2D peak fitting for the analysis of radioxenon beta gamma spectra

Abstract

Atmospheric traces of radioactive xenon, in particular $^{131m}{\text {Xe}}$, $^{133}{\text {Xe}}$, $^{133m}{\text {Xe}}$ and $^{135}{\text {Xe}}$, can provide “smoking gun” evidence to classify underground nuclear fission reactions. Current software used to quantify isomer concentrations relies on a Region of Interest (ROI) method to sort beta-gamma coincidence counts. This experiences errors when classifying nuclides, especially with metastable nuclides, due to the difficulty of deconvoluting overlapping ROIs and accounting for shifts in detector calibration over time. To address this uncertainty, our technique mathematically models the distinctive peaks in an isomer’s beta-gamma spectrum. The function representations are then fitted to measured spectra to determine the concentrations of the primary isomers in the sample. From this proof-of-concept, we hope to create a more precise and accurate system to detect nuclear fission reactions.

Introduction

The International Monitoring System (IMS), with the Comprehensive Nuclear-Test-Ban Treaty Organization, currently utilizes beta-gamma coincidence counting to detect and quantify four xenon nuclides: $^{131m}{\text {Xe}}$, $^{133}{\text {Xe}}$, $^{133m}{\text {Xe}}$ and $^{135}{\text {Xe}}$ [1,2,3]. Radioactive isomers of xenon and krypton are both very likely to be generated by thermal neutron fission of uranium and, being noble gases, tend to be difficult to contain compared to particulate or chemically reactive emissions. Xenon isomers are much more useful than krypton ones, however, due to their half-lives of days to several hours. This is long enough to be detectable downwind of a detonation after diffusing through the ground, while also short enough to have low background levels against which new releases are easily noticeable. By examining the concentrations of the four xenon radionuclides, treaty monitoring agencies can use activity ratios to determine if elevated readings came from peaceful nuclear activities, such as power generation or medical isotope production, or if they came from a nuclear weapon explosion [4]. Beta-gamma coincidence counting greatly simplifies concentration measurements by reducing the background noise of beta particles and gamma radiation not associated with xenon radioisotopes [5]. Coincidence counting is accomplished with simple but robust detectors which enclose an atmospheric sample in a sodium iodide shell and a plastic scintillator shell paired with photomultipliers, all enclosed in lead [6]. Simultaneous beta and gamma radiations are recorded, and plotted according to both radiation energies to create a beta-gamma spectrum.

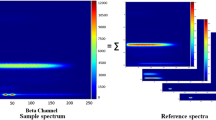
The 2-dimensional (2D) beta-gamma spectra for each of the four radioxenon isomers that we studied are illustrated in Fig. 1. $^{133}{\text {Xe}}$ and $^{135}{\text {Xe}}$ both experience beta decay coincident with a gamma ray, while the metastable states $^{131m}{\text {Xe}}$ and $^{133m}{\text {Xe}}$ experience a conversion electron decay coincident with a gamma ray [7]. Beta decay releases a beta particle and a neutrino from the nucleus, creating an underdefined three-body system—as a result, beta decays appear on beta-gamma spectra as streaks across many beta energies at a single gamma energy. As shown in Fig. 1, $^{133}{\text {Xe}}$ has these streaks at a gamma energy of 31.6 keV and at 80 keV, with a maximum beta energy of 346 keV. $^{135}{\text {Xe}}$ primarily releases 250 keV gamma rays, as well as a few 31.6 keV rays, with a maximum beta energy of 910 keV [7]. Internal conversion decay does not release a neutrino, and so both the released electrons and gamma rays have a definite energy: 130 keV and 30.4 keV for $^{131m}{\text {Xe}}$, and 199 keV and 30.4 keV for $^{133m}{\text {Xe}}$. Note that $^{133m}{\text {Xe}}$ cannot be isolated from its decay product $^{133}{\text {Xe}}$, however its unique spectrum is identifiable by comparing the pure $^{133}{\text {Xe}}$ spectra to the $^{133m}{\text {Xe}}/^{133}{\text {Xe}}$ combined spectra in Fig. 1.

Fig. 1

The 2D beta-gamma energy spectra for $^{131m}{\text {Xe}}$, $^{133}{\text {Xe}}$, $^{133m}{\text {Xe}}$ & $^{133}{\text {Xe}}$, and $^{135}{\text {Xe}}$ [8]

The current software used to classify $^{131m}{\text {Xe}}$, $^{133}{\text {Xe}}$, $^{133m}{\text {Xe}}$ and $^{135}{\text {Xe}}$ relies on Region of Interest (ROI) counting. This subdivides the beta-gamma spectrum into several regions roughly corresponding to the activity from each nuclide. The number of counts in each region are summed, and counts in regions encompassing multiple interfering isomers are deconvoluted, to calculate the concentration of each isomer. While relatively simple, this method can be imprecise due to overlapping regions of isomer activity, where deconvolution becomes especially sensitive to gain shifts in the energy calibration of the detector over time. The meta-stable isomers’ spectra are particularly vulnerable to these deconvolution errors, since their activity is completely overlapped by other nuclides’ spectra [5, 9].

Several groups have developed various analysis techniques for radio-xenon beta-gamma spectra. The Nuclear Explosion Monitoring and Policy program at Pacific Northwest National Laboratory (PNNL) improved upon the ROI method by changing the number of regions of interest. By changing the number of regions, they are able to more easily deconvolute overlapping regions, thus giving a more accurate result in comparison to the normal ROI method, but this method remains vulnerable to gain shifts in energy calibration [5]. Researchers at The University of Texas at Austin developed another improvement to the ROI method known as the Spectral Deconvolution Analysis Tool (SDAT). SDAT utilizes software that deconvolves the 3-D sample spectra into the most probable combination of pure radioisomer signals using the non-negative least-squares method. This method results in a better ability to resolve inferences and improves counting statistics, but, similar to PNNL’s improvement, requires complex corrections to correct for gain shifts [10,11,12,13].

In this work, we aim to address this problem by modeling beta-gamma spectra using mathematical functions, which can be easily and automatically adjusted to account for gain shifts. The energy distributions of two-dimensional spectral histograms can be modeled by two-dimensional functions, allowing the distributions to be summarized by function parameters. Constrained least-squares fitting can then fit multiple functions onto the peaks from sample data, adjusting the location and scaling parameters of the function to match detector gain. Once fitted, function amplitude replaces count number as the proxy for nuclide activity, and with sufficient calibration can be used to compute nuclide concentrations in the sample.

Theory

The two-dimensional energy distributions for each spectral feature is the product of a gamma probability density function (PDF) ($n_\gamma (E_\gamma )$) and an electron PDF ($n_e(T)$);

$$\begin{aligned} n_{\text {2D}\,\text {feature}}(T,E_\gamma ) = A \, n_e(T) \, n_\gamma (E_\gamma ) \end{aligned}$$

(1)

where A is the feature amplitude, $E_\gamma$ is the gamma ray energy, and T is the electron kinetic energy. The functional form of the electron PDF varies depending on the decay type, whether conversion electron or beta decay. The one-dimensional PDFs are normalized so that the area under each distribution is one. One or more 2D spectral feature PDFs sum to fully model a particular isomer

$$\begin{aligned} n_{\text {isomer}}(T,E_\gamma ) = \sum _{\text {2D features}} n_{\text {2D}\,\text {feature}}(T,E_\gamma ) \end{aligned}$$

(2)

and the four isomer PDFs sum to describe the full xenon spectra.

Each 2D spectral feature PDF contains several fitting parameters, determining the peak location, width, and amplitude, which are allowed to vary when calibrating the detector response to a particular isotope. After initial calibration, we improve the algorithm’s performance by reducing the number of fit parameters to only those needed to adjust for detector gain shifts and changes in isomer concentrations. Isomer amplitudes are used to determine nuclide concentrations since they are proportional to the decay counts, and thus the concentration, of each nuclide. Before describing how gain shifts are handled, first we detail the functional forms of the 1D PDFs.

We used three 1D PDFs, with shapes based on the decay mechanisms underlying the data they represent. The first of these functions is the Gaussian Distribution, Eq. (3), used to model gamma ray energy distributions for all four isomers as well as the energies of conversion electrons produced by $^{131m}{\text {Xe}}$ and $^{133m}{\text {Xe}}$. Each isomer produces gamma rays and/or conversion electrons within a narrow energy range, which is then broadened by the detector resolution. In accordance with the Central Limit Theorem, [14] these random errors are distributed normally around the true value, with an energy distribution n(E) given by the expression

$$\begin{aligned} n(E)\propto e^{- \frac{1}{2}\left( \frac{E-E_{peak}}{\sigma } \right) ^2} \end{aligned}$$

(3)

in terms of the peak energy $E_{peak}$ and the standard deviation, or width, $\sigma$. Figure 2 exhibits two such Gaussian functions (orange lines) mapped closely to the conversion electron and gamma ray spectra of $^{131m}{\text {Xe}}$ (blue dots).

Fig. 2

The beta-gamma spectrum 2D histogram of a $^{131m}{\text {Xe}}$ conversion electron emission, with the 2D fit overlaid with contour lines. The 1D electron and gamma Gaussian fits (orange lines) overlay the total beta and gamma counts (blue dots) on the axes, with the residual in the electron fit also plotted. (Color figure online)

The second and third energy distributions we use are described by Fermi beta decay theory and model the variable energies of electrons and neutrinos in the beta decays of $^{133}{\text {Xe}}$ and $^{135}{\text {Xe}}$. The theory predicts the statistical distribution of decay products’ momenta using Fermi’s Golden Rule, which says the decay probability is proportional to daughter particles’ density of states

$$\begin{aligned} dn = dn_e dn_\nu \propto p^2_\beta dp_\beta \, p^2_\nu dp_\nu \, \end{aligned}$$

(4)

where dn are the number of states in a momentum interval dp and $p_\beta$ and $p_\nu$ are the beta particle and neutrino momenta respectively [15]. From the Einstein energy-momentum relation¹$E^2-p^2 = m^2$ we have $p \, dp = E \, dE$ and we can re-write Eq. (4) as

$$\begin{aligned} dn \propto (E_\beta p_\beta E_\nu p_\nu ) \, dE_\beta \, dE_\nu \, . \end{aligned}$$

(5)

The term proceeding the energy differentials is called the statistical factor. It can be expressed entirely in term of the beta particle’s measured kinetic energy T using Einstein’s energy-momentum relation along with the expressions $E_\beta = T + m_\beta$ and $Q = T + E_\nu$, where Q is the total decay kinetic energy.

Two additional terms modify the simple distribution given in Eq. (5). The first is the shape function, S(T), which includes the nuclear matrix element. For beta decays that are well described by the “allowed approximation” the shape function is constant. The second term, called the Fermi function, describes how the shape of the beta kinetic energy distribution is modified by Coulomb interactions with the daughter nucleus. Taken together, the beta particle PDF, n(T), is given by

$$\begin{aligned} n_\beta (T)\propto E_\beta p_\beta E_\nu p_\nu F(T) S(T) \end{aligned}$$

(6)

where the energy and momenta are implicit functions of T [15].

The beta decay of $^{133}{\text {Xe}}$ is an allowed transition ($S(T)=1$) and the Fermi function is well approximated by $F(T) = E_\beta /p_\beta$. The negligible mass of the neutrino means its energy and momentum are nearly equal, thus we may simplify Eq. (6) to

$$\begin{aligned} n_\beta (T)\propto E_\beta ^2 E_\nu ^2 \, , \end{aligned}$$

(7)

or in terms of T as

$$\begin{aligned} n_\beta (T) \propto (T + m_\beta )^2 (Q-T)^2 . \end{aligned}$$

(8)

This curve is fitted to the beta decay of $^{133}{\text {Xe}}$ in Fig. 3.

Fig. 3

The beta-gamma spectrum 2D histogram for the $E_\gamma = 30$ keV spectral feature in $^{133}{\text {Xe}}$ beta decay, with the 2D fit overlaid with contour lines. The 1D Fermi beta fit and gamma Gaussian fit (orange lines) overlay the total beta and gamma counts (blue dots) on the axes, with the residual in the beta fit also plotted. (Color figure online)

Finally, we have the beta decay of $^{135}{\text {Xe}}$, which experiences an allowed transition at a much higher cutoff energy Q than $^{133}{\text {Xe}}$. The higher-energy beta particles will sometimes “punch-through” through the plastic scintillator detectors, depositing only a portion of their energy, which results in detector undercounts of high-energy particles and overcounts of low-energy particles. Rather than trying to correct for this altered shape, we noted that the resulting “S-curve” was close to the distribution predicted by Fermi theory for first forbidden transitions. From Eq. (6), we used a Fermi function $F(T)=1$ and the first-forbidden shape function $S(T)=p_\beta ^2 + p_\nu ^2$ to generate a $^{135}{\text {Xe}}$ beta energy distribution model of

$$\begin{aligned} n_\beta (T)\propto E_\beta p_\beta E_\nu ^2 \left( p_\beta ^2 + p_\nu ^2\right) . \end{aligned}$$

(9)

Substituting the definitions for total beta energy $E_\beta$ and momentum $p_\beta$, and neutrino energy $E_\nu$ and momentum $p_\nu$, in terms of beta mass $m_\beta$, beta kinetic energy T, and total decay kinetic energy Q gives

$$\begin{aligned} n_\beta (T)\propto \left( T+m_\beta \right) \sqrt{T^2 + 2T m_\beta } \left( Q-T\right) ^2 \left( T^2 + 2T m_\beta + \left( Q-T\right) ^2 \right) . \end{aligned}$$

(10)

While not an exact fit, Fig. 4 shows this curve reliably following the measured beta energy distribution of $^{135}{\text {Xe}}$.

Fig. 4

The beta-gamma spectrum 2D histogram of $^{135}{\text {Xe}}$, with the 2D fit overlaid with contour lines. The 1D Fermi beta fit and gamma Gaussian fit (orange lines) overlay the total beta and gamma counts (blue dots) on the axes, with the residual in the beta fit also plotted. (Color figure online)

We substitute these 1D PDFs into Eq. (1) to arrive at the 2D spectral feature PDFs. In particular, we arrive at

$$\begin{aligned} n_{\text {CE}} (T,E_\gamma )= & {} A \cdot \left( N_{\text {CE}} \, e^{- \frac{1}{2} \left( \frac{T-T_{\text {CE peak}}}{\sigma _{\text {CE}}} \right) ^2} \right) \nonumber \\&\cdot \left( N_\gamma \, e^{- \frac{1}{2} \left( \frac{E_\gamma -E_{\gamma \, \text {peak}}}{\sigma _\gamma } \right) ^2} \right) , \end{aligned}$$

(11)

$$\begin{aligned} n_\beta (T,E_\gamma )= & {} A \cdot \left( N_\beta \, (T+m_\beta )^2 (Q - E_\beta )^2 \right) \nonumber \\&\cdot \left( N_\gamma \, e^{- \frac{1}{2} \left( \frac{E_\gamma -E_{\gamma \, \text {peak}}}{\sigma _\gamma } \right) ^2} \right) , \end{aligned}$$

(12)

and

$$\begin{aligned} n_\beta (T,E_\gamma )= & {} A \cdot \left( N_\beta \left( T+m_\beta \right) \sqrt{T^2 + 2T m_\beta } \left( Q-T\right) ^2 \nonumber \right. \\&\left. \cdot \left( T^2 + 2T m_\beta +\left( Q-T\right) ^2\right) \right) \nonumber \\&\cdot \left( N_\gamma \, e^{- \frac{1}{2} \left( \frac{E_\gamma -E_{\gamma \, \text {peak}}}{\sigma _\gamma } \right) ^2} \right) , \end{aligned}$$

(13)

where the N’s in Eqs. (11), (12), and (13) are normalization coefficients chosen so that the area under each 1D distribution is one.² This normalization ensures that the function amplitudes (A) are approximately equal to the number of counts in the histogram bins they cover. The conversion electron 2D peak function, Eq. (11) thus has five parameters for fitting: the peak electron and gamma energies ($T_{\text {CE peak}}$ and $E_{\gamma \, \text {peak}}$) giving the “location” of the peak on the beta-gamma spectrum, the electron and gamma peak widths ($\sigma _{\text {CE}}$ and $\sigma _\gamma$), and the amplitude (A) giving the “height.” Likewise, the beta decay 2D PDFs, Eqs. (12) and (13), have four fitting parameters: the two electron parameters are replaced by the maximum beta kinetic energy (Q), which defines the maximum extent of the Fermi distribution, and serves as the “location” parameter. $^{133}{\text {Xe}}$ and $^{135}{\text {Xe}}$ generate gamma rays at multiple energies creating multiple distinct spectral features: we combine these into a single isomer model by summing the features (with amplitudes in fixed ratios, depending on the particular isomer’s spectra) as in Eq. (2) (Fig. 5).

Fig. 5

Graphics visualizing the shapes of the 2D PDFs for a a conversion electron peak, b a $^{133}{\text {Xe}}$ beta decay peak, and c a $^{135}{\text {Xe}}$ beta decay peak

Our algorithm fits the isomer PDFs to the spectral data via least squares fitting. When an isomer is absent from a sample spectrum, the algorithm should fit that isomer’s corresponding PDF to the data by pushing its amplitude to zero, keeping the other function parameters unchanged. While the function may not fit with exactly zero amplitude, due to uncertainty in the measurement, we look for the amplitude to be small enough that it does not induce significant error in the nonzero PDF models. This requires adding constraints to the fitting routine, as without them, the peak functions would “wander.” This wandering could fit peaks to background noise, giving nonzero amplitudes; or it could fit to portions of spectral features from other nuclides, changing both amplitudes; or the functions could move outside the spectrum where it would behave unpredictably. To address this, we constrained the function parameters by linking the location and width parameters for all four isomer PDFs into four fit parameters describing scale and translation in both dimensions (electron energy and gamma energy) for the entire spectrum, as shown in Fig. 6. The algorithm takes initial values for each 2D PDF, which were generated by an unconstrained least-squares fit of each PDF to only its corresponding feature. This initialization calibration must be done for each detector, due to each detector’s unique biases. Then during subsequent full-spectrum fitting, the model’s electron-dimension parameters can be scaled, but they must all be scaled by the same factor. Likewise, the algorithm can shift all the electron-dimension location parameters by the same amount, and it can adjust the gamma-dimension parameters in the same manner. Thus the algorithm can move or squeeze the entire function mapping to best fit the data, easily adjusting for detector gain shifts, but no single peak’s location or width can change relative to the others.

We incorporated other ancillary constraints to improve performance. We prohibited fitting parameters for PDFs from becoming negative where necessary. We also incorporated a very slight cost to changing the four constrained fit parameters, by treating the difference between each parameter and its initial value as an error to be minimized alongside the difference between each data point and its modeled value. This was weighted enough to prevent wandering from the initial values when fitting to a completely empty spectrum, while also allowing unencumbered adjustments to fit to shifted data. We then used a standard Python least-squares error optimizing function to find the best values of the four scaling/translation parameters and the four isomer amplitudes that fully define the 2D peak functions. Once fitted to the data, these isomer function amplitudes are proportional to the concentrations of the nuclides in the detector measurements.

Fig. 6

An illustration of the concept behind constraining all isomer PDFs to four fit parameters. The scaling parameters control the size of and distance between peaks, while the translation parameters shift all the peaks together

Results

We evaluated the effectiveness of the peak-fitting routine and the constraints applied to it with two tests. The first was designed around the limited spectra from available from real detectors, while the second used a set of simulated data to expose the algorithm to a wide variety of scenarios, allowing a much more rigorous baseline than would be practical from experimental data alone.

The first test assessed the self-consistency of fitting in three cases: in the first (control) case we fit data from a single isomer decay spectra using only the corresponding isomer PDF, in the second (experiment) case we fit all four isomer PDFs to the same single-isomer data, before comparing the results, and in the third (experiment) case we repeated the experiment with a four-isomer mixture. We used spectral data obtained from the 21^st Reconnaissance Squadron at the Air Force Technical Applications Center, which was generated by four detectors, with one sample of isolated $^{131m}{\text {Xe}}$, $^{133}{\text {Xe}}$, and $^{135}{\text {Xe}}$ per detector. Since we did not have detector samples of $^{133m}{\text {Xe}}$, we complemented the data with a simulated spectra, allowing us to study the interactions of all four nuclides. In the control case (single isomer data fitted with a matching single isomer model), the resulting PDF fit amplitudes were taken as the baseline against which the experiment cases (multiple isomer models fitted to data) were compared. Our objective with the first experiment, fitting all four isomer PDFs to data from a single isomer, was to determine if the models interfered with each other during fitting. In proper operation, the peak corresponding to the nuclide present would be identical to the control and the amplitudes of the other three models would be close to zero. Any error in the primary isomer amplitude could then be taken as an indication of interference from another model. For the second experiment, we created four spectra (one for each detector) with a synthetic mixture of all four isomer spectra by summing together the pure isomer data for every detector, and fit the combined isomer PDFs to them. Since the counts from each isomer were the same as the separated controls, each isomer amplitude should be the same as well; our goal was to see if the isomers’ overlapping spectral features would be properly deconvoluted to give the same amplitudes. All three cases from this test are illustrated by Fig. 7 alongside the raw data.

The results from the single-isomer tests are given in Table 1, those from the mixed-isomer tests are in Table 2. Across all four detector data sets, the (control) single isomer data fits to a single matching PDF were almost indistinguishable from the (experiment) multi-model fits to the same data, demonstrating success in using the least-squares error fit to isolate the proper isomer PDF and push the other three to zero amplitude. In this way, the algorithm is simultaneously identifying what isomers are present and which are absent, and measuring the concentration of those present. Measuring all four nuclides at once in the synthetic mixture introduced slightly higher amplitude errors, although most measurements were still well within 1% accuracy. While clearly successful, it should be noted that due to having access to only one sample of each isomer from each detector, the baseline peak location and width calibration for each detector had to be done using the same samples the program was tested on. We addressed this in the simulated-data experiment by obtaining all samples using the same simulator settings, requiring only one calibration.

Fig. 7

Four plots demonstrate stages of the self-consistency experiments. The plot (a) shows a beta-gamma spectrum of pure $^{131m}{\text {Xe}}$ from a detector, with the gamma and the electron distributions below. Plot (b) overlays the $^{131m}{\text {Xe}}$ PDF fitted to the data, the control case. On the 2D spectra, the fitted model is shown with contour lines, with color corresponding to height; on the 1D plots, the model is shown by the orange lines as before. Plot (c) shows all four isomer PDFs fitted to the data: note that it is nearly identical to the control. Plot (d) shows the synthetic mixture with all four models fitted to it

Table 1 Amplitude errors in primary isomer of a four-PDF fit to single-isomer data, using single-isomer PDF fits to the same data as a baseline

Table 2 Amplitude errors in the fits of four isomer PDFs to spectral data from a mixture of all four isomers; single-isomer PDF fits to single-isomer data served as a baseline

For our second set of experiments, we used the BGSim spectra simulator provided by Pacific Northwest National Laboratory to generate 625 beta-gamma spectra. [4] These encompassed all permutations of the four isomers at 5 different concentrations: 0, 10,000, 1,000,000, 3,000,000, and 10,000,000 atoms in a 1.3 cubic centimeter sample. For any particular isomer concentration there were $5^3=125$ spectra from permutations of the other three isotopes at each of the five concentrations. We used four pure-isomer data sets (one for each isomer) with 10,000,000 atoms each to calibrate the algorithm to the simulated detector response, both in terms of PDF shapes and amplitudes. We then analyzed all 625 spectra using a four-isomer fit, and calculated the percent error in each isomer concentration prediction from the value used to generate the simulated data.

Table 3 Simulated dataset fitting results, arranged by true number of atoms

Table 4 Simulated dataset fitting results, arranged by isomer concentration ratios

Fig. 8

These plots illustrate the incorrect shape of the simulated $^{133}{\text {Xe}}$ beta energy distribution. Plot (a) is the beta-gamma spectrum from a detector test: note the nearly linear beta distribution in the center axes, which is well matched by the fit function in orange. Plot (b) shows the simulated spectrum, fitted only with the $^{133}{\text {Xe}}$ model. Note the distinctive curve in the beta distribution, which is not followed by the more linear fit function. Finally, plot (c) shows the same data fitted with all isomer functions, demonstrating how the algorithm attempts to “fill in” the gap between the model and the data by incorrectly adding the $^{133m}{\text {Xe}}$ function, creating a lump in the orange fitted distribution. This behavior is absent when fitting to actual experimental spectra due to the better beta function fit

Results from the simulated-data experiment are summarized in Tables 3 and 4. There are 500 different percent errors associated with each isomer arising from the 125 spectra for each of the four nonzero isomer concentrations. Table 3 summarizes the concentration accuracy for each isomer grouped by the isomer concentration. It lists the minimum, median, maximum, mean, and standard deviation of the 125 isomer concentration percent errors. As can be expected, we see that higher concentrations can be detected with greater accuracy. This is partially due to the better-defined spectral features of high-concentration isomers. More often, however, the increased error which sometimes occurs at lower concentrations is associated with mixtures wherein one isomer’s concentration is less than another isomer’s concentration by an order of magnitude or more, drowning out the smaller isomer’s signal.

To further investigate cases with highly unbalanced isomer concentrations, we summarized the same results re-grouped by isomer concentration ratio in Table 4. For this, each beta-gamma spectrum was classified for each isomer according the smallest ratio between the concentrations of that isomer and the other three. For example, all spectra in the “$^{131m}{\text {Xe}}~\ge 2:1$” grouping have $^{131m}{\text {Xe}}$ at a greater concentration than any other isomer, by at least a 2:1 ratio, whereas spectra in the “$^{131m}{\text {Xe}}~\ge 1:1000$” grouping each have at least one isomer at a concentration over 10 times, but less than or equal to 1000 times, that of $^{131m}{\text {Xe}}$. In this formulation, we see that most of the high-error cases were at very small concentration ratios, where the isomer being measured is outnumbered by others by at least a hundred to one. Outside of these cases, the least-squares fit reliably predicts concentrations within about 5% of the true value, frequently achieving pinpoint accuracy below 1% but occasionally missing by up to 20–30%.

There are three special cases of increased error apparent in the simulated dataset results worth discussing. The first is the presence of significant outliers, single fits with an amplitude error much smaller or much larger than any other in their group. These have been indicated in both data tables by showing them alongside the second-most extreme in their respective groups. The root cause of these outliers is being investigated, but they occur only in very specific situations. The second special case is the low activity of $^{131m}{\text {Xe}}$ compared to the other three nuclides, which causes it to produce significantly fewer decay counts, and thus smaller spectral features, than the other nuclides at the same concentration. This is the primary cause for the higher $^{131m}{\text {Xe}}$ errors when evaluating samples by their concentration. Finally, $^{133}{\text {Xe}}$ experiences much higher error in fits to simulated data because the BGSim program produces $^{133}{\text {Xe}}$ spectra shaped differently from experimental results [4]. Figure 8 illustrates this problem, showing the shape of the beta particle energy distribution from experimental data and from the BGSim simulator. This causes difficulty fitting the Fermi distribution curve to the differently-shaped simulator distribution, and also induces error in $^{131m}{\text {Xe}}$ and $^{133m}{\text {Xe}}$ fits as the algorithm uses their models to reduce the $^{133}{\text {Xe}}$ count discrepancy. Although this problem could be addressed by changing the $^{133}{\text {Xe}}$ shape, we chose to not pursue this since the problem is not present in actual experimental data, where the Fermi PDF matches the data quite accurately. In future work, we hope to obtain a far more extensive set of experimental data to test the algorithm against, hopefully eliminating this issue.

Conclusion and Future Work

Our work aimed to accurately measure radioxenon nuclide concentrations using a constrained least-squares error fitting of two dimensional probability density functions to the beta-gamma spectra generated by detectors. The algorithm was built to identify and robustly handle gain shifts in the detector, and to accurately deconvolute interfering signals from each of the isomers $^{131m}{\text {Xe}}$, $^{133m}{\text {Xe}}$, $^{133}{\text {Xe}}$, and $^{135}{\text {Xe}}$. Against a limited set of real detector results, the algorithm performed remarkably well, reliably predicting the correct isomer function amplitude within 1-4% and usually within 0.5%. The program also made accurate predictions for a much larger and more challenging set of simulated beta-gamma-spectra, with errors in most scenarios of interest below 5%. These results indicate that with further development to address error trends and outlier scenarios, and to incorporate more mathematical tools for real-life spectrum interpretation, the peak fitting methods proposed here can be a viable basis for future radioxenon measurement efforts.

In the immediate future we will be continuing to evaluate the results from the large-batch simulated data experiments, to understand the specific behavior of the least-squares fit in the high-error outlier cases, to identify trends correlating with higher amplitude error, and to develop corrective measures in the functions and constraints. We are also working with Pacific Northwest National Labs and the Air Force Technical Applications Center to acquire more detector test data against which to run our proof-of-concept program, as well as samples with low radioxenon counts, high background noise, or high detector gain to challenge the versatility of the program. In this way, we hope to continue incremental improvements of the algorithm and to drive down its error statistics.

Improvements to the PDF fitting algorithm are also needed. The current algorithm minimizes the sum of the squares of the difference between the PDF and the data. Data uncertainties are not taken into account during the fitting, though future versions of the algorithm will take into account Poisson distribution uncertainties to minimize the chi-squared. Care will be needed in estimating the variance $\lambda$ of the data in the large regions where few, if any, beta-gamma coincidence counts are recorded. A constant background component may be added to improve the algorithm’s fit.

In the longer term, we hope to develop a calibration routine for the isomer peaks to automate the process for each detector, and to develop a rigorous test of the peak-fitting program against the ROI method, SDAT method, and other contemporary proposals for radioxenon measurement.