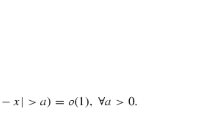On Weak Invariance Principles for Partial Sums

Abstract

Given a sequence of random functionals $\bigl \{X_k(u)\bigr \}_{k \in \mathbb {Z}}$, $u \in \mathbf{I}^d$, $d \ge 1$, the normalized partial sums $\check{S}_{nt}(u) = n^{-1/2}\bigl (X_1(u) + \cdots + X_{\lfloor n t \rfloor }(u)\bigr )$, $t \in [0,1]$ and its polygonal version ${S}_{nt}(u)$ are considered under a weak dependence assumption and $p > 2$ moments. Weak invariance principles in the space of continuous functions and càdlàg functions are established. A particular emphasis is put on the process $\check{S}_{nt}(\widehat{\theta })$, where $\widehat{\theta } \xrightarrow {\mathbb {P}} \theta$, and weaker moment conditions ($p = 2$ if $d = 1$) are assumed.

1 Introduction

Let $\mathbf{I}^d$ (with $\mathbf{I}= \mathbf{I}^1$) be the d-dimensional unit cube, and $\bigl \{X_k(u)\bigr \}_{k \in \mathbb {Z}}$, $u \in \mathbf{I}^d$ be a sequence of stationary and ergodic functionals. In many statistical applications, central limit theorems and invariance principles of partial sums $\check{S}_{nt}(u) = n^{-1/2}\bigl (X_1(u) +\cdots + X_{\lfloor n t \rfloor }(u)\bigr )$, $t \in \mathbf{I}$ are of interest. A particular case is ‘plug-in’ invariance principles, where one is interested in the quantity $\check{S}_{nt}(\widehat{\theta })$, where $\widehat{\theta } = \widehat{\theta }_n$ is a consistent estimator for some parameter $\theta$. Such functionals arise naturally in many contexts, for instance, when dealing with M-estimators, see Sect. 2.2. Due to the nonergodic nature of $\check{S}_n(t,\widehat{\theta })$, a direct application of the related univariate theory is not possible. The most frequently used work around is to consider a multivariate setting in an appropriate space $\mathbf{S}[\mathbf{I}^{d+1}]$. Continuous mapping, given that the limiting process is continuous, then yields the claim. The standard way to achieve this is to employ a ‘moment and tightness condition’ or related criteria (cf.  [8],  [32]), such as (for $d = 1$)

$$\begin{aligned} \mathbb {E}\bigl [|\check{S}_{nt}(u) - \check{S}_{ns}(v)|^{p}\bigr ] \le C \bigl (|t-s|^{2 + \delta } + |u-v|^{2 + \delta } \bigr ), \quad C, \delta > 0. \end{aligned}$$

(1.1)

However, such conditions inevitably require the assumption of at least $p > 4$ moments. The aim of this note is to provide accessible conditions which imply weak convergence of $\check{S}_{nt}(u)$ and its polygonal version ${S}_{nt}(u)$ under weaker moment conditions in $\mathbf{C}[\mathbf{I}^{d+1}]$ (continuous functions) and $\mathbf{D}[\mathbf{I}^d]$ (càdlàg functions). In the particular case of $\check{S}_n(t,\widehat{\theta })$, weaker conditions ($p = 2$ if $d = 1$) are sufficient.

Weak invariance principles in infinite-dimensional (Banach) spaces with $p > 2$ moments have a tradition in probability theory. In case of $\phi$-mixing sequences (see  [10] for details on mixing), Philipp  [41] has shown that a CLT implies a weak invariance principle (see also  [37]). Eberlein  [23, 24] gives related results. A seminal contribution in this context is due to Berkes and Philipp  [6] (see also  [40]), who derived strong invariance principles based on a novel approximation technique, exploiting the Strassen–Dudley Theorem (cf.  [22]). This technique was subsequently refined and extended by Kuelbs and Philipp  [34], Dehling and Philipp  [19] and Dehling  [16], allowing for improved strong invariance principles for $\phi$-mixing and even regular sequences. As was further shown by Dehling  [17], this approximation technique, however, fails for strongly mixing sequences; hence, a further relaxation of the previous results in terms of strong mixing seems to be rather difficult. In this paper, we go down a completely different path, resorting to martingale approximations and another notion of weak dependence instead. Properties of martingales, in particular corresponding maximal inequalities, will play a central role in the proofs.

Apart from its theoretical interest, the number of underlying moments is an important issue in practice due to its relation to ‘fat-tails.’ A common definition of fat-tails for a (positive) random variable X is given by

$$\begin{aligned} \mathbb {P}\bigl (X > x\bigr ) \sim x^{-\nu }L(x), \quad x,\nu > 0, \end{aligned}$$

(1.2)

where L(x) is a slowly varying function. Ever since the seminal work of Mandelbrot  [36], fat-tailed distributions have been an important topic in economics, but have left their landmark also in different fields, for instance hydrology. Note that for $X \ge 0$, (1.2) is related to the $p>0$ moments of X via

$$\begin{aligned} \mathbb {E}\bigl [X^p\bigr ] = \int _0^{\infty } p x^{p-1} \mathbb {P}\bigl (X > x\bigr ) \mathrm{d}x, \end{aligned}$$

(1.3)

which implies $\mathbb {E}\bigl [X^p\bigr ] < \infty$ for $0 < p < \nu$. If $p = \nu$, finiteness of $\mathbb {E}\bigl [X^p\bigr ]$ depends on L(x). A natural question in connection with fat-tailed distributions is the range of $\nu > 0$. If $\nu \in (0,2)$, one often speaks of infinite variance processes (cf.  [3, 5] and the references therein). However, very often authors report ranges of $\nu \in (2,4)$ (cf.  [25, 26]), and thus the existence of the fourth or even third moment is already questionably, justifying interest in weak invariance principles for $\check{S}_{nt}(u)$ and $\check{S}_{nt}(\widehat{\theta })$ for $2 < p < 4$ moments.

The remainder of this paper is organized as follows. In Sect. 2, some notation and the main results are established. Ramifications and some applications are given in Sect. 2.1. The proofs are provided in Sects. 3, 4 and 5.

2 Preliminary Remarks and Main Results

Throughout this exposition, we will use the following notation. For a random variable X, we denote with $\Vert X\Vert _p = \mathbb {E}\bigl [|X|^p\bigr ]^{1/p}$ the $L^p$ norm. We write $\lesssim$, $\gtrsim$, ($\thicksim$) to denote (two-sided) inequalities involving a multiplicative constant, $a \wedge b = \min \{a,b\}$ and $a \vee b = \max \{a,b\}$. For a set $\mathcal {A}$, we denote with $\mathcal {A}^c$ its complement. For a vector $v \in \mathbb {R}^d$, we denote with $|v|_{\infty }$ the maximum norm. Given a filtration $(\mathcal {F}_k)_{k \in \mathbb {Z}}$, we always assume that $\{X_k(u)\}_{k\ge 1}$ is adapted to $\mathcal {F}_{k}$ for each $k \in \mathbb {Z}$, $u \in \mathbf{I}^d$. In this context, we introduce the projection operator $\mathcal {P}_k(\cdot )$. For a process $\{U_i\}_{i \in \mathbb {Z}}$ denote $\mathcal {P}_k(U_i) = \mathbb {E}(U_i|\mathcal {F}_k) - \mathbb {E}(U_i|\mathcal {F}_{k - 1})$. Most of the assumptions will rely on this quantity in some way or other. We also write $X_k = X_k(u)$ if the dependence on u is of no immanent relevance.

In the sequel, it is convenient to work in different function spaces. For $d \ge 1$, we consider the space $\mathbf{C}[\mathbf{I}^d]$ (continuous functions) and $\mathbf{D}[\mathbf{I}^d]$ (càdlàg functions). If we do not specify a particular space, we simply write $\mathbf{S}[\mathbf{I}^d]$. We also use the following metrics: $|\cdot |_{\mathbf{C}} = \sup _{u \in \mathbf{I}^d}|\cdot |$, and the Skorohod metric (cf.  [7, 8]) $|.|_{\mathbf{D}}$. We write $\mathbf{S}[\mathbf{I}^d]$ for a space $\mathbf{S}[\mathbf{I}^d]_{\mathbf{S}}$ if $|\cdot |_\mathbf{S}$ is its natural metric. Note that we only consider the unit cube $\mathbf{I}^d$ for the sake of simplicity, but all results are equally valid for $[-K,K]^d$ for any finite $K > 0$.

Our main interest lies on the following partial sums.

$$\begin{aligned} S_{nt}&= S_{nt}(u) = \frac{1}{\sqrt{n}}\sum _{k = 1}^{\lfloor n t \rfloor }X_k(u) + \frac{nt - \lfloor n t \rfloor }{\sqrt{n}} X_{\lfloor n t \rfloor + 1}(u) \quad \text {and} \nonumber \\ \check{S}_{nt}&= \check{S}_{nt}(u) = \frac{1}{\sqrt{n}}\sum _{k = 1}^{\lfloor n t \rfloor }X_k(u). \end{aligned}$$

(2.1)

In order to avoid any notational complications, we define $X_{k}(u) = 0$ for any $u \not \in \mathbf{I}^d$. This naturally carries over to $S_{nt}(u)$, $\check{S}_{nt}(u)$. The main results will be formulated in terms of the following assumptions.

Assumption 2.1

The process $\{X_k(u)\}_{k \in \mathbb {Z}}$ is stationary, ergodic and adapted to $\mathcal {F}_k$ for every $u \in \mathbf{I}^d$, such that for $p \ge 2$

• (A1) $\bigl |\mathbb {E}[X_0(u)|\mathcal {F}_{-\infty }]\bigr |_{\mathbf{C}} = 0$,

• (A2) $\bigl |\sum _{i = -\infty }^{-K}\Vert \mathcal {P}_i(X_0(u))\Vert _p\bigr |_{\mathbf{C}} \lesssim K^{-\alpha }$, $K, \alpha \ge 0$,

• (A3) $\Vert X_k(u)-X_k(v)\Vert _{p'} \lesssim |u-v|_{\infty }^{\beta }$, $\beta > 0$, $u,v \in \mathbf{I}^d$, for some $2 \le p' \le p$.

Let us briefly discuss the assumptions. (A1) is important for two reasons. First, note that since

$$\begin{aligned} \mathbb {E}\bigl [X_k\bigr ] = \mathbb {E}\bigl [\mathbb {E}\bigl [X_k\bigl |\mathcal {F}_{-\infty }\bigr ]\bigr ] = 0, \end{aligned}$$

it follows that $\mathbb {E}\bigl [S_{nt}] = 0$. Secondly, in conjunction with (A2) it gives the decomposition $X_k = \sum _{i = -\infty }^k \mathcal {P}_i(X_k)$, which allows for applications of martingale theory (cf.  [38, 39, 46] and the references therein). In  [39], a counter example is given in case of univariate sequences, showing that a weak invariance principle may fail if (A2) holds but (A1) is violated. In contrast to (A2), there are many other well-known different notions of weak dependence in the literature; for an overview and more details on this subject, we refer to [10, 14, 38, 39] and the many references therein. It can be expected that the results carry over to such different notions of weak dependence. (A3) is a probabilistic notion of Hölder continuity, which will be indispensable for us. Also note that the norm $|\cdot |_{\infty }$ can be replaced by any other norm in $\mathbb {R}^d$.

Theorem 2.2

Assume that Assumption 2.1 holds with $p > 2$ and $\alpha \beta p' > d(1 + \alpha )$ for some $2 \le p' \le p$. Then

$$\begin{aligned} S_{nt}(u) \xrightarrow {\mathbf{C}[\mathbf{I}^{d+1}]} \mathcal {G}_t(u), \end{aligned}$$

where $\{\mathcal {G}_t(u)\}_{t \in \mathbf{I}, u \in \mathbf{I}^d}$ is a Gaussian process with covariance $\mathbb {E}[\mathcal {G}_t(u)\mathcal {G}_s(v)] = t \wedge s \Gamma (u,v)$, where $\Gamma (u,v) = \phi _0(u,v) + \sum _{h = 1}^{\infty }\bigl (\phi _{h}(u,v) + \phi _{h}(v,u)\bigr )$ with $\phi _{h}(u,v) = {{Cov} }\bigl (X_h(u),X_0(v)\bigr )$. This series is well defined (it converges in absolute value).

Remark 2.3

A priori, it is not clear whether $S_{nt}(u) \in \mathbf{C}[\mathbf{I}^{d+1}]$ or not. On the one hand, the proof shows that there exists a modification $\tilde{S}_{nt}(u) \in \mathbf{C}[\mathbf{I}^{d+1}]$. On the other hand, as was noted by a reviewer, condition $\alpha \beta p' > d(1 + \alpha )$ and Kolmogorovs theorem directly yield that a modification of $X_k(u)$ is continuous. Hence for any finite n, a modification of $S_{nt}(u)$ is continuous.

Remark 2.4

A careful check of the proof reveals that if $\bigl |\sum _{i = -\infty }^{-K}\Vert \mathcal {P}_i(X_0(u))\Vert _p\bigr |_{\mathbf{C}} = 0$ for some finite $K > 0$, then it suffices to demand $p' \beta > d$ instead of $\alpha \beta p' > d(1 + \alpha )$. This is, for instance, the case if $\{X_k(u)\}_{k \in \mathbb {Z}}$ is a martingale difference sequence with respect to $\mathcal {F}_k$ for $u \in \mathbf{I}^d$.

Regarding the space $\mathbf{D}[\mathbf{I}^{d+1}]$, we have the following companion result.

Corollary 2.5

Grant the Assumptions of Theorem 2.2. Then

$$\begin{aligned} \check{S}_{nt}(u) \xrightarrow {{\mathbf{D}}[\mathbf{I}^{d+1}]} \mathcal {G}_t(u), \end{aligned}$$

where $\bigl \{\mathcal {G}_t(u)\bigr \}_{t \in \mathbf{I}, u \in \mathbf{I}^d}$ is as in Theorem 2.2. This result is also valid if we consider the space ${\mathbf{D}}[\mathbf{I}^{d+1}]_{\mathbf{C}}$.

Remark 2.6

The proof actually shows that we may switch between $\check{S}_{nt}(u)$ and ${S}_{nt}(u)$ in ${\mathbf{D}}[\mathbf{I}^{d+1}]$, since the error is asymptotically negligible. This is not an immediate consequence of Theorem 2.2, since $S_{nt}(u) \ne \check{S}_{nt}(u)$ in general. Also note that ${\mathbf{D}}[\mathbf{I}^{d+1}]_{\mathbf{C}}$ is not a separable space (cf.  [8]).

Suppose now that we are given an estimator $\widehat{\theta } \xrightarrow {\mathbb {P}} \theta \in \mathcal {I}^d$, where we assume for simplicity that $\mathcal {I} = (0,1)$. Using Corollary 2.5, one may deduce that $\check{S}_{nt}(\widehat{\theta }) \xrightarrow {{\mathbf{D}}[\mathbf{I}^{d+1}]} \sqrt{\Gamma (\theta ,\theta )}\mathcal {W}_t$ via continuous mapping. However, if $d = 1$, it is possible to establish this result under slightly weaker conditions.

Theorem 2.7

Grant Assumption 2.1 with $d = 1$, $p \ge 2$ and $\alpha \beta p > (1 + \alpha )$. Suppose that $\widehat{\theta } \xrightarrow {P} \theta \in \mathcal {I}$. Then

$$\begin{aligned} \check{S}_{nt}(\widehat{\theta }) \xrightarrow {\mathbf{D}[\mathbf{I}]} \sqrt{\Gamma (\theta ,\theta )}\mathcal {W}_t, \end{aligned}$$

where $\Gamma (u,v)$ is as in Theorem 2.2 and $\{\mathcal {W}_t\}_{0 \le t \le 1}$ is a Brownian motion.

Remark 2.8

Note that if $p = 2$, then we require that $2 \alpha \beta > 1 + \alpha$. If $X_k(u)$ shares in addition a Lipschitz-type behavior with $\beta = 1$, then this simplifies further to $\alpha > 1$. For example in this direction refer to Sect. 2.1.

In statistical applications, it is necessary to estimate the long-run variance $\Gamma (\theta ,\theta )$. This is a highly nontrivial task, and a considerable literature has evolved around this problem (cf.  [11, 27] and the references there). To shed more light on this issue, we introduce some notation. Let $\mu = \mu (u)$, $u \in \mathbf{I}^d$ be some deterministic function with $\bigl |\mu (u)\bigr |_{\mathbf{C}} < \infty$. Put $Y_k = X_k + \mu$, $\phi _h(u) = \phi _h(u,u) = {Cov} \bigl (Y_h(u),Y_0(u)\bigr )$ and let ${\Phi }_{l_n}(u) = \phi _0(u) + 2 \sum _{h = 1}^{l_n} \phi _h(u)$, where $l_n$ denotes a bandwidth. Given the sequence $\{Y_k\}_{1 \le k \le n}$, consider the covariance estimators

$$\begin{aligned} \widehat{\phi }_h(u) = n^{-1} \sum _{k = h + 1}^n \bigl (Y_k(u) - \overline{Y}_{n}(u)\bigr )\bigl (Y_{k-h}(u) - \overline{Y}_{n}(u)\bigr ), \end{aligned}$$

(2.2)

where $\overline{Y}_{n}(u) = n^{-1}\sum _{k = 1}^n Y_k(u)$. In practice, it is more advisable to use the normalizing factor $(n-h)^{-1}$ in (2.2) instead. However, this is negligible for our asymptotic considerations, and indeed all the results remain equally valid. A popular estimator in this context is Bartlett’s estimator (cf.  [11]), or, more general, estimators of the form

$$\begin{aligned} \widehat{\Phi }_{l_n}^{(\omega )}(u) = \sum _{|h| \le l_n} \omega (h/l_n) \widehat{\phi }_{h}(u), \quad l_n \rightarrow \infty \end{aligned}$$

(2.3)

with weight function $\omega (x)$. Considering the triangular weight function $\omega (x) = 1 - |x|$ for $|x| \le 1$ and $\omega (x) = 0$ otherwise, one recovers Bartlett’s estimator in (2.3). As before, we may neglect $\omega (x)$ for our asymptotic analysis; hence, it suffices to consider the simple plug-in estimator $\widehat{\Phi }_{l_n}(u) = \widehat{\Phi }_{l_n}^{(1)}(u)$, given as

$$\begin{aligned} \widehat{\Phi }_{l_n}(u) = \widehat{\phi }_0(u) + 2 \sum _{h = 1}^{l_n} \widehat{\phi }_h(u), \quad l_n \rightarrow \infty . \end{aligned}$$

(2.4)

Let us formally introduce ${\Phi }({\theta },\infty ) = \phi _0(\theta ) + 2 \sum _{h = 1}^{\infty } \phi _h(\theta )$. Then we have the following result.

Proposition 2.9

Grant Assumption 2.1 with $p > 2$ and $\alpha \beta p > d(1 + \alpha )$, and suppose that $\widehat{\theta } \xrightarrow {\mathbb {P}} \theta \in \mathcal {I}^d$. Assume in addition

• (B1) $\sup _{h \ge 0}\bigl |\sum _{i = - \infty }^{-K}\Vert \mathcal {P}_i(Y_{k-h}(u) Y_k(u))\Vert _{p/2}\bigr |_{\mathbf{C}} \lesssim K^{-\gamma }$, $\gamma > 0$,

• (B2) $\beta \gamma p/2 > d(1 + \gamma )$, and $l_n = \mathcal {O}\bigl (n^{p/2 - p/2p^*} \wedge n^{p/4}\bigr )^{2/(p+2)}$, where $p^* = \min \{2, p/2\}$.

Then ${\Phi }_{\infty }({\theta }) = \Gamma (\theta ,\theta )$ and $\widehat{\Phi }_{l_n}(\widehat{\theta }) \xrightarrow {\mathbb {P}} {\Phi }_{\infty }({\theta })$ as $l_n \rightarrow \infty$.

Remark 2.10

Note that if $p \le 4$, then $p^* = p/2$ and hence $l_n = \mathcal {O}\bigl (n^{\frac{p-2}{p+2}}\bigr )$.

2.1 Examples and Ramification

In this section, we connect the assumptions of the previous results to fairly general, yet easy verifiable weak dependence conditions. Given a sequence $\{\epsilon _k\}_{k \in \mathbb {Z}}$ of independent and identically distributed random variables, we define the $\sigma$-algebra $\mathcal {E}_k := \sigma ( \epsilon _j, \, j \le k )$. We always assume that $\{ X_k\}_{k\ge 1}$ is adapted to $\mathcal {E}_{k}$, implying that $X_{k}$ can be written as a function

$$\begin{aligned} X_{k}(u) = g_u\bigl (\epsilon _{k}, \epsilon _{k-1}, \ldots \bigr ). \end{aligned}$$

(2.5)

For convenience, we write $g_u(\xi _{k})$, with $\xi _k = (\epsilon _k, \epsilon _{k - 1},\ldots )$. Note that we did not specify an underlying space for the sequence $\{\epsilon _k\}_{k \in \mathbb {Z}}$ so far, we just assume that $g_u(\xi _{k})$ is well defined. In fact, $\epsilon _k$ may depend on $u \in \mathbf{I}^d$ as well, i.e., $\epsilon _k = \epsilon _k(u)$. The class of processes that fits into this framework is large and contains a variety of linear and nonlinear processes including ARCH, GARCH and related processes, see, for instance,  [43, 46]. A nice feature of the representation given above is that it allows to give simple, yet very efficient and general dependence conditions. Following Wu  [45], let $\{\epsilon _k'\}_{k \in \mathbb {Z}}$ be an independent copy of $\{\epsilon _k\}_{k \in \mathbb {Z}}$ on the same probability space, and define the ’filters’ $\xi _{k}^{(m, ')}$, $\xi _{k}^{(m,*)}$ as

$$\begin{aligned} \xi _{k}^{(m,')} = (\epsilon _{k}, \epsilon _{k - 1},\ldots ,\epsilon _{k - m}',\epsilon _{k - m - 1},\ldots ) \end{aligned}$$

(2.6)

and

$$\begin{aligned} \xi _{k}^{(m,*)} = (\epsilon _{k}, \epsilon _{k - 1},\ldots ,\epsilon _{k - m},\epsilon _{k - m - 1}',\epsilon _{k - m - 2}'\ldots ). \end{aligned}$$

(2.7)

We put $\xi _{k}' = \xi _{k}^{(k, ')} = (\epsilon _{k}, \epsilon _{k - 1},\ldots ,\epsilon _0',\epsilon _{-1},\ldots )$ and $\xi _{k}^* = \xi _{k}^{(k,*)} = (\epsilon _{k }, \epsilon _{k - 1},\ldots ,\epsilon _{0},\epsilon _{- 1}',\epsilon _{- 2}'\ldots )$. In analogy, we put $X_{k}^{(m,')}(u) = g_{u}\bigl (\xi _{k}^{(m,')} \bigr )$ and $X_{k}^{(m,*)}(u) = g_{u}\bigl (\xi _{k}^{(m,*)} \bigr )$; in particular, we have $X_{k}'(u) = X_{k}^{(k,')}(u)$ and $X_{k}^{*}(u) = X_{k}^{(k,*)}(u)$. As a dependence measure, one may now consider the quantities $\Vert X_{k}(u) - X_{k}'(u)\Vert _p$ or $\Vert X_{k}(u) - X_{k}^*(u)\Vert _p$, $p \ge 1$. For example, if we define the (functional) linear processes $X_{k}(u) = \sum _{i = 0}^{\infty } \alpha _{i}(u) \epsilon _{k - i}$, condition

$$\begin{aligned} \bigl |\sum _{k = 0}^{\infty } \Vert X_{k}(u) - X_{k}'(u)\Vert _2\bigr |_{\mathbf{C}} < \infty \quad \text {amounts to} \quad \bigl |\sum _{i = 0}^{\infty }|\alpha _{i}(u)|\bigr |_{\mathbf{C}} < \infty \end{aligned}$$

if $\mathbb {E}\bigl (\epsilon _0^2\bigr ) < \infty$. Dependence conditions of this type are quite general and easy to verify in many cases, see the examples given below or  [13, 21, 46] and the references therein. As pointed out earlier, the aim of this section is to verify some of the main results under the following conditions.

Assumption 2.11

For $d \ge 1$, the process $\{X_k(u)\}_{k \in \mathbb {Z}}$ is adapted to $\mathcal {E}_k$ for every $u \in \mathbf{I}^d$, such that for some $p \ge 2$ and $\tau \ge 0$

• (C1) $\mathbb {E}\bigl [X_k(u)\bigr ] = 0$ for $u \in \mathbf{I}^d$,

• (C2) $\bigl |\sum _{k = K}^{\infty }\Vert X_k(u) - X_k'(u)\Vert _p\bigr |_{\mathbf{C}} \lesssim K^{-\tau }$ for $k \ge 1$,

• (C3) $\Vert X_k(u)-X_k(v)\Vert _p \lesssim |u-v|_{\infty }^{\beta }$, $\beta > 0$, $u,v \in \mathbf{I}^d$.

Proposition 2.12 below now essentially tells us to what extent Assumption 2.11 implies Assumption 2.1.

Proposition 2.12

Assume that (C1), (C2) and (C3) hold with $p \ge 2$ such that $\tau \ge 0$. Then (A1), (A2) with $\alpha = \tau$, and (A3) are valid.

In applications, one typically has a process $\{L_k\}_{k \in \mathbb {Z}}$ that does not depend on $u \in \mathbf{I}^d$, a real-valued (measurable) function f(x, u), and the quantity of interest is the combined sequence $X_k(u) = f(L_k,u)$. Suppose that $L_k \in \mathcal {E}_k$ and $\big \Vert L_k - L_k'\bigr \Vert _p \lesssim k^{-\mathfrak {l} - 1}$ with $\mathfrak {l} > 0$. Consider the real-valued function f(x, u), with

$$\begin{aligned} \bigl |f(x,u)-f(y,v)\bigr | \le C_f\bigl (|x-y|^{\mathfrak {h}_1} + |u-v|_{\infty }^{\mathfrak {h}_2}\bigr ), \quad \mathfrak {h}_i > 0, \, i \in \{0,1\}, \, C_f < \infty . \end{aligned}$$

(2.8)

Then $X_k(u) = f(L_k,u) - \mathbb {E}\bigl [f(L_k,u)\bigr ]$ meets (C1), (C2), (C3) with $\tau = (\mathfrak {l} + 1)\mathfrak {h}_1 - 1$ and $\beta = \mathfrak {h}_2$.

The literature (cf.  [1, 2, 15, 18, 20, 29, 35, 42]) offers a huge variety of empirical central limit theorems. Given a family of functions $\mathcal {F}$, the process $\{S_n(f)\}_{f \in \mathcal {F}}$ with $S_n(f) = n^{-1/2}\sum _{k = 1}^n f(L_k)$ is considered. Usually the aim here is to allow the function class $\mathcal {F}$ to be as general (resp. large) as possible, which is often expressed in terms of entropy conditions. This usually comes at the cost of heavier dependence assumptions compared to standard invariance principles, and often a uniformly bounded like condition such as $\sup _{f \in \mathcal {F}}|f| < \infty$ is required. Also note that in general, a sequential version of a uniform central limit theorem is by no means for free, often requiring additional conditions. On the contrary, the results presented here are more adapted to the case where the functions in question possess a certain minimum smoothness, thereby being less general. On the other hand, no uniformly boundedness of the corresponding random variables is required, which in view of  [25, 26] can be very restrictive. As already mentioned, such smoothness conditions are naturally present in many statistical problems (see Sects. 2.1, 2.2), in which case our results allow for a significantly wider range of application. In addition, the present dependence assumptions are more related to martingale approximations instead of mixing conditions, and in many cases easy to verify.

Regarding Proposition 2.9, we have the following companion result of Proposition 2.12.

Proposition 2.13

Grant Assumption 2.11 with $p > 2$ such that $\tau \beta p/2 > 1 + \tau$. Let $l_n$ be as in Proposition 2.9. Then ${\Phi }({\theta },\infty ) = \Gamma (\theta ,\theta )$ and $\widehat{\Phi }_n(\widehat{\theta },l_n) \xrightarrow {\mathbb {P}} {\Phi }({\theta },\infty )$ as $l_n \rightarrow \infty$.

We now give two prominent examples from the time-series literature that are within our framework, and in particular meet the conditions of the previous Propositions.

Example 2.14

(ARMA($\mathfrak {p},\mathfrak {q}$) sequences) Let $\{L_k\}_{k \in \mathbb {Z}}$ be an ARMA($\mathfrak {p},\mathfrak {q})$ sequence, defined as

$$\begin{aligned} L_k = \alpha _1 \epsilon _{k} +\cdots + \alpha _\mathfrak {p} \epsilon _{k - \mathfrak {p}} + \beta _1 L_{k - 1} +\cdots + \beta _{\mathfrak {q}} L_{k - \mathfrak {q}}, \end{aligned}$$

where $\{\epsilon _{k}\}_{k \in \mathbb {Z}}$ is a zero mean I.I.D. sequence and $\alpha _1,..,\alpha _\mathfrak {p}, \beta _1,\ldots ,\beta _{\mathfrak {q}} \in \mathbb {R}$. Consider the polynomials

$$\begin{aligned} \mathbf{A}(z) = \sum _{j = 0}^{\mathfrak {p}} \alpha _j z^{j}, \quad \mathbf{B}(z) = \sum _{j = 0}^{\mathfrak {q}} \beta _j z^{j}, \end{aligned}$$

(2.9)

where $\mathbf{A}(z)$ and $\mathbf{B}(z)$ are assumed to be relative prime. It is well known (cf.  [11]) that if the associated polynomial $\mathbf{C}(z) = \mathbf{A}(z) \mathbf{B}^{-1}(z)$ satisfies

$$\begin{aligned} \mathbf{C}(z) \ne 0 \quad \text {for } |z| \le 1, \end{aligned}$$

then $L_k$ admits a causal representation

$$\begin{aligned} L_k = \sum _{i = 0}^{\infty } \theta _i \epsilon _{k - i}, \quad k \in \mathbb {Z}, \end{aligned}$$

where $|\theta _i| \lesssim \rho ^{i}$ for $0 < \rho < 1$, hence exponential decay. One thus easily concludes

$$\begin{aligned} \bigl \Vert L_k - L_k'\bigr \Vert _p \lesssim \rho ^{-k}, \quad \text {where } 0 < \rho < 1. \end{aligned}$$

(2.10)

Example 2.15

(GARCH($\mathfrak {p},\mathfrak {q}$) sequences) Let $\{L_k\}_{k \in \mathbb {Z}}$ be a GARCH($\mathfrak {p},\mathfrak {q})$ sequence, given through the relations

$$\begin{aligned}&L_k = \epsilon _k \sigma _{k} \quad \text {where } \{\epsilon _{k}\}_{k \in \mathbb {Z}} \hbox { is a zero mean I.I.D. sequence and}\\&\sigma _k^2 = \mu + \alpha _1 \sigma _{k - 1}^2 +\cdots + \alpha _\mathfrak {p} \sigma _{k - \mathfrak {p}}^2 + \beta _1 L_{k - 1}^2 +\cdots + \beta _{\mathfrak {q}} L_{k - \mathfrak {q}}^2, \end{aligned}$$

with $\mu , \alpha _1,..,\alpha _\mathfrak {p}, \beta _1,\ldots ,\beta _{\mathfrak {q}} \in \mathbb {R}$. A very important quantity in this context is

$$\begin{aligned} \gamma _C = \sum _{i = 1}^{r} \bigl \Vert \alpha _i + \beta _i \epsilon _i^2\bigr \Vert _2, \quad \text {with } r = \max \{\mathfrak {p},\mathfrak {q}\}, \end{aligned}$$

(2.11)

where we replace possible undefined $\alpha _i, \beta _i$ with zero. If $\gamma _C < 1$, then $\{L_k\}_{k \in \mathbb {Z}}$ is stationary (cf.  [9]). It was shown in  [4] that $\{L_k\}_{k \in \mathbb {Z}}$ may then be represented as

$$\begin{aligned} L_k = \sqrt{\mu }\epsilon _k\biggl (1 + \sum _{n = 1}^{\infty } \sum _{1 \le l_1,\ldots ,l_n\le r} \prod _{i = 1}^n\bigl (\alpha _{l_i} + \beta _{l_i}\epsilon _{j - l_1 -\cdots - l_i}^2\bigr ) \biggr )^{1/2}. \end{aligned}$$

(2.12)

Using this representation and the fact that $|x-y|^p \le |x^2 - y^2|^{p/2}$ for $x,y \ge 0$, $p \ge 1$, one readily deduces that

$$\begin{aligned} \bigl \Vert L_k - L_k'\bigr \Vert _p \lesssim \rho ^{-k}, \quad \text {where } 0 < \rho < 1. \end{aligned}$$

(2.13)

2.2 Applications

An important concept in statistics is so-called M-estimators $\widehat{\theta }_n$, which among others include and generalize MLE-estimators. Given an ergodic sequence $\{L_k\}_{k \in \mathbb {Z}}$, the characterizing definition for $\widehat{\theta }_n$ is usually given as

$$\begin{aligned} {\varvec{\Psi }}_n(\widehat{\theta }_n) = 0, \quad \text {where } \quad {\varvec{\Psi }}_n(\theta ) = n^{-1}\sum _{k = 1}^n \psi (L_k,\theta ), \quad \theta \in \mathbb {R}^d. \end{aligned}$$

(2.14)

Such estimators are also referred to as Z-estimators (Z for zero), but the name M-estimator is widespread. Often $\psi (\cdot ,\theta ) = \bigl (\psi _1(\cdot ,\theta ),\ldots ,\psi _d(\cdot ,\theta ) \bigr )^{\top }$ stands for a d-dimensional gradient vector, the prototype of such a case being many MLE-estimators. For a more detailed discussion of M-estimators, see, for instance,  [44].

In this section, we are interested in the problem of testing for changes in the parameter $\theta$, based on the estimation principle of $\widehat{\theta }_n$. Particularly in the I.I.D. setting, a lot of literature has been developed in this area, see, for instance,  [12, 30] and the references therein. A (technical) key feature in this context is invariance principles for

$$\begin{aligned} n^{1/2} {\varvec{\Psi }}_{\lfloor nt \rfloor }(\theta ) = n^{-1/2}\sum _{k = 1}^{\lfloor nt \rfloor } \psi (L_k,\theta ), \end{aligned}$$

(2.15)

which is exactly the kind of problem studied earlier in Sects. 2 and 2.1. Such expressions can either be used to directly construct a (CUSUM) test (see, e.g.,  [30]), or naturally arise in the study of $n^{1/2}(\widehat{\theta }_{nt} - \theta )$, which in turn is useful to construct test procedures. We again refer to  [12] on how to construct a variety of tests based on such invariance principles.

In order to study the limiting behavior of M-estimators, a key minimum requirement is (uniform) consistency of the estimators in question. Conditions for such consistency results are more attached to properties of the function $\psi (\cdot , \theta )$ than to the underlying sequence $\{L_k\}_{k \in \mathbb {Z}}$, where typically a (strong) law of large numbers is sufficient, which in our case is provided by the ergodicity of $\{L_k\}_{k \in \mathbb {Z}}$. In the sequel, we take such a consistency result for granted and refer to  [44] for more details regarding this subject. To simplify the present discussion, we focus on the univariate case $\theta \in (0,1)$ for the remainder of this section. Following  [44], we obtain the following result.

Theorem 2.16

For each $\theta \in (0,1)$ let $x \mapsto \psi (x,\theta )$ be a measurable, real-valued map such that, for every $\theta _1, \theta _2$ in a neighborhood of $\theta _0$ and a measurable function $\psi '$ with $\mathbb {E}[\psi '(L_0)^2] < \infty$

• (M1) $\bigl |\psi (x,\theta _1) - \psi (x,\theta _2)\bigr | \le \psi '(x) \bigl |\theta _1 - \theta _2\bigr |$.

Assume that $\mathbb {E}[\psi (L_0,\theta _0)^2] < \infty$ and that the map $\theta \mapsto \mathbb {E}[\psi (L_0,\theta )]$ is differentiable at a zero $\theta _0$ (i.e., $\mathbb {E}[\psi (L_0,\theta _0)] = 0$) with nonzero derivative $V(\theta _0)$. If $\{L_k\}_{k \in \mathbb {Z}}$ is ergodic, and

• (M2) $\bigl |\sum _{i = -\infty }^{-K}\Vert \mathcal {P}_i(\psi (L_0,\theta ))\Vert _2\bigr |_{\mathbf{C}} \lesssim K^{-\alpha }$, $\alpha > 1$,

• (M3) $\sup _{0 \le t \le 1}n^{-1/2}\bigl |\sum _{k = 1}^{\lfloor n t \rfloor }\psi (L_k,\widehat{\theta }_{\lfloor nt \rfloor }) \bigr | = \mathcal {O}_{\mathbb {P}}(1), \quad \bigl |\widehat{\theta }_n - \theta _0 \bigr | = \mathcal {O}_{\mathbb {P}}(\delta _n)$,

where $\delta _n \rightarrow 0$ monotonously, then

$$\begin{aligned} n^{-1/2}\sup _{0 \le t \le 1}\bigl |\widehat{\theta }_{\lfloor nt \rfloor } - \theta _0 +\sum _{k = 1}^{\lfloor n t \rfloor } \psi (L_k,\theta _0)/V(\theta _0) \bigr | = \mathcal {O}_{\mathbb {P}}(1). \end{aligned}$$

Moreover, we also have

$$\begin{aligned} n^{-1/2}\bigl (\widehat{\theta }_{\lfloor nt \rfloor } - \theta _0\bigr ) \xrightarrow {\mathbf{D}[\mathbf{I}]} \sqrt{\sigma ^2(\theta _0)}\mathcal {W}_t, \end{aligned}$$

where $\sigma ^2(\theta _0) = \sum _{k \in \mathbb {Z}} \mathbb {E}[\psi (L_k,\theta _0)\psi (L_0,\theta _0)]/V^2(\theta _0)$.

Remark 2.17

Observe that the first part of condition (M3) is a relaxation of the stronger version (2.14), which requires that ${\varvec{\Psi }}_{\lfloor n t \rfloor }(\widehat{\theta }_{\lfloor nt \rfloor }) = 0$.

Theorem 2.16 covers a large number of examples, see for instance  [44]. Further extensions to related results (e.g., Theorem 5.23 in  [44]) can be obtained in the same manner.

3 Proofs of the Main Results

To simplify the discussion and notation, we only consider the case $d = 1$ in the proofs of Theorem 2.2, Corollary 2.5, Theorem 2.7 and Proposition 2.9. The more general case $1 \le d < \infty$ follows from straightforward adaptations, and we omit the details.

Remark 3.1

We will frequently make use of the following property. It holds that (cf. Lemma 3.84 in  [31])

$$\begin{aligned} \mathcal {P}_{i + h}\bigl (X_{k + h}(u)\bigr )\mathop {=}\limits ^{d} \mathcal {P}_{i}\bigl (X_{k}(u)\bigr ), \quad h \in \mathbb {Z},\, u \in [0,1]. \end{aligned}$$

This implies in particular $\bigl \Vert \mathcal {P}_{i + h}\bigl (X_{k + h}(u)\bigr )\bigl \Vert _p = \bigl \Vert \mathcal {P}_{i}\bigl (X_{k}(u)\bigr )\bigr \Vert _p$.

Proof of Theorem 2.2

Before going into details, let us briefly outline the proof of Theorem 2.2. The main tool is to combine the classic dyadic-grid expansion with a maximal inequality. Unlike to the classical proofs (cf.  [8, 32]), this allows for a grid expansion where the size is different in the two coordinates. It is therefore very likely that our approach carries over to other notions of weak dependence, where the actual result then depends on the corresponding maximal inequality. In our setup, we use the maximal inequality given in Lemma 5.1, due to Wei Biao Wu [46] and based on martingale approximations.

The proof proceeds along the classical lines by first establishing finite-dimensional convergence and then tightness. The claim then follows from Theorem 7.5 in  [8] (multivariate version). Finite-dimensional convergence follows from Lemma 5.7. It thus remains to show tightness in $\mathbf{C}[0,1]^2$. To this end, for $X(t,u) \in \mathbf{C}[0,1]^2$ we define the modulus of continuity $w(X,\delta )$ as

$$\begin{aligned} w\bigl (X,\delta \bigr ) = \sup _{\begin{array}{c} |t-s|\le \delta ,\\ |u-v|\le \delta \end{array}}\bigl |X(t,u) - X(s,v)\bigr |, \quad \text {where } 0 \le \text {s, t, u, v } \le 1. \end{aligned}$$

(3.1)

Note that due to the norm equivalence in $\mathbb {R}^2$, any other norm for the vectors $(t,u)^{\top }$, $(s,v)^{\top } \in \mathbf{I}^2$ could be used [the maximum norm is used in (3.1)]. By Theorem 14.5 in  [32] (see also  [8]), it thus suffices to establish that for any $\epsilon > 0$, it holds that

$$\begin{aligned} \lim _{\delta \rightarrow 0}\lim \sup _{n \rightarrow \infty } \mathbb {P}\bigl (w(S_n,\delta ) \ge \epsilon \bigr ) = 0. \end{aligned}$$

(3.2)

In order to show (3.2), we will use a modification of the dyadic expansion, employed, for instance, in  [8, 32, 33]. Let $\tau _1, \tau _2, N, L \in \mathbb {N}^+$, where $L < N$ and $\mathbb {N}^+$ denotes the strictly positive natural numbers. Consider $0 \le l_1,l_2 \le 2^L$ and introduce

$$\begin{aligned} t_{i,l_1} = \frac{l_1}{2^L} + \frac{i}{2^{\tau _1 N}}, \quad u_{j,l_2} = \frac{l_2}{2^L} + \frac{j}{2^{\tau _2 N}}. \end{aligned}$$

(3.3)

To avoid any notational problems, we also put $t_{2^{\tau _1 N} + 1,l_1} = t_{2^{\tau _1 N},l_1}$ and $u_{2^{\tau _2 N} + 1,l_2} = u_{2^{\tau _2 N},l_2}$. For $\tau , N \in \mathbb {N}^+$, we also introduce the index set $\mathcal {I}(\tau N) = \bigl \{i = 0,\ldots ,2^{\tau N}\bigr \}$ and the set of numbers

$$\begin{aligned} D_{l}{(\tau N)} = \biggl \{\frac{l}{2^L} + \frac{i}{2^{\tau N + L}}, \, i = 0,\ldots ,2^{\tau N} \biggr \} = \biggl \{\frac{l}{2^L} + \frac{i}{2^{\tau N + L}}, \, i \in \mathcal {I}(\tau N) \biggr \}. \end{aligned}$$

For $M > N$, we denote with $U_l^{M}(\tau ) = \bigcup _{N = 0}^M D_{l}{(\tau N)}$, where we point out that $U_l^{\infty }(\tau )$ contains all the rational dyadic points that lie within $[l/2^L,(l+1)2^L]$, i.e.,

$$\begin{aligned} U_l^{\infty }(\tau ) = [l/2^L,(l+1)2^L] \cap \mathbb {Q}_2, \end{aligned}$$

(3.4)

where $\mathbb {Q}_2$ denotes the set of all rational dyadic points. Let us now fix $\tau _1, \tau _2 \in \mathbb {N}$, $0 \le l_1,l_2 \le 2^L$, and consider the grid $G(N) = D_{l_1}{(\tau _1 N )} \times D_{l_2}{(\tau _2 N)}$. We can move along the grid G(N) stepwise, where in each step we can move one unit $2^{-\tau _1 N}$ within $D_{l_1}{(\tau _1 N )}$, and one unit $2^{-\tau _2 N}$ within $D_{l_2}{(\tau _2 N )}$; it is not necessary to move in both coordinates in one step. This means, for instance, from $\bigl (t_{i,l_1}, u_{j,l_2}\bigr )$ to $\bigl (t_{i+1,l_1}, u_{j+1,l_2}\bigr )$, or from $\bigl (t_{i,l_1}, u_{j,l_2}\bigr )$ to $\bigl (t_{i-1,l_1}, u_{j,l_2}\bigr )$. Suppose that the point $p_{N+1}$ lies on $G(N+1)\setminus G(N)$ and the point $p_{N}$ on G(N). Then moving along the grid $G(N+1)$, it takes at the most $2^{\tau _1 \vee \tau _2}$ steps to reach $p_{N}$, starting off from the point $p_{N+1}$. Obviously, this is true for every $N \ge L$. Put

$$\begin{aligned} \nonumber&\mathrm{II}(l_1,l_2,N) = \max _{i \in \mathcal {I}(\tau _1 N)} \max _{j \in \mathcal {I}(\tau _2 N)}\bigl |S_{n t_{i+1,l_1}}(u_{j,l_2}) - S_{n t_{i,l_1}}(u_{j,l_2})\bigr |,\\&\mathrm{III}(l_1,l_2,N) = \max _{i \in \mathcal {I}(\tau _1 N)} \max _{j \in \mathcal {I}(\tau _2 N)}\bigl |S_{nt_{i,l_1}}(u_{j+1,l_2}) - S_{nt_{i,l_1}}(u_{j,l_2})\bigr |. \end{aligned}$$

(3.5)

The quantities $\mathrm{II}(l_1,l_2,N)$ and $\mathrm{III}(l_1,l_2,N)$ refer to the maximal coordinatewise error that we make in each step. Using this methodology, we readily obtain the bound

$$\begin{aligned}&\max _{\begin{array}{c} t,s \in U_{l_1}^{(M)}(\tau _1)\\ |t-s| \le 2^{-L} \end{array}}\max _{\begin{array}{c} u,v \in U_{l_2}^{(M)}(\tau _2)\\ |u-v| \le 2^{-L} \end{array}}\biggl |S_{nt}(u) - S_{ns}(v) \biggr | \le 2^{\tau _1\vee \tau _2}\sum _{N = L}^M \bigl (\mathrm{II}(l_1,l_2,N) + \mathrm{III}(l_1,l_2,N)\bigr ). \end{aligned}$$

Let $\epsilon > 0$. Then since $\sum _{i = 1}^{\infty } i^{-2} \le 2$, we have that

$$\begin{aligned}&\mathbb {P}\biggl (\sum _{N = L}^M \mathrm{II}(l_1,l_2,N) + \mathrm{III}(l_1,l_2,N) \ge \epsilon \biggr )\\ {}&\le \sum _{N = L}^M \biggl (\mathbb {P}\bigl (\mathrm{II}(l_1,l_2,N) \ge N^{-2}\epsilon /4 \bigr ) + \mathbb {P}\bigl (\mathrm{III}(l_1,l_2,N) \ge N^{-2}\epsilon /4 \bigr ) \biggr ). \end{aligned}$$

An application of Lemma 5.5 and Lemma 5.6 yields that for some constant $C_1(p) > 0$ and $2 \le p' \le p$ we have

$$\begin{aligned}&\sum _{N = L}^M \biggl (\mathbb {P}\bigl (\mathrm{II}(l_1,l_2,N) \ge N^{-2}\epsilon /4 \bigr ) + \mathbb {P}\bigl (\mathrm{III}(l_1,l_2,N) \ge N^{-2}\epsilon /4 \bigr ) \biggr )\nonumber \\&\lesssim \epsilon ^{-p} \sum _{N = L}^{M} N^{2p}\biggl (2^{-(p/2-1)\tau _1N - p/2L + \tau _2 N} + 2^{-(\alpha \beta p'/(1 + \alpha ) -1)\tau _2N - L \alpha \beta p'/(1+\alpha )} \biggr ). \end{aligned}$$

(3.6)

Choosing $\tau _1, \tau _2 > 0$ such that $\tau _1 > (1 + \tau _2)(p/2 - 1)^{-1}$ and $\tau _2 > (\alpha \beta p'/(1 + \alpha ) -1)^{-1}$, it follows that for absolute constants $c_1, c_2 > 0$, the above is bounded by

$$\begin{aligned} \thicksim \epsilon ^{-p} 2^{-2L}\sum _{N = L}^{M}N^{2p}\bigl (2^{-c_1N} + 2^{-c_2 N} \bigr ). \end{aligned}$$

(3.7)

For any $M \in \mathbb {N}$, we thus obtain that

$$\begin{aligned} \nonumber&\mathbb {P}\biggl (\max _{0 \le l_1,l_2 \le 2^L}\max _{\begin{array}{c} t,s \in U_{l_1}^{(M)}(\tau _1)\\ |t-s| \le 2^{-L} \end{array}}\max _{\begin{array}{c} u,v \in U_{l_2}^{(M)}(\tau _2)\\ |u-v| \le 2^{-L} \end{array}}\biggl |S_{nt}(u) - S_{ns}(v) \biggr |\ge \epsilon \biggr ) \\ \nonumber&\quad \le \sum _{l_1 = 0}^{2^L}\sum _{l_2 = 0}^{2^L}\mathbb {P}\biggl ( \max _{\begin{array}{c} t,s \in U_{l_1}^{(M)}(\tau _1)\\ |t-s| \le 2^{-L} \end{array}}\max _{\begin{array}{c} u,v \in U_{l_2}^{(M)}(\tau _2)\\ |u-v| \le 2^{-L} \end{array}}\biggl |S_{nt}(u) - S_{ns}(v) \biggr | \ge \epsilon \biggr )\\ {}&\quad \lesssim \epsilon ^{-p} \sum _{N = L}^{\infty }N^{2p}\bigl (2^{-c_1N} + 2^{-c_2 N} \bigr ) \lesssim \epsilon ^{-p} L^{-1}. \end{aligned}$$

(3.8)

Note that by construction, $\bigcup _{l = 0}^{2^L} U_l^{\infty }(\tau _1) \times \bigcup _{l = 0}^{2^L} U_l^{\infty }(\tau _2)$ contains $[0,1]^2 \cap \mathbb {Q}_2 \times \mathbb {Q}_2$. Hence we deduce from the above that

$$\begin{aligned} \mathbb {P}\biggl (\sup _{\begin{array}{c} t,s \in \mathbb {Q}_2 \cap [0,1]\\ |t-s| \le 2^{-L} \end{array}}\sup _{\begin{array}{c} u,v \in \mathbb {Q}_2 \cap [0,1]\\ |u-v| \le 2^{-L} \end{array}}\bigl |S_{nt}(u) - S_{ns}(v) \bigr | \ge \epsilon \biggr ) \lesssim \epsilon ^{-p} L^{-1}. \end{aligned}$$

(3.9)

Proceeding in the same manner, and, using the classical arguments for proving the Kolmogorov–Centsov theorem (cf.  [32, 33]), it follows that there exists a continuous modification $\tilde{S}_{nt}(u)$ of $S_{nt}(u)$ which satisfies (3.9). This implies (3.2) if we set $\delta = 2^{-L -1}$. $\square$

Proof of Corollary 2.5

For the proof of Corollary 2.5, it suffices to show that

$$\begin{aligned} \lim _{n \rightarrow \infty }\mathbb {P}\biggl (\max _{1 \le k \le n}\sup _{0 \le u \le 1}\bigl |X_k(u)\bigr | \ge \sqrt{n} \epsilon \biggr ) = 0, \quad \epsilon > 0. \end{aligned}$$

Note first that we have the simple upper bound

$$\begin{aligned} \mathbb {P}\biggl (\max _{1 \le k \le n}\sup _{0 \le u \le 1}\bigl |X_k(u)\bigr | \ge \sqrt{n} \epsilon \biggr ) \le \sum _{k = 1}^n \mathbb {P}\biggl (\sup _{0 \le u \le 1}\bigl |X_k(u)\bigr | \ge \sqrt{n} \epsilon \biggr ). \end{aligned}$$

Fix $L > 0$, and, for $0 \le l \le 2^L - 1$, let $\Lambda _l = [l 2^{-L}, (l+1)2^{-L}]$. Then the above is bounded by

$$\begin{aligned}&\sum _{k = 1}^n \sum _{l = 0}^{2^L} \mathbb {P}\biggl (\sup _{u \in \Lambda _l}\bigl |X_k(u) - X_k(l 2^{-L})\bigr | \ge \sqrt{n} \epsilon 2^{- L - 1} \biggr )\\&\quad + \sum _{k = 1}^n \sum _{l = 0}^{2^L}\mathbb {P}\bigl (|X_k(l2^{-L})| \ge \sqrt{n} \epsilon 2^{- L - 1}\bigr ). \end{aligned}$$

Proceeding exactly in the same way as in the proof of Theorem 2.2, one shows that the first sum is of magnitude $\thicksim \sum _{k = 1}^n (\epsilon n)^{-p/2} = \mathcal {O}\bigl (1\bigr )$. The second sum can be dealt with by Markov’s inequality, which also yields a magnitude of $\thicksim \sum _{k = 1}^n (\epsilon n)^{-p/2} = \mathcal {O}\bigl (1\bigr )$. $\square$

Proof of Theorem 2.7

Introduce the quantity

$$\begin{aligned} \mathrm{V}_n(u) = \max _{1 \le k \le n}\bigl |\check{S}_k(u) - \check{S}_k(\theta )\bigr |. \end{aligned}$$

(3.10)

Since $|\widehat{\theta } - \theta | \xrightarrow {\mathbb {P}} 0$ by assumption, there exists a $\delta _n \rightarrow 0$ such that

$$\begin{aligned} \mathbb {P}(\mathrm{V}_n(\widehat{\theta }) \mathbf {1}(|\widehat{\theta } - \theta | \ge \delta _n) \ge \epsilon \bigr ) \le \mathbb {P}\bigl (|\widehat{\theta } - \theta | \ge \delta \bigr ) \rightarrow 0, \end{aligned}$$

(3.11)

Consider now the quantity

$$\begin{aligned} \mathbb {P}\bigl (\mathrm{V}_n(\widehat{\theta }) \mathbf {1}(|\widehat{\theta } - \theta | < \delta _n) \ge \epsilon \bigr ) \le \mathbb {P}\bigl (\sup _{|u - \theta | \le \delta _n}|\mathrm{V}_n(u)| \ge \epsilon \bigr ). \end{aligned}$$

Proceeding in the same manner as in Theorem 2.2 (the part which deals with $\mathrm{III}(l_1,l_2,N)$), one shows that the above is bounded by $\lesssim (-\log \delta _n')^{-1}$, hence

$$\begin{aligned} \mathbb {P}\bigl (\mathrm{V}_n(\widehat{\theta }) \mathbf {1}(|\widehat{\theta } - \theta | < \delta _n) \ge \epsilon \bigr ) \lesssim (-\log \delta _n')^{-1} = \mathcal {O}\bigl (1\bigr ). \end{aligned}$$

(3.12)

Combining (3.11) and (3.12), we conclude that treating $\check{S}_{nt}(\theta )\mathbf {1}(|\widehat{\theta } - \theta | < \delta _n)$ is sufficient. However, since $\mathbf {1}\bigl (|\widehat{\theta } - \theta | < \delta _n \bigr ) \xrightarrow {\mathbb {P}} 1$, Slutzkys Lemma implies that it suffices to have $\check{S}_{nt}(\theta ) \xrightarrow {\mathbf{D}[\mathbf{I}]} \sqrt{\Gamma (\theta ,\theta )}\mathcal {W}_t$. This, however, follows from Lemma 5.8. $\square$

Proof of Proposition 2.9

The proof mainly employs some of the arguments already encountered in the proofs of Theorem 2.2 and Theorem 2.7. We thus sometimes use these as reference instead of repeating all the details. The first claim ($\Gamma (\theta , \theta ) = \Phi _{\infty }(\theta )$) is trivial; hence, it remains to show that $\widehat{\Phi }_{l_n}(\widehat{\theta }) \xrightarrow {\mathbb {P}} {\Phi }_{\infty }({\theta })$. To this end, note that by Lemma 5.7

$$\begin{aligned} \bigl |{\Phi }_{\infty }(\theta ) - {\Phi }_{l_n}(\theta )\bigr | \le 2\sum _{h > l_n} \bigl |\phi _h(\theta )\bigr | = \mathcal {O}\bigl (1\bigr ), \end{aligned}$$

(3.13)

hence we may replace ${\Phi }_{\infty }({\theta })$ with ${\Phi }_{l_n}({\theta })$. Introduce the set $\mathcal {A}_{\delta } = \bigl \{|\widehat{\theta } - \theta | < \delta \bigr \}$, and consider the complement $A_{\delta }^c$. Then by the triangle inequality

$$\begin{aligned} \bigl |\widehat{\Phi }_{l_n}(\widehat{\theta }) - {\Phi }_{l_n}(\theta )\bigr |&\le \bigl |\widehat{\Phi }_{l_n}({\theta }) - {\Phi }_{l_n}(\theta )\bigr | + \sup _{|\theta - u|_{\infty }\le \delta }\bigl |\widehat{\Phi }_{l_n}(u) - \widehat{\Phi }_{l_n}({\theta })\bigr |\mathbf {1}\bigl (\mathcal {A}_{\delta }\bigr ) \\ {}&+ \bigl |\widehat{\Phi }_{l_n}(\widehat{\theta }) - {\Phi }_{l_n}(\theta )\bigr |\mathbf {1}\bigl (\mathcal {A}_{\delta }^c\bigr ). \end{aligned}$$

Since we have for $\epsilon > 0$ that

$$\begin{aligned} \mathbb {P}\biggl (\bigl |\widehat{\Phi }_{l_n}(\widehat{\theta }) - {\Phi }_{l_n}(\theta )\bigr | \mathbf {1}\bigl (\mathcal {A}_{\delta }^c\bigr )\ge \epsilon \biggr ) \le \mathbb {P}\biggl (\bigl |\widehat{\theta } - \theta | \ge \delta \biggr ) \rightarrow 0, \end{aligned}$$

(3.14)

it suffices to consider

$$\begin{aligned} \mathrm{IV}_n(\theta ,l_n) = \bigl |\widehat{\Phi }_{l_n}({\theta }) - {\Phi }_{l_n}(\theta )\bigr | \quad \text {and} \quad \mathrm{V}_n(\theta ,l_n) = \sup _{|\theta - u|_{\infty }\le \delta }\bigl |\widehat{\Phi }_{l_n}(u) - \widehat{\Phi }_{l_n}({\theta })\bigr |\mathbf {1}\bigl (\mathcal {A}_{\delta }\bigr ). \end{aligned}$$

To this end, put $A_{k - h}(u) = Y_{k - h}(u) - \overline{Y}_{n}(u)$, where we write $A_k$ for $A_{k - 0}$. In addition, put $B_{k,h}(u,v) = Y_{k-h}(u) Y_k(u) - Y_{k-h}(v) Y_k(v)$. We then have the decomposition

$$\begin{aligned} \sum _{k = h + 1}^n A_k(u)A_{k - h}(u)&= \sum _{k = h+1}^n Y_k(u) Y_{k-h}(u) - \overline{Y}_{n}(u)\sum _{k = h+1}^n Y_k(u)\nonumber \\&\quad - \overline{Y}_{n}(u)\sum _{k = 1}^{n-h} Y_k(u) + \overline{Y}_{n}^2(u). \end{aligned}$$

(3.15)

We separately deal with $\mathrm{IV}_n(\theta ,l_n)$ and $\mathrm{V}_n(\theta ,l_n)$.

Case $\mathrm{IV}_n(\theta ,l_n)$: It holds that

$$\begin{aligned} \mathrm{IV}_n(\theta ,l_n) = \bigl |\widehat{\Phi }_{l_n}({\theta }) - {\Phi }_{l_n}(\theta )\bigr | \le 2 l_n \max _{0 \le h \le l_n} \bigl |\widehat{\phi }_h(\theta ) - {\phi }_h(\theta ) \bigr |. \end{aligned}$$

(3.16)

Let $T_n(\theta ) = n^{-1} \sum _{k = h + 1}^n Y_k(\theta ) Y_{k - h}(\theta ) - \mathbb {E}\bigl [Y_k(\theta ) Y_{k - h}(\theta )\bigr ]$. By the decomposition given in (3.15), it follows that it suffices to deal with $T_n(\theta )$ and $\overline{Y}_n^2(\theta ) - \mu ^2(\theta )$, the other (related) quantities can be dealt with in the same manner. Using $a^2 - b^2 = (a-b)(a+b)$ and Cauchy–Schwarz, it follows that $\bigl \Vert \overline{Y}_n^2(\theta ) - \mu ^2(\theta )\bigr \Vert _{p/2} \le \bigl \Vert \overline{Y}_n(\theta ) - \mu (\theta )\bigr \Vert _{p} \bigl \Vert \overline{Y}_n(\theta ) + \mu (\theta )\bigr \Vert _{p}$. Lemma 5.2 now implies that this is bounded by $\thicksim n^{-1/2}$, uniformly for $0 \le \theta \le 1$. Hence

$$\begin{aligned} \sup _{\theta \in \mathbf{I}^d}\bigl \Vert \overline{Y}_n^2(\theta ) - \mu ^2(\theta )\bigr \Vert _{p/2} \lesssim n^{-1/2}. \end{aligned}$$

(3.17)

Recall that $p^* = \min \{2,p/2\}$. Then an application of Lemma 5.2 yields

$$\begin{aligned} \bigl \Vert T_n(\theta )\bigr \Vert _{p/2} \lesssim n^{-1 + 1/p^*}\sup _{u \in \mathbf{I}}\sum _{i = - \infty }^0 \bigl \Vert \mathcal {P}_{i}\bigl (Y_0(u) Y_{-h}(u) \bigr )\bigr \Vert _{p/2} \lesssim n^{-1 + 1/p^*}. \end{aligned}$$

(3.18)

We deduce from (3.17) and (3.18) via the triangle and Markov’s inequality that

$$\begin{aligned} \nonumber \epsilon ^{p/2}\mathbb {P}\big (\bigl |\widehat{\phi }_h(\theta ) - \phi _h(\theta )\bigr | \ge \epsilon \bigr )&\lesssim \bigl \Vert T_n(\theta )\bigr \Vert _{p/2} + \bigl \Vert \overline{Y}_n^2(\theta ) - \mu ^2(\theta )\bigr \Vert _{p/2} \\ {}&\lesssim n^{-p/2 + p/2p^*} + n^{-p/4}. \end{aligned}$$

(3.19)

Hence it follows that

$$\begin{aligned} \nonumber \mathbb {P}\big (\max _{0 \le h \le l_n} \bigl |\widehat{\phi }_h(\theta ) - \phi _h(\theta )\bigr | \ge \epsilon \bigr )&\lesssim \epsilon ^{-p/2}\sum _{h = 0}^{l_n} \bigl (n^{-p/2 + p/2p^*} + n^{-p/4}\bigr ) \\ {}&\lesssim \epsilon ^{-p/2} l_n \bigl (n^{-p/2 + p/2p^*} + n^{-p/4}\bigr ). \end{aligned}$$

(3.20)

From condition (ii) (upper bound for $l_n$), we conclude that $\max _{0 \le h \le l_n} \bigl |\widehat{\phi }_h(\theta ) - \phi _h(\theta )\bigr | = \mathcal {O}_{\mathbb {P}}\bigl (l_n^{-1}\bigr )$, which yields

$$\begin{aligned} \bigl |\mathrm{IV}_n(\theta ,l_n)\bigr | = \mathcal {O}_{\mathbb {P}}\bigl (1\bigr ). \end{aligned}$$

(3.21)

Case $\mathrm{V}_n(\theta ,l_n)$: We are first interested in controlling the difference

$$\begin{aligned} \Delta _{n,h}(u,v) = \sum _{k = h + 1}^n A_k(u)A_{k - h}(u) - \sum _{k = h + 1}^n A_k(v)A_{k - h}(v), \quad \text {uniformly for } 0 \le u, v \le 1. \end{aligned}$$

(3.22)

Recall $B_{k,h}(u,v)$ and the decomposition in (3.15). If we consider the difference $\Delta _{n,h}(u,v)$, we need to deal with $\mathrm{VI}_{n,h}(u,v) = \sum _{k = h + 1}^n B_{k,h}(u,v)$, and expressions of the type $\mathrm{VII}_{n}(u,v) = \overline{Y}_{n}^2(u) - \overline{Y}_{n}^2(v)$. The latter can all be handled in the same manner; hence, we only consider $\mathrm{VII}_{n}(u,v)$ explicitly. Let us fist deal with $\mathrm{VI}_{n,h}(u,v)$. Recall that $p^* = \min \{2,p/2\}$. Then Lemma 5.1 implies

$$\begin{aligned} \biggl \Vert \sum _{k = h + 1}^{n}B_{k,h}(u,v)\biggr \Vert _{p/2} \lesssim n^{1/{p^*} } \sum _{i = - \infty }^0 \bigl \Vert \mathcal {P}_{i}\bigl (B_{0,h}(u,v)\bigr )\bigr \Vert _{p/2}. \end{aligned}$$

By adding and subtracting $X_{k-h}(u) X_k(v)$, the triangle and Jensens inequality imply that

$$\begin{aligned}&\bigl \Vert \mathcal {P}_{i}\bigl (B_{0,h}(u,v)\bigr )\bigr \Vert _{p/2} \le 2\bigl \Vert \bigl (Y_k(u) - Y_k(v)\bigr )Y_{k-h}(u)\bigr \Vert _{p/2}\\&\quad +\, 2\bigl \Vert \bigl (Y_{k-h}(u) - Y_{k-h}(v)\bigr )Y_{k}(v)\bigr \Vert _{p/2}, \end{aligned}$$

which by Cauchy–Schwarz is bounded by

$$\begin{aligned} 2\bigl \Vert Y_k(u) - Y_k(v)\bigr \Vert _{p} \bigl \Vert Y_{k-h}(u)\bigr \Vert _{p} + 2\bigl \Vert Y_{k-h}(u) - Y_{k-h}(v)\bigr \Vert _{p} \bigl \Vert Y_{k}(v)\bigr \Vert _{p}. \end{aligned}$$

Assumption 2.1 now implies that

$$\begin{aligned} \bigl \Vert \mathcal {P}_{i}\bigl (B_{0,h}(u,v)\bigr )\bigr \Vert _{p/2} \lesssim |u-v|_{}^{\beta }. \end{aligned}$$

(3.23)

On the other hand, by assumption we have $\sup _{u \in \mathbf{I}^d}\sum _{i = - \infty }^{-K}\bigl \Vert \mathcal {P}_i\bigl (Y_{k-h}(u) Y_k(u)\bigr )\bigr \Vert _{p/2} \lesssim K^{-\gamma }$. Hence setting $K^{-\gamma } \thicksim K |u-v|_{\infty }^{\beta }$, we obtain the choice $K \thicksim |u-v|_{}^{-\beta /(1 + \gamma )}$. It follows that

$$\begin{aligned} \biggl \Vert \sum _{k = h + 1}^{n}B_{k,h}(u,v)\biggr \Vert _{p/2} \lesssim n^{1/{p^*} } |u-v|_{}^{\beta \gamma /(1 + \gamma )}. \end{aligned}$$

(3.24)

Recall that by assumption $\beta \gamma p/2 > 1 + \gamma$. Combining (3.24) with the same arguments for establishing (3.9) in the proof of Theorem 2.2, one obtains that

$$\begin{aligned} \mathbb {P}\biggl (\sup _{\begin{array}{c} |u - v|_{} \le \delta ,\\ u,v \in \mathbf{I}^d \end{array}}\bigl |\sum _{k = h + 1}^{n}B_{k,h}(u,v)\bigr | \ge \eta \biggr ) \lesssim \eta ^{-p/2} n^{p/{2p^*} }, \quad \delta , \eta > 0. \end{aligned}$$

(3.25)

Employing this result, we deduce that

$$\begin{aligned} \nonumber \mathbb {P}\biggl (\max _{0 \le h \le l_n} \sup _{|\theta - v|_{}\le \delta }\bigl |\mathrm{VI}_{n,h}(\theta ,v)\bigr | \ge n \epsilon \biggr )&\le \sum _{h = 0}^{l_n} \mathbb {P}\biggl (\sup _{|\theta - v|_{}\le \delta } \sum _{k = h + 1}^n B_{k,h}(\theta ,v) \ge n \epsilon \biggr ) \\ {}&\lesssim \epsilon ^{-p/2} l_n n^{-p/2 + p/{2p^*}}. \end{aligned}$$

(3.26)

We now deal with $\mathrm{VII}_{n}(\theta ,v)$. We have the trivial expansion

$$\begin{aligned} \overline{Y}_{n}(u) \overline{Y}_{n}(u) - \overline{Y}_{n}(v) \overline{Y}_{n}(v) = \overline{Y}_{n}(u) \bigl (\overline{Y}_{n}(u) - \overline{Y}_{n}(v)\bigr ) + \overline{Y}_{n}(u) \bigl (\overline{Y}_{n}(u) - \overline{Y}_{n}(v)\bigr ). \end{aligned}$$

For random variables X, Y, we have $\mathbb {P}\bigl (|XY| \ge \epsilon \bigr ) \le \mathbb {P}\bigl (|X| \ge \sqrt{2 \epsilon }\bigr ) + \mathbb {P}\bigl (|Y| \ge \sqrt{2 \epsilon }\bigr )$; hence, it suffices to consider $\overline{Y}_{n}(u) - \overline{Y}_{n}(v)$ and $\overline{Y}_{n}(u)$ (resp. the counter part $\overline{Y}_{n}(u) - \overline{Y}_{n}(v)$ and $\overline{Y}_{n}(u)$) separately.

Since $\alpha \beta p > 1 + \alpha$ by assumption, we may use (3.9) in the proof of Theorem 2.2 together with the argument employed in the proof of Corollary 2.1. This implies that

$$\begin{aligned} \mathbb {P}\biggl (\sup _{u \in \mathbf{I}}\bigl |\overline{Y}_{n}(u)\bigr | \ge \sqrt{\epsilon } \biggr ) \lesssim \epsilon ^{-p/2} n^{-p/2}, \quad \epsilon > 0, \end{aligned}$$

(3.27)

where the above right-hand side does not depend on h. Similarly, one concludes that

$$\begin{aligned} \mathbb {P}\biggl (\sup _{\begin{array}{c} |u - v|_{} \le \delta ,\\ u,v \in \mathbf{I} \end{array}}\bigl |\overline{Y}_{n}(u) - \overline{Y}_{n}(v)\bigr | \ge \sqrt{\epsilon } \biggr ) \lesssim \epsilon ^{-p/2} n^{-p/2} \quad \delta , \epsilon > 0. \end{aligned}$$

(3.28)

Combining (3.27) and (3.28) and arguing as in (3.26), it follows that

$$\begin{aligned} \mathbb {P}\biggl (\max _{0 \le h \le l_n} \sup _{|\theta - v|_{}\le \delta }\bigl |\mathrm{VII}_{n}(\theta ,v)\bigr | \ge \epsilon \biggr ) \lesssim l_n \epsilon ^{-p/2} n^{-p/2}. \end{aligned}$$

(3.29)

Piecing together the bounds for $\mathrm{VI}_{n}(\theta ,v)$ and $\mathrm{VII}_{n}(\theta ,v)$, we deduce that for $0 < \epsilon \le 1$

$$\begin{aligned} \mathbb {P}\biggl (\max _{0 \le h \le l_n} \sup _{|\theta - v|_{} \le \delta }\bigl |\Delta _{n,h}(\theta ,v)\bigr | \ge \epsilon \biggr )&\le \sum _{h = 0}^{l_n} \mathbb {P}\biggl (\sup _{|\theta - v|_{} \le \delta }\bigl |\Delta _{n,h}(\theta ,v)\bigr | \ge \epsilon \biggr ) \\ \nonumber&\lesssim \epsilon ^{-p/2} l_n n^{-p/2 + p/{2p^*}} + l_n \epsilon ^{-p} n^{-p/2}. \end{aligned}$$

Setting $\epsilon = \mathcal {O}\bigl (l_n^{-1}\bigr )$, condition (ii) (upper bound for $l_n$) implies that the above is of magnitude $\mathcal {O}\bigl (1\bigr )$, hence by the triangle inequality we conclude

$$\begin{aligned}&V_n(\theta ,l_n) \le l_n \max _{0 \le h \le l_n} \biggl (\sup _{|\theta - v|_{}\le \delta }\bigl |VI_{n,h}(\theta ,u)\bigr | + \sup _{|\theta - v|_{}\le \delta }\bigl |VII_{n}(\theta ,u)\bigr |\biggr ) \nonumber \\&\quad = \mathcal {O}_{\mathbb {P}}\bigl (l_nl_n^{-1} \bigr )= \mathcal {O}_{\mathbb {P}}\bigl (1\bigr ). \end{aligned}$$

(3.30)

Piecing together the bound for $\mathrm{IV}_n(\theta ,l_n)$ in (3.21) and $\mathrm{V}_n(\theta ,l_n)$ in (3.30), the claim follows. $\square$

4 Proofs of Examples and Applications

Proof of Proposition 2.12

Note first that since $\bigl \{\epsilon _k\bigr \}_{k \in \mathbb {Z}}$ is ergodic, this is also true for $X_k(u) = g_u(\xi _k)$ (cf. Lemma 9.5  [32]). As underlying $\sigma$-algebra $\mathcal {F}_k$, we use from now on $\mathcal {F}_k = \mathcal {E}_k$. Next, we verify that (A1) is valid. Due to Kolmogorovs zero-one law, it follows that $\mathcal {E}_{- \infty } = \bigcap _{i \in \mathbb {N}} \mathcal {E}_{i}$ is the trivial $\sigma$-algebra $\bigl \{\emptyset , \Omega \bigr \}$. Hence $\mathbb {E}\bigl [X_k(u)\bigl |\mathcal {E}_{-\infty }\bigr ] = \mathbb {E}\bigl [X_k(u)\bigr ] = 0$ and the claim follows. In order to show that (A2) holds, note that by Jensens inequality $\bigl \Vert \mathcal {P}_0\bigl (X_k(u)\bigr )\bigr \Vert _{p} \le \bigl \Vert X_k(u) - X_k'(u)\bigr \Vert _p$, hence we obtain that

$$\begin{aligned} \sup _{u \in \mathbf{I}^d}\sum _{i = - \infty }^{-K} \bigl \Vert \mathcal {P}_i\bigl (X_k(u)\bigr )\bigr \Vert _{p} \lesssim K^{-\tau }. \end{aligned}$$

(4.1)

Setting $\alpha = \tau$, the claim follows. $\square$

Proof of Proposition 2.13

It suffices to verify the conditions of Proposition 2.9. As underlying $\sigma$-algebra $\mathcal {F}_k$, we use from now on $\mathcal {F}_k = \mathcal {E}_k$. By Proposition 2.12, we have that the choice $\alpha = \tau$ implies $\alpha \beta p > d(1 + \alpha )$, since we have $\tau \beta p/2 > d(1 + \tau )$. It thus remains to express $\gamma$ in terms of $\tau$. To this end, we will first derive a bound for $\bigl \Vert \mathcal {P}_0\bigl (X_k(u) X_{k-h}(u)\bigr )\bigr \Vert _{p/2}$. By Jensens, the triangle and Cauchy–Schwarz inequality we have

$$\begin{aligned}&\bigl \Vert \mathcal {P}_0\bigl (X_k(u) X_{k-h}(u)\bigr )\bigr \Vert _{p/2} \le \bigl \Vert \mathbb {E}\bigl [X_k(u) X_{k-h}(u) - X_k'(u) X_{k-h}'(u)\bigl |\mathcal {E}_0\bigr ]\bigr \Vert _{p/2} \\ {}&\le \bigl \Vert X_k(u) - X_k'(u)\bigr \Vert _{p} \bigl \Vert X_{k-h}(u)\bigr \Vert _p + \bigl \Vert \mathbb {E}\bigl [X_k'(u) \bigl (X_{k-h}(u) - X_{k-h}'(u)\bigr )\bigl |\mathcal {E}_0\bigr ]\bigr \Vert _{p/2}. \end{aligned}$$

Let $\mathcal {H}_k = \sigma \bigl (\mathcal {E}_{k}, \epsilon _0'\bigr )$. Then $\mathbb {E}\bigl [X_k'\bigl |\mathcal {H}_{k-h}\bigr ] = \mathbb {E}\bigl [X_k \bigl |\mathcal {E}_{k-h}\bigr ]$ if $k - h \ge 0$. Hence we deduce from the Jensen and Cauchy–Schwarz inequality that

$$\begin{aligned}&\bigl \Vert \mathbb {E}\bigl [X_k'(u) \bigl (X_{k-h}(u) - X_{k-h}'(u)\bigr )\bigl |\mathcal {E}_0\bigr ]\bigr \Vert _{p/2} \le \bigl \Vert \mathbb {E}\bigl [ X_k'(u)\bigl |\mathcal {H}_{k-h}\bigr ] \bigl (X_{k-h}(u)\\&\quad - X_{k-h}'(u)\bigr )\bigr \Vert _{p/2} \\&\le \bigl \Vert \mathbb {E}\bigl [X_k(u) \bigl |\mathcal {E}_{k-h}\bigr ]\bigr \Vert _p \bigl \Vert X_{k-h}(u) - X_{k-h}'(u)\bigr \Vert _p, \end{aligned}$$

if $k-h \ge 0$. Jensens inequality and Theorem 1 in  [45] yield that

$$\begin{aligned} \bigl \Vert \mathbb {E}\bigl [X_k(u) \bigl |\mathcal {E}_{k-h}\bigr ]\bigr \Vert _p^2 \lesssim \sum _{k = h}^{\infty }\bigl \Vert X_k(u) - X_k'(u) \bigr \Vert _p^2, \end{aligned}$$

hence we deduce from the above and Assumption 2.11 that

$$\begin{aligned} \nonumber \bigl \Vert \mathcal {P}_0\bigl (X_k(u) X_{k-h}(u)\bigr )\bigr \Vert _{p/2}&\lesssim \bigl \Vert X_k(u) - X_k'(u)\bigr \Vert _{p} + \sum _{l = h}^{\infty }\bigl \Vert X_l(u) - X_l'(u) \bigr \Vert _p\\ {}&\lesssim \bigl \Vert X_k(u) - X_k'(u)\bigr \Vert _{p} + h^{-\tau }. \end{aligned}$$

(4.2)

If $k - h \le -1$ then by Jensens and the Cauchy–Schwarz inequality we have

$$\begin{aligned} \bigl \Vert \mathcal {P}_0\bigl (X_k(u) X_{k-h}(u)\bigr )\bigr \Vert _{p/2} \le \bigl \Vert X_k(u) - X_k'(u)\bigr \Vert _p \bigl \Vert X_{k-h}(u)\bigr \Vert _p. \end{aligned}$$

(4.3)

Suppose now that $h > K$. Then by (4.2), (4.3) and Assumption 2.11, we have

$$\begin{aligned}&\sum _{k = K}^{\infty } \bigl \Vert \mathcal {P}_0\bigl (X_k(u) X_{k-h}(u)\bigr )\bigr \Vert _{p/2} = \sum _{k = K}^{h-1} \bigl \Vert \mathcal {P}_0\bigl (X_k(u) X_{k-h}(u)\bigr )\bigr \Vert _{p/2}\\&\quad + \sum _{k = h}^{\infty } \bigl \Vert \mathcal {P}_0\bigl (X_k(u) X_{k-h}(u)\bigr )\bigr \Vert _{p/2}\lesssim K^{-\tau } + h^{-\tau } \lesssim K^{-\tau } \end{aligned}$$

since $h > K$. Consider now the case where $h \le K$. By (4.2) we have

$$\begin{aligned} \sum _{k = K}^{\infty } \bigl \Vert \mathcal {P}_0\bigl (X_k(u) X_{k-h}(u)\bigr )\bigr \Vert _{p/2}&\lesssim K^{-\tau } + h^{-\tau }(K - h)^{-\tau } \wedge 1. \end{aligned}$$

The right-hand side is maximal if we choose $h = K/2 < K$, which amounts to $K^{-\tau } + K^{-\tau } \thicksim K^{-\tau }$. Hence we obtain the total bound

$$\begin{aligned} \sup _{h \ge 0}\sum _{k = K}^{\infty } \bigl \Vert \mathcal {P}_0\bigl (X_k(u) X_{k-h}(u)\bigr )\bigr \Vert _{p/2} \lesssim K^{-\tau }, \quad \text {uniformly for } u \in \mathbf{I}^d. \end{aligned}$$

(4.4)

Setting $\gamma = \tau$, we find that the conditions of Proposition 2.9 are satisfied, which completes the proof. $\square$

Proof of Theorem 2.16

Let $\overline{\psi }(\theta ) = \mathbb {E}[\psi (L_k,\theta )]$, Then (M1), the uniform consistency of $\widehat{\theta }_n$ and Theorem 2.7 yield that

$$\begin{aligned} \nonumber&n^{-1/2}\sup _{0 \le t \le 1}\bigl |\sum _{k = 1}^{\lfloor n t \rfloor } \bigl (\psi (L_k,\widehat{\theta }_{nt}) - \psi (L_k,\theta _0) - \overline{\psi }(\widehat{\theta }_{nt}) + \overline{\psi }(\theta _0)\bigr ) \bigr | \\&\le \mathcal {O}_{\mathbb {P}}(n^{-1/6}) + \sup _{n^{-2/3} \le t \le 1}\bigl |\sum _{k = 1}^{\lfloor n t \rfloor } \bigl (\psi (L_k,\widehat{\theta }_{nt}) - \psi (L_k,\theta _0) - \overline{\psi }(\widehat{\theta }_{nt}) + \overline{\psi }(\theta _0)\bigr ) \bigr | = \mathcal {O}_{\mathbb {P}}(1). \end{aligned}$$

(4.5)

Using this result, we may now proceed as in the proof of Theorem 5.21 in  [44]. $\square$

5 Some Auxiliary Results

The following Lemma is essentially a restatement of Theorem 1 in  [46], adapted to our setting.

Lemma 5.1

Grant Assumption 2.1 with $p > 1$. Let $p' = \min \{p,2\}$. Then for $1 \le m \le n$

$$\begin{aligned} \biggl \Vert \max _{0 \le k \le m}\bigl |\check{S}_k(u)\bigr |\biggr \Vert _p \lesssim m^{1/p'} n^{-1/2} \sum _{i = - \infty }^{0}\bigl \Vert \mathcal {P}_i\bigl (X_k(u)\bigr )\bigr \Vert _p. \end{aligned}$$

Proof of Lemma 5.1

Using Remark 3.1, the claim immediately follows from Theorem 1 in  [46]. $\square$

Lemma 5.2

Grant Assumption 2.1 with $p \ge 2$. Then for $0 \le t-h \le t \le 1$ we have

$$\begin{aligned} \biggl \Vert \sup _{t-h \le s \le t}\bigl |S_{nt}(u) - S_{ns}(u)\bigr |\biggr \Vert _p \lesssim \sqrt{|h|} \sum _{i = -\infty }^{0} \bigl \Vert \mathcal {P}_i\bigl (X_0(u)\bigr ) \bigr \Vert _p. \end{aligned}$$

Lemma 5.3

Grant Assumption 2.1 $p \ge 2$. Then for $0 \le u,v \le 1$ we have

$$\begin{aligned} \biggl \Vert \sup _{0 \le t \le 1}\bigl |S_{nt}(u) - S_{nt}(v)\bigr |\biggr \Vert _p \lesssim \sum _{i = -\infty }^{0} \bigl \Vert \mathcal {P}_i\bigl (X_0(u) - X_0(v)\bigr ) \bigr \Vert _p. \end{aligned}$$

Remark 5.4

Note that since the maximum values of $S_{nt}(u)$ are attained at the values $t = k/n$, $k = 0,\ldots ,n$, Lemma 5.2 and Lemma 5.3 remain valid if we replace $S_{nt}(u)$ with $\check{S}_{nt}(u)$.

Proof of Lemma 5.2

Suppose first that $\lfloor n t \rfloor - \lfloor n(t-h) \rfloor \ge 2$. Then

$$\begin{aligned}&S_{nt}(u) - S_{n(t-h}(u) \\ {}&= \frac{\sum _{k = \lfloor n(t-h) \rfloor + 2}^{\lfloor n t \rfloor }X_k(u)}{\sqrt{n}} + \frac{nt - \lfloor n t\rfloor }{\sqrt{n}}X_{\lfloor n t\rfloor + 1}(u)\\&\quad + \frac{1 - n(t-h) + \lfloor n (t-h)\rfloor }{\sqrt{n}}X_{\lfloor n (t-h)\rfloor + 1}(u). \end{aligned}$$

Let $M_{l}(u) = n^{-1/2}\sum _{k = \lfloor n(t-h) \rfloor + 2}^{l}X_k(u)$. Then an application of Lemma 5.1 yields that

$$\begin{aligned} \bigl \Vert \max _{\lfloor n (t-h)\rfloor + 2 \le l \le \lfloor nt \rfloor } \bigl |M_l(u)\bigr | \bigr \Vert _p \lesssim \sqrt{\frac{\lfloor nt \rfloor - \lfloor n (t-h)\rfloor - 1}{n}} \sum _{i = -\infty }^{0} \bigl \Vert \mathcal {P}_i\bigl (X_0(u)\bigr ) \bigr \Vert _p. \end{aligned}$$

(5.1)

Since $nx - \lfloor nx \rfloor \le 1$, $x \in [0,1]$, Assumption 2.1 and some computations yield

$$\begin{aligned}&\bigl \Vert \sup _{t-h \le s \le t}\bigl |S_{nt}(u) - S_{ns}(u)\bigr |\bigr \Vert _p \\ {}&\lesssim \biggl (\sqrt{\frac{\lfloor nt \rfloor - \lfloor n (t-h)\rfloor - 1}{\sqrt{n}}} + \sqrt{\frac{nt - \lfloor n t\rfloor }{n}} + \sqrt{\frac{1 - n(t-h) + \lfloor n (t-h)\rfloor }{n}}\biggr ), \end{aligned}$$

which by Jensens inequality is bounded by $\lesssim \sqrt{h}$. The case where $\lfloor n t \rfloor - \lfloor n(t-h) \rfloor < 2$ can be treated in the same way and hence the claim follows. $\square$

Proof of Lemma 5.3

Since $\{X_k(u) - X_k(v)\}_{k \in \mathbb {Z}}$ is a stationary sequence that clearly meets Assumption 2.1, the claim follows from Lemma 5.1. $\square$

Lemma 5.5

Grant Assumption 2.1 with $\alpha > 0$ and $p \ge 2$. Then

$$\begin{aligned} \mathbb {P}\bigl (\mathrm{III}(l_1,l_2,N) \ge \epsilon \bigr ) \lesssim \epsilon ^{-p} \, 2^{-(\alpha \beta p/(1 + \alpha ) - 1)N\tau _2 - L\alpha \beta p/(1 + \alpha )}, \end{aligned}$$

where $\mathrm{III}(l_1,l_2,N)$ is given in (3.5).

Proof of Lemma 5.5

It holds that

$$\begin{aligned} \mathbb {P}\bigl (\mathrm{III}(l_1,l_2,N) \ge \epsilon \bigr ) \le \sum _{j = 0}^{2^{\tau _2 N}} \mathbb {P}\biggl (\max _{i \in \mathcal {I}(\tau _1N)}\bigl |S_{nt_{i,l_1}}(u_{j+1,l_2}) - S_{nt_{i,l_1}}(u_{j,l_2})\bigr | \ge \epsilon \biggr ). \end{aligned}$$

(5.2)

Now $\{X_k(u) - X_{k}(v)\}_{k \in \mathbb {Z}}$, $0 \le u,v \le 1$, clearly is a stationary process that meets Assumption 2.1. Hence Markov’s inequality together with Lemma 5.3 yields

$$\begin{aligned} \mathbb {P}\bigl (\max _{i \in \mathcal {I}(\tau _1N)}\bigl |S_{nt_{i,l_1}}(u_{j+1,l_2})&- S_{nt}(u_{j,l_2})\bigr | \ge \epsilon \bigr ) \\ {}&\lesssim \epsilon ^{-p} \biggl (\sum _{i = -\infty }^{0} \bigl \Vert \mathcal {P}_i\bigl (X_0(u_{j+1,l_2}) - X_0(u_{j,l_2})\bigr ) \bigr \Vert _p \biggr )^p. \end{aligned}$$

Let $x = u_{j+1,l_2} - u_{j,l_2} = 2^{-\tau _2 N - L}$. By Assumption 2.1, we have $\sup _{u \in \mathbf{I}}\sum _{i = -\infty }^{-K}\bigl \Vert \mathcal {P}_i\bigl (X_0(u)\bigr )\bigr \Vert _p \lesssim K^{-\alpha }$. Equating $K^{-\alpha } = K x^{\beta }$ and solving for K, we obtain $K \thicksim 2^{(\tau _2 N + L)\beta /(1 + \alpha )}$. We thus conclude that

$$\begin{aligned} \sum _{i = -\infty }^{0} \bigl \Vert \mathcal {P}_i\bigl (X_0(u_{j+1,l_2}) - X_0(u_{j,l_2})\bigr ) \bigr \Vert _p \lesssim 2^{-(\tau _2 N + L)\alpha \beta /(1 + \alpha )}, \end{aligned}$$

(5.3)

which in turn implies

$$\begin{aligned} \mathbb {P}\bigl (\max _{i \in \mathcal {I}(\tau _1N)}\bigl |S_{nt_{i,l_1}}(u_{j+1,l_2}) - S_{nt_{i,l_1}}(u_{j,l_2})\bigr | \ge \epsilon \bigr )\lesssim \epsilon ^{-p} 2^{-(\tau _2 N + L)\alpha \beta p /(1 + \alpha )}. \end{aligned}$$

(5.4)

Using inequality (5.2), this gives the bound

$$\begin{aligned} \mathbb {P}\bigl (\mathrm{III}(l_1,l_2,N) \ge \epsilon \bigr ) \lesssim \epsilon ^{-p} \, 2^{-(\alpha \beta p/(1 + \alpha ) - 1)N\tau _2 - L\alpha \beta p/(1 + \alpha )}, \end{aligned}$$

(5.5)

which completes the proof. $\square$

Lemma 5.6

Grant Assumption 2.1 with $p > 2$. Then

$$\begin{aligned} \mathbb {P}\bigl (\mathrm{II}(l_1,l_2,N) \ge \epsilon \bigr ) \lesssim \epsilon ^{-p} 2^{-(p/2 -1)\tau _1N - p/2L + \tau _2 N}, \end{aligned}$$

where $\mathrm{II}(l_1,l_2,N)$ is given in (3.5).

Proof of Lemma 5.6

We will proceed similarly as in the proof of Lemma 5.5. Then it holds that

$$\begin{aligned} \mathbb {P}\bigl (\mathrm{II}(l_1,l_2,N) \ge \epsilon \bigr ) \le \sum _{i = 0}^{2^{\tau _1 N}}\sum _{j = 0}^{2^{\tau _2 N}} \mathbb {P}\bigl (\bigl |S_{ nt_{i+1,l_1}}(u_{j,l_2}) - S_{nt_{i,l_1}}(u_{j,l_2})\bigr | \ge \epsilon \bigr ). \end{aligned}$$

(5.6)

The Markov inequality together with Lemma 5.1 now yields

$$\begin{aligned}&\mathbb {P}\bigl (\bigl |S_{nt_{i+1,l_1}}(u_{j,l_2}) - S_{nt_{i,l_1}}(u_{j,l_2})\bigr | \ge \epsilon \bigr ) \lesssim \epsilon ^{-p}\\&\quad \times \biggl (\sqrt{t_{i+1,l_1} - t_{i,l_1}} \sum _{i = -\infty }^{0} \bigl \Vert \mathcal {P}_i\bigl (X_0(u_{j,l_2})\bigr ) \bigr \Vert _p \biggr )^p. \end{aligned}$$

Hence we deduce from Assumption 2.1 that

$$\begin{aligned} \sup _{j \in \mathcal {I}(\tau _2 N)}\mathbb {P}\bigl (\bigl |S_{nt_{i+1,l_1}}(u_{j,l_2}) - S_{nt_{i,l_1}}(u_{j,l_2})\bigr | \ge \epsilon \bigr ) \lesssim \epsilon ^{-p} 2^{-(\tau _1N + L)p/2}. \end{aligned}$$

(5.7)

Using inequality (5.6), this in turn gives the bound

$$\begin{aligned} \mathbb {P}\bigl (\mathrm{II}(l_1,l_2,N) \ge \epsilon \bigr ) \lesssim \epsilon ^{-p} 2^{-(p/2 -1)\tau _1N -p/2 L + \tau _2 N}, \end{aligned}$$

(5.8)

which completes the proof. $\square$

Lemma 5.7

Grant Assumption 2.1 with $\alpha = 0$ and $p \ge 2$. Let $\phi _{h}(u,v) = {Cov} \bigl (X_h(u),X_0(v)\bigr )$. Then $\Gamma (u,v) = \phi _0(u,v) + \sum _{h = 1}^{\infty }\bigl (\phi _{h}(u,v) + \phi _{h}(v,u)\bigr )$ is well defined, and

$$\begin{aligned} S_{nt}(u) \xrightarrow {fdd} \mathcal {G}_t(u), \end{aligned}$$

where $\{\mathcal {G}_t(u)\}_{0 \le t,u \le 1}$ is a Gaussian process with covariance $\mathbb {E}\bigl [\mathcal {G}_t(u)G_s(v)\bigr ] = t \wedge s\Gamma (u,v)$.

Proof of Lemma 5.7

First note that using the expansion $X_k(u) = \sum _{i = - \infty }^{k} \mathcal {P}_i\bigl (X_k(u)\bigr )$, we obtain by the orthogonality of the martingale increments

$$\begin{aligned} \mathbb {E}\bigl [X_k(u) X_0(v)\bigr ] = \sum _{i = - \infty }^0 \mathbb {E}\bigl [\mathcal {P}_i\bigl (X_k(u)\bigr )\mathcal {P}_i\bigl (X_0(v)\bigr )\bigr ]. \end{aligned}$$

(5.9)

Hence an application of the Cauchy–Schwarz inequality and Tonellis theorem yields

$$\begin{aligned}&\sum _{k = 0}^{\infty }\bigl |\mathbb {E}\bigl [X_k(u) X_0(v)\bigr ]\bigr | \le \sum _{k = 0}^{\infty }\sum _{i = - \infty }^0 \bigl \Vert \mathcal {P}_i\bigl (X_k(u)\bigr \Vert _2 \bigl \Vert \mathcal {P}_i\bigl (X_0(v)\bigr )\bigr \Vert _2\\&\quad \le \sup _{u \in \mathbf{I}}\biggl (\sum _{i = -\infty }^0 \bigl \Vert \mathcal {P}_i\bigl (X_0(u)\bigr )\bigr \Vert _2 \biggr )^2, \end{aligned}$$

and in a similar manner, we particularly obtain

$$\begin{aligned} \lim _{K \rightarrow \infty }\sum _{k = K}^{\infty }\bigl |\mathbb {E}\bigl [X_k(u) X_0(v)\bigr ]\bigr | = 0. \end{aligned}$$

(5.10)

We thus conclude that the function $\Gamma (u,v)$ is well defined. Similarly, one readily derives that

$$\begin{aligned} \mathbb {E}\bigl [S_{nt}(u)S_{nt}(v)\bigr ] \xrightarrow {n \rightarrow \infty } t \Gamma (u,v), \end{aligned}$$

and using (5.10) it follows more generally that

$$\begin{aligned} \mathbb {E}\bigl [S_{nt}(u)S_{ns}(v)\bigr ] \xrightarrow {n \rightarrow \infty } t\wedge s \Gamma (u,v). \end{aligned}$$

Since $\sup _{u \in \mathbf{I}} \sum _{i = -\infty }^{0} \bigl \Vert \mathcal {P}_{i}\bigl (X_0(u)\bigr )\bigr \Vert _p < \infty$ by assumption, the claim follows from Theorem 1 in  [28] and the Cramer–Wold device. $\square$

Lemma 5.8

Grant Assumption 2.1 with $\alpha = 0$ and $p \ge 2$. Then for fixed $u \in \mathbf{I}$, it holds that

$$\begin{aligned} \check{S}_{nt}(u) \xrightarrow {{\mathbf{D}}[\mathbf{I}]} \sqrt{\Gamma (u,u)}\mathcal {W}_t, \end{aligned}$$

where $\Gamma (u,u)$ is as in Lemma 5.7 and $\{\mathcal {W}_t\}_{0 \le t \le 1}$ is a Brownian motion.

Proof of Lemma 5.8

This follows from Proposition 8 in  [38] and Lemma 5.7. $\square$