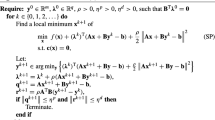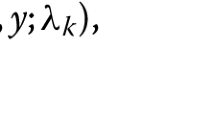On the Convergence Properties of a Majorized Alternating Direction Method of Multipliers for Linearly Constrained Convex Optimization Problems with Coupled Objective Functions

Abstract

In this paper, we establish the convergence properties for a majorized alternating direction method of multipliers for linearly constrained convex optimization problems, whose objectives contain coupled functions. Our convergence analysis relies on the generalized Mean-Value Theorem, which plays an important role to properly control the cross terms due to the presence of coupled objective functions. Our results, in particular, show that directly applying two-block alternating direction method of multipliers with a large step length of the golden ratio to the linearly constrained convex optimization problem with a quadratically coupled objective function is convergent under mild conditions. We also provide several iteration complexity results for the algorithm.

1 Introduction

In this paper, we discuss the convergence of the alternating direction method of multipliers (ADMM) for minimizing linearly constrained convex optimization problems with coupled objective functions. More precisely, the concerned objective function consists of two nonsmooth separable functions and a coupled smooth one. This type of problems arises frequently in many fields of applications, including signal processing, image restoration, machine learning, and etc.

One popular way to solve this class of problems is the well studied classic augmented Lagrangian method (ALM). The ALM minimizes the augmented Lagrangian function with respect to all the decision variables simultaneously, regardless of whether the objective function is coupled or not before updating the Lagrangian multiplier along the (sub-)gradient ascent direction of the dual problem. Numerically, however, to solve the inner subproblems exactly or approximately with a high accuracy in the ALM, which may not be necessary at early stages, can be a time consuming task due to the non-separable structure combined with the two nonsmooth functions in the augmented Lagrangian function.

When the objective function is separable, i.e., the coupled smooth function is not present, one can alleviate the numerical difficulty in the ALM by directly applying the ADMM. The global convergence of the ADMM with separable objective functions has been extensively studied in the literature; see, for examples, [1–5]. For a recent survey, see Eckstein and Yao [6]. Meanwhile, there are very few papers on the ADMM targeting the optimization problems with coupled objective functions except for the work of Hong et al. [7], where the authors studied a majorized multi-block ADMM for linearly constrained optimization problems with non-separable objectives. Hong et al. [7] provided a very general convergence analysis of their majorized ADMM, assuming that the step length is a sufficiently small fixed number or converging to zero, among other conditions. Since a large step length is almost always desired in practice, one needs to develop a new convergence theorem beyond the one in [7].

In this paper, we conduct a thorough convergence analysis on our proposed majorized ADMM (see Sect. 3) when it is applied to the optimization problems with non-separable objective functions. This majorized ADMM reduces to the classic ADMM when the coupled term is absent from the objective. By making use of nonsmooth analysis, especially the generalized Mean-Value Theorem, we are able to establish the global convergence and the iteration complexity for our majorized ADMM with the step length taken as large as 1.618. To the best of our knowledge, this is the first paper providing the convergence properties of the (majorized) ADMM with a large step length for solving linearly constrained convex optimization problems with coupled smooth objective functions.

The remaining parts of our paper are organized as follows. In next section, we state the targeted optimization problems and provide some preliminary results. Section 3 focuses on our framework of a majorized ADMM and two important inequalities for the convergence analysis. In Sect. 4, we prove the global convergence and several iteration complexity results of the proposed algorithm. We conclude our paper in the last section.

2 Preliminaries

Consider the following convex optimization problem:

(1)

where $p: \mathcal {U}\rightarrow ]-\infty ,\infty ]$, $q: \mathcal {V}\rightarrow ]-\infty ,\infty ]$ are two closed and proper convex functions (possibly nonsmooth), $\phi :\mathcal {U}\times \mathcal {V}\rightarrow ]-\infty , \infty [$ is a smooth and convex function, whose gradient mapping is Lipschitz continuous, $\mathcal {A}: \mathcal {X}\rightarrow \mathcal {U}$ and $\mathcal {B}:\mathcal {X}\rightarrow \mathcal {V}$ are two given linear operators, $c\in \mathcal {X}$ is a given vector, and $\mathcal {U},\mathcal {V}$ and $\mathcal {X}$ are three real finite dimensional Euclidean spaces, each equipped with an inner product $\langle \cdot ,\cdot \rangle$ and its induced norm $\Vert \cdot \Vert$.

One particular example of problem (1) is the following problem, whose objective is the sum of a quadratic function and a squared distance function to a closed and convex set:

$$\begin{aligned} \displaystyle \min _{u,v} \displaystyle \left[ \frac{1}{2}\bigg \langle \left( \begin{array}{c} u\\ v \end{array}\right) , \widetilde{\mathcal {Q}}\left( \begin{array}{c} u\\ v\end{array}\right) \bigg \rangle + \frac{\rho }{2}\bigg \Vert \left( \begin{array}{c} u\\ v \end{array}\right) -\varPi _{{\mathcal {K}_1}}\left( \begin{array}{c} u\\ v \end{array}\right) \bigg \Vert ^2\,\bigg |\, \mathcal {A}^*u + \mathcal {B}^*v = c, \quad u\in \mathcal {K}_2, ~v\in {\mathcal {K}_3}\right] ,\nonumber \\ \end{aligned}$$

(2)

where $\rho >0$ is a penalty parameter, $\widetilde{\mathcal {Q}}:\mathcal {U}\times \mathcal {V}\rightarrow \mathcal {U}\times \mathcal {V}$ is a self-ajoint positive semidefinite linear operator, $\mathcal {K}_1\subseteq \mathcal {U}\times \mathcal {V}$, $\mathcal {K}_2\subseteq \mathcal {U}$ and $\mathcal {K}_3\subseteq \mathcal {V}$ are closed and convex sets and $\varPi _{\mathcal {K}_1}(\cdot , \cdot )$ denotes the metric projection onto $\mathcal {K}_1$.

The augmented Lagrangian function for problem (1) associated with the parameter $\sigma >0$ is defined as

$$\begin{aligned} \mathcal {L}_\sigma (u,v;x):= & {} \theta (u,v) + \langle x, \mathcal {A}^*u + \mathcal {B}^*v - c\rangle +\frac{\sigma }{2}\Vert \mathcal {A}^*u\nonumber \\&+ \,\mathcal {B}^*v -c\Vert ^2, \quad \forall \, (u,v,x)\in \mathcal {U}\times \mathcal {V}\times \mathcal {X}. \end{aligned}$$

(3)

Even if $\phi (\cdot ,\cdot )$ is not separable, one can still apply the classic ADMM scheme for solving problem (1) as follows:

$$\begin{aligned} \begin{array}{ll} u^{k+1} =\displaystyle \arg \min _{u} \mathcal {L}_\sigma (u,v^k; x^k),\\ v^{k+1} = \displaystyle \arg \min _{v} \mathcal {L}_\sigma (u^{k+1},v; x^k), \\ x^{k+1} = x^k + \tau \sigma (\mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1} - c), \end{array} \end{aligned}$$

(4)

where $\tau >0$ is the step length. However, its convergence analysis is largely non-existent in the literature. One way to deal with the non-separability of $\phi (\cdot ,\cdot )$ is to introduce a new variable $w = \left( \begin{array}{c}u\\ v\end{array}\right)$. By letting ${\widetilde{\mathcal {A}}^*} = \left( \begin{array}{c} \mathcal {A}\\ {\mathcal {I}}_1\\ 0 \end{array}\right)$, ${\widetilde{\mathcal {B}}^*} = \left( \begin{array}{c}\mathcal {B}\\ 0\\ {\mathcal {I}}_2 \end{array}\right)$, $\widetilde{\mathcal {C}}^* = \left( \begin{array}{cc}0 &{} 0\\ -{\mathcal {I}}_1 &{} 0\\ 0 &{}-{\mathcal {I}}_2\end{array}\right)$ and $\tilde{c} = \left( \begin{array}{c} c\\ 0 \\ 0 \end{array}\right)$ with identity maps $\mathcal {I}_1:\mathcal {U}\rightarrow \mathcal {U}$ and $\mathcal {I}_2:\mathcal {V}\rightarrow \mathcal {V}$, we can rewrite the optimization problem (2) equivalently as

$$\begin{aligned} \displaystyle \min _{u,v,w} [ \tilde{\theta }(u,v,w): = p(u) + q(v) + \phi (w)\,|\, \widetilde{\mathcal {A}}^*u + \widetilde{\mathcal {B}}^*v + \widetilde{\mathcal {C}}^*w = \tilde{c}]. \end{aligned}$$

(5)

For given $\sigma >0$, the corresponding augmented Lagrangian function for problem (5) is

$$\begin{aligned} \widetilde{L}_\sigma (u,v,w; x) = \tilde{\theta }(u,v,w) + \langle x, \widetilde{\mathcal {A}}^*u + \widetilde{\mathcal {B}}^*v + \widetilde{\mathcal {C}}^*w - \tilde{c}\rangle + \displaystyle \frac{\sigma }{2}\Vert \widetilde{\mathcal {A}}^*u + \widetilde{\mathcal {B}}^*v + \widetilde{\mathcal {C}}^*w - \tilde{c}\Vert ^2, \end{aligned}$$

where $(u,v,w)\in \mathcal {U}\times \mathcal {V}\times (\mathcal {U}\times \mathcal {V})$ and $x\in \mathcal {X}$. Directly applying the three-block ADMM yields the following framework:

$$\begin{aligned} u^{k+1}= & {} \displaystyle \arg \min _{u} \widetilde{\mathcal {L}}_\sigma (u,v^k,w^k; x^k),\\ v^{k+1}= & {} \displaystyle \arg \min _{v} \widetilde{\mathcal {L}}_\sigma (u^{k+1},v,w^k; x^k),\\ w^{k+1}= & {} \displaystyle \arg \min _{w} \widetilde{\mathcal {L}}_\sigma (u^{k+1},v^{k+1},w; x^k),\\ x^{k+1}= & {} x^k + \tau \sigma (\widetilde{\mathcal {A}}^*u^{k+1} + \widetilde{\mathcal {B}}^*v^{k+1} + \widetilde{\mathcal {C}}^*w^{k+1} - \tilde{c}), \end{aligned}$$

where $\tau >0$ is the step length. Even though numerically the three-block ADMM works well for many applications, generally it is not a convergent algorithm even if $\tau$ is as small as $10^{-8}$, as shown in the counterexamples given by Chen et al. [8].

As is mentioned in the Introduction section, Hong et al. [7] proposed to combine the majorization technique within the ADMM framework. When specialized to the two-block case for problem (1), their algorithm works as follows:

$$\begin{aligned} u^{k+1}= & {} \displaystyle \arg \min _{u}\, [ p(u) +\langle x^k,\mathcal {A}^*u \rangle + \hat{h}_1(u; u^k, v^k)],\nonumber \\ v^{k+1}= & {} \displaystyle \arg \min _{v}\, [q(v) + \langle x^k, \mathcal {B}^*v\rangle +\hat{h}_2(v; u^{k+1}, v^k)], \nonumber \\ x^{k+1}= & {} x^k + \alpha _k\sigma (\mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1} - c), \end{aligned}$$

(6)

where $\hat{h}_{1}(u; u^k,v^k)$ and $\hat{h}_{2}(v; u^{k+1},v^k)$ are majorization functions of $\phi (u,v) + \frac{\sigma }{2}\Vert \mathcal {A}^*u + \mathcal {B}^*v - c\Vert ^2$ at $(u^k,v^k)$ and $(u^{k+1}, v^{k})$, respectively, and $\alpha _k >0$ is the step length.

Similar to Hong et al.’s work [7], our approach also relies on the majorization technique applied to the smooth coupled function $\phi (\cdot ,\cdot )$. One difference is that we majorize $\phi (u,v)$ at $(u^k,v^k)$ before the $(k+1)$th iteration instead of changing the majorization function based on $(u^{k+1},v^k)$ when updating $v^{k+1}$ as in (6). Interestingly, if $\phi (\cdot ,\cdot )$ merely consists of quadratically coupled functions and separable smooth functions, then our majorized ADMM is exactly the same as the one proposed by Hong et al. under a proper choice of the majorization functions. Moreover, for applications such as (2), a potential advantage of our method is that we only need to compute the projection $\varPi _{\mathcal {K}_1}(\cdot ,\cdot )$ once in order to compute $\nabla \phi (\cdot , \cdot )$ as a part of the majorization function within one iteration, while the procedure (6) needs to compute $\varPi _{\mathcal {K}_1}(\cdot ,\cdot )$ at two different points $(u^k,v^k)$ and $(u^{k+1}, v^k)$.

Next, we summarize several necessary results to be used in our subsequent analysis.

Denote $w:= \left( \begin{array}{c} u\\ v \end{array}\right)$. Since $\phi (\cdot )$ is assumed to be a convex function with a Lipschitz continuous gradient, $\nabla ^2 \phi (\cdot )$ exists almost everywhere. Thus, the following Clarke’s generalized Hessian at given $w\in \mathcal {U}\times \mathcal {V}$ is well defined [9]:

$$\begin{aligned} \partial ^2 \phi (w) := \text {conv}\left\{ \displaystyle \lim _{w^k\rightarrow w} \nabla ^2 \phi (w^k), \nabla ^2 \phi (w^k) \,\text {exists}\right\} , \end{aligned}$$

(7)

where “conv$\{S\}$” denotes the convex hull of a given set S. Note that for any $\mathcal {W}\in \partial ^2\phi (w)$ with $w\in \mathcal {U}\times \mathcal {V}$, $\mathcal {W}$ is self-adjoint and positive semidefinite. In [10], Hiriart-Urruty et al. provide a second order Mean-Value Theorem for $\phi$, which states that for any $w'$ and w in $\mathcal {U}\times \mathcal {V}$, there exists $z\in [w',w]$, which is the line segment connecting $w'$ and w, and $\mathcal {W}\in \partial ^2\phi (z)$ such that

$$\begin{aligned} \phi (w) := \phi (w') + \langle \nabla \phi (w') , w-w'\rangle +\frac{1}{2}\langle w-w', \mathcal {W}(w-w')\rangle \, . \end{aligned}$$

Since $\nabla \phi$ is assumed to be globally Lipschitz continuous, there exist two self-adjoint positive semidefinite linear operators $\mathcal {Q}$ and $\mathcal {H}: \mathcal {U}\times \mathcal {V}\rightarrow \mathcal {U}\times \mathcal {V}$ such that for any $w\in \mathcal {U}\times \mathcal {V}$,

$$\begin{aligned} \mathcal {Q} \preceq \mathcal {W} \preceq \mathcal {Q}+\mathcal {H}, \quad \forall \,\mathcal {W}\in \partial ^2 \phi (w). \end{aligned}$$

(8)

Here, $\mathcal {Q}$ and $\mathcal {H}$ are independent of w. Thus, for any $w, w'\in \mathcal {U}\times \mathcal {V}$, we have

$$\begin{aligned}&\phi (w)\ge \phi (w') + \langle \nabla \phi (w'), w - w' \rangle +\frac{1}{2}\Vert w'-w\Vert ^2_{\mathcal {Q}}, \end{aligned}$$

(9)

$$\begin{aligned}&\phi (w) \le \hat{\phi }(w; w'): = \phi (w') + \langle \nabla \phi (w'), w - w' \rangle +\frac{1}{2}\Vert w'-w\Vert ^2_{\mathcal {Q}+\mathcal {H}}. \end{aligned}$$

(10)

In this paper, we further assume that

$$\begin{aligned} \mathcal {H} = \text {Diag}\,(\mathcal {D}_1, \mathcal {D}_2), \end{aligned}$$

(11)

where $\mathcal {D}_1: \mathcal {U}\rightarrow \mathcal {U}$ and $\mathcal {D}_2: \mathcal {V}\rightarrow \mathcal {V}$ are two self-adjoint positive semidefinite linear operators. In fact, this kind of structure naturally appears in applications like (2), where the best possible lower bound of the generalized Hessian is $\widetilde{\mathcal {Q}}$ and the best possible upper bound of the generalized Hessian is $\widetilde{\mathcal {Q}}+\mathcal {I}$, where $\mathcal {I}: \mathcal {U}\times \mathcal {V}\rightarrow \mathcal {U}\times \mathcal {V}$ is the identity operator. For this case, the tightest estimation of $\mathcal {H}$ is $\mathcal {I}$, which is block diagonal. Since the coupled function $\phi (u,v)$ consists of two block variables u and v, the operators $\mathcal {Q}$ and $\mathcal {W}$ can be decomposed accordingly as $\mathcal {Q} = \begin{pmatrix} \mathcal {Q}_{11} &{} \mathcal {Q}_{12}\\ \mathcal {Q}_{12}^* &{} \mathcal {Q}_{22}\end{pmatrix}$ and $\mathcal {W} = \begin{pmatrix} \mathcal {W}_{11} &{} \mathcal {W}_{12}\\ \mathcal {W}_{12}^* &{} \mathcal {W}_{22}\end{pmatrix}$, where $\mathcal {W}_{11},~\mathcal {Q}_{11}: \mathcal {U}\rightarrow \mathcal {U}$ and $\mathcal {W}_{22}, ~\mathcal {Q}_{22}: \mathcal {V}\rightarrow \mathcal {V}$ are self-adjoint positive semidefinite linear operators, and $\mathcal {W}_{12}, ~\mathcal {Q}_{12}:\mathcal {V}\rightarrow \mathcal {U}$ are two linear mappings, whose adjoints are denoted by $\mathcal {W}_{12}^*$ and $\mathcal {Q}_{12}^*$, respectively. Denote $\eta \in [0,1]$ as a constant that satisfies

$$\begin{aligned} |\langle u, (\mathcal {W}_{12}-\mathcal {Q}_{12}) v\rangle |\le \frac{\eta }{2}(\Vert u\Vert ^2_{\mathcal {D}_1} + \Vert v\Vert ^2_{\mathcal {D}_2}), \quad \forall \,\mathcal {W}\in \partial ^2 \phi (u,v), ~u\in \mathcal {U}, ~v\in \mathcal {V}.\nonumber \\ \end{aligned}$$

(12)

Note that (12) always holds true for $\eta = 1$, according to the Cauchy-Schwarz inequality.

In order to prove the convergence of the proposed majorized ADMM, the following constraint qualification is needed:

Assumption 2.1

There exists $(\hat{u},\hat{v})\in {\mathrm{ri}}\;({\mathrm{dom}}(p)\times {\mathrm{dom}}(q))$ such that $\mathcal {A}^*\hat{u} + \mathcal {B}^*\hat{v} = c$.

Let $\partial p$ and $\partial q$ be the subdifferential mappings of p and q, respectively. Define the set-valued mapping $\mathcal {F}$ by

$$\begin{aligned} {{F}(u,v,x)}: = \nabla \phi (w) + \left( \begin{array}{cc} \partial p(u) + \mathcal {A}x\\ \partial q(v) + \mathcal {B}x \end{array}\right) , \quad \forall \, (u,v,x)\in \mathcal {U}\times \mathcal {V}\times \mathcal {X}. \end{aligned}$$

Under Assumption 2.1,¹ $(\bar{u}, \bar{v})$ is optimal to (1) if and only if there exists $\bar{x}\in \mathcal {X}$ such that the following Karush–Kuhn–Tucker (KKT) condition holds:

$$\begin{aligned} 0\in F(\bar{u},\bar{v},\bar{x}),\quad \mathcal {A}^*\bar{u} + \mathcal {B}^*\bar{v} = c, \end{aligned}$$

(13)

which is equivalent to the following variational inequality:

$$\begin{aligned}&(p({u}) + q({v}) ) -( p(\bar{u}) + q(\bar{v}) ) + \langle {w}-\bar{w},\nabla \phi (\bar{w})\rangle + \langle u - \bar{u}, \mathcal {A}\bar{x}\rangle + \langle v - \bar{v} , \mathcal {B}\bar{x}\rangle \nonumber \\&\quad - \langle x - \bar{x}, \mathcal {A}^*\bar{u} + \mathcal {B}^*\bar{v} - c\rangle \ge 0, \quad \forall \, (u,v,x)\in \mathcal {U}\times \mathcal {V}\times \mathcal {X}. \end{aligned}$$

(14)

Also recall that for any $\xi$, $\zeta$ in the same space and a self-adjoint positive semidefinite operator $\mathcal {G}$, it holds that

$$\begin{aligned} \langle \xi , \mathcal {G}\zeta \rangle = \frac{1}{2}\left( \Vert \xi \Vert _\mathcal {G}^2 + \Vert \zeta \Vert _\mathcal {G}^2 - \Vert \xi -\zeta \Vert _\mathcal {G}^2\right) = \frac{1}{2}\left( \Vert \xi +\zeta \Vert _\mathcal {G}^2 - \Vert \xi \Vert _\mathcal {G}^2 - \Vert \zeta \Vert _\mathcal {G}^2\right) .\nonumber \\ \end{aligned}$$

(15)

3 A Majorized Alternating Direction Method of Multipliers with Coupled Objective Functions

In this section, we will first present the framework of our majorized ADMM, and then prove two important inequalities that play an essential role for our convergence analysis.

Let $\sigma >0$. For given $w' = (u',v')\in \mathcal {U}\times \mathcal {V}$, define the following majorized augmented Lagrangian function associated with problem (1):

$$\begin{aligned} \widehat{\mathcal {L}}_\sigma (w; (x,w')):= p(u) + q(v) +\hat{\phi }(w; w') + \langle x,\mathcal {A}^*u + \mathcal {B}^*v - c\rangle +\displaystyle \frac{\sigma }{2}\Vert \mathcal {A}^*u + \mathcal {B}^*v - c\Vert ^2, \end{aligned}$$

where $(w,x) = (u,v,x)\in \mathcal {U}\times \mathcal {V}\times \mathcal {X}$, and the majorized function $\hat{\phi }$ is given by (10). Then, our proposed algorithm works as follows:

In order to simplify subsequent discussions, for $k = 0,1,2,\ldots$, define

$$\begin{aligned} \tilde{x}^{k+1}:= & {} x^k + \sigma \left( \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1} - c\right) ,\nonumber \\ \varXi _{k+1}:= & {} \left\| v^{k+1} - v^k\right\| ^2_{\mathcal {D}_2+ \mathcal {T}} + \eta \left\| u^{k+1} - u^k\right\| ^2_{\mathcal {D}_1},\nonumber \\ \varTheta _{k+1}:= & {} \left\| u^{k+1} - u^k\right\| ^2_{\mathcal {S} } + \left\| v^{k+1} - v^k\right\| ^2_{\mathcal {T}} + \frac{1}{4}\left\| w^{k+1}-w^k\right\| ^2_{\mathcal {Q}},\nonumber \\ \varGamma _{k+1}:= & {} \varTheta _{k+1}+ \min \left( \tau , 1+\tau - \tau ^2\right) \left\| v^{k+1} - v^k\right\| ^2_{\sigma \mathcal {B}\mathcal {B}^* } \nonumber \\&- \left\| u^{k+1} - u^k\right\| ^2_{\eta \mathcal {D}_1} - \left\| v^{k+1} - v^k\right\| ^2_{\eta \mathcal {D}_2 } \end{aligned}$$

(16)

and denote, for $(u,v,x)\in \mathcal {U}\times \mathcal {V}\times \mathcal {X}$,

$$\begin{aligned} \varPhi _{k}(u,v,x):= & {} \frac{1}{\tau \sigma }\left\| x^{k}-x\right\| ^2 + \left\| u^{k}-u\right\| ^2_{\mathcal {D}_1+ \mathcal {S}} + \left\| v^{k}-v\right\| ^2_{\mathcal {Q}_{22}+ \mathcal {D}_2 + \mathcal {T}}\nonumber \\&+\frac{1}{2}\left\| w^{k}-w\right\| ^2_\mathcal {Q} + \sigma \left\| \mathcal {A}^*u+\mathcal {B}^*v^k-c\right\| ^2,\nonumber \\ \varPsi _{k}(u,v,x):= & {} \varPhi _{k}(u,v,x)+\left\| w^{k}-w\right\| ^2_{\mathcal {Q}}\nonumber \\&+\max (1-\tau ,1-\tau ^{-1})\sigma \left\| \mathcal {A}^*u^{k} + \mathcal {B}^*v^{k} - c\right\| ^2. \end{aligned}$$

(17)

Proposition 3.1

Suppose that the solution set of problem (1) is nonempty and Assumption 2.1 holds. Assume that $\mathcal {S}$ and $\mathcal {T}$ are chosen such that the sequence $\{(u^k,v^k,x^k)\}$ is well defined. Then, the following conclusions hold:

• (i) For $\tau \in ]0,1]$, we have that for any $k\ge 0$ and $(u,v,x)\in \mathcal {U}\times \mathcal {V}\times \mathcal {X}$,

  $$\begin{aligned}&\displaystyle \left( p\left( u^{k+1}\right) + q\left( v^{k+1}\right) \right) -(p(u) + q(v) ) +\left\langle w^{k+1}-w,\nabla \phi (w)\right\rangle \nonumber \\&\quad + \left\langle u^{k+1} - u, \mathcal {A}x\right\rangle + \left\langle v^{k+1} - v , \mathcal {B}x\right\rangle \nonumber \\&\quad \displaystyle - \left\langle \tilde{x}^{k+1} - x , \mathcal {A}^*u + \mathcal {B}^*v - c\right\rangle + \frac{1}{2}\left( \varPhi _{k+1}({u}, {v}, {x}) - \varPhi _k({u}, {v}, {x})\right) \nonumber \\&\qquad \le \displaystyle -\frac{1}{2}\left( \varTheta _{k+1}+ \sigma \left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^k - c\right\| ^2 \right. \nonumber \\&\qquad \quad \left. +(1-\tau )\sigma \left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1} - c\right\| ^2 \right) . \end{aligned}$$

  (18)

• (ii) For $\tau \ge 0$, we have that for any $k\ge 1$ and $(u,v,x)\in \mathcal {U}\times \mathcal {V}\times \mathcal {X}$,

  $$\begin{aligned}&\left( p\left( u^{k+1}\right) + q\left( v^{k+1}\right) \right) -\left( p(u) + q(v) \right) +\left\langle w^{k+1}-w,\nabla \phi (w)\right\rangle \nonumber \\&\quad + \left\langle u^{k+1} - u, \mathcal {A}x\right\rangle + \left\langle v^{k+1} - v , \mathcal {B}x\right\rangle \nonumber \\&\quad \displaystyle - \left\langle \tilde{x}^{k+1} - x , \mathcal {A}^*u + \mathcal {B}^*v - c\right\rangle + \frac{1}{2}\left( \varPsi _{k+1}({u}, {v}, {x}) \right. \nonumber \\&\quad \left. + \varXi _{k+1} - \left( \varPsi _k({u}, {v}, {x}) +\varXi _k\right) \right) \nonumber \\&\qquad \le \displaystyle -\frac{1}{2}\left( \varGamma _{k+1} +\min (1,1+\tau ^{-1} - \tau )\sigma \left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1} - c\right\| ^2\right) .\nonumber \\ \end{aligned}$$

  (19)

Proof

In the majorized ADMM iteration scheme, the optimality condition for $(u^{k+1},v^{k+1})$ is

$$\begin{aligned} 0\in & {} \partial p\left( u^{k+1}\right) + \nabla _u \phi \left( w^k\right) + \mathcal {A}\tilde{x}^{k+1} \nonumber \\&\quad + \left( \mathcal {Q}_{11} + \mathcal {D}_1+ \mathcal {S}\right) (u^{k+1} - u^k) + \sigma \mathcal {A}\mathcal {B}^*\left( v^k - v^{k+1}\right) ,\nonumber \\ 0\in & {} \partial q\left( v^{k+1}\right) + \nabla _v \phi (w^k) + \mathcal {B}\tilde{x}^{k+1} \nonumber \\&\quad + \left( \mathcal {Q}_{22} + \mathcal {D}_2+\mathcal {T}\right) \left( v^{k+1} - v^k\right) + \mathcal {Q}_{12}^*\left( u^{k+1} - u^k\right) , \end{aligned}$$

(20)

which can be reformulated as

$$\begin{aligned} \begin{array}{ll} &{}-\mathcal {A}\tilde{x}^{k+1} -\nabla _u \phi \left( w^k\right) - \left( \mathcal {Q}_{11} + \mathcal {D}_1+ \mathcal {S}\right) \left( u^{k+1} - u^k\right) -\sigma \mathcal {A}\mathcal {B}^*\left( v^k- v^{k+1}\right) \in \partial p(u^{k+1}),\\ &{}-\mathcal {B}\tilde{x}^{k+1} - \nabla _v \phi \left( w^k\right) -\left( \mathcal {Q}_{22} + \mathcal {D}_2 + \mathcal {T}\right) \left( v^{k+1} - v^k\right) - \mathcal {Q}_{12}^*\left( u^{k+1} - u^k\right) \in \partial q\left( v^{k+1}\right) . \end{array}\nonumber \\ \end{aligned}$$

(21)

Therefore, by the convexity of p and q, we have that for any $u\in \mathcal {U}$ and $v\in \mathcal {V}$,

$$\begin{aligned} p(u)\ge & {} p\left( u^{k+1}\right) - \left\langle u - u^{k+1},\mathcal {A}\tilde{x}^{k+1} +\nabla _u \phi \left( w^k\right) + \left( \mathcal {Q}_{11}+\mathcal {D}_1+ \mathcal {S}\right) \left( u^{k+1} - u^k\right) \right. \nonumber \\&\quad \left. +\,\sigma \mathcal {A}\mathcal {B}^*\left( v^k - v^{k+1}\right) \right\rangle ,\nonumber \\ q(v)\ge & {} q\left( v^{k+1}\right) - \left\langle v - v^{k+1}, \mathcal {B}\tilde{x}^{k+1} + \nabla _v \phi \left( w^k\right) +\left( \mathcal {Q}_{22} + \mathcal {D}_2 + \mathcal {T}\right) \left( v^{k+1}-v^k\right) \right. \nonumber \\&\quad \left. +\,\mathcal {Q}^*_{12}\left( u^{k+1}- u^{k}\right) \right\rangle . \end{aligned}$$

(22)

By taking $(w, w') = ({w}, w^k)$ and $(w^{k+1}, {w})$ in (9), and $(w, w') = (w^{k+1}, w^k)$ in (10), we know that

$$\begin{aligned} \begin{array}{rl} \phi ({w}) &{}\ge \phi \left( w^k\right) + \left\langle \nabla \phi \left( w^k\right) , {w} - w^k\right\rangle + \frac{1}{2}\left\| {w} - w^k\right\| ^2_{\mathcal {Q}},\\ \phi \left( w^{k+1}\right) &{}\ge \phi ({w}) + \left\langle \nabla \phi ({w}),w^{k+1} - {w}\right\rangle + \frac{1}{2}\left\| w^{k+1} - {w}\right\| ^2_{\mathcal {Q}},\\ \phi \left( w^{k+1}\right) &{}\le \phi \left( w^{k}\right) + \left\langle \nabla \phi \left( w^{k}\right) , w^{k+1} - w^k\right\rangle +\frac{1}{2}\left\| w^{k+1} - w^k\right\| ^2_{\mathcal {Q} +\mathcal {H}}. \end{array} \end{aligned}$$

(23)

Putting the above three inequalities together, we get

$$\begin{aligned} \left\langle \nabla \phi \left( w^k\right) - \nabla \phi ({w}), w^{k+1}-w\right\rangle\ge & {} \frac{1}{2}\left( \left\| w^k-w\right\| ^2_{\mathcal {Q}}+\left\| w^{k+1}-w\right\| ^2_{\mathcal {Q}}\right) \nonumber \\&\quad -\frac{1}{2}\left\| w^{k+1} - w^k\right\| ^2_{\mathcal {Q} +\mathcal {H}}. \end{aligned}$$

(24)

Substituting (24) into the sum of the two inequalities in (22) and by the assumption (11) and the identity (15), we can further obtain that

$$\begin{aligned}&\left( p\left( u^{k+1}\right) + q\left( v^{k+1}\right) \right) -(p(u) + q(v) ) +\left\langle w^{k+1}-w,\nabla \phi (w)\right\rangle + \left\langle u^{k+1} - u, \mathcal {A}x\right\rangle \nonumber \\&\quad + \left\langle v^{k+1} - v , \mathcal {B}x\right\rangle - \left\langle \tilde{x}^{k+1} - x , \mathcal {A}^*u + \mathcal {B}^*v - c\right\rangle \nonumber \\&\qquad \le \sigma \left\langle \mathcal {B}^*(v^{k+1} - v^k),\mathcal {A}^*(u^{k+1}-u)\right\rangle +\left\langle v^{k+1}-v^k, \mathcal {Q}_{12}^*(u^{k+1} - u)\right\rangle \nonumber \\&\qquad \quad -\frac{1}{2}\left( \left\| u^{k+1} - u^k\right\| _{\mathcal {S}}^2+ \left\| u^{k+1} - u\right\| _{\mathcal {D}_1+\mathcal {S}}^2 - \left\| u^k - u\right\| _{\mathcal {D}_1+\mathcal {S}}^2\right) \nonumber \\&\qquad \quad -\displaystyle \frac{1}{2}\left( \left\| v^{k+1} - v^k\right\| _{ \mathcal {T}}^2 + \left\| v^{k+1}- v\right\| _{\mathcal {D}_2+ \mathcal {T}}^2 - \left\| v^k -v\right\| ^2_{\mathcal {D}_2 + \mathcal {T}}\right) \nonumber \\&\qquad \quad - \displaystyle \frac{1}{2\tau \sigma }\left( \left\| x^{k+1} - x^k\right\| ^2 + \left\| x^{k+1} - x\right\| ^2 - \left\| x^k - x\right\| ^2\right) \nonumber \\&\qquad \quad - (1-\tau )\sigma \left\| \mathcal {A}^*u^{k+1}+ \mathcal {B}^*v^{k+1} - c\right\| ^2- \left\| w^{k+1}-w\right\| ^2_{\mathcal {Q}}.\nonumber \\ \end{aligned}$$

(25)

(i) Assume that $\tau \in ]0,1]$. Then, we get that

$$\begin{aligned}&\left\langle {v^{k+1} - v^{k}}{\mathcal {Q}_{12}^*\left( u^{k+1}-u\right) }\right\rangle \nonumber \\&\quad = \left\langle \left( \begin{array}{c} 0\\ v^{k+1} - v^{k}\end{array}\right) ,\,\mathcal {Q}( w^{k+1}-w ) \right\rangle \nonumber \\&\qquad - \left\langle \mathcal {Q}_{22}\left( v^{k+1}- v^{k}\right) , v^{k+1}-v \right\rangle \nonumber \\&\quad \le \displaystyle \frac{1}{2}\left( \left\| v^{k+1} - v^k\right\| ^2_{\mathcal {Q}_{22}} + \left\| w^{k+1}-w\right\| ^2_{\mathcal {Q}}\right) \nonumber \\&\qquad - \frac{1}{2}\left( \left\| v^{k+1} - v^k\right\| ^2_{\mathcal {Q}_{22}} + \left\| v^{k+1}-v\right\| ^2_{\mathcal {Q}_{22}} - \left\| v^k-v\right\| ^2_{\mathcal {Q}_{22}}\right) \nonumber \\&\quad =\displaystyle \frac{1}{2}\left\| w^{k+1}-w\right\| ^2_{\mathcal {Q}} + \frac{1}{2}\left( \left\| v^{k}-v\right\| ^2_{\mathcal {Q}_{22}} - \left\| v^{k+1}-v\right\| ^2_{\mathcal {Q}_{22}}\right) , \end{aligned}$$

(26)

where the inequality is obtained by the Cauchy-Schwarz inequality. By some simple manipulations we can also see that

$$\begin{aligned}&\sigma \left\langle \mathcal {B}^*\left( v^{k+1} - v^k\right) , \mathcal {A}^*\left( u^{k+1}-u\right) \right\rangle \nonumber \\&\quad = \displaystyle \frac{\sigma }{2}\left( \left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1}- c\right\| ^2 - \left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^k - c\right\| ^2\right) \nonumber \\&\qquad \displaystyle \quad +\frac{\sigma }{2}\left( \left\| \mathcal {A}^*u + \mathcal {B}^*v^k-c\right\| ^2 -\left\| \mathcal {A}^*u + \mathcal {B}^*v^{k+1}-c\right\| ^2\right) . \end{aligned}$$

(27)

Finally, by substituting (26) and (27) into (25) and recalling the definition of $\varPhi _{k+1}(\cdot , \cdot , \cdot )$ and $\varTheta _{k+1}$ in (16) and (17), we have that

$$\begin{aligned}&\left( p\left( u^{k+1}\right) + q\left( v^{k+1}\right) \right) -(p(u) + q(v) ) +\left\langle w^{k+1}-w,\nabla \phi (w)\right\rangle + \left\langle u^{k+1} - u, \mathcal {A}x\right\rangle \\&\quad + \left\langle v^{k+1} - v , \mathcal {B}x\right\rangle \displaystyle - \left\langle \tilde{x}^{k+1} - x , \mathcal {A}^*u + \mathcal {B}^*v - c\right\rangle + \frac{1}{2}\left( \varPhi _{k+1}({u}, {v}, {x}) - \varPhi _k({u}, {v}, {x})\right) \\&\qquad \le \displaystyle - \frac{1}{2} \left( \left\| u^{k+1} - u^k\right\| ^2_{\mathcal {S} } + \left\| v^{k+1} - v^k\right\| ^2_{\mathcal {T}} + \frac{1}{2}\left\| w^{k+1}-w\right\| ^2_{\mathcal {Q}}+\frac{1}{2} \left\| w^k-w\right\| ^2_{\mathcal {Q}}\right. \\&\qquad \quad \left. + \sigma \left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^k - c\right\| ^2 +(1-\tau )\sigma \left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1} - c\right\| ^2\right) \\&\qquad \le \displaystyle - \frac{1}{2}\left( \varTheta _{k+1} + \sigma \left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^k - c\right\| ^2+ (1-\tau )\sigma \left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1} - c\right\| ^2\right) , \end{aligned}$$

where the last inequality comes from the fact that $\frac{1}{2}\Vert w^{k+1}-w\Vert ^2_{\mathcal {Q}} + \frac{1}{2}\Vert w^{k}-w\Vert _{\mathcal {Q}}^2\ge \frac{1}{4}\Vert w^{k+1} - w^k\Vert ^2_{\mathcal {Q}}.$ This completes the proof of part (i).

(ii) Assume that $\tau \ge 0$. In this part, first we shall estimate the following term

$$\begin{aligned} \sigma \left\langle \mathcal {B}^*\left( v^{k+1} - v^k\right) , \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1} - c\right\rangle + \left\langle v^{k+1} - v^k, \mathcal {Q}_{12}^*\left( u^{k+1}-u\right) + \mathcal {Q}_{22}\left( v^{k+1}-v\right) \right\rangle . \end{aligned}$$

It follows from (21) that

$$\begin{aligned}&-\mathcal {B}\tilde{x}^{k+1} - \nabla _v \phi \left( w^k\right) -\left( \mathcal {Q}_{22}+\mathcal {D}_2 + \mathcal {T}\right) \left( v^{k+1} - v^k\right) - \mathcal {Q}_{12}^*\left( u^{k+1} - u^k\right) \in \partial q\left( v^{k+1}\right) ,\nonumber \\&-\mathcal {B}\tilde{x}^{k} - \nabla _v \phi \left( w^{k-1}\right) -\left( \mathcal {Q}_{22}+\mathcal {D}_2 + \mathcal {T}\right) \left( v^{k} - v^{k-1}\right) -\mathcal {Q}_{12}^*\left( u^k-u^{k-1}\right) \in \partial q\left( v^{k}\right) .\nonumber \\ \end{aligned}$$

(28)

Since $\nabla \phi$ is globally Lipschitz continuous, it is known from Clarke’s Mean-Value Theorem [9, Proposition 2.6.5] that there exists a self-adjoint and positive semidefinite operator $\mathcal {W}^k \in \text {conv}\{\partial ^2\phi ([w^{k-1}, w^k])\}$ such that

$$\begin{aligned} \nabla \phi \left( w^k\right) - \nabla \phi \left( w^{k-1}\right) = \mathcal {W}^k\left( w^k-w^{k-1}\right) , \end{aligned}$$

where the set $\text {conv}\{\partial ^2\phi [w^{k-1},w^k]\}$ denotes the convex hull of all points $\mathcal {W}\in \partial ^2\phi (z)$ for any $z\in [w^{k-1},w^k]$. Denote $\mathcal {W}^k: = \begin{pmatrix} \mathcal {W}_{11}^k &{} \mathcal {W}_{12}^k \\ (\mathcal {W}_{12}^k)^* &{} \mathcal {W}_{22}^k\end{pmatrix}$, where $\mathcal {W}_{11}^k: \mathcal {U}\rightarrow \mathcal {U}$, $\mathcal {W}_{22}^k: \mathcal {V}\rightarrow \mathcal {V}$ are self-adjoint positive semidefinite operators and $\mathcal {W}_{12}^k: \mathcal {U}\rightarrow \mathcal {V}$ is a linear operator. By using (28) and the monotonicity of $\partial q(\cdot )$, we obtain that

$$\begin{aligned}&-\left\langle \mathcal {B}\left( \tilde{x}^{k+1} - \tilde{x}^k\right) , v^{k+1} - v^k\right\rangle -\left\langle \mathcal {Q}_{22}\left( v^{k+1} - v^{k}\right) +\mathcal {Q}_{12}^* \left( u^{k+1} - u^{k}\right) , v^{k+1} - v^k\right\rangle \\&\quad \ge \left\langle \nabla _v\phi \left( w^k\right) - \nabla _v \phi \left( w^{k-1}\right) , v^{k+1} -v^k\right\rangle -\left\langle \left( \mathcal {Q}_{22} + \mathcal {D}_2+ \mathcal {T}\right) \left( v^{k} - v^{k-1}\right) , v^{k+1} - v^k\right\rangle \\&\qquad + \left\| v^{k+1} - v^k\right\| ^2_{\mathcal {T}+\mathcal {D}_2} -\left\langle u^k-u^{k-1}, \mathcal {Q}_{12}\left( v^{k+1} - v^k\right) \right\rangle \\&\quad = \left\langle u^k-u^{k-1},\left( \mathcal {W}_{12}^k-\mathcal {Q}_{12}\right) \left( v^{k+1} - v^k\right) \right\rangle \\&\qquad -\left\langle \left( \mathcal {Q}_{22}+ \mathcal {D}_2+\mathcal {T} - \mathcal {W}_{22}^k\right) \left( v^{k} - v^{k-1}\right) , v^{k+1} - v^k\right\rangle + \left\| v^{k+1} - v^k\right\| ^2_{\mathcal {T}+\mathcal {D}_2} \\&\quad \ge \displaystyle -\frac{\eta }{2}\left( \left\| u^k - u^{k-1}\right\| ^2_{\mathcal {D}_1} + \left\| v^{k+1} - v^k\right\| ^2_{\mathcal {D}_2}\right) \\&\qquad - \frac{1}{2}\left( \left\| v^{k+1} - v^k\right\| ^2_{\mathcal {T}+ \mathcal {D}_2} + \left\| v^k-v^{k-1}\right\| ^2_{\mathcal {T}+ \mathcal {D}_2}\right) +\left\| v^{k+1} - v^k\right\| ^2_{\mathcal {T}+\mathcal {D}_2}\\&\quad = \displaystyle \frac{1}{2}\left\| v^{k+1} - v^k\right\| ^2_{\mathcal {T} +(1-\eta )\mathcal {D}_2} - \frac{1}{2}\left\| v^k - v^{k-1}\right\| ^2_{\mathcal {T} +\mathcal {D}_2} - \frac{\eta }{2}\left\| u^k-u^{k-1}\right\| ^2_{\mathcal {D}_1}, \end{aligned}$$

where the second inequality is obtained from (12) and the fact that $\mathcal {W}_{22}^k\succeq \mathcal {Q}_{22}$. Therefore, in light of $\mu _{k+1} = (1-\tau )\sigma \langle \mathcal {B}^*(v^{k+1} - v^k), \mathcal {A}^*u^{k} + \mathcal {B}^*v^{k} - c\rangle ,$ we can estimate the cross term

$$\begin{aligned}&\sigma \left\langle \mathcal {B}^*\left( v^{k+1} - v^k\right) , \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1} - c\right\rangle \nonumber \\&\quad + \left\langle \mathcal {Q}_{12}^*\left( u^{k+1}-u\right) + \mathcal {Q}_{22}\left( v^{k+1}-v\right) , v^{k+1} - v^k\right\rangle \nonumber \\&\qquad = (1-\tau )\sigma \left\langle \mathcal {B}^*\left( v^{k+1} - v^k\right) , \mathcal {A}^*u^{k} + \mathcal {B}^*v^{k} - c\right\rangle \nonumber \\&\qquad \quad + \left\langle \mathcal {B}^*\left( v^{k+1} - v^k\right) , \tilde{x}^{k+1}-\tilde{x}^{k}\right\rangle \nonumber \\&\qquad \quad + \left\langle \mathcal {Q}_{12}^*\left( u^k-u\right) + \mathcal {Q}_{22}\left( v^k-v\right) , v^{k+1} - v^k\right\rangle \nonumber \\&\quad \qquad + \langle \mathcal {Q}_{12}^*\left( u^{k+1} - u^k\right) +\mathcal {Q}_{22}\left( v^{k+1} - v^k\right) , v^{k+1} - v^k\rangle \nonumber \\&\qquad \le \displaystyle \mu _{k+1} + \frac{1}{2}\left( \left\| w^k-w\right\| ^2_{\mathcal {Q}} + \left\| v^{k+1} - v^k\right\| ^2_{\mathcal {Q}_{22}}\right) \nonumber \\&\qquad \quad - \frac{1}{2}\left\| v^{k+1} - v^k\right\| ^2_{\mathcal {T} +(1-\eta )\mathcal {D}_2} + \frac{1}{2}\left\| v^k - v^{k-1}\right\| ^2_{\mathcal {T} + \mathcal {D}_2}\nonumber \\&\qquad \quad + \displaystyle \frac{\eta }{2}\left\| u^k-u^{k-1}\right\| ^2_{\mathcal {D}_1}. \end{aligned}$$

(29)

Finally, by the Cauchy-Schwarz inequality we know that

$$\begin{aligned} \mu _{k+1} \le \left\{ \begin{array}{ll} \displaystyle \frac{1}{2}(1-\tau )\sigma \left( \left\| \mathcal {B}^*\left( v^{k+1} - v^k\right) \right\| ^2 + \left\| \mathcal {A}^*u^k + \mathcal {B}^*v^k - c\right\| ^2\right) , \quad \tau \in ]0,1],\\ \displaystyle \frac{1}{2}(\tau -1)\sigma \left( \tau \left\| \mathcal {B}^*\left( v^{k+1} - v^k\right) \right\| ^2 +\tau ^{-1} \left\| \mathcal {A}^*u^k + \mathcal {B}^*v^k - c\right\| ^2\right) , \quad \tau >1. \end{array}\right. \end{aligned}$$

(30)

Substituting (29) and (30) into (25) and by some manipulations, we can obtain (19). This completes the proof of part (ii). $\square$

4 Convergence Analysis

With all the preparations given in the previous sections, we can now discuss the main convergence results of our paper.

4.1 The Global Convergence

First we prove that under mild conditions, the iteration sequence $\{(u^k, v^k, x^k)\}$ generated by the majorized ADMM with $\tau \in ]0,\frac{1 +\sqrt{5}}{2}[$ converges to an optimal solution of problem (1) and its dual.

Let $\bar{w} = (\bar{u}, \bar{v})\in \mathcal {U}\times \mathcal {V}$ be an optimal solution of (1) and $\bar{x}\in \mathcal {X}$ be the corresponding optimal multiplier. For $k = 0,1,2,\ldots$, define

$$\begin{aligned}\begin{array}{cc} u_e^k := u^k - \bar{u}, \quad v_e^k := v^k - \bar{v}, \quad w_e^k := w^k - \bar{w}, \quad x_e^k := x^k - \bar{x}. \end{array} \end{aligned}$$

Theorem 4.1

Suppose that the solution set of (1) is nonempty and Assumption 2.1 holds. Assume that $\mathcal {S}$ and $\mathcal {T}$ are chosen such that

$$\begin{aligned} \mathcal {Q}_{11} + \sigma \mathcal {A}\mathcal {A}^*+\mathcal {S}\succ 0\quad \text {and} \quad \mathcal {Q}_{22} + \sigma \mathcal {B}\mathcal {B}^*+\mathcal {T}\succ 0. \end{aligned}$$

(i) Assume that $\tau \in ]0,1]$. If for any $w = \left( \begin{array}{c}u\\ v\end{array}\right) \in \mathcal {U}\times \mathcal {V}$, it holds that

$$\begin{aligned} \langle w, [\mathcal {Q}+\text {Diag}\,(\mathcal {S}+(1-\tau )\sigma \mathcal {A}\mathcal {A}^*, \mathcal {T} + (1-\tau )\sigma \mathcal {B}\mathcal {B}^*)]w\rangle = 0 \Rightarrow \Vert u\Vert \Vert v\Vert = 0,\nonumber \\ \end{aligned}$$

(31)

then the generated sequence $\{(u^k, v^k)\}$ converges to an optimal solution of (1), and $\{x^k\}$ converges to the corresponding optimal multiplier.

(ii) Assume that $\tau \in ]0, \frac{1+\sqrt{5}}{2}[$. Under the conditions that

$$\begin{aligned} \begin{array}{cc} \displaystyle \mathcal {M}: = \frac{1}{4}\mathcal {Q} + \text {Diag}\,(\mathcal {S}-\eta \mathcal {D}_1, ~\mathcal {T} -\eta \mathcal {D}_2 )\succeq 0,\\ \displaystyle \frac{1}{4} \mathcal {Q}_{11}+\mathcal {S} + \sigma \mathcal {A}\mathcal {A}^* - \eta \mathcal {D}_1\succ 0,\quad \frac{1}{4}\mathcal {Q}_{22}+\mathcal {T} + \sigma \mathcal {B}\mathcal {B}^* - \eta \mathcal {D}_2\succ 0, \end{array} \end{aligned}$$

(32)

and for any $w = \left( \begin{array}{c}u\\ v\end{array}\right) \in \mathcal {U}\times \mathcal {V}$, it holds that

$$\begin{aligned} \langle w, [\mathcal {M}+ \sigma \text {Diag}\,(\mathcal {A}\mathcal {A}^*, \mathcal {B}\mathcal {B}^* )]w\rangle = 0 \Rightarrow \Vert u\Vert \Vert v\Vert = 0, \end{aligned}$$

(33)

the generated sequence $\{(u^k, v^k)\}$ converges to an optimal solution of (1) and $\{x^k\}$ converges to the corresponding optimal multiplier.

Proof

(i) Let $\tau \in ]0,1]$. By letting $(u,v,x) = (\bar{u}, \bar{v}, \bar{x})$ in (18) and the optimality condition (14), we can obtain that for any $k\ge 0$,

$$\begin{aligned}&\varPhi _{k+1}(\bar{u}, \bar{v}, \bar{x}) - \varPhi _k(\bar{u}, \bar{v}, \bar{x}) \le \nonumber \\&\quad -\left( \varTheta _{k+1}+ \sigma \Vert \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^k - c\Vert ^2 +(1-\tau )\sigma \Vert \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1} - c\Vert ^2 \right) .\nonumber \\ \end{aligned}$$

(34)

The above inequality shows that $\{\varPhi _{k+1}(\bar{u}, \bar{v}, \bar{x})\}$ is bounded, which implies that $\{\Vert x^{k+1}\Vert \}$, $\{\Vert w_e^{k+1}\Vert _{\mathcal {Q}}\}$, $\{\Vert u_e^{k+1}\Vert _{S}\}$ and $\{\Vert v_e^{k+1}\Vert _{\mathcal {Q}_{22} + \sigma \mathcal {B}\mathcal {B}^*+\mathcal {T} }\}$ are all bounded. From the positive definiteness of $\mathcal {Q}_{22} + \sigma \mathcal {B}\mathcal {B}^*+\mathcal {T}$, we can see that $\{\Vert v_e^{k+1}\Vert \}$ is bounded. By using the inequalities

$$\begin{aligned} \left\| \mathcal {A}^*u_e^{k+1}\right\|\le & {} \left\| \mathcal {A}^*u_e^{k+1} + \mathcal {B}^*v_e^{k+1}\right\| + \left\| \mathcal {B}^*v_e^{k+1}\right\| \nonumber \\\le & {} \tau \sigma \left( \left\| x_e^{k+1}\right\| + \left\| x_e^k\right\| \right) + \left\| \mathcal {B}^*v_e^{k+1}\right\| ,\left\| u^{k+1}_e\right\| _{\mathcal {Q}_{11}} \nonumber \\\le & {} \left\| w_e^{k+1}\right\| _{\mathcal {Q}} + \left\| v_e^{k+1}\right\| _{\mathcal {Q}_{22}}, \end{aligned}$$

we know that the sequence $\{\Vert u_e^{k+1}\Vert _{\sigma \mathcal {A}\mathcal {A}^* + \mathcal {Q}_{11}}\}$ is also bounded. Therefore, $\{\Vert u_e^{k+1}\Vert _{\mathcal {Q}_{11} + \sigma \mathcal {A}\mathcal {A}^*+\mathcal {S}} \}$ is bounded. By the positive definiteness of $\mathcal {Q}_{11} + \sigma \mathcal {A}\mathcal {A}^*+\mathcal {S}$, we know that $\{\Vert u_e^{k+1}\Vert \}$ is bounded. On the whole, the sequence $\{(u^k,v^k,x^k)\}$ is bounded. Thus, there exists a subsequence $\{(u^{k_i},v^{k_i}, x^{k_i})\}$ converging to a cluster point, say $(u^{\infty },v^{\infty },x^{\infty })$. Next, we will prove that $(u^{\infty },v^{\infty })$ is optimal to (1) and $x^\infty$ is the corresponding optimal multiplier.

The inequality (34) also implies that

$$\begin{aligned}&\displaystyle \lim _{k\rightarrow \infty } \left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k} - c\right\| = 0,\quad \displaystyle \lim _{k\rightarrow \infty } (1-\tau )\left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1} - c\right\| = 0, \nonumber \\&\quad \displaystyle \lim _{k\rightarrow \infty } \left\| w^{k+1} - w^k\right\| _{\mathcal {Q}+\text {Diag}\,(\mathcal {S}, \mathcal {T})} =0. \end{aligned}$$

(35)

For $\tau \in ]0,1[$, since $\displaystyle \lim _{k\rightarrow \infty } \Vert \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1} - c\Vert =0$, by using (35) we see that

$$\begin{aligned}&\displaystyle \lim _{k\rightarrow \infty } \left\| \mathcal {A}^*(u^{k+1} - u^k)\right\| \le \displaystyle \lim _{k\rightarrow \infty } \left( \left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k} - c\right\| + \left\| \mathcal {A}^*u^{k} + \mathcal {B}^*v^{k} - c\right\| \right) = 0,\\&\quad \displaystyle \lim _{k\rightarrow \infty } \left\| \mathcal {B}^*(v^{k+1} - v^k)\right\| \le \displaystyle \lim _{k\rightarrow \infty }\left( \left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1} - c\right\| + \left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k} - c\right\| \right) = 0, \end{aligned}$$

which implies $\displaystyle \lim _{k\rightarrow \infty } \Vert w^{k+1} - w^k\Vert _{\mathcal {Q}+\text {Diag}\,(\mathcal {S}+\sigma \mathcal {A}\mathcal {A}^*, \mathcal {T} + \sigma \mathcal {B}\mathcal {B}^*)} = 0$. Therefore, for $\tau \in ]0,1]$, we have $\displaystyle \lim _{k\rightarrow \infty } \Vert w^{k+1} - w^k\Vert _{\mathcal {Q}+\text {Diag}\,(\mathcal {S}+(1-\tau )\sigma \mathcal {A}\mathcal {A}^*, \mathcal {T} + (1-\tau )\sigma \mathcal {B}\mathcal {B}^*)} = 0$. By picking a subsequence of $\{(u^{k_i}, v^{k_i})\}$ if necessary, we can see that either $\displaystyle \lim _{k_i\rightarrow \infty }\Vert u^{k_i+1} - u^{k_i}\Vert = 0$ or $\displaystyle \lim _{k_i\rightarrow \infty }\Vert v^{k_i+1} - v^{k_i}\Vert = 0$ by the condition (31). Without any loss of generality we assume that $\displaystyle \lim _{k_i\rightarrow \infty } \Vert v^{k_i+1} - v^{k_i}\Vert = 0$. Thus,

$$\begin{aligned} \displaystyle \lim _{k_i\rightarrow \infty } \left\| \mathcal {A}^*(u^{k_i+1} - u^{k_i})\right\|\le & {} \displaystyle \lim _{k\rightarrow \infty }\left( \left\| \mathcal {A}^*u^{k_i+1} + \mathcal {B}^*v^{k_i} - c\right\| + \left\| \mathcal {A}^*u^{k_i} + \mathcal {B}^*v^{k_i-1} - c\right\| \right. \nonumber \\&\quad \left. + \left\| \mathcal {B}^*\left( v^{k_i}-v^{k_i-1}\right) \right\| \right) = 0,\nonumber \\ \displaystyle \lim _{k_i\rightarrow \infty } \left\| u^{k_i+1} - u^{k_i}\right\| _{\mathcal {Q}_{11}}\le & {} \displaystyle \lim _{k_i\rightarrow \infty }\left( \left\| w^{k_i+1} - w^{k_i}\right\| _{\mathcal {Q}} + \left\| v^{k_i+1} - v^{k_i}\right\| _{\mathcal {Q}_{22}}\right) = 0. \end{aligned}$$

(36)

Therefore, $\displaystyle \lim _{k_i\rightarrow \infty } \Vert u^{k_i+1} - u^{k_i}\Vert _{\mathcal {Q}_{11}+\mathcal {S}+\sigma \mathcal {A}\mathcal {A}^*} = 0$. This implies $\displaystyle \lim _{k_i\rightarrow \infty } \Vert u^{k_i+1} - u^{k_i}\Vert =0$ by the positive definiteness of $\mathcal {Q}_{11}+\mathcal {S}+\sigma \mathcal {A}\mathcal {A}^*$.

Now, taking limits on both sides of (20) along the subsequence $\{(u^{k_i},v^{k_i},x^{k_i})\}$, and by using the closedness of the graphs of $\partial p$, $\partial q$ and the continuity of $\nabla \phi$, we obtain

$$\begin{aligned} 0\in F(u^\infty , v^\infty ,x^\infty ),\quad \mathcal {A}^*u^\infty + \mathcal {B}^*v^\infty = c. \end{aligned}$$

This indicates that $(u^\infty ,v^\infty )$ is an optimal solution to (1) and $x^\infty$ is the corresponding optimal multiplier. Since $(u^\infty , v^\infty , x^{\infty })$ satisfies (13), all the above arguments involving $(\bar{u},\bar{v},\bar{x})$ can be replaced by $(u^\infty , v^\infty , x^{\infty })$. Thus the subsequence $\{\varPhi _{k_i}(u^\infty , v^\infty , x^{\infty }) \}$ converges to 0 as $k_i\rightarrow \infty$. Since $\{\varPhi _{k_i}(u^\infty , v^\infty , x^{\infty }) \}$ is non-increasing, we obtain that

$$\begin{aligned} \displaystyle \lim _{k\rightarrow \infty } \varPhi _{k+1}\left( u^\infty , v^\infty , x^{\infty }\right)= & {} \displaystyle \lim _{k\rightarrow \infty }~ (\tau \sigma )^{-1}\left\| x^{k+1} - x^\infty \right\| ^2 \nonumber \\&\quad + \left\| v^{k+1}-v^{\infty }\right\| ^2_{\sigma \mathcal {B}\mathcal {B}^*} \nonumber \\&\quad +\mathcal {T}+{\mathcal {Q}_{22}}+ \left\| u^{k+1} - u^{\infty }\right\| ^2_{\mathcal {S}}\nonumber \\&\quad +\left\| w^{k+1} - w^{\infty }\right\| _{\mathcal {Q}}^2 = 0. \end{aligned}$$

(37)

From this we can immediately get $\displaystyle \lim _{k\rightarrow \infty } x^{k+1} = x^\infty$ and $\displaystyle \lim _{k\rightarrow \infty } v^{k+1} = v^\infty$. Similar to (36), we have that $\displaystyle \lim _{k\rightarrow \infty } \sigma \Vert \mathcal {A}^*(u^{k+1} - u^{\infty })\Vert = 0$ and $\displaystyle \lim _{k\rightarrow \infty } \Vert u^{k+1} - u^{\infty }\Vert _{\mathcal {Q}_{11}} = 0$, which, together with, (37) imply that $\displaystyle \lim _{k\rightarrow \infty } \Vert u^{k+1} - u^{\infty }\Vert = 0$ by the positive definiteness of $\mathcal {Q}_{11}+\mathcal {S}+\sigma \mathcal {A}\mathcal {A}^*$. Therefore, the whole sequence $\{(u^k,v^k,x^k)\}$ converges to $(u^{\infty },v^\infty , x^\infty )$, the unique limit of the sequence. This completes the proof for the first case.

(ii) From the inequality (19) and the optimality condition (14) we know that for any $k\ge 1$,

$$\begin{aligned}&(\varPsi _{k+1}(\bar{u}, \bar{v}, \bar{x}) + \varXi _{k+1}) - (\varPsi _k(\bar{u}, \bar{v}, \bar{x}) +\varXi _k) \nonumber \\&\quad \le -\left( \varGamma _{k+1}+\min \left( 1,1+\tau ^{-1} - \tau \right) \sigma \left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1} - c\right\| ^2\right) . \end{aligned}$$

(38)

By the assumptions $\tau \in ]0, \frac{1+\sqrt{5}}{2}[$ and $\mathcal {M}\succeq 0$, we can obtain that $\varGamma _{k+1}\ge 0$ and $\min (1,1+\tau ^{-1} - \tau )\ge 0$. Then, both $\{\varPsi _{k+1}(\bar{u}, \bar{v}, \bar{x})\}$ and $\{\varXi _{k+1}\}$ are bounded. Thus, by a similar approach to case (i), we see that the sequence $\{(u^k,v^k,x^k)\}$ is bounded. Therefore, there exists a subsequence $\{(u^{k_i},v^{k_i}, x^{k_i})\}$ that converges to a cluster point, say $(u^{\infty },v^{\infty },x^{\infty })$. Next, we will prove that $(u^{\infty },v^{\infty })$ is optimal to problem (1) and $x^\infty$ is the corresponding optimal multiplier. The inequality (38) also implies that

$$\begin{aligned} \begin{array}{ll} \displaystyle \lim _{k\rightarrow \infty } \left\| x^{k+1} - x^k\right\| = \displaystyle \lim _{k\rightarrow \infty }(\tau \sigma )^{-1}\left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1} - c\right\| = 0, \\ \displaystyle \lim _{k\rightarrow \infty } \left\| w^{k+1} - w^k\right\| _{\mathcal {M}} = 0,\quad \displaystyle \lim _{k\rightarrow \infty }\left\| \mathcal {B}^*\left( v^{k+1} - v^k\right) \right\| = 0. \end{array} \end{aligned}$$

By the relationship

$$\begin{aligned} \displaystyle \lim _{k\rightarrow \infty } \left\| \mathcal {A}^*(u^{k+1}-u^k)\right\|\le & {} \displaystyle \lim _{k\rightarrow \infty } \left( \left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1}-c\right\| \right. \\&\quad + \left\| \mathcal {A}^*u^k + \mathcal {B}^*v^k - c\right\| \\&\quad + \left. \left\| \mathcal {B}^*\left( v^{k+1} - v^k\right) \right\| \right) = 0, \end{aligned}$$

we can further get $\displaystyle \lim _{k\rightarrow \infty } \Vert w^{k+1} - w^k\Vert _{\mathcal {M} + \text {Diag}\,(\sigma \mathcal {A}\mathcal {A}^*, \sigma \mathcal {B}\mathcal {B}^*)}= 0$. Thus, by the condition (33) and taking a subsequence of $\{(u^{k_i}, v^{k_i})\}$ if necessary, we can get either $\displaystyle \lim _{k\rightarrow \infty } \Vert u^{k_i+1} - u^{k_i}\Vert = 0$ or $\displaystyle \lim _{k\rightarrow \infty } \Vert v^{k_i+1} - v^{k_i}\Vert = 0$. Again, similar to case (i), we can see that, in fact, both of them would hold by the positive definiteness of $\frac{1}{4} \mathcal {Q}_{11}+\mathcal {S} + \sigma \mathcal {A}\mathcal {A}^* - \eta \mathcal {D}_1$ and $\frac{1}{4} \mathcal {Q}_{22}+\mathcal {T} + \sigma \mathcal {B}\mathcal {B}^* - \eta \mathcal {D}_{22}$. The remaining proof about the convergence of the whole sequence $\{(u^k,v^k,x^k)\}$ follows exactly the same as in case (i). This completes the proof for the second case. $\square$

Remark 4.1

In Theorem 4.1, for $\tau \in ]0,1]$, a sufficient condition for the convergence is

$$\begin{aligned} \mathcal {Q}+\text {Diag}\,\left( \mathcal {S}+(1-\tau )\sigma \mathcal {A}\mathcal {A}^*, \mathcal {T} + (1-\tau )\sigma \mathcal {B}\mathcal {B}^*\right) \succ 0, \end{aligned}$$

and for $\tau \in [1, \frac{1+\sqrt{5}}{2}[$, a sufficient condition for the convergence is

$$\begin{aligned}&\displaystyle \frac{1}{4}\mathcal {Q} + \text {Diag}\,\left( \mathcal {S}-\eta \mathcal {D}_1, ~\mathcal {T} -\eta \mathcal {D}_2 \right) \succeq 0\quad \text {and}\\&\quad \frac{1}{4}\mathcal {Q} +\text {Diag}\,\left( \mathcal {S}+\sigma \mathcal {A}\mathcal {A}^*-\eta \mathcal {D}_1, \mathcal {T} +\sigma \mathcal {B}\mathcal {B}^* -\eta \mathcal {D}_2\right) \succ 0. \end{aligned}$$

Remark 4.2

An interesting application of Theorem 4.1 is for the linearly constrained convex optimization problem with a quadratically coupled objective function of the form

$$\begin{aligned} \phi (w) = \frac{1}{2}\left\langle w, \widetilde{\mathcal {Q}}w\right\rangle + f(u) + g(v), \end{aligned}$$

where $\widetilde{\mathcal {Q}}:\mathcal {U}\times \mathcal {V}\rightarrow \mathcal {U}\times \mathcal {V}$ is a self-adjoint positive semidefinite linear operator, $f: \mathcal {U}\rightarrow ]-\infty , \infty [$ and $g: \mathcal {V}\rightarrow ]-\infty , \infty [$ are two convex and smooth functions with Lipschitz continuous gradients. In this case, there exist four self-adjoint positive semidefinite operators $\varSigma _f, \widehat{\varSigma }_f: \mathcal {U}\rightarrow \mathcal {U}$ and $\varSigma _g, \widehat{\varSigma }_g:\mathcal {V}\rightarrow \mathcal {V}$ such that

$$\begin{aligned} \varSigma _f\preceq \xi \preceq \widehat{\varSigma }_f, \quad \forall \xi \in \partial ^2 f(u), \,u\in \mathcal {U} \quad \text {and} \quad \varSigma _g\preceq \zeta \preceq \widehat{\varSigma }_g ,\quad \forall \zeta \in \partial ^2 g(v), \, v\in \mathcal {V}, \end{aligned}$$

where $\partial ^2 f$ and $\partial ^2 g$ are defined in (7). Then, by letting $\mathcal {Q} = \widetilde{\mathcal {Q}} + \text {Diag}\,(\varSigma _f, \varSigma _g)$ in (9) and $\mathcal {Q} + \mathcal {H} = \widetilde{\mathcal {Q}} + \text {Diag}\,(\widehat{\varSigma }_f, \widehat{\varSigma }_g)$ in (10), we have $\eta = 0$ in (12). This implies that $\mathcal {M}\succeq 0$ always holds in (32). Therefore, for $\tau \in ]0,\frac{1+\sqrt{5}}{2}[$, the conditions for the convergence can be equivalently written as

$$\begin{aligned} \begin{array}{ll} \widetilde{\mathcal {Q}}_{11} +\varSigma _f+ \mathcal {S} + \sigma \mathcal {A}\mathcal {A}^*\succ 0, ~\widetilde{\mathcal {Q}}_{22}+\varSigma _g + \mathcal {T} + \sigma \mathcal {B}\mathcal {B}^*\succ 0 \end{array} \end{aligned}$$

(39)

and

$$\begin{aligned} \left\langle w, \left[ \widetilde{\mathcal {Q}}+\text {Diag}\,\left( \varSigma _f + \mathcal {S}+\sigma \mathcal {A}\mathcal {A}^*, \varSigma _g + \mathcal {T} + \sigma \mathcal {B}\mathcal {B}^*\right) \right] w\right\rangle = 0 \Rightarrow \Vert u\Vert \Vert v\Vert = 0.\nonumber \\ \end{aligned}$$

(40)

A sufficient condition for ensuring (39) and (40) to hold is

$$\begin{aligned} \widetilde{\mathcal {Q}} + \text {Diag}\,\left( \varSigma _f + \mathcal {S} + \sigma \mathcal {A}\mathcal {A}^*, \varSigma _g + \mathcal {T} + \sigma \mathcal {B}\mathcal {B}^*\right) \succ 0. \end{aligned}$$

If $\widetilde{\mathcal {Q}} = 0$, i.e., if the objective function of the original problem (1) is separable, then we will recover the convergence conditions given in [11] for a majorized ADMM with semi-proximal terms.

4.2 The Non-ergodic Iteration Complexity for General Coupled Objective Functions

In this subsection, we will present the non-ergodic iteration complexity for the majorized ADMM in terms of the KKT optimality condition.

Before showing the main result, we first present the following Lemma, which shows the nonincreasing property of the difference between two consecutive iteration points when the step length $\tau =1$. This property has also been discussed by He and Yuan [12] for the classic ADMM with $\tau =1$. For $k=0,1,2,\ldots$, denote the following notation:

$$\begin{aligned} \varDelta x^{k+1}:= & {} x^{k+1} - x^k, \quad \varDelta u^{k+1} := u^{k+1} - u^k, \quad \varDelta v^{k+1} := v^{k+1} - v^k,\\&\varDelta w^{k+1} := w^{k+1} - w^k. \end{aligned}$$

Lemma 4.1

Assume that $\tau =1$. Then, for any $k\ge 1$, it holds that

$$\begin{aligned}&\left\| \varDelta x^{k+1}\right\| ^2_{\sigma ^{-1}\mathcal {I}} + \left\| \varDelta u^{k+1}\right\| ^2_{\mathcal {S}} + \left\| \varDelta v^{k+1}\right\| ^2_{\mathcal {T} + \sigma \mathcal {B}\mathcal {B}^* + \mathcal {Q}_{22}}+\left\| \varDelta w^{k+1}\right\| ^2_{{\mathcal {Q} + \mathcal {H}}}\nonumber \\&\quad \le \left\| \varDelta x^{k}\right\| ^2_{\sigma ^{-1}\mathcal {I}} + \left\| \varDelta u^{k}\right\| ^2_{\mathcal {S}} + \left\| \varDelta v^{k}\right\| ^2_{\mathcal {T} + \sigma \mathcal {B}\mathcal {B}^* + \mathcal {Q}_{22}}+\left\| \varDelta w^k\right\| ^2_{{\mathcal {Q} + \mathcal {H}}}. \end{aligned}$$

(41)

Proof

For $\tau =1$ and $k\ge 1$, the optimality conditions at the $(k+1)$th and kth iterations can be written as

$$\begin{aligned} -\mathcal {A} x^{k+1} -\nabla _u \phi \left( w^k\right) - \left( \mathcal {Q}_{11} + \mathcal {D}_1+ \mathcal {S}\right) \varDelta u^{k+1} +\sigma \mathcal {A}\mathcal {B}^*\varDelta v^{k+1}\in & {} \partial p\left( u^{k+1}\right) ,\\ -\mathcal {B} x^{k+1} - \nabla _v \phi \left( w^k\right) -\left( \mathcal {Q}_{22} + \mathcal {D}_2 + \mathcal {T}\right) \varDelta v^{k+1} - \mathcal {Q}_{12}^*\varDelta u^{k+1}\in & {} \partial q\left( v^{k+1}\right) \end{aligned}$$

and

$$\begin{aligned} -\mathcal {A} x^{k} -\nabla _u \phi \left( w^{k-1}\right) - \left( \mathcal {Q}_{11} + \mathcal {D}_1+ \mathcal {S}\right) \varDelta u^{k} +\sigma \mathcal {A}\mathcal {B}^*\varDelta v^{k}\in & {} \partial p\left( u^{k}\right) ,\\ -\mathcal {B} x^{k} - \nabla _v \phi \left( w^{k-1}\right) -\left( \mathcal {Q}_{22} + \mathcal {D}_2 + \mathcal {T}\right) \varDelta v^{k} - \mathcal {Q}_{12}^*\varDelta u^{k}\in & {} \partial q\left( v^{k}\right) . \end{aligned}$$

By the monotonicity of the subdifferential of the convex functions p and q, we have the following inequalities:

$$\begin{aligned}&\left\langle \varDelta u^{k+1}, \mathcal {A}\varDelta x^{k+1}+\left( \nabla _u \phi \left( w^{k}\right) -\nabla _u \phi \left( w^{k-1}\right) \right) + \left( \mathcal {Q}_{11} + \mathcal {D}_1+ \mathcal {S}\right) \right. \\&\quad \left. \times \left( \varDelta u^{k+1} - \varDelta u^{k}\right) -\sigma \mathcal {A}\mathcal {B}^*\left( \varDelta v^{k+1} - \varDelta v^{k}\right) \right\rangle \le 0,\\&\langle \varDelta v^{k+1}, \mathcal {B} \varDelta x^{k+1} + \left( \nabla _v \phi \left( w^k\right) - \nabla _v \phi \left( w^{k-1}\right) \right) +\left( \mathcal {Q}_{22} + \mathcal {D}_2 + \mathcal {T}\right) \\&\qquad \times \left( \varDelta v^{k+1} - \varDelta v^k\right) + \mathcal {Q}_{12}^*\left( \varDelta u^{k+1} - \varDelta u^k\right) \rangle \le 0. \end{aligned}$$

Adding the above two inequalities together, and using the fact that

$$\begin{aligned} \varDelta x^{k+1} - \varDelta x^k = \sigma (\mathcal {A}^*\varDelta u^{k+1} + \mathcal {B}^* \varDelta v^{k+1}), \end{aligned}$$

we get

$$\begin{aligned}&\sigma ^{-1}\left\langle \varDelta x^{k+1}, \varDelta x^{k+1} - \varDelta x^k\right\rangle +\left\langle \varDelta u^{k+1}, \mathcal {S}\left( \varDelta u^{k+1} - \varDelta u^k\right) \right\rangle \nonumber \\&\quad + \left\langle \varDelta v^{k+1}, \mathcal {T}\left( \varDelta v^{k+1} - \varDelta v^k\right) \right\rangle \nonumber \\&\quad +\left\langle \varDelta w^{k+1}, \nabla \phi \left( w^k\right) - \nabla \phi \left( w^{k-1}\right) \right. \nonumber \\&\quad \left. + \left( {\mathcal {Q}} + \mathcal {H}\right) \left( \varDelta w^{k+1} - \varDelta w^k\right) \right\rangle \nonumber \\&\quad -\left\langle \varDelta u^{k+1}, \left( \sigma \mathcal {A}\mathcal {B}^* + \mathcal {Q}_{12}\right) \left( \varDelta v^{k+1} - \varDelta v^k\right) \right\rangle \le 0. \end{aligned}$$

(42)

Since $\nabla \phi$ is globally Lipschitz continuous, there exists a self-adjoint positive semidefinite linear operator $\mathcal {W}^k \in \,\text {conv}\{\partial ^2\phi ([w^{k-1}, w^k])\}$ such that

$$\begin{aligned} \nabla \phi \left( w^k\right) - \nabla \phi \left( w^{k-1}\right) = \mathcal {W}^k\left( w^k - w^{k-1}\right) . \end{aligned}$$

(43)

By using the Cauchy-Schwarz inequality and (15), we see that

$$\begin{aligned}&\left\langle \varDelta u^{k+1}, \sigma \mathcal {A}\mathcal {B}^*\left( \varDelta v^{k+1} - \varDelta v^k\right) \right\rangle \nonumber \\&\quad = \sigma \left\langle \mathcal {A}^*\varDelta u^{k+1}, \mathcal {B}^*\varDelta v^{k+1}\right\rangle - \sigma \left\langle \mathcal {A}^*\varDelta u^{k+1}, \mathcal {B}^*\varDelta v^k\right\rangle \nonumber \\&\quad \le \frac{1}{2}\left( \sigma \left\| \mathcal {A}^*\varDelta u^{k+1} + \mathcal {B}^*\varDelta v^{k+1}\right\| ^2 - \left\| \varDelta u^{k+1}\right\| ^2_{\sigma \mathcal {A}\mathcal {A}^*} - \left\| \varDelta v^{k+1}\right\| ^2_{\sigma \mathcal {B}\mathcal {B}^*}\right) \nonumber \\&\qquad + \frac{1}{2}\left( \left\| \varDelta u^{k+1}\right\| ^2_{\sigma \mathcal {A}\mathcal {A}^*} + \left\| \varDelta v^{k}\right\| ^2_{\sigma \mathcal {B}\mathcal {B}^*}\right) \nonumber \\&\quad = \frac{1}{2}\left\| \varDelta x^{k+1} - \varDelta x^k\right\| ^2_{\sigma ^{-1}\mathcal {I}} -\frac{1}{2}\left( \left\| \varDelta v^{k+1}\right\| ^2_{\sigma \mathcal {B}\mathcal {B}^*} -\left\| \varDelta v^k\right\| ^2_{\sigma \mathcal {B}\mathcal {B}^*}\right) . \end{aligned}$$

(44)

By substituting (43) and (44) into (42) and some simple calculations, we have that

$$\begin{aligned}&\left( \left\| \varDelta x^{k+1}\right\| ^2_{\sigma ^{-1}\mathcal {I}} - \left\| \varDelta x^k\right\| ^2_{\sigma ^{-1}\mathcal {I}}+\left\| \varDelta x^{k+1} - \varDelta x^k\right\| ^2_{\sigma ^{-1}\mathcal {I}}\right) \\&\quad + \left( \left\| \varDelta u^{k+1}\right\| ^2_{\mathcal {S}}- \left\| \varDelta u^k\right\| ^2_{\mathcal {S}}+ \left\| \varDelta u^{k+1} - \varDelta u^k\right\| ^2_{\mathcal {S}} \right) \\&\quad +\left( \left\| \varDelta v^{k+1}\right\| ^2_{\mathcal {T}} -\left\| \varDelta v^k\right\| ^2_{\mathcal {T}} + \left\| \varDelta v^{k+1} - \varDelta v^k\right\| ^2_{\mathcal {T}}\right) \\&\quad + 2\left\| \varDelta w^{k+1}\right\| ^2_{{\mathcal {Q}} + \mathcal {H}} \\&\quad - \left( \left\| \varDelta w^{k+1}\right\| ^2_{{\mathcal {Q}} + \mathcal {H}- \mathcal {W}^k} -\left\| \varDelta w^{k+1} - \varDelta w^k\right\| ^2_{{\mathcal {Q}} + \mathcal {H} - \mathcal {W}^k} +\left\| \varDelta w^k\right\| ^2_{{\mathcal {Q}} + \mathcal {H} - \mathcal {W}^k}\right) \\&\quad -\left( \left\| \varDelta w^{k+1}\right\| ^2_{\mathcal {Q}} +\left\| \varDelta v^k\right\| ^2_{\mathcal {Q}_{22}} - \left\| \varDelta v^{k+1}\right\| ^2_{\mathcal {Q}_{22}}\right) \\&\quad -\left( \left\| \varDelta x^{k+1} - \varDelta x^k\right\| _{\sigma ^{-1}\mathcal {I}}^2- \left\| \varDelta v^{k+1}\right\| _{\sigma \mathcal {B}\mathcal {B}^*}^2 + \left\| \varDelta v^k\right\| _{\sigma \mathcal {B}\mathcal {B}^*}^2\right) \le 0, \end{aligned}$$

which can be recast as

$$\begin{aligned}&\left\| \varDelta x^{k+1}\right\| ^2_{\sigma ^{-1}\mathcal {I}} + \left\| \varDelta u^{k+1}\right\| ^2_{\mathcal {S}} + \left\| \varDelta v^{k+1}\right\| ^2_{\mathcal {T} + \sigma \mathcal {B}\mathcal {B}^* + \mathcal {Q}_{22}} + \left\| \varDelta w^{k+1}\right\| ^2_{{\mathcal {Q}} + \mathcal {H}} \\&\quad \le \left\| \varDelta x^{k}\right\| ^2_{\sigma ^{-1}\mathcal {I}} + \left\| \varDelta u^{k}\right\| ^2_{\mathcal {S}} + \left\| \varDelta v^{k}\right\| ^2_{\mathcal {T} + \sigma \mathcal {B}\mathcal {B}^* + \mathcal {Q}_{22}}+\left\| \varDelta w^k\right\| ^2_{{\mathcal {Q}} + \mathcal {H}} \\&\qquad - \left( \left\| \varDelta u^{k+1} - \varDelta u^k\right\| ^2_{\mathcal {S}}+ \left\| \varDelta v^{k+1} - \varDelta v^k\right\| ^2_{\mathcal {T}} + \left\| \varDelta w^{k+1} - \varDelta w^k\right\| ^2_{{\mathcal {Q}} + \mathcal {H} - \mathcal {W}^k}\right. \\&\qquad + \left. \left\| \varDelta w^{k+1}\right\| ^2_{\mathcal {W}^k-\mathcal {Q}} + \left\| \varDelta w^k\right\| ^2_{\mathcal {W}_k}\right) \\&\quad \le \left\| \varDelta x^{k}\right\| ^2_{\sigma ^{-1}\mathcal {I}} + \left\| \varDelta u^{k}\right\| ^2_{\mathcal {S}} + \left\| \varDelta v^{k}\right\| ^2_{\mathcal {T} + \sigma \mathcal {B}\mathcal {B}^* + \mathcal {Q}_{22}} + \left\| \varDelta w^k\right\| ^2_{{\mathcal {Q}} + \mathcal {H}}, \end{aligned}$$

where the last inequality is obtained by the relationship (8).

Theorem 4.2

Suppose that the solution set of (1) is nonempty and Assumption 2.1 holds. Assume that one of the following conditions holds:

• (i) $\tau \in ]0,1]$, $\mathcal {O}_1: = \displaystyle \frac{1}{4}\mathcal {Q} + \text {Diag}\,\left( \mathcal {S}+(1-\tau )\sigma \mathcal {A}\mathcal {A}^*, \mathcal {T} + (1-\tau )\sigma \mathcal {B}\mathcal {B}^*\right) \succ 0$;

• (ii) $\tau \in ]0,\frac{1+\sqrt{5}}{2}[$, $\displaystyle \frac{1}{4}\mathcal {Q} + \text {Diag}\,\left( \mathcal {S}- \eta \mathcal {D}_1, \mathcal {T} - \eta \mathcal {D}_2\right) \succeq 0$ , $\mathcal {O}_2: = \displaystyle \frac{1}{4}\mathcal {Q} + \text {Diag}\,(\mathcal {S}+\sigma \mathcal {A}\mathcal {A}^* - \eta \mathcal {D}_1, \mathcal {T} + \sigma \mathcal {B}\mathcal {B}^* - \eta \mathcal {D}_2)\succ 0.$

Then, there exists a constant C only depending on the initial point and the optimal solution set, such that the sequence $\{(u^k, v^k,x^k)\}$ generated by the majorized ADMM satisfies that for $k\ge 1$,

$$\begin{aligned} \displaystyle \min _{1\le i\le k} \left[ \text {dist}^2\left( 0, F\left( u^{i+1}, v^{i+1}, x^{i+1}\right) \right) + \left\| \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^{i+1}-c\right\| ^2\right] \le C/k. \end{aligned}$$

(45)

and for the limiting case we have that

$$\begin{aligned} \displaystyle \lim _{k\rightarrow \infty } k\left( \min _{1\le i\le k} \left[ \text {dist}^2\left( 0, F\left( u^{i+1}, v^{i+1}, x^{i+1}\right) \right) + \left\| \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^{i+1}-c\right\| ^2 \right] \right) = 0.\nonumber \\ \end{aligned}$$

(46)

Furthermore, when the step length $\tau =1$, it holds that

$$\begin{aligned} \displaystyle \lim _{k\rightarrow \infty } k\left( \text {dist}^2\left( 0, F\left( u^{k+1}, v^{k+1}, x^{k+1}\right) \right) + \left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1}-c\right\| ^2\right) = 0.\nonumber \\ \end{aligned}$$

(47)

i.e., the “$\displaystyle \min _{1\le i\le k}$” can be removed from (46).

Proof

From the optimality condition for $(u^{k+1}, v^{k+1})$, we know that

$$\begin{aligned}&\left( \begin{array}{cc} -(1-\tau )\sigma \mathcal {A}\left( \mathcal {A}^*u^{k+1} +\mathcal {B}^*v^{k+1} - c\right) - \sigma \mathcal {A}\mathcal {B}^*\left( v^{k} - v^{k+1}\right) - \mathcal {S}\left( u^{k+1} - u^k\right) \\ + \mathcal {Q}_{12}\left( v^{k+1}- v^k\right) -(1-\tau )\sigma \mathcal {B}\left( \mathcal {A}^*u^{k+1} +\mathcal {B}^*v^{k+1} - c\right) - \mathcal {T}\left( v^{k+1} - v^k\right) \end{array}\right) \\&\quad - \left( \mathcal {Q}+\mathcal {H}\right) \left( w^{k+1} - w^k\right) + \nabla \phi \left( w^{k+1}\right) - \nabla \phi \left( w^k\right) \in F\left( u^{k+1}, v^{k+1}, x^{k+1}\right) . \end{aligned}$$

Therefore, we can obtain that

$$\begin{aligned}&\text {dist}^2\left( 0, F\left( u^{k+1}, v^{k+1}, x^{k+1}\right) \right) + \left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1}-c\right\| ^2\nonumber \\&\quad \le 5\left\| \sigma \mathcal {A}\mathcal {B}^*\left( v^{k+1} - v^k\right) \right\| ^2 \nonumber \\&\qquad + 5(1-\tau )^2\sigma ^2\left( \left\| \mathcal {A}\right\| ^2+\left\| \mathcal {B}\right\| ^2\right) \left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1} - c\right\| ^2\nonumber \\&\qquad + 5\left\| \left( \mathcal {Q} + \mathcal {H}\right) \left( w^{k+1} - w^k\right) -\nabla \phi \left( w^{k+1}\right) +\nabla \phi \left( w^k\right) \right\| ^2\nonumber \\&\qquad +5\left\| \mathcal {Q}_{12}\left( v^{k+1} - v^k\right) \right\| ^2 + 5\left\| \mathcal {T}\left( v^{k+1} - v^k\right) \right\| ^2 \nonumber \\&\qquad + 5\left\| \mathcal {S}\left( u^{k+1} - u^k\right) \right\| ^2+\left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1} - c\right\| ^2\nonumber \\&\quad \le 5\sigma \left\| \mathcal {A}\right\| ^2\left\| v^{k+1} - v^k\right\| _{\sigma \mathcal {B}\mathcal {B}^*}^2\nonumber \\&\qquad + \left( 5(1-\tau )^2\sigma ^2\left( \left\| \mathcal {A}\Vert ^2 + \Vert \mathcal {B}\right\| ^2\right) +1\right) \left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1}-c\right\| ^2 \nonumber \\&\qquad + 5\left\| \sqrt{\mathcal {Q}_{12}^*\mathcal {Q}_{12}}\right\| \left\| v^{k+1} - v^k\right\| _{\sqrt{\mathcal {Q}_{12}^*\mathcal {Q}_{12}}}^2\nonumber \\&\qquad + 5\left\| \mathcal {H}\right\| \left\| w^{k+1} - w^k\right\| _{\mathcal {H}}^2 + 5\left\| \mathcal {S}\right\| \left\| u^{k+1} - u^k\right\| ^2_{\mathcal {S}}\nonumber \\&\qquad + 5\left\| \mathcal {T}\right\| \left\| v^{k+1} - v^k\right\| ^2_{\mathcal {T}}\le C_1\left\| w^{k+1} - w^k\right\| ^2_{\widehat{\mathcal {O}}} \nonumber \\&\qquad + C_2\left\| \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1}-c\right\| ^2, \end{aligned}$$

(48)

where

$$\begin{aligned} \begin{array}{ll} &{}C_1 = 5\max (\sigma \Vert \mathcal {A}\Vert ^2,\Vert \sqrt{\mathcal {Q}_{12}^*\mathcal {Q}_{12}}\Vert , \Vert \mathcal {H}\Vert ,\Vert \mathcal {S}\Vert ,\Vert \mathcal {T}\Vert ), \\ {} &{}C_2 = 5(1-\tau )^2\sigma ^2(\Vert \mathcal {A}\Vert ^2 + \Vert \mathcal {B}\Vert ^2)+1,\\ &{}\widehat{\mathcal {O}} = \mathcal {H} + \text {Diag}\,(\mathcal {S}, \mathcal {T} + \sigma \mathcal {B}\mathcal {B}^* + \sqrt{\mathcal {Q}_{12}^*\mathcal {Q}_{12}}), \end{array} \end{aligned}$$

and the second inequality comes from the fact that there exists some $\mathcal {W}^k\in \text {conv}\{\partial ^2\phi ([w^{k-1}, w^k])\}$ such that

$$\begin{aligned}&\Vert (\mathcal {Q} + \mathcal {H})(w^{k+1} - w^k)-\nabla \phi (w^{k+1}) + \nabla \phi (w^k)\Vert ^2 \\&\quad =\Vert (\mathcal {Q} + \mathcal {H}-\mathcal {W}^k)(w^{k+1} - w^k)\Vert ^2 \le \Vert \mathcal {H}\Vert \Vert w^{k+1} - w^k\Vert ^2_{\mathcal {H}}. \end{aligned}$$

Next, we will estimate the upper bounds for $\Vert w^{k+1} - w^k\Vert ^2_{\widehat{\mathcal {O}}}$ and $\Vert \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1} - c\Vert ^2$ by only involving the initial point and the optimal solution set under the two different conditions.

First, assume condition (i) holds. For $\tau \in ]0,1]$, by using (34) in the proof of Theorem 4.1, we have that,

$$\begin{aligned}&\Vert w^{i+1} - w^i\Vert ^2_{\frac{1}{4}\mathcal {Q} + \text {Diag}\,(\mathcal {S}, \mathcal {T})} + \sigma \Vert \mathcal {A}^*u^{i+1} \\&\qquad + \mathcal {B}^*v^i - c\Vert ^2 + (1-\tau )\sigma \Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^{i+1} -c\Vert ^2 \\&\quad \le \varPhi _i(\bar{u}, \bar{v}, \bar{x}) - \varPhi _{i+1}(\bar{u}, \bar{v}, \bar{x}),\quad i\ge 1, \end{aligned}$$

which implies

$$\begin{aligned}&\displaystyle \sum _{i=1}^k (\Vert w^{i+1} - w^i\Vert ^2_{\frac{1}{4}\mathcal {Q} + \text {Diag}\,(\mathcal {S}, \mathcal {T})} + \sigma \Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^i - c\Vert ^2 + (1-\tau )\sigma \Vert \mathcal {A}^*u^{i+1}\\&\quad + \mathcal {B}^*v^{i+1} -c\Vert ^2 \le \varPhi _1(\bar{u}, \bar{v}, \bar{x}) - \varPhi _{k+1}(\bar{u}, \bar{v}, \bar{x})\le \varPhi _1(\bar{u}, \bar{v}, \bar{x}). \end{aligned}$$

This shows that

$$\begin{aligned}&\displaystyle \sum _{i=1}^k \Vert w^{i+1} - w^i\Vert ^2_{\frac{1}{4}\mathcal {Q} + \text {Diag}(\mathcal {S}, \mathcal {T})} \le \varPhi _1(\bar{u}, \bar{v}, \bar{x}),\nonumber \\&\quad \displaystyle \sum _{i=1}^k \sigma \Vert \mathcal {A}^*u^{i+1}+\mathcal {B}^*v^{i} -c\Vert ^2 \le \varPhi _1(\bar{u}, \bar{v}, \bar{x}),\nonumber \\&\quad \displaystyle \sum _{i=1}^k (1-\tau )\sigma \Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^{i+1} - c\Vert ^2 \le \varPhi _1(\bar{u}, \bar{v}, \bar{x}). \end{aligned}$$

(49)

From the above three inequalities we can also get that

$$\begin{aligned}&(1-\tau )\displaystyle \sum _{i=1}^k \Vert u^{i+1} - u^i\Vert ^2_{\sigma \mathcal {A}\mathcal {A}^*}\le (1-\tau )\displaystyle \sum _{i=1}^k (2\sigma \Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^i - c\Vert ^2\\&\quad + 2\sigma \Vert \mathcal {A}^*u^{i} + \mathcal {B}^*v^{i} - c\Vert ^2)\le 2(2-\tau )\varPhi _1(\bar{u}, \bar{v}, \bar{x}),\\&(1-\tau )\displaystyle \sum _{i=1}^k \Vert v^{i+1} - v^i\Vert ^2_{\sigma \mathcal {B}\mathcal {B}^*} \le (1-\tau )\displaystyle \sum _{i=1}^k (2\sigma \Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^i \\&\quad - c\Vert ^2 + 2\sigma \Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^{i+1} - c\Vert ^2) \le 2(2-\tau )\varPhi _1(\bar{u}, \bar{v}, \bar{x}). \end{aligned}$$

With the notation of operator $\mathcal {O}_1$ we have that

$$\begin{aligned} \displaystyle \sum _{i=1}^k \Vert w^{i+1} - w^i\Vert ^2_{\mathcal {O}_1}= & {} \displaystyle \sum _{i=1}^k \Vert w^{i+1} - w^i\Vert ^2_{\frac{1}{4}\mathcal {Q} + \text {Diag}(\mathcal {S}, \mathcal {T})} \nonumber \\&+ \displaystyle \sum _{i=1}^k \Vert w^{i+1} - w^i\Vert ^2_{(1-\tau )\text {Diag}(\sigma \mathcal {A}\mathcal {A}^*, \mathcal {B}\mathcal {B}^*)} \nonumber \\\le & {} (9-4\tau )\varPhi _1(\bar{u}, \bar{v}, \bar{x}). \end{aligned}$$

(50)

If $\tau \in ]0,1[$, then we further have that

$$\begin{aligned} \begin{array}{ll} \displaystyle \sum _{i=1}^k \Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^{i+1} - c\Vert ^2 \le (1-\tau )^{-1}\sigma ^{-1}\varPhi _1(\bar{u}, \bar{v}, \bar{x}). \end{array} \end{aligned}$$

(51)

If $\tau = 1$, then by the condition that $\mathcal {O}_1 = \displaystyle \frac{1}{4}\mathcal {Q} + \text {Diag}\,(\mathcal {S}, \mathcal {T})\succ 0$, we have that

$$\begin{aligned}&\displaystyle \sum _{i=1}^k \Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^{i+1} - c\Vert ^2 \nonumber \\&\quad \le \displaystyle \sum _{i=1}^k (2\Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^{i} - c\Vert ^2 + 2\Vert v^{i+1} - v^i\Vert ^2_{\mathcal {B}\mathcal {B}^*})\nonumber \\&\quad \le \displaystyle \sum _{i=1}^k (2\Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^{i} - c\Vert ^2 + 2\Vert \mathcal {O}_1^{-\frac{1}{2}}\text {Diag}\,(0,\mathcal {\mathcal {B}\mathcal {B}^*})\mathcal {O}_1^{-\frac{1}{2}}\Vert \Vert w^{i+1} - w^i\Vert ^2_{\mathcal {O}_1})\nonumber \\&\quad \le (2\sigma ^{-1} + (18-8\tau )\Vert \mathcal {O}_1^{-\frac{1}{2}}\text {Diag}\,(0,\mathcal {\mathcal {B}\mathcal {B}^*})\mathcal {O}_1^{-\frac{1}{2}}\Vert )\varPhi _1(\bar{u}, \bar{v}, \bar{x}), \end{aligned}$$

(52)

where the second inequality is obtained by the fact that for any $\xi$, a self-adjoint positive definite operator $\mathcal {G}$ with square root $\mathcal {G}^{\frac{1}{2}}$ and a self-adjoint positive semidefinite operator $\widehat{G}$ defined in the same Euclidean space, it always holds that $\Vert \xi \Vert ^2_{\widehat{\mathcal {G}}} = \langle \xi , \widehat{\mathcal {G}}\xi \rangle = \langle \xi , (\mathcal {G}^{\frac{1}{2}}\mathcal {G}^{-\frac{1}{2}})\widehat{\mathcal {G}}(\mathcal {G}^{-\frac{1}{2}}\mathcal {G}^{\frac{1}{2}})\xi \rangle = \langle \mathcal {G}^{\frac{1}{2}}\xi , (\mathcal {G}^{-\frac{1}{2}}\widehat{\mathcal {G}}\mathcal {G}^{-\frac{1}{2}})\mathcal {G}^{\frac{1}{2}}\xi \rangle \le \Vert \mathcal {G}^{-\frac{1}{2}}\widehat{\mathcal {G}}\mathcal {G}^{-\frac{1}{2}}\Vert \Vert \xi \Vert ^2_{\mathcal {G}}.$

Therefore, by using (48), (50) and the positive definiteness of operator $\mathcal {O}_1$, we know that

$$\begin{aligned}&\displaystyle \min _{1\le i\le k} [\text {dist}^2(0, F(u^{i+1}, v^{i+1}, x^{i+1})) + \Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^{i+1}-c\Vert ^2]\\&\quad \le (\displaystyle \sum _{i=1}^k(\text {dist}^2(0, F(u^{i+1}, v^{i+1}, x^{i+1})) + \Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^{i+1}-c\Vert ^2))/k \\&\quad \le C\varPhi _1(\bar{u}, \bar{v}, \bar{x})/k, \end{aligned}$$

where

$$\begin{aligned}C =\left\{ \begin{array}{ll} C_1(9-4\tau )\Vert \mathcal {O}_1^{-\frac{1}{2}}\widehat{\mathcal {O}}\mathcal {O}_1^{-\frac{1}{2}}\Vert + C_2(1-\tau )^{-1}\sigma ^{-1}, \quad \tau \in ]0,1[,\\ C_1(9-4\tau )\Vert \mathcal {O}_1^{-\frac{1}{2}}\widehat{\mathcal {O}}\mathcal {O}_1^{-\frac{1}{2}}\Vert + C_2(2\sigma ^{-1} + (18-8\tau )\Vert \mathcal {O}_1^{-\frac{1}{2}}\text {Diag}\,(0,\mathcal {\mathcal {B}\mathcal {B}^*})\mathcal {O}_1^{-\frac{1}{2}}\Vert ) ,\quad \tau = 1. \end{array}\right. \end{aligned}$$

To prove the limiting case (46), by using inequalities (50), (51), (52) and [11, Lemma2.1], we have that

$$\begin{aligned} \min _{1\le i\le k}\Vert w^{i+1} - w^i\Vert ^2_{\mathcal {O}_1} = o(1/k),\quad \min _{1\le i\le k}\Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^{i+1} - c\Vert ^2 = o(1/k), \end{aligned}$$

which, together with (48), imply that

$$\begin{aligned}&\displaystyle \lim _{k\rightarrow \infty } k (\min _{1\le i\le k} [\text {dist}^2(0, F(u^{i+1}, v^{i+1}, x^{i+1})) + \Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^{i+1}-c\Vert ^2]) \\&\quad \le \displaystyle \lim _{k\rightarrow \infty } k (\min _{1\le i\le k} [C_1\Vert \mathcal {O}_1^{-\frac{1}{2}}\widehat{\mathcal {O}}\mathcal {O}_1^{-\frac{1}{2}}\Vert \Vert w^{i+1} - w^i\Vert ^2_{\mathcal {O}_1} + C_2\Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^{i+1} - c\Vert ^2]) = 0. \end{aligned}$$

Next, we shall prove (47) under the condition (i) and $\tau = 1$. By (49), (52) and the positive definiteness of the self-adjoint linear operator $\frac{1}{4}\mathcal {Q}+ \text {Diag}\,(\mathcal {S},\mathcal {T})$, we know that

$$\begin{aligned} \displaystyle \sum _{i=1}^\infty \Vert w^{i+1} - w^i\Vert ^2<\infty , \quad \displaystyle \sum _{i=1}^\infty \Vert x^{i+1} - x^i\Vert ^2<\infty . \end{aligned}$$

(53)

Then, by using Lemma 4.1, (53) and [13, Lemma1.2], we know that

$$\begin{aligned} \displaystyle \lim _{k\rightarrow \infty } k (\Vert w^{k+1} - w^k\Vert ^2_{\mathcal {Q}+ \mathcal {H}+ \text {Diag}\,(\mathcal {S}, \mathcal {T} + \sigma \mathcal {B}\mathcal {B}^* + \mathcal {Q}_{22})} + \Vert x^{k+1} - x^k\Vert ^2_{\sigma ^{-1}\mathcal {I}} )= 0. \end{aligned}$$

Since $\mathcal {Q}+\mathcal {H}+ \text {Diag}\,(\mathcal {S}, \mathcal {T} + \sigma \mathcal {B}\mathcal {B}^* + \mathcal {Q}_{22}) \succeq \mathcal {Q}+ \text {Diag}\,(\mathcal {S},\mathcal {T})\succ 0,$ we obtain that

$$\begin{aligned} \displaystyle \lim _{k\rightarrow \infty }k\Vert w^{k+1} - w^k\Vert ^2=0, \quad \lim _{k\rightarrow \infty }k\Vert x^{k+1} - x^k\Vert _{\sigma ^{-1}\mathcal {I}}^2=0, \end{aligned}$$

which, together with (48), imply

$$\begin{aligned} \displaystyle \lim _{k\rightarrow \infty } k(\text {dist}^2(0, F(u^{k+1}, v^{k+1}, x^{k+1})) + \Vert \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1}-c\Vert ^2) = 0. \end{aligned}$$

It completes the proof of the conclusions under condition (i).

For $\tau \in ]0,\frac{1+\sqrt{5}}{2}[$, let $\rho (\tau ) = \min (\tau ,1+\tau -\tau ^2)$. We know from (32) that for $\tau \in ]0,\frac{1+\sqrt{5}}{2}[$ and any $k\ge 1$,

$$\begin{aligned}&\displaystyle \sum _{i=1}^k \Vert w^{i+1} - w^i\Vert ^2_{\frac{1}{4}\mathcal {Q} + \text {diag}\,(\mathcal {S} - \eta \mathcal {D}_1,\mathcal {T} - \eta \mathcal {D}_2)} + \rho (\tau ) \Vert v^{i+1} - v^i\Vert ^2_{\sigma \mathcal {B}\mathcal {B}^*}\\&\quad + \frac{\rho (\tau )}{\tau }\sigma \Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^{i+1} - c\Vert ^2 \le \\&\qquad (\varPsi _1(\bar{u}, \bar{v}, \bar{x}) +\varXi _1) - (\varPsi _{k+1}(\bar{u}, \bar{v}, \bar{x}) + \varXi _{k+1})\le \varPsi _1(\bar{u}, \bar{v}, \bar{x}) + \varXi _1. \end{aligned}$$

Thus, by the positive semidefiniteness of $\frac{1}{4}\mathcal {Q} + \text {Diag}\,(\mathcal {S}- \eta \mathcal {D}_1, \mathcal {T} - \eta \mathcal {D}_2)$, we can get that

$$\begin{aligned}&\displaystyle \sum _{i=1}^k \Vert w^{i+1} - w^i\Vert ^2_{\frac{1}{4}\mathcal {Q} + \text {diag}\,(\mathcal {S} - \eta \mathcal {D}_1,\mathcal {T} - \eta \mathcal {D}_2)} \le \varPsi _1(\bar{u}, \bar{v}, \bar{x}) + \varXi _1,\nonumber \\&\quad \displaystyle \sum _{i=1}^k \Vert v^{i+1} - v^i\Vert ^2_{\sigma \mathcal {B}\mathcal {B}^*} \le (\varPsi _1(\bar{u}, \bar{v}, \bar{x})+\varXi _1)/\rho (\tau ),\nonumber \\&\qquad \displaystyle \sum _{i=1}^k \sigma \Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^{i+1} - c\Vert ^2 \le \tau (\varPsi _1(\bar{u}, \bar{v}, \bar{x})+\varXi _1)/\rho (\tau ), \end{aligned}$$

(54)

which implies

$$\begin{aligned}&\displaystyle \sum _{i=1}^k \Vert u^{i+1} - u^i\Vert ^2_{\sigma \mathcal {A}\mathcal {A}^*} \le \displaystyle \sum _{i=1}^k(3\sigma \Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^{i+1} - c\Vert ^2 + 3\sigma \Vert \mathcal {A}^*u^i\nonumber \\&\qquad + \mathcal {B}^*v^i - c\Vert ^2 + 3\Vert v^{i+1} - v^i\Vert _{\sigma \mathcal {B}\mathcal {B}^*}^2)\nonumber \\&\quad \le (6\tau +2)(\varPsi _1(\bar{u}, \bar{v}, \bar{x})+\varXi _1)/\rho (\tau ). \end{aligned}$$

(55)

Combining (54) and (55) one can find that

$$\begin{aligned}&\displaystyle \sum _{i=1}^k \Vert w^{i+1} - w^i\Vert ^2_{\mathcal {O}_2}= \displaystyle \sum _{i=1}^k \Vert w^{i+1} - w^i\Vert ^2_{\frac{1}{4}\mathcal {Q} + \text {diag}\,(\mathcal {S} - \eta \mathcal {D}_1,\mathcal {T} - \eta \mathcal {D}_2)} \nonumber \\&\qquad + \displaystyle \sum _{i=1}^k \Vert w^{i+1} - w^i\Vert ^2_{\text {Diag}\,(\sigma \mathcal {A}\mathcal {A}^*, \sigma \mathcal {B}\mathcal {B}^*)} \nonumber \\&\quad \le (1+ (6\tau +3)/\rho (\tau ))(\varPsi _1(\bar{u}, \bar{v}, \bar{x}) +\varXi _1). \end{aligned}$$

(56)

Therefore, by using (48), (54), (56), and recalling the positive definiteness of operator $\mathcal {O}_2$, we finally have that

$$\begin{aligned}&\displaystyle \min _{1\le i\le k} [\text {dist}^2(0,F(u^{i+1}, v^{i+1}, x^{i+1})) + \Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^{i+1}-c\Vert ^2]\\&\quad \le \big (\displaystyle \sum _{i=1}^k (\text {dist}^2(0,F(u^{i+1}, v^{i+1}, x^{i+1})) + \Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^{i+1}-c\Vert ^2\big )/k\\&\quad \le C'(\varPsi _1(\bar{u}, \bar{v}, \bar{x})+\varXi _1)/k, \end{aligned}$$

where $C' = C_1\Vert \mathcal {O}_2^{-\frac{1}{2}}\widehat{\mathcal {O}}\mathcal {O}_2^{-\frac{1}{2}}\Vert (1+ (6\tau +3)/\rho (\tau ))+ C_2\sigma ^{-1}\tau /\rho (\tau )$. The limiting property (46) and (47) can be derived in the same way as for the case under condition (i).

This completes the proof of Theorem 4.2. $\square$

Remark 4.3

Theorem 4.2 gives the non-ergodic complexity of the KKT optimality condition, which does not seem to be known even for the classic ADMM with separable objective functions. For the latter, related results about the non-ergodic iteration complexity for the primal feasibility and the objective functions of the special classic ADMM with $\tau = 1$ can be found in Davis and Yin [14]. When $\tau \ne 1$, instead of showing the behavior of the current kth iteration point, we provide a non-ergodic complexity property on the “best point among the first k iterations”, indicating that the iteration sequence may satisfy the O(1 / k) tolerance of the KKT system before the kth step. Thus, it may be of some interest to see whether the slightly better result with the “$\min _{1\le i\le k}$” being removed from (46) holds for $\tau \ne 1$.

4.3 The Ergodic Iteration Complexity for General Coupled Objective Functions

In this subsection, we will discuss the ergodic iteration complexity of the majorized ADMM for solving problem (1). For $k = 1,2,\cdots ,$ denote

$$\begin{aligned}\begin{array}{ll} \hat{x}^k := \displaystyle \frac{1}{k}\displaystyle \sum _{i=1}^k \tilde{x}^{i+1}, \quad \hat{u}^k := \frac{1}{k}\displaystyle \sum _{i=1}^k u^{i+1}, \quad \hat{v}^k := \frac{1}{k}\displaystyle \sum _{i=1}^k v^{i+1}, \quad \hat{w}^k := (\hat{u}^k, \hat{v}^k) \end{array} \end{aligned}$$

and

$$\begin{aligned}\begin{array}{ll} \varLambda _{k+1} := \Vert u^{k+1}_e\Vert ^2_{\mathcal {D}_1 + \mathcal {S}} +\Vert v^{k+1}_e\Vert ^2_{\mathcal {D}_2 +\mathcal {T}+\mathcal {Q}_{22}+\sigma \mathcal {B}\mathcal {B}^*} +(\tau \sigma )^{-1}\Vert x^{k+1}\Vert ^2, \\ \overline{\varLambda }_{k+1} := \varLambda _{k+1} + \varXi _{k+1} + \Vert w^{k+1}_e\Vert ^2_{\mathcal {Q}} + \max (1-\tau , 1-\tau ^{-1})\sigma \Vert \mathcal {A}^*u^{k+1} + \mathcal {B}^*v^{k+1} - c\Vert ^2. \end{array} \end{aligned}$$

Theorem 4.3

Suppose that $\mathcal {S}$ and $\mathcal {T}$ are chosen such that

$$\begin{aligned} \mathcal {Q}_{11} + \sigma \mathcal {A}\mathcal {A}^*+\mathcal {S}\succ 0 \quad \text {and} \quad \mathcal {Q}_{22} + \sigma \mathcal {B}\mathcal {B}^*+\mathcal {T}\succ 0. \end{aligned}$$

Assume that either (a) $\tau \in ]0,1]$ and (31) holds, or (b) $\tau \in ]0,\frac{1+\sqrt{5}}{2}[$ and (32) and (33) hold. Then, there exist constants $D_1$ and $D_2$ that depend only on the initial point and the optimal solution set such that for $k\ge 1$, the following conclusions hold:

• (i)
  $$\begin{aligned} \Vert \mathcal {A}^*\hat{u}^{k} + \mathcal {B}^*\hat{v}^{k} - c\Vert \le D_1/k. \end{aligned}$$

  (57)

• (ii) For case (b), if we further assume that $\mathcal {S}- \eta \mathcal {D}_1\succeq 0$ and $\mathcal {T}- \eta \mathcal {D}_2\succeq 0$, then

  $$\begin{aligned} |\theta (\hat{u}^{k} ,\hat{v}^{k}) - \theta (\bar{u}, \bar{v}) | \le D_2/k. \end{aligned}$$

  (58)

The inequality (58) holds for case (a) without additional assumptions.

Proof

(i) Under the conditions for case (a), (34) indicates that $\{\varPhi _{k+1}(\bar{u}, \bar{v}, \bar{x})\}$ is a non-increasing sequence, which implies that

$$\begin{aligned} (\tau \sigma )^{-1}\Vert x^{k+1} - \bar{x}\Vert ^2 \le \varPhi _{k+1}(\bar{u}, \bar{v}, \bar{x}) \le \varPhi _1(\bar{u}, \bar{v}, \bar{x}). \end{aligned}$$

Similarly, under the conditions for case (b), we can get from (38) that

$$\begin{aligned} (\tau \sigma )^{-1}\Vert x^{k+1} - \bar{x}\Vert ^2\le \varPsi _{k+1}(\bar{u}, \bar{v}, \bar{x})+\varXi _{k+1}\le \varPsi _1(\bar{u}, \bar{v}, \bar{x}) + \varXi _1. \end{aligned}$$

Therefore, in terms of the ergodic primal feasibility, we have that

$$\begin{aligned}&\Vert \mathcal {A}^*\hat{u}^{k} + \mathcal {B}^*\hat{v}^{k} - c\Vert ^2 \nonumber \\&\quad = \Vert \displaystyle \frac{1}{k}\sum _{i=1}^k (\mathcal {A}^*{u}^{i+1} + \mathcal {B}^*{v}^{i+1} - c)\Vert ^2 \nonumber \\&\quad = \Vert (\tau \sigma )^{-1}(x^{k+1} - x^1)\Vert ^2/k^2\nonumber \\&\quad \le 2\Vert (\tau \sigma )^{-1}(x^{k+1} - \bar{x})\Vert ^2/k^2 + 2\Vert (\tau \sigma )^{-1}(x^1 - \bar{x})\Vert ^2/k^2 \le C_3/k^2, \end{aligned}$$

(59)

where

$$\begin{aligned} C_3 = \left\{ \begin{array}{ll} 2(\tau \sigma )^{-1}\varPhi _1(\bar{u}, \bar{v}, \bar{x}) +2\Vert (\tau \sigma )^{-1}(x^1 - \bar{x})\Vert ^2 \quad \text {for case (a)},\\ 2(\tau \sigma )^{-1}(\varPsi _1(\bar{u}, \bar{v}, \bar{x}) + \varXi _1) +2\Vert (\tau \sigma )^{-1}(x^1 - \bar{x})\Vert ^2 \quad \text {for case (b)}. \end{array}\right. \end{aligned}$$

Then, by taking the square root on inequality (59), we can obtain (57).

(ii) For the complexity of primal objective functions, first, we know from (13) that

$$\begin{aligned}\begin{array}{ll} p(u)\ge p(\bar{u}) + \langle -\mathcal {A}\bar{x} - \nabla _u\phi (\bar{w}), u-\bar{u}\rangle , \quad \forall u\in \mathcal {U},\\ q(v)\ge q(\bar{v}) + \langle -\mathcal {B}\bar{x} - \nabla _v\phi (\bar{w}), v - \bar{v}\rangle , \quad \forall v\in \mathcal {V}. \end{array} \end{aligned}$$

Therefore, summing them up and by noting $\mathcal {A}^*\bar{u} + \mathcal {B}^*\bar{v} = c$ and the convexity of function $\phi$, we have that

$$\begin{aligned}\begin{array}{ll} \theta (u,v) - \theta (\bar{u}, \bar{v}) &{} \ge -\langle \bar{x}, \mathcal {A}^*u + \mathcal {B}^*v - c\rangle + \phi (w) - \phi (\bar{w}) - \langle \nabla \phi (\bar{w}), w-\bar{w}\rangle \\ &{}\ge -\langle \bar{x}, \mathcal {A}^*u + \mathcal {B}^*v - c\rangle , \quad \forall u\in \mathcal {U}, v\in \mathcal {V}. \end{array} \end{aligned}$$

Thus, with $(u,v) = (\hat{u}^{k},\hat{v}^{k})$, it holds that

$$\begin{aligned} \theta (\hat{u}^{k},\hat{v}^{k}) - \theta (\bar{u}, \bar{v})\ge & {} -\langle \bar{x}, \mathcal {A}^*\hat{u}^{k} + \mathcal {B}^*\hat{v}^{k} - c\rangle \nonumber \\\ge & {} \displaystyle -\frac{1}{2}(\frac{1}{k}\Vert \bar{x}\Vert ^2 + k\Vert \mathcal {A}^*\hat{u}^{k} + \mathcal {B}^*\hat{v}^{k} - c\Vert ^2)\nonumber \\\ge & {} \displaystyle -\frac{1}{2}(\Vert \bar{x}\Vert ^2 + C_3)/k, \end{aligned}$$

(60)

where $C_3$ is the same constant as in (59).

For the reverse part, by (9) and (10) we can obtain that for any $i\ge 1$,

$$\begin{aligned}&\phi (w^{i+1}) \le \displaystyle \phi (w^{i}) + \langle \nabla \phi (w^{i}),w^{i+1} - w^i\rangle + \frac{1}{2}\Vert w^{i+1} - w^i\Vert ^2_{\mathcal {Q} + \mathcal {H}},\\&\quad \phi (\bar{w}) \ge \displaystyle \phi (w^{i}) + \langle \nabla \phi (w^{i}),\bar{w}-w^i\rangle + \frac{1}{2}\Vert \bar{w}-w^i\Vert ^2_{\mathcal {Q}}, \end{aligned}$$

which indicates that

$$\begin{aligned} \phi (w^{i+1}) - \phi (\bar{w})\le \langle \nabla \phi (w^i), w^{i+1} - \bar{w}\rangle + \frac{1}{2}\Vert w^{i+1} - w^i\Vert ^2_{\mathcal {Q} + \mathcal {H}} - \frac{1}{2}\Vert w^i - \bar{w}\Vert ^2_{\mathcal {Q}}.\nonumber \\ \end{aligned}$$

(61)

Thus, (22) and (61) imply that for $\tau \in ]0,1]$ and any $i\ge 1$,

$$\begin{aligned}&\theta (u^{i+1}, v^{i+1}) -\theta (\bar{u},\bar{v})\nonumber \\&\quad \le \displaystyle \frac{1}{2}\Vert w^{i+1} - w^i\Vert ^2_{\mathcal {Q}+\mathcal {H}} - \frac{1}{2}\Vert w^i-\bar{w}\Vert ^2_{\mathcal {Q}} +\langle \bar{w} - w^{i+1}, \mathcal {Q}(w^{i+1}- w^i)\rangle \nonumber \\&\qquad + \langle \bar{u} - u^{i+1}, \mathcal {A}\tilde{x}^{i+1}\rangle \displaystyle + \langle \bar{v} - v^{i+1}, \mathcal {B}\tilde{x}^{i+1}\rangle - \langle v^{i+1} - v^i, \mathcal {Q}_{12}^*(\bar{u} - u^{i+1})\rangle \nonumber \\&\qquad +\sigma \langle \mathcal {A}^*( u^{i+1}-\bar{u}), \mathcal {B}^*(v^{i+1}-v^i)\rangle \displaystyle +\langle \bar{u} - u^{i+1}, ( \mathcal {D}_1 + \mathcal {S})(u^{i+1} - u^i)\rangle \nonumber \\&\qquad + \langle \bar{v} -v^{i+1}, ( \mathcal {D}_2+\mathcal {T})(v^{i+1} - v^i)\rangle \nonumber \\&\quad \le \displaystyle \frac{1}{2}(\varLambda _{i} - \varLambda _{i+1}) - \frac{1}{2}(\Vert u^{i+1} - u^i\Vert ^2_{\mathcal {S}} +\Vert v^{i+1} - v^i\Vert ^2_{\mathcal {T}} + \sigma \Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^i - c\Vert ^2 \nonumber \\&\qquad \displaystyle +\sigma (1-\tau )\Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^{i+1} - c\Vert ^2) \le \displaystyle \frac{1}{2}(\varLambda _{i} - \varLambda _{i+1}). \end{aligned}$$

(62)

Therefore, summing up the above inequalities over $i = 1, \cdots k$ and by using the convexity of function $\theta$ we can obtain that

$$\begin{aligned} \theta (\hat{u}_k,\hat{v}_k) - \theta (\bar{u}, \bar{v}) \le (\varLambda _{1}(u,v,x) - \varLambda _{k+1}(u,v,x))/2k \le \varLambda _1/2k. \end{aligned}$$

(63)

The inequalities (60) and (63) indicate that (58) holds for case (a).

Next, assume that the conditions for case (b) hold. Similar to (62), we have that

$$\begin{aligned}&\theta (u^{i+1}, v^{i+1}) -\theta (\bar{u},\bar{v})\\&\quad \le \displaystyle \frac{1}{2}(\overline{\varLambda }_{i} - \overline{\varLambda }_{i+1}) - \frac{1}{2}(\Vert u^{i+1} - u^i\Vert ^2_{\mathcal {S}-\eta \mathcal {D}_1} +\Vert v^{i+1} - v^i\Vert ^2_{\mathcal {T} + \min (\tau , 1+\tau - \tau ^2)\sigma \mathcal {B}\mathcal {B}^* - \eta \mathcal {D}_2} \\&\qquad +\min (1,1 + \tau ^{-1}-\tau )\sigma \Vert \mathcal {A}^*u^{i+1} + \mathcal {B}^*v^{i+1} - c\Vert ^2). \end{aligned}$$

By the assumptions that $\mathcal {S}-\eta \mathcal {D}_1\succeq 0$ and $\mathcal {T} - \eta \mathcal {D}_2\succeq 0$, we can obtain that

$$\begin{aligned} \theta (\hat{u}^{k},\hat{v}^{k}) - \theta (\bar{u}, \bar{v})\le (\overline{\varLambda }_1 - \overline{\varLambda }_{k+1})/2k\le \overline{\varLambda }_1/2k. \end{aligned}$$

(64)

Thus, by (63) and (64) we can obtain (58). $\square$

Below we make a remark about the results in Theorem 4.3.

Remark 4.4

The results in Theorem 4.3, which are on the ergodic complexity of the primal feasibility and the objective function, respectively, are extended from the work of Davis and Yin [14] on the classic ADMM with separable objective functions. However, there is no corresponding result available on the dual problem. Therefore, it will be very interesting to see if one can develop a more explicit ergodic complexity result containing all the three parts in the KKT condition.

5 Conclusions

In this paper, we establish the convergence properties for the majorized ADMM with a large step length to solve linearly constrained convex programming, whose objective function includes a coupled smooth function. From Theorem 4.1, one can see the influence of the coupled objective on the convergence condition. For $\tau \in ]0,\frac{1+\sqrt{5}}{2}[$, a joint condition like (31) or (33) is needed to analyze the behaviour of the iteration sequence. One can further observe that the parameter $\eta$, which controls the off-diagonal term of the generalized Hessian, also affects the choice of proximal operators $\mathcal {S}$ and $\mathcal {T}$. However, as is pointed out in Remark 4.2, when the coupled function is convex quadratic, $\eta = 0$ and the corresponding influence would disappear. Although, in this paper we focus on the two-block case, it is not hard to see that, with the help of the Schur complement technique introduced in  [15], one can apply our majorized ADMM to solve large scale convex optimization problems with many smooth blocks.