On the Behaviour of a Periodically Forced and Thermostatted Harmonic Chain

Abstract

We consider a chain consisting of $n+1$ harmonic oscillators subjected on the right to a time dependent periodic force ${{\mathcal {F}}}(t)$ while Langevin thermostats are attached at both endpoints of the chain. We show that for long times the system is described by a Gaussian measure whose covariance function is independent of the force, while the means are periodic. We compute explicitly the work and energy due to the periodic force for all n including $n\rightarrow \infty$.

1 Introduction

In this work we consider the conversion of work into heat in a simple model system: a pinned harmonic chain of $n+1$ particles on which work is performed by an external periodic force acting at one of the endpoints. The system is also in contact with thermal reservoirs, placed at both of its endpoints, which absorb the energy generated by the work. In the absence of the reservoirs the response of the system to the external forcing depends entirely on whether the frequency $\omega$ of the external force coincides with the normal frequencies of the chain $\{ \omega _j, j=0,\ldots , n\}$. When $\omega \ne \omega _j$ the system adjusts itself to be out of phase with the force so that there is no work done on the average. If on the other hand the system is in resonance with the force, i.e. $\omega =\omega _j$ for some j, then the amplitude of the oscillation tends to infinity as time $t\rightarrow \infty$.

The situation is different in the presence of the thermostats. They cause the oscillations at resonance to be damped and as a result the work done by the force is strictly finite for all values of $\omega$.

There is still a strong dependence on $\omega$, as far as the magnitude of the work is concerned, when n gets large. This difference becomes qualitative when $n\rightarrow \infty$ and the spectrum of the harmonic chain becomes dense in an interval ${\mathcal {I}}$. The work done and the internal energy of the chain depend strongly on whether $\omega$ lies in the interior of ${\mathcal {I}}$, or not.

Due to the linearity of the system there is a clear division, in the long time properties of the system, between those due to temperatures of the thermal reservoirs and those due to the external force. The energy flowing through the system as a result of the presence of the thermal reservoirs we call thermal energy. It is not influenced by the external force and its behavior is the same as in [14] and [12]. The energy flow due to the work of the external force we call mechanical energy. It is independent of the temperatures of the reservoirs, and it is influenced only by the corresponding damping. For finite n and pure damping equal on both sites this was computed in section 4 of [13] in terms of the Green function of the corresponding damped harmonic chain. The main objective of the present note is the exact calculation of the asymptotic behavior as $n\rightarrow \infty$ of the work and the mechanical energy. Calculation of these quantities, turns out to be quite complicated, but leads to explicit expressions for their asymptotics. In particular we show that, for forcing frequency outside ${\mathcal {I}}$, the work, the mechanical energy and its flow become negligible as $n\rightarrow \infty$. Inside ${\mathcal {I}}$ these quantities oscillate fast and their asymptotic behavior can be described in terms of Young measures.

The results of the present work remain also valid in the case of unpinned harmonic chain. It suffices to set the pinning constant $\omega _0=0$ in our formulas describing the work and energy functionals. Obviously we now always have $\omega >\omega _0=0$ and consider the motion relative to the center of mass positioned at zero.

Agarwalla et.al. [1] consider a physical situation similar to ours in a quantum setup using the Keldysh formalism of nonequilibrium Green’s functions. They investigate, among other things, the following setup: an infinite harmonic chain on the integer lattice ${\mathbb {Z}}$ without pining. The continuous spectrum of this chain lies in [0, 2]. They calculate then the work done on this system by applying various types of periodic forces, with frequencies in the interval [0, 2], to the $N_c$ particles in the middle, with $N_c$ varying between 1 and 40. The sign of the forces alternate from even to odd sites as if the particles had opposite charges on odd and even lattice sites in an external electric field. The left and right parts of the infinite chain, are initially taken at equilibrium at temperatures $T_L$ and $T_R$, respectively, that corresponds to Rubin baths, see [15] and also [16]. Since the spectrum of their system is continuous they do not have problems with resonances.

For anharmonic interaction the situation is qualitatively very different. The non-linearity produces many new effects, see [7, 13]. The case of a harmonic chain with a random velocity flip has been studied in [9,10,11], see also [18, 19].

2 Description of the System

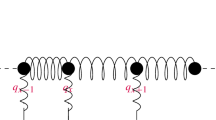
The configurations of our system, consisting of $n+1$ pinned harmonic oscillators, are described by

$$\begin{aligned} ({\textbf{q}}, {\textbf{p}}) = (q_0, \dots , q_n, p_0, \dots , p_n) \in \Omega _n:={{\mathbb {R}}}^{n+1}\times {{\mathbb {R}}}^{n+1}. \end{aligned}$$

(2.1)

We should think of the positions $q_x$ as the relative displacement of an atom from a point x belonging to the integer lattice interval ${{{\mathbb {I}}}_n= \{0,\ldots ,n\}}$ and $p_x$ as its respective momentum.

The total energy of the chain is given by the Hamiltonian:

$$\begin{aligned} \mathcal {H}_n ({\textbf{q}}, {\textbf{p}}):= \sum _{x=0}^n e_x ({\textbf{q}}, {\textbf{p}}), \end{aligned}$$

(2.2)

where the microscopic energy density at x is given by

$$\begin{aligned} e_x ({\textbf{q}}, {\textbf{p}}):= \frac{p_x^2}{2} + \frac{1}{2} (q_{x}-q_{x-1})^2 +\frac{\omega _0^2 q_x^2}{2},\quad x \in {{\mathbb {I}}}_n. \end{aligned}$$

(2.3)

Here we let $q_{-1}:=q_0$.

The microscopic dynamics of the process describing the total chain is given by

$$\begin{aligned} \begin{aligned} \dot{q}_x(t)&= p_x(t), \qquad \qquad x\in {{\mathbb {I}}}_n,\\ \dot{p}_x(t)&= \Delta _x q_x-\omega _0^2 q_x,\quad x\in {{\mathbb {I}}}_n^o= \{1, \dots , n-1\} \end{aligned} \end{aligned}$$

(2.4)

and at the boundaries by

$$\begin{aligned} \textrm{d}p_0(t)&= \; \Big (q_1(t)-q_0(t) - \omega _0^2 q_0 \Big ) \textrm{d}t - 2 \gamma _- p_0(t) \textrm{d}t +\sqrt{4 \gamma _- T_-} \textrm{d}\widetilde{w}_-(t), \nonumber \\ \textrm{d}p_n(t)&= \; \Big (q_{n-1}(t) -q_n(t) -\omega _0^2 q_n(t) \Big ) \textrm{d}t + \; {{\mathcal {F}}}(t/\theta ) \textrm{d}t - 2 \gamma _+ p_n(t) \textrm{d}t +\sqrt{4 \gamma _+ T_+} \textrm{d}{\widetilde{w}}_+(t). \end{aligned}$$

(2.5)

Here $\Delta q_x=q_{x+1}+q_{x-1}-2q_x$, $x\in {{\mathbb {Z}}}$ is the laplacian on the integer lattice ${{\mathbb {Z}}}$, $\omega _0>0$ is a pinning constant, ${\widetilde{w}}_-(t)$ and ${\widetilde{w}}_+(t)$ are two independent standard one dimensional Wiener processes and $\gamma _\pm$ are non-negative constants that describe the respective strengths of the Langevin thermostats.

We assume the force ${{\mathcal {F}}}(t)$ to be a smooth periodic function of period 1 and parameter $\theta$ rescales the period. We will suppose, without losing generality, that

$$\begin{aligned} \int _0^1 {{\mathcal {F}}}(t) \textrm{d}t = 0, \qquad \int _0^1 {{\mathcal {F}}}(t)^2 \textrm{d}t > 0. \end{aligned}$$

(2.6)

The generator of the dynamics is given by

$$\begin{aligned} {\mathcal {G}}_t = {\mathcal {A}}_t + 2\sum _{\iota \in \{-,+\}}\gamma _{\iota } S_\iota , \end{aligned}$$

(2.7)

where

$$\begin{aligned} {\mathcal {A}}_t = \sum _{x=0}^n p_x \partial _{q_x} + \sum _{x=0}^n (\Delta q_{x}-\omega ^2_0q_x) \partial _{p_x} + {{\mathcal {F}}}(t/\theta ) \partial _{p_n}. \end{aligned}$$

(2.8)

By convention we let $q_{n+1}:=q_n$ and $q_{-1}= q_0$. Furthermore

$$\begin{aligned} S_-= T_- \partial _{p_0}^2 - p_0 \partial _{p_0},\qquad S_+= T_+ \partial _{p_n}^2 - p_n \partial _{p_n} \end{aligned}$$

(2.9)

The energy currents are

$$\begin{aligned} \begin{aligned}&{\mathcal {G}}_t e_x = j_{x-1,x} - j_{x,x+1},\\&j_{x,x+1}:=- p_x (q_{x+1}- q_x), \qquad \text {if } x \in \{0,...,n-1\}, \end{aligned} \end{aligned}$$

(2.10)

and at the boundaries

$$\begin{aligned} j_{-1,0}:= 2 { \gamma }_- \left( T_- - p_0^2 \right) \qquad j_{n,n+1}:= -2 { \gamma }_+ \left( T_+ - p_n^2 \right) - {{\mathcal {F}}}(t/\theta ) p_n. \end{aligned}$$

(2.11)

We are interested in the long time behavior of the system. In the absence of the external forcing, ${{\mathcal {F}}}(t)\equiv 0$, this is just the model considered in [14], with $\omega _0=0$, and in [12] for $\omega _0>0$. In the case when ${{\mathcal {F}}}(t)\equiv 0$, starting with any initial configuration $({\textbf{q}}(0), \textbf{p}(0))$ (or any initial probability distribution $\mu _0(\textrm{d}{\textbf{q}}, \textrm{d}{\textbf{p}})$) the system approaches a stationary Gaussian distribution $\mu _{\textrm{stat}}(\textrm{d}{\textbf{q}}, \textrm{d}{\textbf{p}})$, in which the expectation values of $q_x$ and $p_x$ vanish, i.e. $\overline{q}_x(t)=0$ and ${\overline{p}}_x(t)=0$, while the covariances between components of $({\textbf{q}}, {\textbf{p}})$ are given explicitly.

In particular the expectation of the energy current ${\overline{j}}_{x,x+1}$ between sites x and $x+1$, that is independent of x and t, is given by

$$\begin{aligned} {\overline{j}}_{x,x+1}=(c+o(1))(T_--T_+),\quad \text{ as } n\gg 1, \end{aligned}$$

(2.12)

with

$$\begin{aligned} c=\frac{\gamma }{1+4\gamma ^2+2\gamma \omega _0(\gamma \omega _0+\sqrt{1+4\gamma ^2+ (\gamma \omega _0)^2})}, \end{aligned}$$

when $\gamma _-=\gamma _+=\gamma$, see [12, formula (37), p. 240]. In the case $\omega _0=0$ the term o(1) in the formula (2.12) can be omitted (no dependence on n) and we have $c=\frac{\gamma }{1+4\gamma ^2}$, see [12, formula (40), p. 241].

Equation (2.12) implies that the thermal conductivity is proportional to n - the size of the system - and becomes infinite in the limit $n\rightarrow +\infty$, see also [14]. In fact the ”temperature” $T_x$, defined as the variance of $p_x^2$, is independent of x, except near the boundary points $x=0,n$. Adding now the periodic force of period $\theta$ leads, as $t\rightarrow +\infty$, to a Gaussian, periodic stationary state $\{\mu _t^P, t\in [0,+\infty )\}$, whose covariances are the same as in the case when no force is applied. For any functions $F=F(\textbf{q},\textbf{p})$ and $G=G(t)$ define

$$\begin{aligned} {\overline{F}}(t) = \int _{\Omega _n} F \textrm{d}\mu _t^P\quad \text{ and }\quad \langle \langle G\rangle \rangle = \frac{1}{\theta }\int _0^\theta G(t) \textrm{d}t. \end{aligned}$$

(2.13)

The periodic stationary state has the property that $\langle \langle \overline{{\mathcal {G}} F}\rangle \rangle = 0$ for any F in the domain of ${\mathcal {G}}_t$.

The expectation values of the position and momentum ${\overline{q}}_x(t)$ and ${\overline{p}}_x(t)$ are now $\theta$-periodic and independent of the temperature of the reservoirs. They are given by

$$\begin{aligned} \left( \begin{array}{c}\overline{\textbf{q}}(t)\\ \overline{\textbf{p}}(t) \end{array}\right) =\int _{-\infty }^t e^{-A(t-s)}\;{{\mathcal {F}}}(s/\theta )\textrm{e}_{p,n+1}\textrm{d}s. \end{aligned}$$

Here A is a $2\times 2$ block matrix made of $(n+1)\times (n+1)$ matrices of the form

$$\begin{aligned} A= \left( \begin{array}{cc} 0&{}-\textrm{Id}_{n+1}\\ -\Delta _{\textrm{N}}+\omega _0^2&{} \Gamma \end{array} \right) , \end{aligned}$$

where $\textrm{Id}_{n+1}$ is the $(n+1)\times (n+1)$ identity matrix, $\Delta _{\textrm{N}}$ is the Neumann laplacian on ${{\mathbb {I}}}_n$:

$$\begin{aligned} \Delta _{\textrm{N}} f_x:= \Delta f_x,\quad x\in {{\mathbb {I}}}_n^o\quad \text{ and } \quad \Delta _{\textrm{N}} f_0=f_1-f_0,\quad \Delta _{\textrm{N}} f_n=f_{n-1}-f_n. \end{aligned}$$

(2.14)

Furthermore $\Gamma$ is the diagonal matrix

$$\begin{aligned} \Gamma =2\left( \begin{array}{ccccc} \gamma _-&{}0&{}\ldots &{}0&{}0\\ 0&{} 0&{}\ldots &{}0&{}0\\ \vdots &{} \vdots &{}\vdots &{}\vdots &{}\vdots \\ 0&{} 0&{}\ldots &{}0&{}0\\ 0&{} 0&{}\ldots &{}0&{}\gamma _+ \end{array} \right) . \end{aligned}$$

The column vector $\textrm{e}_{p,n+1}$ is given by $\textrm{e}_{p,n+1}^T=[\underbrace{0,\ldots ,0}_{2n+1 - \textrm{times}},1].$ Notice that the first of the conditions (2.4) implies that $\langle \langle {\overline{p}}_x\rangle \rangle = 0$, while the second gives $\langle \langle \overline{q}_x\rangle \rangle = 0$.

The expected value of energy, averaged over a period, breaks up into the mechanical part, coming from the averaged position $\overline{\textbf{q}}(t)$ and momentum $\overline{\textbf{p}}(t)$, which is independent of the temperature of the reservoirs, and the thermal part, which is independent of the external force. More precisely

$$\begin{aligned} \langle \langle e_x\rangle \rangle =\langle \langle e_x^{\textrm{mech}}\rangle \rangle +\langle \langle e_x^{\textrm{th}}\rangle \rangle , \end{aligned}$$

(2.15)

where the mechanical component of the energy is given by

$$\begin{aligned} e_x^{\textrm{mech}}(t):=\frac{1}{2}\Big [{\overline{p}}_x^2(t)+\omega _0^2 {\overline{q}}_x^2(t)+\big ({\overline{q}}_x(t)-{\overline{q}}_{x-1}(t)\big )^2\Big ],\quad x\in {{\mathbb {I}}}_n \end{aligned}$$

(2.16)

and the thermal part is

$$\begin{aligned} e_x^{\textrm{th}}(t):=\frac{1}{2}{{\mathbb {E}}}\Big [ p_x'(t)^2+\omega _0^2 q_x'(t)^2+\big (q_x'(t)- q_{x-1}'(t)\big )^2\Big ],\quad x\in {{\mathbb {I}}}_n, \end{aligned}$$

(2.17)

where $q_x'(t)=q_x(t)-{\overline{q}}_x(t)$ and $p_x'(t) =p_x(t)-{\overline{p}}_x(t)$ and ${{\mathbb {E}}}$ denotes the average with respect to the initial data and the realizations of the Wiener processes in (2.5). As before, we adopt the convention ${\overline{q}}_{-1}(t):={\overline{q}}_{0}(t)$ and likewise $q_{-1}'(t):= q_{0}'(t)$.

As already mentioned in the Introduction one of the goals of the present paper is to describe the work done by the force on the system. It is given by

$$\begin{aligned} W(n)=\frac{1}{\theta }\int _0^\theta {{\mathcal {F}}}(t/\theta ) {\overline{p}}_n(t) \textrm{d}t. \end{aligned}$$

(2.18)

W(n) is always positive, generates energy fluxes into the two heat reservoirs. Furthermore, we describe the time average of the mechanical energy functional given by eq. (2.16). Its thermal counterpart does not depend on time and has been described in [12, 14]. We mention here also that the case $n=0$, i.e. a single oscillator in contact with a heat bath and driven by an external unbiased time-periodic force, has been fully characterized in [17].

3 Results

In what follows we will use the dispersion relation of the infinite chain given by

$$\begin{aligned} \omega (r)=\sqrt{\omega _0^2+4\sin ^2\left( \frac{\pi r}{2}\right) }, \qquad r\in [0,1] \end{aligned}$$

(3.1)

and its inverse defined for $\omega \in {\mathcal {I}}:= [\omega _0, \sqrt{\omega _0^2 +4}]$ by the formula

$$\begin{aligned} r(\omega ) =\frac{2}{\pi }\arcsin \left( \frac{1}{2} \sqrt{\omega ^2 - \omega _0^2}\right) . \end{aligned}$$

(3.2)

3.1 Work Done by the Force on the System

The work W(n) performed by the force on the system, see (2.18), depends on the period $\theta$. Considering for simplicity the simple mode case when

$$\begin{aligned} {{\mathcal {F}}}(t/\theta )=F\cos (\omega t),\quad \omega :=\frac{2\pi }{\theta } \end{aligned}$$

(3.3)

the work done is given by (see Appendix):

$$\begin{aligned} W(\omega ,n)=\big (\omega F\big )^2 \frac{N(\omega ,n)}{D(\omega ,n)}. \end{aligned}$$

(3.4)

Here

$$\begin{aligned} N(\omega ,n)=\&\gamma _-G^{1}(\omega ,n)^2+\gamma _+G^{0}(\omega ,n)^2 +4{\gamma _-^2\gamma _+}\omega ^2\left( G^{0}(\omega ,n)^2-G^{1}(\omega ,n)^2\right) ^2\nonumber \\ D(\omega ,n)=\ {}&1+8\gamma _-\gamma _+ {\omega ^2}G^1(\omega ,n)^2 +4\omega ^2G^0(\omega ,n)^2(\gamma _-^2+\gamma _+^2)\nonumber \\&+16\gamma _-^2\gamma _+^2\omega ^4\left( G^{0}(\omega ,n)^2-G^{1}(\omega ,n)^2\right) ^2, \end{aligned}$$

(3.5)

where

$$\begin{aligned} G^s(\omega ,n)=G_{0,sn}(\omega ,n), \quad s=0,1, \end{aligned}$$

(3.6)

and

$$\begin{aligned} G_{x,y}(\omega ,n)=\frac{1}{n+1}\cdot \frac{1}{\omega _0^2-\omega ^2} +\frac{2}{n+1}\sum _{j=1}^n\frac{ \cos (\frac{\pi j(2x+1)}{2(n+1)}) \cos (\frac{\pi j(2y+1)}{2(n+1)})}{\omega _j^2-\omega ^2},\quad x,y\in {{\mathbb {I}}}_n\nonumber \\ \end{aligned}$$

(3.7)

is the Green’s functions of $-\Delta _N+\omega _0^2-\omega ^2$, and $\pm \omega _j$, $j=0,\ldots ,n$ are the eigenvalues of $-\Delta _N+\omega _0^2$ defined by $\omega _j = \omega \left( \frac{j}{n+1}\right)$ where $\omega (r)$ is given by (3.1).

It is easy to see from (3.5) that $4\omega ^2\gamma _-N\leqslant D+\gamma _-^2\,G^{1}(\omega ,n)^2$. Therefore, the following bound can be found

$$\begin{aligned} W(\omega ,n)\leqslant \frac{\big (\omega F\big )^2}{4}\Big (\frac{1}{\gamma _-}+\frac{1}{\gamma _+}\Big ),\quad n=1,2,\ldots . \end{aligned}$$

(3.8)

The functions $G^s(\omega ,n)$ can be computed explicitly:

$$\begin{aligned} G^s(\omega ,n)=\frac{1}{n+1}\cdot \frac{1}{\omega _0^2-\omega ^2} +\frac{2}{n+1}\sum _{j=1}^n\frac{(-1)^{j s}\cos ^2(\frac{\pi j}{2(n+1)})}{\omega _j^2-\omega ^2}\quad ,\quad s=0,1, \end{aligned}$$

(3.9)

There are very different behaviors of $W(\omega ,n)$ depending on whether $\omega$ is in the spectrum of the harmonic chain, or not, see Fig. 1.

Fig. 1

Behavior of the work for $\omega _0=1$, $n=50$ with $\gamma _\pm =1$ (left figure) and $\gamma _-=1$, $\gamma _+=1/10$ (right figure). The red points are the values of work computed at the points $\omega _j$ of the harmonic spectra using equation (3.11). Note the larger magnitude of the vertical scale on the right diagram

In particular, the formula (3.4) cannot be applied directly when $\omega =\omega _j$ as then both $G^s(\omega ,n)$, $s=0,1$ are divergent. However, we can still use the formula to find $W(\omega _j,n)$, because both $N(\omega ,n)$ and $D(\omega ,n)$ have the same order of magnitude in the neighborhood of $\omega _j$ and, due to the cancellation, the work remains finite.

More precisely, assume that given j we have $\omega ^2=\omega ^2_{j}+\epsilon$ for some $\epsilon \ll 1/n$. The Green’s functions can be then written in the form

$$\begin{aligned} G^s(\omega ,n)=\frac{2 (-1)^{js}}{n+1}\cos ^2\left( \frac{\pi j}{2(n+1)}\right) \epsilon ^{-1}+{\overline{G}}^s(\omega ,n) \end{aligned}$$

(3.10)

where ${\overline{G}}^s(\omega ,n)$ is of order O(1) for $\epsilon \ll 1/n$. We obtain then

$$\begin{aligned} W(\omega _j,n)=\frac{F^2}{4}\cdot \frac{\gamma _++\gamma _-+16\gamma _+\gamma _-^2\omega _j^2 S(\omega _j,n)}{(\gamma _++\gamma _-)^2+16\gamma _+^2\gamma _-^2\omega _j^2 S(\omega _j,n)} \end{aligned}$$

(3.11)

where

$$\begin{aligned} S(\omega _j,n)={\overline{G}}^0(\omega _j,n)-(-1)^j{\overline{G}}^1(\omega _j,n). \end{aligned}$$

(3.12)

In particular, (3.11) implies that

$$\begin{aligned} W(\omega _j,n)\sim \frac{F^2}{4\gamma _{-}, },\quad \text{ as } \gamma _{+}\rightarrow 0\quad \text{ and } \quad W(\omega _j,n)\sim \frac{F^2}{4\gamma _{+}, },\quad \text{ as } \gamma _{-}\rightarrow 0. \end{aligned}$$

If $\gamma _+ = 0$ the formula (3.4) for the work simplifies to

$$\begin{aligned} W(\omega ,n) = \left( \omega F\right) ^2 \frac{\gamma _- G^1(\omega ,n)^2}{1+4\gamma _-^2\omega ^2 G^0(\omega ,n)^2} \end{aligned}$$

(3.13)

that gives $W(\omega ,n) \rightarrow 0$, as $\gamma _- \rightarrow 0$, if $\omega \ne \omega _j$. This means that outside the resonance frequences, no work is done on the system if dissipation is absent. Recall also that when $\gamma _+ = \gamma _-= 0$ the stationary periodic state does not exist as the energy keeps accumulating inside the system.

3.1.1 Work in the Case $n\rightarrow +\infty$ when $\omega$ Lies Outside the Harmonic Chain Spectrum

Consider now the case $n\gg 1$. The spectrum becomes then the interval ${{\mathcal {I}}}:=[\omega _0,\sqrt{\omega _0^2+4}].$ For $\omega$ outside ${{\mathcal {I}}}$ the right hand side of the formula for the Green’s function, see (3.9), does not contain any singular term and $G^s(\omega ,n)$ can be approximated by:

$$\begin{aligned} \begin{aligned} G^0(\omega ,n)&= { 2\int _0^1 \frac{\cos ^2\left( \frac{\pi r}{2}\right) }{\omega _0^2 -\omega ^2 + 4 \sin ^2\left( \frac{\pi r}{2}\right) } \; dr+ O\Big (\frac{1}{n}\Big )}\\&=-\frac{1}{2}+\frac{1}{2\pi }\left( \omega _0^2+4-\omega ^2\right) \int _0^\pi \,\frac{\textrm{d}q}{\omega _0^2+2-\omega ^2-2\cos q}+O\Big (\frac{1}{n}\Big ). \end{aligned} \end{aligned}$$

(3.14)

Using [8, formula 2.553.3] we get¹

$$\begin{aligned} \overline{G}^0(\omega )=\lim _{n\rightarrow \infty }G^0(\omega ,n)=-\frac{1}{2}+\frac{\vert \omega _0^2+4-\omega ^2\vert }{2\sqrt{(\omega _0^2-\omega ^2)(\omega _0^2+4-\omega ^2)}}\quad \omega \notin {{\mathcal {I}}}. \end{aligned}$$

(3.15)

Likewise, we can show

$$\begin{aligned} {\overline{G}}^1(\omega )=\lim _{n\rightarrow \infty }G^1(\omega ,n)=0, \quad \omega \notin {{\mathcal {I}}}. \end{aligned}$$

(3.16)

Combining the above, the work corresponding to $\omega$ outside the harmonic spectra is given by

$$\begin{aligned} \overline{W}(\omega )=\lim _{n\rightarrow \infty }W(\omega ,n)=\frac{\gamma _+\Big (FH\Big )^2 \Big [1+4\Big (\gamma _-H\Big )^2\Big ]}{1+4(\gamma _+^2+\gamma _-^2)H^2+16\Big (\gamma _+\gamma _- H^2\Big )^2}, \end{aligned}$$

(3.17)

where

$$\begin{aligned} H(\omega ):=\omega {\overline{G}}^0(\omega ). \end{aligned}$$

(3.18)

Observe that ${\overline{W}}(\omega )$ tends to 0, when $\gamma _+\rightarrow 0$. Likewise ${\overline{W}}(\omega ) \rightarrow 0$, when either $\omega \rightarrow \infty$ or $\omega \rightarrow 0$. Notice that there is still a strictly positive work done even if $\omega \notin {\mathcal {I}}$, as long as there is dissipation on the point where work is applied ($\gamma _+ >0$) and $\omega$ is finite. We will see in Sect. 4 that this work flows directly into the right reservoir while the current of mechanical energy through the system vanishes as $n\rightarrow \infty$. In particular, it follows from (3.17) that

$$\begin{aligned} \begin{aligned} \lim _{\omega \uparrow \omega _0} {\overline{W}}(\omega )&={\overline{W}}(\omega _0):= \frac{F^2}{4 {\gamma _+}},\\ \lim _{\omega \downarrow \sqrt{\omega _0^2 +4}} {\overline{W}}(\omega )&= \overline{W}(\sqrt{\omega _0^2 +4})\\&=\frac{\gamma _+ F^2 (\omega _0^2 +4) }{4}\cdot \frac{1+ \gamma _-^2 (\omega _0^2 +4)}{1+ (\gamma _-^2 + \gamma _+^2) (\omega _0^2 +4) + \gamma _-^2 \gamma _+^2 (\omega _0^2 +4)^2}. \end{aligned} \end{aligned}$$

(3.19)

This helps to understand the different scales on vertical lines in Fig. 1 depending on the value of $\gamma _-$.

3.1.2 The Case $n\rightarrow +\infty$ and $\omega$ is Inside of the Harmonic Chain Spectrum

The computation of the $n\rightarrow \infty$ limit for the Green’s functions when $\omega$ is inside the harmonic spectral interval ${{\mathcal {I}}}$ is more complicated because there are singularities at the harmonic frequencies $\omega _j$ and the distance between singularities is of order 1/n.

Fix $\omega$ inside of ${{\mathcal {I}}}$. To describe the behavior of $W(\omega ,n)$ near the selected frequency $\omega$ we introduce a function ${\overline{W}}(r,u)$, see formula (B.14). This function is 1-periodic in both variables and satisfies $W(\omega ,n)= {\overline{W}}\big (r(\omega ),(n+1)r(\omega ))+o(1)$, as $n\rightarrow +\infty$. The description of $W(\omega ,n)$ in terms of the associated family of Young measures is given in (B.15) below. The work $W(\omega ,n)$ in the limit, when n is large, is plotted in Fig. 2.

Fig. 2

Behavior of the work functional. First row: $(\gamma _-,\gamma _+)=(1,1)$. Second row: $(\gamma _-,\gamma _+)=(1,1/10)$. Left column: work inside the harmonic spectrum computed using limiting expression (3.4) for $n\rightarrow \infty$. Black dotted curve represents $W(\omega ,n)$ with $n=50$. Red dashed lines stand for the limit of the harmonic spectrum. Blue, cyan and orange lines indicate the harmonic frequencies $\omega =1.0478$, 1.41421 and 2.101, respectively. Right column: diagrams of ${\overline{W}}\big (r,u\big )$, $u\in [-1,1]$ around the harmonic frequencies $\omega =1.0478$ ($r=0.1$, blue), 1.41421 ($r=0.66$, cyan) and 2.101 ($r=0.75$, orange). Note the larger magnitude of the vertical scale in the second row

3.1.3 The Case of a General Periodic Force

Finally, we remark that in the general case of a $\theta$-periodic force of the form

$$\begin{aligned} {{\mathcal {F}}}(t/\theta )=\sum _{\ell =1}^{+\infty }F_{\ell }\cos (\omega (\ell ) t),\quad \text{ where } \omega (\ell ):=\frac{2\pi \ell }{\theta } \end{aligned}$$

(3.20)

whose real valued Fourier coefficients satisfy $\sum _{\ell =1}^{+\infty }(\ell F_{\ell })^2<+\infty$, the work performed by the force can be determined from the formula:

$$\begin{aligned} W(n)=\sum _{\ell =1}^{+\infty }\big (\omega (\ell ) F_{\ell }\big )^2 \frac{N(\omega (\ell ),n)}{D(\omega (\ell ),n)}. \end{aligned}$$

(3.21)

Therefore its behavior, as n gets large, can be determined from the term by term analysis of the series appearing on the right hand side of (3.21).

3.2 Energy

As in Sect. 3.1 we assume that the periodic force ${\mathcal {F}}(t)$ is given by (3.3). The time average of the expectation of the total energy of the chain $E(\omega ,n)$ breaks up into the sum of thermal component $E_\textrm{th}(\omega ,n)=\sum _{x\in {{\mathbb {I}}}_n}\langle \langle e_x^{\textrm{th}}\rangle \rangle$ and the mechanical one $E_{\textrm{mech}}(\omega ,n)=\sum _{x\in {{\mathbb {I}}}_n}\langle \langle e_x^\textrm{mech}\rangle \rangle$, with $e_x^{\textrm{th}}$ and $e_x^{\textrm{mech}}$ defined in (2.17) and (2.16), respectively.

Considering the behavior of the thermal energy functional, defined in (2.15), it has been shown in [14], that in the case $\omega _0=0$ and $\gamma _-=\gamma _+$ we have $\langle \langle e_x^\textrm{th}\rangle \rangle =\frac{1}{2}(T_-+T_+)$ for all $x=1,\ldots ,n-1$. If $\omega _0>0$ and $\gamma _-=\gamma _+$, then [12, formulas (38) and (42)] give

$$\begin{aligned} \langle \langle e_x^{\textrm{th}}\rangle \rangle =\frac{1}{2}(T_-+T_+)(1+o_x), \quad \text{ where } |o_x|\leqslant \frac{C}{g^{x\wedge (n+1-x)}} \end{aligned}$$

for some constants $C>0$, $g>1$ independent of n. As a result we have $E^{\textrm{th}}(\omega ,n)\sim n$, as $n\rightarrow +\infty$.

3.2.1 Formula for the Total Mechanical Energy Functional for a Single Mode Oscillating Force

In what follows we consider the behavior of the mechanical component of the energy. Again, assume that the force is given by (3.3). It turns out, see Sect. 1 of the Appendix, that the time average over the period of the microscopic mechanical energy density equals

$$\begin{aligned} \langle \langle e_x^{\textrm{mech}}\rangle \rangle =\frac{F^2}{2}\cdot \frac{M_x(\omega ,n)}{D(\omega ,n)}, \end{aligned}$$

(3.22)

where $D(\omega ,n)$ is given by (3.5) and

$$\begin{aligned} M_x(\omega ,n)= & {} G^1_x(\omega ,n)^2(\omega ^2+\omega _0^2)+(\nabla ^\star G^1_x)(\omega ,n)^2\\{} & {} +(2\omega \gamma _-)^2 \Big [ {\mathcal {G}}_x(\omega ,n)^2 +(\nabla ^\star {\mathcal {G}}_x)(\omega ,n)^2\Big ], \end{aligned}$$

with (see (3.7))

$$\begin{aligned} G^0_x(\omega ,n)=G_{0,x}(\omega ,n)\quad \text{ and } \quad G^1_x(\omega ,n)=G_{x,n}(\omega ,n). \end{aligned}$$

(3.23)

Using (3.7) we get

$$\begin{aligned} G^s_x(\omega ,n)=\frac{1}{n+1}\cdot \frac{1}{\omega _0^2-\omega ^2} +\frac{2}{n+1}\sum _{j=1}^n\frac{(-1)^{j s}\cos (\frac{\pi j}{2(n+1)})\cos (\frac{\pi j(2x+1)}{2(n+1)})}{\omega _j^2-\omega ^2}\quad ,\quad s=0,1 \end{aligned}$$

and (recall $G^s=G^s_0$, $s=0,1$)

$$\begin{aligned} {\mathcal {G}}_x(\omega ,n)=G^0(\omega ,n) G^1_x(\omega ,n)-G^1(\omega ,n) G^0_x(\omega ,n). \end{aligned}$$

The explicit formula for the total mechanical energy functional, obtained by summing over all x expression (3.22), is presented in (C.1) below.

3.2.2 Energy in the Case $\omega$ lies Outside Harmonic Chain Spectrum

Analogously as in the case of the work functional the behavior $E_{\textrm{mech}}(\omega ,n)$ depends on whether the force frequency belongs to the inside or outside of the spectrum of the harmonic chain. If $\omega \not \in {{\mathcal {I}}}$ the asymptotics of $E_{\textrm{mech}}(\omega ,n)$, as $n\rightarrow +\infty$, can be obtained by a Riemann sum approximation. Then,

$$\begin{aligned} \lim _{n\rightarrow +\infty } E(\omega ,n)=\frac{F^2\left\{ 1 +4\big (\gamma _-H \big )^2\right\} }{4[1+ 4( \gamma _-^2 +\gamma _+ ^2) H^2 +16(\gamma _+\gamma _- H^2)^2] } \Big [K_0 \left( \omega ^2+\omega _0^2\right) +K_1\Big ].\nonumber \\ \end{aligned}$$

(3.24)

Here H is given by (3.18) and

$$\begin{aligned} K_0= \frac{\textrm{d}H}{\textrm{d}\omega ^2},\qquad K_1= \frac{\textrm{d}}{\textrm{d}\omega ^2}\left( \Gamma _0(\omega )-\Gamma _2(\omega )\right) , \end{aligned}$$

where $\Gamma _x(\omega )$ is the Green’s function of the lattice ${{\mathbb {Z}}}$ laplacian. It is given by

$$\begin{aligned}&\Gamma _x(\omega )= \left\{ \Big [\omega _0^2 -\omega ^2\Big ]\Big [ 4+ \omega _0^2 -\omega ^2\Big ]\right\} ^{-1/2}\\&\times \left\{ 1+\frac{1}{2}\Big [\omega _0^2 -\omega ^2\Big ]+\frac{1}{2}\left\{ \Big [\omega _0^2 -\omega ^2\Big ]\Big [4+\omega _0^2 -\omega ^2\Big ]\right\} ^{1/2}\right\} ^{-|x|},\quad \text { when} \quad \omega _0^2 >\omega ^2 \end{aligned}$$

and

$$\begin{aligned}&\Gamma _x(\omega )=- \left\{ \Big [\omega ^2-\omega _0^2 \Big ]\Big [\omega ^2-\omega _0^2-4 \Big ]\right\} ^{-1/2}\\&\times \left\{ 1-\frac{1}{2}\Big [\omega ^2-\omega _0^2 \Big ]- \frac{1}{2} \left\{ \Big [\omega ^2-\omega _0^2 \Big ]\Big [\omega ^2-\omega _0^2-4 \Big ]\right\} ^{1/2} \right\} ^{-|x|},\quad \text {when}\quad \omega _0^2 +4 <\omega ^2. \end{aligned}$$

Note that when $\gamma _+\rightarrow 0$, the formula (3.24) simplifies and we have

$$\begin{aligned} \lim _{n\rightarrow +\infty } E(\omega ,n)=\frac{F^2 }{4 } \Big [K_0 \left( \omega ^2+\omega _0^2\right) +K_1\Big ]. \end{aligned}$$

(3.25)

3.2.3 The Case When $\omega$ is Inside of the Harmonic Chain Spectrum

If, $\omega$ is inside of ${{\mathcal {I}}}$, the time average of $E_\textrm{mech}(\omega ,n)$ is proportional to the size of the system. After normalization we obtain, see Sect. 1 of the Appendix,

$$\begin{aligned} \frac{1}{n}E(\omega ,n)={\overline{E}} \big (r,(n+1)r\big )+o(1) \end{aligned}$$

as $n\rightarrow +\infty$, where ${\overline{E}} \big (r,u\big )$ is 1-periodic in the first and 2-periodic in the second variable. It is described by formulas (C.5) and (C.6). Here r is determined from $\omega$ by formula (3.1).

Behavior of the energy functional is illustrated in Fig. 3.

Fig. 3

Behavior of the energy for $n=50$ with $\gamma _\pm =1$ (left) and $\gamma _+=1$, $\gamma _-=1/10$ (right)

4 Current of Mechanical Energy

The currents of the mechanical energy are given by

$$\begin{aligned} \begin{aligned} \overline{ j_{x,x+1}^{\text {mech}}}(t)&= - {\overline{p}}_x(t)\left( \overline{q}_{x+1}(t) - {\overline{q}}_{x}(t)\right) , \qquad x=0,\dots ,n-1\\ \overline{ j_{-1,0}^{\text {mech}}}(t)&= -\gamma _- {\overline{p}}_0(t)^2, \qquad \overline{ j_{n,n+1}^{\text {mech}}}(t) = \gamma _+ {\overline{p}}_n(t)^2 - {\mathcal {F}}(t/\theta ) {\overline{p}}_n(t). \end{aligned} \end{aligned}$$

(4.1)

They have all the same time average over the period:

$$\begin{aligned} J^{\text {mech}}(n):= \langle \langle \overline{ j_{x,x+1}^{\text {mech}}}\rangle \rangle . \end{aligned}$$

(4.2)

Note that $W^-(n):=-J^{\text {mech}}(n)$ is the amount of work that goes into the left reservoir. Of course when $\gamma _+ = 0$ we have $W^-(n)= W(n)$. If however $\gamma _+ >0$, then some of the work, denoted by $W^+(n)= W(n)-W^-(n)$, goes into the right reservoir.

We compute first $W^-(n)$, using $\overline{ j_{-1,0}^{\text {mech}}}(t)$, as it involves simpler formulas. From (A.5) we have

$$\begin{aligned} \begin{aligned}&{\overline{p}}_0(t) = \text {Re}\left( i\omega {e^{i\omega t}} {\widetilde{q}}_0(\omega )\right) \\&= \frac{F G^1(\omega ,n) \left[ \text {Re}({\widetilde{D}}(\omega ,n)) \omega \cos (\omega t) - \text {Im}({\widetilde{D}}(\omega ,n)) \omega \sin (\omega t)\right] }{\left| {\widetilde{D}}(\omega ,n)\right| ^2} \end{aligned} \end{aligned}$$

(4.3)

and, recalling that $\omega = \frac{2\pi }{\theta }$,

$$\begin{aligned} \begin{aligned} J^{\text {mech}}(n) = -\frac{\gamma _-}{\theta } \int _0^\theta \overline{p}_0(t)^2 \textrm{d}t = - \gamma _-\Big ( F\omega G^1(\omega ,n)\Big )^2 \end{aligned} \end{aligned}$$

(4.4)

As a result, combining with (3.4), we get

$$\begin{aligned} W^-(n)=\gamma _-\Big ( F\omega G^1(\omega ,n)\Big )^2,\qquad W^+(n)= W(n)- W^-(n). \end{aligned}$$

(4.5)

Notice that if $\omega \notin {\mathcal {I}}$, since $G^1(\omega ,n) \mathop {\longrightarrow }_{n\rightarrow \infty } 0$, we have $J^{\text {mech}}(n) \mathop {\longrightarrow }_{n\rightarrow \infty } 0$. Comparing with (3.17) we deduce that if $\omega \notin {\mathcal {I}}$, all the work goes to the right thermostat as $n\rightarrow \infty$.

If $\omega \in (\omega _0, \sqrt{\omega _0^2+4})$, then $W^-(n)=\overline{W}^-\Big (r(\omega ),(n+1)r(\omega )\Big )+o(1),$ where the formula for $\overline{W}^- (r, u)$ can be obtained from (4.5) by replacing $G^1(\omega ,n)$ by the function ${\overline{G}}^1(r,u)$ defined in (B.13). We also have $W^+(n)=\overline{W}^+\Big (r(\omega ),(n+1)r(\omega )\Big )+o(1),$ where $\overline{W}^+ (r, u) =\overline{W}(r, u)-\overline{W}^- (r, u)$, where $\overline{W}(r, u)$ is given by (B.14).

5 Conclusion

In summary, in the present paper we consider a finite, one dimensional harmonic chain in contact with thermal reservoirs, placed at both of its endpoints. In addition, an external periodic force acts at one endpoint. We present exact analytical expressions for the work done by the force (see formula (3.4)), the mechanical component of the energy density (see (3.22)) and its current (see (4.3)). The asymptotics of these expresssions is described when the size of the system grows to infinity both in the case when the frequency $\omega$ of the external forcing lies outside and inside the harmonic chain spectrum. In the latter case the limit of the work and energy functionals are characterized in Sects. 1 and 1 of the Appendix. If $\omega$ is outside the spectrum the asymptotics of the work and energy are given by (3.17) and (3.25), respectively.

Appendices

Appendix A. Time Harmonics of the Position and Momenta Averages

Recall that ${\mathcal {F}}(t/\theta )=\textrm{Re}\Big (Fe^{i\omega t}\Big )$. Consider the Fourier coefficients of the means of the positions and momenta

$$\begin{aligned} {\widetilde{p}}_x =\frac{1}{\theta }\int _0^\theta e^{- i\omega t}{\overline{p}}_x(t)\textrm{d}t,\quad {\widetilde{q}}_x=\frac{1}{\theta }\int _0^\theta e^{- i\omega t}{\overline{q}}_x (t)\textrm{d}t,\quad x\in {{\mathbb {I}}}_n. \end{aligned}$$

(A.1)

We have ${\overline{p}}_x(t)=\textrm{Re}\Big ({\widetilde{p}}_xe^{i\omega t}\Big )$ and ${\overline{q}}_x(t)=\textrm{Re}\Big ({\widetilde{q}}_xe^{i\omega t}\Big )$.

From (2.4) and (2.5) we obtain ${\widetilde{p}}_x =i\omega {\widetilde{q}}_x$ and

$$\begin{aligned} i\omega {\widetilde{p}}_x =\Big ( \Delta _\textrm{N} -\omega _0^2 -2i\gamma _x \omega \Big ){\widetilde{q}}_x+F\delta _{x,n}, \; \quad x\in {{\mathbb {I}}}_n. \end{aligned}$$

(A.2)

Here $\gamma _x= \gamma _-\delta _{0,x}+ \gamma _+\delta _{n,x}$. Substituting into (A.2) for ${\widetilde{p}}_x$ we get the equation

$$\begin{aligned} 0 = \Big (\Delta _x +\omega ^2-\omega _0^2 - 2i\omega \gamma _x \Big ){\widetilde{q}}_x + F\delta _{x,n}, \; \quad x\in {{\mathbb {I}}}_n. \end{aligned}$$

(A.3)

Hence, using the notation of (3.23), we can write

$$\begin{aligned} \Big (F-2i\gamma _+ \omega {\widetilde{q}}_n \Big )G^1_x(\omega ,n) -2i\gamma _+ \omega {\widetilde{q}}_0 G^0_x(\omega ,n) = {\widetilde{q}}_x,\quad x\in {{\mathbb {I}}}_n. \end{aligned}$$

(A.4)

For $x=0,n$ we get a closed system of 2 equations for $\widetilde{q}_0$ and ${\widetilde{q}}_n$ that can be solved explicitly and we obtain

$$\begin{aligned} {\widetilde{q}}_0 =\frac{F G^1 (\omega ,n)}{{\widetilde{D}}( \omega ,n)},\quad {\widetilde{q}}_n =\frac{F{\widetilde{N}}(\pm \omega ,n)}{{\widetilde{D}}( \omega ,n)}, \end{aligned}$$

(A.5)

where, using the notation of (3.6), we have

$$\begin{aligned}&{\widetilde{N}}(\omega ,n)=G^0(\omega ,n)+2i\omega \gamma _ -\left( G^0(\omega ,n)^2-G^1(\omega ,n)^2\right) \nonumber \\&{\widetilde{D}}(\omega ,n)=1-4\gamma _+\gamma _-\omega ^2\left( G^0(\omega ,n)^2 -G^1(\omega ,n)^2\right) +2i\omega (\gamma _++\gamma _-)G^0(\omega ,n). \end{aligned}$$

(A.6)

Substituting back into (A.4) we conclude that

$$\begin{aligned} \begin{aligned}&{\widetilde{q}}_x =F\Big (a G^0_x(\omega ,n) +b G^1_x(\omega ,n) \Big ),\quad \text{ where },\\&a=1-2i\omega \gamma _+\frac{{\widetilde{N}}(\omega ,n)}{\widetilde{D}(\omega ,n)},\quad b =-2i\omega \gamma _-\frac{G^1(\omega ,n)}{\widetilde{D}(\omega ,n)}. \end{aligned} \end{aligned}$$

(A.7)

Using (2.18) and the fact that ${\overline{p}}_n(t)=-\omega \textrm{Im}\Big ( {\widetilde{q}}_ne^{i\omega t} \Big )$ we obtain (3.4).

Appendix B.Time Average of Work Functional When $\omega$ is Inside ${{\mathcal {I}}}$ and $n\rightarrow +\infty$

We consider now $\omega \in (\omega _0,\sqrt{\omega _0^2+4})$. We will parametrize the spectrum using $r(\omega ) \in (0,1)$, defined by (3.2), and we study here the asymptotic behaviour of $\widetilde{W}(r,n) =W(\omega (r),n)$. Similarly we define ${\widetilde{G}}^{s}(r,n), s=0,1$.

Denote $j(r) = [(n+1) r]$ (where [x] denotes the integer part of x) and

$$\begin{aligned} u(r) = (n+1) r - [(n+1) r] \in (0,1). \end{aligned}$$

(B.1)

Since we are choosing $\omega \ne \omega _j$, we have that $u(r)\in (0,1)$.

To compute ${\widetilde{G}}^0(r,n)$ we start with extracting the singular term at $\omega _j$. From (3.9) we get

$$\begin{aligned} {{\widetilde{G}}^0(r,n)} =\frac{1}{n+1}\cdot \frac{1}{\omega _0^2-\omega (r)^2} +I_-(r;0,j-1)+I_+(r;1,n-j), \end{aligned}$$

(B.2)

where

$$\begin{aligned} I_\pm (r;m,k)=\frac{2}{n+1}\sum _{\ell =m}^{k} \frac{\cos ^2(\frac{\pi (j(r) \pm \ell )}{2(n+1)})}{\omega \left( \frac{j (r)\pm \ell }{n+1}\right) ^2 -\omega (r)^2}. \end{aligned}$$

(B.3)

For any $1\leqslant k_0\leqslant k$ we break $I_\pm (\omega ;1,k)$ in two terms: one with the first $k_0$ terms and the other with the remaining $k-k_0$ ones. The idea is to assume that k is of order n and $k_0$ is of order $n^a$, with $a\in (0,1)$, when $n\rightarrow \infty$. The first term can be summed up explicitly and for the second we can use the Riemann sum approximation, since we are far away from the singularity that occurs at $\omega _j$. More precisely we can write $I_+(r;0,k)=I_+(r;0,k_0)+I_+(r;k_0+1,k)$. Using the formula

$$\begin{aligned} \cot (\pi x)=\frac{1}{\pi x}-\frac{2x}{\pi }\sum _{j=1}^{+\infty }\frac{1}{j^2-x^2}, \end{aligned}$$

(B.4)

for $k_0 \sim n^a$, $a<1$, and large n we have

$$\begin{aligned} \begin{aligned} I_+(r;0,k_0)= \frac{1}{n+1}\sum _{\ell =0}^{k_0} \frac{\cos ^2(\frac{\pi (j(r) + \ell )}{2(n+1)})}{\cos (\pi r) - \cos \left( \pi \frac{j(r) + \ell }{n+1}\right) }\\ = \frac{1}{n+1}\sum _{\ell =0}^{k_0} \frac{\cos ^2(\frac{\pi (j(r) + \ell )}{2(n+1)})}{-\sin \left( \frac{j(r) + \ell }{n+1}\right) \frac{\pi }{n+1}\left( (n+1)r - j(r) - \ell \right) } + o(1) \\ = - \frac{1}{2\pi }\sum _{\ell =0}^{k_0} \frac{\cot \left( \frac{\pi (j(r) + \ell )}{2(n+1)}\right) }{\left( u(r) - \ell \right) } + o(1) = \frac{\cot (\pi r/2)}{2\pi }\sum _{\ell =0}^{k_0}\frac{1}{\ell - u(r)} + o(1). \end{aligned} \end{aligned}$$

(B.5)

The sum in the last expression diverges, when $k_0\rightarrow \infty$. However, in the expression (B.2) for ${\widetilde{G}}^0$ we have also

$$\begin{aligned} I_-(r;1,k_0)=-\frac{\cot (\pi r/2)}{2\pi }\sum _{\ell =1}^{k_0}\frac{1}{\ell + u(r)}+o(1) \end{aligned}$$

(B.6)

and, as a result of the cancelation, the sum of them has a finite limit as $k_0\rightarrow \infty$. It can be computed and the result is:

$$\begin{aligned} \lim _{k_0\rightarrow \infty }\big (I_+(r;0,k_0)+I_-(r;1,k_0)\big )= -\frac{1}{2}\cot (\pi r/2)\cot (\pi u(r)). \end{aligned}$$

(B.7)

Now we compute the remaining expressions $I_\pm (r;k_0+1,k)$ by using the Riemann sum approximation:

$$\begin{aligned} \begin{aligned}&I_\pm ( r;k_0+1,k)= \frac{2}{n+1}\sum _{\ell =k_0+1}^k \frac{\cos ^2(\frac{\pi (j(r) \pm \ell )}{2(n+1)})}{\omega \left( \frac{j(r) \pm \ell }{n+1}\right) ^2-\omega ^2(r)}\\&= 2 \int _{v_0}^{v} \frac{\cos ^2\left( \frac{\pi }{2}(r \pm \overline{v})\right) }{\omega (r \pm {\overline{v}})^2- \omega (r)^2} d{\overline{v}} +o(1)= \frac{1}{2}\int _{v_0}^{v}\,\frac{\big [1+\cos \big ( \pi (r \pm \overline{v})\big )\big ]}{\cos (\pi r)-\cos (\pi (r \pm {\overline{v}}))} dv +o(1), \end{aligned} \end{aligned}$$

(B.8)

where $v_0=k_0/(n+1)$, $v=k/(n+1)$. The last integral has a logarithmic singularity when $v_0\rightarrow 0$ (i.e. $k_0\ll n$). Nevertheless, when putting together the two terms, we obtain the principal value of the integral at the singular point and, as a result,

$$\begin{aligned}&I(r)=\lim _{n\rightarrow +\infty }\Big (I_+(r;k_0,j) +I_-(r;k_0,n-j)\Big ) = \frac{1}{2} \mathrm{p.v.}\int _{-r}^{1-r}\,\frac{\big [1+\cos \big ( \pi (r+\overline{v})\big )\big ]\textrm{d}{\overline{v}}}{\cos (\pi r)-\cos (\pi (r+ {\overline{v}}))} \nonumber \\&=-\frac{1}{2}+ \cos ^2\big ( \pi r/2\big ) \mathrm{p.v.}\int _{0}^{1}\,\frac{\textrm{d}{\overline{v}}}{\cos (\pi r)-\cos (\pi {\overline{v}})} \end{aligned}$$

(B.9)

(we recall that $k_0\simeq n^a$ with $a\in (0,1)$, and $j=[r (n+1)]$). Using [8, formula 2.551.3, p. 171]

$$\begin{aligned} \int \,\frac{\textrm{d}{\overline{v}}}{\cos (\pi r)-\cos (\pi \overline{v})}=\frac{1}{\pi \sin (\pi r)}\log \Big |\frac{(1+\sin (\pi r))/\cos (\pi r)-\tan \left( \frac{\pi }{2}\big (\overline{v}+\frac{1}{2}\big )\right) }{(1-\sin (\pi r))/\cos (\pi r)-\tan \left( \frac{\pi }{2}\big ({\overline{v}}+\frac{1}{2}\big )\right) } \Big |. \end{aligned}$$

we conclude that that the principal value of the integral on the utmost right hand side of (B.9) equals null. Hence $I(r) = -1/2$.

Finally, putting together (B.7) and (B.9) we find:

$$\begin{aligned}&{{\widetilde{G}}^0(r,n)={\overline{G}}^0\big (r, (n+1)r \big )} + o(1),\quad \text{ where }\nonumber \\&{\overline{G}}^0(r,u)=-\frac{1}{2}\Big (\cot (\pi r/2)\cot (\pi u) +1\Big ). \end{aligned}$$

(B.10)

We will consider $u\in {{\mathbb {R}}}$ and extend periodically the function ${\overline{G}}^0(r,u)$.

We compute ${\overline{G}}^1(r) =\lim _{n\rightarrow +\infty }{\widetilde{G}}^1(r,n)$ by using formula:

$$\begin{aligned} \frac{1}{2}\Big ({\widetilde{G}}^0(r,n)+ {\widetilde{G}}^1(r,n)\Big )= \frac{1}{n+1}\cdot \frac{1}{\omega _0^2-\omega (r)^2}+ \frac{2}{n+1}\sum _{\ell =1}^{n/2}\frac{\cos ^2(\frac{\pi \ell }{n+1})}{4\sin ^2(\frac{\pi \ell }{n+1}) +\omega _0^2-\omega (r)^2}.\nonumber \\ \end{aligned}$$

(B.11)

That is a very similar expression to the original one for $\widetilde{G}^0(r,n)$, see (3.9) with $s=0$, but with factors 2 not present in the denominators of fractions appearing in the infinite sum. Following analogous arguments to the ones used before we find, in the limit $n\rightarrow +\infty$

$$\begin{aligned} \begin{aligned}&\frac{1}{2}\Big ({\widetilde{G}}^0(r,n)+ {\widetilde{G}}^1(r,n)\Big ) = {\overline{H}}\Big (r, (n+1)r \Big ) +o(1),\quad \text{ where }\\&{\overline{H}}(r,u)= -\frac{1}{4}\Big (\cot (\pi r/2)\cot (\pi u/2) +1\Big ). \end{aligned} \end{aligned}$$

(B.12)

Therefore we get ${\widetilde{G}}^1(r,n)={\overline{G}}^1\big (r, (n+1)r \big )+o(1)$, as $n\rightarrow +\infty$, where

$$\begin{aligned} {\overline{G}}^1(r,u)=(-1)^{[u]+1}\frac{ \cot (\pi r/2)}{ 2\sin (\pi u)}. \end{aligned}$$

(B.13)

We have shown therefore that

$$\begin{aligned} \begin{aligned}&{\widetilde{W}}(r,n)= {\overline{W}}(r,(n+1)r) +o(1),\quad \text{ where }\\&{{\overline{W}}(r,u) = F^2 \omega (r)^2\frac{{\overline{N}}(r,u) }{{\overline{D}}(r,u) } }. \end{aligned} \end{aligned}$$

(B.14)

The functions ${\overline{N}}(r,u)$ and ${\overline{D}}(r,u)$ are given by analogues of (3.5), with $G^s(\omega ,n)$ replaced by $\overline{G}^s(r,u)$, respectively for $s=0,1$. As in (3.8) we get

$$\begin{aligned} 0\leqslant {\overline{W}}(r,u)\leqslant \frac{F^2}{4} \left( \frac{1}{\gamma _{-}}+\frac{1}{\gamma _{+}}\right) . \end{aligned}$$

Equality (B.14) can be used to find the family of Young measures that is associated with ${\widetilde{W}}(r,n)$. This is defined, see e.g. [6, Section 1.E.3, p. 16], as a family of measures $\mu (r,\textrm{d}v)$, $v\in {{\mathbb {R}}}$ such that for any test function $\varphi \in L^1[0,1]$ and a bounded continuous function $\Phi \in C_b({{\mathbb {R}}})$

$$\begin{aligned} \lim _{n\rightarrow +\infty } \int _{0}^{1} \Phi \Big (\widetilde{W}(r,n)\Big ) \varphi (r)\textrm{d}r = \int _{0}^{1} {\overline{\Phi }} (r) \varphi (r)\textrm{d}r, \end{aligned}$$

(B.15)

with ${\overline{\Phi }} (r):=\int _{{\mathbb {R}}}\Phi (v)\mu (r,\textrm{d}v).$ Thanks to (B.14) we conclude that the probability measures $\mu (r,\textrm{d}v)$ obtained by transporting the Lebesgue measure $\textrm{m}(\textrm{d}u)$ on (0, 1) by the mapping $u\mapsto {\overline{W}}\big (r,u\big )$ constitute the family of Young measures associated with the sequence ${\widetilde{W}}(r,n)$. We have $\mu (r,A)=\textrm{m}\Big [u: \overline{W}\big (r,u\big ) \in A\Big ]$ for any Borel measurable subset A of ${{\mathbb {R}}}$. Since ${\overline{W}}\big (r,u\big )$ is bounded, piecewise $C^1$-smooth and $\{u: {\overline{W}}\big (r,u\big ) = v\}$ is finite for each r, the Young measures $\mu (r,\textrm{d}v)$, have compactly supported densities. Using the frequency domain in the description of the Young measures, we conclude from (B.15) that

$$\begin{aligned} \lim _{n\rightarrow +\infty } \int _{{\mathcal {I}}} \Phi \Big ( W(\omega ,n)\Big ) \varphi (\omega )\textrm{d}\omega = \int _{{\mathcal {I}}} {\overline{\Phi }} (\omega ) \varphi (\omega )\textrm{d}\omega , \end{aligned}$$

(B.16)

for any function $\varphi \in C_b({{\mathcal {I}}})$. Here ${\overline{\Phi }} (\omega ):=\int _{{\mathbb {R}}}\Phi (v)\mu (r(\omega ),\textrm{d}v).$ We have

$$\begin{aligned}&\lim _{\omega \downarrow \omega _0 } \mu (r(\omega ),\textrm{d}v)=\delta _{\overline{W}(\omega _0)}(\textrm{d}v),\\&\lim _{\omega \uparrow \sqrt{\omega _0^2+4} } \mu (r(\omega ),\textrm{d}v)= \delta _{{\overline{W}}(\sqrt{\omega _0^2 +4}) }(\textrm{d}v), \end{aligned}$$

where, as we recall ${\overline{W}}(\omega _0)$ and ${\overline{W}}(\sqrt{\omega _0^2 +4})$ are given in (3.19). The limit holds in the sense of the weak convergence of measures.

Appendix C. Time Average of Energy in Case $\mathbf \omega$ is Inside of ${{\mathcal {I}}}$

Formula (3.22) is a direct consequence of (2.16) and formula (A.7). Summing over all x we conclude that

$$\begin{aligned} E_{\textrm{mech}}(\omega ,n)&=F^2 \Biggl \{ (\vert a\vert ^2+\vert b\vert ^2)\biggl [ (\omega ^2+\omega _0^2)I_0(\omega ,n)+J_0(\omega ,n) \biggl ] \end{aligned}$$

(C.1)

$$\begin{aligned}&+\textrm{Re}\big (a^*b) \biggl [ (\omega ^2+\omega _0^2)I_1(\omega ,n)+J_1(\omega ,n) \biggl ] \Biggl \}, \end{aligned}$$

(C.2)

where

$$\begin{aligned} I_s(\omega ,n)=\frac{\textrm{d}}{\textrm{d}\omega ^2}G_s(\omega ,n),\quad J_s(\omega ,n)=\frac{\textrm{d}}{\textrm{d}\omega ^2}R_s(\omega ,n) \end{aligned}$$

(C.3)

and

$$\begin{aligned} R_s=\frac{2}{n+1}\sum _{j=1}^n\frac{(-1)^{j s}\sin ^2(\frac{\pi j}{(n+1)})}{4\sin ^2(\frac{\pi j}{2(n+1)})+\omega _0^2-\omega ^2},\quad s=0,1. \end{aligned}$$

(C.4)

The remaining terms have been defined in Section A.

The four functions: $I_s(\omega ,n)$ and $J_s(\omega ,n)$, $s=0,1$, appearing in (C.3) diverge, as $n\rightarrow \infty$, for $\omega$ inside of ${{\mathcal {I}}}$. Computations involving these functions use the same technique as in the case of the asymptotics of the work functional considered in Section B of the Appendix. We obtain

$$\begin{aligned}&e(\omega ,n) =\frac{E_{\textrm{mech}}(\omega ,n)}{n}= \overline{e}\big (r,(n+1)r\big )+o(1),\quad \text{ where } \nonumber \\&{\overline{e}}\big (r,u\big ), = F^2\left[ (\omega ^2+\omega _0^2)\left[ (\vert {\overline{a}}\vert ^2+\vert {\overline{b}}\vert ^2)I_0\big (r,u\big ) +({\overline{a}}^*{\overline{b}}+{\overline{a}}{\overline{b}}^*)I_1\big (r,u\big ) \right] \right. \nonumber \\&+\left. (\vert {\overline{a}}\vert ^2+\vert \overline{b}\vert ^2)J_0\big (u\big )+({\overline{a}}^*{\overline{b}}+{\overline{a}}\overline{b}^*)J_1\big (u\big )\right] +o(1), \end{aligned}$$

(C.5)

with the formulas for terms ${\overline{a}}$ and ${\overline{b}}$ given by analogues of (A.7), where the Green’s functions $G^s(\omega ,n)$ are replaced by ${\overline{G}}^s(r,u)$, $s=0,1$, defined in (B.10) and (B.13). Here r is determined from $\omega$ by eqt. (3.1) and

$$\begin{aligned}&I_s(r,u)=\frac{(-1)^{s[ u]}}{8}\cdot \frac{\cos (s\pi u)}{\sin (\pi r/2)\sin ^2(\pi u)},\nonumber \\&J_s(u)=\frac{ (-1)^{s[u]}}{2}\cdot \frac{\cos (s\pi u)}{\sin ^2(\pi u)},\quad \quad s=0,1. \end{aligned}$$

(C.6)

Figure 4 illustrates the behaviour of $e(\omega )$.

Fig. 4

Behavior of the energy per-oscillator. First row: $(\gamma _-,\gamma _+)=(1,1)$. Second row: $(\gamma _-,\gamma _+)=(1,1/10)$. Left column: energy computed with the limiting expressions for $n\rightarrow \infty$. The oscillating part is obtained directly using the Green’s function expressions with $n=40$ and black dotted curves inside the harmonic spectra zone are computed used the energy expression for $n\rightarrow \infty$. Red dashed lines define the limits of the harmonic spectra. Blue, cyan and orange lines indicate the harmonic frequencies $\omega =1.0478$, 1.41421 and 2.101. Right column: Scaled energy ${\overline{e}}(r,u)$ around the harmonic frequencies $\omega =1.0478$ (blue), 1.41421 (cyan) and 2.101 (orange)