1 Introduction

Markov models have been thoroughly investigated in population dynamics and queueing theory due to their numerous applications in demography, epidemiology, biology, ecology, telecommunications, and social sciences [1–7]. One of the basic examples is a birth-death process which is defined by a set of birth and death rates depending on the population size. As a consequence, the population size plays the role of the state variable while individuals are indistinguishable. More elaborate models include other mechanisms such as migration, catastrophes, food/energy limited supply, or multi-species competition (e.g., prey-predator models). In turn, individuals are distinguishable in queueing theory, e.g., customers are usually served according to their order of arrival into the queue (i.e., their age in the queue), the most common examples being “first in–first out” and “last in–first out” queues. More generally, the service order can be either set by a given deterministic function of customers’ ages, or be random with prescribed age-dependent probabilities.

In this paper, we analyze the extreme case when the service order is fully randomized, i.e., the customers are served independently of their ages. This case can be relevant when the service order is not determined by the age but by other criteria such as, e.g., health state or priority. When these criteria are unknown or hidden, the resulting choice by a server can appear as random. In turn, the age of a randomly chosen customer can affect the “service efficiency” through the probability \(q_k\) with which the customer of age k leaves the queue after receiving the service (e.g., curing a disease). Alternatively, this model can describe “impatient” clients leaving the waiting room with probability \(q_k\) [8]. In the context of population dynamics, an individual is chosen randomly (e.g., by an accident) while the death probability \(q_k\) depends on its age k.

More precisely, we consider the following discrete-time toy model. At the beginning, there is no individuals (or customers). At every time step, a uniformly chosen individual of the population dies (a customer leaves the queue) with a prescribed probability \(q_k\) which depends on its age k. The age of all other individuals (customers) is increased by 1. During the same time step, a new individual is born (a new customer arrives) with probability r. This individual (customer) is assigned with the age 1. In this model, the “birth” (arrival of a new customer) and the “death” (departure of the served customer) are independent of the number of customers and settled by a serving system. These features (random choice of individuals and population-independent rates) make the model distinct from common models in population dynamics (in which the birth-death rates are typically proportional to the population size, yielding exponential-like behavior in the simplest setting) and queueing theory (in which the service order is typically determined by the age).

When all \(q_k = q\), individuals are indistinguishable, and one retrieves an elementary birth-death process governing the population size. Understanding the impact of the age-dependence of death probabilities \(q_k\) onto the population dynamics is the main motivation of the paper. In particular, we will show that in the critical regime, when \(q_k\) asymptotically approach to r (i.e., the birth and death events seem to be equilibrated), the mean population size still grows due to fluctuations as a power law, \(t^\beta \). The scaling exponent \(\beta \) equals 1 / 2 for a fast enough (e.g., exponential) approach of the death probabilities \(q_k\) to the limit r but, most surprisingly, \(\beta \) takes nonuniversal values between 1 / 2 and 1 for a slow (e.g., power law) approach. This unexpected behavior highlights the intricate role of the age-dependence of death probabilities that results in long-time memory effects in the population dynamics. Although the model might be too simplistic to accurately describe physical or social phenomena, it allows one to inspect the essence of the anomalous population growth caused by the age-dependent structure. Note that the role of age-dependent death rates has been thoroughly studied in population dynamics in the context of the McKendrick partial differential equation [9, 10] and its extensions [11–17]. The present model and the related challenges are different.

The paper is organized as follows. In Sect. 2, we formalize the model as a Markov chain and compute the mean population size at first time steps. In Sect. 3, a mean field approximation is introduced to derive the recurrence relations for the mean population size and to investigate its long-time asymptotic behavior. In Sect. 4, these relations are solved for the particular case of truncated age-dependence when \(q_k = q\) for \(k > T\). In this case, the long-time asymptotic behavior can be derived explicitly. In Sect. 5, we distinguish three asymptotic regimes according to the limiting death probability q (\(q_k \rightarrow q\)): the linear growth for \(r > q\), the critical regime at \(r = q\), and the saturation at \(r < q\). The validity of the mean field approximation is discussed and confirmed by Monte Carlo simulations. Finally, Sect. 6 reports conclusions and elucidates some open problems.

2 Markov Chain Formulation

Let \(\eta _k(t)\) denote the number of individuals of age k at time t. Since only one individual can be born at one time step, \(\eta _k(t)\) takes values 0 or 1. At every time step, one individual is uniformly chosen from the population and removed with probability \(q_k\), where k is the age of the chosen individual. During the same time step, a new individual is born with probability r:

$$\begin{aligned} \eta _1(t) = {\left\{ \begin{array}{ll} 1 &{}\,\,\,{\text {with probability }} r ,\\ 0 &{}\,\,\,{\text {with probability }} 1-r . \end{array}\right. } \end{aligned}$$
(1)

We are interested in the population size,

$$\begin{aligned} \eta (t) = \sum \limits _{k=1}^\infty \eta _k(t) , \end{aligned}$$
(2)

i.e., the number of individuals at time t. Since the death probability \(q_k\) depends on the age of the chosen individual, the population size does not fully characterize the state of the system so that the model cannot be reduced to a standard birth-death process. At the same time, the model can be formulated as a Markov chain on an infinite-dimensional space of states. In fact, each state of the system is characterized by a binary sequence whose k-th element encodes whether the individual of age k is present (\(\eta _k(t) = 1\)) or not (\(\eta _k(t) = 0\)). The space of states is therefore formed by all binary sequences. It is convenient to denote the states by integer numbers: \(0 = (0,0,0,0,\ldots )\), \(1 = (1,0,0,0,\ldots )\), \(2 = (0,1,0,0,\ldots )\), etc. The above birth-death rules determine the transition matrix \(W_{m,n}\) describing the probability of passing from the state m to the state n. The first elements of this matrix are

where prime denotes the complementary probability, i.e. \(r' = 1 - r\), etc. For instance, \(W_{3,4} = \frac{1}{2} q_1(1-r)\) describes the transition from \((1,1,0,0,\ldots )\) to \((0,0,1,0,\ldots )\) which occurs if the individual of age 1 is chosen (with probability 1 / 2) and removed (with probability \(q_1\)), while no new individual is born (with probability \(1-r\)). In general, the line of the matrix W corresponding to a state

$$\begin{aligned} \begin{array}{ll} m = &{} (0,\ldots ,0,1,0,\ldots ,0,1,0,\ldots ,0,1,0,\ldots ) \\ &{}\qquad \quad \qquad \, j_1 \qquad \qquad \quad \, j_2 \qquad \ldots \quad \,\, j_\ell \\ \end{array} \end{aligned}$$

with \(\ell \) individuals of ages \(j_1,\ldots , j_\ell \) contains \(4\ell \) nonzero elements describing four options for each of \(\ell \) individuals: death with probability \(q_{j_i}/\ell \) or survival with probability \((1-q_{j_i})/\ell \) (\(i=1,\ldots ,\ell \)), as well as birth of a new individual with probability r, or not.

Once the matrix is constructed, the distribution at time t can be computed as \(P(t) = P(0) W^t\), where P(0) is the vector representing the initial state: \(P_n(0) = \delta _{n,0}\) (no individuals). In particular, the probability distribution at first steps is

$$\begin{aligned} P(0) = \left( \begin{array}{c} 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ \cdots \\ \end{array} \right) , \quad P(1) = \left( \begin{array}{c} r' \\ r \\ 0 \\ 0 \\ 0 \\ \cdots \\ \end{array} \right) , \quad P(2) = \left( \begin{array}{c} r'^2 + rr'q_1 \\ rr'+r^2q_1 \\ rr'q'_1 \\ r^2 q'_1 \\ 0 \\ \cdots \\ \end{array} \right) , \quad \ldots \end{aligned}$$

The elements of the vector P(t) are related to the mean number of individuals of age k at time t as

$$\begin{aligned} {\langle \eta _k(t)\rangle = 0\cdot {\mathbb P}\{\eta _k(t) = 0\} + 1\cdot {\mathbb P}\{\eta _k(t) = 1\} = \sum \limits _{[n]_k = 1} P_n(t),} \end{aligned}$$
(3)

where\([n]_k\) denotes the k-th element in the binary expansion of n, and the sum is taken over all n for which \([n]_k = 1\). In other words, one adds the complementary probabilities of all states that contain an individual of age k. Finally, the mean population size is

$$\begin{aligned} {\langle \eta (t)\rangle = \sum \limits _{k=1}^\infty \sum \limits _{[n]_k = 1} P_n(t).} \end{aligned}$$
(4)

This explicit construction yields for the first time steps:

$$\begin{aligned} \begin{array}{ll} \langle \eta (1)\rangle &{} = r, \\ \langle \eta (2)\rangle &{} = r(2-q_1) , \\ \langle \eta (3)\rangle &{} = r\bigl (1 + (1-q_1)(2-q_2 + r(q_1+q_2)/2)\bigr ) . \\ \end{array} \end{aligned}$$
(5)

One can see that the exact expressions are rapidly getting very complicated.

An explicit solution for any time t can be obtained in several special cases:

  1. (i)

    When all \(q_j = 0\), the individuals are produced at a fixed rate r so that \(\langle \eta (t)\rangle = rt\).

  2. (ii)

    When \(q_1 = 1\) (i.e., certain death of the individual of age 1), one gets \(\langle \eta (t)\rangle = r\) at any t, as the system remains trapped in the state 1. Note that the condition \(q_j = 1\) for any other \(j >1\) does not imply such trapping because, for two or more individuals, there is a chance of choosing the individual of age which is different from j.

  3. (iii)

    When all \(q_j = q\), individuals are indistinguishable, and one recovers a simple birth-death process. The population size \(\eta (t)\) can be described as a biased reflected random walk. When \(\eta (t) > 0\), one of the three events can occur: the population size is increased by 1 with probability \(r(1-q)\), decreased by 1 with probability \((1-r)q\), or kept the same with the complementary probability \(1 - r(1-q) - (1-r)q\). In turn, if \(\eta (t) = 0\), only two events can occur: \(\eta (t)\) is increased by 1 with probability r, or kept the same with probability \(1-r\). The special consideration of the case \(\eta (t) = 0\) is equivalent to imposing the reflecting boundary condition at 0 that ensures that the number of individuals remains nonnegative. If this condition was ignored, the mean population size would be \(\langle \eta (t)\rangle = \langle \eta (1)\rangle + (t-1)[r(1-q) - q(1-r)] = (r-q)t + q\), as expected. This relation describes the long-time asymptotic behavior of \(\langle \eta (t)\rangle \) for \(r > q\) but it is not exact (compare with Eq. (5) at small times). If \(r = 1\), the condition \(\eta (t) = 0\) is never satisfied for \(t > 0\), and one gets the trivial exact solution \(\langle \eta (t)\rangle = (1-q)t + q\). Finally, if \(r = q,\) the population size is increased or decreased by 1 with equal probabilities \(q(1-q)\), and the population dynamics is reduced to an unbiased reflected random walk on the positive semi-axis (whose mean one-step displacement is zero). Since the mean position of reflected Brownian motion on the positive semi-axis is \(\sqrt{2\sigma ^2 t/\pi }\), setting the one-step variance \(\sigma ^2\) to be \(2q(1-q)\) yields

    $$\begin{aligned} \langle \eta (t)\rangle \simeq \sqrt{4q(1-q)/\pi } \sqrt{t}. \end{aligned}$$
    (6)

In other words, one gets the long-time asymptotic growth of the population size as the square-root of time at the critical regime when \(r = q\). The square-root behavior will be universally retrieved in the general case of age-dependent death probabilities \(q_k\) that rapidly converge to r as \(k\rightarrow \infty \). In turn, slow convergence of \(q_k\) will result in a faster mean population size growth.

(iv) When \(r = 1\), \(q_k = 0\) for \(k \le T\), and \(q_k = 1\) for \(k > T\), the exact solution is given in Appendix.

The first two cases represent the fastest and the slowest population dynamics so that in general, \(r \le \langle \eta (t)\rangle \le rt\). We checked numerically for the first time steps that \(\langle \eta (t)\rangle \) grows monotonously. Moreover, \(\langle \eta (t+1)\rangle = \langle \eta (t)\rangle \) was observed only in two extreme cases: \(r = 0\) (no birth event) or \(q_1 = 1\) (trapped case). We conjecture that the strictly monotonous growth of \(\langle \eta (t)\rangle \) holds at all times. As a consequence, \(\langle \eta (t)\rangle \) either converges to a finite limit, or grows up to infinity at long times.

3 Mean Field Approximation

Although the model is formalized as a Markov chain, the exact computation of the mean population size does not seem to be feasible at long times. In fact, the binary encoding of the population states by integers suggests thinking about the model as a random hopping on a nonnegative integer semi-axis. However, this random walk is nonlocal, i.e., its jumps can be arbitrarily large. For instance, the process can jump from the state \(2^{j-1}\) (representing one individual of age j) to the state 0 (no individuals) with probability \((1-r)q_j\), or to the state \(2^j\) (one individual of age \(j+1\)) with probability \((1-r)(1-q_j)\). Since we are interested in the long-time behavior of the population dynamics, all these transitions have to be accounted. This nonlocal character is related to a highly nonlinear relation between binary encoded states and the number of individuals (the latter being the number of bits in the binary expansion). These features make an exact solution of the model challenging.

To overcome this difficulty, we propose a mean field approximation which consists in two steps. (i)While the death event concerns only one individual per time step, one can approximate the changes in the population as an averaged effect, as though each individual could die at every time step so that all \(\eta _k(t)\) are effectively updated as

$$\begin{aligned} \eta _{k+1}(t+1) = {\left\{ \begin{array}{ll} \eta _k(t) &{}\,\,\, {\text {with probability }} 1 - q_k/\eta (t) ,\\ 0 &{}\,\,\, {\text {with probability }} q_k/\eta (t). \end{array}\right. } \end{aligned}$$
(7)

In other words, an individual of age k that was alive at time t, is getting older (of age \(k+1\)) at time \(t+1\) with probability \(1 - q_k/\eta (t)\), or dies with the complementary probability. The factor \(1/\eta (t)\) accounts for the uniform choice over \(\eta (t)\) individuals. The above dynamic rule is ignored when there is no individual (i.e., when \(\eta (t) = 0\)). We emphasize that this dynamic rule is slightly different from the original one: although this scheme reproduces the dynamics on average, it allows for several individuals to die during one time step. (ii)The mean number of individuals of age k, \(\langle \eta _k(t)\rangle \), can be approximately found by replacing the random population size \(\eta (t)\) in Eq. (7) by its mean value \(\langle \eta (t)\rangle \). The average of Eq. (7) becomes

$$\begin{aligned} N_{k+1}(t+1) = N_k(t) \bigl (1 - q_k/{\mathcal N}(t)\bigr ), \end{aligned}$$
(8)

where \(N_k(t)\) and \({\mathcal N}(t)\) are the mean field approximations of \(\langle \eta _k(t)\rangle \) and \(\langle \eta (t)\rangle \), respectively. The set of inequalities

$$\begin{aligned} {\mathcal N}(t) \ge q_k \qquad \text {for all }t \text { and }k \end{aligned}$$
(9)

is the necessary condition for this approximation to be meaningful (otherwise some \(N_k(t)\) could become negative). Its validity and accuracy will be discussed later. Given that

$$\begin{aligned} N_1(t-k+1) = \langle \eta _1(t-k+1)\rangle = {\left\{ \begin{array}{ll} r &{}\,\,\, (k \le t), \\ 0 &{}\,\,\, (k > t), \end{array}\right. } \end{aligned}$$
(10)

the repeated application of Eq. (8) yields

$$\begin{aligned} N_{k+1}(t+1) = {\left\{ \begin{array}{ll} \displaystyle r \prod \limits _{j=1}^k \left( 1 - \frac{q_j}{{\mathcal N}(t-k+j)}\right) &{}\,\,\, (k \le t), \\ 0 , &{}\,\,\, (k > t). \end{array}\right. } \end{aligned}$$
(11)

Substituting this relation into the definition of \(\langle \eta (t)\rangle \) leads to a closed expression for \({\mathcal N}(t)\)

$$\begin{aligned} {\mathcal N}(1) = r, \qquad {\mathcal N}(t+1) = r \sum \limits _{k=0}^t \prod \limits _{j=1}^k \left( 1 - \frac{q_j}{{\mathcal N}(t-k+j)}\right) . \end{aligned}$$
(12)

The inequalities (9) at \(t = 1\) require that

$$\begin{aligned} q_k \le r \qquad \text {for all }k. \end{aligned}$$
(13)

This condition is also sufficient for recovering the main features of the original population dynamics. In fact, from the first relation \({\mathcal N}(1) = r\), one can demonstrate by induction that all factors \((1 - q_j/{\mathcal N}(t-k+j))\) in Eq. (12) are positive and \({\mathcal N}(t)\) monotonously grows. Finally, the approximate mean population size remains bounded, \(r \le {\mathcal N}(t) \le rt\), in agreement with the similar bounds for \(\langle \eta (t)\rangle \) (see Sect. 2).

We emphasize that the inequalities (13) are needed for the mean field approximation while no restriction on \(q_k\) and r was imposed in the original model. For instance,the mean field approximation \({\mathcal N}(2) = 2r - q_1\) becomes negative if \(r < q_1/2\), while \(\langle \eta (2)\rangle = r(2-q_1)\) is positive for any r and \(q_1\). The above restriction is not surprising because the substitution of the integer random population size \(\eta (t)\) by its mean value is expected to be valid for large \(\langle \eta (t)\rangle \) but may not be applicable for small values. More generally, the mean field approximation aims at capturing the long-time asymptotic behavior but may be inaccurate or even invalid at small times. As a consequence, the inequalities (13) can potentially be relaxed if only the asymptotic behavior matters. In particular, we will show that the approximate solution may still be accurate asymptotically even if some \(q_j\) exceed r. In what follows, we focus on the regular case \(q_k \le r\) keeping in mind possible extensions. In the age-independent case, \(q_j = q\), the solution (12) is reduced to the trivial linear dynamics:

$$\begin{aligned} {\mathcal N}(t) = t (r - q) + q . \end{aligned}$$
(14)

In turn, age-dependent death probabilities lead to a rich population dynamics due to the memory effects in Eq. (12). In general, the death probabilities \(\{q_k\}\) are arbitrary real numbers from 0 to 1. We focus on the relevant situation when the sequence \(\{q_k\}\) converges to a limit q as \(k\rightarrow \infty \). We also exclude the trivial dynamics with \(q_1 = 1\) in which case the population growth would be blocked at the age 1, with \({\mathcal N}(t) = \langle \eta (t)\rangle = r\).

4 Truncated Death Probabilities

When the death probabilities \(q_k\) converge to a limit q, one can expect that, for a large enough age T, the \(q_k\) for \(k > T\) are so close to q that they can be replaced by q. To explore this idea, we consider the case of truncated age-dependence: \(q_k = q\) for \(k > T\) (while \(q_k\) are arbitrary for \(k \le T\)).

Due to this truncation, Eq. (12) can be rewritten, by applying the similar formula for \({\mathcal N}(t)\), as

$$\begin{aligned} {\mathcal N}(t+1) - {\mathcal N}(t) = r - q + \frac{r}{{\mathcal N}(t)} \sum \limits _{k=1}^T (q - q_k) \prod \limits _{j=1}^{k-1} \biggl (1 - \frac{q_j}{{\mathcal N}(t-k+j)}\biggr ) \end{aligned}$$
(15)

for \(t > T\). In contrast to the general relation (12), in which the mean population size \({\mathcal N}(t+1)\) at time \(t+1\) depends on all \({\mathcal N}(t), \ldots , {\mathcal N}(1)\), the memory effect in Eq. (15) is limited by a time span T, i.e., \({\mathcal N}(t+1)\) depends on \({\mathcal N}(t),\ldots , {\mathcal N}(t-T+1)\).

When \(r > q\), the population size exhibits a linear growth at large times:

$$\begin{aligned} {\mathcal N}(t) \simeq (r-q)t + {\mathcal N}_0 \qquad (t \gg T), \end{aligned}$$
(16)

where the constant \({\mathcal N}_0\) results from the short-time dynamics. The asymptotic behavior can be checked by substituting this relation into Eq. (15) and noting that the sum in the second term is bounded by \(\sum \nolimits _{k=1}^T |q-q_k|\). In turn, \({\mathcal N}(t)\) in the denominator grows up to infinity, thus cancelling this term.

The above argument does not hold when \(r = q\), in which case the above relation reads

$$\begin{aligned} {\mathcal N}(t)[{\mathcal N}(t+1) - {\mathcal N}(t)] = r \sum \limits _{k=1}^T (q - q_k) \prod \limits _{j=1}^{k-1} \biggl (1 - \frac{q_j}{{\mathcal N}(t-k+j)}\biggr ) . \end{aligned}$$

If \({\mathcal N}(t)\) grows up to infinity, the right-hand side converges to a constant \(r\sum \nolimits _{k=1}^T (q-q_k)\) which does not depend on time t. At large t, \({\mathcal N}(t+1) - {\mathcal N}(t)\) can be interpreted as the derivative of \({\mathcal N}(t)\), yielding the differential equation \({\mathcal N}(t) {\mathcal N}'(t) \simeq r\sum \nolimits _{k=1}^T (q-q_k)\) that is integrated up to t to get the asymptotic behavior

$$\begin{aligned} {\mathcal N}(t) \simeq \left( 2r \sum \limits _{k=1}^T (q-q_k)\right) ^{1/2} \sqrt{t} \qquad (t \gg T). \end{aligned}$$
(17)

The condition (13) ensures the positive sign of the sum under the square root. One can see that the square-room asymptotic behavior (6) is extended to the case of truncated age-dependent death probabilities.

4.1 Death After a Fixed Age

To provide a specific example, we consider a simple situation when any selected individual of age k below (or equal to) T surely survives while an individual of age above T dies with probability q: \(q_k = 0\) for \(k \le T\) and \(q_k = q\) otherwise. Substituting these \(\{q_k\}\) into Eq. (12) yields the linear growth \({\mathcal N}(t) = r t\) for \(t \le T\) and

$$\begin{aligned} {\mathcal N}(t+1) - {\mathcal N}(t) = r - q + \frac{qr T}{{\mathcal N}(t)} \qquad (t > T). \end{aligned}$$
(18)

This equation could be directly obtained from Eq. (15). Setting \(T = 0\), one retrieves the trivial dynamics (14).

If \(r > q\), the right-hand side of Eq. (18) is positive. While \({\mathcal N}(t)\) progressively increases, the last term diminishes, and one recovers asymptotically the linear growth. If \(r < q\), the sign of the growth rate is controlled by \({\mathcal N}(t)\): too small \({\mathcal N}(t)\) yields the positive sign of the right-hand side and thus triggers an increase of \({\mathcal N}(t)\), and vice-versa. One approaches the stationary limit \({\mathcal N}(\infty ) = qr T/(q-r)\). Finally, at the critical regime \(r = q\), one gets

$$\begin{aligned} {\mathcal N}(t) \bigl [{\mathcal N}(t+1) - {\mathcal N}(t)\bigr ] = qr T . \end{aligned}$$

Replacing \({\mathcal N}(t+1) - {\mathcal N}(t)\) at large t by the derivative of \({\mathcal N}(t)\) yields the differential equation \({\mathcal N}(t) {\mathcal N}'(t) \simeq qrT\) that is integrated from T to t to get \({\mathcal N}(t)^2 - {\mathcal N}(T)^2 = 2qrT(t-T)\), from which

$$\begin{aligned} {\mathcal N}(t) \simeq {\left\{ \begin{array}{ll} rt &{}\,\,\, (t \le T), \\ r\sqrt{T(2t - T)} &{}\,\,\, (t > T). \end{array}\right. } \end{aligned}$$
(19)

This mean field solution agrees well with the exact solution of the original model for \(r = q =1\) presented in Appendix.

5 Asymptotic Regimes

In order to validate the predicted asymptotic regimes and the mean field approximation, we computed the mean population size \(\langle \eta (t)\rangle \) by averaging \(\eta (t)\) over 1000 simulated dynamics governed by the original model. The mean field approximation \({\mathcal N}(t)\) was calculated numerically by recurrence relations (12). Note that a straightforward implementation of these relations would require \(O(t^3)\) operations that starts to be time-consuming for \(t \gtrsim 1000\). One can speed up the computation by re-arranging the terms in Eq. (12) as follows

$$\begin{aligned} \begin{array}{l | l l l l l} t=2 &{} (1-q_1c_1) &{} 0 &{} 0 &{} 0 &{} \ldots \\ t=3 &{} (1-q_1c_1)(1-q_2c_2) &{} (1-q_1c_2) &{} 0 &{} 0 &{} \ldots \\ t=4 &{} (1-q_1c_1)(1-q_2c_2)(1-q_3c_3) &{} (1-q_1c_2)(1-q_2c_3) &{} (1-q_1c_3) &{} 0 &{} \ldots \\ \ldots &{} \ldots &{} \ldots &{} \ldots &{} \ldots &{} \ldots \\ \end{array} \end{aligned}$$

where \(c_t = 1/{\mathcal N}(t)\). Using this structure, one computes the elements of the k-th line by adjusting the elements of the previous \((k-1)\)-th line, while \({\mathcal N}(k)\) is obtained by summing these contributions, adding 1, and multiplying by r. In this algorithm, the computation of \({\mathcal N}(t)\) requires \(O(t^2)\) operations.

For illustrative purposes, we focus on two families of the death probabilities: (i) rapidly converging sequence \(q_k = q(1 - e^{-\alpha k})\), and (ii) slowly converging sequence \(q_k = q(1 - k^{-\alpha })\), both characterized by \(\alpha > 0\). The sign in front of the second term ensures the inequality \(q_k \le q\) which, in turn, implies the condition (13) if \(r \ge q\). Although an additional coefficient could be introduced in front of the second term, it does not affect the asymptotic behavior (except through some constants). We do not truncate the above sequences at a fixed age T in order to investigate the relevance of this threshold that we used to derive the asymptotic regimes in Sect. 4.

We consider three cases: \(r > q\), \(r = q\), and \(r < q\). In the latter case, the mean field approximation may be invalid. However, we show that it is still applicable and accurate under certain conditions even in this case.

Fig. 1
figure 1

The mean population size at the linear regime (\(r = 1\), \(q = 0.8\)) with the death probabilities \(q_k\) following an exponential law \(q_k = q(1 - e^{-\alpha k})\) (a), or a power law \(q_k = q(1-k^{-\alpha })\) (b). Symbols show the empirical mean \(\langle \eta \,(t)\rangle \) from Monte Carlo simulations, whereas thick lines present the mean field approximation \({\mathcal N}(t)\) from Eq. (12). The thin line indicates the linear asymptotic growth \((r-q)t\)

Full size image

5.1 Linear Regime: \(r > q\)

Figure 1 illustrates the linear asymptotic growth (16) of the mean population size. For both exponential and power-law convergence and all \(\alpha \), the slope of the asymptotic growth is only determined by \(r-q\). In turn, the convergence features (e.g., the exponent \(\alpha \)) determine the constant shift term \({\mathcal N}_0\) and how fast the asymptotic regime is established. Smaller values of \(\alpha \) correspond to slower convergence of \(q_k\) to q and result in slower convergence to the asymptotic behavior and in larger shift terms. In particular, the curve for \(\alpha = 0.5\) on Fig. 1b does not even reach the linear asymptotic growth. We also conclude that the mean field solution (12) accurately approximates the empirical mean \(\langle \eta (t)\rangle \), justifying the mean field approximation introduced in Sect. 3.

Fig. 2
figure 2

The mean population size at the saturation regime (\(r = 0.8\), \(q = 1\)) with the death probabilities \(q_k\) following an exponential law \(q_k = q(1 - e^{-\alpha k})\) (a), or a power law \(q_k = q(1-k^{-\alpha })\) (b). Symbols show the empirical mean \(\langle \eta (t)\rangle \) from Monte Carlo simulations, whereas thick lines present the mean field approximation \({\mathcal N}(t)\) from Eq. (12)

Full size image

5.2 Saturation Regime: \(r < q\)

For \(r < q\), the saturation regime is expected at long times. This regime is characterized by a finite population size \({\mathcal N}(\infty )\) that can be found by solving numerically the limiting equation

$$\begin{aligned} {\mathcal N}(\infty ) = r \sum \limits _{k=0}^\infty \prod \limits _{j=1}^k \left( 1 - \frac{q_j}{{\mathcal N}(\infty )}\right) . \end{aligned}$$
(20)

Figure 2 shows the saturation of the mean population size \({\mathcal N}(t)\) for both exponential and power-law convergence of the death probabilities \(q_k\). Whatever the choice of the convergence, \({\mathcal N}(t)\) saturates to a limit \({\mathcal N}(\infty )\). The convergence features (e.g., the exponent \(\alpha \)) determine the limiting value \({\mathcal N}(\infty )\) and how fast the saturation occurs.

According to Eq. (11), the stationary population age profile \(N_{k+1}(\infty )\) reads

$$\begin{aligned} N_{k+1}(\infty ) = r \prod \limits _{j=1}^k \left( 1 - \frac{q_j}{{\mathcal N}(\infty )}\right) . \end{aligned}$$
(21)

Since \(\{q_j\}\) converge to q, the age profile exhibits an exponential decay at large k:

$$\begin{aligned} N_k(\infty ) \propto \exp (k \ln (1 - q/{\mathcal N}(\infty ))) \simeq \exp (-k q/{\mathcal N}(\infty )), \end{aligned}$$

where the last approximate relation is valid for large \({\mathcal N}(\infty )\).

The comparison to the empirical mean \(\langle \eta (t)\rangle \) shows that the mean field approximation provides an accurate solution \({\mathcal N}(t)\) even for \(r < q\), i.e., formally beyond its validity range. This observation is related to the particular choice of r and \(q_k\). For the chosen parameters, the first death probabilities \(q_k\) are below r that allows one to apply the mean field approximation at the first steps up to some \(t_0\). As a consequence, the mean population size \({\mathcal N}(t)\) has grown enough to ensure the inequalities \({\mathcal N}(t) \ge q_k\) for \(t > t_0\) and therefore the applicability of the mean field approximation at longer times. At the same time, the mean field approximation would fail for all examples from Fig. 2 if the birth rate r was chosen small enough (e.g., it is sufficient to take \(r < q_1/2\) for getting a negative \({\mathcal N}(2)\)).

5.3 Critical Regime: \(r = q\)

With no loss of generality, we set \(r = q = 1\) at the critical regime (one can check that Eq. (12) remains invariant under rescaling \(r\rightarrow ar\), \(q\rightarrow aq\), \({\mathcal N}(t)\rightarrow a{\mathcal N}(t)\)).

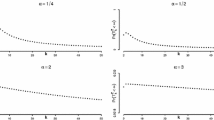
Figure 3 illustrates the behavior of the mean population size \({\mathcal N}(t)\) at the critical regime. In contrast to both linear and saturation regimes (\(r \ne q\)), for which only the probabilities r and q determined the asymptotic behavior, the population dynamics at the critical regime (\(r = q\)) turns out to be sensitive to the convergence rate. On one hand, Fig. 3a shows the square-root asymptotic behavior of \({\mathcal N}(t)\) for all sets of exponentially converging death probabilities, in agreement with Eq. (17) derived for the truncated case. In other words, the exponential convergence is fast enough so that it can be truncated and yield the universal square-root behavior. On the other hand, Fig. 3b reveals a non-universal power-law growth of the mean population size,

$$\begin{aligned} {\mathcal N}(t) \propto t^\beta \qquad (t\rightarrow \infty ), \end{aligned}$$
(22)

for a slower, power-law decay of the death probabilities: \(q_k = q(1-k^{-\alpha })\). The exponent \(\beta \), which was equal to 1 / 2 for an exponentially fast convergence and for any truncated set of death probabilities, depends on \(\alpha \) for a power-law convergence.

Fitting the slope of \({\mathcal N}(t)\) in the log-log plot is not enough to accurately estimate the exponent \(\beta \) due to next-order terms (we emphasize that Eq. (22) captures only the leading term). For this purpose, we first computed the local exponent \(\beta (t)\) as the slope between two neighboring points in the log-log plot,

$$\begin{aligned} \beta (t) = \frac{\ln ({\mathcal N}(t+1)/{\mathcal N}(t))}{\ln ((t+1)/t)} , \end{aligned}$$

and then extrapolated its values to \(t = \infty \) by fitting \(\beta (t)\) versus \(1/\sqrt{t}\) by a fourth-order polynomial over the broad range of t (from 1000 to 50000). A somewhat artificial choice of \(1/\sqrt{t}\) instead of 1 / t allowed us to get the dependence closer to a linear one. Figure 4 shows the extrapolated \(\beta \) as a function of \(\alpha \). One can note the exponentially fast approach of the exponent \(\beta \) to 1 / 2 as \(\alpha \) increases.

Fig. 3
figure 3

The mean population size at the critical regime (\(r = q = 1\)) with the death probabilities \(q_k\) following an exponential law \(q_k = q(1 - e^{-\alpha k})\) (a), or a power law \(q_k = q(1-k^{-\alpha })\) (b). Symbols show the empirical mean \(\langle \eta (t)\rangle \) from Monte Carlo simulations, thick lines present the mean field approximation \({\mathcal N}(t)\) from Eq. (12), whereas thin lines indicate the power law (22), with \(\beta \) being either 0.5 (a) or 0.6673, 0.5346, and 0.5004 for \(\alpha = 0.5, 1, 2\), respectively (b). To ease visual comparison, the coefficient in front of \(t^\beta \) in Eq. (22) is set to 6.0, 4.3 and 3.0 for \(\alpha = 0.05, 0.1, 0.2\) (a), and to 1.9, 2.4, 1.8 for \(\alpha = 0.5, 1, 2\) (b)

Full size image

This example shows that the truncated case analyzed in Sect. 4 does not capture all features of the population dynamics at the critical regime. In particular, a slow convergence of the death probabilities results in a faster, anomalous growth of the population size.

Fig. 4
figure 4

The dependence of the exponent \(\beta \) of the anomalous population growth (22) on the exponent \(\alpha \) at the critical regime, with \(q_k = 1 - c k^{-\alpha }\), \(q = r = 1\), and \(c = 1\) (circles) and \(c = 2\) (line). As expected, the factor c in front of \(k^{-\alpha }\) does not affect the scaling exponent

Full size image

In the limit \(t\rightarrow \infty \), the mean population size \({\mathcal N}(t)\) is large according to Eq. (22). Expanding the product of k factors in Eq. (11) and keeping only the leading terms, one gets

$$\begin{aligned} {N_k(t+1) \simeq 1 - \sum \limits _{j=1}^k \frac{q_j}{{\mathcal N}(t-k+j)} \simeq 1 - \frac{1}{{\mathcal N}(t)} \sum \limits _{j=1}^k q_j \qquad (k\ll t),} \end{aligned}$$
(23)

where we used \({\mathcal N}(t-k+j) \approx {\mathcal N}(t)\) for \(|j-k| \ll t\) in the last relation. One can see that the mean number of individuals of age k progressively saturates to the maximum level 1 as \(t\rightarrow \infty \), though the rate of this saturation decreases with k, as illustrated on Fig. 5.

Fig. 5
figure 5

The mean number \(N_k(t)\) of individuals of age k as a function of t at the critical regime, with \(q = r = 1\), \(q_k = 1 - k^{-\alpha }\), and \(\alpha = 0.5\)

Full size image

6 Discussion and Conclusion

We considered a simple model of population dynamics in which the death probability depends on the age of a randomly chosen individual. While this model was formalized as a Markov chain, the complicated structure of the transition matrix did not allow us to investigate the long-time asymptotic behavior of the mean population size. To overcome this difficulty, a mean field approximation was introduced in two steps: (i) a single death event for one individual was replaced by an average impact over the whole population through the dynamic rule (7), and (ii) the random population size \(\eta (t)\) in Eq. (7) was replaced by its mean value \(\langle \eta (t)\rangle \). These two approximations resulted in the recurrence relation (12) for the mean population size, as well as Eq. (11) for the mean population age profile. The recurrence relation (12) expresses the (approximate) mean population size \({\mathcal N}(t+1)\) through the mean population sizes at earlier times. While the original model is a Markov chain, the dynamics of the mean population size exhibits strong memory effects. The mean field solution \({\mathcal N}(t)\) was shown to be bounded between r and rt, and to exhibit a monotonous growth. The same features were observed numerically for the original model but a proof is missing. The accuracy of the mean field approximation was confirmed by Monte Carlo simulations. The set of inequalities (13) was positioned as the necessary and sufficient condition for the validity of the mean field approximation. However, Monte Carlo simulations showed that the approximate solution \({\mathcal N}(t)\) accurately captured the long-time asymptotic behavior of \(\langle \eta (t)\rangle \) even if the inequalities (13) are not satisfied for some j. Further analysis of the original model is needed to clarify the validity range of this approximation.

The analytical mean field solution allowed us to investigate the long-time asymptotic behavior of the mean population size. As intuitively expected, three different regimes have been identified according to the ratio between the birth probability r and the asymptotic death probability q: linear growth for \(r > q\), saturation for \(r < q\), and critical regime for \(r = q\). The age dependence of the death probabilities \(q_k\) was shown to be irrelevant for the two former cases (\(r \ne q\)): what matters is the balance between birth and death events. In contrast, the age dependence becomes crucial at the critical regime. When the convergence of the death probabilities \(q_k\) to the limit q is fast (e.g., exponential), old individuals behave similarly, and the mean population size \({\mathcal N}(t)\) grows as \(\sqrt{t}\), as expected from the analogy with a reflected random walk. In turn, when the death probabilities converge as a power law, \(q_k = q(1-k^{-\alpha })\), the distinction between old individuals remains significant, and the mean population size grows faster, as \(t^\beta \), with an exponent \(\beta \) between 1 / 2 and 1. A rigorous determination of the relation between \(\beta \) and \(\alpha \) remains an open problem.