1 Introduction

Stochastic differential equations are preeminently adopted to model, among others, population dynamics, protein kinetics, turbulence and even finance [1, 2]. From such equations, a partial differential equation can be derived to inform on the probability transition function of the stochastic process. Notwithstanding, many of the stochastic differential equations have no analytical solutions, imposing the requirement of other methods to analyze the properties of the stochastic phenomena. In this sense, one of the most appreciated stochastic differential equation is the Fokker–Planck equation (FPE), used originally not only to study stochastic phenomena, but also the Brownian motion.

There are several methods to solve the FPE, such as numerical integration methods, simulation methods, analytic solution for some potentials [3] and the method of formally transform a given FPE in a Schrödinger equation. Methods and techniques that describe the relation between Fokker–Planck and Schrödinger equations are widely applicable in many areas, including life sciences, engineering and physics. Frequently, this last method is applied only when confined potentials are chosen [4]. Nevertheless, in recent years this method has been the subject of interest in many fields of physics and considerable classes of potentials are being explored to obtain analytic solutions [5, 6], in particular all the shape-invariant potentials of supersymmetric quantum mechanics.

Concerning the solvability of the Schrödinger equation to central problems, different methods have been used to solve this equation for many potentials. Variational methods [7, 8], Lie group theoretical approaches [9, 10], Nikiforov-Uvarov method [11], Fourier analysis [12] and semi-classical estimates [13] can be highlighted. Specially, as already cited, an alternative method which is known as generalization of the factorization method or supersymmetry method has been introduced to solve the Schrödinger equation [14–16]. However, this method is still little explored concerning FPE-Schrödinger analogy formalisms. In this way, potentials of supersymmetric quantum mechanics give exactly solvable FPEs [17] and they will be the main subjects covered by the present report besides general solutions of the Schrödinger equation for generalized Morse and Hulthén potentials [7, 18].

One of the present work motivations is that Morse and Hulthén potentials are excellent examples of potentials to be applied in models of tumor growth and mechanisms involving differentiated cells [19, 20], addressing effective manners to comprehend mechanisms of tumor growth and consequently enlightening possible effective paths on cancer treatment [21, 22]. The generalized Morse potential also is used to describe diatomic molecular and physical models for DNA [23, 24]. The Hulthén potential describes atomic interactions as well, with applications in nuclear physics, solid state physics and physical chemistry [25, 26].

The present paper is organized as follows. After a brief presentation of the FPE (Sect. 2), in Sect. 3 we introduce a brief review on supersymmetric quantum mechanics methods [16], describing the main features of how to associate the generalized Morse and Hulthén potentials to such approach. Following this, we derive the solving method of the FPE in Sect. 4, using those solutions to calculate the transition probability for the potentials. In Sect. 5 we present the results and the most relevant effects of this analysis. We address some conclusions in Sect. 6.

2 The Fokker–Planck Equation and Its Formal Analogy with Schrödinger Equation

The Fokker–Planck equation gives the temporal evolution of the probability distribution P(x, t):

$$\begin{aligned} \frac{\partial }{\partial t}P(x,t) = \frac{\partial }{\partial x} \Big [f(x,t)P(x,t)\Big ] +\frac{\Gamma }{2}\frac{\partial ^2}{\partial x^{2}}P(x,t), \end{aligned}$$
(1)

where \(\Gamma \) is a constant of diffusion and f(x) is the function associated to a potential V(x). Following [5] and using the method of separation of variables, it is possible to yield the probability distribution as a series of functions:

$$\begin{aligned} P(x,t)=\sum _{l=0}^{\infty }a_{l}\phi _{l}(x)e^{-t|\Lambda _{l}|}, \end{aligned}$$
(2)

where \(\phi _{l}(x)\) are the eigenfunctions given by \(\phi _{l}(x)=\psi _l(x)\psi _0(x)\) and \(\Lambda _l\) are the eigenvalues. In this way, solutions of the Fokker–Planck equation can be written as (see e.g. [4])

$$\begin{aligned} P(x,t)=\psi _0(x)\sum _{l=0}^{\infty }a_{l}\psi _{l}(x)e^{-t|\Lambda _{l}|}, \end{aligned}$$
(3)

where the coefficients \(a_l\) are

$$\begin{aligned} a_l=\frac{\psi _l(0)}{\psi _0(0)}. \end{aligned}$$
(4)

The connection between FPE and Schrödinger equation is detailed discussed in [5, 17], where some solutions of the FPE are also presented. In few words, Eq. (3) permits one to rewrite the FPE as the following Schröndiger equation:

$$\begin{aligned} \frac{\Gamma }{2}\frac{d^{2}}{dx^{2}}\psi (x)- V_{eff}(x) \psi (x) =\Lambda _{n}\psi (x), \end{aligned}$$
(5)

where \(V_{eff}(x)=\frac{1}{2}\left\{ \frac{1}{\Gamma }f(x)^{2}+\frac{\partial f(x)}{\partial x}\right\} \).

3 Solutions of Schrödinger Equation from Supersymmetric Quantum Mechanics

The quantum mechanics formalism carried out by supersymmetry emerged during the 1970s. Particularly, Witten [14] introduced Supersymmetry in (1 + 0) Field Theory, calling it the Supersymmetric Quantum Mechanics. Here the time t is the coordinated and the position x is the field itself.

One of the preeminent applications for such formalism is to obtain solutions of the Schrödinger equation. In this way, supersymmetry is considered a generalization of the factorization method [15], where one can find elegant solutions of the Schrödinger equation for several types of potentials [16]. Firstly, in such approach, the original factorized radial Hamiltonian \(H_1\) is written as

$$\begin{aligned} H_1=\frac{\hbar ^{2}}{2m}\frac{d^2}{dx^2}+V_1(x)=a_{1}^{+}a_{1}^{-}+E_{0}^{(1)}, \end{aligned}$$
(6)

where \(a^{\pm }\) are respectively the operators of creation and annihilation (the bosonic operators), defined by

$$\begin{aligned} a^{\pm }=\mp \frac{d}{dx}+W_1(x), \end{aligned}$$
(7)

where \(W_1(x)\) is called the superpotential. For simplicity, \(\hbar =2m=1\) is adopted. As a result of the factorization of the Hamiltonian in the Eq. (6), we find that the superpotential \(W_1\) satisfies the Riccati equation

$$\begin{aligned} W_{1}^2-W_{1}^{\prime }+E_{0}^{1}=V_1(x), \end{aligned}$$
(8)

where \(E_{0}^{1}\) is the eigenvalue of the ground state and \(V_1(x)\) is the potential. The eigenfunction for the lowest state is associated to the superpotential \(W_1\) by

$$\begin{aligned} \Psi _{0}^{1}(x)=N e^{-\int _0^{x} W(\bar{x})d\bar{x}}, \end{aligned}$$
(9)

where N is constant of normalization. The general solution is

$$\begin{aligned} H_n= & {} a_{n}^{+}a_{n}^{-}+E_{0}^{n}, \nonumber \\ a_{n}^{\pm }= & {} \mp \frac{d}{dx}+W_n(x), \nonumber \\ \Psi _{n}^{(1)}= & {} a_{1}^{+}a_{2}^{+}...a_{n}^{+}\psi _{0}^{(n+1)}, E_{n}^{(1)}=E_{0}^{(n+1)}. \end{aligned}$$
(10)

Thus, all hierarchy of Hamiltonians can be constructed, connecting the eigenvalues and eigenfunctions of the n-members [16].

3.1 Schrödinger Equation with the Generalized Morse Potential (GMP)

The generalized Morse potential (GMP) [18, 23] is defined by

$$\begin{aligned} V(x)=D\biggl [1-\frac{b}{e^{ax}-1}\biggl ]^{2}, \ \ \ \ \ b=e^{ax_{e}}-1, \end{aligned}$$
(11)

where \(0 < x < \infty \), and D, b, \(a>1\) are parameters related respectively to the depth, the position of the minimum \(x_e\) and the radius of the potential. The Schrödinger equation for the GMP can be written as [5, 6]

$$\begin{aligned} \biggl (-\frac{d^2}{dx^{2}}+v(x)\biggl )\psi (x)=\epsilon \psi (x),\ \ \ \ \ \ v(x)=k\biggl (1-\frac{b}{e^{x}-1}\biggl )^{2}, \end{aligned}$$
(12)

where

$$\begin{aligned} \Psi (x)=\sqrt{a}\psi (x), \ \ \ \ k\equiv \frac{2\mu D}{a^{2}\hbar ^{2}}, \ \ \ \ \epsilon =\frac{2\mu E}{a^{2}\hbar ^{2}}. \end{aligned}$$
(13)

From the described method of supersymmetric quantum mechanics, the solution of Eq. (12) is

$$\begin{aligned} \Psi _n{(x)}=N_{n}y^{\alpha _n}(1+y)^{-\beta _n}\ _{2}F_{1}(-n,-n+1-2l;2\alpha _{n}+1;-y), \ \ \ y=(e^{ax}-1)^{-1}, \end{aligned}$$
(14)

where

$$\begin{aligned} \alpha _n=\frac{1}{2}\biggl (\frac{kb(b+2)}{n+l}-n-l\biggl ), \ \ \ \beta _n=\frac{1}{2}\biggl (\frac{kb(b+2)}{n+l}+n+l\biggl ), \end{aligned}$$
(15)
$$\begin{aligned} l=\frac{1}{2}\Big (1+\sqrt{1+4kb^{2}} \Big ) \end{aligned}$$
(16)

and \(N_n\) is the normalization constant. The corresponding eigenvalues are

$$\begin{aligned} E_n=D-\frac{a^{2}}{4}\biggl (n+l-\frac{b(b+2)k}{n+l}\biggl )^{2}, \ \ \ \ n=0,1,2... \end{aligned}$$
(17)

The Morse potential can be written as [5]

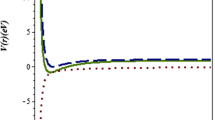
$$\begin{aligned} V(x)=D \Big [1-e^{-a(x-x_e)} \Big ]^{2}, \end{aligned}$$
(18)

with the same parameters of the Generalized Morse potential. Figure 1 shows the plots comparing the potentials. The principal difference between potentials appears at \(x\sim 0\).

Fig. 1
figure 1

Graphics of the generalized Morse and Morse potentials to \(a=1\), \(x_{e}=2,5\) and \(D=10\)

Full size image

3.2 Schrödinger Equation with the Hulthén Potential

The Hulthén potential has recently been studied by many authors [25, 26]. The potential has the form,

$$\begin{aligned} V(x)=-\frac{V_{1}e^{-2ax}}{1-qe^{-2ax}}, \end{aligned}$$
(19)

where \(V_1\), \(a>0\) and q are parameters. The energy eigenvalues and wave functions of the Hulthén potential to Schrödinger equation are [7]

$$\begin{aligned} E_n=-a^{2}\biggl [n+1-\frac{V_1}{4qa^{2}(n+1)}\biggl ]^{2} \ \ n\ge 0, \; q\ge 1 \end{aligned}$$
(20)
$$\begin{aligned} \Psi _n(s)=N_ns^{\sqrt{\epsilon }}(1-qs)P_n^{(2\sqrt{\epsilon },1)}(1-2qs), \end{aligned}$$
(21)

where \(s=e^{-2ax}\), \(\epsilon =-\frac{2mE}{4a^{2}\hbar ^{2}}\), \(N_n\) is the normalization constant and \(P_n\) are Jacobi polynomials.

4 Solving Fokker–Planck Equation with GMP and Hulthén as Effective Pontentials

4.1 Fokker–Planck Equation for the Generalized Morse Potential

From the connection between the FPE and the Schrödinger equation, Eq. (5), one can observe that the function f(x) is associated to an effective potential. For the case of GMP, the effective potential is

$$\begin{aligned} \frac{1}{2}\left\{ \frac{1}{\Gamma }f(x)^{2}+\frac{\partial f(x)}{\partial x}\right\} =V_{eff}(x)=D\left[ 1-\frac{b}{e^{ax}-1}\right] ^{2}+ D\biggl (\frac{\rho ^2}{2\Gamma D}-1\biggl ), \end{aligned}$$
(22)

where \(\rho =\frac{u}{2}-\frac{\Gamma D}{u}(2b+b^{2})\) and \(u=\frac{1}{2}(\Gamma a +\sqrt{(\Gamma a)^{2}+8\Gamma Db^{2}})\). The solution to f(x) is

$$\begin{aligned} f(x)=\frac{\rho e^{ax}-\gamma }{e^{ax}-1}, \end{aligned}$$
(23)

with \(\gamma =-\frac{u}{2}-\frac{\Gamma D}{u}(2b+b^{2})\). Substituting the Eq. (23) in the FPE associated with Schrödinger equation [5] we find

$$\begin{aligned} \frac{\Gamma }{2}\frac{d^{2}}{dx^{2}}\psi (x)-\frac{1}{2}\left\{ \frac{1}{\Gamma }f(x)^{2}+\frac{\partial f(x)}{\partial x}\right\} \psi (x) =\Lambda _{n}\psi (x). \end{aligned}$$
(24)

Therefore, Eq. (24) is a differential equation that can be determined by comparison with the Schrödinger equation. We consider \(\Gamma \rightarrow -\frac{\hbar ^{2}}{m}\) and the eigenvalues can be written in terms of the eigenvalues (17),

$$\begin{aligned} \Lambda _{n} = \frac{a^{2}\Gamma ^{2}}{8}\left( n+l-\frac{b(b+2)D}{a^{2}(n+l)}\right) ^{2}-2D+\frac{\rho ^{2}}{2\Gamma }. \end{aligned}$$
(25)

Replacing the values \(\Lambda _n\) in (3) we obtain the distribution of probability P(x, t). The Fig. 2 shows the distribution of probability to different values of time.

Fig. 2
figure 2

Distribution of probability P(x, t) as a function of x to generalized Morse potential with parameters \(a=1\), \(D=10\), \(\Gamma =2\) and \(x_e\) to times \(t=0.001\) and \(t=0.1\)

Full size image
Fig. 3
figure 3

Distribution of probability P(x, t) as a function of x to Hulthén potential with parameters \(a=1\), \(q=1\), \(V_1=3\) and \(\Gamma =2\) to times \(t=0.35\) and \(t=3.00\)

Full size image
Fig. 4
figure 4

The plots show P(x, t) as a function of x to generalized Morse potential, calculated by using the relation between Fokker–Planck and the Schrödinger equation using techniques from supersymmetry quantum mechanics. a Shows the dependence of P(x, t) on x for fixed \(a=1\), \(D=10\), \(\Gamma =2\) and \(x_e\) to values of \(t=0.001\), \(t=0.02\) and \(t=0.05\). b Shows the dependence of P(x, t) on x for fixed \(a=1\), \(D=10\), \(\Gamma =2\) and \(x_e\) to values of time \(t=0.5\), \(t=2.0\) and \(t=5.0\)

Full size image
Fig. 5
figure 5

The plots show P(x, t) as a function of x to Hulthén potential, calculated by using the relation between Fokker–Planck and the Schrödinger equation using techniques from supersymmetry quantum mechanics. a Shows the dependence of P(x, t) on x for fixed \(a=1\), \(D=10\) and \(\Gamma =2\) to values of \(t=0.35\), \(t=0.40\) and \(t=0.50\). b Shows the dependence of P(x, t) on x for fixed \(a=1\), \(D=10\) and \(\Gamma =2\) to values of time \(t=0.65\), \(t=3.0\) and \(t=8.0\)

Full size image

4.2 Fokker–Planck Equation for Hulthén Potential

The transformation of the Fokker–Planck equation to Schrödinger equation introduces the following effective potential

$$\begin{aligned} \frac{1}{2}\left\{ \frac{1}{\Gamma }f(x)^{2}+\frac{\partial f(x)}{\partial x}\right\} =V_{eff}(x)=-V_1\frac{e^{-2ax}}{1-qe^{-2ax}} + \frac{1}{2\Gamma }\Biggl (\frac{-V_1+2qa^{2}\Gamma }{4aq}\Biggl )^{2}. \end{aligned}$$
(26)

The ansatz to f(x) is

$$\begin{aligned} f(x)=-\frac{\xi e^{-2ax}}{1-qe^{-2ax}}+\eta , \end{aligned}$$
(27)

with \(\xi = -2aq\Gamma \) and \(\eta = \frac{-V_1+2qa^{2}\Gamma }{4aq}\). As we have seen in the previous section, replacing (27) in the FPE analog of the Schrödinger equation leads to the calculation of the eigenvalues

$$\begin{aligned} \Lambda _{n} = 2a^{2}\Gamma \Biggl (n+1-\frac{V_1}{4qa^{2}(n+1)}\Biggl )^{2} + \frac{1}{2\Gamma }\Biggl (\frac{2qa^{2}\Gamma -V_1}{2aq}\Biggl )^{2}. \end{aligned}$$
(28)

The distribution of probability P(x, t) with the Hulthén potential background is obtained replacing (28) in (3). The main characteristics of the distribution of probability P(x, t) to different values of time t are shown in the Fig. 3.

5 Results

Several conclusions can be drawn from the analysis of results. The Figs. 2 and 3 show the distribution of probability P(x, t) as a function of x to generalized Morse and Hulthén potentials. The solutions were obtained replacing the values of the eigenfunctions and eigenvalues for generalized Morse and Hulthén potential in Eq. (3). The previous comparison between the solutions to potentials shows that although the Figs. 2 and 3 display the same behavior, they present a discrepancy between increase of time and decrease of the probability.

The main features from the calculation of P(x, t) can be summarized as follows (see Figs. 4 and 5): The curves presented in Fig. 4 illustrate the distribution of probability P(x, t) as a function of x to the generalized Morse potential with parameters \(a=1\), \(D=10\) and \(\Gamma =2\) to different values of time. The Fig.  4a shows the distribution to short times (\(t=0.001,0.02,0.05\)) and 4b shows the distribution to large times (\(t=0.5,2.0,5.0\)). It can be observed that for small values of time the probability of finding the particle at position x is (\(P(x,t)\sim 0.98\) ), Fig.  4a. The probability decreases (\(P(x,t)\sim 0.92\)) as time increases, Fig. 4b. For times of order \(t \sim 2.0\) the system can be considered stationary, given that for such time values the curves coincide.

Results of distribution of probability to Hulthén potential are presented in Fig. 5. The parameters used to find the numerical solutions are \(a=1\), \(D=10\) and \(\Gamma =2\). Figure 5a also shows the distribution to short times (\(t=0.35,0.40,0.50\)) while 5b shows the distribution to large times (\(t=0.65,3.00,8.00\)). In this case, the more time increases, the larger is probability of finding the particle at position x. Again, the system is considered stationary at \(t \sim 2.0\).

6 Conclusions

In recent years there has been a considerable increase in research activities directed toward the development of solutions of the FPE to different potentials. The purpose of the present contribution was to calculate solutions of the FPE for two specific effective potentials: generalized Morse and Hulthén potentials. Also, it was illustrated how to find solving shortcuts from supersymmetric quantum mechanics and its method to yield solutions from Schröndiger equation. Namely, solutions for the two mentioned potentials was achieved by the formal analogy of FPE with the Schröndiger equation.

In this way, the algebraic relation between the corresponding eigenfunctions and eigenvalues of the Schrödinger equation and the relationship between FPE and Schrödinger equation provides the solutions of the distribution of probability. We note, as well, that such technique is a powerful and an elegant prescription to obtain the Fokker–Planck distribution of probability in the presence of several potentials.

Finally, the generalized Morse and Hulthén potentials are excellent examples of potentials to be applied in models of tumor growth and mechanisms involving differentiated cells, addressing effective manners to comprehend mechanisms of tumor growth and consequently enlightening possible effective paths on cancer treatment.