1 Introduction

Recently, the derivation of different thermodynamic parameters from experimental values of various physico-chemical properties, and their meaningful correlations with one another, introduces a new framework of scientific research on binary liquid mixtures. The studied isobutyric acid + water solvent system is most attractive, and a great deal of work has been performed by many researchers, especially when two phases are in equilibrium [1–6]. Considering the values reported in our earlier papers [1, 3], here it is extended to study the viscosity Arrhenius behavior along with a new parameter designated as the Arrhenius temperature (T A ), in isobutyric acid (IBA) + water (W) binary mixtures from 302.15–313.15 K (i.e. over the entire range of mole fractions at six different temperatures, close to the critical temperature (2.055 < (T − T C)/K < 12.055). Here, we determine the temperature effect in the Arrhenius region (T − T C) >2 K on the viscosities, where T C is the critical temperature {T C (IBA + W) = 300.095 K}. From our study, we can deduce the thermodynamic properties of IBAW far away from the critical point. In addition, partial molar activation energies have been determined to reveal the individual interaction contributions from each pure component within the mixture at each composition, and the new introduced parameter designated as the current Arrhenius temperature (T Ai ), which is for each component (i) and allows us to make a good estimations of the boiling temperatures of the corresponding pure components at atmospheric pressure.

2 Viscosity Arrhenius Behavior

2.1 Viscosity Results

In earlier works the experimental values of dynamic viscosity (η) and density (ρ) as a function of the mole fraction of IBA in the IBA (1) + W (2) system were used to calculate the excess molar volumes (V E) of this system in the single phase (T > T C), and viscosity deviations (∆η), that were correlated with composition by using two procedures. First, the Redlich–Kister expression was fitted in least-squares polynomials, series of Legendre polynomials and Hermite polynomials. Second, the Herráez correlation equation, using an exponent polynomial versus the mole fraction x 1 of isobutyric acid, IBA, at seven different temperatures, was recently proposed [3, 4]. It was observed that there were marked negative and positive deviations of the V E and ∆η values, respectively, over the entire mole fraction range of IBA and at the seven investigated temperatures. The maximum value of ∆η is obtained in the mole fraction region of (0.10–0.45), with a critical region centered around x c  = 0.1114. We did not detect any anomaly near the critical composition x c  = 0.1114 mol fraction of IBA. This behavior is similar to that reported in the literature [6, 7]. We can add that in this region the viscosity η is characterized by a scaling law [7]:

$$ \eta = \eta_{ 0} \cdot t^{{ - y_{\eta } }} $$
(1)

where \( t = \frac{{T - T_{\text{C}}^{{}} }}{{T_{\text{C}}^{{}} }} \) is the reduced temperature and \( y_{\eta } \) is a universal critical exponent \( y_{\eta } \)  = 0.04). Also, in the water-rich region, the viscosity η increases as the temperature T approaches to the critical temperature T C and x 1 tends to x C. We observe a decrease of Δη when x 1 increases in the IBA-rich region [1–3]. It was also observed that the magnitude of positive values of ∆η marginally decreases with increase of the molecular correlation, which is characterized by a correlation length according to the scaling law [3]. On the other hand, we observed that the magnitude of positive values of Δη marginally decreases with the increase of molecular correlation, which is characterized by a correlation length according to the scaling law (Eq. 2),

$$\xi = \xi_{0} (t)^{ - \upsilon } \left[ {1 + a_{\xi } (t) + \cdots } \right]$$
(2)

where ξ 0 is the critical amplitude of (IBA–W) mixtures and ν is the universal critical exponent (ν = 0.63). The correlation length ξ diverges at T = T C and all of the molecules of (IBA) are correlated with water molecules. This phenomenon has been known for a long time in critical mixtures.

It is well known that the IBA molecule is a proton donor and the water molecule is a proton acceptor. Therefore, the negative values of the excess volume are an indication of strong heteromolecular interactions in the liquid mixtures and, according to Fort et al. [8], this can be attributed to specific interactions (hydrogen bonding) and non-specific interactions (dipole–dipole, dipole-induced–dipole, dispersion interactions), which depend on the temperature [8, 9]. Hence, there will be a significant degree of H-bounding, leading to strong correlation between the molecules; the difference in the size of the molecules can also play a role in this respect [10].

In the same context, Desnoyers and Perron [11] showed that an examination of the trends of the dependence of V E and ∆η on x 1 suggested that many of these systems are similar, and the differences in interactions are mostly significant in solutions that are very rich in component 2. From the treatment of excess thermodynamic quantities for liquid mixtures proposed by Desnoyers and Perron [11], we can conclude that an excess quantity (V E and ∆η) gives an overall view of the origin of the non-ideality in the mixtures but still can be quite misleading, especially for systems that show strong interactions at high dilution. Desnoyers and Perron [11] suggested that, in agreement with the original statements of Redlich–Kister (R–K) [12], it is better to use the reduced R–K excess property i.e., the ratio V E/x 1(1 − x 1) or ∆η/x 1(1 − x1) for this purpose. We note that the reduced R–K excess property is more sensitive than the direct excess properties, Y E and ∆η, to interactions that occur at low concentrations [11, 12]. In fact, in the present system noteworthy changes in curvature [1, 3] are found for the reduced Redlich–Kister viscosity deviation Q exp,η,T (x 1) for dilute solutions of IBA. In the same context, Belda [13] recently proposed a new empirical correlation equation for four properties (density, viscosity, surface tension, and refractive index) which introduces a correcting factor F B,Y (x 1) as an homographic function applied to the system [5]. It was found that in the dilute region of isobutyric acid, the calculated Belda correcting factor F B,V (x 1) shows a pronounced deviation from the experimental one F B,Y,exp(x 1). A rapid comparison shows that the reduced Redlich–Kister property implicit in Belda’s equation exhibits nonlinear behavior versus the molar fraction x 1 of IBA in opposition to the explicit Redlich–Kister equation. Taking into account this nonlinear behavior, it was suggested that for most experimental reduced Redlich–Kister properties, the Belda equation offers better representation than the Redlich–Kister ones when only two free parameters (A 0 and A 1) are used for the latter.

2.2 Correlation Between Arrhenius Parameters

Investigation of the viscosity Arrhenius parameters (E a and ln(A S )) leads us to conclude that these distinct behaviors are clearly shown when the correlation between disorder and order is schematized through the viscosity Arrhenius activation energy E a against the logarithm of the entropic factor of Arrhenius, Rln(A S ) as shown in Fig. 1. Generally, the Arrhenius activation energy E a(x 1) of viscosity increases against the logarithm of the Arrhenius entropic factor Rln(A S ), which is also observed for some other binary mixtures such as water with 1.4-dioxane or N,N-dimethylacetamide (DMA) [14, 15]. Likewise, the pre-exponential entropic factor (A S ), equivalent to the viscosity at infinite temperature (As = η ∞), is very closely related to the viscosity of the same system in the vapor phase at the normal boiling temperature and at the same pressure, and can also be compared with the viscosity of the fluid in the ideal state for pure components as well as their mixtures. In this system it was found that structural order is not destroyed much by the activation process, and consequently most bonds are broken between the associated molecules to form smaller clusters (IBA:8 W). We conclude that there are two association-type structures in two distinct ranges separated by the critical composition around x C = 0.1114, where the Arrhenius activation energy Ea(x 1) and the logarithm of the Arrhenius entropic factor Rln(A S ) take their maximum values (Fig. 1).

Fig. 1
figure 1

Correlation between the Arrhenius activation energy E a (kJ·mol−1) of viscosity and the logarithm of the entropic factor of Arrhenius −Rln(As/Pa·s)/(J·K−1·mol−1) for isobutyric acid (1) + water (2) mixtures in the temperature range (302.15–313.15) K: (filled square), experimental data points; (solid line), linear least-squares fit of Eq. 3

Full size image

We can add that for each mixture, even in the case of different domains with distinct behaviors, we note that all different branches exhibit approximately the same slope of their quasi-straight line for which we can write the following standardized empirical equation:

$$ {-}E_{\text{a}} /R = T_{A} { \ln }\left( {A_{S} } \right) + B $$
(3)

where B is a constant related to the viscosity of the liquid system at the boiling temperature and which is the intercept on the ordinate when ln A S is mathematically null, while the slope T A characterizes each binary system and is equivalent to an absolute temperature for which we suggest as a name the viscosity Arrhenius temperature for the corresponding binary system. Noteworthy, we observe that the T A values for all the studied systems are near the boiling temperatures (T bi ) of the corresponding pure components. In the case of the IBA–W mixtures, the T A value is equal to 344.0 K with correlation factor 0.97195, while the boiling temperature of IBA and W are 428.15 and 373.15 K, respectively; we conclude that the viscosity Arrhenius temperature T A is closely related to the temperature of the isobaric liquid–vapor equilibrium of the system IBA–W.

We can add that our next goal is to show that the Arrhenius temperature T A is closely correlated to the average value of the temperature function T(x 1) against molar composition (x 1) in the interval [0,1] for the T–X isobaric binary liquid–vapor diagram, which can be expressed as:

$$ \mathop \smallint \limits_{0}^{1} T(x_{1} )dx_{1 \sim } T_{A} , $$
(4)

and the Arrhenius temperature T A is approximately the average height of the graph of temperature–composition (T − x 1) of the corresponding isobaric phase diagram at atmospheric pressure of the studied binary liquid mixture. In the same way and depending on whether the T A value is at, is undervalued or overvalued by one of the boiling points T bi , we can estimate the graph-type of the temperature-composition (T − x 1) diagram (azeotropic or regular with low or high boiling point).

3 Thermodynamic Characters

3.1 Enthalpy of Activation of Viscous Flow

In the case of a liquid phase we can add that the absolute reaction rate theory of Eyring et al. [16] and Ali et al. [17] relates kinematic viscosity with the Gibbs energy (ΔG*) of activation of viscous flow, then the temperature dependence of (ΔG*) leads us to determinate the enthalpy ΔH* and entropy ΔS* of activation of viscous flow [17, 18].

Inspection of the E a values and those of the enthalpy (ΔH*) of activation of viscous flow [18, 19] shows that the E a and ΔH* values are very closely related. So, we can write that the difference between E a values and those of the enthalpy (ΔH*) of activation of viscous flow can be considered as an increment of ΔH* which is expressed linearly as:

$$ \Delta H* \, = E_{\text{a}} {-}\delta H* $$
(5)

We also consider the entropy of activation of viscous flow (ΔS*) that is closely correlated with the difference between the Arrhenius entropic factor (−R·lnA S ) and an entropy increment (ΔS*) as [19–23]:

$$ \Delta S* = {-}R{\ln}\,A_{S} + \delta S* $$
(6)

3.2 Partial Molar Activation Energy

Considering the quasi-equality between the Arrhenius activation energy E a and the enthalpy of activation of viscous flow ΔH*, and between logarithm of the Arrhenius entropic factor −Rln(As) and the entropy of activation of viscous flow ΔS*, mentioned in the Sect. 3.1, we can assume that E a(x 1) is approximately a thermodynamic function [14, 15, 19–23], then we can define the partial molar quantities Y 1 and Y 2 for IBA (1) and W(2), respectively, through the following equations:

$$ Y_{1} (x_{1} ) = Y(x_{1} ) + (1 - x_{1} )\frac{{\partial Y(x_{1} )}}{{\partial (x_{1} )}} $$
(7)
$$ Y_{2} (x_{1} ) = Y(x_{1} ) - x_{1} \frac{{\partial Y(x_{1} )}}{{\partial (x_{1} )}} $$
(8)

where Y i represents the partial molar activation energies E a1 and E a2 or the partial molar quantity relative to the Arrhenius entropic factor –Rln(A Si ).

This action is interesting because the partial molar activation energy E ai (x 1) values give the individual contribution of each pure component (i) and specific interaction in competition at each fixed binary mixture composition (x 1, x 2).

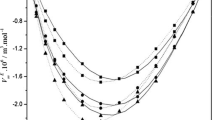
Values of E a1(x 1), E a2(x 1), −Rln(A S1) and –Rln(As 2) are reported in Table 1, and E a1(x 1) and E a2(x 1) are plotted in Fig. 2 against the mole fraction (x 1) of IBA. We divide the full range into multiple parts with a similar behavior, in which the fit is made with polynomials of different optimal degrees, while ensuring continuous extension and differentiability. In fact, this is clearly shown in Fig. 2 where, in the water-rich region and before reaching the critical composition x 1c = 0.1114 [1–5, 24–28], the E a values increase with increasing mole fraction of IBA, showing an effect on E a resulting from strong interactions between the W and IBA molecules in the vicinity of x 1c = 0.1114. After that, the value of E a(x 1) decreases with increasing mole fraction of IBA (1). This fact suggests that the structural order is not much destroyed by the activation process, and consequently most bonds are not broken between the associated molecules to form smaller clusters (IBA:8 W). We conclude again that there are two association type structures in two distinct ranges separated by the critical composition around x 1c. These distinct behaviors are clearly shown when the correlation between disorder and order is plotted in Fig. 3 (enthalpy factor against the corresponding entropy one).

Table 1 Partial molar quantities relative to the activation energies Ea i /(kJ·mol−1) and the logarithm of the entropic factor of Arrhenius −Rln(As i /Pa·s)/(J·K−1·mol−1) for {isobutyric acid (1) + water (2)} mixtures as a function of the mole fraction of isobutyric acid (x 1) over the temperature range (302.15 to 313.15) K
Full size table
Fig. 2
figure 2

Arrhenius activation energy Ea/(kJ·mol−1) and partial molar activation energies of viscosity (Eqs. 7, 8) Ea i /(kJ·mol−1) for {isobutyric acid (1) + water (2)} mixtures as a function of the mole fraction of isobutyric acid (x 1) over the temperature range (302.15–313.15) K: (filled triangle), Ea(x 1); (filled circle), Ea1(x 1); (open circle), Ea2(x 1)

Full size image
Fig. 3
figure 3

Correlation between the partial molar Arrhenius activation energies Ea1(x 1) and Ea2(x 1) for {isobutyric acid (1) + water (2)} mixtures over the temperature range (302.15–313.15) K

Full size image

We note that the observed slope changes and anomaly in the curvature (Fig. 1) in the very dilute region can be associated with the thermodynamic dissociation equilibrium (Eq. 9). In fact, in the highly dilute region (0 < x 1 < 0.02 and molar concentration C 1 less than 1 mol·L−1), we must take into account the ionization of IBA and the fractional dissociation α (Eq. 10) that is not negligible (0.05 < α < 1),

$$ \left( {{\text{CH}}_{ 3} } \right)_{ 2} {\text{CHO}}_{ 2} {\text{H}} \underset {} \,\leftrightarrows\, (\text{CH}_{3} )_{2} \text{CHO}_{2}^{ - } + {\text{H}}^{ + } $$
(9)
$$ \alpha = [(\text{CH}_{3} )_{2} \text{CHO}_{2}^{ - } ]/C_{1} \approx 10^{ - \text{pH}} /C_{1} $$
(10)

where the IBA molarity is C 1 < 0.15 mol·L−1, which corresponds to mole fraction x 1 < 0.003. We add that this acid dissociation region is clearly delimited in Fig. 3. Furthermore, the asymmetrical behavior at very high dilutions can be confirmed by the value of Herráez exponent. Hence, we can add that the universal exponent B 0 of the Herráez equation [29, 30] at infinite dilution investigated in previous works [3] shows that B 0,T takes a (1.0) value in the two cases of the IBA in W and the W in IBA. Then, we can conclude that at very high dilution solute–solute interactions are absent in the two cases of IBA in W and W in IBA.

Moreover, the distinct shape variation of the E ai (x 1) curves (Fig. 2) leads us to eliminate the mole fraction x 1 as a variable and to plot the correlation between the two partial molar activation energies E a1(x 1) and E a2(x 1) (Fig. 3); we can conclude that the individual contributions of IBA and W in the activation energy clearly show the delimitation of domains of IBA solvation in W and inversely (x 1 ≈ 0.1114), which corresponds approximately to a cluster (IBA:8 W) as revealed in previous work [31].

Then, if we abandon the assumption that the Arrhenius temperature (T A ) is no longer a constant over the whole range of composition (Eq. 3), we can redefine it as Arrhenius’ current temperatures (T Ai ) by the derivative of the partial molar Arrhenius activation energy E ai (x 1) with respect to the partial molar quantity corresponding to the logarithm of the Arrhenius entropic factor –Rln(A Si ) at selected molar fraction (x 1):

$$ T_{Ai} = \frac{{\partial \left( {E_{{\text{a}}i} } \right)}}{{\partial \left( { - R{ \ln }A_{Si} } \right)}} $$
(11)

The experimental T Ai values are equal to the slope of the tangent line at a selected point of the curve (i.e., at selected mixture composition x 1). As an application of this definition, we obtain very interesting results especially in the vicinity of the two limits of composition range. So, we obtain Arrhenius’ current temperatures (T Ai ) from the slopes of the two curves given in Fig. 4 such that in the case of the very high concentration of one component (i) we find that T A1(x 1 ≈ 1) = 433 K ≈ T b1 for the first curve (i = 1), T A2(x 2 ≈ 1) = 362.9 K ≈ T b2 for the second curve (i = 2), while in the case of very high dilution of the component (i) in the second one (j) we find that T A1(x 1 ≈ 0) = 320 K < T b1 for the first curve, and T A2(x 2 ≈ 0) = 360 K < T b2 for the second curve.

Fig. 4
figure 4

Correlation between the partial molar quantities relative to the activation energies Ea i /(kJ·mol−1) and the logarithm of the entropic factors of Arrhenius −Rln(As i /Pa·s)/(J·K−1·mol−1) for {isobutyric acid (1) + water (2)} mixtures over the temperature range (302.15–313.15) K. (filled circle): Ea 1(x 1) versus −Rln(As 1) and Ea2(x 1) versus −Rln(As 2)

Full size image

Note that these mathematical manipulations are delicate and could be improved with more experimental points (with high precision) in the two limits of the composition range (very high to dilute regions). Thus, due to the imposed experimental data taken from the literature and used in our investigations, we face constraints on the estimated accuracy of the calculated values, and, a good verification of the reliability and predictive capability of the developed method and its accuracy should be provided with our own well chosen experimental data in the next work. We can add that the temperature range can affect values and accuracy for the Arrhenius parameters, because of the viscosity doesn’t follow exactly the linear Arrhenius behavior in all of the temperature the range.

With this finding, we can predict the boiling point of the two pure components at constant pressure through investigation of the viscosity–temperature dependence in the corresponding liquid phase. We can add that this very interesting finding was also verified for other studied previous works for some binary mixtures consisting of the following solvents DMA [14], 2-ethoxyethanol (EOE) [32], formamide (FA) [33], N,N-dimethylformamide (DMF), methanol (Met), water and 1,4-dioxane [14, 15, 32–36] (Table 2). Taking into account the accuracy of data and the errors made in the calculations, we can conclude that Arrhenius’ current temperature at very high concentration of one component (T Ai ) at (x i  ≈ 1) is very close to its corresponding boiling temperature, while in the other cases the Arrhenius’ current temperatures (T Ai ) at (x i  ≠ 1) strongly correlates with the vaporization temperature of the isobaric liquid–vapor equilibrium of the corresponding binary mixture.

Table 2 Comparison between the current Arrhenius temperature (T Ai )/K for (x i  ≈ 1) and the corresponding boiling temperature T bi /K of the pure component (i) in some binary mixtures
Full size table

So, we can then summarize these observations by the following equation:

$$ \mathop {\lim }\limits_{x_i \to \infty } \left( {\frac{{\frac{{\partial (E_{{\text{a}}i} )}}{{\partial x_{i} }}}}{{\frac{{\partial (InA_{Si} )}}{{\partial x_{i} }}}}} \right) \approx - R \cdot T_{{\text{b}}i} $$
(12)

and, we can then estimate the boiling temperature (T bi ) of the pure component (i) with a good approximation.

In addition, a new proposed Hajkacem–Ouerfelli equation [37] presents curious causal correlation and good concordance between the two viscosity Arrhenius parameters (E a and lnA S ) for low and moderately viscous pure fluids (Eq. 13) which do not have very high values of the activation energy (E a < 30 kJ·mol−1) and do not very low values of the pre-experimental factor (A S  = 42 nPa·s, i.e. ln(A S /Pa·s) > −17).

$$ E_{\text{a}} = \lambda \cdot R( - {\ln}A_{s} )^{{\alpha_{0} }} $$
(13)

where R is the perfect gas constant, λ ≈ 1 K and α 0 = 2.933.

We note that this equation can be also used for the two parameters related to some binary liquid mixtures with a good approximation. More, this model could be very important in several branches of the chemical sciences. In addition, it will be very useful for engineering data and it will permit the estimation of one non-available parameter when the second one is available (Eqs. 13 or  14), or can be otherwise evaluated by some theories suggested in the literature [38].

$$ { \ln }A_{S} = - \left( {\frac{{E_{\text{a}} }}{\lambda R}} \right)^{{\frac{1}{{\alpha_{0} }}}} $$
(14)

4 Conclusion

Based on the same experimental of dynamic viscosity and density data of IBA + W binary mixtures at seven different temperatures, both near and close to the critical temperature [1–3], some new theoretical approaches have been pointed out for improving investigations of the variation of Arrhenius activation energy and derived partial molar properties against the molar fraction composition.

Arrhenius parameters of pure components (IBA and W) can be estimated and the correlation between the two Arrhenius parameters for binary mixtures permits us to bring to light the Arrhenius viscosity temperature that characterizes the studied binary liquid mixtures and can provide information on the average of the vaporization temperature of the isobaric liquid–vapor equilibrium. Also, this correlation can give evidence for the existence of distinct composition regions with different behaviors.

Therefore, assuming that the activation energy can be treated as a complete differential thermodynamic quantity, we have determined the partial molar activation energies to reveal contributions of individual interactions of each pure component within the binary mixture at each well-defined molar fraction. Also, the variation of logarithm of the Arrhenius entropic factor deviation versus mole fraction (x 1) of IBA shows the presence of a minimum and maximum at two molar fractions, which was interpreted as due to complex formation between IBA and W [1–3]. Correlation between the partial molar quantities relative to the activation energies and the logarithm of the Arrhenius entropic factors for IBA + W mixtures over the temperature range gives an approximately linear behavior, i.e., no observable crucial change in curvature. This quasi-straight line behavior suggested to us to make an empirical linear equation by introducing a new parameter T A denoted as viscosity Arrhenius temperature that characterizes each binary system. In the case of partial molar quantities, we consider that the Arrhenius temperature (T A ) is no longer a constant over the full range of composition and we introduce a new concept of the Arrhenius’ current temperature (T Ai ) for each pure component (i) to find its value at the two extreme compositions i.e., at very high concentration and very high dilution, respectively. The results derived in the studied binary system gives an interesting fact that the isobaric boiling point (T bi ) of the pure components is very close or strongly depends upon the viscosity Arrhenius’ current temperature (T Ai ). In conclusion, we can ascertain that with more mathematical manipulations, we will be able to reveal some physical significances of the viscosity Arrhenius parameters, and it definitely develops as well as improves the thermodynamic theories and also predicts some information on liquid–vapor diagram through the study of the viscosity against temperature and composition only in the liquid phase of the binary mixture.

We can add that a supplemental study on the eventual relationship between the Arrhenius temperature and the properties of numerous binary mixtures can prove how the method estimates the properties of other non treated fluid mixtures. In order to tightly establish the utility of the Arrhenius temperature and develop a means for predicting such quantities, more mixtures will be studied in the future to give a clearer discussed protocol. To our knowledge, there is no strong theoretical and physical basis of this study or any developed predictive techniques for our initial suppositions and so we are unable to provide our verifications more clearly. We are very much hopeful that these original and interesting experimental findings can be well received by the theorists for developing new theoretical approaches. Also, in a future work, we will address the effect of pressure on the viscosity and how correlations can be deduced with the previously available theories.