Novel-Shape-Based HTS Magnet Coil for SMES Application

Abstract

Solenoid is the most preferred geometry for MJ class–based HTS-based SMES; however, current carrying capacity is limited by the radial component of magnetic field. Optimization of dimensions is required for reducing the refrigeration cost, cost of 2 G HTS tape, structural support, and cryostat dimensions. A new optimized shape, which looks like a solenoid from the outside but has a different inner radius for each double pancake (DP) coil, is obtained using teaching learning-based optimization (TLBO) for minimum length and 1 MJ stored energy. The structural integrity and the operating current of SMES coil degrade due to high Lorentz force; therefore, stress is also included in optimization process as a constraint. COMSOL along with MATLAB is used for shape optimization. The operating current is increased by reducing the perpendicular component in these novel shapes thereby, reducing the total HTS tape length. These shapes are compared with the optimized perfect solenoid in terms of HTS tape length, stress, and inductance.

1 Introduction

In numerous applications, such as load-leveling, pulsing power supplies, and instantaneous voltage drop compensation, superconducting magnetic energy storage, or SMES, stores energy in the form of magnetic fields [1, 2]. SMES made out of 2nd-generation (2 G) high-temperature superconductors (HTS), having flat tape-like structures, are wound in a flat pancake coil. These coils can be arranged in solenoid or toroid geometries. A toroid has less energy density and low stray field whereas a solnoid has high energy density but high stray field [3, 4]. A long length of HTS tape can increase the thermal mass of SMES and refrigeration cost as well as the cost of the tape itself. An optimized length of HTS tape can save both without losing the superconductivity.

The stored energy in SMES depends on the operating current (I) and inductance according to $\frac{1}{2}LI^2$, here L is the inductance. The B-I characteristic ($B_\perp -I_c$ and $B_\parallel -I_c$) of the tape and the maximum radial ($B_r$) and axial ($B_z$) components of magnetic field density in the HTS coil are all necessary for determining operational current. However, the perpendicular component ($B_\perp$) is the determining factor in the case of HTS solenoid magnet coil in the absence of background magnetic field [5]. The maximum $B_r$ depends on the coil’s size and operating current. Optimization is a challenging topic since determining the operating current is an iterative process. Since there is no closed-form equation for the stored energy in terms of dimensions, gradient-based optimization techniques cannot be employed in this situation. Even after determining the operating current, estimating stored energy still requires a numerical approach. These things also add to the difficulty in the optimization process. However, population-based non-traditional optimization methods like genetic algorithm (GA) [6], particle swarm optimization (PSO) [7], and teaching learning-based optimization (TLBO) [8, 9] can be utilized for optimization. These techniques allow for parallel computation and do not require the derivative. Table 1 lists out parameters required for optimization and current status of utilization in SMES coil dimension optimization. A fine tuning is required for these algorithm-specific parameters in GA and PSO to avoid local optima; however, TLBO does not require these parameters, thereby saving the time of parameter tuning.

Table 1 Some popular population-based optimization algorithm details

All superconducting magnets designed for SMES application belong in either solenoid or toroidal geometry. For MJ class HTS SMES, solenoid requires less length in comparison with toroidal geometry [3, 4]. Most of the designed HTS SMES in solenoid geometry had equal number of turns in all DP coils [5, 10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25], which makes it a perfect solenoid. Few HTS SMES [10,11,12,13,14] were designed without any optimization. Some HTS projects [5, 15,16,17,18,19, 21, 23, 24] used optimization based on parametric sweep. Although Zheng et al. [20] and Kim et al. [18] both used the GA, algorithm-specific parameters for the GA, such as the mutation index and crossover index, are not stated. SMES has not yet undergone shape optimization. There are very few case studies that use non-conventional optimization techniques (GA, TLBO, PSO) to optimize magnet dimensions.

In this paper, TLBO is used to obtain the novel HTS SMES shapes with minimum length of HTS tape for a fixed stored energy (1 MJ) operating at 4.2 K having maximum von-Mises stress less than 250 MPa. Section 2 describes the shape changing dynamic geometry and design requirements. It also defines the fitness function used for optimization. Section 3 gives the methodology to calculate the length and stored energy required for fitness function calculation along with FEM validation. Section 4 describes the TLBO implementation and provides the complete flowchart utilized for optimization. Section 5 outlines the new shapes obtained after optimization and compares them with the perfect solenoid in terms of HTS tape length, stored energy, von-Mises stress, and inductance. Section 6 concludes the paper.

2 Shape Changing Dynamic Geometry and Objective Function

To perform shape optimization with the varying number of turns ($n_r$) in each DP coil, a quarter axis-symmetric geometry is created, in terms of all design variables. The design variables required to make geometry include number of turns for each DP coil ($nr_1$, $nr_2$.....$nr_{10}$), clearance between neighboring turns ($c_r$), clearance between DP coils ($c_z$), and number of DP coils ($n_z$). Clearance between turns $c_r$ is provided for turn-by-turn insulation and support layer for reduction in stress in magnet due to Lorentz force. The clearance between DP coils and inter DP coils is kept the same ($c_z$) for ease of geometry creation during optimization. These total 13 variables (10 $n_r$, 1 $c_r$, 1 $c_z$, and 1 $n_z$) are the design variables which need to be obtained after optimization process. The full 3D sectional view of geometry is shown in Fig. 1. To reduce the computation time during optimization, a quarter axis-symmetry geometry is modeled. The outer diameter of each DP coil is kept the same for easy electrical connection between neighboring coils. The position and numbering of the DP coils are also shown in Fig. 1. This geometry is dynamic in the sense that depending upon the variables, the unique shape will be generated.

Fig. 1

Geometry generation with different inner radius of each DP coil

The upper bound (UB) and lower bound (LB) of variables that relate to maximum and minimum values of variables taken for this optimization are given in Table 2.

Table 2 Lower and upper limits of variables used for optimization

Table 3 Design parameters

The objective is to design a 1 MJ SMES (Eq. (2)) with minimum length of 2 G HTS tape (Eq. (1)) operating at 4.2 K. Stress due to Lorentz force can be very high and degrades ${I_c}$ beyond a critical limit [26, 27]. This makes structural aspects of SMES coil equally important as electromagnetic. A limit in maximum von-Mises stress (250 MPa) is set as a constraint in objective function (Eq. (3)). The design requirement and 2 G HTS tape details are given in Table 3.

$$\begin{aligned} F=Min(Length) \end{aligned}$$

(1)

$$\begin{aligned} E_{Desired} \approx 1~MJ \end{aligned}$$

(2)

$$\begin{aligned} \sigma _{Allowed} \le 250~MPa \end{aligned}$$

(3)

To include energy requirement and stress limitation in the optimization process, a penalty method is used to modify the fitness function. The deviation in energy from required energy ($E_{Desired}$) is treated as energy penalty as given in Eq. (4). For stress constraint, the penalty only acts if maximum stress is more than allowed stress; otherwise, it will be zero. The penalty function created for stress is given in Eq. (5).

$$\begin{aligned} E_P=\left( \frac{E-E_{{Desired }}}{E_{\max }}\right) ^{2} \end{aligned}$$

(4)

$$\begin{aligned} \sigma _P=\left\{ \begin{array}{cl} 0 &{} \sigma <250~\textrm{MPa} \\ \left( \frac{\sigma -\sigma _{{allowed }}}{\sigma _{\max }}\right) ^{2} &{} \sigma \ge 250~\textrm{MPa} \end{array}\right. \end{aligned}$$

(5)

These penalty functions ($E_{P}$ and $\sigma _{P}$) are added into objective function with suitable scaling factors ($P_E$, $P_S$) for optimization process. The modified normalized scalar fitness function is given by Eq. (6).

$$\begin{aligned} F=\left( \frac{ { Length~of~HTS~Tape }}{ { Maximum~Length }{ }}\right) ^{2}+P_E\times E_{P}^{2}+P_S\times \sigma _{P}^2 \end{aligned}$$

(6)

$P_E$ and $P_S$ are the penalty factors used for scaling the energy penalty function and stress penalty function respectively. These scaling factor values are determined based on the modified fitness function behavior. $E_{max}$ and $Length_{max}$ are the maximum values of stored energy and corresponding tape length possible in LB and UB of variables. $\sigma _{\max }$ is the maximum von-Mises stress obtained for corresponding $E_{max}$.

3 Fitness Function Calculation

Fitness function calculation requires calculation of the length, stored energy, and stress. The calculation of energy and stress requires the calculation of $B_r$ maximum, operating current ($I_{op}$), and magnetic flux density distribution.

Fig. 2

$B_\perp$-I characterization of HTS tape and load line [28]

3.1 Total Length Calculation

The total length of HTS tape required can be calculated by adding the length requirement of each coil. The inner radius (IR) of each coil is different and it depends upon the outer radius (OR) and the number of turns in DP coil. The IR of $i^{th}$ DP coil can be calculated using $OR_{i}$ and number of turns in $i^{th}$ coil ($nr_{i}$) as given by Eq. (7).

$$\begin{aligned} IR_{i}=OR_{i}-nr_{i}*(t+c_r) \end{aligned}$$

(7)

Here $c_r$, t is the thickness of support layer including insulation and thickness of HTS tape respectively. The clearance is here meant for providing layer-by-layer insulation and mechanical support. For each DP coil, the HTS tape length required is different. Total length can be calculated using IR, OR, and the number of turns using Eq. (8). A factor of 2 is multiplied because a DP consists of two SP coils.

$$\begin{aligned} { Tape~Length }=2\sum _{i=1}^{N_{z}}2 \pi \frac{\left( IR_{i}+O R_{i}\right) }{2} Nr_{i} \end{aligned}$$

(8)

3.2 Energy Calculation

Energy stored (E) in superconducting coil can be calculated either by $\frac{1}{2}LI_{op}^2$ where L is the inductance and $I_{op}$ is the operating current or, $\int \frac{B^{2}}{2 \mu } d v$ (integrating the energy density in full volume), where B is the magnetic flux density. However, both the methods require prior knowledge of $I_{op}$, which depends upon the shape of coil and B-I characterization of chosen HTS tape. Similar to solenoid, load line slope of shape considered in this paper will remain constant. The standard method to calculate operating current by solving load line equation and B-I curve fitted equation simultaneously can be used. However, unlike the analytical method used by [22] to obtain load line slope (using analytical expression for $B_r$ given by [29]) cannot be used due to non-solenoid shape. Only a numerical method can be utilized to calculate load line slope to determine $I_{op}$. The model is solved for magnetic vector potential (A) and magnetic flux density (B) using Eqs. (9) and (10) for a given test current ($I_{test}$).

$$\begin{aligned} \nabla \times \left( \frac{1}{\mu } \nabla \times \textbf{A}\right) =\textbf{J} \end{aligned}$$

(9)

$$\begin{aligned} \textbf{B}=\bigtriangledown \times \textbf{A} \end{aligned}$$

(10)

Load line slope (m) is calculated by dividing the $I_{test}$ by maximum $B_r$. With this load line slope, an equation of the line is written passing through the origin. $B_\perp -I$ characterization plot as shown in Fig. 2 is taken from [28] and curve fitted. The fitted equation is also mentioned in the plot. This can be easily solved by Matlab and gives us the intersection point. The operating current ($I_{op}$) is taken as 90% of the maximum possible value for safety reasons. Energy stored in this coil can be calculated by using Eq. (11) after solving Eqs. (9) and (10) for calculated operating current ($I_{op}$).

$$\begin{aligned} E_{stored}=\int \frac{B^{2}}{2 \mu } d v \end{aligned}$$

(11)

3.3 Stress Calculation

Analytical expression for hoop and radial stresses for perfect solenoid (central plane, where stress is maximum) is readily available [30, 31]. However for shapes considered in this paper, it cannot be used, as magnetic flux density is not similar to perfect solenoid. Once again, the numerical method is utilized to calculate the stress. Operating current obtained during energy calculation is again used in the same model to obtain the magnetic field distribution. The impact of screening current on stress calculations is neglected due to the absence of an ultra high background magnetic field, such as that found in the HTS inset coil [32], which results in a rotation effect in the end coil HTS tape [33, 34]. A static structural model is created with similar boundary conditions used in perfect solenoid as shown in Fig. 3. The inner and outer diameters are free to deform, while the top and bottom surfaces are given a roller support, i.e., free to move only in radial direction.

Fig. 3

Boundary condition applied in each coil for stress calculation

Volumetric force ($F_{vol}$) is calculated using the current density (J) and magnetic flux density (B) given by Eq. (12).

$$\begin{aligned} \mathbf {F_{vol}}=\textbf{J}\times \textbf{B} \end{aligned}$$

(12)

This $F_{vol}$ along with boundary conditions is used in static structural simulation. Equation (13) is solved to calculate the stress distribution in full coil.

$$\begin{aligned} \bigtriangledown .s+F_{vol}=0 \end{aligned}$$

(13)

Here s denotes the surface force.

Fig. 4

Geometry created using dimension from [35] along with magnetic flux density, hoop stress, radial stress, and axial stress surface plot for FEM validation

Fig. 5

DP fabrication process along with I-V characteristic (77 K, self-field) submerged in liquid nitrogen, using 50 m SuNAM, makes SCNk04200 for operating current validation

3.4 FEM Model Validation

Given that it incorporates calculations for both the magnetic field and stress, Kwak et al.’s [35] 600 kJ SMES numerical model is used to validate the FEM modeling approach using COMSOL. A small DP HTS coil is created and put to the test at 77 K to confirm operating current calculations.

3.4.1 Numerical Validation

Figure 4a illustrates the creation and resimulation of an axisymmetric geometry in accordance with the specified dimension in [35]. It consists of 22 DP coils with respective IR, OR, and $c_z$ dimensions of 500, 619.26, and 4 mm. With 89.5 GPa, 0.35 Young’s modulus (E), and 0.35 Poisson’s ratio (v), the operating current used was 275 A. The magnetic flux density, hoop stress, radial stress, and axial stress, respectively, after simulation are shown in Fig. 4b–e. Only hoop and radial stress were calculated; Von-Mises stress was not provided. Table 4 compares author’s FEM model against [35].

Table 4 Comparison of$B_r$,$B_z$, hoop, and radial stress between FEM model of [35] and this paper

3.4.2 Experimental Validation of Operating Current

Using a small HTS DP coil made from 50 ms of SuNAM-made SCNk4200 HTS 2 G tape with an 80-mm ID, the FEM model was experimentally validated. The HTS tape was already Kapton-insulated and had a total thickness of 0.17 mm with insulation. For I-V characterization, a DC current source was used to excite the coil. The coil was tested for I-V characteristic to determine operating current at 77 K using liquid nitrogen. Figure 5i and a–h display, respectively, the I-V characteristic result and DP coil test setup picture. A total of 70 A at 77 K, self-field, was the maximum permitted operating current with 1 microvolt criterion obtained.

An axisymmetric geometric model with dimensions taken from the DP coil is generated in COMSOL for the numerical calculation of maximum operational current. The load line slope was determined through simulation using FEM and the $B_\perp -I$ curve, which was taken from [36], in order to compute the operating current. The computed maximum operational current was 69.7 A. The numerical value and the operating current discovered through experimentation were comparable (70 A). This supports the FEM model’s validity in this study.

Fig. 6

Flowchart for shape optimization of HTS SMES using TLBO

4 Implementation of TLBO for Shape Optimization

TLBO is a population-based optimization algorithm proposed by Rao et al. [8, 9], developed on classroom environment, where students learn from the teacher, as well as learn from each other. This algorithm is different from the evolutionary algorithm (GA), and swarm intelligence (PSO) by the fact that it does not have any algorithm-specific parameters. Only number of initial population and number of iterations are required for implementation. Number of students is treated as population and various subjects are treated as design variables. Students’ result is treated as the fitness function value of the optimization problem. This algorithm is divided into two phases, the teaching phase and the learning phase. In the teaching phase, teacher tries to increase the average result of the class taught by him. The population, having the best fitness function value, is treated as teacher. In the learner’s phase, the students increase their knowledge by learning from each other. A student interacts randomly with other students for enhancing their knowledge. A student only learns new things, if other students have more knowledge than him, i.e., better fitness value.

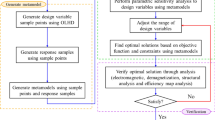
The 13 variables ($nr_1$, $nr_2$,......, $nr_{10}$, $c_r$, $c_z$, $n_z$) are treated as subjects with number of students (population) taken as 400. The implementation of optimization is done using MATLAB and COMSOL. COMSOL is used for FEM simulation to calculate the stored energy, $B_z$ and MATLAB for the optimization process. Steps for implementation of TLBO are as follows (Fig. 6).

• 1. Initialization: random population generation: At first, marks for each subject for all students are given randomly.

• 2. Fitness function calculation: Fitness function value is calculated for each student as given by Eq. (6). The right side of the flowchart (Fig. 6) shows the procedure of fitness function calculation.

• 3. Calculation of average marks in each subject ($X_{Mean}$)

• 4. Teacher selection ($X_{teacher}$): A teacher is selected from all students based on fitness function calculated in step 2. The student having the best fitness function value will act as a teacher.

• 5. Improve the student’s marks: Each subject mark for every student will be modified based on average marks (($X_{Mean}$)) as given by Eq. (14). TF is teaching factor, which can be 1 or 2.

  $$\begin{aligned} X_{ {new }}=X_{ {old }}+r\left( X_{ {teacher }}-(T F) X_{ Mean }\right) \end{aligned}$$

  (14)

• 6. Fitness function value calculation after teaching for each student

• 7. Comparison between before teaching and after teaching: The old fitness and new fitness value are compared. The one with increased fitness function value will be changed to new marks; otherwise, it will be kept the same as before teaching

• 8. Learning phase: Two students ($X_i$, $X_j$) are selected randomly and their fitness values are compared. The student having higher fitness function value is treated as more knowledgeable than others. More knowledgeable students will try to increase the marks of other students as given by Eqs. (15) and (16).

  $$\begin{aligned} X_{ {new }}=X_{ {old }}+r\left( X_{j}-X_{i}\right) ~~for~X_i~ better~than~X_j \end{aligned}$$

  (15)
  $$\begin{aligned} X_{ {new }}=X_{\ {old }}+r\left( X_{i}-X_{j}\right) ~~for~X_j~ better~than~X_i \end{aligned}$$

  (16)

• 9. Comparison between before learning and after learning phases: Once again, the fitness values of each student is compared between before learning and after learning processes. If the fitness function value is improved, the change in subject marks is kept, otherwise rejected.

• 10. Check the termination criteria: If the algorithm is reached for the total number of iterations given, the program will stop; otherwise, it will go into the teaching phase again. The student with the highest fitness function value is treated as an optimization result and marks of each subject are optimized variable values.

Table 5 Values of variables obtained after optimization

Fig. 7

Minimum fitness function value vs iteration showing optimization process

Because there was no change in the minimal fitness function value during a continuous 30 iterations, a total of 90 iterations were chosen. The values of the minimum fitness function for increasing iterations are shown in Fig. 7.

Fig. 8

Quarter axis symmetric geometry of some selected shapes each having 1 MJ stored energy obtained at the end of $70^{th}$ iteration using TLBO

5 Results and Discussion

After the termination of optimization process, all 400 population variables are grouped and sorted based on the minimum length value obtained. Table 5 lists out 6 selected optimized design variables with column (a) having minimum length and the rest are in increasing order. It also tabulates the parameters related to SMES coil such as $B_r$, $B_z$, $I_{op}$, von-Mises stress, and inductance. Each shape is unique with varying inner radius and individual DP coil positions but same stored energy of 1 MJ. The 1st result is having total 10 DP with 3 DP’s having single turn. Single turn is present due to the lower limit of number of turns kept as 1. For practical purpose, the effective number of DP coils can be taken as 7 by eliminating these 3 DP coils. The inner radius of each DP can be calculated by Eq. (7). The operating current given in the table is uniquely determined during the optimization process itself for a particular shape, which is 90% of the maximum allowable operating current.

The quarter axis-symmetric geometry of the tabulated results (Table 5) is shown in Fig. 8. Figure 8a is the geometry of the 1st result of Table 5 having length 7723.16 m. This unique topology has allowed to minimize the $B_\perp$ for maximizing of operating current, thus a reduction in HTS tape length. The optimization process has eliminated one or more DP coils in Fig. 8a to f, thereby making their positions more important in z coordinate. The increase of clearance between DP coils at the end is certainly helpful in increasing the current density, as inferred by Fig. 8a to e. In Fig. 8c, the top coil is having less IR in comparison with other coils. This has allowed the central coils to keep the maximum stress within the limit. Some shapes closely resemble to the solenoid in the final population. One of such shapes is given in Fig. 8f. Figure 8f is very close to the regular solenoid and the length required ($\approx$8357 m) for this is more than that for rest of the designs ($\approx$7700–8000 m). It can be said that a simple solenoid is not optimized in the view of minimum length. In the view of inductance also, Fig. 8a has less inductance (10.18 H) in comparison with Fig. 8f (16.83 H). For SMES application, during fast discharging, voltage may increase due to the sudden change in current and hence a low inductance is preferred in comparison with high inductance.

5.1 Comparison with Solenoid Geometry

To compare with a solenoid, optimization is performed for solenoid geometry. Total variables reduce down to 4 ($n_r$, $c_r$, $c_z$, $n_z$) from 13, by fixing the same number of turns in each coil. The fitness function, LB, and UB remain the same for shape optimization. With 50 initial random populations and for 50 iterations, the optimization is performed. At the end of the program, results are sorted based on minimum length. Figure 9 shows the results selected with varying number of DP coils. Figure 9a is having 4 DP coils while Fig. 9f consists of 9 DP coils. All the geometries in Fig. 9 have the same stored energy of 1 MJ. Figure 9a has the minimum length in comparison with other geometries. For increasing number of DP coils, the required length increases. For DP coils, less than 4, the stress is more than 250 MPa; therefore, it is not present in the final result. As the 1st result (Fig. 9a) is having minimum length for perfect solenoid geometry, it is selected for the comparison with shape-optimized geometry (Fig. 8a).

Fig. 9

Result of optimization for solenoid geometry (quarter axis symmetric geometry with 1 MJ stored energy)

Table 6 Comparison between shape-optimized vs simple solenoid for 1 MJ stored energy

The comparison of both the geometry in terms of length, maximum value of radial component of magnetic flux density ($B_r$ max), maximum value of axial component of magnetic flux density ($B_z$max), operating current ($I_{op}$), maximum von-Mises stress in whole of SMES coil, and inductance is given in Table 6.

The central field, $B_z$ max, and $B_r$ max for shape optimized are less than those for a simple solenoid. The increase in operating current capacity by 97 A for shape optimized in comparison with perfect solenoid can be explained by reduction in $B_r$. Although the inductance of simple solenoid is approximately 1.6 times that of shape optimized, stored energy (1 MJ) is the same in both. For SMES magnet coil, the higher inductance may lead to higher induced voltage ($V=L\frac{dI}{dt}$) during fast discharging and lower inductance value is preferred in this view the shape-optimized SMES is superior in comparison with perfect solenoid geometry. An increase in operating current has resulted in reduction in total length requirement by 7%.

Fig. 10

Magnetic flux density (a shape optimized, c perfect solenoid) and von-Mises stress (b shape optimized, d perfect solenoid) surface plot comparison

Figure 10c and a show the magnetic flux density surface plot for perfect solenoid and shape-optimized solenoid respectively. This shows that the magnetic flux lines are different due to change in the shape that has resulted in increase of operating current by reduction of $B_r$. In general, a perfect solenoid has maximum $B_r$ on the top surface of coil, but in shape-optimized geometry the location is no longer at the top surface. Moreover by looking at the flux lines at top DP coils, the angle is altered by unique topology.

Figure 10d and b show the von-Mises stress distribution in simple solenoid and shape-optimized solenoid respectively. Although the maximum stress is higher in shape-optimized geometry, it is less than the required design stress (250 MPa).

6 Conclusion

Shape optimization of HTS SMES coil is performed to obtain minimum length for 1 MJ of stored energy by varying the number of turns in each DP coil with fixed OD and maximum von-Mises stress limited to 250 MPa. TLBO is used as optimizer due to its simplicity as it does not require any algorithm-specific parameters. Several new and unique novel shapes are obtained. These shapes require less length in comparison with optimized solenoid geometry. The shape having minimum tape length required is compared with perfect solenoid geometry in terms of HTS tape length requirement, stored energy, inductance, and maximum stress. The shape-optimized SMES coil has significantly increased operating current due to reduction in $B_r$ as compared to perfect solenoid.