1 Introduction

Superconductors are generally in complex physical environments such as strong magnetic fields and high currents, whose critical properties are affected by the applied magnetic fields, currents, and mechanical loads. Superconducting materials generate AC loss when transmitting current and undergo mechanical deformation and magnetostriction or even destruction under electromagnetic stress.

Ikuta et al. [1] first proposed the magnetostriction of high-temperature superconductors caused by flux pinning and also developed a quantitative model of magnetostriction of superconducting plates by analyzing the experimental findings. Koziol et al. [2] tested the magnetostriction of a single crystal sample of Bi2Sr2CaCu2O8 through experiments and explained the magnetostriction properties present in the superconductor using a modified Kim-Anderson model. Nabialek et al. [3] proposed a model that can effectively simulate isotropy high-temperature superconductors by approximate simplification and studied the magnetostriction caused by flux pinning in some specially shaped superconducting samples. Yang et al. [4] investigated the effect of critical current density and elastic modulus non-uniformity on magnetostriction of superconductors when the applied magnetic field is perpendicular to the direction of change of the elastic modulus. Yong et al. [5] used an equivalent model to analyze the influence of non-superconducting state particle inclusions on the magnetostriction of bulk high-temperature superconductors. The results indicated that both the elastic modulus and the volume fraction of particles significantly affect the magnetostriction of the bulk superconductors. In addition, Gao et al. [6] proposed a fully coupled model to calculate the magnetostriction properties induced by flux pinning in a type II superconductor under the effect of an alternating magnetic field. Yong et al. [7] quantitatively illustrated the effects of coupling parameters on the magnetostriction and magnetization. Gao et al. [8,9,10,11] discussed the magnetostriction effect of high-temperature superconducting materials under uniform and non-uniform magnetic fields considering the critical current density, external magnetic field amplitude, frequency, and Meissner current fish-tail effect and coexistence of critical and normal states.

Mawatari et al. [12,13,14,15] theoretically analyzed the AC loss of a polygonal arrangement of superconducting cables and the AC loss of a circular arrangement of cylindrical superconducting cables. Savvides et al. [16] measured the AC loss of monofilament and multifilament Bi-2223/Ag strips under transmitted alternating currents by experimental means. Subsequently, Zhang et al. [17] experimentally measured the transmission AC loss of Bi-2223/Ag stainless steel strips at different tensile strains and gave a formula for the transmission loss considering the strain factor based on the Norris equation. The analytical results could be in good agreement with the experimental values. Clem et al. [18] proposed an anisotropic homogeneous medium to calculate approximately the current distribution and AC loss in a finite stacked superconducting strips carrying equivalent transfer currents. Yang et al. [19, 20] developed a set of finite difference numerical solutions to calculate the magneto-thermal diffusion equations of infinitely large high-temperature superconducting plates and considered the influence of magneto-thermal coupling effects on the superconductor AC loss as well as flux jump.

High-temperature superconductors are anisotropic materials, and the critical current density \(J_{c}\) is affected not only by the magnitude of the external magnetic field, but also by changes in the temperature field. For the study of magnetostriction phenomena and AC loss effects in high-temperature superconductors, most scholars define the material properties as isotropic materials and the critical current density \(J_{c}\) as the Bean or Kim model without considering the effect of temperature in order to simplify the study, which will have an impact on the accuracy of the results. For example, the premise of the magnetostriction studies in the Refs [6,7,8] is to define the material as isotropic, while the Ref [4] considers the anisotropy of the material but not the influence of the temperature field on the current density \(J_{c}\). Similarly, the Ref [18] defined high-temperature strips as anisotropic materials to investigate the effects of AC loss, but the Bean model independent of the applied field and temperature was chosen as critical current density model. The Ref [20] studied the AC loss effect in high-temperature superconducting plates under the condition of considering the influence of the temperature field on the critical current density, but the anisotropic properties of the model material were not considered. In this paper, cylindrical superconducting materials are defined as anisotropic and placed in a periodic alternating magnetic field for magnetization. The AC loss and magnetostriction of the superconductors under the electro-magnetic-thermal coupling effect are investigated. The whole research adopts the controlled variable method, and the effects of the four physical parameters (applied field amplitude \(H_{0}\), frequency \(f\), non-uniform coefficient of elastic modulus \(\beta\), and ambient temperature \({T}_{0}\)) on the trapped magnetic field, temperature field, magnetic moment distribution, AC loss, and magnetostriction of the superconductor at different values are discussed separately.

When a high-temperature superconductor is placed in an external magnetic field, the bucking current induced by the magnetic field flows in the superconductor along a toroidal loop. The electromagnetic field inside the superconductor satisfies the Maxwell equation as follows:

$$\nabla \times B={\mu }_{0}J$$
(1)
$$\nabla \times E+\frac{\partial B}{\partial t}=0$$
(2)

where \(B\) is the magnetic induction, \(J\) and \(E\) are the current density and electric field strength, respectively, and \(\mu_{0}\) is the permeability of vacuum.

The relationship between the electric field and the current density is given by the power law model [21, 22]:

$$E={\rho }_{s}\left(B,J,T\right)J={E}_{c}{(\frac{J}{{J}_{c}})}^{n}$$
(3)

where \(\rho_{s} (B,J,T)\) is the equivalent resistivity of the bulk superconductor and \(E_{c}\) is the characteristic electric field and \(n = {{U_{0} } \mathord{\left/ {\vphantom {{U_{0} } {kT}}} \right. \kern-\nulldelimiterspace} {kT}}\) represents the chance of creep occurrence.

From Eqs. (1)–(3), the governing equation of H-equation under the two-dimensional axisymmetric condition can be obtained:

$$\left\{\begin{array}{c}\mu_0\frac{\partial H_r}\partial-\frac1r\frac{\partial\left[r\rho_s\left(\partial H_r/\partial z-\partial H_z/\partial r\right)\right]}{\partial z}=0\\\mu_0\frac{\partial H_z}\partial+\frac1r\frac{\partial\left[r\rho_s\left(\partial H_r/\partial z-\partial H_z/\partial r\right)\right]}{\partial z}=0\end{array}\right.$$
(4)

where \(B = \mu_{0} H\), \(H_{r}\), and \(H_{z}\) represent the magnetic field components of \(H\) along the \(r\) direction and \(z\) direction, respectively.

Considering thermal activation and flux creep effects, the electric field in a superconductor can be described by the Anderson-Kim flux creep model [23,24,25]:

$$E=2{Bv}_{0\;}\exp(\frac{-U_0}{kT})\sinh(\frac{JU_0}{J_ckT})$$
(5)

where \(k\) is the Boltzmann constant; \(\nu_{0}\) is the velocity of the flux creep when the Lorentz force increases to equal the pinning force; for flux lines moving inside a superconductor, the part of the pinning center that plays a role in the pinning force density constitutes the effective pinning barrier, the average height of the barrier is \(U_{0}\); and the flux line must overcome this barrier in order to move. So \(U_{0}\) is the activation energy, which is a function of the magnetic field and temperature, and can be expressed explicitly as [26, 27]:

$${U}_{0}={U}_{00}\left[1-{\left(T/{T}_{c}\right)}^{4}\right]\left[1-B/{B}_{c2}(T)\right]$$
(6)

in which \(U_{00}\) is a constant, \(T_{c}\) is the superconducting transition temperature, and \(B_{c2} (T) = B_{c2} (0)[1 - ({T \mathord{\left/ {\vphantom {T {T_{c} }}} \right. \kern-\nulldelimiterspace} {T_{c} }})^{2} ]\) is the upper critical magnetic field. \(J_{c}\) is the critical current density, which is also a function of temperature and magnetic field. And here it is assumed to satisfy the Kim model form; the expression for the critical current can be obtained using the experimental fitting relationship of the superconducting material \({\mathrm{BiSr}}_{2}{\mathrm{CaCu}}_{2}{\mathrm{O}}_{8+\updelta }\) [28]:

$$J_c=J_c\left(T,B\right)=J_{c0}\;\exp\left\{-T/\lbrack T_c(1-{(T/T_c)}^2)\rbrack\right\}\frac{B_0}{\left|B\right|+B_0}$$
(7)

among them, \(J_{c0}\), \(T_{c}\), and \(B_{0}\) are constants that do not depend on temperature and magnetic field.

In the two-dimensional axisymmetric model, the heat transfer law can be described by the following equation. In superconductors, Eq. (8) is the controlling equation for the electro-magnetic-thermal coupling effect:

$$\rho_mc\frac{\partial T}{\partial t}=\frac1r\frac\partial{\partial r}(rk_s\frac{\partial T}{\partial r})+\frac\partial{\partial z}(k_s\frac{\partial T}{\partial z})+E_\varphi\cdot J_\varphi$$
(8)

where \({\rho }_{m}\) and c are the mass density and specific heat of the superconductor, respectively. \({k}_{s}\) denotes the thermal conductivity of the superconductor. \({E}_{\varphi }\) and \({J}_{\varphi }\) are the strength of the circulating current and the density of the circulating current induced in the superconductor, respectively.

The equation for the AC loss in the superconductor is as follows [29]:

$$Q={\int }_{{T}^{cycle}}dt{\int }_{-R}^{R}{E}_{\varphi }\cdot {J}_{\varphi }dr$$
(9)

in which \({T}^{cycle}\) denotes the period of the external magnetic field and R is the radius of the superconductor.

The time-varying power loss can be described as:

$$P={\int }_{-R}^{R}{E}_{\varphi }\cdot {J}_{\varphi }dr$$
(10)

The heat transfer problem at the superconductor-air interface is more complicated. According to the practical situation, the simple empirical formula proposed in the Ref [30] is used as the temperature boundary condition for the heat transfer part. During immersion cooling, the heat flux density at the interface between the superconductor and the coolant can be expressed as:

$${\varvec{n}}\cdot \left(-{k}_{s}\nabla T\right)=A({T}^{{\sigma }_{A}}-{T}_{0}^{{\sigma }_{A}})$$
(11)

where \({\varvec{n}}\) is the unit vector in the direction of the outer normal of the superconducting surface, \({T}_{0}\) is the ambient temperature, and A as a fixed empirical constant, generally taking the value \({{0.05W} \mathord{\left/ {\vphantom {{0.05W} {(m^{2} \cdot K^{{\sigma_{A} }} )}}} \right. \kern-\nulldelimiterspace} {(m^{2} \cdot K^{{\sigma_{A} }} )}}\). \({\sigma }_{A}\) is a dimensionless variable parameter that reflects the heat transfer capacity of the interface. If \(T>{T}_{0}>1K\) , the heat flux density of the interface increases with the increase of \({\sigma }_{A}\), which generally takes a value in 3 ~ 4.

Gao and Zhou proposed a numerical model to calculate the magnetostriction induced by magnetic pinning of superconductors under an alternating magnetic field [6]. The magnetic field generated by the electromagnet in the \(z\) direction can be described as that:

$${H}_{z}={H}_{0}\mathrm{sin}(2\pi ft)$$
(12)

where \({H}_{0}\) is the amplitude of the applied magnetic field and \(f\) is the frequency of the applied magnetic field.

The magnetization direction of a two-dimensional axisymmetric high-temperature superconductor is mainly in the axial direction (z-axis), while its magnetization intensity \({M}_{z}\) in the z-axis direction can be expressed as [31]:

$${M}_{z}=(\frac{1}{2}{\int }_{{D}_{SC}}r\cdot {J}_{\varphi }dV)/V$$
(13)

The magnetostriction of cylindrical superconductors can be expressed as [32]:

$$\frac{\Delta R}{R}=\frac{1-v}{{E}_{s}{\mu }_{0}{R}^{2}}{\int }_{0}^{R}r[{B}^{2}\left(r\right)-{B}_{a}^{2}]dr$$
(14)

where v denotes the Poisson’s ratio of the superconducting material, \({E}_{s}\) represents the elastic modulus of the superconductor, B(r) is the magnetic field distribution in the superconductor, and \({B}_{a}\) denotes the external magnetic field magnitude.

High-temperature superconductors are generally heterogeneous materials. In order to describe the non-uniformity of its elastic modulus, it is assumed that the elastic modulus of a two-dimensional axisymmetric high-temperature superconductor is a function of the coordinate r, which is distributed in the \(r\)-axis direction in the following form [33]:

$${E}_{s}\left(r\right)={E}_{0}\cdot {e}^{\beta r}$$
(15)

where \({E}_{0}\) is a constant and \(\beta\) is the non-uniform coefficient of elastic modulus of high-temperature superconductor material.

In this paper, we study the AC loss and magnetostriction of a cylindrical superconductor placed in an alternating magnetic field magnetization process under the electro-magnetic-thermal coupling effect. Due to the symmetry of the cylinder, we can simplify the three-dimensional model to a two-dimensional axisymmetric model. A large volume \({\mathrm{BiSr}}_{2}{\mathrm{CaCu}}_{2}{\mathrm{O}}_{8+\updelta }\) sample with a diameter of 120 mm and a thickness of 40 mm is used, as shown in Fig. 1. The sinusoidal periodic excitation model proposed by Gao and Zhou is used for the alternating external field. The external magnetic field applied to the superconducting sample is parallel to the z-axis direction of the specimen. The numerical model used in this paper is based on the two-dimensional \({\text{H}}\) formula of the \({\mathrm{BiSr}}_{2}{\mathrm{CaCu}}_{2}{\mathrm{O}}_{8+\updelta }\) superconductor, which was implemented with the commercial finite element software COMSOL Multiphysics [34,35,36], and the parameters are shown in Table 1.

Fig. 1
figure 1

Sample size

Full size image
Table 1 Parameters used in the simulations [37,38,39,40,41,42]
Full size table

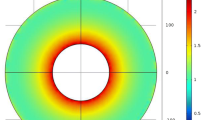
According to the H formula and heat transfer law, the distribution state of the electromagnetic field with radius can be obtained by numerical calculation. Controlling the frequency of the alternating magnetic field \(f{ = }5{\text{Hz}}\), the non-uniform coefficient of the material elastic modulus \(\beta { = 0}\), the ambient temperature \(T_{0} { = }15{\text{K}}\) is a fixed value, and the external magnetic field loaded to \({{(1} \mathord{\left/ {\vphantom {{(1} 4}} \right. \kern-\nulldelimiterspace} 4})T^{cycle}\). When the external field amplitude is taken as \(H_{0} = 1 \times 10^{5} ({\text{A/m}})\), \(H_{0} = 2 \times 10^{5} ({\text{A/m}})\), and \(H_{0} = 3 \times 10^{5} ({\text{A/m}})\), respectively, the magnetic flux density distribution inside the superconductor is shown in Fig. 2. From the figure, it can be observed that the magnetic flux gradually penetrates from the boundary of the superconductor to the inside of the superconductor. The magnetic field does not completely penetrate the superconductor when \(H_{0} = 1 \times 10^{5} ({\text{A/m}})\), while when \(H_{0} = 3 \times 10^{5} ({\text{A/m}})\), the magnetic field has completely penetrated the superconductor.

Fig. 2
figure 2

Contour diagram of the variation of magnetic flux density with radius inside the superconductor

Full size image

Take different values of amplitude \(H_{0}\), frequency \(f\), non-uniform coefficient of elastic modulus \(\beta\), and ambient temperature \({T}_{0}\), respectively. The trend of the trapped magnetic field inside the superconductor is plotted with the value of radius \(r\) taken when the external magnetic field is loaded to \({{(1} \mathord{\left/ {\vphantom {{(1} 4}} \right. \kern-\nulldelimiterspace} 4})T^{cycle}\), as shown in Fig. 3.

Fig. 3
figure 3

Trend of trapped magnetic field strength with radius. (a) \(H_{0}\) takes \(H_{0} = 1 \times 10^{5} (A/m)\), \(H_{0} = 2 \times 10^{5} (A/m)\), and \(H_{0} = 3 \times 10^{5} (A/m)\). (b) \(\beta\) takes \(\beta = 0\), \(\beta = 5\), and \(\beta = 10\), respectively. (c) \(f\) takes \(f = 5{\text{Hz}}\), \(f = 10{\text{Hz}}\), and \(f = 50{\text{Hz}}\), respectively. (d) \({T}_{0}\) takes \(T_{0} = 15{\text{K}}\), \(T_{0} = 18{\text{K}}\), and \(T_{0} = 20{\text{K}}\), respectively

Full size image

In Fig. 3a, the frequency \(f\), the non-uniform coefficient \(\beta\) of the elastic modulus, and the ambient temperature \(T_{0}\) are taken as constant values. As the amplitude of the applied alternating magnetic field \(H_{0}\) increases, the ability of superconductor to trap the magnetic field continuously strengthens. And the penetration depth of the magnetic field inside the superconductor also deepens until it penetrates completely. Figure 3b shows that the ability of the superconductor to trap the magnetic field is essentially constant as the non-uniform coefficient of elastic modulus \(\beta\) increases when the other parameters are taken to be definite. In other words, variations in the non-uniform coefficient of elastic modulus do not cause changes in the magnetic flux and magnetic moment inside the superconductor. Figure 3c and d show that when the external magnetic field penetrates the superconductor, controlling the other parameters constant while increasing the external field excitation frequency \(f\), the ability of the superconductor to trap the magnetic field gradually decreases; i.e., the magnetic flux into the superconductor also gradually decreases. When the ambient temperature \({T}_{0}\) increases, the ability of the superconductor to trap the magnetic field appears to be slightly enhanced, but the increase is not significant.

As shown in Fig. 4, the applied alternating magnetic field amplitude \({H}_{0}\), frequency f, the non-uniform coefficient of elastic modulus \(\beta\), and ambient temperature \({T}_{0}\) take different values, respectively. Figure 4 shows the trend of the temperature field T inside the superconductor with the value of the radius r taken when the external magnetic field is loaded to a period \({T}^{cycle}\).

Fig. 4
figure 4

Trend of temperature field inside the superconductor with radius. (a) \(H_{0}\) takes \(H_{0} = 1 \times 10^{5} (A/m)\),\(H_{0} = 2 \times 10^{5} (A/m)\), and \(H_{0} = 3 \times 10^{5} (A/m)\), respectively. (b) \(\beta\) takes \(\beta = 0\), \(\beta = 5\), and \(\beta = 10\), respectively. (c) \(f\) takes \(f = 5{\text{Hz}}\), \(f = 10{\text{Hz}}\), and \(f = 50{\text{Hz}}\). (d) \({T}_{0}\) takes \(T_{0} = 15{\text{K}}\), \(T_{0} = 18{\text{K}}\), and \(T_{0} = 20{\text{K}}\), respectively

Full size image

Figure 4a demonstrates that when the other parameters remain unchanged, the temperature inside the superconductor tends to increase with the increase of the external magnetic field amplitude \(H_{0}\), and the rate of increase is accelerating. It is observed through Fig. 4b that the internal temperature of the superconductor remains essentially constant as the non-uniform coefficient of elastic modulus \(\beta\) increases. That is to say, the variation in the non-uniform coefficient of elastic modulus will not cause the change in the internal temperature field of the superconductor. Figure 4c reveals that with the growth of the external magnetic frequency \(f\), the internal temperature of the superconductor remains basically unchanged, but there is an obvious rise in temperature at the surface. Figure 4d shows that the temperature inside the superconductor increases gradually with the increase of the ambient temperature \({T}_{0}\). However, it is noteworthy that under different ambient temperatures, the tendency of the internal temperature field \(T\) of superconductors to vary with radius \(r\) remains basically consistent.

As a magnetic medium with special electromagnetic properties, high-temperature superconductors, like general magnetic media, have electromagnetic effects that can be reflected by the magnetization of the medium. Moreover, the investigation of the magnetization properties of high-temperature superconductors is one of the significant ways to study the relevant behavior of high-temperature superconductors. Figure 5 shows the variation of the magnetization intensity with loading and unloading process of the alternating external field when \(H_{0}\), \(f\), and \(\beta\) and \({T}_{0}\) are taken to different values, respectively.

Fig. 5
figure 5

Trend of internal magnetic moment of superconductor with external field loading and unloading process. (a) \(H_{0}\) takes \(H_{0} = 1 \times 10^{5} (A/m)\), \(H_{0} = 2 \times 10^{5} (A/m)\), and \(H_{0} = 3 \times 10^{5} (A/m)\), respectively. (b) \(\beta\) takes \(\beta = 0\), \(\beta = 5\), and \(\beta = 10\), respectively. (c) \(f\) takes \(f = 5{\text{Hz}}\), \(f = 10{\text{Hz}}\), and \(f = 50{\text{Hz}}\), respectively. (d) \({T}_{0}\) takes \(T_{0} = 15{\text{K}}\), \(T_{0} = 18{\text{K}}\), and \(T_{0} = 20{\text{K}}\), respectively

Full size image

From Fig. 5a, it can be observed that the magnetic moment increases with the increase of the external magnetic field amplitude \(H_{0}\), and the change of the external field amplitude has a remarkable effect on the magnetization curve. The area of the magnetization intensity curve also shows a significant increase with the increase of the external field amplitude. And it can be noticed from Fig. 5b and d that changes in both the non-uniform coefficient of elastic modulus \(\beta\) and the ambient temperature \({T}_{0}\) do not have an obvious effect on the magnetization curve. Therefore, when studying the effect of \(\beta\) and \({T}_{0}\) on the magnetization strength, the influence of magnetic flux and magnetic moment on its mechanical properties can be ignored. The law is in accordance with the conclusions given in Fig. 3b and d. Figure 5c indicates that there is a slight increase in the area and magnetic moment of the magnetization region with the increase of the external field excitation frequency \(f\) when the other parameters remain unchanged. Gao et al. [6] present a fully coupled model to account for the flux pinning induced giant magnetostriction in type II superconductors under alternating magnetic field, The results show that an increase in the external field amplitude \(B_{0}\) causes a significant increase in the area of the magnetization curve, while an increase in the alternating external field frequency \(f\) causes only a slight increase in the magnetization curve. The conclusions obtained are fully consistent with the variation pattern of Fig. 5a and c in this paper.

AC loss assessment is related to the safe and stable operation of superconducting magnets. And it is a key issue to be considered in the electromagnetic design of superconducting magnets, topology design, cryogenic system, and quench protection system design process. In order to investigate in depth the influence of different physical parameters on AC losses, the time-varying power loss conditions for different cases of \({H}_{0}\), \(\beta\), f, and \({T}_{0}\) are given in Fig. 6.

Fig. 6
figure 6

Time-varying power loss distribution. (a) \(H_{0}\) takes \(H_{0} = 1 \times 10^{5} (A/m)\), \(H_{0} = 2 \times 10^{5} (A/m)\), and \(H_{0} = 3 \times 10^{5} (A/m)\), respectively. (b) \(\beta\) takes \(\beta = 0\), \(\beta = 5\), and \(\beta = 10\), respectively. (c) \(f\) takes \(f = 5{\text{Hz}}\), \(f = 10{\text{Hz}}\), and \(f = 50{\text{Hz}}\), respectively. (d) \({T}_{0}\) takes \(T_{0} = 15{\text{K}}\), \(T_{0} = 18{\text{K}}\), and \(T_{0} = 20{\text{K}}\), respectively

Full size image

It can be observed from Fig. 6a and c that when the external field penetrates the superconductor, the power loss increases with the rise of the external magnetic field amplitude \(H_{0}\) and frequency \(f\). The time response of the power loss basically exhibits a periodic variation with half the variation period of the external field period. In addition, in the case of considering the initial magnetization phase, that is, after the magnetization phenomenon reaches a steady state, the time response of the power loss lags behind the change in the magnetic field scanning rate. When the magnetic field scanning rate reaches the maximum value, for example, at the moment \(t = 0.15{\text{s}}\), the power loss does not reach its peak, as shown in Fig. 6a. Figure 6c illustrates that the increase in frequency \(f\) speeds up the movement of the magnetic flux lines, and induces a higher magnetization intensity and current density, thus resulting in greater loss. The law conforms to the conclusion given in Fig. 5c. Huang et al. [20] investigated the AC loss of high-temperature superconducting plate transmission. When varying the applied electric field amplitude \(I_{0}\) and alternating current frequency \(f\), the AC loss variation curves are consistent with the patterns shown in Fig. 6a and c of this paper. Figure 6b shows that the variation of the non-uniform coefficient \(\beta\) has almost no effect on the power loss, which means that the non-uniformity of the elastic modulus of the superconducting material is negligible in the calculation of the AC loss. Figure 6d reveals that the variation of the ambient temperature \({T}_{0}\) has also little effect on the power loss. High-temperature superconducting materials in the liquid nitrogen temperature region have a large specific heat capacity, generally in \({10}^{5}\sim {10}^{6}{\mathrm{JK}}^{-1}{\mathrm{m}}^{-3}\). So, in a good cooling environment, superconductors do not show a significant temperature rise. And the temperature term can be ignored when calculating the electromagnetic behavior and AC losses in superconductors in this temperature region. However, it is worth noting that there is a significant difference in the time to reach the peak value. The higher the external ambient temperature, the earlier the peak loss will be reached. If we want to investigate quench of superconductivity, flux jump, and flux avalanche [30, 42, 43], which are accompanied by obvious temperature fluctuations, it is necessary to introduce a temperature term in the model and to calculate the evolutionary behavior of the temperature with time.

In order to further investigate the effects of different physical parameters on the AC loss, two cases of the external magnetic field not penetrating and penetrating the superconductor will be discussed separately in this paper. \(B_{p}\) is the magnitude of the external field that corresponds to when the magnetic field can just completely penetrate the superconductor. It can be calculated with the formula \(B_{p} = \mu_{0} J_{c} R\), but the \(J_{c}\) model is more complicated and it is difficult to solve the value of \(B_{p}\). In this paper, when the applied field amplitude \(H_{0} = 1 \times 10^{5} ({\text{A/m}})\), the superconductor is not penetrated by the observation of the trapped magnetic field inside the superconductor in the numerical calculation. When the applied field amplitude \(H_{0} = 3 \times 10^{5} ({\text{A/m}})\), the magnetic field has completely penetrated the superconductor. By changing the magnitude of the applied magnetic field \(H_{0}\), the trend of the AC loss with the external field strength at different excitation frequencies is shown in Fig. 7.

Fig. 7
figure 7

Time-varying power loss distribution. (a) The external magnetic field does not penetrate the superconductors. (b) The external magnetic field penetrates the superconductor completely

Full size image

Based on Bean model to derive the AC loss analysis calculation formula, the formula reflects that when the external field does not completely penetrate the superconductor, \(B_{a} < B_{p}\), \(Q = {{2B_{a}^{3} } \mathord{\left/ {\vphantom {{2B_{a}^{3} } {3\mu_{0} B_{p} }}} \right. \kern-\nulldelimiterspace} {3\mu_{0} B_{p} }}\), the loss value is proportional to the third power of the external field amplitude [29]. A cubic polynomial fit of five different sets of external field amplitudes and corresponding AC loss values for the unpenetrated case with a fit of \(R^{2} > 0.99\) indicates that the fit results are fully consistent with the theoretical reality, as shown in Fig. 7a. And when the given external field amplitude is not enough to penetrate the superconductor, the larger the external field excitation frequency \(f\), the smaller the area of the magnetization curve at the same amplitude, and the smaller the AC loss of the superconductor. When the external field completely penetrates the superconductor, \(B_{a} \ge B_{p}\), \(Q = {{(6B_{p} B_{a} - 4B_{p}^{2} )} \mathord{\left/ {\vphantom {{(6B_{p} B_{a} - 4B_{p}^{2} )} {3\mu_{0} }}} \right. \kern-\nulldelimiterspace} {3\mu_{0} }}\), at which time the AC loss value is linearly related to the external field amplitude [29]. Similarly, linear fitting is performed for five different sets of external field amplitudes and the corresponding AC loss values in the case of complete penetration, and the fitting degree is \(R^{2} > 0.99\) which again shows that the fitting results are fully consistent with the theoretical reality, as shown in Fig. 6b. It can be seen that when the external field amplitude can penetrate the superconductor, the larger the frequency, the larger the area of the magnetization curve and the corresponding AC loss under the same amplitude condition. The law is fully consistent with the conclusion given in Fig. 6c.

The distribution of the magnetic field in the superconductor not only satisfies the constitutive relationship between the critical current density and the magnetic field, but also satisfies the Ampere law that ignores the electric displacement vector, where a change in either of the two quantities will be followed by a change in the other. The Lorentz force in a superconductor is the vector product of the magnetic field and the current density. When the magnetic field and current density change, the Lorentz force will also change accordingly. The change of Lorentz force will be reflected in the magnetostriction of the superconductor; that is, the magnetostriction of the superconductor can reflect the magnitude and distribution of the magnetic field in the superconductor and the force condition. The magnetostriction for different cases of external magnetic field amplitude \(H_{0}\), non-uniform coefficient \(\beta\), frequency \(f\), and ambient temperature \({T}_{0}\) is given in Fig. 8.

Fig. 8
figure 8

The circuit diagram of superconducting magnetostriction. (a) \(H_{0}\) takes \(H_{0} = 1 \times 10^{5} (A/m)\),\(H_{0} = 2 \times 10^{5} (A/m)\), and \(H_{0} = 3 \times 10^{5} (A/m)\), respectively. (b) \(\beta\) takes \(\beta = 0\), \(\beta = 5\), and \(\beta = 10\), respectively. (c) \(f\) takes \(f = 5{\text{Hz}}\), \(f = 10{\text{Hz}}\), and \(f = 50{\text{Hz}}\), respectively. (d) \({T}_{0}\) takes \(T_{0} = 15{\text{K}}\), \(T_{0} = 18{\text{K}}\), and \(T_{0} = 20{\text{K}}\), respectively

Full size image

Figure 8a shows that the magnetostriction curve and the peak value of magnetostriction become larger as the amplitude H increases when controlling the other parameters unchanged. When the amplitude \(H_{0} = 1 \times 10^{5} {\text{(A/m)}}\) of the applied magnetic field, the applied magnetic field has not yet penetrated the superconductor. And the magnetostriction is all negative, and the magnetostriction does not change obviously with the process of loading and unloading the external magnetic field. When the amplitude \(H_{0} = 3 \times 10^{5} {\text{(A/m)}}\) of the applied magnetic field, the applied magnetic field has completely penetrated the superconductor. At this time, the magnetostriction has changed significantly with the loading and unloading process of the external magnetic field. The Ref [8] investigates that the magnetostriction in a superconductor-magnet system under non-uniform magnetic field, and the obtained magnetostriction variation curves under the different external field amplitudes are more consistent with the variation pattern shown in Fig. 8a of this paper. In Fig. 8b, as the non-uniform coefficient \(\beta\) increases, the peak of magnetostriction decreases gradually during both the ascending and descending fields, and the area of the magnetostriction loop also decreases gradually. For high-temperature superconductors, there is no change in the magnetic flux and magnetic moment inside the superconductor when the non-uniformity coefficient \(\beta\) increases. And from the conclusions given in Figs. 3b and 5b, it is clear that the internal electromagnetic stress has not changed at this time. In this case, the deformation produced by the entire high-temperature superconductor will decrease as the average value of the elastic modulus increases, leading to a decrease in its magnetostriction. It is indicated that the non-uniformity of the elastic modulus of superconductor materials can have a significant effect on the magnetostriction of superconductors. In the Ref [4], the effect of material inhomogeneity on the magnetostriction phenomenon of superconductors was studied by the analytical method. The material elastic modulus was also defined as an extended exponential model to obtain the variation law of the magnetostriction curve for different values of non-uniform coefficient of elastic modulus \(\beta\). This law is in accordance with Fig. 8b obtained by the numerical solution in this paper.

Figure 8c shows a slight decreasing trend of magnetostriction as the excitation frequency \(f\) of the external magnetic field increases. Zhao et al. [44] plotted the variation curves of the magnetostriction loop under different external field excitation frequencies \(f\) by analytical calculations, and the curve variation law is completely consistent with the conclusion obtained in Fig. 8c of this paper. Figure 8d reveals that the morphology of the magnetostriction loop remains basically the same when the ambient temperature \({T}_{0}\) is changed. In other words, the ambient temperature does not have a significant effect on the magnetostriction.

This paper presents numerical simulations of the trapped and temperature field variations, magnetization properties, AC loss, and magnetostriction effects of superconductors with anisotropic materials during the magnetization of periodic alternating fields. Considering the cylindrical symmetry, the three-dimensional model is simplified to a two-dimensional axisymmetric model. Based on the electro-magnetic-thermal coupling effect, the trapped magnetic field, temperature field, and magnetization distribution law can be obtained according to the H formula and heat transfer law, and the AC loss and magnetostriction in the process of loading and unloading with the external magnetic field are calculated. The results show that when the external field amplitude is increased, the trapped magnetic field, temperature field, magnetic moment, and AC loss as well as magnetostriction in the superconductor all increase significantly. When increasing the non-uniformity coefficient of elastic modulus of superconducting materials, only the magnetostriction and the area of magnetostriction loop are significantly reduced. If the excitation frequency of the external magnetic field is increased, the trapped magnetic field and magnetostriction tend to decrease, while the magnetic moment inside the superconductor tends to increase. If the temperature of the external field is changed, there is no apparent change in the trend of the trapped magnetic field, magnetic moment and AC loss, and magnetostriction of the superconductor. Since high-temperature superconducting materials in the liquid nitrogen temperature region have a large specific heat capacity, the superconductor will not have a significant temperature rise in a good cooling environment. It is worth noting that when the external magnetic field has not completely penetrated the superconductor, the AC loss tends to decrease with the increase of the excitation frequency. When the external magnetic field completely penetrates the superconductor, the AC loss tends to increase with the increase of the excitation frequency.