1 Introduction

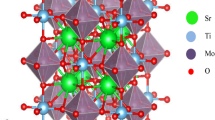
The field of magnetoelectronics, also known as spintronics, can be referred to as one of the most important and promising branches of solid-state physics and condensed matter [1,2,3]. For application in spintronic devices, materials must have high magnetic moment, high spin polarization, and high critical transition temperature. Some half-metallic ferromagnetic materials are used in spintronic applications such as magnetic sensors [4, 5], memory storages [6,7,8], spin filters [9], spin valves [10,11,12,13], and tunneling magnetoresistance effect [14,15,16,17]. During the last few years, a huge number of materials, including Heusler alloys (full, half, and quaternary) [18,19,20,21,22,23,24,25], dilute magnetic semiconductors [26,27,28,29,30], transition metal oxides [31, 32], perovskites [33,34,35,36], and double perovskites [37,38,39,40,41,42,43,44,45,46,47,48,49,50,51], with different chemical compositions and structural types, have been investigated to show the possibilities of obtaining new half-metallic systems. One of the most important families of compounds among them is strontium double perovskite oxides with the stoichiometric composition Sr2MM′O6, where Sr, M, and M′ atoms are arranged on octahedral sites according to the rock salt type. The exploration of new members of this class of double perovskite oxides in terms of their structures and their compositions to achieve desired properties is an active area of research in condensed matter physics and beyond. Different charming properties have been observed in these strontium double perovskite oxides, such as the half-metallic behavior in Sr2FeMO6 (M =Mo, Re) and Sr2CrMO6 (M=Mo, W) [41,42,43], half-metallic antiferromagnetic behavior in Sr2OsMoO6 [44], room-temperature colossal magnetoresistance in Sr2MMoO6 (M = Cr, Fe) [41, 46], tunnel magnetoresistance in Sr2FeMoO6 [47], and magnetoelectric behavior in Sr2CoMoO6 [48].

To the best of our knowledge, only a few studies on Sr2(Cr, V)NbO6 have been reported until now [49,50,51,52,53,54]. Experimentally, Sr2CrNbO6 has been prepared, and characterized to investigate the bonding nature of the metal–ligand bond and its relationship with crystal structure and magnetic properties [49]. Furthermore, the electrical properties of Sr2CrNbO6 in oxidizing and reducing atmospheres were investigated by Xia et al. [50]. Cheah et al. [51] reported the synthesis and phase transitions of the solid solutions of Sr2-xCaxCrNbO6 using powder neutron diffraction. In the same context, Sr2CrNbO6 has been also investigated for use as buffer layer material to aid in high-quality thin film growth of the half-metallic double perovskite Sr2FeMoO6 [52]. A combined experimental and theoretical study of Sr2CrNbO6 has been carried out on the effects of cation ordering/disordering upon photocatalytic activity [53]. Recently, the authors in reference [54] shed light on the cation order (layered vs rock salt) control of correlations in double perovskite Sr2VNbO6.

The present work provides us a further understanding of the stability of Sr2MNbO6 (M = V, Cr) and a deep comprehension of the relationship between their physical properties and chemical composition. Furthermore, our contribution covers the deficiency of theoretical investigation on the thermo-elastic and magneto-electronic properties of these strontium oxides. In our Sr-based double perovskites Sr2MNbO6, the results clearly demonstrate that the M3+ (3dn-\({\mathrm{t}}_{2g}^{n}\)) ions (n = 2or 3) have a significant effect on magnetic moment and electronic conducting, contrary to the nonmagnetic Nb5+ (4d0-\({\mathrm{t}}_{2g}^{0}\)) ions.

2 Computational Details

The calculations of transition metal oxides Sr2MNbO6 (M = V, Cr) were made using the WIEN2k code [55, 56], which is an implementation within the scheme of density functional theory [57]. The exchange–correlation effects were estimated by the well-known generalized gradient approximation (GGA) [58], which is a functional of the local electron spin densities ρ(r) and their gradients written in equation form:

$${E}_{xc}^{GGA}\left[{\rho }_{\uparrow } , {\rho }_{\downarrow }\right]=\int {\epsilon }_{xc} \rho \uparrow \left(\overrightarrow{r}\right),\rho \downarrow \left(\overrightarrow{r}\right),\nabla \rho \uparrow \left(\overrightarrow{r}\right),\nabla \rho \downarrow \left(\overrightarrow{r}\right),\rho (r){d}^{3}r$$
(1)

where the terms in the above equation, ρ↑, ρ↓, ∇ρ↑, and ∇ρ↓, denote the electron and gradient densities of electrons in spin-up and spin-down, respectively, while \({\epsilon }_{xc}\) defines the exchange correlation energy. Moreover, the Hubbard parameter U was used to overcome the inefficiency of the GGA functional to predict the magneto-electronic properties and understand the underlying physics of the strongly correlated d transition metal-based system limits [59]. Additionally, the hybrid functional approach of exact exchange for correlated electrons (EECE) was also used [60]. The charge densities of the Fourier expansion and maximum values of angular momentum were set to be lmax = 10 and Gmax = 14, respectively. To certify that there is no outflow of charge from the core, the non-overlapped muffin–tin radius (RMT) and converged energy value should be selected. The product of RMT and Kmax restricts the number of plane waves for Brillouin zone (BZ) integration, and its value used to perform the calculations was 8.5. The convergence criterion used for energy was 10–4 Ry, whereas the charge was converged up to 10−3e. A dense k-mesh of 20 × 20 × 20 was used to calculate all physical properties of considered compounds, and the separation between the core and valence states was set to -6.0 Ry.

3 Results and Discussion

The results obtained using the various ground-state parameters are discussed as below.

3.1 Structural Phase Stability

Structure stability is an important issue for evaluating and predicting compounds including hypothetical materials. In order to study the structural stability of the transition-metal double perovskite oxides, we firstly assessed the Goldschmidt tolerance (t) factor [61]. For Sr2MNbO6 (M = V, Cr), t can be calculated as follows:

$$\mathrm{t}=\frac{\left({\mathrm{r}}_{\mathrm{Sr}}+{\mathrm{r}}_{\mathrm{O}}\right)}{\sqrt{2}\left({\mathrm{r}}_{\mathrm{M},\mathrm{Nb}}+{\mathrm{r}}_{\mathrm{O}}\right)}=\frac{\sqrt{2}\left({\mathrm{r}}_{\mathrm{Sr}}+{\mathrm{r}}_{\mathrm{O}}\right)}{\left({(\mathrm{r}}_{\mathrm{M}}+{\mathrm{r}}_{\mathrm{Nb}})+2{\mathrm{r}}_{\mathrm{O}}\right)}$$
(2)

The ionic radii in 6-coordinate octahedral arrangements are r (Sr2+) = 1.44 Å, r (Cr3+) = 0.615 Å, r (V3+) = 0.64 Å, r (Nb5+) = 0.64 Å, and r (O2−) = 1.4 Å [62]. The divergence of the tolerance factor t from unity decreases the probability of the formation of a cubic phase as the stable structure, whereas it increases the probability of the formation of less symmetric states. As seen in Table 1, the calculated values are found to be amid (0.984 ≤ t ≤ 0.995) for \({\mathrm{Sr}}_{2}^{2+}{\mathrm{M}}^{3+}{\mathrm{Nb}}^{5+}{\mathrm{O}}_{6}^{2-}\) materials, confirming the stability of the cubic structure. The bond angle < M–O–Nb >  = 180° and thus no MO6–NbO6-octahedral distortions. The main reason for the deviation from the cubic symmetry can be explained by the magnitude of the octahedral tilt angle. The rotation of the octahedra can be explained by using the Glazer tilt system (GTS) [63, 64]. The GTS describes the tilt system by the rotations of the MO6/NbO6 octahedra about the cubic crystallographic directions a, b, and c. Therefore, no octahedral tilt or (a0a0a0) in terms of GTS rotation exists in Sr2MNbO6, as mentioned in Table 1. The overall structure stability can be examined by means of the global instability index (GII), i.e., the deviation of the bond valence sums with the ideal formal valences [65, 66]. The GII value is typically < 0.1 v.u., valence units, for unstrained structures, while it is large as 0.2 v.u. in structures with lattice-induced strains [65]. The GII values of Sr2MNbO6 (M = V, Cr) are calculated using the Structure Prediction Diagnostic Software [67] and found to be 0.0853 v.u. and 0.0502 v.u., respectively.

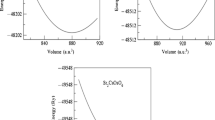
Table 1 The calculated and experimental crystallographic data for Sr2MNbO6 (M = V, Cr); tolerance factors (t), Glazer tilt system (GTS), lattice constants a, oxygen positions u, bulk modulus (B), pressure derivative of bulk modulus (B′), standard enthalpy of formation energies (\(\Delta {H}_{f}^{o}\)), and the average bond lengths. Values within parentheses represent the predicted results at RT via the SPuDS Software
Full size table

To confirm the structural stability in these double perovskites, the total energies are calculated for the four different polymorph structures, i.e., cubic (Fm-3 m; No. 225), tetragonal (I4/m; No. 87), monoclinic (P21/n; No. 14), and orthorhombic (Pmm2; No. 25). The calculated total energies reveal that the cubic structure is more stable than the other structures, as shown in Fig. 1. The curves were obtained by fitting the calculated values to the Murnaghan equation of state [68].

Fig. 1
figure 1

The total energy versus volume (cubic, tetragonal, monoclinic, and orthorhombic) of Sr2CrNbO6 and Sr2VNbO6 compounds

Full size image

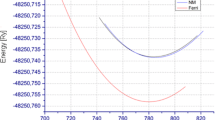
Next, to confirm the stable state of Sr2MNbO6 (M = V, Cr) in the cubic crystal phase, we calculate the total energies, in which we assume three magnetic orderings: paramagnetic (PM), ferromagnetic (FM), and antiferromagnetic (AFM). Each state was organized by the spin alignments of the (M = V, Cr) and Nb ions in Sr2MNbO6. The energy optimization curves are depicted in Fig. 2. Based on the results, it was clear that the FM ordering state has the lowest energy among the three configurations. It is important to see that these double perovskites were previously reported as ferromagnetic compounds [49,50,51,52,53,54].

Fig. 2
figure 2

The total energy versus volume of the cubic phase of Sr2CrNbO6 and Sr2VNbO6 in paramagnetic (PM), ferromagnetic (FM), and antiferromagnetic (AFM) states

Full size image

The optimized parameters of the ferromagnetic cubic phase are collected in Table 1, and obtained values are consistent with the available experimental measurements and theoretical predictions [49,50,51,52,53,54]. The oxygen position u remains unchanged with the choice of the transition metal M (3d).

For a better comparison, these structural parameters were also estimated using the SPuDS Software based on an ionic crystal model [67]. Thus, it was established that the optimized parameters are close to the predicted values. We can observe also that the bulk modulus decreases as the lattice constant increases, which means that the compressibility of the double perovskite is reduced.

On the other hand, the thermodynamic stability of double perovskite oxides has been assessed by calculating the enthalpy of the formation energy \(\Delta {H}_{f}^{o}\), which is nothing other than the energy difference \(\Delta E\) between the double perovskite compound Sr2MNbO6 and existing materials, such as M2O3 (M = Cr,V) and NbO3, based on their thermochemical equations using the solid-state reaction procedure as follows:

$${4\mathrm{SrCO}}_{3}+{\mathrm{M}}_{2}{\mathrm{O}}_{5}+{2\mathrm{NbO}}_{2}+{\mathrm{H}}_{2}\to {2\mathrm{Sr}}_{2}{\mathrm{MNbO}}_{6}+{4\mathrm{CO}}_{2}+{\mathrm{H}}_{2}\mathrm{O}$$
(3)

Hence, \(\Delta {H}_{f}^{o}\) can be calculated via the following equation:

$$\Delta H_f^o=\Delta E=E_{Tot}-{\textstyle\sum_i^N}n_iE_i=2E_{Tot}-(n_1E_{Sr}+n_2E_M+n_3E_{Nb}+n_4E_{O_2})$$
(4)

where ETot is the total energy per unit cell volume (Z = 2) of Sr2MNbO6, Ei = ESr, EM (M = V and Cr), ENb and EO are the energy of individual elements in the unit cell, and ni denotes the number of atoms of the ith element in a single formula unit: n1 = 4, n2 = 2, n3 = 2, and n4 = 6, respectively. The results of formation energies are negative for both compounds, which imply that this cubic structure is thermodynamically stable. This result does not surprise when we know that Sr2CrNbO6 was already experimentally synthesized. Hence, the calculations of thermo-elastic and magneto-electronic characteristics were performed based on the cubic phase.

Turning now, to the average bond distances in Sr2CrNbO6 and Sr2VNbO6, as mentioned in Table 1, it is important to note that the Cr − O 1.9807-Å and V − O 1.9801-Å bond distances are almost equal. This is mainly attributed to the fact that the ionic radii of Cr3+ and V3+ are nearly equal. Experimentally, this was also observed by Choy et al. using powder X-ray diffraction data collected [49].

3.2 Mechanical Stability and Anisotropic Character

After determining the structural stability of the titled double perovskite oxides, the elastic constants were calculated to further determine the mechanical stability. Moreover, the elastic constants are of great importance to respond to mechanical parameters, such as Young’s modulus, shear modulus, and Poisson’s ratio.

To calculate the elastic parameters, one can use the volume conserving tetrahedral and rhombohedral distortions on the ground-state structure. As it is well known, the Born Huang elastic stability criteria [69] for the cubic phases are given by

$${\mathrm C}_{11}+2{\mathrm C}_{12}>0,\;{\mathrm C}_{11}-{\mathrm C}_{12}>0,\;{\mathrm C}_{44}>0$$
(5)

The computed values of the elastic constants presented in Table 2 are positive and follow the stability criteria, thereby authenticating the stability in the cubic phase for Sr2MNbO6 double perovskites.

Table 2 Calculated elastic constants Cij, shear modulus G, Young’s modulus E, Poisson’s ratio v, Zener coefficient A, and B/G ratio of Sr2(V, Cr) NbO6. The units for Cij, G, and E are gigapascals
Full size table

Turning now to the mechanical properties, the shear modulus (G) describes the response to shear stress, Young modulus (E) represents the ability of a material to deform elastically, Poisson’s ratio (υ) can give an idea about the nature of the deformation, and shear anisotropic factor (A) (also called Zener coefficient) gives a measure of the anisotropy of the elastic wave velocity in a crystal; they were calculated and are listed in Table 2. The relationship between these parameters and elastic constants are displayed as follows [70]:

$$\text{B} = \frac{{\text{C}}_{11}\text{+}{2}{\text{C}}_{12}}{3}$$
(6)
$$G=\frac{G_V+G_R}2\left\{\begin{array}{l}G_R=\frac{5C_{44}\left(C_{11}-C_{12}\right)}{\left[4C_{44}+3\left(C_{11}-C_{12}\right)\right]}\\G_V=\frac{\left[C_{11}-C_{12}+3C_{44}\right]}5\end{array}\right.$$
(7)
$$E=\frac{9GB}{3B+G}$$
(8)
$$v=\frac{3B-E}{6B}$$
(9)
$$A=\frac{2C_{44}}{C_{11}-C_{12}}$$
(10)

The mechanical parameters and the ratio of the bulk and shear modulus (B/G) known as Pugh’s ratio, describe the behavior of a deformed material. This ratio is related to the transition between brittle and ductile character of a solid, and it was observed by Pugh in 1954 [71]; 1.75 is specified as a critical value. The data in Table 2 confirm that these double perovskites are brittle materials.

According to the Frantsevich rule, the value of Poisson ratio υ could also be used as a criterion for judging whether the material has ductility, and 0.26 is defined as the critical value [72]. From Table 2, the values of the Poisson ratio are observed to be 0.23 for Sr2VNbO6 and 0.25 for Sr2CrNbO6, indicating that they are brittle materials, which are consistent with the results of B/G. We have analyzed the anisotropic behavior of the double perovskites by evaluating the shear anisotropic factor (A). The deviation of A from unity, as shown in Table 2, signifies the presence of anisotropic nature, and so the possibility of developing structural defects during the synthesis of these materials is little.

3.3 Electronic and Magnetic Properties

The knowledge of the magneto-electronic properties is essential for spintronic device applications. These transition-metal double perovskite oxides are complicated and need strong electron correlation systems with better description rather than GGA calculations. However, GGA calculations can be corrected using a strong-correlation correction called GGA + U functional. Here, we used values of Ueff = 1.0, 4.0, and 3.0 eV for Nb (4d), V (3d), and Cr (3d) electrons, respectively, and similarly to Ref. [54]. Undoubtedly, this functional is highly successful in a large class of highly correlated systems. But its quality of results depends on the choice of the optimal value of the Hubbard Ueff. For further confirmation, we have also used the exact exchange for the correlated electron (EECE) functional.

The spin-polarized electronic band structures of Sr2MNbO6 (M = V, Cr) double perovskite oxides determined via the GGA, GGA + U, and EECE approximations are shown in Figs. 3 and 4. Results reveal that Sr2VNbO6 exhibits half-metallic ferromagnetism in the three approximations, whereas Sr2CrNbO6 is a ferromagnetic insulator.

Fig. 3
figure 3

Band structures of Sr2CrNbO6 (spin-up and spin-down) with GGA, GGA + U, and EECE. The Fermi level is located at 0 eV

Full size image
Fig. 4
figure 4

Band structures of Sr2VNbO6 (spin up and spin down) with GGA, GGA + U, and EECE. The Fermi level is located at 0 eV

Full size image

GGA + U gives the band-gap value of 2.92 eV in the minority spin channel, while GGA gives 2.50 eV for the Sr2VNbO6 compound. The band gap energies in both minority and majority spins changed their values from 2.31 eV to 2.68 eV and 2.78 eV to 3.08 eV for Sr2CrNbO6 in GGA and GGA + U, respectively. In the case of the EECE approach, the results are very close to the values from the GGA + U functional. All these values are qualitatively consistent with previous experimental findings reported in references [44, 53], as mentioned in Table 3.

Table 3 The calculated band gaps of Sr2MNbO6 (M = V, Cr) by GGA, EECE, and GGA + U approaches along with previously reported experimental measurements is given
Full size table

In order to get further insight into the band structures, we plot the atom and orbital projected DOS (PDOS) for Sr2CrNbO6 and Sr2VNbO6, respectively. The figures for the three functionals GGA, GGA + U, and ECCE are equivalent in shape. Therefore, only the results obtained through GGA + U functional are presented, as shown in Fig. 5.

Fig. 5
figure 5

The total density of states and partial (spin up and spin down) of Sr2CrNbO6 and Sr2VNbO6. The Fermi level is located at 0 eV

Full size image

The influence of M ions in Sr2MNbO6 is to supply spin-polarized (2 and 3) electrons per formula unit since M is in 3 + valence-state V3+ (3d2; \({\mathrm{t}}_{2g}^{2}\uparrow {\mathrm{t}}_{2g}^{0}\downarrow {\mathrm{e}}_{g}^{0}\uparrow {\mathrm{e}}_{g}^{0}\downarrow ;S=1\)) and Cr3 + (3d3; \({\mathrm{t}}_{2g}^{3}\uparrow {\mathrm{t}}_{2g}^{0}\downarrow {\mathrm{e}}_{g}^{0}\uparrow {\mathrm{e}}_{g}^{0}\downarrow ;S=\frac{3}{2}\)), respectively. In Sr2CrNbO6, the spin-down valence band maximum (VBM) is mainly contributed by 2p states of the O atoms, while the spin-down conduction band minimum (CBM) is mostly constructed from Nb (\({\mathrm{t}}_{2g}^{0}\downarrow\)) and Cr (\({\mathrm{t}}_{2g}^{0}\downarrow {\mathrm{e}}_{g}^{0}\downarrow\)) states, whereas in spin-up the VBM is mainly attributed by Cr-3d (\({\mathrm{t}}_{2g}^{3}\uparrow\)) states with a small contribution from p states of O, while the CBM is mostly constructed from Nb (\({\mathrm{t}}_{2g}^{0}\uparrow\)) and Cr (\({\mathrm{e}}_{g}^{0}\uparrow\)) states. In case of Sr2VNbO6, the V (\({\mathrm{t}}_{2g}^{2}\uparrow\)) states are responsible for the half-metallicity as they occupy the Fermi level in the spin up.

The presence of the cation magnetic (V, Cr)-3d states at different energy values in the spin-up and down channels indicates that the electrons in these channels do not cancel each other’s magnetic moment and thereby lead to its ferromagnetic character. However, the presence of Sr and O-atoms states at the same energy value in the spin-up and down channels reflects the symmetric character of the valence states of these atoms. This implies complete cancellation of the magnetic moment of these constituents. The total spin magnetic moment and individual contributions to it are presented in Table 4 for Sr2 (V, Cr) NbO6.

Table 4 Calculated interstitial, individual, and total magnetic moments of Sr2(V,Cr)NbO6 double perovskites (in units of µB) using GGA, EECE, and GGA + U calculations
Full size table

Higher Curie temperature is another key factor for the application of magnetic materials in spintronic devices. The empirical formula is often used to estimate the Curie temperature (Tc) of materials [73, 74]:

$$Tc=23+181 {M}_{tot}$$
(11)

The calculated GGA Curie temperatures are 385 K and 554 K for Sr2VNbO6 and Sr2CrNbO6, respectively. These temperatures make these inorganic double perovskites suitable for use in spintronics and magneto-electronic applications.

3.4 Thermal Properties

The use of materials in devices is usually at different temperatures and pressures. Therefore, characterization of the thermodynamic parameters with pressure and temperature is essential in view of potential future applications. The quasi-harmonic Debye approximation [23, 75,76,77,78,79] is used to describe the effects of temperature and pressure on the thermodynamic properties of the double perovskites Sr2MNbO6(M = V, Cr). In this model, Gibbs free energy G* (V, P, T) in the non-equilibrium state was determined by the following formula:

$${G}^{*}\left(V,P,T\right)=E\left(V\right)+PV+{A}_{Vib}({\theta }_{D}\left(V\right),T)$$
(12)

where E(V) is the total energy of the cell calculated using a GGA functional, PV corresponds to the constant pressure, \({A}_{Vib}\) represents the vibrational Helmholtz free energy.

The Gibbs free energy G*(V, P, T) can be minimized with respect to volume V is as follows:

$${\left[\frac{\partial {G}^{*}(V,P,T)}{\partial V}\right]}_{P,T}=0$$
(13)

By solving (07), we can get the thermal equation of state V(P,T) and the heat capacity Cv.

The temperature has been varied from 0 to 1000 K and pressure ranges from 0 to 20 GPa. In this range of temperatures, the quasi-harmonic Debye model remains unconditionally valid. Figure 6 shows the variation relationship of the lattice parameter with respect to temperature and pressure. It is observed from the figure that the lattice parameter of both compounds was increased with the increase of temperature. Pressure has a reverse effect on this parameter. The predicted value of the lattice constant at 300 K and 0 GPa is 8.004 and 7.968 Å, respectively, for Sr2MNbO6(M = V, Cr). Figure 7 depicts the variation of bulk modulus (B) with pressure at different temperature points respectively at 0, 300, 600, and 900 K. Our results present a clear increase in bulk modulus with pressure at different temperature values, and a decrease is observed with the temperature. This is attributed to the fact that the temperature reduces the hardness of a crystal, while pressure tends to raise the same. The calculated value of bulk modulus at 300 K and 0 GPa is 157.21 and 164.25 GPa, respectively, for Sr2MNbO6 (M = V, Cr). Figure 8 presents the variation of a specific heat at the constant volume (CV) with temperature and pressure. The graph shows clearly an exponential increasing trend at low temperatures while in a high temperature range a constant value is achieved. The high temperature variation defines the Dulong–Petit law, as seen in all solids [80]. From this limit value of Dulong–Petit, as the temperature increases, each of the atoms in the Sr2MNbO6 compound absorbs the same amount of energy proportional to this temperature increase. The calculated value of CV at 300 K and 0 GPa of pressure for Sr2MNbO6 (M = V, Cr) was found to be 207.15 and 205.36 J mol−1 K−1, respectively. Our results on the thermal properties for these compounds are almost of the same magnitude as that of the double perovskite oxides of the same variant like, Ba2ZnOsO6, Ba2InTaO6, and Ba2MTaO6 (M = Er and Tm) [81,82,83]. Presently, these values are of academic interest only as measured data on them are not available. However, they follow the same trend as the other double perovskites follow.

Fig. 6
figure 6

The variation lattice parameters with temperature at different pressures of Sr2CrNbO6 and Sr2VNbO6 compounds, respectively

Full size image
Fig. 7
figure 7

The variation of the bulk modulus versus pressure at different temperatures of Sr2CrNbO6 and Sr2VNbO6 compounds

Full size image
Fig. 8
figure 8

Variation of the heat capacities Cv versus temperature at different pressures for Sr2CrNbO6 and Sr2VNbO6 compounds

Full size image

4 Conclusion

In the study, detailed investigations of the thermo-elastic and magneto-electronic characteristics of double perovskite oxides Sr2MNbO6 (M = V and Cr) are performed using the ab initio FPLAPW method within the DFT theory. The structural optimization, tolerance factor, formation energy, and stability criteria confirm the stability of these double perovskites in the cubic polymorph. The analysis of mechanical parameters reveals that both compounds are brittle in nature with anisotropic behavior. More importantly, for Sr2VNbO6, a half-metallic ferromagnetism is predicted with a narrow band gap in the minority spin, whereas Sr2CrNbO6 shows a ferromagnetic insulator nature, and the estimated Curie temperatures are higher than the room temperature. Finally, some thermodynamic quantities of Sr2MNbO6 are investigated in the temperature range (0–1000) K and pressure range (0–20) GPa based on the quasi-harmonic Debye model. The calculated value of CV at the room temperature for Sr2MNbO6 (M = V, Cr) was found to be 207.15 and 205.36 J mol−1 K−1, respectively. At higher temperatures, the Cv approaches the Dulong–Petit limit.

The present theoretical estimation of various physical parameters can prove as a valuable reference with respect to their future experimental work.