1 Introduction

It is well established that three types of vortices can be found within polycrystalline samples of high Tc superconductors: Abrikosov (A), Abrikosov-Josephson (AJ), and Josephson (J) [1, 2]. It is also well established that, in the limit of low misorientation angle (𝜃 < 5∘) between neighboring crystallites, vortices behave as A vortices: they have core sizes comparable to the coherence length, ξ, and are essentially pinned by defects [2, 3]. As 𝜃 increases, the superconducting critical current density, Jc, across grain boundaries (GBs) decreases exponentially [3, 4] and, as a consequence, vortices become anisotropic. Such an anisotropy is related to an increase in the size l of the core of the vortices along GBs, which is not observed along the perpendicular direction. These vortices, different from the A vortices, are called AJ vortices [1, 2]. For much higher values of 𝜃, the condition l > λ, where λ is the London penetration depth, is fulfilled and a transition from AJ vortices to J vortices is expected to occur [2]. Gurevich and co-workers have calculated the flux flow resistivity of the AJ vortices, identified in transport data by taken 𝜃\(\sim \) 7∘ in unirradiated and irradiated YBCO bicrystals [2]. From these results, the core size and the intrinsic depairing current density on nanoscale of few GB dislocations were measured for the first time.

More recently, clusters of superconducting oxides have been associated with intragranular defects as colonies of low-angle c-axis boundaries [5]. Thus, the magnetic trapped flux within the clusters was found to be due to AJ vortices [6]. In order to identify such kind of vortices, flux-trapping curves [7] as a function of the average minimum boundary angle, 𝜃min, were constructed. It was possible because the maximum applied magnetic field, Ham, was written as a function of 𝜃min. Within this scenario, one is able to determine graphically, from the flux-trapping curves, values of the GB angles for which the superconducting critical current density exhibits appreciable decrease due to the trapped flux within the specimen. Moreover, different types of vortices present in the material, according to the value of Ham, could be determined. The model also offers the possibility of studying separately the dynamics of J, AJ, and A vortices located at grain boundaries of a polycrystalline sample in anisotropic superconducting materials. The discussion was focused on the region of the flux-trapping curves in which the maximum applied magnetic field, Ham, is less than the lower critical field of the crystallites, Hc1c, because the main objective there was the study of the intragranular medium of the materials.

In this paper, we clear up the role of the low-angle grain boundaries and the doping with α-Al2O3 nanoparticles in the intragranular flux trapping of Bi-2223 ceramic samples. We first discuss certain microstructural characteristics of the samples used in this study that are important support to confirm the theoretical results. This has been done by a generalization of the relationship between Ham and 𝜃min published elsewhere [6]. The next step was to compare: the required energy to create an AJ vortex in a low-angle boundary and the one required for the creation of a vortex in a pore, an extra phase region, or even a nanoparticle located in the vicinity of a low-angle boundary. From the results of this comparison, we have found an inequality, which correlates the following parameters: the angle of the grain boundary, its transparency, the size of the nanoparticles, and the coherence length of the superconducting material. Finally, based on these theoretical tools, the general features of the experimental flux-trapping curves are analyzed. Our results clearly indicate that the role played by the doping with α-Al2O3 nanoparticles is to pin the AJ vortices in grain boundaries with misorientation angles \(\theta \sim 10^{\circ }\). As far as the authors know, the combination of these experimental and theoretical results is reported for the first time.

2 Experimental Details

Details of the preparation of the samples are described elsewhere [8,9,10]. In this work, three samples were studied: two of them have been used for other studies and their general physical properties are described elsewhere [10]. A third sample of Bi1.65Pb0.35Sr2Ca2Cu3O10+δ (Bi-2223), without α-Al2O3 nanoparticles (0.0% (B00)), was synthesized, under the same conditions, in order to compare its behavior with those of the doped samples. We have also employed for the B00 sample the same two experimental techniques applied in other investigations [10]: X-ray diffraction analysis (XRD) and the dependence of Jc(0, Ham). This type of measurement corresponds to the so-called flux-trapping curves which were measured at 77 K [7].

To estimate the mean size of the α-Al2O3 NPs located within the Bi-2223 matrix, two techniques were employed: high-resolution transmission electron microscopy (HRTEM) and atomic force microscopy (AFM). By using a field-emission transmission electron microscope, JEM-2200FS (200 kV), several micrographies were obtained with 0.19-nm resolution in the TEM mode. For this purpose, a dry powder sample was dispersed in isopropanol and deposited onto a Formvar carbon copper grid. The AFM technique was applied by means of an CPII (SPM) model of a scanning probe microscope in scanning mode. Several images were obtained and size profiles of α-Al2O3 nanoparticles were extracted.

3 Results and Discussion

3.1 Microstructural Characterizations

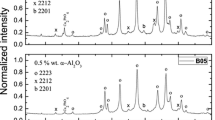
The studied samples are composed by a mixture of phases in which the Bi-2223 phase coexists, along with α-Al2O3, with three other phases: Bi-2212, Bi-2201, and Ca2PbO4 (see Fig. 1) [10]. The determination of the phase composition was performed similar to Li and Han [11] and the results, displayed in Table 1, are slightly different from those reported for a similar material studied elsewhere [12]. Differences between both sample preparation methods [9] provoked these differences in their phase compositions.

Fig. 1
figure 1

X-ray diffraction patterns of the samples B00, B03, and B05

Full size image
Table 1 Phase composition of the Bi-2223 ceramic samples
Full size table

The unit-cell parameters of the Bi-2223 phase were calculated with respect to an orthorhombic unit cell and the obtained values are displayed in Table 2.

Table 2 Crystallographic data of each sample
Full size table

By using several images similar to those shown in Figs. 2 and 3, the mean size of the α-Al2O3 nanoparticles has been estimated. In order to obtain this important result, the images from HRTEM and AFM were analyzed by the softwares Gatan Digital Micrograph and WSxM 5.0 Develop 8.1 [13], respectively.

Fig. 2
figure 2

HRTEM image of the sample B03. The black circles correspond to α-Al2O3 nanoparticles

Full size image
Fig. 3
figure 3

AFM image of the sample B03. The white particles correspond to α-Al2O3 nanoparticles

Full size image

From the analysis of the HRTEM images, the mean size of the nanoparticles measured inside the superconducting matrix was 42 nm. In the case of the AFM images, the explored area was approximately 10.4 μm2 and the obtained mean size was 35.6 nm. Both values (42 nm and 35.6 nm) are close to 40 nm, the mean size of the α-Al2O3 nanoparticles.

3.2 Flux-Trapping Curves and Doping Effects

Figure 4 displays the different behaviors of the magnetic trapping flux starting from the results of the critical current density dependence as a function of the maximum applied magnetic field for the three studied samples. These differences can be summarized in the following way [10]:

  1. 1.

    Samples B03 and B05 begin to trap the magnetic flux in Ham lower than that of the pristine sample B00.

  2. 2.

    Sample B03 exhibits the minor relative values of the critical current density in the Ham region 35 Oe ≤ Ham ≤ 65 Oe.

  3. 3.

    The flux-trapping phenomenon occurs more abruptly in sample B03.

Fig. 4
figure 4

Normalized critical current density as a function of Ham of the three samples studied: B00, B03, and B05. The inset displays the same dependence of the sample B03

Full size image

Although our samples have percentages of extra phases between 4 and 16% according to Table 1, an appreciable change in the magnetic flux trapping is mainly observed for the sample B03. It confirms that the trapping of the magnetic flux not only depends on the percentage of the extra-phases but also depends on its distribution, at nanometric scale, inside the superconducting matrix. Figure 3 is a good example for the case of α-Al2O3 nanoparticles. A similar result for the flux pinning has been reported elsewhere [12].

In the case of Fig. 5, the model proposed in reference [6] has been applied. The main features of these curves are as follows: (i) the two α-Al2O3-doped samples start to trap flux at \(\theta _{\min \nolimits }\sim 15^{\circ }\), a feature not observed in sample B00, in which magnetic flux starts to trap in the vicinity of 12∘; (ii) sample B03 displays a sudden drop in the normalized critical current density close to 12∘; (iii) the normalized critical current density increases with increasing \(\theta _{\min \nolimits }\) in all samples; (iv) sample B03 displays an almost constant value of the normalized critical current density for \(6^{\circ } < \theta _{\min \nolimits } < 10^{\circ }\); (v) sample B03 clearly displays the most pronounced change in its Jc(0, Ham)/Jc(0) vs. \(\theta _{\min \nolimits }\) dependence. Here, the negative values of the angles correspond to values of maximum applied magnetic field where the transition AJ to A vortices happens and the crystallites are penetrated by the magnetic flux as discussed in reference [6]. The different behaviors regarding the magnetic flux trapping will be discussed in detail later.

Fig. 5
figure 5

Flux-trapping curves of samples B00, B03, and B05. The independent variable Ham has been replaced by 𝜃min following (1). Continuous lines divide the graphs into four different regions according to the flux-trapping mechanism

Full size image

3.3 Generalizing a Previous Result

As already reported [6], the maximum applied magnetic field Ham may be expressed as a function of the minimum penetrated misorientation angle by the following equation:

$$ \theta_{1}=-\theta_{0}\left[\ln\left( \frac{3\sqrt{3}}{4\kappa}\right)+a\ln\kappa+a\gamma_{1}-\gamma_{2}\right]. $$
(1)

Here, 𝜃0, κ, γ1, and γ2 are the misorientation angles, 5∘ (Ref. [14]), 83 (Ref. [15]), 0.497 (Ref. [16]), and 0.423 (Ref. [17]), respectively. As a is Hc1d normalized to the lower critical field of the crystallites (known as intragranular region free of defects), then we have obtained the desired function.

As shown in a previous paper [6], the relative error in determining 𝜃 from (1) is approximately 6% and the average of geometric factors of the grains G is considered to be approximately 0.

To express (1) in a more general form, we introduce a factor β (β < 1) in (2) as follows:

$$ {J}_{s}=\beta\textit{J}_{d}\exp\left( -\frac{\theta}{\theta_{0}}\right). $$
(2)

This factor represents the effect of the transparency of the junctions (defects) and also models the decrease of Jd when the junction thickness is greater than the London penetration depth. Both conditions may be presented in any junction of a ceramic superconducting material. Thus, taking into account the results of Ref. [18], one obtains (3) more general than (1):

$$ \theta_{2}=-\theta_{0}\left[\ln\left( \frac{3\sqrt{3}}{4\kappa\beta}\right)+a\ln\kappa+a\gamma_{1}-\gamma_{2}\right]. $$
(3)

Figure 6 displays the theoretical dependence of the misorientation angle versus the parameter β in the magnetic field window where AJ vortices are majority (40 Oe < Hc1c < 80 Oe). It is the result of plotting (3) to different values of β from 0.05 to 1 with a step size of 0.05, for five different values of the parameter a. The interpretation of Fig. 6 allows us to determine the permissible values of β. As the misorientation angle should be positive, hence for a = 0.5, β may take values inside the interval 0.15 ≤ β < 1. For a = 1, no allowed values for β are expected.

Fig. 6
figure 6

Misorientation angle versus β dependence for different values of a

Full size image

3.4 On The Role of Doping with Nanoparticles in the Flux-Trapping Mechanism

In order to clarify the role of doping with α-Al2O3 nanoparticles in the flux-trapping mechanism of Bi-2223, we should compare both: the required energy to create an AJ vortex in a low-angle boundary and that required to create a similar one, but in the vicinity of a pore (nanoparticle with certain dimensions). We will first focus on determining the lower critical field of the pore, Hc1p.

Regarding cylindrical pores, as a first approximation, and taking into account the Helmholtz equation [19], where α is the radius of cylinder, one obtains:

$$ {B}_{z}=\frac{\phi_{0}}{2\pi\lambda^{2}}\left[\frac{K_{0}(\rho/\lambda)}{1/2\frac{\alpha^{2}}{\lambda^{2}}K_{0}(\alpha/\lambda)+\frac{\alpha}{\lambda} K_{1}(\alpha/\lambda)}\right]. $$
(4)

On the other hand, the generalized (anisotropic) expression for the energy per unit length, (Wl), equation 6.226 in Ref. [19], is:

$$ {W}_{l}=\frac{1}{2\mu_{0}}\int\mathbf{B}\cdot\mathbf{V}dxdy, $$
(5)

where \(\vec {V}=\phi _{0}\delta (x)\delta (y)\hat {k}\) is the vorticity and, dividing by ϕ0, the lower critical field for the vortex in the vicinity of the pore is given by the expression:

$$ {H}_{c1p}=\frac{\phi_{0}}{4\pi\mu_{0}\lambda^{2}}\left[\frac{K_{0}(\alpha/\lambda)}{1/2\frac{\alpha^{2}}{\lambda^{2}}K_{0}(\alpha/\lambda)+\frac{\alpha}{\lambda} K_{1}(\alpha/\lambda)}\right]. $$
(6)

In order to compare the lower critical fields of pores and defects, we can obtain those expressions normalized with respect to the lower critical field of the crystallites by using equations to the lower critical fields of the crystallites and the defects, respectively, as they are written in reference [18]:

$$ {H}_{c1c}=\frac{\phi_{0}\left[\ln\left( \frac{\lambda}{\xi}\right)+\gamma_{1}\right]}{4\pi\mu_{0}\lambda^{2}} $$
(7)

and:

$$ {H}_{c1d}=\frac{\phi_{0}\left[\ln\left( \frac{\lambda}{l}\right)+\gamma_{2}\right]}{4\pi\mu_{0}\lambda^{2}}. $$
(8)

Thus, we may divide (6) and (8) by (7) and obtain:

$$ \frac{{H}_{c1p}}{{H}_{c1c}}=\frac{1}{ln{\kappa}+\gamma_{1}}\left[\frac{K_{0}(\alpha/\lambda)}{1/2\frac{\alpha^{2}}{\lambda^{2}}K_{0}(\alpha/\lambda)+\frac{\alpha}{\lambda} K_{1}(\alpha/\lambda)}\right] $$
(9)

and

$$ \frac{{H}_{c1d}}{{H}_{c1c}}=\frac{\ln\left( \frac{\lambda}{l}\right)+\gamma_{2}}{\ln(\kappa)+\gamma_{1}}. $$
(10)

Applying the curl to (4), the critical current density as a function of the radial coordinate is obtained:

$$ {J}_{p}=\frac{\phi_{0}}{2\pi\mu_{0}\lambda^{3}}\left[\frac{K_{1}(\rho/\lambda)}{1/2\frac{\alpha^{2}}{\lambda^{2}}K_{0}(\alpha/\lambda)+\frac{\alpha}{\lambda} K_{1}(\alpha/\lambda)}\right], $$
(11)

the denominator of the second factor approaches 1 for small values of the Bessel function parameter [19], so one can obtain:

$$ {J}_{p}=\frac{\phi_{0}}{2\pi\mu_{0}\lambda^{3}}{K_{1}(\rho/\lambda)}. $$
(12)

The previous expression evaluated at the radius of the pore ρ = α yields the maximum current density of the vortex:

$$ {J}_{pmax}=\frac{\phi_{0}}{2\pi\mu_{0}\lambda^{3}}{K_{1}(\alpha/\lambda)}. $$
(13)

Moreover, the critical current density of the defects as a function of the grain boundary angle is:

$$ {J}_{cd}=\frac{\phi_{0}}{2\pi\mu_{0}\lambda^{3}}{K_{1}(\xi/\lambda)}\beta\exp\left( -\frac{\theta}{\theta_{0}}\right). $$
(14)

As Jpmax ≤ Jcd, then one obtains:

$$ {K}_{1}(\alpha/\lambda)\leq{K}_{1}(\xi/\lambda)\beta\exp\left( -\frac{\theta}{\theta_{0}}\right). $$
(15)

For small arguments K1(x) = (1/x) and:

$$ \alpha\beta\geq{\xi}\exp\left( \frac{\theta}{\theta_{0}}\right) $$
(16)

On the other hand, taking into account that the lower critical field is proportional to the energy per unit length as follows:

$$ {H}_{c1d}=\frac{W_{c1d}}{\phi_{0}}. $$
(17)

One can write this equation for the pores and crystallites. After that, we may normalize the equations for the clusters and pores with respect to the equation of crystallites:

$$ \frac{{H}_{c1d}}{{H}_{c1c}}=\frac{W_{c1d}}{W_{c1c}}, $$
(18)
$$ \frac{{H}_{c1p}}{{H}_{c1c}}=\frac{W_{c1p}}{W_{c1c}}, $$
(19)

Figure 7 displays both magnitudes as a function of the ratios \(\frac {\lambda }{l}\) and \(\frac {\lambda }{\alpha }\), respectively. The main result here is that the energy of the vortices in the vicinity of a pore is lower than that of the vortices in the low-angle boundary free of pores.

Fig. 7
figure 7

Energy per unit length of an AJ vortex and for a vortex in a pore normalized to the energy per unit length of an A vortex vs λ/l and λ/α dependence, respectively

Full size image

Based on the theoretical framework described above, the next step is to explain our experimental results displayed in the flux-trapping curves. First of all, the presence of α-Al2O3 nanoparticles in the matrix of Bi-2223 is responsible for a decrease in the energy to create an AJ vortex, which can be explained by using the results displayed in Fig. 7. Under this circumstance, the doped samples start trapping flux for lower applied magnetic fields than the pristine sample. Secondly, taking β = 1 in the expression (16), it is possible to determine if the inequality is fulfilled. As the model assumes pores located at GBs (planar defects), it is reasonable to assume that our samples have misorientation angles \(\theta \sim 10^{\circ }\). Then, taking 𝜃0 = 5∘ [14] and \(\xi \sim 3\) nm [20], one obtains α ≥ 22 nm. This result is of interest and explains well the sudden drop in the flux-trapping curve of sample B03. The presence of nanoparticles is responsible for an improvement of the flux trapping as a consequence of the increase of the pinning energy, but such an effect is critical starting from the fulfillment of the condition given by the expression (16). It demonstrates that the nanoparticles used for doping our samples, with mean diameter \(\sim \) 40 nm, favor the increase of the trapping of AJ vortices, which emerge at low-angle boundaries. Finally, sample B05 does not exhibit the same behavior of the B03 due to a decrease of the transparency of the junctions, a feature caused by the excess of α-Al2O3 nanoparticles throughout the material. Within this scenario, the apparent size of the nanoparticales (αβ) decreases and the condition given by expression (16) is not fulfilled in the range of the low-angle boundaries. For this reason, the general superconducting behavior of sample B05 is similar to that observed in sample B00.

4 Conclusions

We successfully correlated the effects of the size of α-Al2O3 manoparticles and the superconducting properties of Bi-2223 to get an effective pinning of the AJ vortices in the intragranular low-angle boundaries. This correlation was established by comparison of the energies required to create an AJ vortex in a planar defect free of nanoparticles with that required for the presence of α-Al2O3 nanoparticles. The α-Al2O3 nanoparticles embedded in the superconducting matrix have two main effects related to the parameters of the model described in this paper: (a) an increase of the pinning centers, mainly for the AJ vortices due to the size of the nanoparticle, α, and the angle of the planar defects, 𝜃 ≤ 10∘; (b) a decrease of the junction transparency, β, which can be modified by the excess of α-Al2O3 nanoparticles within the Bi-2223 matrix. The model captures important features of the combined data and is sufficient to explain why the flux trapping and pinning of the AJ vortices first increase with the α-Al2O3 nanoparticle content, and then decreases for values above a certain percentage in weight in the samples, as has been observed by other authors [12]. Although the model described here has been applied to a specific doping and superconducting matrix, it may be useful in other superconducting systems.