1 Introduction

Superconductors have always attracted the attention of the scientific community due to possible technological applications such as digital circuits, superconducting electromagnets, and magnetometers. At the same time, with the continuous advances in nanotechnology, the drive for decreasing the size of superconducting devices is unavoidable. In the nanoscale regime, size effects can be crucial for many material properties, which makes studies aiming to understand the influences of sample size for superconducting properties indispensable.

When a type II superconducting film is submitted to an external magnetic field perpendicular to the sample surface in the range \(H_{c_{1}}<H<H_{c_{2}}\), quantized magnetic flux lines penetrate the material, characterizing the mixed state. The movement of these magnetic vortices creates an electric potential that dissipates energy. In the absence of external forces, these vortices arrange themselves in a hexagonal vortex lattice, also called the Abrikosov lattice [1]. However, when external forces are applied, e.g., temperature increase or the presence of a transport current, these flux lines will freely move, dissipating energy [2]. A method to avoid the vortex motion is the introduction of artificial pinning centers (APCs) [3, 4]. The APCs are capable of pinning vortices at specific positions, hindering the loss of superconductivity.

The vortex behavior under the influence of APC arrays has been extensively investigated over the years. Periodic pinning landscapes induce several matching effects that can enhance the critical current for certain values of magnetic field [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. These matching effects are associated to the commensurability between the vortex and the pinning lattices. As an example, it is usual to observe matching effects and, consequently, critical current peaks when the ratio between the applied magnetic field (H) and first matching field (Hϕ) is an integer or a rational fraction.

Recently, aiming to overcome some of the drawbacks of periodic pinning lattices, different quasi-periodic pinning arrays started to be tested, such as Penrose lattices [20,21,22,23,24], hyperbolic tessellations [25], and conformal pinning arrays [26,27,28,29,30,31,32]. As an example, Ray et al. [26] proposed the construction of pinning lattices by applying a conformal transformation, showing promising results. They demonstrated that this pinning landscape can avoid the high fluctuations of the critical current as a function of the applied magnetic field with the conformal (angle-preserving) transformation sustaining high values of critical current over a much wider range of fields than the other pinning geometries.

However, most of the research regarding dynamical properties of vortex lattices under the influence of pinning arrays were made with type II superconducting films with a width much larger than the London penetration depth (λ). For mesoscopic samples, where the width is comparable with λ, most of the theoretical work focused on studies of superconductors with different geometries within TDGL theory [33,34,35,36,37,38,39,40,41,42,43]. Meanwhile, for semi-finite systems like superconducting strips, we still have unanswered questions which could help us to understand better how sample size affects the vortex dynamics.

For finite superconductor samples, the surface creates an energy barrier known as the Bean-Livingston surface barrier [44]. The shielding Meissner supercurrents from the surface repel the vortices. Meanwhile, the superconductor-normal interface generates an attractive interaction, which was included in the model of Bean and Livingston as an attractive interaction between the vortices and their anti-images, to satisfy the boundary condition at the surface [44]. The concurrence of these two interactions is the origin of the energy barrier, which leads to deformations of the perfect Abrikosov lattice [45,46,47] and delays the vortex penetration [48].

Theoretical studies demonstrated that the size effects influence properties like magnetization, vortex lattice geometry, critical currents, and dynamical phases for superconducting strips [45,46,47,48,49,50,51,52,53]. As an example, Carneiro [45] analyzed the minimum energy configuration for several vortex lattices in superconducting thin strips, observing changes in the vortex configuration with the increase of the applied magnetic field. Meanwhile, de Souza Silva et al. [48] studied matching effects, magnetization curves, and vortex states in mesoscopic superconductors, concluding that the surface barrier induces the formation of metastable vortex structures and a hysteretic behavior. They also observed the presence of jumps in the magnetization curves, attributed to the penetration and expulsion of vortices in the sample.

Another valuable result on mesoscopic samples is the observation of vortex chains, as the applied magnetic field increases [33, 45,46,47,48, 54]. Bronson et al. [47] studied the pinning effects in mesoscopic systems, showing that in the presence of pinning sites, the penetration of vortices begins at lower magnetic fields when compared with the same strip with no APCs. The explanation for this effect is that the attractive pinning potential in the sample induces the vortex penetration at lower values of magnetic field. Recently, Vizarim et al. [53] also showed that the vortex penetration may be influenced on how the pinning centers are distributed in the sample.

Regarding dynamical properties for superconducting strips, Reis et al. [49] simulated the vortex behavior in a thin strip with the presence of a random pinning distribution under the effects of an applied transport current in the finite direction of the strip. The results show that for transport forces above a critical value, vortices flow through narrow channels due to the surface effect, reducing the vortex diffusion in the transversal direction. Concerning the vortex dynamical phases, they found a behavior similar to the one observed for infinite samples with random pinning, i.e., plastic flow, smectic flow, and the frozen transverse solid phases. However, the plastic and smectic regimes were observed in a reduced range of forces when the strip width is reduced. Meanwhile, using the TDGL theory, Berdiyorov et al. [51] also investigated the pinning effects in the vortex dynamical phases. They simulated the strip in three situations: without APCs, with square array of APCs, and with a random pinning distribution. As a result, they found that the inclusion of a pinning lattice reduces the resistive state transition current. Moreover, they characterize the vortex dynamical phases as (i) flux-flow states at low currents, (ii) phase-slip phase at intermediate values of applied current, and (iii) the hot-spot state at larger currents, which evolves into a complete transition to the normal state.

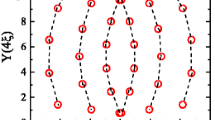
In this work, we study vortex dynamical phases in superconducting strips in the presence of APCs, aiming to understand how the size of the sample affects the vortex dynamical behavior. We perform our simulations using two types of triangular pinning lattices: the regular one and a flattened triangular lattice, which mimics the flattening of the vortex lattice in strips due to the geometrical constraint. In Fig. 1, both pinning arrays are plotted to overlap in order to see the difference between the arrays. The flattened triangular pinning array has the pinning sites dislocated toward the center of the strip, mimicking the vortex lattice deformed by the surface effect. We compared our results with those for infinite superconducting films [5,6,7, 15,16,17,18,19, 55,56,57,58,59], searching for differences and similarities between these systems. In order to analyze the effect of the strip width, we computed three sample widths with the same applied magnetic field and pinning density.

Fig. 1
figure 1

Pinning site locations used in the strip for Lx = 1.00λ, where the black open circles represent the regular triangular pinning array and the red open circles represent the flattened pinning array. The grey regions in the figure illustrates the difference in the x coordinate between the flattened and the regular pinning site positions. The flattened pinning array mimics the flattening of the vortex lattice in a superconducting strip due to the surface energy barrier. The lengths x and y are normalized by 4ξ

Full size image

The outline of the paper is the following. In Section 2, we present the model used in our simulations. In Section 3, we show our results using a regular triangular pinning lattice in the strips. We show how the width of the strip influences the number of dynamic phases and vortex regimes. In Section 4, we show the results obtained using the flattened triangular pinning array. We also highlight the differences observed in the flattened lattice compared with the regular one. In Section 5, we present the conclusions of this work, emphasizing the main factors that influence the dynamical behavior of vortices in strips and comparing the results observed in strips with the infinite film cases.

2 Model

In this work, we simulate a type II superconducting thin strip, finite in the x direction and infinite in y, considering vortices in the London limit interacting with two types of triangular pinning landscapes, as shown in Fig. 1, the regular one and a flattened pinning lattice.

The dynamical properties of vortex systems interacting with pinning arrays were simulated by solving a set of Langevin equations, as described in (1), using molecular dynamics.

$$ \eta \frac{d\mathrm{\mathbf{r}}_{i}\left( t \right)}{dt}=-\sum\limits_{i\ne j,p} {\mathrm{\mathbf{\nabla}}_{i}U_{eff}} +\mathrm{\mathbf{F}}_{\mathrm{y}} $$
(1)

In this equation, the left term is the drag force, where η is the Bardeen-Stephen [60] friction constant η = Φ0Hc2/c2ρn. The first term on the right side of (1) represents the sum of all forces present in the system, where the interactions between the vortices i and j and the pinning centers p are calculated. The force Fy results from the interaction of the vortex and the applied transport current J, \(\mathrm {\mathbf {F}}_{\mathrm {y}}=\left (\mathrm {{\Phi } }_{0}/c \right )\mathrm {\mathbf {J}}\times \hat {z}\).

For simulations of an infinite superconducting thin strip, we define the effective potential (Ueff), including the energy expression provided by Carneiro [45] and the pinning potential term, as described in (2).

$$ U_{\text{eff}}=U_{vv}+U_{p}+U_{H}+U_{S} $$
(2)

The potentials used in our model can be describe as follows:

$$U_{vv}\left( r_{ij} \right)=\thinspace \frac{C_{v}}{2}\sum\limits_{k,\thinspace j\ne i} {\ln\left\{ \frac{\cosh \left[ \frac{\pi \left( {kL_{y}+y}_{i}-y_{j} \right)}{L_{x}} \right]-\cos \left[ \frac{\pi \left( x_{i}+x_{j} \right)}{L_{x}} \right]}{\cosh \left[ \frac{\pi \left( {kL_{y}+y}_{i}-y_{j} \right)}{L_{x}} \right]-\cos \left[ \frac{\pi \left( x_{i}-x_{j} \right)}{L_{x}} \right]} \right\}} $$
$$U_{p}\left( r_{ip} \right)=-C_{p}e^{-\left( r_{ip} {\left/ {\vphantom {r_{ip} a_{p}}} \right. \kern-\nulldelimiterspace} a_{p} \right)^{2}} $$
$$U_{H}\left( r \right)=\thinspace \frac{C_{v}\thinspace 4\pi \thinspace \mathrm{\lambda }^{\mathrm{2}}H}{\mathrm{{\Phi} }_{0}}\sum\limits_{i} \left\{ \frac{\cosh \left[ \frac{\left( x_{i}-L_{x}/2 \right)}{\lambda } \right]}{\cosh \left[ \frac{L_{x}}{2\lambda } \right]}-\thinspace 1 \right\} $$
$$U_{s}\left( r \right)=\thinspace \frac{C_{v}}{2}\sum\limits_{i} {\ln\left\{ \frac{4\sin^{2}\left[ \frac{\pi x_{i}}{L_{x}} \right]+\left( \frac{\pi \xi }{L_{x}} \right)^{2}}{\left( \frac{\pi \xi }{L_{x}} \right)^{2}} \right\}} $$

The potential Uvv(rij) represents the interaction between vortices and the interaction of the vortices with the images excluding self-images, where Lx is the strip width, and k is the index of the image boxes in the infinite direction \(L_{y}= 2\lambda {\left / {\vphantom {\lambda \sqrt {3}}} \right . \kern -\nulldelimiterspace } \sqrt 3 \), modeled by the inclusion of periodic boundary conditions in the y direction. The second term (UP(rip)) represents the vortex-pinning interaction, where CP is the pinning strength and rip is the distance between a vortex i and a pinning center p. The pinning sites were modeled by a Gaussian function adjusting the pinning strength with CP = 0.2Cv and considering the pinning range as ap = ξ. The pinning density was maintained constant in this work for all samples simulated, using np = 55.42/λ2.

The third term (UH(r)) is the energy related to the vortex interacting with the screening Meissner supercurrents and the fourth term (US(r)) is the potential energy given by the interaction of the vortices and their self-images anti-vortices outside the superconducting strip, as included by Bean and Livingston [44] to satisfy the boundary condition at the surface.

The external magnetic field was adjusted to H = 68Φ0/λ2 in order to match the vortex density with the pinning density. Then, a careful minimization procedure was performed using the Generalized Simulated Annealing [61] method (GSA), where Ueff was minimized as a function of the vortices positions. We use η = 1, the length scales normalized by 4ξ, the energy scale by Cv, the time scale by 0.0016ηλ2/Cv, the magnetic field H by Φ0/λ2, and the force scales by 25Cv/λ, where ξ is the coherence length and λ the London penetration depth. We consider the Ginzburg-Landau parameter κ = λ/ξ = 100. The transport current was applied in the finite direction of the strip, creating a driving force in the infinite direction. The force associated with the transport current started at Fy = 0 and was increased in steps of ΔFy = 0.002 up to Fy = 1.0. For each force value, we performed 100,000 equilibration time steps to obtain the time averages and the overall analysis.

To evaluate the depinning forces, we calculate the time average of the vortex velocity, \(\langle V_{y}\rangle = \langle V_{y}(t)\rangle =\langle \frac {1}{N_{v}}{\sum }_{i}\frac {dy_{i}}{dt}\rangle \), which is proportional to the macroscopically measured voltage-current curve [62, 63]. The threshold for considering the vortex system static is 〈Vy〉 = 1 × 10− 3. Moreover, to characterize the dynamical phases, we plotted snapshots of the vortex trajectories and analyzed the time average of the vortex velocity derivative which is proportional to the differential resistance \({dV}_{y}/ {dF}_{D}=\rho _{f}^{-1}{dE}/{dJ}\), where ρf is the flux flow resistivity.

3 Dynamical Phases on the Regular Triangular Array

In order to analyze only the size effects in the regular triangular pinning array, we investigate three samples with different widths (Lx = 0.50λ, 0.75λ, and 1.00λ), but with the same pinning density, size, strength, and applied magnetic field. For this purpose, it was necessary to use the GSA to search for the vortex ground state for each sample. Then, the ground state was used as initial boundary condition for the integration of Langevin equations.

The vortex ground state for the case of Lx = 0.50λ is illustrated in Fig. 2a. As pointed out before, we are interested in analyzing the vortex behavior under the influence of a regular triangular pinning array at the first matching field, that is, nv/np = 1, where nv and np correspond to the vortex and pinning densities respectively. In order to find the groundstate magnetic field, we compared the energy of the states with N and N + 1 vortices in a similar way as done by Venegas [64]. The minimization shows that the first matching field is H = 68Φ0/λ2, therefore, this is the field value used in our simulations for all sample widths. For the other strip widths, we used the same field value and compared the energies of the system with N and N + 1 vortices, choosing the vortex density and configuration that corresponds to the minimum energy.

Fig. 2
figure 2

Main simulation box, where open circles represent the pinning centers and black dots represent vortices, with H = 68Φ0/λ2, Lx = 0.50λ, nv/np = 1, Cp = 0.2Cv, and ap = ξ. Numbers on top of each figures indicate the dynamic phase according to the plot shown on Fig. 3. a The static phase, b the first moving phase, where vortices near the edge of the sample flow in narrow channels, c the beginning of the second moving phase, where vortices flow in channels with significant transversal displacement, and d the second moving phase with vortices flowing in narrow channels with small bumps due to the pinning centers. The lengths x and y are normalized by 4ξ

Full size image

Figure 3 shows the average vortex velocity (〈Vy〉) and the differential resistance (dVy/dFy) as functions of the applied transport force (Fy). It is possible to see three distinct vortex dynamic phases, indicated by changes in the slope of the velocity curve and pronounced peaks in the differential resistance curve. Each of them is directly associated to the vortex regimes illustrated in Fig. 2.

Fig. 3
figure 3

Average vortex velocity (〈Vy〉) and vortex derivative velocity (dVy/dFy) as a function of the applied force (Fy) for the strip under the influence of the regular pinning array with Lx = 0.50λ, Cp = 0.2Cv, and ap = ξ. Vertical dashed lines represent the dynamic phase transitions

Full size image

The dynamic phases of regions II and III are illustrated in Fig. 2. In region II, the vortex chains close to the edge of the strip depin at the same transport force value Fy = 0.178. Both channels of vortices flow in narrow and well-defined channels without interconnectivity. Region III begins when the transport force reaches the value Fy = 0.608. In that case, the inner vortex chains depin together in vortex channels with significant transversal fluctuations (see Fig. 2c). After a further increase of the transport force, the transversal fluctuation of vortices is reduced resulting in four well-defined vortex channels, which can be seen in Fig. 2d. It is also possible to see that the outer channels behave differently compared with the inner channels. The inner vortex channels flow with small bumps due to the presence of the attractive pinning sites Meanwhile the outer vortices flow in straighter channels because the surface currents push them far from the surface and, consequently, far from the outer pinning column.

It is interesting to point out that the depinning process depends on the commensurability of each vortex chain. For example, the inner chains are fully commensurate; therefore, they can endure higher transport forces without depinning when compared with non-fully commensurate chains. The competition between the vortex-vortex and vortex-surface interactions stabilize vortices near the edge of the sample. Only a few vortices are trapped at the top of the pinning sites, but most of them are interstitial vortices, which provokes a premature depinning when compared with the commensurate vortex chains near the center of the sample.

Numerical simulations were also performed with Lx = 0.75λ using the same pinning size, density and applied magnetic field than that used for Lx = 0.50λ. The energy minimization process leads to the vortex ground state illustrated in Fig. 4a with nv/np = 1.042. That is, as the sample is enlarged, the same applied magnetic field induces a higher vortex density. Figure 5 shows the 〈Vy〉 and dVy/dFy as a function of the applied transport force Fy. In this case, six distinct vortex dynamic phases are observed. Each of them is directly associated to the vortex regimes illustrated in Fig. 4.

Fig. 4
figure 4

Main simulation box, where open circles represent the pinning centers and black dots represent vortices, with H = 68Φ0/λ2, Lx = 0.75λ, nv/np = 1.042, Cp = 0.2Cv, and ap = ξ. Numbers on top of each figures indicate the dynamic phase according to the plot shown on Fig. 5. a The static phase, b the first moving phase, where vortices near the left edge of the sample flow in a narrow channel, c the second moving phase, where vortices of the right edge of the strip depin in a narrow channel, d the third moving phase where the chain of vortices in which the number of vortices exceed the number of pinning sites depin in a tortuous narrow channel, e the beginning of the fourth moving phase, where the last non-fully commensurate vortex chain depin in a plastic flow with interconnectivity (see also the animation of this regime in the Electronic Supplementary Material—vortex4e.avi), f the fourth moving phase where all channels flow almost linearly, and g the fifth moving phase where the fully commensurate vortex chains depin and all vortices flow. The lengths x and y are normalized by 4ξ

Full size image
Fig. 5
figure 5

Average vortex velocity (〈Vy〉) and vortex derivative velocity (dVy/dFy) as a function of the applied force (Fy) for the strip under the influence of the regular pinning array with Lx = 0.75λ, Cp = 0.2Cv, and ap = ξ. Vertical dashed lines represent the dynamic phase transitions

Full size image

The vortex ground state (see Fig. 4a) exhibits two fully commensurate chains and four with different commensurability degree. At Fy = 0.074 occurs the depinning transition resulting in one narrow vortex channel in the left side of the sample (see Fig. 4b). However, this vortex dynamic phase remains just for a short range of transport force values denoted by region II of Fig. 5 At Fy = 0.090, which corresponds to the beginning of region III, the outer vortex chain in the right side of the sample depins forming a narrow channel of vortices (see Fig. 4c). It is interesting to note that these channels close to the edge of the strip exhibit similar commensurability degree but do not depin at the same transport force. The explanation is related to the different pinning landscape seen by each vortex chain. At Fy = 0.135 occurs another dynamic phase transition, where the vortices move according to the region IV of Fig. 4d. In that case there is a depinning of another vortex chain with vortices moving in tortuous channels. After further increases in the transport force, at Fy = 0.360 the last non-commensurate vortex chain depin in a plastic flow with interconnectivity with the neighbor channel (see Fig. 4e and the animation of this regime in the Electronic Supplementary Material—vortex4e.avi). As can be seen in Fig. 5, this vortex regime exhibits several changes in the average vortex velocity and peaks in the differential resistance curve. However, these instabilities cease at Fy = 0.412, where the vortices move in almost straight channels along the strip (see Fig. 4f). Note that the regimes from Fig. 4e, f correspond to the same vortex dynamic phase (region V), i.e., the vortex regime of Fig. 4e is transient. The final depinning transition occurs at Fy = 0.584, where the fully commensurate vortex chains depin and all channels flow along the strip (see Fig. 4g).

We also performed simulation with Lx = 1.00λ, aiming to understand the size effects in the dynamical phases of superconducting strips. Using the same pinning parameters and applied magnetic field, we found the vortex ground state illustrated in Fig. 6a, with nv/np = 1.031. Note again that as the sample width is enlarged with the same applied magnetic field, the vortex density changes. In Fig. 7, we show the 〈Vy〉 and dVy/dFy as a function of the Fy. As a result, it is possible to see six distinct vortex dynamic phases. Each of them is directly associated to the vortex regimes illustrated in Fig. 6.

Fig. 6
figure 6

Open circles represent the pinning centers, and the black dots represent vortices, with H = 68Φ0/λ2, Lx = 1.00λ, nv/np = 1.031, Cp = 0.2Cv, and ap = ξ. Numbers on top of each figure indicate the dynamic phase according to the plot shown on Fig. 7. a The static phase, b the first moving phase, where vortices near the left edge of the sample flow in a narrow channel, c the beginning of the second moving phase, where vortices in the central region and right edge depin together in a transient motion (see also the animation of this regime in the Electronic Supplementary Material—vortex6c.avi), d the third moving phase, e the fourth moving phase where the last non-commensurate vortex chain depin in a plastic flow (see also the animation of this regime in the Electronic Supplementary Material—vortex6e.avi), f the fifth moving phase where the system exhibits a symmetric distribution of channels, g the beginning of the sixth moving phase, where all vortices move through the strip with interconnectivity in the outer channels (see also the animation of this regime in the Electronic Supplementary Material—vortex6h.avi), and h where all vortices move without interconnectivity. The lengths x and y are normalized by 4ξ

Full size image
Fig. 7
figure 7

Average vortex velocity (〈Vy〉) and vortex derivative velocity (dVy/dFy) as a function of the applied force (Fy) for the strip under the influence of the regular pinning array with Lx = 1,00λ, Cp = 0.2Cv, and ap = ξ. Vertical dashed lines represent the dynamic phase transitions

Full size image

Figure 6a illustrates the vortex ground state for the strip with Lx = 1,00λ. In the central region of the strip the number of vortices exceeds the number of pinning centers, i.e., there is a formation of incommensurate vortex chains. Besides that, the chains next to the edge of the sample exhibit vortices stabilizing themselves in interstitial positions due to the surface barrier pushing vortices toward the center of the sample. Our calculations show that there are several vortex transient motions below the depinning current (region I), which can be seen by small fluctuations in the differential resistance curve. A similar type of transient motion was already reported before in simulations with infinite samples [65,66,67]. This kind of motion reorders the vortex lattice into a new static one. As an example, we can see the vortices close to the right edge of the sample: in the ground state only one is pinned and in Fig. 6b, three vortices are pinned due to the transient effects.

When the transport force reaches its critical value Fy = 0.098 the depinning occurs, where vortices begin to flow in a narrow channel in the left side of the sample, denotated by region II (see Fig. 6b). At Fy = 0.144, three vortex chains depin at the same time initiating region III (see Fig. 6c and the animation of this regime in the Electronic Supplementary Material—vortex6c.avi). The central chains, where the number of vortices exceeds the pinning centers, depin together exhibiting almost straight channels with small bumps. Meanwhile, the chain next to the right edge of the sample starts to depin In the lower part of the figure vortices move by tortuous trajectories and in the upper part, all of them join forming only one straight channel At Fy = 0.156, the dynamic phase denotated as region III stabilizes. Vortices that initially were moving through tortuous channels are now moving through almost straight channels (see Fig. 6d). After a further increase of the transport force, the depinning of the last non-commensurate vortex chain in a plastic flow with interconnectivity occurs at Fy = 0.360 (see Fig. 6e and the animation of this regime in the Electronic Supplementary Material—vortex6e.avi). However, at Fy = 0.386 the vortex regime stabilizes in straight channels flowing through the strip (see Fig. 6f). At Fy = 0.542, there is a new depinning transition leading to a symmetric distribution of channels. In that case, the system exhibits six moving channels and two trapped chains of vortices (see Fig. 6g) However, this regime does not persist for a wide range of transport force values. At Fy = 0.556, the vortices that were trapped in the previous phase, depin and flow through the strip with interconnectivity in the outer channels (see Fig. 6h and the animation of this regime in the Electronic Supplementary Material—vortex6h.avi). Interestingly, vortices near the edge flow in thicker channels while inner channels flow in narrower ones due to the higher magnetic pressure, as shown in Fig 6i.

For all strip widths with the regular triangular pinning array, even at high vortex speed, the vortices do not organize themselves in a moving crystal phase.

4 Dynamical Phases on the Flattened Triangular Array

The flattened triangular pinning array is a pinning distribution that mimics the vortex lattice in a type II superconducting strip without pinning centers. As we are interested only in the size effects, three samples with different widths (Lx = 0.50λ, 0.75λ and 1.00λ) are simulated using the same pinning density, size, strength, and applied magnetic field. For all strip widths, the vortex ground state is fully commensurate with the pinning lattice, as shown in Fig. 8a, c, and e. Figure 9 shows the 〈Vy〉 as a function of the Fy for all values of strip widths. It is possible to see that for the narrower strips, there are only two distinct vortex phases; however, for the larger one, three vortex dynamic phases can be observed. Besides that, all systems exhibit the same critical depinning force value. Each phase is directly associated to the vortex regimes illustrated in Fig. 8.

Fig. 8
figure 8

Strips with the flattened triangular pinning lattice, where open circles represent the pinning centers and black dots represent the vortices, with H = 68Φ0/λ2, nv/np = 1, Cp = 0.2Cv, and ap = ξ. Numbers on top of each figure indicate the dynamic phase according to the plot shown on Fig. 9. a The static and b moving phases for the strip with Lx = 0.50λ; c the static and d moving phases for Lx = 0.75λ; e the static phase, f the disordered moving phase (0.684 ≤ Fy ≤ 0.770) and g the perfectly moving flattened triangular lattice for Lx = 1.00λ. The lengths x and y are normalized by 4ξ

Full size image
Fig. 9
figure 9

Average vortex velocity (〈Vy〉) as a function of the applied transport force (Fy) for strips under the influence of the flattened pinning array with Lx = 0.50λ, 0.75λ and 1.00λ, using Cp = 0.2Cv and ap = ξ. The narrower strips show only two phases: the static (I) and moving phases (II), where all vortices move in a perfectly flattened triangular lattice. For Lx = 1.00λ, the system exhibits three phases: the static (I) and two moving phases (II and III). Phase II corresponds to a disordered regime and phase III to a perfectly moving flattened triangular lattice. In all cases, the strips depin at Fy = 0.684

Full size image

The fact that the depinning force is the same for all strips is because the pinning and vortex lattices are fully commensurate in all the cases. Therefore, the vortex pinning is maximum and the depinning occurs at the same force value.

As shown in Fig. 9, it is evident that for Lx = 0.50λ and 0.75λ, the dynamical behavior is different than for Lx = 1.00λ For narrower strips, all vortices show only one dynamical phase, where all of them behave as a perfectly moving flattened triangular lattice. However, for Lx = 1.00λ and in the range of forces 0.684 ≤ Fy ≤ 0.770 (region II of Fig. 9), the vortices begin to move in disordered thicker channels with small bumps. For Fy > 0.770, vortices slightly reduce their average velocities and move in narrower channels forming a perfectly moving flattened triangular lattice That is, at Fy = 0.770 there is a dynamic phase transition, where vortices change from a disordered to an ordered phase. This behavior is similar to what was found by Reichhardt and Olson Reichhardt analyzing particles flowing in neighboring channels [68]. Comparing with our case, here the system also exhibits a transition where the velocities of the different vortex channel change from a decoupled (where different channels exhibits different velocities) to a coupled motion (where all channels move with the same velocity).

5 Conclusions

In summary, we simulated for the first time the vortex behavior in thin superconducting strips of three widths Lx = 0.50λ, 0.75λ and 1.00λ in the presence of a regular triangular and a flattened triangular pinning array at zero temperature. The pinning density and applied magnetic field were the same for all samples to investigate the size effects only. The vortex ground state was obtained with a simulated annealing procedure, and then, a transport force was applied along the infinite direction of the strip. For the regular triangular pinning lattice, we found that in all samples sizes, the depinning occurs by columns following the degree of commensurability of each vortex chain. Different than in infinite films, the Meissner supercurrents push vortices toward the center of the sample, destroying the commensurability of the chains close to the surface favoring the depinning of vortices. However, this is not the only mechanism that contributes to lower the critical depinning force. As the strip is enlarged and the applied magnetic field remains the same, the vortex density changes, provoking that some vortices may stabilize in interstitial positions. Moreover, the influence of the surface energy barrier becomes less important, and the transversal fluctuation of vortices is higher, favoring the arising of new vortex dynamic regimes.

For the flattened triangular pinning array, we observed that for all the calculated widths the critical depinning force was the same (Fy = 0.684) and much higher than in the strips with the regular pinning array. This may be explained because the vortex and pinning lattice are fully commensurate. For the narrower strips with the flattened pinning array, we only observed one dynamical phase, where vortices move in an ordered and perfectly flattened triangular lattice. For Lx = 1.00λ, the system shows two dynamic phases. The first one is characterized by vortices moving through decoupled thicker channels with different velocities. The second dynamic phase happens for Fy > 0.770, where the vortices move in narrower coupled channels forming a perfectly moving flattened triangular array.

Comparing the dynamic phases obtained by our simulations in strips with that of infinite films with same pinning lattice [57], our results show that in the strips there is a greater richness of dynamic phases. In infinite samples it is observed only three dynamic phases: (i) the static, (ii) a sinuous moving phase with interconnectivity between channels and (iii) a sinuous moving channel with smaller amplitude [57]. That richness may be associated to the following idea: in strips, as the width is varied at a constant field, the ratio between vortices and pinning sites changes, giving rise to several different ground states, with different degrees of commensurability. Thus, as the strip width vary, the number of vortex dynamical phases and regimes may also change.

The high critical depinning forces observed with the flattened pinning lattice and the similarities between the dynamical phases observed for these pinning arrays when compared with the hexagonal lattice in infinite samples show an indication of how to partially recover the results obtained with regular pinning lattices in the infinite sample limit. In the future, these results might be useful to carefully obtain a systematic way of flattening regular lattices to create efficient pinning lattices for superconducting strips using the vast expertise from the scientific community on infinite two-dimensional systems obtained throughout the years.