1 Introduction

In contrast with low-temperature superconductors (LTS), high-temperature superconducting (HTS) YBCO tape has high critical current at very high background fields and low temperature or can be used at elevated temperature, and thus they have potential advantages in superconducting magnets, superconducting fault current limiters, and so on [1,2,3,4,5,6,7,8]. Since the conductor with large current-carrying capacity is required in many power applications, the cable is usually assembled with multi-tapes or stacked tapes [9,10,11]. In the practical operation, the cable experiences complicated electromagnetic field. Due to energy disturbances in superconducting devices, the dramatic change of local temperature may occur in the cable [12], which can result in the quench of the cable. The quench propagation velocity (QPV) of HTS is much smaller than that of LTS, which leads to high local temperature in the vicinity of the quench point [13]. In addition, serious damage may be caused in the superconducting devices without timely quench protection. Thus, it is necessary to study the quench behaviour to ensure stability and safety of the superconducting structure. At present, many numerical researches are presented to simulate and analyse the quench characteristics of YBCO tape [14]. Roy et al. established a 3D magneto-thermal coupling model to investigate the effect of substrate made by different materials on the QPV of YBCO tape [15]. Moreover, Chan et al. analysed the effects of resistivity, thermal conductivities of silver layer and buffer layer in YBCO tape on QPV with a two-dimensional (2D) thermoelectric coupling model, and maximum temperature rise of the quench area was presented [16]. Then, they studied the quench propagation characteristics of multi-layer composite YBCO tape in an adiabatic environment based on 3D coupling model [17, 18]. In order to reduce the calculation, the superconducting layer is simplified as a two-dimensional surface, and the results were in good agreement with the experimental results [19]. They also discussed the effects of the geometric dimensions and material parameters. In addition, Levin et al. investigated the variation of QPV with the interface resistance between the superconducting layer and the copper stabilisation layer [20, 21]. Zhang et al. found that the quench was induced with the increase of heat-pulse energy and QPV was small for a 40-turn YBCO coil based on the H-formulation [22]. The quench behaviours in stacked superconducting composite tape with defects were also studied.

However, with the presence of termination resistances, the transport current in superconducting cable composed of several tapes will be redistributed [23]. Grilli et al. presented three dc models to calculate the distribution of current of individual tape for a stacked-tape cable composed of four tapes with considering the effects of the termination resistances [24]. However, the effects of the termination resistances on the quench are not discussed.

In this paper, a 2D stacked-tape cable composed of four tapes is used to study the effects of the termination resistances on the quench of HTS tape by loading a pulse heat source. The distribution of temperature can be obtained by solving the coupled heat conduction equation and the Maxwell’s equations. The E-J constitutive law and Ohm’s law are adopted for superconducting layer and other layers. Meanwhile, the mechanical behaviours during the quench are also analysed. In Section 2, we describe the computational model and the underlying equations. Section 3 discusses the effects of the termination resistances on the quench characteristics by considering different ways of transport current and different locations of heat source. The final section summarises the main results of this work.

2 Numerical Model

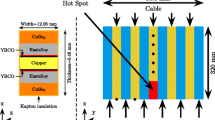
It is assumed that the length of the tapes has no effect on their properties in the cable [24]. The model composed of four tapes can be simplified as a 2D model to study the effects of the termination resistances on the quench characteristics in the section when the pulsed heat source is loaded on the individual tape, as shown in Fig. 1. The model of tape is based on SCS4050 [25], and each tape consists of insulation layer (59 μ m), copper stabiliser (20 μ m), hastelloy substrate (50 μ m) and YBCO (1 μ m). The width of the tape is 4 mm. Note that the Kapton with small thermal conductivity is used as the insulation material for HTS tape, and thus the heat can propagate between the adjacent tapes [22].

Fig. 1
figure 1

The schematic diagram of the cable model. The heater is located at the hastelloy substrate with 0.4 mm width and 50 μ m height. The points P1, P2, P3 and P4 which are located in the superconducting layer of each tape represent temperature probes and are used to monitor the change of the temperature

Full size image

The model is numerically investigated by solving the thermal transient equation coupled with the 2D H-formulation of Maxwell equations. Here, the heat conduction equation can be expressed as

$$ dC(T)\frac{\partial T}{\partial t}-\nabla \times (k(T)\nabla T)=Q $$
(1)

where d, C(T) and k(T) are the material mass density, the heat capacity and the thermal conductivity, respectively. It is to be noted that the heat capacity and thermal conductivity are dependent on the temperature, and the relationships between the parameters and temperature are given in ref. [22]. Q represents the power density dissipated, which is equal to the product of the current density and local electric field. The heat transfer to the coolant through the boundaries of the cable is not taken into account, and thus the adiabatic condition is assumed in the simulation.

The 2D H-formulation is used to calculate the current density and local electric field of individual tapes with time. The magnetic field only has two components (Hx and Hy) along the x-axis and y-axis, and the critical current density and electrical field only have one components (Jz and Ez) along the z-axis. The corresponding H-formulation [26, 27] governing equations can be obtained by Faraday’s law, Ampere’s law and the E-J constitutive law,

$$ \left[ {{\begin{array}{*{20}c} {\mu_{0} \mu_{r} \frac{\partial H_{x} }{\partial t}+\frac{\partial }{\partial y}\left[\rho \left( \frac{\partial H_{y} }{\partial x}-\frac{\partial H_{x} }{\partial y}\right)\right]} \hfill \\ {\mu_{0} \mu_{r} \frac{\partial H_{y} }{\partial t}+\frac{\partial }{\partial x}\left[\rho \left( \frac{\partial H_{x} }{\partial y}-\frac{\partial H_{y} }{\partial x}\right)\right]} \hfill \end{array} }} \right]=\left[ {{\begin{array}{*{20}c} 0 \hfill \\ 0 \hfill \end{array} }} \right] $$
(2)

where μ0 and μr are the permeability of vacuum and the relative permeability, respectively. And ρ obtained by the E-J constitutive law is given in the following.

In order to simplify the model, total voltage drop is composed of two parts including the voltage of superconducting tapes and termination resistances, and thus the governing equations need to be modified [24]. In the dc case, the voltage equations generated by the termination resistances for the individual tapes are

$$ E_{tr} =R_{i} I_{i} $$
(3)

where I(i = 1,2,3,4) is the transport current in the i th tape. And represents the scaled termination resistance (Ω m− 1) at the end of tape, and the scaling is obtained by considering the length of the superconducting tape. The corresponding values for R1, R2, R3 and R4 are 0.328, 2.101, 0.533 and 0.6 μΩ m− 1, respectively [24]. The governing equations are modified as

$$ \left[ {{\begin{array}{*{20}c} {\mu_{0} \mu_{r} \frac{\partial H_{x} }{\partial t}+\frac{\partial }{\partial y}\left[\rho \left( \frac{\partial H_{y} }{\partial x}-\frac{\partial H_{x} }{\partial y}\right)+R_{i} I_{i} \right]} \\ {\mu_{0} \mu_{r} \frac{\partial H_{y} }{\partial t}+\frac{\partial }{\partial x}\left[\rho \left( \frac{\partial H_{x} }{\partial y}-\frac{\partial H_{y} }{\partial x}\right)+R_{i} I_{i} \right]} \hfill \end{array} }} \right]=\left[ {{\begin{array}{*{20}c} 0 \hfill \\ 0 \hfill \end{array} }} \right] $$
(4)

The model is solved in self-field. When the direction and magnitude of the magnetic field is taken into account, the expression of the critical current density is given as [24]

$$ J_{c} \left( {B_{\parallel } ,B_{\bot } } \right)=\frac{s_{i} J_{c0} }{\left( {1+{\sqrt {\left( {kB_{\parallel } } \right)^{2}+B_{\bot }^{2} } } \mathord{\left/ {\vphantom {{\sqrt {\left( {kB_{\parallel } } \right)^{2}+B_{\bot }^{2} }} {B_{c} }}} \right.} {B_{c} }} \right)^{b}} $$
(5)

where Jc0 = 21.218 GA m− 2, k = 0.275, b = 0.6 and Bc = 32.5 mT. si is a tuning factor of the critical current in the i th tape and the values for s1, s2, s3 and s4 are 1, 0.9904, 0.9604 and 0.8643, respectively [24]. And B|| and B⊥ represent the parallel and perpendicular components of magnetic field, respectively. Furthermore, the critical current density is also affected by the temperature. Thus, when the temperature is less than the critical temperature of YBCO (Tc = 92 K), the relationship between them is [22]

$$ J_{c} (T)=\beta \times [1-(T/T_{c} )^{2}]^{\frac{3}{2}} $$
(6)

where the value β is determined by Jc0 at 77 K. The resistivity of YBCO below Tc is usually represented with a nonlinear power-law relation [28, 29]

$$ \rho_{s} =\frac{E_{c} }{J_{c} (T)}\times \left[\frac{J_{z} }{J_{c} (T)}\right]^{n-1} $$
(7)

where Ec represents the electrical field criterion and its value is 1 μ V cm− 1. And the n value is 21 [24]. When the temperature is more than critical temperature, we use ρnormal = 3 × 10− 6 Ω m to replace the resistivity of YBCO in the paper [22]. In order to assure the convergence of computation, a smooth transition is assumed between the superconducting state and normal state. The expression is given as [30, 31]

$$ \rho =\left\{ {{\begin{array}{*{20}l} {\frac{\rho_{s} \times \rho_{\text{norm}} }{\rho_{s} +\rho_{\text{norm}} }} \hfill & \quad{T<T_{c} } \hfill \\ {\rho_{\text{norm}}} \hfill &\quad {T\ge T_{c} } \hfill \end{array} }} \right. $$
(8)

In addition, the coil will experience remarkable strain and stress during the quench. Thus, the mechanical model is built to analyse the variation of mechanical behaviour. Due to the temperature differences, the strain and stress can be calculated as

$$\begin{array}{@{}rcl@{}} {\Delta} T&{=}&T-T_{{re}f} \\ \varepsilon_{x} &{=}&\frac{1-\mu^{2}}{E_{young} }\left( {\sigma_{x} -\frac{\mu }{1-\mu }\sigma_{y} } \right)+\left( {1+\mu } \right)\alpha {\Delta} T \\ \varepsilon_{y} &{=}&\frac{1-\mu^{2}}{E_{young} }\left( {\sigma_{y} -\frac{\mu }{1-\mu }\sigma_{x} } \right)+\left( {1+\mu } \right)\alpha {\Delta} T,\\ \\ &&\gamma_{xy} =\frac{2\left( {1+\mu} \right)}{E_{young} }\tau_{xy} \\ \sigma_{x} &{=}&\frac{E_{young} }{\left( {1+\mu } \right)\left( {1-2\mu} \right)}\left( {\left( {1-\mu } \right)\varepsilon_{x} +\mu \varepsilon _{y} -\alpha {\Delta} T} \right) \\ \sigma_{y} &{=}&\frac{E_{young} }{\left( {1+\mu } \right)\left( {1-2\mu} \right)}\left( {\left( {1-\mu } \right)\varepsilon_{y} +\mu \varepsilon _{x} -\alpha {\Delta} T} \right),\\ &&\tau_{xy} =\frac{E_{young} }{2\left( {1+\mu } \right)}\gamma_{xy} \end{array} $$
(9)

where Tref is 77 K. The coefficients α of thermal expansion of superconducting layer, hastelloy substrate, copper stabiliser and insulation layer are 1.34 × 10− 5, 1.09 × 10− 5, 1.67 × 10− 5 and 2 × 10− 5 K− 1, respectively. And their Young’s moduli Eyoung and Poisson’s ratios μ are 157, 209, 117, and 30 GPa and 0.3, 0.3, 0.35, and 0.3, respectively [32, 33].

In self-field, the Lorentz force is much smaller than the thermal stress so that it can be neglected in the simulation. The governing equations of mechanical equilibrium are

$$\begin{array}{@{}rcl@{}} \frac{\partial \sigma_{x} }{\partial x}+\frac{\partial \tau_{xy} }{\partial y}= 0 \\ \frac{\partial \sigma_{y} }{\partial y}+\frac{\partial \tau_{xy} }{\partial x}= 0 \end{array} $$
(10)

The lower boundary is fixed, and other boundaries are free. The numerical model is built and solved by commercial finite element software COMSOL Multiphysics [34].

3 Results and Discussions

In the simulation, the outer boundaries of the model are the thermal insulation conditions and the initial temperature is 77 K. The transport current reaches maximum at 0.1 s, and the current keeps unchanged. After this, the heater is pulsed for 30 ms with an energy. Note that the heater is 0.4 mm long, height is equal to the thickness of layer and the location is in the middle of layer.

3.1 The Effect of the Termination Resistances on the Quench

The termination resistance is an important factor for the redistribution of the current among the tapes, which can affect the energy loss and lead to different sequences of the quench due to the heat generated by the termination resistances.

The transport current 45 A is loaded in each tape, and the heater is located in the hastelloy substrate of tape 1 with an energy of 11 J m− 1. Figure 2 shows the distributions of temperature, where the results are presented for the cable with and without the termination resistances. It can be seen that the termination resistances will also generate the heat, which speeds up the quench of tapes. After considering the effect of the termination resistances, the quench is trigged at the upper end (tape 4) firstly, which is far away from the heater. The reason is that the heat begins to propagate towards upper and bottom boundaries when the heater is turned on. Because of using adiabatic condition in the simulation, the heat is accumulated in the tapes 1 and 4. However, the termination resistance of tape 4 is larger than that of tape 1. Thus, the temperature rise in tape 4 is larger than that in tape 1. Moreover, the critical current of tape 4 is smallest in the cable, and thus it is easier to induce a quench. As the entire cable experiences quench, the temperature of tapes 2 and 3 is slightly lower than that of tapes 1 and 4 due to heat accumulation in upper and bottom boundaries. Thus, the termination resistance has a large effect on the location and the sequence of quench.

Fig. 2
figure 2

The temperature distributions during the quench a with the termination resistances and b without the termination resistances, where the pulsed energy is 11 J m− 1

Full size image

However, the quench will occur in both tapes 1 and 4 firstly for the case without the termination resistances. Because the heat cannot be exchanged with the outer space in time so that it is accumulated in the tapes 1 and 4. When the time is long enough, the distribution of heat is symmetrical for the cable with and without the termination resistances during the quench, respectively. With the increase of pulsed energy, compared with Fig. 2, it can be expected that the maximal temperature is larger for the higher pulsed energy at the same time, as shown in Fig. 3. Note that the sequences of the quench are the same for the cable with and without termination resistances, as shown in the inset of Fig. 3. The quench appears successively from tapes 1 to 4. The reason is that high pulsed energy can firstly induce quench in the heater location (The heater location of Fig. 3 is in tape 1). Then, the heat propagates toward the top of the cable due to adiabatic boundary, and thus tape 2, tapes 3 and 4 quench successively. The temperature of all tapes increases during the heat disturbance. When the heater turns off, the temperature of tape 1 drops and the temperature of other tapes continues to rise. Then, the temperature of tape 1 also starts to increase after a while so that the overall cable experiences a quench finally. And the quench is triggered at tape 1 first. The reason is that the heat is not able to exchange in time with a higher energy, which leads to the accumulation of a large amount of heat in the location of the heater.

Fig. 3
figure 3

The temperature distributions during the quench a with the termination resistances and b without the termination resistances, where the pulsed energy is 12 J m− 1. The insert figures can clearly show that the sequences of the quench are the same for two cases

Full size image

3.2 Effects of Transport Current and Location of Heat Source

During the above investigation, the transport current in each tape is 45 A. Next, we consider the different cases where the power supply current is equal to the sum of the current of four tapes and the transport current is different in each tape. Figure 4 shows the change of temperature and current in the superconducting layer with termination resistances, and the total transport current is 180 A. It indicates that the cable with the termination resistances has no quench with an energy of 12 J m− 1. In other words, the thermal stability is higher and the energy induced the quench is higher for the case. When the heat-pulsed energy reaches 14 J m− 1, both cables with and without the termination resistances quench, as shown in Fig. 5. As the cable with termination resistance is under the stable operation, the transport current in tape 1 is largest and in tape 2 is smallest, which is related to the magnitude of termination resistance (see Fig. 5b). While for the cable without termination resistance, the transport current in each tape is the same. Moreover, the heater is located in tape 1, and the current in superconductor layer of tapes 1 and 2 reduces and flows into tapes 3 and 4 during the heat disturbance. Then, with the recovery of temperature in tapes 1 and 2, the current of the superconducting layers in the two tapes also increases. When the cable quenches, the current of superconducting layers in all tapes drops to zero and all current flows in the substrate and copper. It is interesting to find the sequence of quench will also change, as shown in inset of Fig. 5a, c. The sequence of quench is tapes 1, 4, 2 and 3 with termination resistance (Fig. 5a). Because the critical current of tape 4 is minimum and the transport current of tape 4 exceeds critical current firstly for this loading-current way (Fig. 5b), the quench of tape 4 is faster than tapes 2 and 3. The trend is different with that in Fig. 3a. In Fig. 5c (without termination resistance), the quench appears in tapes 1 and 4 almost simultaneously. Then, tapes 2 and 3 also quench. This result means that the quench is dependent on the termination resistance and distribution of transport current.

Fig. 4
figure 4

Time dependence of a temperature and b current of superconducting layer in each tape with the termination resistances, where the pulsed energy is 12 J m− 1

Full size image
Fig. 5
figure 5

Time dependence of temperature and current for the cable a, b with the termination resistances and c, d without the termination resistances, where the energy is 14 J m− 1. Inserts in (a) and (c) clearly show that the sequences of the quench are different for two cases

Full size image

Then, we consider the effect of location of heater, where the current 45 A is loaded in each tape. When the temperature of entire cable is close to critical temperature, the temperature distributions are presented in Fig. 6. As can be seen from Fig. 6a, the sequence of quench is not related with the location of heater with an energy of 10 J m− 1. The reason is that low energy cannot induce a quench in the location of the heater. Moreover, tape 4 has a larger termination resistance than tape 1 and the critical current of tape 4 is lowest. Thus, the heat accumulation in the top boundary of cable firstly leads to the quench. It can be also found that when the heater is placed in tape 4, the heat can rapidly propagate to the top boundary so that the quench is induced in shorter time. Although the heater is located in different layers of the superconducting thin tape, the time of quench is almost the same for the cable based on the rapid heat propagation along the thickness direction. However, when the energy is 12 J m− 1, the quench is firstly induced in the place of the heater, as shown in Fig. 6b. This is because high energy can directly induce a quench in the tape located in the heater. Thus, when the heater is located in tape 1, the sequence of the quench is different by comparing with the left of Fig. 6. Furthermore, high energy can accelerate the quench and the termination resistances no longer have effect on the sequence of quench. However, the time of quench is still affected by the termination resistances.

Fig. 6
figure 6

The effect of different heater locations on the distribution of temperature with the termination resistances in the cable. The pulsed energy is a 10 and b 12 J m− 1. The heater locations of each side from top to bottom are in the upper copper layer and superconducting layer of tape 4 and the hastelloy substrate, superconductor layer and bottom copper layer of tape 1, respectively

Full size image

3.3 Mechanical Behaviours During the Quench

During the quench, much heat will be generated in the cable. Then, the cable or coil will be subjected to a large thermal stress due to the change of temperature [35]. The mechanical strain can also be used to predict the quench of HTS tape [36]. In this section, the heater is located in the hastelloy substrate of the bottom of the model with an energy of 12 J m− 1. Figure 7 shows the Von Mises stress profile distributions during the quench with and without the termination resistances, respectively. During the heat disturbance, the electromagnetic force has little effect on the mechanical behaviours, which is mainly affected by the thermal expansion. Thus, the variational trend of Von Mises stress is similar to that of temperature. As the temperature of the tape increases in the cable, the tape continues to expand which leads to the increase of Von Mises stress. Due to the decrease of the temperature after the heat disturbance, tape 1 in the cable starts to recover so that Von Mises stress also reduces. In addition, the termination resistances have a little effect on the Von Mises stress. Figure 8 indicates the strain rate profile along the y-axial direction with and without termination resistances, respectively. The termination resistances still have a little effect on the strain rate. It can be seen that when the local temperature reaches the critical temperature and quench is induced, the strain rate of each tape has an inflection point. The reason is that the resistivity of superconducting layer becomes a larger constant when the temperature is more than the critical temperature. Thus, the strain rate can be also used to predict the quench of stacked tape, as report in ref. [36].

Fig. 7
figure 7

The heater is located in the hastelloy substrate of the bottom of the model with an energy of 12 J m− 1. Von Mises stress profiles: a with the termination resistances and b without the termination resistances

Full size image
Fig. 8
figure 8

The heater is located in the hastelloy substrate of the bottom of the model with an energy of 12 J m− 1. The strain rate profiles along the y-axial direction: a with the termination resistances and b without the termination resistances

Full size image

4 Conclusions

Due to the heat generated by the termination resistances, the termination resistance has the obvious effect on the distribution of the current in the cable during the quench. It can be found that the quench is easier to be induced in the cable with the termination resistances by comparing with the cable without the termination resistances. The top tape has a larger termination resistance and a smallest critical current so that the quench appears firstly for the low pulsed energy. For the high pulsed energy, the quench is induced in the location of heater. Moreover, when the transport current in each tape is different, a large pulsed energy is needed to induce the quench in the cable with the termination resistances. The sequence of the quench is affected by the pulsed energy and termination resistance. Because the deformation of the cable is mainly generated by the change of the temperature, the Von Mises stress profile has the same trend as the temperature distribution. When the temperature is more than the critical temperature, the strain rate of each tape has an inflection point. Thus, the strain rate may be also able to be used to detect the quench of stacked-tape cable. It can be also found that the termination resistances have little effect on the mechanical behaviours of stacked-tape cable.