First-Principles Studies of the Magnetic Anisotropy of Monolayer VS₂

Abstract

First-principles calculations are performed to study the magnetic anisotropy of monolayer VS₂. The magnetic anisotropy energy (MAE) for H-VS₂ is −0.213 meV, and the magnetic preferential direction is in the monolayer plane, while the corresponding value for T-VS₂ is only 0.004 meV, which can be ignored for two-dimensional materials. According to the second-order perturbation of the spin–orbit coupling (SOC) interactions, the physical origin of magnetic anisotropy for H-VS₂ is derived from the occupied and unoccupied dxy/dx ²-y ² states with different spin channels in light of the electronic structure. In the reciprocal space, the negative contributions mainly stem from the corners of hexagonal Brillouin zone. Interestingly, there are non-equivalent K and K ^′ for the MAEs, which are observed for the first time for MAE in the reciprocal space. We predict that the lack of inversion symmetry results in the different signs of MAEs in the K and K ^′. Our studies open up broad prospects to trace the physical origin of magnetic anisotropy in the reciprocal space.

1 Introduction

Since the discovery of graphene, two-dimensional (2D) layered materials have drawn extensive concerns [1–3]. Among various kinds of layered materials, 2D transition metal dichalcogenides (TMDs) stand out because some of them exhibit many more exciting properties compared with graphene. For instance, the MoS₂ monolayer was found to be a semiconductor with a sizable direct band gap of approximately 1.8 eV, overcoming the disadvantage of zero band gap in graphene when applied in field-effect transistors (FETs) and optoelectronic devices [4]. Furthermore, though being a very young field, there have been several reviews on 2D TMDs that address the history of their development [5]; synthesis [5, 6]; electronic [6–8], optoelectronic, and nanophotonic applications [6, 9–11]; and the spin and valley physics and photonics [7].

In most of existing pristine 2D TMDs, no magnetic ordering is observed, though magnetic properties play an important role in practical applications. Several approaches haven been reported to tune magnetic properties among 2D TMDs, such as introducing transition metal atoms [12–15], point defects [16], and adatom adsorption [17, 18]. But, it is difficult to put them into practice, which hampers their applications in many aspects. Monolayer VS₂, as a kind of 2D TMDs, has received special attentions due to its intrinsic magnetism [19, 20]. VS₂ is formed by a graphene-like hexagonal arrangement of V and S atoms stacked together like S-V-S sandwiches. VS₂ monolayers have two phases, H and T phases, and different crystal structures demonstrate distinct physical properties [21]. Using first-principles calculations, Ma et al. predicted that monolayer VS₂ exhibits exciting ferromagnetic behavior [19]. Inspired by the research of Ma et al., Gao et al. obtained ultrathin VS₂ nanosheets, and ferromagnetism was verified experimentally [20]. Ma et al. regarded T-VS₂ monolayer as the stable structure [19], but it was found that H-VS₂ monolayer is more stable in the subsequent researches [22, 23]. In a recent study, monolayer H-VS₂ is predicted to be ferromagnetic and its easy axis is in the plane of monolayer VS₂ [24].

In term of the Mermin–Wagner theorem, the isotropic Heisenberg system cannot ensure long-range magnetic ordering in 2D materials above zero temperature [25]. However, the magnetic anisotropy can generate an energy gap for the long wavelength spin waves to remove the limitations of Mermin–Wagner theorem [26]. Two famous modes, XY model and Ising model, can show magnetic ordering in 2D materials [27, 28]. XY model corresponds to an easy plane, while the Ising model corresponds to an easy axis [24, 29]. Magnetic anisotropy is an important property in magnetic materials which is the prerequisite and foundation to verify whether a 2D material exhibits a magnetically ordered phase above zero temperature, but few researches go deeply into this aspect of monolayer VS₂ [24].

In this work, we perform first-principles calculations to study the magnetic anisotropy of monolayer VS₂. The magnetic preferential axis for H-VS₂ is in-plane. Meanwhile, the magnetic anisotropy energy (MAE) for T-VS₂ is so small that can be ignored. The microscopic origin of magnetic anisotropy in monolayer H-VS₂ is our focus in this research. To our surprise, there are non-equivalent K and K ^′ for the MAEs in H-VS₂, which are observed for the first time for MAE in the reciprocal space.

2 Computational Details

First-principles calculations are performed within the framework of the density functional theory (DFT) with the Perdew–Burke–Ernzerhof (PBE) version of the generalized gradient approximation (GGA) exchange–correlation functional programmed in the Vienna Ab initio Simulation Package (VASP) code. In the calculations, we use projector-augmented wave (PAW) potential and plane-wave cutoff energy of 450 eV. The positions of atoms and the cell parameters are fully optimized. In the structural optimizations, the force acting on each atom is less than 0.01 eV/Å, and the total energies of the optimized structures are well converged with criteria of 10 ⁻⁵ eV per cell. The Brillouin zone is sampled using a set of 15 × 15 × 1 and 30 × 30 × 1 gamma-centered k-mesh for the structural optimizations and electronic structure calculations, respectively. In order to avoid any interaction between monolayers perpendicular to the plane of monolayer VS₂, a vacuum space of 20 Å is used. We calculate the MAE based on the force theorem by

$$ \text{MAE}=E(\theta =90^{0})-E(\theta =0^{0}) $$

(1)

where E stands for the total energy with the inclusion of the spin–orbit coupling (SOC) interactions for each spin orientation. 𝜃=90⁰ and 𝜃=0⁰ denote that the magnetization direction is in-plane and perpendicular to the monolayer VS₂ sheet, respectively [30].

3 Results and Discussions

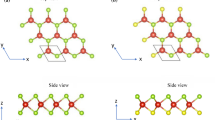
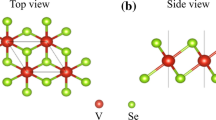
As shown in Fig. 1, VS₂ monolayers possess trigonal prismatic (H-VS₂) and octahedral (T-VS₂) polymorphs, whose point groups are D_3h and D_3d , respectively. The structural parameters for H-VS₂ and T-VS₂ are listed in Table 1. As depicted in Fig. 2, the results of energy band indicate that both phases in the spin-up and spin-down channels are metallic. All these results coincide well with previous theoretical studies, which give our confidence to pursue further studies [31–33].

Fig. 1

a Top view of monolayer H-VS₂. b Top view of monolayer T-VS₂. c Side view of monolayer H-VS₂. d Side view of monolayer T-VS₂. V atoms are red, and S atoms are yellow

Fig. 2

Spin-polarized band structures of a H-VS₂ and b T-VS₂. Red and blue lines correspond to the majority and minority spin bands, respectively

Table 1 Structural parameters of monolayer VS₂ polytypes

Under the crystal field with D_3h symmetry in H-VS₂, the five V 3d orbitals are split into a single state $\text {{a}}^{\prime }_{1}$ (dz ²) and two twofold degenerate states e ^′ (dx ²-y ²,dxy) and e ^″ (dxz,dyz), as shown in Fig. 2. Accordingly, the five V 3d orbitals of T-VS₂ under the D_3d symmetry are split into a single state a _1g (dz ²) and two twofold degenerate states e _g (dx ²-y ²,dxy) and e _g (dxz,dyz), as shown in Fig. 3.

Fig. 3

a The total density of states of monolayer H-VS₂. b The projected DOS of the 3d orbitals of V atom

The magnetic moments per unit cell are 0.990 and 0.479 μ _B for H-VS₂ and T-VS₂, respectively. The magnetic moment in H phase is larger than that in T phase, which is due to the fact the H-VS₂ has a stronger spin splitting than the T-VS₂, as shown in Figs. 3 and 4. The magnetic moments mainly stem from V 3d orbitals which are 0.924 and 0.485 μ _B, and the neighboring sulfur atoms are polarized antiferromagnetically with magnetic moments of −0.043 and −0.029 μ _B for H-VS₂ and T-VS₂, respectively. In this case, the S atoms act as a good bridge for the magnetic coupling between V ions.

Fig. 4

a The total density of states of monolayer T-VS₂. b The projected DOS of the 3d orbitals of V atom

The calculated MAE based on the force theorem approach for H-VS₂ is −0.213 meV, which has an easy plane. The corresponding value for T-VS₂ is only 0.004 meV, and it is too small for 2D materials [34]. In the reciprocal space, the MAE can be defined by

$$\begin{array}{@{}rcl@{}} {\Delta} E=E_{//} -E_{\bot} &=&\sum\limits_{i,k} \left[ \varepsilon_{i,//} (k)\cdot n_{i,//} (k)\right.\\ &&\left.-\varepsilon_{i,\bot} (k)\cdot n_{i,\bot} (k) \right] \cdot w(k), \end{array} $$

(2)

where ε _i,//(k) and ε _i,⊥ are the ith band energy for each k-point with in-plane and out-of-plane magnetizations, respectively. n _i,k is the corresponding number of occupation, and w(k) is the weight of each k-point. The calculated MAEs for H-VS₂ and T-VS₂ by using (2) are −0.213 and 0.004 meV, respectively, which have the same values as the results from the differences of total energies. The calculated MAE of the H-VS₂ monolayer is in good accordance with the previous result, −0.21 meV [35]. The value of MAE for T-VS₂ can be ignored, and we will not discuss it any more.

The SOC interactions are responsible for the MAE’s microscopic origin [36]. For 2D magnetic systems, the second-order perturbation between occupied and unoccupied states shall prevail [34]. The contributions to MAE can be divided into two parts [37, 38], one involving the same spin channel and the other involving different spin channels, i.e.,

$$ {\Delta} E_{\pm ,\pm} =\left( {\frac{\xi} {2}} \right)^{2}\frac{\left| {\left\langle {o^{\pm} \left| {\hat{{L}}_{z}} \right|u^{\pm} } \right\rangle} \right|^{2}-\left| {\left\langle {o^{\pm} \left| {\hat{{L}}_{x}} \right|u^{\pm} } \right\rangle} \right|^{2}}{\varepsilon_{\mathrm{u}} -\varepsilon_{\mathrm{o}}} $$

(3)

$$ {\Delta} E_{\pm ,\mp} =\left( {\frac{\xi} {2}} \right)^{2}\frac{\left| {\left\langle {o^{\pm} \left| {\hat{{L}}_{x}} \right|u^{\mp} } \right\rangle} \right|^{2}-\left| {\left\langle {o^{\pm} \left| {\hat{{L}}_{z}} \right|u^{\mp} } \right\rangle} \right|^{2}}{\varepsilon_{\mathrm{u}} -\varepsilon_{\mathrm{o}}} $$

(4)

where o ⁺(u ⁺) and o ⁻(u ⁻) represent the occupied (unoccupied) spin-up and spin-down states, respectively, and ξ is the SOC constant. ε _o(ε _u) denotes the energy of occupied (unoccupied) states. Only a few of the angular momentum matrix elements between the d orbitals are non-vanishing: $\left \langle {d_{z^{2}} \left | {\hat {{L}}_{x}} \right |d_{yz}} \right \rangle \quad \left \langle {d_{xy} \left | {\hat {{L}}_{x}} \right |d_{xz}} \right \rangle$ $\left \langle {d_{x^{2}-y^{2}} \left | {\hat {{L}}_{x}} \right |d_{yz}} \right \rangle \quad \left \langle {d_{xz} \left | {\hat {{L}}_{z}} \right |d_{yz}} \right \rangle \quad \left \langle {d_{x^{2}-y^{2}} \left | {\hat {{L}}_{z}} \right |d_{xy}} \right \rangle$ (bra and ket can be exchanged) [26]. In the case of contributions involving interactions between the states with the same spin channel in (3), the SOC interaction between states with the same (different) magnetic quantum number(s) through the $\hat {{L}}_{z} (\hat {{L}}_{x} )$ operator gives a positive (negative) contribution to MAE. The results are reversed for the contributions involving states with different spin channels, as described in (4). The energy difference (ε _u−ε _o) between the unoccupied state and the occupied state is inversely proportional to the absolute value of MAE; thus, the states in the vicinity of Fermi level play a decisive role in the contributions to MAE.

From the DOS of monolayer H-VS₂ in Fig. 3, there is a strong spin splitting in the vicinity of Fermi level for spin-up and spin-down states; thus, the occupied and unoccupied states have the same orbital compositions. The occupied and unoccupied states are mainly derived from the same orbital compositions: ${a}^{\prime }_{1}$ (dz ²) and e ^′ (dx ²-y ²,dxy) states, but they are in different spin channels. Only some interactions among these states are non-vanishing on the basis of the abovementioned analyses. Therefore, the contributions mainly stem from the occupied spin-up e ^′ (dx ²-y ²,dxy) and unoccupied spin-down e ^′ (dx ²-y ²,dxy) states through the operator of $\hat {{L}}_{\mathrm {z}}$, which are negative and make the easy axis turn to in-plane orientation.

The total energy of an uniaxial system can be well approximated in the form

$$ E(\theta )=E_{0} +K_{2} \sin^{2}(\theta ) $$

(5)

and the calculated results of H-VS₂ fit (5) well, as shown in Fig. 5. The term of K ₂ sin2𝜃 includes the contributions from the second-order perturbation, and the negative K ₂ of the H-VS₂ system means that the easy axis is in-plane, which provides further evidence of our previous analysis.

Fig. 5

The calculated angular dependence of the total energy for monolayer H-VS₂, and 𝜃 is the angle between the magnetic moment and the normal of the layer plane

In the reciprocal space, the negative contributions to the MAE are mainly from the corners of hexagonal Brillouin zone, which should be responsible for the easy plane of monolayer H-VS₂, as shown in Fig. 6. What is particularly intriguing is the existence of non-equivalent K and K ^′ for MAE in the reciprocal space. To the best of our knowledge, it has not been shown in the previous reports. In Fig. 7, it is noted that the band structures in K and K ^′ have the same occupations when the calculations are performed without including the SOC interactions. According to the previous study, the MAE for the 2D systems mainly stems from the second-order perturbation of the SOC interactions, and the MAEs in K and K ^′ seem to have the same result that is the negative contributions. However, the reality in this research is in conflict with the previous studies, and the distributions of MAE in the reciprocal space show sharp contrasts in a large surrounding region around the corners of hexagonal Brillouin zone, as shown in Fig. 6. That just means that there may be some other factors to influence the magnetic anisotropy. Due to the lack of inversion symmetry, the Berry curvatures of monolayer H-VS₂ and H-MoS₂ have shown different signs of Ω _z (k) in the K and K ^′ points in the reciprocal space [24, 39]. Here, we predict that the inversion symmetry also influences the magnetic anisotropy. The lack of inversion symmetry results in the different signs of MAE in the K and K ^′. Our studies open up broader prospects to trace the physical origin of magnetic anisotropy in the reciprocal space.

Fig. 6

The distributions of the MAEs in the reciprocal space

Fig. 7

The projected band structure of monolayer H-VS₂ for the a spin-up channel and b spin-down channel

4 Conclusions

In this work, we have investigated the magnetic anisotropy of monolayer VS₂. The MAEs for H-VS₂ and T-VS₂ are −0.213 and 0.004 meV, respectively. The MAE for T-VS₂ is so small that can be ignored. According to the second-order perturbation of the SOC interactions, the microscopic origin of monolayer H-VS₂ is derived from the occupied spin-up e ^′ (dx ²-y ²,dxy) and unoccupied spin-down e ^′ (dx ²-y ²,dxy) states, and the fitted curve for the dependence of total energy on the angle (𝜃) for H-VS₂ provides further evidence for our analysis. From the distributions of MAE in the reciprocal space, the negative MAE mainly arises from the corners of hexagonal Brillouin zone. Interestingly, there are non-equivalent K and K ^′ for MAE in the reciprocal space. We attribute it to the lack of inversion symmetry in the monolayer H-VS₂. Certainly, more works should be done in the future to provide a more precise understanding of this phenomenon in the reciprocal space.

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.