1 Introduction

Spatial correlations belong to the most important properties of superconducting systems. Very unconventional features of coherency were found recently in magnetic response of multi-band compounds [1–6]. The various aspects of spatially inhomogeneous multi-gap superconducting ordering were studied in Refs. [3, 7–15].

Coherence lengths for two-band superconductivity were first obtained almost 30 years ago by means of the two-component Ginzburg-Landau equations [16]. It was shown that the spatial variations of superconductivity gaps are determined by the mixture of coherency modes characterized by qualitatively different length-scales: conventional (critical) one which diverges at phase transition temperature and unconventional (non-critical) one which stays finite. The dependencies of the contributions of coherency modes on the parameters of the system and temperature were analyzed in Ref. [17].

Probably the most natural way for the determination of coherence lengths is the calculation of relevant correlation functions. The intra- and interband spatial correlation functions of two-band superconductivity, derived in Ref. [15], contain critical and non-critical coherence lengths. The spatial behavior of fluctuations in a bulk two-band superconductor is characterized by length-scales which coincide with the coherence lengths [17]. In the present paper, we want to find out what happens with characteristic length-scales if two-band superconductivity is distorted by the presence of the interface.

2 Basic Equations

We consider the weak coupling s-wave superconductivity in a system with two partially overlapping bands. It is supposed that the superconducting ordering is created by the intraband effective electron-electron attractions with constants W 11,22<0 and by interband pair-transfer interaction with the constant W 12 = W 21. These interaction channels are supposed to be operative in the energy layer \(\pm \hbar \omega _{c}\) around the Fermi level intersecting both bands.

The spatially inhomogeneous two-band superconductivity is described by the appropriate free energy functional following from the BCS-type microscopic theory. In the absence of magnetic field, it reads as [18]

$$\begin{array}{@{}rcl@{}} F=&&\int \mathrm{d}V\left\{\sum\limits_{\alpha =1}^{2}\rho_{\alpha}\left( a_{\alpha}\left|\delta_{\alpha}\right|^{2}+\frac{b}{2}\left|\delta_{\alpha}\right|^{4} + \beta_{\alpha}\left|\nabla \delta_{\alpha}\right|^{2}\right)\right.\\ &&\left. - \sqrt{\rho_{1}\rho_{2}} c\left( \delta_{1}\delta^{\ast}_{2}+\delta^{\ast}_{1}\delta_{2}\right){\vphantom{\sum\limits_{\alpha =1}^{2}}}\right\} \,. \end{array} $$
(1)

Here, α=1,2 is the band index, ρ α are the densities of electron states at the Fermi level per one spin direction, δ α are the non-equilibrium superconductivity gaps, and coefficients are given by

$$\begin{array}{@{}rcl@{}} a_{\alpha}&=&-w_{\alpha\alpha}/{\det}\hat w-g,\qquad b=7\zeta(3)/[8\pi^{2}\left( k_{\mathrm{B}}T_{c}\right)^{2}] \,, \\ c&=&-w_{12}/{\det}\hat w,~~\quad\qquad \beta_{\alpha}=b\hbar^{2}v_{\text{F}\alpha}^{2}/6 \, , \end{array} $$
(2)

where \(g=\ln \left [1.13\hbar \omega _{c}/(k_{\mathrm {B}}T)\right ]\) and w α α = W α α ρ α and \(w_{12}=w_{21}=W_{12}\sqrt {\rho _{1}\rho _{2}}\) are the dimensionless interaction constants forming a 2×2 matrix \(\hat {w}\). We assume clean limit where bands are characterized by the Fermi velocities v Fα .

Due to the surface, equilibrium superconductivity gaps vary with the distance x from the boundary. By using an ansatz \(\delta _{\alpha }(x)=\left |{\Delta }^{\infty }_{\alpha }\right |f_{\alpha }(x)\mathrm {e}^{i\phi _{\alpha }}\), where \(\left |{\Delta }^{\infty }_{\alpha }\right |\) are the modula of gaps in the bulk homogeneous state, and taking constant phases ϕ α , the minimization of the free energy functional (1) leads to the following differential equations

$$\begin{array}{@{}rcl@{}} \beta_{1}f_{1}^{\prime\prime}&=&a_{1}f_{1}+b\left|{\Delta}^{\infty}_{1}\right|^{2}{f^{3}_{1}}+{\Xi}_{12}f_{2}\,,\\ \beta_{2}f_{2}^{\prime\prime}&=&a_{2}f_{2}+b\left|{\Delta}^{\infty}_{2}\right|^{2}{f^{3}_{2}}+{\Xi}_{21}f_{1} \,, \end{array} $$
(3)

where

$$\begin{array}{@{}rcl@{}} {\Xi}_{12,21}=-|c|\sqrt{\rho_{1,2}/\rho_{2,1}}\left|{\Delta}^{\infty}_{2,1}\right|/\left|{\Delta}^{\infty}_{1,2}\right|\,. \end{array} $$
(4)

Here, we have taken into account the bulk relation between the sign of interaction constant w 12 and the difference of phases ϕ 1−ϕ 2. If interband interaction channel is absent, i.e., Ξ12=Ξ21=0, the system (3) splits into two equations for independent bands.

The system of non-linear differential (3) must be solved numerically. For the sake of simplicity, we will use the first-type homogeneous boundary conditions at the surface, f α (0)=0. The situation can be achieved by means of a ferromagnetic film coating the surface of a superconductor [19]. Far from the boundary f α =1 and \(f_{\alpha }^{\prime }=0\).

3 Length-Scales Near the Surface and Near the Bulk Superconducting State

Characteristic length-scales for superconductivity manifest themselves in the asymptotic behavior of gap functions. Close to the boundary, we linearize (3) as follows:

$$\begin{array}{@{}rcl@{}} {\gamma_{1}^{2}}f^{\prime\prime}_{1}=f_{1}+\frac{{\Xi}_{12}}{a_{1}}f_{2} \, ,\quad\qquad {\gamma_{2}^{2}}f^{\prime\prime}_{2}=f_{2}+\frac{{\Xi}_{21}}{a_{2}}f_{1} \, , \end{array} $$
(5)

where \(\gamma ^{2}_{\alpha }=\beta _{\alpha }/a_{\alpha }\). Near the bulk superconducting state, we consider small deviations 𝜖 α =1−f α which satisfy

$$\begin{array}{@{}rcl@{}} {\xi^{2}_{1}}\epsilon^{\prime\prime}_{1}=\epsilon_{1}+\frac{{\Xi}_{12}}{A_{1}}\epsilon_{2} \, ,{\qquad\quad\xi^{2}_{2}}\epsilon^{\prime\prime}_{2}=\epsilon_{2}+\frac{{\Xi}_{21}}{A_{2}}\epsilon_{1} \, , \end{array} $$
(6)

where \(\xi ^{2}_{\alpha }=\beta _{\alpha }/A_{\alpha }\) and \(A_{\alpha }=a_{\alpha }+3b\left |{\Delta }^{\infty }_{\alpha }\right |^{2}\).

The temperature dependencies of the reciprocal values of the coefficients \(\xi _{1,2}^{2}\) and \(\gamma _{1,2}^{2}\) are shown in Fig. 1. One can see that in the superconducting state (T<T c ) the quantities \(\xi _{\alpha }^{2}\) are always finite and positive, while \(\gamma _{\alpha }^{2}\) change their signs at the certain temperatures passing through infinity. This difference is one of the reasons for the modification in the characteristic length-scales near the surface compared to the region far from it.

Fig. 1
figure 1

The quantities \(\xi _{1,2}^{-2}\) and \(\gamma _{1,2}^{-2}\) vs temperature for |w 12|=0.007. The other parameters are as follows: \(w_{11}=-0.25, w_{22}=-0.24, \hbar \omega _{c}=0.05 \, eV, v_{\mathrm {F}1}=5\times 10^{5} \, m/s\), and v F2=5.1×105 m/s. It is supposed that ρ 1/ρ 2=(v F2/v F1)3

Full size image

If interband interaction is switched off, w 12=0, the quantities ξ 1 and ξ 2 transform into coherence lengths for corresponding independent bands with autonomous superconducting phase transitions at the critical points T c1 and T c2,

$$\begin{array}{@{}rcl@{}} k_{\mathrm{B}}T_{c\alpha}=1.13\hbar\omega_{c}\exp\left( 1/w_{\alpha\alpha}\right). \end{array} $$
(7)

At the same time, the quantities γ 1 and γ 2 coincide with ξ 1 and ξ 2 in the regions T≥T c1 and T≥T c2, respectively.

The general solution of the system (5) has the following form:

$$\begin{array}{@{}rcl@{}} f_{\alpha}(x)&=&K_{\alpha-}\left[\exp\left( x/\gamma_{-}\right)-\exp\left( -x/\gamma_{-}\right)\right] \\ &&+K_{\alpha+}\left[\exp\left( x/\gamma_{+}\right)-\exp\left( -x/\gamma_{+}\right)\right], \end{array} $$
(8)

where K α± are constants and

$$\begin{array}{@{}rcl@{}} 2\gamma_{\pm}^{-2}\,=\,\gamma_{1}^{-2}\,+\,\gamma_{2}^{-2}\!\pm\!\sqrt{\left( \gamma_{1}^{-2}-\gamma_{2}^{-2}\right)^{2}\,+\,4c^{2}/ (a_{1}a_{2}{\gamma_{1}^{2}}{\gamma_{2}^{2}})}.\\ \end{array} $$
(9)

The solutions (8) satisfy the boundary conditions chosen.

One easily finds (see also Fig. 2) that

$$\begin{array}{@{}rcl@{}} &&\gamma^{-2}_{-}\leq 0 \,\,\,\, \text{if} \,\,\,\,\,\, T\leq T_{c}^{-}=T_{c},\\ &&\gamma_{+}^{-2}> 0 \,\,\,\, \text{if} \,\,\,\,\,\, T > T_{c}^{+}, \\ &&\gamma_{+}^{-2}\leq 0 \,\,\,\, \text{if} \,\,\,\,\,\, T \leq T_{c}^{+}. \end{array} $$
(10)

Here,

$$\begin{array}{@{}rcl@{}} k_{\mathrm{B}}T_{c}^{\pm}=1.13\hbar\omega_{c}\exp\left( 2/\chi^{\pm}\right) \end{array} $$
(11)

with \(\chi ^{\pm }=\text {tr}\hat w\pm \sqrt {(\text {tr}\hat w)^{2}-4{\det }\hat w}\). The inequality \(T_{c}^{+}<T_{c}^{-}\) is always valid. For vanishing interband interaction \(T_{c}^{-}\rightarrow T_{c1}\) and \(T_{c}^{+}\rightarrow T_{c2}\), if T c1>T c2. The dependencies of \(T^{\pm }_{c}\) on the constant of interband interaction are depicted in Fig. 3. If interband interaction is sufficiently strong, \(w^{2}_{12}\geq w_{11}w_{22}\), the temperature \(T_{c}^{+}\) disappears.

Fig. 2
figure 2

The quantities \(\gamma _{\pm }^{-2}\) vs temperature for |w 12|=0.001. Rest parameters are given in the caption of Fig. 1

Full size image
Fig. 3
figure 3

The dependencies of \(T^{\pm }_{c}\) on the interband interaction constant. Rest parameters are given in the caption of Fig. 1

Full size image

By taking into account (10), the asymptotes near the surface take the following form

$$\begin{array}{@{}rcl@{}} && T_{c}^{+}<T<T_{c}^{-} : \\ &&f_{\alpha}(x)=C_{\alpha-}^{0}\sin\left( x/\left|\gamma_{-}\right|\right)+C_{\alpha+}^{0} \sinh\left( x/\left|\gamma_{+}\right|\right) \, , \end{array} $$
(12)
$$\begin{array}{@{}rcl@{}} &&T<T_{c}^{+} : \\ &&f_{\alpha}(x)=C_{\alpha-}^{0}\sin\left( x/\left|\gamma_{-}\right|\right)+C_{\alpha+}^{0} \sin\left( x/\left|\gamma_{+}\right|\right) \, . \end{array} $$
(13)

Approaching the bulk state, the solution of the system (6) yields

$$\begin{array}{@{}rcl@{}} f_{\alpha}(x)=1-C_{\alpha-}^{\infty}\exp\left( -x/\xi_{-}\right)-C_{\alpha+}^{\infty}\exp\left( -x/\xi_{+}\right), \end{array} $$
(14)

where

$$\begin{array}{@{}rcl@{}} 2\xi_{\pm}^{-2}\,=\,\xi_{1}^{-2}\,+\,\xi_{2}^{-2}\!\pm\! \sqrt{\left( \xi_{1}^{-2}-\xi_{2}^{-2}\right)^{2}\,+\,4c^{2}/(A_{1}A_{2}{\xi_{1}^{2}}{\xi_{2}^{2}})}\\ \end{array} $$
(15)

are the coherence lengths of a two-gap superconductor [11, 15].

The coefficients \(C_{\alpha \pm }^{0}\) and \(C_{\alpha \pm }^{\infty }\) in the expressions of the asymptotes (12–-14) can be determined by using the fitting to the exact solutions found numerically.

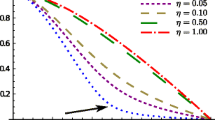
It is seen from (12) and (13) that one must consider the modula |γ ±| as characteristic length-scales near the surface. At the same time, according to (14), the coherence lengths ξ ± play the role of length-scales as one is approaching the bulk superconducting state. The functions |γ ±(T)| and ξ ±(T) exhibit different temperature dependencies, see Figs. 4 and 5. Both |γ −| and ξ − diverge at T c , but at \(T^{+}_{c}\) only the length |γ +| is singular, while ξ + remains finite everywhere. In Figs. 4 and 5, one can observe how the curves |γ ±(T)| and ξ ±(T) change with the variation of the strength of interband interaction in comparison with the functions |γ 1,2(T)| and ξ 1,2(T) taken for the condensates in non-interacting bands.

Fig. 4
figure 4

The temperature dependencies of length-scales near the surface (upper panel) and far from the surface (lower panel) for |w 12|=0.001. Upper panel: |γ −(T)|—thick solid line, |γ +(T)|—thin solid line; dotted and dashed lines represent the dependencies |γ 1(T)| and |γ 2(T)|, correspondingly, in the case w 12=0. Lower panel: ξ −(T)—thick solid line, ξ +(T)—thin solid line; dotted and dashed lines represent the dependencies ξ 1(T) and ξ 2(T) correspondingly for w 12=0

Full size image
Fig. 5
figure 5

The temperature dependencies of length-scales near the surface (upper panel) and far from the surface (lower panel) for |w 12|=0.007. The functions depicted are the same as in Fig. 4

Full size image

We notice that coherence length is a characteristic of bulk state so that |γ ±| cannot be treated as coherence lengths. Therefore, the singularity of |γ +| at \(T_{c}^{+}\) is not related to any phase transition unless w 12=0.

In Fig. 6, an example of the asymptotes calculated by means of (12) (upper panel) and by means of (14) (lower panel) have been presented compared to exact dependencies f 1,2(x). The coefficients \(C_{\alpha \pm }^{0}\) and \(C_{\alpha \pm }^{\infty }\) were found by fitting to the numerical solutions of non-linear equations providing matching with exact curves in remarkably wide domains.

Fig. 6
figure 6

The dependencies of f 1,2 on x. Dashed-dotted linesin the upper panel: asymptotic behavior of f 1,2(x) near the surface. Dotted lines in the lower panel: asymptotic behavior of f 1,2(x) near the bulk superconducting state. Solid lines represent the exact dependencies f 1,2(x) calculated numerically. Parameters: \(w_{11}=-0.25, w_{22}=-0.26, |w_{12}|=0.003, \hbar \omega _{c}=0.05 \, eV, v_{F1}=5\times 10^{5} \, m/s, v_{F2}=5.2\times 10^{5} \, m/s, T=0.9T_{c}>T_{c}^{+}\)

Full size image

4 Conclusion

We have found that the recovery of two-gap superconductivity suppressed by the surface of a sample is described by the linear combination of two spatial modes characterized by length-scales which diverge at different temperatures \(T_{c}^{\pm }\). Approaching the bulk superconducting state, the singularity at \(T_{c}^{+}\) disappears and the length-scales become equal to the coherence lengths in a macroscopic two-band superconductor.