Up to now, polycrystalline high-T c superconductors have not yet been widely used as kinds of largescale applications because of their low critical current densities which are limited by the grain boundaries (GBs) [1]. There have been a large number of attempts which were made at interpreting this phenomenon and revealing its mechanisms. For example, a conventional model [2, 3] treated symmetric low-angle GBs as serials of edge dislocations and assumed that the strain fields around the dislocations and compositional variations near GBs give rise to structural and chemical inhomogeneities along GBs. Mannhart et al. [4, 5] pointed out a classic exponential dependence of the critical current density on the misorientation angle which was explained after by Chaudhari et al. [6] who introduced some effects. The first effect they introduced was the relative orientation of the d-wave order parameters pinned to the crystal lattices on either side of the boundary which induce the angle variation. However, this model cannot explain the exponential suppression of J c over the full range of misorientation angles. The second one assumed that the density of dislocation cores grows with increasing angles and can suppress the total through current. Gurevich and Pashitskii [7] developed a model which assumed that the insulating dislocation cores nucleate antiferromagnetic regions and destroy superconducting order. Besides these two effects, critical current density is also regarded to be affected by the variation of the stoichiometry in grain boundary regions, such as in the oxygen concentration. Graser et al. [8] simulated the microscopic evaluation of fully 3D YBa2CuO7−δ GBs by the molecular dynamics (MD) method and obtained the critical current densities following an exponential suppression with the grain boundary angle. They concluded that the buildup of charge inhomogeneities is the dominant mechanism for the suppression of the supercurrent.

Dislocations, which play an effective pinning role in superconductors, have been studied on their pinning forces for a long time. Campbell et al. [9] studied the flux vortices and transport currents in type II superconductors and gave an interaction potential between a flux vortex and an edge dislocation. A model of flux pinning by grain boundaries in type II superconductors was suggested by Pande et al. [10] in which the GB was modeled as a distribution of edge dislocations. The interaction between a flux line and a point defect was investigated by Yu et al. [11]. A molecular dynamics (MD) simulation of vortex transport properties in a type II superconductor with a grain boundary was studied by Jiang et al. [12]. Besides, there are many other works which made great contributions to the study of the effects of grain boundaries on critical current density of superconductors [13–19]. In this work, a distribution of flux vortices in a GB is assumed based on the interaction between the flux vortices and the edge dislocations which constitute a GB. The critical current density along the GB of the superconductor is then obtained through a gradient calculating of the flux vortices. For a lowangle grain boundary, our results satisfy the classic exponential relationship with the misorientation angles. However, the model is not suitable for high-angle grain boundaries.

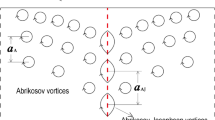
In a symmetric low-angle tilt grain boundary, edge dislocations are arranged in a periodic array as shown in Fig. 1. The dislocation spacing D along the grain boundary can be expressed by the misorientation angle 𝜃

$$ D=\frac{b}{2\sin (\theta /2)}\approx \frac{b}{\theta} , $$
(1)

in which b is the Burgers vector of the dislocation.

Fig. 1
figure 1

Schematic diagram of a low-angle grain boundary

Full size image

Let us consider a bicrystalline high-T c superconducting film like YBCO which is subjected to a transport current or placed in a perpendicular magnetic field paralleled to its c-axis. It is known that if the transport current is small, it flows within about λ of the surface (λ ≪ W, width of the film) and decays exponentially beyond this length. However, the critical currents will flow in the form of the penetrated vortices into the film to a depth which is determined by the strength of the pinning. The current density can be expressed as the gradient of B, that is

$$ \text{\textbf{j}}=\frac{1}{\mu_{0}} \nabla \times \text{\textbf{B}}=\frac{\phi_{0}} {\mu_{0}} \nabla \times n\text{\textbf{k}}, $$
(2)

where n is the density of flux lines per unit area and per unit length of the flux line, ϕ 0 is a magnetic flux quantum, μ 0 is the permeability of vacuum, and k is the unit vector of magnetic direction. For the case that supercurrents flow through the grain boundary perpendicularly, with the fluxoids distributed as shown in Fig. 2, (2) can be simplified as

$$ j(y)=\frac{\phi_{0}} {\mu_{0}} \frac{dn(y)}{dy}, $$
(3)

where the density of flux lines n(y) is the function of y along the grain boundary. The high critical current density J E of hightemperature superconductors is due to a larger number of flux pinning centers such as defects, dislocations and artificial particles. Among several criticalstate models, the Bean model assumes that J c is a constant value in a superconductor. Denote J c0 as the critical current density in the grain which is formed from the competition between the flux lines’ interaction, Lorenz force and flux pinning effect. While in the grain boundary, the critical current density is not J c0 anymore since the flux lines’ density can be affected by the boundary or by the distributed dislocation within it. In view of this effect, the interaction between a flux line and a dislocation should be introduced.

Fig. 2
figure 2

The physical model of the coexistence of dislocations and the flux vortices

Full size image

The interaction potential between an edge dislocation and a flux line per unit length is [9]

$$ E(r,\alpha )=\frac{A\xi^{2}b}{r}\sin \alpha , $$
(4)

where ξ is the ab-plane coherence length of the superconductor, r is the distance between the dislocation and the flux line, α is the relative angle between the two, and A=−δ ε v G(1 + ν)/3(1−ν)=−γ G, in which G is the shear modulus of the superconducting material; ν is Poisson’s ratio; \(\gamma =\frac {\beta (1+\nu )}{3(1-\nu )}\) in which β is the ratio of the difference of normal and superconducting volume to superconducting volume [20]; and ε v is the dilation of the flux core with respect to the normal state.

If a flux vortex is located in the grain boundary, for example, between two neighboring dislocations as shown in Fig. 2, the interaction potential per unit length between the flux vortex and the grain boundary can be expressed as

$$ E(y)\approx A\xi^{2}b\left( {\frac{1}{D-y}-\frac{1}{y}} \right), $$
(5)

in which the effects by the dislocations far apart from the flux vortex are negligible. It is assumed that the distribution of flux vortices along the grain boundary is determined by E(y); the following density equation is obtained

$$ n(y)=n_{0} (y)\exp \left( -\frac{E(y)l}{k_{\mathrm{B}} T}\right), $$
(6)

where n 0(y) is the density of flux vortices without a grain boundary, l is the length of the flux line, k B is Boltzmann’s constant, and T is the temperature. Since the interflux energy and the Lorentz force have been considered in the determination of n 0(y), the only potential from the dislocations is included in E(y). However, the density of fluxoids cannot be infinity when the flux vortex is close to the attractive dislocation. Thus, the following density equation is assumed

$$ n(y)=n_{0} (y)\exp \left( -\frac{A\xi^{2}b}{k_{\mathrm{B}} T}\frac{l}{D-y}\right). $$
(7)

The shielding supercurrent density within the grain boundary can be obtained by substituting (7) into (3)

$$\begin{array}{@{}rcl@{}} j(y)&=&j_{\text{c0}} \exp \left( -\frac{A\xi^{2}b}{k_{\mathrm{B}} T}\frac{l}{D-y}\right)+\frac{n_{0} (y)\varphi_{0}} {\mu_{0}}\\ &&\times \left[ {\exp \left( -\frac{A\xi^{2}b}{k_{\mathrm{B}} T}\frac{l}{D-y}\right)} \right]^{\prime}, \end{array} $$
(8)

where \(j_{\mathrm {c}0} =\frac {\varphi _{0}} {\mu _{0}} \frac {dn_{0} (y)}{dy}\) is the critical current density without a grain boundary; the second term of (8) is \(\frac {n_{0} (y)\varphi _{0} A\xi ^{2}bl}{\mu _{0} k_{\mathrm {B}} T(D-y)^{2}}\exp (-\frac {A\xi ^{2}b}{k_{\mathrm {B}} T}\frac {l}{D-y})\) which is small relative to the first one; thus, (8) can be further simplified as

$$ j(y)=j_{\mathrm{c}0} \exp \left( -\frac{A\xi^{2}b}{k_{\mathrm{B}} T}\frac{l}{D-y}\right). $$
(9)

The critical current density in the grain boundary can be obtained as

$$ J_{\text{c,GB}} =<j(y)>, $$
(10)

in which < ... > means the average value over the GB, and the dislocation spacing D is enough for this averaging. Therefore, the critical current density can be rewritten as

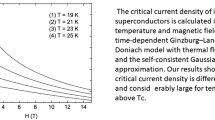
$$ J_{\text{c,GB}} =\frac{J_{\text{c0}} \theta} {b}{\int}_{\xi}^{b/\theta -\xi} {\exp \left( -\frac{A\xi^{2}b}{k_{\mathrm{B}} T}\frac{l}{b/\theta -y}\right)dy} , $$
(11)

Figure 3 shows the relation between the critical current density and the misorientation angle. The material parameters of a high-T c superconductor such as YBCO [21, 22] are γ=10−4, E=148 GPa, ν=0.255, ξ=1.5×10−9 m, b=3.82×10−10 m, l≈2ξ c=4×10−10 m, and T=77 K. While for Bi-2212, the parameters are E=81 GPa, ν=0.44, b=5.4×10−10 m, and 2ξ c=2×10−10 m. It is known that the elastic model (4) is invalid in the dislocation core; the integration can only be carried out from ξ to D−ξ. Therefore, the dislocation spacing D should be large enough to guarantee the validity of the model. Here, D ≥ 4ξ is assumed to be the value range of D and, thus, the range of the misorientation angles can be estimated as 𝜃≤4∘. For a high-angle grain boundary with 𝜃 > 4∘, our dislocation model is not suitable anymore. It can be found from Fig. 3 that the results of our model have a good agreement with the classic exponential model in the low-angle range.

Fig. 3
figure 3

Suppression of the critical current density with the increasing misorientation angles

Full size image

In this paper, a relatively simple model is developed to study the effect of the grain boundary on the critical current density of high-T c superconductors. For simplicity, a Boltzmann distribution of flux lines is obtained within a GB under the action of elastic potential from dislocations. The results show a consistence with the classic exponential suppressing equation. The model can be helpful for understanding the mechanisms of the effect of grain boundaries on the critical current density. However, our model is only valid for low-angle grain boundaries. The suppression of critical current density for high-angle grain boundaries cannot be interpreted from this perspective.