1 Introduction

Bi2223/Ag superconducting multifilamentary composite tapes, as one of important practical high-temperature superconducting structures, have many large-scale potential applications such as electric devices for power industry [1], high-field magnets [2], and superconducting magnetic energy storages (SMES) [3]. During the fabrication/winding process and current-carrying operation, they are unavoidably subjected to mechanical loads and electromagnetic forces. On these loads, for thin film-like composite tapes (the cross section is shown in Fig. 1) which are usually made to be winding coils or magnets, the bending deformation is principal. Such bending for Bi2223/Ag composite tapes not only results in some serious mechanical problems but also affects the current-carrying capacity, in most cases degrades the critical current [4]. Therefore, it is very significant to deeply understand the effect of bending deformation on the critical current for the design and safety operation of superconducting magnets related to Bi2223/Ag composite tapes.

Fig. 1
figure 1

The typical optical micrograph of the cross section of a Bi2223/Ag superconducting multifilamentary composite tape. This picture cited from ref. [22], in which the sample’s width is 3.7 mm, thickness 0.27 mm, the number of the filament (black spots in central area) 55, the matrix material (gray part in central area) is silver, and its filling factor is about 26 %

Full size image

For decades, many researches made the efforts on the bending [4–8] or uniaxial [8, 9] strain dependence of the critical current of Bi2223/Ag composite tapes, but few of them [9–13] tried to explore the mechanism of how the deformation is affecting the critical current, particularly from the theoretical aspect. For this point, Ochiai et al. [11, 12, 14] made some studies focusing on the effect of the bending strain on the critical current, in which the modeling of the relation of the critical current versus the bending strain was the most significant one [14]. On these bases, Gou et al. [13] developed the modified model, in which the damage stress of Bi2223 superconducting filaments was introduced as the failure criterion, and the influence of the elastic modulus of each component (Bi2223 superconducting filaments, Ag matrix, and Ag alloy sheath) in the Bi2223/Ag composite tape was taken into account. However, for this type of superconducting composite structures including metal and metal alloy components, due to the significant difference in the coefficients of thermal expansion among the different components in the process of cooling down during the heat treatment, the residual stress can be accumulated even up to the relatively high stress level [15]. For example, the Ag matrix with lower yield stress (˜12.2 MPa [10]) usually has been partly or completely yielded when the temperature decreases to room temperature [11]. Under the initial residual stress, once the superconducting composite structure is bent, the neutral axis can shift off the center of the cross section due to the Bauschinger effect of metal components (Ag matrix and/or Ag alloy sheath). Indeed, previous investigations found that not only for Bi2223/Ag composite tapes [4, 10] but also for YBCO-coated conductors [16] and Nb 3Sn wires [17] (their common feature is that the composite structure includes metal or metal alloy components), when they are under the bending deformation, the neutral axis moves away from the center of the cross section. Thus, a significant problem naturally arising is how the movement of the neutral axis makes the stress-strain in these superconducting composite structures redistribute, and further affects the current-carrying capacity - the critical current.

In this article, for the bending of Bi2223/Ag composite tape, the aim is to investigate the movement of the neutral axis and further the influence of the movement on the relation of the critical current versus the bending strain. For this point, based on our previous model [13], firstly, the movement of the neutral axis of the Bi2223/Ag composite tape was studied, and its moved position on the cross section was further determined. Then, the relation of the critical current versus the bending strain (described by the curvature 1/ R) and the distributions of the stress and strain on the cross section along the thickness direction were obtained. Furthermore, in the different cases of the Bauschinger effect factor (BEF) of metal components (Ag matrix and Ag alloy sheath), the elastic modulus and volume fraction of the superconducting filaments in the Bi2223/Ag composite tape, the movement of the neutral axis, and correspondingly the relation of the critical current versus the bending strain were comprehensively investigated.

2 The Damage Stress-Based Model on Taking Account of the Bauschinger Effect of Ag and Ag Alloy in the Bending of Bi2223/Ag Composite Tape

2.1 The Planar Outline of the Superconducting Core

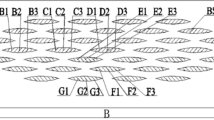
A typical optical micrograph of the cross section of a Bi2223/Ag superconducting composite tape is shown in Fig. 1. Apparently, the Bi2223 composite tape consists of two components: the superconducting core and Ag alloy sheath, and the superconducting core is composed of the superconducting filaments and Ag matrix. According to this micrograph, the schematic diagram of the cross section of Bi2223 composite tapes is presented as shown in Fig. 2, in which the outline of the superconducting core is simplified as an ellipse. For the consideration of the Bi2223 composite tape, the volume fraction and elastic modulus of these components are listed in Table 1. According to the fraction volume of each component, and the sizes of the sample (width 3.7 mm, thickness 0.27 mm), the shape of the ellipse can be uniquely determined. As a result, based on the above data, in the coordinate system shown in Fig. 2, the shape of the superconducting core on the cross section can be described by

$$ \frac{x^{2}}{1.76^{2}} + \frac{y^{2}}{0.12^{2}} = 1\, . $$
(1)
Fig. 2
figure 2

The cross section of Bi2223/Ag composite tapes with an elliptical configuration of the superconducting core. According to Fig. 1, the rectangle cross section with an elliptical configuration of the superconducting core is assumed. The width of the core is noted as W core, and the thickness of the composite tape is noted as t

Full size image
Table 1 The volume fraction and elastic modulus of each component in the Bi2223 composite tape
Full size table

It is noted that, even the more complex functional form [12] can be used to describe the outline of the core; ellipse, mathematically as a convex function, is easy to be used to characterize the relation of the critical current with strain. Besides, the minor semiaxis of the ellipse is accurately calculated as 0.1168 mm. For unified description of decimals, the parameters a and b (corresponding to the elliptic (1)) are here written as 1.76 and 0.12 mm, respectively.

Discussed in ref. [13] is a relatively rational description of the ellipse approximation to the shape of the superconducting core. Besides, other two assumptions on the geometric model are here presented as,

  1. 1.

    Complete contact at the interface between superconducting filaments and Ag matrix and the superconducting core and Ag alloy sheath

  2. 2.

    No initial microstructure defects and therefore whole continuity for all the materials in the Bi2223 composite tape

2.2 The Position Determination of the Neutral Axis on the Cross Section

As discussed in ref. [13], in this article, we also consider the elastic modulus of each component (Bi2223 superconducting filaments, Ag matrix, and Ag alloy sheath) in the Bi2223 composite tape and then obtain the variation of the elastic modulus of the Bi2223 tape with y coordinates.

To investigate the influence of the movement of the neutral axis on the macro electromechanical behaviors of the Bi2223/Ag composite tape, the position determination of the neutral axis in different bending deformations should be the first key step. According to mechanics of materials [18], for the thin film-like composite tape (usually called as beam) with bending deformation, because there is no resultant force acting on the cross section, thus, the position of the neutral axis can be determined by the equation of static equilibrium as

$$ {\int}_{A} {\sigma dA} = 0 \, , $$
(2)

in which σ is the normal stress on the cross section and A denotes its area. Generally, for the structure with homogeneous materials, when it is bent, the position of the neutral axis keeps still at the center of the cross section. But, for a composite structure with different materials, particularly including metal or metal alloy, as discussed in Section 1, because of the existence of thermally residual stress, the compressive yield stress is different from the tensile one due to the Bauschinger effect. Therefore, the distribution of the normal stress on the cross section is not symmetric with the neutral axis any more. Thus, according to (2), it results in shifting of the neutral axis away from the center of the cross section.

As the longitudinal section of bending Bi2223 composite tape shown in Fig. 3, the position of the neutral axis can be described by the coordinate y n (the intersection point of the moved neutral axis and the z-axis). In this case, setting the neutral axis as a dividing line, the upper part (y >y n) is in tension and the lower one (y <y n) is in compression. The neutral axis moves to the tensile side if y n >0 and to the compressive side if y n <0. For the bending Bi2223 composite tape, on the assumption of small deformation (In other words, in this case, the relation of stress with strain keeps still linear.), the strain ε(y) of the arbitrary point y (its coordinate y) of the tape can be given by

$$ \varepsilon (y)=\frac{y-y_{\mathrm{n}}} {R+y_{\mathrm{n}}} \, . $$
(3)

According to (2), given that the distribution of the normal stress on the cross section has been known, the position of the neutral axis can be determined. As shown in Fig. 2, the cross section is divided into three parts along the thickness direction, i.e., Ag alloy sheath, core 2, and Ag alloy sheath. So, (2) can be further written as

$$\begin{array}{@{}rcl@{}} {\int}_{-t/2}^{-y_{\text{core1,max}}} \sigma_{\text{Ag}{\kern 1pt}{\kern 1pt}\text{alloy}} dy &+& {\int}_{-y_{\text{core1,max}}}^{y_{\text{core1,max}}} {\sigma_{\text{core2}}} dy\\ &+& {\int}_{y_{\text{core1,max}}}^{t/2} {\sigma_{\text{Ag}{\kern 1pt}{\kern 1pt}\text{alloy}} dy=0} , \end{array} $$
(4)

in which, σ Agalloy and σ core2 are the normal stresses in the Ag alloy sheath and core 2, respectively. The core 2 consists of Bi2223 superconducting filaments, Ag matrix, and Ag alloy, in which the stress can be obtained through the simple superposition principle, described by (5), (7), and (8) in ref. [13].

Fig. 3
figure 3

The longitudinal section of a bending Bi2223 composite tape with the bending radius R and the moved neutral axis. The dash curve indicates the moved neutral axis, and its movement can be described by the coordinate y n (i.e., the intersection point of the moved neutral axis and the z-axis)

Full size image

For Ag and Ag alloy, the Bauschinger effect will be particularly considered here. The BEF is defined as the ratio of the reverse yield stress to the tensile one. For simplicity, the BEFs of the Ag and Ag alloy are selected as same. In this condition, the stress-strain relation of Ag and Ag alloy can be approximately described by the following [10]:for Ag,

$$ \sigma_{\text{Ag}} =\sigma_{y,\text{Ag}} +K_{\text{Ag}} \left( {\varepsilon_{\text{Ag}} -\varepsilon_{y,\text{Ag}}} \right), $$
(5a)

and for Ag alloy,

$$\begin{array}{@{}rcl@{}} \sigma_{\text{Ag}\text{ alloy}} \,=\, \sigma_{y1,\text{Ag }\text{alloy}} \!\! &+& \!\! K_{1,\text{Ag }\text{alloy}}\left( {\varepsilon_{\text{Ag }\text{alloy}} \,-\, \varepsilon_{y1,\text{Ag}{\kern 1pt}{\kern 1pt}\text{alloy}}} \right)\\ &&\! \text{if}\left( {\varepsilon_{y1,\text{Ag}{\kern 1pt}{\kern 1pt}\text{alloy}} \!\!<\!\!\varepsilon_{\text{Ag} \text{ alloy}} \!\!<\! \varepsilon_{y2,\text{Ag} \text{ alloy}}} \right),\\ \sigma_{\text{Ag}{\kern 1pt}{\kern 1pt}\text{alloy}}\,=\, \sigma_{y2,\text{Ag }\text{alloy}} \!\! &+& \! \!K_{2,\text{Ag }\text{alloy}}\left( {\varepsilon_{\text{Ag }\text{alloy}} \,-\, \varepsilon_{y2,\text{Ag }\text{alloy}}}\right)\\ && \!\text{if}\left( {\varepsilon_{\text{Ag }\text{alloy}} >\varepsilon_{y2,\text{Ag }\text{alloy}}} \right) \end{array} $$
(5b)

in which σ Ag and ε Ag and σ Agalloy and ε Agalloy are the stress and strain of Ag and Ag alloy, respectively, σ y,i and ε y,i (i denotes Ag or Ag alloy) are the yield stress and strain of Ag and Ag alloy, respectively, and K i,Ag and K i,Agalloy (here i = 1, 2) are the coefficients of hardening of Ag and Ag alloy, respectively. These parameters are listed in Table 2. The stress-strain relation of Bi2223 is estimated to be linear until final fracture.

Table 2 Work hardening parameters of the Ag matrix and Ag alloy sheath
Full size table

Besides, in the calculation of the stress through (5a) and (5b), the residual strain ε R,i (i = Bi2223 filaments, Ag, and Ag alloy) accumulated in the process of the temperature cooling down should be included. It can be calculated by

$$ \varepsilon_{\mathrm{R},\mathrm{i}} =(\alpha_{c}^{\ast} -\alpha_{i} ){\Delta} T, $$
(6)

in which α i and \(\alpha _{c}^{\ast }\) represent the coefficient of thermal expansion of each component and the composite tape, respectively; ΔT is the change of the kelvin temperature. In the calculation, α Bi2223 = 15 × 10−6K−1 and α Ag = α Agalloy = 20 × 10−6K−1. Then, \(\alpha _{c}^{\ast } \) can be obtained by

$$ \sum\limits_{i}{V_{i} \sigma_{\mathrm{R},i} =0} , $$
(7)

in which V i and σ R,i are the volume fraction (it is given in Table 1) and the thermally residual stress of each component, respectively. Then, after the ε R,i is obtained by (6), finally, the stress of each component is written by the following:in elastic period,

$$ \sigma_{i} =E_{i} \left( {\varepsilon +\varepsilon_{\mathrm{R},i}} \right), $$
(8a)

and in plastic period,

$$ \sigma_{i} =\sigma_{yk,i} +K_{k,i} \left( {\varepsilon + \varepsilon_{\mathrm{R},i} -\varepsilon_{yk,i}} \right), (K = 1 and 2) $$
(8b)

in which ε is the strain of the whole tape which can be calculated by (3).

Finally, the position of the neutral axis (the coordinate y n ) can be determined by (4), in which, the stress in the core 2 can be given by

$$ \sigma_{\text{core2}} =\sum\limits_{i} {V_{i}{~}^{\prime}}\sigma_{i} , $$
(9)

in which σ i and \(V_{i}^{\prime } \) are the stress and the volume fraction of each component in the core 2, respectively. σ i can be calculated by (8a) and (8b), and \(V_{i}^{\prime }\) can be estimated by the area of each component in the core 2. In this paper, \(V_{\text {Bi2223}}^{\prime } :V_{\text {Ag}}^{\prime } :V_{\text {Ag}{\kern 1pt}\text {alloy}}^{\prime } =0.30:0.45:0.25\).

After substituting (9) with the stress-strain relation described by (8a) and (8b) into (4), we can obtain the coordinate y n, i.e., the position of the moved the neutral axis. It is noted that the determination of the coordinate y n is actually coupled with the bending deformation of the tape. As the discussion above, the determination of the coordinate y n needs to solve (4), and according to the stress-strain relation described by (8a) and (8b), the precondition of solving (4) is that the strain ε must be known. However, as shown in (3), the strain ε is related with the coordinate y n, which is obviously related to the bending radius R. Thus, the determination of the coordinate y n is coupled with the bending strain ε. Accordingly, the iterative method is used in the calculation for the determination of the coordinate y n.

According to above the approach, the coordinate y n, i.e., the position of the moved neutral axis with the bending radius R is calculated as shown in Fig. 4. Firstly, the negative value of the coordinate y n means that the movement of the neutral axis is always to the compressive side of the bending Bi2223 composite tape. Furthermore, the monotonically increasing of the curve indicates that, the less bending radius R is, which means the larger the bending deformation is, the bigger the movement of the neutral axis is (actually the less the coordinate y n is).

Fig. 4
figure 4

The movement of the neutral axis versus the bending radius R of the bending Bi2223 composite tape. The parameters used here are listed in Tables 1 and 2, and the Bauschinger effect factor (BEF) is adopted as 0.4

Full size image

2.3 The Variation of the Critical Current with the Curvature 1/R

In this section, we still use the modified model of describing the bending strain dependence of the critical current developed in our previous paper [13]. The main feature of the model lies in establishing the correlation between the critical current and the damage strength of the superconducting filaments in the Bi2223 composite tape. It is noted that we just focus the influence of tension damage of superconducting filaments on the critical current in this article, even though the compression one also has the influence on the capacity of current-carrying of the Bi2223 composite tape [8]. Based on the assumptions and the main equations, which are the same as those in ref. [13], except the replacement of (6) in ref. [13] with (3), particularly, according to the key formula, the criterion of having the current-carrying capacity as follows

$$ I_{\mathrm{c}} /I_{\text{c0}} = \left\{ {\begin{array}{ll} 1 & {\sigma (y_{\text{core1,max}} )<\sigma_{\mathrm{D}}}\\ 1-{\int}_{-W_{\text{core1}} /2}^{W_{\text{core1}} /2} {(y-y^{\prime})dx/S_{\text{core1}}} & {\sigma (y_{\text{core1,max}} )\ge \sigma_{\mathrm{D}}} \end{array}} \right., $$
(10)

the normalized critical current I c/I c0 can be calculated. In (10), the I c/ I c0 is defined as the ratio of the critical current (I c) on some bending strain to the one (I c0) on the zero bending strain. With the coordinate y ′ as the boundary between damaged and undamaged parts in the core 1 (see Fig. 2; it consists of the superconducting filaments and Ag matrix), the core 1 can be divided into two parts: y ′ ≤ y ≤ y core1,max(damaged) and −y core1.max ≤ y<y ′ (undamaged). And in (10), σ D is the damage stress of the superconducting filaments, which can be experimentally obtained. Thus, on the base of the modified model, given that the damage stress σ D of the superconducting filaments is known, the relation of the critical current versus the bending strain ε (specified by the curvature 1/ R) can be obtained.

3 Results and Discussion

The main purpose of the paper is to investigate the influence of the movement of the neutral axis on the relation of the critical current versus the strain in bending Bi2223/Ag composite tapes. For this point, on the parameters listed in Tables 1 and 2, and the Bauschinger effect factor (BEF) adopted as 0.4 [10], in two cases of with/without taking account of the movement of the neutral axis, the normalized critical current I c/ I c0 versus the curvature 1/R of the bending Bi2223 composite tape has been calculated and compared with the experimental data [12]. As shown in Fig. 5, apparently, the normalized critical current I c/ I c0 with the movement of the neutral axis is smaller than that without the movement of the neutral axis, and most importantly, the former is closer to the experimental data than the latter in the region of the I c sharply decreasing with the curvature 1/R. Further, with the curvature 1/R increasing, the difference between the two cases of with/without the movement of the neutral axis gradually increases. This comparison indicates that, (i) the modeling on the approach in this paper is enough to be accurate and (ii) the influence of the movement of the neutral axis on the relation of the critical current versus the bending strain has not to be neglected, and with the curvature 1/R increasing, the influence gets more and more significant. When the Bi2223 composite tape is bent, according to the calculated result shown in Fig. 4, the neutral axis moves always to the compressive side of the tape. It means that the distance of the edge of the core 2 at the tensile side (i.e., y core1,max) from the neutral axis increases, which results in the maximum tensile stress at the edge of the core 2 getting bigger than that in the situation in which the neutral axis keeps at the center of the cross section of the Bi2223 composite tape. Accordingly, from (10), the critical current with the movement of the neutral axis is smaller.

Fig. 5
figure 5

Comparison of the calculated results of the normalized critical current I c/ I c0 versus the curvature 1/R of the bending Bi2223 composite tape in two cases of with/without the movement of the neutral axis with the experimental data [12]. The parameters used here are listed in Tables 1, and 2, and the Bauschinger effect factor (BEF) is here adopted as 0.4

Full size image

The current-carrying capacity of the Bi2223 composite tape is closely related to the tensile strength of the superconducting filaments [19]. To explore the mechanism of the dependence of the critical current on the bending deformation, and further accurately assess the current-carrying capacity through the dependence, the first important thing is to be aware of the distributions of the stress and strain on the cross section of the bending Bi2223 composite tape. As shown in Fig. 6, the distributions of the stress and strain on the cross section of the Bi2223 composite tape along the thickness direction (i.e., y direction) in the two cases of the bending radius R have been obtained. It is found that, (i) the strain varies monotonically and continuously, but the stress changes as a broken line; (ii) the position that the stress equals to zero is not at the position y= 0, but at the position y<0, which clearly means the neutral axis is at the compressive side; (iii) the smaller the bending radius R is, the bigger the distance of the position of the zero stress away from the position y= 0 is; (iv) the vertical line of the variation of the stress with the coordinate y, particularly for the core 2, means stress reaches the strength of the superconducting filaments due to its limited tensile strength (i.e., the damage tensile stress σ D, for the Bi2223 superconductor—a typical brittle material, generally less than compressive one); and (v) according to the bending deformation and corresponding stress state (shown in the left of Fig. 6), the superconducting filament (colored thick lines) with a black spot (schematically shown in the right of Fig. 6) indicates that it has been broken due to its stresses reach to the tensile strength of Bi2223 superconducting filaments. The similar results have been obtained by Hojo et al. [10], but the results in this paper are still significant. Because our results are based on different geometric model (shown in Fig. 2) and modeling approach, thus, we think that the mechanical failure of the superconducting filaments always occurs from the edge of the core 2 at the tensile side of the composite tape, and consequently, they lose the current-carrying capacity. It is noted that, the analysis of mechanical failure is here based on the macro homogenization theory for heterogeneous materials and the assumption that the mechanical failure related to the current-carrying is mainly controlled by the tensile strength of the superconducting filaments, i.e., the damage tensile stress σ D. Further, more accurate and in-depth study needs to consider the local deformation of the superconducting filaments [9] or even of the polycrystalline structure of BSCCO [20].

Fig. 6
figure 6

The distributions of the stress and strain on the cross section of the Bi2223 composite tape along the thickness direction (i.e., y direction) under the bending deformation for the cases of a R= 13.8 mm and b R= 22.3 mm. The corresponding Bi2223 superconducting filaments damaged in these two cases are illustrated respectively. The superconducting filaments with a black spot indicate they have been already broken due to the tensile failure

Full size image

As in the above discussion, for the bending of Bi2223/Ag composite tape, on the existence of the thermally residual stress (in most cases, Ag matrix has already been partly or completely yielded), the Bauschinger effect of metal components causes the movement of the neutral axis. Generally, for the different samples of Bi2223/Ag composite tapes, the components of metal and/or metal alloy are different, and correspondingly, the BEF should be different. For this point, in the two cases of the BEF, we obtained the movement of the neutral axis, the normalized critical current I c/ I c0 versus the curvature 1/R, and the distributions of the stress on the cross section as shown in Fig. 7a–c, respectively. Even the difference of the BEFs are relatively small; a notable difference of the movement of the neutral axis is displayed, while no very clear differences of the normalized critical current I c/ I c0 versus the curvature 1/R and of the distribution of the stress on the cross section along the thickness direction (just in the core 2) are found. Obviously, from Fig. 7a, the larger the BEF is, the bigger the movement of the neutral axis is. The main reason is that, the larger the BEF is, the bigger the compressive stress limit of Ag and Ag alloy is (according to the definition of the BEF, in Sect. 2.2) and correspondingly the bigger the movement of the neutral axis is. The result in Fig. 7b is consistent with that in Fig. 5. From Fig. 7c, just the clear difference in the Ag alloy sheath at the compressive side is found. The larger the BEF is, the smaller the stress is.

Fig. 7
figure 7

The two cases of the Bauschinger effect factors (BEFs) of Ag and Ag alloy in the Bi2223 composite tape: a the movement of the neutral axis versus the bending radius R, b the normalized critical current I c/ I c0 versus the curvature 1/R, and c the distributions of the stress on the cross section along the thickness direction (i.e., y direction) under the bending deformation

Full size image

Besides the BEF, the elastic modulus of superconducting filaments also has a strong influence on the movement of the neutral axis. As previously reported in ref. [21], the Bi2223 superconducting filaments from different fabrication have elastic moduli that are quite different. If the BEF is fixed as 0.4, in two cases of the elastic modulus of superconducting filaments, we modeled the movement of the neutral axis, the normalized critical current I c/ I c0 versus the curvature 1/R, and the distributions of the stress on the cross section as shown in Fig. 8a–c, respectively. Apparently, similar results with those in Fig. 7 are found. However, a notable difference lies in the results of the distributions of the stress on the cross section (see Figs. 7c and 8c). That is, for the different BEFs, the notable difference lies in the Ag alloy sheath at the compressive side (see Fig. 7c), but for the different elastic moduli, the notable one lies in the core 2 (see Fig. 8c). The larger elastic modulus of superconducting filaments leads to the bigger stress in the core 2. Besides, the result of the normalized critical current I c/ I c0 versus the curvature 1/R is consistent with that in ref. [13].

Fig. 8
figure 8

The influences of the elastic modulus of superconducting filaments in the Bi2223 composite tape on a the movement of the neutral axis versus the bending radius R, b the normalized critical current I c/ I c0 versus the curvature 1/R, and c the distributions of the stress on the cross section along the thickness direction (i.e., y direction) under the bending deformation. In calculation, the BEF is fixed as 0.4

Full size image

In addition, we further studied the influences of the volume fraction of superconducting filaments in the Bi2223 composite tape on the movement of the neutral axis, the normalized critical current I c/ I c0 versus the curvature 1/R, and the distributions of the stress in the cross section. As shown in Fig. 9, the results are similar with those in Figs. 7 and 8. The larger the volume fraction of superconducting filaments is, the bigger the movement of the neutral axis is (see Fig. 9a), the smaller the normalized critical current I c/ I c0 is (see Fig. 9b), and the slightly bigger the stress in the core 2 is (see Fig. 9c). Since the elastic modulus of superconducting filaments is normally larger than that of the Ag, the results of the movement of the neutral axis and the distributions of the stress on the cross section are similar with those in Fig. 8. And, the larger the volume fraction is, on the damage stress-based model in this paper, the smaller the normalized critical current I c/ I c0.

Fig. 9
figure 9

The influences of the volume fraction of superconducting filaments in the Bi2223 composite tape on a the movement of the neutral axis versus the bending radius R, b the normalized critical current I c/ I c0 versus the curvature 1/R, and c the distributions of the stress on the cross section along the thickness direction (i.e., y direction) under the bending deformation. In calculation, the BEF is fixed as 0.4

Full size image

In addition, from Figs. 7a, 8a, and 9a, we can also find that, with the bending radius R increasing, the movement of the neutral axis approaches to zero, and when it increases beyond about 45 mm, in the different cases (i.e., the different BEFs in Fig. 7a, the elastic moduli in Fig. 8a, and the volume fractions in Fig. 9a), the movements of the neutral axis reach to a convergence. In other words, for the Bi2223 composite tape, the movement of the neutral axis with the bending radius R has a critical value. When the bending radius R increases to be larger than the critical one, for the different BEFs, the elastic moduli, and the volume fractions of the superconducting filaments, no notable difference of the movement of the neutral axis has been found. In fact, when the bending radius R increases, i.e., the bending deformation of the tape decreases, accordingly the movement of the neutral axis diminishes. When the bending radius R increases beyond a certain value, the influences of the BEF, the elastic modulus, and the volume fraction of the superconducting filaments on the movement of the neutral axis are gradually weak, and the results in different cases are hard to be identified.

4 Conclusions

For the bending of Bi2223/Ag composite tape, on our modified model with the damage stress of the superconducting filaments, we studied the influence of the movement of the neutral axis on the relation of the critical current versus the bending strain. Specifically, on taking account of the BEF of Ag and Ag alloy, we comprehensively investigated the movement of the neutral axis of the Bi2223/Ag composite tape, the relation of the normalized critical current I c/ I c0 versus the bending strain, and the distributions of the stress (or strain) on the cross section in different cases of the BEF, the elastic modulus, and volume fraction of the superconducting filaments. The results clearly show that, the movement of the neutral axis cannot to be neglected and it indeed has a strong effect on the relation of the critical current versus bending strain, especially for the Bi2223/Ag composite tape with larger bending deformation (correspondingly smaller bending radius).