Introduction

The aging and senescence of blood cells such as platelets and red cells have been studied for almost a century. The lifespan of circulating cells is a key factor of the cell homeostasis that is often altered by a disease. The lifespan of red blood cells (RBCs) is a major determinant of time to reach new steady state values of hemoglobin in anemic patients undergoing treatment with erythropoietin [1]. The RBC heterogeneity is sufficient to alter the concentration of glycated hemoglobin A1c that is a standard measure of glycemic control in patients with diabetes mellitus [2].

One can determine the lifespan distribution for a cell population present in the circulation by labeling a representative subpopulation with a radioactive isotope or a fluorescent tag and recording the signal as a function of time. The ratio of the signal to the initial signal plotted versus time is called the survival curve. Survival analysis allows one to determine the mean and standard deviation of the cell lifespan distribution [3]. Labeling with chromium 51 is a commonly used clinical method for red cell survival analysis [4]. Recently, biotin labeling of RBCs has been more frequently used as a nonradioactive, nontoxic alternative for red cell survival studies [5]. We will apply this technique in our studies of RBC survival. A cohort of RBCs is a set of red cells that were born at the same time, and consequently have the same age. Signal decay from a labeled RBC cohort can also be used for the determination of the RBC lifespan. The most widely used cohort labeling methods require the biosynthetic introduction of a label into a newly synthesized cells, followed by the quantitative determination of the persistence of the label in circulating erythrocytes [4]. The most frequently used precursor is glycine, labeled with radioactive isotopes. Its value derives from it serving to make the protoporphyrin backbone of heme and as a precursor for the globin portion of hemoglobin. In the presence of minimal reutilization the amount of isotope in the circulating red cells would reflect the fate of the cohort sample. We will use this technique as alternative to the random labeling method described above.

All labeling methods are inherently flawed resulting in potentially inaccurate estimates of cell survival parameters. The most common problem is elution and reuse of the label. This can be caused by decay of the radioactive signal or detachment of label from the cell surface. The hemoglobin vesiculation from RBCs reduces the signal from radioactive tags incorporated in heme [6]. The incorporation of label into the precursor cells in the bone marrow is not instantaneous and release of the cells in the circulation takes some time making labeled cells an imperfect cohort. In the random labeling method, ex vivo manipulation of cells followed by injection in the circulation can damage the cells and thus might affect their subsequent survival.

Equations describing survival curves have been derived assuming that the cells of interest are in homeostasis with the system [7, 8]. For non-stationary systems with perturbed homeostasis, e.g. when drug was administered, a more general interpretation of survival curves has been applied [9, 10]. In more recent approaches cell survival is modeled as a dynamic process controlling turnover of the cell population [11, 12]. In this framework, the population size is controlled by the production and elimination rates and the cell lifespan is a major determinant of the cell loss. The variable of interest in the cell survival studies is cell age. The canonical models of cell dynamics account only for the population size (cell count) as the modeling endpoint. Age-structured population models have been proposed to include the cell age as another independent variable describing age-dependent processes controlling the cell population. The effect of the environment on the individual cell state as well as the state of the entire age-structured population has been encompassed by the physiologically structured population models [13]. We adopted this framework to describe the drug effects on age-structured cell populations where the drug plasma concentration played role of the environment [14]. In this report we expand the pharmacodynamic models of age-structured cell populations to dynamic models of cell survival.

The objective of this work was to propose a universal approach based on the age-structured cell population models to describe cell survival data. We used the mortality rate as a dynamic representation of the death hazard and described the time dependent effect of the environment on the cell senescence. The drug plasma concentration served as an environmental variable. The approach was tested on RBC survival data in rats obtained from two studies employing both cohort and random cell labeling techniques. The data were fitted using the mixed effects model implemented in Monolix 4.3.3.

Theoretical

Age-structured cell population models

The age a of a cell is defined as the time that has elapsed since its entry to the circulation. The distribution of ages among circulating cells at time t is described by the density function \(n(a,t)\). By definition, the number of cells in the population at time t is

$$N\left( t \right) = \mathop \smallint \limits_{0}^{\infty } n\left( {a,t}\right)\,da$$
(1)

Consequently, the probability density function (p.d.f.) for the age distribution at time t can be calculated as follows:

$$p\left( {a,t} \right) = \frac{n(a,t)}{N(t)}$$
(2)

The theory of age-structured populations describes the density \(n(a,t)\) as a population state (p-state) that can be affected by the environment (e-state) [13]. In the context of pharmacodynamic models, the natural environment affecting circulating cells is the drug plasma concentration \(C(t)\). Then the e-state equation is described by a pharmacokinetic model. The p-state equation for a cell population affected by drug has been introduced in [14]

$$\frac{\partial n}{\partial t} + \frac{\partial n}{\partial a} = - \mu \left( {a,C(t)} \right)n$$
(3)

with the boundary condition at \(a = 0\)

$$n\left( {0,t} \right) = k_{in} (C(t))$$
(4)

and the initial condition determined by the steady-state for Eqs. (3) and (4)

$$n\left( {a,0} \right) = n_{ss} \left( a \right) = k_{in} (0)exp\left( { - \mathop \smallint \limits_{0}^{a} \mu \left( {\alpha ,0} \right)\,d\alpha } \right)$$
(5)

where we assume that for \(t < 0\) drug plasma concentration is 0 (\(C\left( t \right) = 0)\). A solution of Eqs. (3)–(5) can be obtained by the method of characteristics and it assumes the following form [14]:

$$n\left( {a,t} \right) = k_{in} (C\left( {t - a} \right))exp\left( { - \mathop \smallint \limits_{0}^{a} \mu \left( {\alpha ,C\left( {\alpha + t - a} \right)} \right)\,d\alpha } \right)$$
(6)

The cell number \(N\left( t \right)\) can be determined from the integral equation obtained by integration of Eq. (6) over \(a\) and utilizing Eq. (1):

$$N\left( t \right) = \mathop \smallint \limits_{ - \infty }^{t} k_{in} (C(s))exp\left( { - \mathop \smallint \limits_{s}^{t} \mu \left( {\alpha - s,C\left( \alpha \right)} \right)d\alpha } \right)ds$$
(7)

The equivalent differential equation defining \(N\left( t \right)\) is

$$\frac{dN}{dt} = k_{in} (C(t)) - \mathop \smallint \limits_{0}^{\infty } \mu \left( {a,C(t)} \right)n\left( {a,t} \right)\,da$$
(8)

with the initial condition

$$N\left( 0 \right) = N_{ss}$$
(9)

Cell lifespan and mortality rate

A lifespan of a cell at time t is defined as a period of time between the entry and exit of the cell into and from the population. The cell lifespan is a time dependent random variable that has its p.d.f. \(\ell (\tau ,t)\). For a cell population with the constant baseline understood as a time invariant age distribution prior to drug administration, the lifespan distribution is uniquely determined by the mortality rate [14]:

$$\ell \left( {\tau ,t} \right) = \mu \left( {\tau ,C\left( {\tau + t} \right)} \right)exp\left( { - \mathop \smallint \limits_{0}^{\tau } \mu \left( {\alpha ,C\left( {\alpha + t} \right)} \right)d\alpha } \right)$$
(10)

Conversely, Eq. (10) implies that the lifespan distribution uniquely determines the mortality rate:

$$\mu \left( {a,C(t)} \right) = \frac{{\ell \left( {a,t - a} \right)}}{{\mathop \smallint \nolimits_{a}^{\infty } \ell \left( {\tau ,t - a} \right)d\tau }}$$
(11)

Equation (10) implies that the mortality rate \(\mu \left( {a,C(t)} \right)\) can be interpreted as the hazard function of cell death (removal from the population). Equations (10) and (11) have been derived previously for a non-stationary model of platelets survival [10].

Random labeling of cell population

A population of cells that have been randomly labeled (called an index population) at index time \(t_{0} \ge 0\) does not have an influx of new cells for times \(t > t_{0}\) [12]. Therefore

$$k_{inind} \left( {C(t)} \right) = 0\;{\text{for}}\;t > t_{0}$$
(12)

It should be noted that, in general, due to events such as label elution or cell stress introduced during the labeling process both the mortality rate and the lifespan for the index population might be different from the analogous ones for the original population. To keep this distinction a subscript “ind” is used for all relevant variables. Then the age density for the index population becomes

$$n_{ind} \left( {a,t} \right) = \left\{ {\begin{array}{*{20}l} {k_{inind} \left( {C\left( {t - a} \right)} \right)exp\left( { - \mathop \smallint \limits_{t - a}^{t} \mu_{ind} \left( {s - t + a,C\left( s \right)} \right)ds} \right), \quad{\text{if}}\; t - a \le t_{0} } \\ {0,\quad if \; t - a > t_{0} } \\ \end{array} } \right.$$
(13)

The fraction of survived cells in the index population can be calculated from Eq. (7):

$$SF\left( t \right) = \frac{{N_{ind} \left( t \right)}}{{N_{ind} \left( {t_{0} } \right)}} = \frac{{\mathop \smallint \nolimits_{ - \infty }^{{t_{0} }} k_{inind} (C\left( s \right))exp\left( { - \mathop \smallint \nolimits_{s}^{t} \mu_{ind} \left( {\alpha - s,C\left( \alpha \right)} \right)d\alpha } \right)ds}}{{\mathop \smallint \nolimits_{ - \infty }^{{t_{0} }} k_{inind} (C\left( s \right))exp\left( { - \mathop \smallint \nolimits_{s}^{{t_{0} }} \mu_{ind} \left( {\alpha - s,C\left( \alpha \right)} \right)d\alpha } \right)ds}},{\text{for}}\;\;t > t_{0}$$
(14)

In case of absence of drug and lack of the impact of the population size on the cell production and elimination rates:

$$k_{inind} \left( {C(t)} \right) \equiv k_{inind} ,\mu \left( {a,C} \right) \equiv \mu \left( a \right),\;{\text{and}}\;t_{0} = 0$$
(15a,b,c)

where \(k_{inind}\) is constant. Equation (14) reduces to

$$SF\left( t \right) = \frac{{\mathop \smallint \nolimits_{t}^{\infty } exp\left( { - \mathop \smallint \nolimits_{0}^{s} \mu_{ind} \left( \alpha \right)d\alpha } \right)ds}}{{\mathop \smallint \nolimits_{0}^{\infty } exp\left( { - \mathop \smallint \nolimits_{0}^{s} \mu_{ind} \left( \alpha \right)d\alpha } \right)ds}}$$
(16)

Cohort labeling of cell population

By definition, a cohort is a population of cells of the same age. For index populations, cell age counts from the moment the cell enters the circulation. If labeling takes place extravascularly (e.g. in the bone marrow), then the labeled cells require some time interval of length \(T_{e}\) > 0 to be released to the circulation. If we assume that the cell labeling was instantaneous and occurred at index time \(t_{0} \ge 0\), then the influx of cells of age 0 into the index population can be approximated by a rectangular wave function:

$$k_{inind} (C(t)) = \frac{{N_{ind0} }}{{T_{e} }}\theta (t - t_{0} )\theta (t_{0} + T_{e} - t)$$
(17)

where \(N_{ind0}\) is the number of cells in the index population and \(\theta \left( x \right) = 0\), if \(x < 0\), and \(\theta \left( x \right) = 1,\) otherwise. The assumption Eq. (3) that \(C(t)\) is the only factor that regulates the production rate of cells in the index population requires interpretation of the labeling event as the drug effect defined by Eq. (17). Equation (17) implies that as \(t \to \infty\), \(k_{inind} \left( {C\left( t \right)} \right) \to 0\), and therefore the cell production at steady-state is 0

$$k_{inind} \left( 0 \right) = 0$$
(18)

and the initial condition Eq. (5) becomes 0 as well. Notice that if the entrance time approaches 0, \(T_{e} \to 0\), then the cell production rate becomes the Dirac delta function:

$$k_{inind} (C(t)) \to N_{ind0} \delta (t - t_{0} )$$
(19)

This ensures that for small \(T_{e}\) the only cells that enter the index population are cells of age 0 at time \(t_{0}\). According to Eq. (6) the age density for the cohort population is

$$\begin{aligned} n_{ind} \left( {a,t} \right) = & \frac{{N_{ind0} }}{{T_{e} }}\theta \left( {t - a - t_{0} } \right)\theta (t_{0} + T_{e} - t + a)) \\ &\times exp\left( { - \mathop \smallint \limits_{0}^{a} \mu_{ind} \left( {\alpha ,C\left( {\alpha + t - a} \right)} \right)d\alpha } \right) \\ \end{aligned}$$
(20)

The cell number in the cohort is

$$N\left( t \right) = \left\{ {\begin{array}{*{20}l} {0,} & {if \; t < t_{0} } \\ {\frac{{N_{ind0} }}{{T_{e} }}\mathop \smallint \limits_{{t_{0} }}^{t} exp\left( { - \mathop \smallint \limits_{s}^{t} \mu_{ind} \left( {\alpha - s,C\left( \alpha \right)} \right)d\alpha } \right)ds,} & {if \; t_{0} \le t \le t_{0} + T_{e} } \\ {\frac{{N_{ind0} }}{{T_{e} }}\mathop \smallint \limits_{{t_{0} }}^{{t_{0} + T_{e} }} exp\left( { - \mathop \smallint \limits_{s}^{t} \mu_{ind} \left( {\alpha - s,C\left( \alpha \right)} \right)d\alpha } \right)ds,} & {if \; t > t_{0} + T_{e} } \\ \end{array} } \right.$$
(21)

For the ideal cohort (\(T_{e} \to 0\))

$$n_{ind} \left( {a,t} \right) = N_{0} \delta \left( {t - a - t_{0} } \right)exp\left( { - \mathop \smallint \limits_{{t_{0} }}^{{a + t_{0} }} \mu_{ind} \left( {\alpha - t_{0} ,C\left( \alpha \right)} \right)\,d\alpha } \right)\;for\;t > t_{0}$$
(22)

and

$$N_{ind} \left( t \right) = N_{ind0} exp\left( { - \mathop \smallint \limits_{{t_{0} }}^{t} \mu_{ind} \left( {\alpha - t_{0} ,C\left( \alpha \right)} \right)d\alpha } \right)\;{\text{for}}\;t > t_{0}$$
(23)

Consequently, the survived fraction of cells for the cohort population is

$$SF\left( t \right) = \frac{{N_{ind} \left( t \right)}}{{N_{ind0} }} = exp\left( { - \mathop \smallint \limits_{{t_{0} }}^{t} \mu_{ind} \left( {\alpha - t_{0} ,C\left( \alpha \right)} \right)d\alpha } \right)$$
(24)

If simplifying conditions Eq. (15b,c) apply, then

$$SF\left( t \right) = exp\left( { - \mathop \smallint \limits_{0}^{t} \mu_{ind} \left( \alpha \right)d\alpha } \right)$$
(25)

Hazard functions

The hazard function for the index population is a sum of the death hazard and the loss of the signal hazard. The latter can be caused by elution of the label and/or the cell loss due to harshness of the labeling procedure:

$$\mu_{ind} \left( {a,t} \right) = \mu \left( a \right) + \mu_{loss} \left( t \right)$$
(26)

The hazard of losing the signal not related to cell senescence can vary with time and, in principle, should be cell age independent.

$$\mu_{loss} \left( t \right) = \theta \left( {t - t_{0} } \right)\mu_{0} exp\left( { - \beta t} \right)$$
(27)

Although not related to the drug effect on the index population, the loss of the signal can be interpreted as the environment effect on the population and formally \(\mu_{loss} \left( t \right)\) can be substituted for \(C(t)\) in all presented equations. Equation (27) actually describes a monoexponential decay of the signal with the peak value \(\mu_{0}\) and the half-life \(\ln \left( 2 \right)/\beta\), and assumes that the hazard is proportional to the signal. For the hazard described by Eq. (26) the following integral simplifies to

$$\mathop \smallint \limits_{s}^{t} \mu_{ind} \left( {\alpha - s,C\left( \alpha \right)} \right)d\alpha = \mathop \smallint \limits_{0}^{t - s} \mu \left( \alpha \right)d\alpha + \frac{{\mu_{0} }}{\beta }\left( {exp\left( { - \beta s} \right) - exp\left( { - \beta t} \right)} \right),t \ge s \ge t_{0}$$
(28)

and

$$\mathop \smallint \limits_{s}^{t} \mu_{ind} \left( {\alpha - s,C\left( \alpha \right)} \right)d\alpha = \mathop \smallint \limits_{0}^{t - s} \mu \left( \alpha \right)d\alpha + \frac{{\mu_{0} }}{\beta }\left( {exp\left( { - \beta t_{0} } \right) - exp\left( { - \beta t} \right)} \right),t \ge t_{0} \ge s$$
(29)

In the case \(\beta = 0\), the last term in Eqs. (28) and (29) becomes \(\mu_{0} (t - t_{0} )\). Consequently, the survived fraction for the ideal cohort (\(T_{e} \to 0\)) Eq. (24) becomes:

$$SF\left( t \right) = exp\left( { - \frac{{\mu_{0} }}{\beta }\left( {exp\left( { - \beta t_{0} } \right) - exp\left( { - \beta t} \right)} \right)} \right)exp\left( { - \mathop \smallint \limits_{0}^{{t - t_{0} }} \mu \left( \alpha \right)d\alpha } \right),t \ge t_{0}$$
(30)

and for the random sample Eq. (14) becomes:

$$SF\left( t \right) = exp\left( { - \frac{{\mu_{0} }}{\beta }\left( {exp\left( { - \beta t_{0} } \right) - exp\left( { - \beta t} \right)} \right)} \right)\frac{{\mathop \smallint \nolimits_{t}^{\infty } exp\left( { - \mathop \smallint \nolimits_{0}^{a} \mu \left( \alpha \right)d\alpha } \right)da}}{{\mathop \smallint \nolimits_{{t_{0} }}^{\infty } exp\left( { - \mathop \smallint \nolimits_{0}^{a} \mu \left( \alpha \right)d\alpha } \right)da}},t \ge t_{0}$$
(31)

Methods

Animals

Male Wistar rats (Harlan Sprague–Dawley, Indianapolis, IL) of weights 340–580 g were used for RBC cohort labeling (N = 4) and random labeling (N = 8) studies. The initial signal from a random RBC sample in one animal was too weak to be detected for more than week and the animal was removed from the study. The animals were kept on a schedule of 12 h light and 12 h dark cycle. All animals were allowed food and water ad libitum. This study had been carried out with the approval of the Institutional Animal Care and Use Committee of the University at Buffalo.

Random RBC labeling

A sample of RBCs was labeled with biotin. The biotinylation technique has been shown to yield similar results as the random labeling method using radioactive 51Cr [5]. A blood sample of about 2.5 mL was drawn from the tail vain of an animal, washed with Dulbecco modified medium (RPMI Medium 1640, Gibco, Grand Island, NY), and incubated at 10% hematocrit in RPMI medium containing 100 μg/mL of water-soluble biotin (Sulfo-NHS-Biotin, Pierce, Rockford, IL) at room temperature for 30 min. After the incubation cells were thoroughly washed with the RPMI medium, re-suspended in 2.5 mL of PBS and injected to an animal via the tail vain. The blood samples of 50 μL for assessment of the decay of the biotinylated RBC were collected for days 0–7 and then twice a week until the signal reached the limit of detection. To determine the percentage of the biotinylated RBCs in the circulation the blood sample was washed with the RPMI medium and incubated for 30 min in Dulbecco’s Phosphate Saline (DPBS, Gibco, Grand Island, NY) containing streptavidin conjugated to R-phycoerythrin (Molecular Probes, Eugene, OR) for 30 min. Next, the sample was washed and re-suspended in 1 mL of DPBS. The fluorescent signal from the streptavidin–biotin complex was recorded by a FL2 filter band of the flow cytometer (FACSCalibur, Becton–Dickinson). The number of labeled cells was normalized by the number of labeled cells on day \(t_{0} = 0\) and expressed as the survived fraction SF.

Cohort RBC labeling

Incorporation of 14C-glycine in hemoglobin was applied as a labeling technique as described previously [15]. Briefly, 200 µCi of 14C-glycine (New England Nuclear Corporation, Boston, MA) was dissolved in sterile saline and injected to the tail vein of rats. Blood was collected daily from the tail vein for the first 4 days, every 3 days from day 4 to day 16 and then every week until the radioactive signal reached the background activity. RBCs were washed three times with PBS by centrifuging (2 min, 1000 RPM) and lysed with 250 μL of 5 mM Tris–HCl buffer with pH 8.6 at room temperature. Cell membranes were removed by centrifugation at 20,000×g for 30 min, and the total 14C-glycine radioactivity was measured by the gamma liquid scintillation counter (Wallac 1409, PerkinElmer, Waltham, MA). To measure hemoglobin concentration in the lysate, an aliquot of 25 µL was added to 3 mL of hemolytic buffer Drabkin’s/TritonX100 0.5 mL/L and measured by using UV–Vis spectrophotometer (PTI, Birmingham, NJ) at wave-length 540 nm. l4C-incorporation into hemoglobin was determined as dpm/mg hemoglobin. The time of 14C-glycine injection was set as the index time \(t_{0} = 0\) days.

Probability density function for RBC lifespan distribution

The Weibull p.d.f. for the cell lifespan distribution is often assumed to model cell survival data [12]:

$$l\left( \tau \right) = \lambda \gamma \left( {\lambda \tau } \right)^{\gamma - 1} exp\left( { - \left( {\lambda \tau } \right)^{\gamma } } \right)$$
(32)

where \(1/\lambda\) is the time scale and \(\gamma\) is the shape factor. The death hazard associated with it is given by Eq. (11):

$$\mu \left( a \right) = \lambda \gamma \left( {\lambda a} \right)^{\gamma - 1}$$
(33)

Fixed effects model

The observed data comprised of measurements of 14C activity and SF at series of time points per animal. Due to significant between subject variability in observed data mixed effects modeling approach has been applied to data analysis. Since the radioactive signal from initially labelled cells in the cohort labeling group was unknown, the measured 14C activity of the index cells was assumed to be proportional to the cell number:

$$A\left( t \right) = \kappa N_{ind} (t)$$
(34)

where \(\kappa\) is the proportionality coefficient and \(N_{ind} (t)\) is described by Eq. (23):

$$A\left( t \right) = \left\{ {\begin{array}{*{20}c} {\frac{{\kappa N_{ind0} }}{{T_{e} }}\mathop \smallint \limits_{0}^{t} \exp \left( { - \left( {\lambda (t - s)} \right)^{\gamma } - \frac{{\mu_{0} }}{\beta }\left( {\exp \left( { - \beta s} \right) - \exp \left( { - \beta t} \right)} \right)} \right)ds, \quad if\,\, 0 \le t \le T_{e} } \\ {\frac{{\kappa N_{ind0} }}{{T_{e} }}\mathop \smallint \limits_{0}^{{T_{e} }} \exp \left( { - \left( {\lambda (t - s)} \right)^{\gamma } - \frac{{\mu_{0} }}{\beta }\left( {\exp \left( { - \beta s} \right) - \exp \left( { - \beta t} \right)} \right)} \right)ds,\quad if\,\, t > T_{e} } \\ \end{array} } \right.$$
(35)

The survived fraction defined by Eq. (31) with the Weibull hazard Eq. (33) was used to model the RBC random labeling data.

$$SF\left( t \right) = \exp \left( { - \frac{{\mu_{0} }}{\beta }\left( {1 - \exp \left( { - \beta t} \right)} \right)} \right)\frac{{\mathop \smallint \nolimits_{t}^{\infty } \exp \left( { - \left( {\lambda a} \right)^{\gamma } } \right)da}}{{\mathop \smallint \nolimits_{0}^{\infty } \exp \left( { - \left( {\lambda a} \right)^{\gamma } } \right)da}},t \ge 0$$
(36)

The Weibull hazard function \(\mu \left( a \right)\) Eq. (33) was same for both groups whereas the hazard of signal loss \(\mu_{loss} \left( t \right)\) Eq. (27) was allowed to differ between groups. The model parameters were assumed to be log-normally distributed among animals:

$$P = \theta_{P} { \exp }(\eta_{P} )$$
(37)

where \(\theta_{P}\) is the parameter typical value and \(\eta_{P} \sim N\left( {0,\omega_{P}^{2} } \right).\) Upon testing constant and proportional residual error models, the former was assumed for the cohort RBC labeling data:

$$Y_{ij} = A\left( {t_{ij} } \right) + { \epsilon }_{cohij}$$
(38)

where \(\epsilon_{cohij} \sim N(0,\varepsilon_{coh}^{2} )\) is the residual error for \(i\)-th animal at time \(t_{ij}\). The proportional residual error model was assumed for the random labeling RBC data:

$$Y_{ij} = SF\left( {t_{ij} } \right) + \epsilon_{ranij} SF\left( {t_{ij} } \right)$$
(39)

where \(\epsilon_{ranij} \sim N(0,\varepsilon_{ran}^{2} )\). The population and individual parameters were estimated using the SAEM algorithm implemented in Monolix 4.3.3 (Lixoft). The numerical evaluation of the integrals was done by the MATLAB function integral available to Monolix.

Results

Population RBC survival data analysis

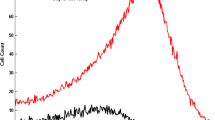
The individual animal 14C activity data spanned up to 72 days (see Fig. 1). The activity increased within two days to the maximal value that persisted to about 44 days and gradually declined to reach the background noise at day 72. The onset in the data time course is explained by the model as the time interval \(T_{e}\) during which the cells labeled by 14C are released to the circulation. The plateau and offset of the time course is explained by the probability of cell survival given by Eq. (24). The model well described individual onset and offset part of the data while reasonable captured the plateau due to relatively high within subject variability as seen in Fig. 1 and observed versus predicted diagnostics plots (Fig. 1S, Supplementary material). The survived fraction of index cells in the random labeling study reached the detection limit after approximately 43–55 days (see Fig. 2). The initial decline of the RBC survival data in few animals was more rapid than accounted by the model cell loss hazard function. Only Rat 6, 8, and 9 had increased the initial SF decline rate compared to other animals in the study (see Table 1S, Supplementary material). The model well captured the SF data for all animals as seen in Fig. 2 and observed versus predicted diagnostics plots (Fig. 1S, Supplementary material).

Fig. 1
figure 1

14C activity time courses in (N = 4) Wistar rats following injection of the 14C-glycine on day 0. The symbols represent measurements whereas the lines are individual model predictions based on Eq. (35)

Full size image
Fig. 2
figure 2

RBC survival curves in (N = 7) Wistar rats following re-injection of the biotin-labeled blood sample on day 0. The data is expressed as the survived fraction of the injected cells. The symbols represent measurements whereas the lines are individual model predictions based on Eq. (36)

Full size image

The estimates of the typical values of the model parameters as well as between subject variability are shown in Table 1. The estimates of the \(\mu_{loss} \left( t \right)\) parameters for the cohort RBC labeling group could not be obtained with a reasonable precision and therefore were set to 0, which effectively eliminated this process from the model. The relative standard errors of the remaining fixed effects parameters did not exceed 21%. The between subject variability of \(T_{e}\) was estimated with low precision that we attribute to small number of animals involved in the studies. Subsequently, \(\omega_{Te}\) was set to 0, resulting in same \(T_{e}\) for all animals in the group. For the random RBC labeling group, the estimate of \(\omega_{\beta }\) was close to 0 and subsequently fixed at this value. The remaining between subject variability parameters were estimated with RSEs not exceeding 34%. The visual predictive check plots shown in Fig. 2S (Supplementary material) indicate that the estimates of the between subject variability parameters for the cohort RBC labeling group are inflated whereas for the random RBC labeling group they predict the observed variability.

Table 1 Estimates of population parameters for simultaneous fits of random and cohort RBC labeling groups of Wistar rats
Full size table

Rat RBC mean lifespan and age

Given \(\mu \left( a \right)\) and \(\ell \left( a \right)\) one can determine from Eqs. (2) and (5) the RBC age distribution at steady state

$$p\left( a \right) = \frac{{exp\left( { - \mathop \smallint \nolimits_{0}^{a} \mu \left( \alpha \right)d\alpha } \right)}}{{\mathop \smallint \nolimits_{0}^{\infty } exp\left( { - \mathop \smallint \nolimits_{0}^{a} \mu \left( \alpha \right)d\alpha } \right)da}} = \frac{{exp\left( { - \mathop \smallint \nolimits_{0}^{a} \mu \left( \alpha \right)d\alpha } \right)}}{{\mathop \smallint \nolimits_{0}^{\infty } a\ell \left( a \right)da}}$$
(40)

Since the mean of the Weibull p.d.f. Eq. (33) is

$$Mean\; RBC \; lifespan = ML = \mathop \smallint \limits_{0}^{\infty } \tau \ell \left( \tau \right)d\tau = \frac{1}{\lambda }{{\varGamma }}\left( {1 + \frac{1}{\gamma }} \right)$$
(41)

then Eqs. (10) and (40) imply

$$Mean\; RBC\; age = MA = \mathop \smallint \limits_{0}^{\infty } ap\left( a \right)da = \frac{{\mathop \smallint \nolimits_{0}^{\infty } a^{2} \ell \left( a \right)da}}{{2\mathop \smallint \nolimits_{0}^{\infty } a\ell \left( a \right)da}} = \frac{{{{\varGamma }}\left( {1 + \frac{2}{\gamma }} \right)}}{{2\lambda {{\varGamma }}\left( {1 + \frac{1}{\gamma }} \right)}}$$
(42)

where \({{\varGamma }}\left( z \right)\) is the Euler gamma function. Using the typical values \(\theta_{\lambda }\) and \(\theta_{\gamma }\) from Table 1, one can calculate the mean RBC lifespan to be 53.7 days and the mean RBC age to be 27.8 days. The mean of individual RBC age estimates for the cohort RBC labeling group was 32.1 ± 0.3 days and for the random RBC labeling group 26.1 ± 3.4 days. The analogous means of the individual RBC lifespans were 62.8.1 ± 1.13 and 50.1 ± 7.8 days, respectively. Both RBC age and lifespan means were significantly different between two groups (p < 0.005, Student t test).

Simulations

Figure 3 shows the RBC age and lifespan distributions at steady state for a typical animal. Equations (10) and (40) imply that \(p(a)\) and \(\ell (\tau )\) are dependent:

$$p\left( a \right) = \frac{1}{ML}\mathop \smallint \limits_{a}^{\infty } \ell (\tau )d\tau$$
(43)
Fig. 3
figure 3

p.d.f.s for lifespan distribution \(\ell (t)\) and age distribution \(p(t)\) of a typical animal (upper panel) and the death hazard function \(\mu (t)\) (lower panel) for a typical Wistar rat. The curves were simulated based on Eqs. (32), (40), and (33), respectively

Full size image

Hence, the RBC age p.d.f. is proportional to the RBC lifespan complementary cumulative distribution function (c.c.d.f.). While \(\ell (\tau )\) versus \(\tau\) plot features the Weibull p.d.f. with the shape factor \(\gamma > 1\), the \(p\left( a \right)\) versus \(a\) plot has all characteristics of a c.c.d.f.: a monotonic decline to 0 with a flat plateau over RBC ages coinciding with RBC lifespans for which \(\ell (\tau )\) is near 0. The mode of the typical RBC lifespan distribution is at \(\frac{1}{\lambda }\left( {\frac{\gamma - 1}{\gamma }} \right)^{1/\gamma }\) = 56.3 days and standard deviation \(\frac{1}{\lambda }\left[ {{{\varGamma }}\left( {1 + \frac{2}{\gamma }} \right) - {{\varGamma }}^{2} \left( {1 + \frac{1}{\gamma }} \right)} \right]^{1/2}\) = 9.7 days. The corresponding Weibull hazard function \(\mu (a)\) determining both \(\ell (\tau )\) and \(p\left( a \right)\) increases as the power of \(a\), as described by Eq. (34).

To study the impact of the time dependent hazard of cell loss from the index population \(\mu_{loss} \left( t \right)\) on the shape of SF, a series of simulations was performed to generate SF versus time plots for varying \(\mu_{0}\) and \(\beta\). The results are shown in Fig. 4. According to Eq. (34) \(\mu_{loss} \left( t \right)\) has characteristics of the monoexponential decay with the peak value \(\mu_{0}\) and the half-life \(\ln \left( 2 \right)/\beta\). Accordingly, for \(\beta\) = 0, the hazard of cell loss is constant \(\mu_{loss} \left( t \right) \equiv \mu_{0}\) and present throughout the study, yielding the maximal impact on the survival curve. Increasing \(\beta\) results in shorten duration of the hazard of cell loss that affects the initial onset of the SF versus time curve. If \(\beta = \infty\), \(\mu_{loss} \left( t \right) \equiv 0\), and the death hazard for the index cell population coincides with the death hazard for RBCs. This can be also achieved by setting \(\mu_{0} = 0\). Increasing \(\mu_{0}\) dramatically affects the overall hazard for the index cells \(\mu_{ind} \left( {a,t} \right)\) and results in elimination of cells at early times and an increased initial slope of the survival curve. As \(\mu_{0}\) approaches \(\infty\), most of the index cells are removed from the population at times approaching 0. These simulations illustrate flexibility of the empirical monoexponential decay hazard function \(\mu_{loss} \left( t \right)\) in describing the initial cell loss from the index population in addition to the time invariant loss due to senescence \(\mu (a)\).

Fig. 4
figure 4

The effect of the correction due to cell loss on the survival curve. The typical values for \(\beta = 0.16\) day−1 and \(\mu_{0}\) = 0.08 day−1 were varied several fold to show the change in the shape of the RBC survival curve for a typical Wistar rat. The curves were simulated based on Eq. (36)

Full size image

Discussion

Hazard as driving force of survival in age-structured cell population models

The presented age-structured model of cell survival falls into category of dynamic models of cell survival controlled by their lifespan distribution [11, 12]. It differs from the previous approaches by including the cell age as an additional independent variable. The age-structured cell population approach allowed for the integration into a single model, individual cell characteristics (e.g. age), population characteristics (e.g. mortality rate), and environment (e.g. drug plasma concentration) [14]. Consequently, the model focuses on the hazard of cell death rather than the lifespan distribution which allows for more mechanistic modeling of processes affecting the cell removal. The use of the hazard function rather than lifespan distribution has been applied previously to model platelet kinetics [10]. In addition to the inherent death hazard for circulating cells that depends on the cell age, we introduced a time dependent hazard of cell loss due to experimental processing of blood sample \(\mu_{loss} \left( t \right)\). Another feature of the presented model is its ability to simultaneously describe cell survival for two different populations created by two distinct labeling techniques. We adopted the concept of index cell populations introduced by Shresta et al. [12] to define cohort sample and random sample of cell population. While the cell production rates reflected the differences between the index populations, the cell death hazards were modeled the same way allowing for cell lifespan and cell age distributions to be common to both populations. This demonstrates that the age-structured model is universal and can be applied to describe survival of various cell populations.

Drug plasma concentration replaced by time variant hazard of cell loss

In the presented framework for age-structured cell population models the environment affecting the cell removal is represented by the drug plasma concentration \(C\left( t \right).\) However, the model was applied to data involving cells at steady-state that were not treated with any drug. Instead, \(C\left( t \right)\) was replaced by the hazard of cell loss due to experimental processing of blood sample \(\mu_{loss} \left( t \right)\). In this context, cell labeling can be viewed as impact of the environment on the index cell population, keeping valid all model equations derived for \(C\left( t \right).\) Under assumption that the labelling is independent of other processes affecting cell death, the key equation describing the survived fraction of the random sample of cell population is Eq. (31) where the SF described solely by death hazard is corrected by a factor due to the transient labelling effect. The presence of this correction factor is unique to our model. Its impact on the shape of the survival curve has been studied in Fig. 4. Other functions can be considered to describe \(\mu_{loss} \left( t \right)\) to account for more gradual cell loss (e.g. linear hazard). This might be the case for allogenic RBC sample reinfused to another recipient [16].

Non-stationarity

The stationarity assumption is often applied in other models of cell survival [7]. In our model the stationarity assumption applies only for times before the drug treatment. This means that prior to drug intervention (\(t \le 0)\) the cell population was at steady-state. The labeling must occur at or later than the drug administration (\(t_{0} \ge 0\)). Consequently, if there was any perturbation of the circulating cells state before drug treatment such as disease progression or treatment with other drugs or therapies affecting the cells, then the presented equations do not apply. With this restriction our model is qualified to describe non-stationary cell survival data within the scope defined by model assumptions [10].

Label elution

A common problem to all labeling techniques is elution of the label from the index cells and possible label reutilization [17]. Since the index cells are detected based on the signal emitted from the label, loss of the label can be interpreted as loss of the cell and it impacts the estimation of the cell lifespan distribution parameters. Many models of cell survival account for the label elution by modifying the cell survival curve [4, 18]. However, the label elution is a factor to consider if the index cell number is assumed to be proportional to the signal emitted by the labeled cells (see Eq. (34)). If the signal is used only for cell detection and cell enumeration is done by another method (e.g. flow cytometry event count), the label elution is insignificant, and only affects cells emitting signals at the detection level.

In the presented model the hazard of cell loss \(\mu_{loss} \left( t \right)\) can only account for the signal loss that makes cells undetectable (e.g. reaching the background noise), and should not be considered as a correction for the label elution. Consequently, the age-structured model in the current form does not account for the label elution. In order to do so in agreement with the framework of the physiologically structured population models one must recognize that the signal s from a labeled cell is another structure and its loss rate defines the state of the cell on par with the cell age a. Therefore, the density function for the index cell population should account both for a and s distribution \(n(a,s,t)\). Then the total signal from the index cell population \(S\left( t \right)\) and the number of cells \(N\left( t \right)\) can be calculated as follows:

$$S\left( t \right) = \mathop \smallint \limits_{0}^{\infty } \mathop \smallint \limits_{0}^{\infty } sn(a,s,t)\,dsda\;{\text{and}}\;N\left( t \right) = \mathop \smallint \limits_{0}^{\infty } \mathop \smallint \limits_{0}^{\infty } n(a,s,t)\,dsda$$
(44)

In the presence of label elution the quantities \(S\left( t \right)\) and \(N\left( t \right)\) are not, in general, proportional to each other. If the total signal is used for index cell enumeration, \(S\left( t \right)\) rather than \(N\left( t \right)\) should be applied. This however requires extension of the presented model onto an \((a,s)\)-structured cell population.

For 14C-glycine cohort labeling of RBCs, the label elution is apparent due to due to vesiculation of hemoglobin [6]. Given the variability of the data we expect that the label elution would not be identifiable for our cohort RBC labeling group.

Selection of Weibull function for p.d.f. of RBC lifespan

Our choice of the Weibull p.d.f. for the RBC lifespan distribution was motivated by its flexibility and computational properties allowing closed formulas for calculation of many integrals. Another reason for choosing the Weibull function was the explicit cell death hazard in the form of the power function. One can consider other p.d.f.s such as lognormal or gamma functions that have been shown to perform equally well for RBC survival analyses [12]. Selection of more realistic p.d.f. that will account for cell death of young RBCs (neocytolysis) [19], or random destruction will increase the number of model parameters and might cause identifiability problems [18]. The age-structured cell population model offers development of more mechanistic p.d.f. through assumptions regarding the hazard of cell removal that can vary with cell age rather than multi-modal lifespan distributions.

Parameter estimates

Our estimates of the mean RBC lifespan for Wistar rats 53.7 days is close to 59.8 days reported in literature for this strain of animals [20]. This typical value was obtained for a population of animals comprising cohort and random RBC labeling groups. However, the means of individual animal RBC lifespans for those two groups were significantly different (62.8.1 ± 1.13 and 50.1 ± 7.8 days). Given substantial cell loss due to blood sample processing detected in the random RBC labeling group we attribute this to lower the mean RBC lifespan estimates despite the presence of \(\mu_{loss} \left( t \right)\) in the model. The objective of our study was to provide a universal approach describing RBC survival data obtained by two different techniques, and not to validate one technique against the other.

We are unaware of any reports of the mean RBC age for rats. Therefore our estimates of 27.8 days cannot be compared to other values. Interestingly, we established a relationship between the mean RBC age and the mean RBC lifespan Eqs. (41) and (42) that is independent of the mathematical form of lifespan and age distributions:

$$MA \cdot ML = \frac{1}{2}\mathop \smallint \limits_{0}^{\infty } a^{2} p\left( a \right)da$$
(45)

This explains the difference in the means of ages between cohort and random RBC labeling groups due the same reasons as for the means of the lifespans.

Another question pertinent to our study is identifiability of the model parameters from individual subject cell survival data. Since we applied mixed effects modeling approach for data analysis, the individual estimates of model parameters benefit from combined information for the population, that limits our ability to address their estimability based on the individual data only. According to the literature reports using p.d.f.s for the RBC lifespan distribution defined by means of two parameters (e.g. lognormal, gamma, and Weibull functions), estimates of these are readily available from fitting individual random labeling cell survival data. Our simulations shown in Fig. 4 imply that the parameters describing \(\mu_{loss} \left( t \right)\) are identifiable if there is noticeable impact of cell loss due to sample processing that manifests itself as a visible curvature of the survival curve. In case \(\mu_{loss} \left( t \right)\) parameters cannot be estimated with a reasonable precision we recommend removing this process from the model (as we did for the cohort RBC labeling group) and claim the data to be uninformative about the cell loss.

Summary

We introduced the age-structured cell population model to describe cell survival. The role of the environment is represented by the drug plasma concentration that can be replaced by any time dependent process affecting cells. The model provides a mechanistic framework flexible enough to account for various experimental designs to generate the cell survival data. Contrary to existing models, our approach utilizes the hazard of cell removal as a key variable subjected to the effect of the environment. Our model reproduces the basic cell survival relationships published elsewhere for cohort and random labeling of cell populations. In addition, it accounts for cell loss due to labeling of cell sample. Our model still lacks ability to describe the effect of label elution on the survival data, but offers a possible extension to age and signal structured cell populations to mechanistically account for that phenomenon. We applied our model to simultaneously fit data from two separate experiments in rats, one involving 14C-glycine cohort labeling of RBCs, and another random labeling of RBCs with biotin. We were able to adequately describe the data and obtain consistent estimates of the mean RBC lifespan. Despite model qualification on the animal data, the model has the same potential to be applied to cell survival data analysis in humans.