An Efficient Spectral-Galerkin Method for Second Kind Weakly Singular VIEs with Highly Oscillatory Kernels

Abstract

In this paper, we construct an efficient spectral Galerkin method to deal with the classical second kind linear VIEs with weakly singular and highly oscillatory kernel. We first study the oscillation and singularity of the exact solution and then based on those results, we propose an efficient fully discrete spectral Galerkin method. The proposed algorithm reaches an optimal convergence order without the influence of the wave number. At last, two numerical examples are provided to verify the efficiency of our proposed method.

1 Introduction

Integral equations arise in applications as mathematical models of various physical processes and biological phenomena. In general, they can not be solved analytically and many numerical method for the non-oscillatory or low-oscillatory integral equations has been devised in the books by Atkinson and Brunner, which convey a good picture of these developments and contain an extensive bibliography [1,2,3]. In recent years, highly oscillatory equations coming from applications have received more and more attention. For such problems, conventional numerical methods for them may be expensive because of the oscillatory factor. Therefor, it is meaningful to construct special numerical methods for them.

We firstly introduce some works on the integral equation with VIEs with highly oscillatory kernels. Brunner study the theory of VIEs with highly oscillatory kernel in [2, 4, 5], where the kernels are separable oscillatory ones. Xiang and Wang in [6, 7] solved certain Volterra integral equations of the first kind with a highly oscillatory Bessel kernel, where they resorted to the analytical expression and got the results by treating oscillatory integral in the solution with the Filon type method. Consequently, Xiang and Brunner introduces piecewise constant and linear collocation method based on the direct Filon method for solving second kind weakly singular VIEs with a highly oscillatory Bessel kernel in [8]. They proved that the methods have asymptotic and desirable order. However, these methods do not consider the influence of the highly oscillatory behavior of the solutions. Recently, in [9], Wang and Xu first introduced the notion of the degree of oscillation of the solution in the oscillatory structured spaces, and then presented the oscillation-preserving finite-element Galerkin method for the numerical approximation of the solution of the second kind oscillatory Fredholm integral equations with smooth kernels by incorporating the conventional approximate subspace with a finite number of oscillatory functions. Later, Fermo and Dermee in [10] combined the classical product rule with a dilation quadrature formula to develop a Nystr$\ddot{o}$m-type method for solving VIEs with highly oscillatory kernels. Motivated by the idea in [9], we presented an oscillation-preserving Legendre-Galerkin algorithm for VIEs with highly oscillatory and smooth kernels in [11]. However, when the kernel function possesses both oscillation and weakly singularity, as far as the authors know, the results on theoretical analysis and numerical approximation for this-type VIEs remain a challenging problem.

In this paper, we are concerned with the second kind linear VIEs with weakly singular and highly oscillatory kernels of the next form

$$\begin{aligned} u(x)=({\mathscr {B}}u)(x)+f(x),\ \ x\in I:=[0,1], \end{aligned}$$

(1.1)

where ${\mathscr {B}}: C(I)\rightarrow C(I)$ defined by

$$\begin{aligned} ({\mathscr {B}}v)(x):=\int _{0}^x(x-t)^{-\mu }e^{i\omega (x-t)}B(x,t)v(t)dt, \ \ x\in I, \end{aligned}$$

where $\mu \in (0,1)$, $\omega$ is the wave number and i is the imaginary unit such that $i^2:=-1$. f and B are two given functions with $B(t,t)\not =0$ for $t\in I$, u is the output function to be determined in an appropriate function space. When the wave number $\omega$ is small, the singularity of the solution of (1.1) has been systematically studied in [2].

Theorem 1.1

Let m be a nonnegative integer. Suppose that $B\in C^{m,m}(I^2)$ and f has the form

$$\begin{aligned} f(x):=\sum _{j+k\mu <m}c_{j,k}x^{j+k\mu }+{f_m}(x),\ \ \ f_m\in C^m(I), \end{aligned}$$

then Eq. (1.1) has a unique solution $u\in C(I)$. Moreover, there exist some constants $d_{j,k}$ such that

$$\begin{aligned} u(x):=\sum _{j+k\mu <m}d_{j,k}x^{j+k\mu }+{f_m}(x),\ \ \ f_m\in C^m(I). \end{aligned}$$

But when $\omega \gg 1$, the exact solution may possess both the singularity and oscillation. To the author’s knowledge, there is rarely theoretical result and numerical simulation on VIEs (1.1) with the huge wave number $\omega$. The purpose of this paper is to present the analysis of the structure of the analytic solution and the correspondingly efficient numerical approach. To derive our schemes, we employ the resolvent representation theory and the Cauchy residue theorem to study the singularity and oscillation of the analytic solution of (1.1). Then, we present an efficient fractional spectral Galerkin method, which incorporates the fractional approximate subspace with a finite number of oscillatory functions. The spectral Galerkin scheme could not always be used in practical because of the highly oscillatory or singular integrals in the matrices, so we propose an appropriate numerical simulation, which yields a fully discrete scheme. At last, we conduct error estimates between the exact solution and the proposed approximate solution. Especially, our estimate reflects the optimal convergence independent of the wave number $\omega$.

The rest of the paper is organized as follows. In Sect. 2, the oscillation and singularity of the exact solution is constructed by using the resolvent solution and Cauchy residue theory. In Sect. 3, an efficient numerical algorithm is constructed by combining fractional spectral Galerkin methods and numerical integration schemes. Some useful lemmas and theorems are introduced in Sect. 4, We also derive the convergence result of the scheme in this part as well. Section 5 gives two illustrative numerical examples. At last, some conclusions are drawn in Sect. 6.

2 Singularity and Oscillation Analysis

In the section, we are going to analyze the singularity and oscillation of the original solution of Eq. (1.1) by using the resolvent solution theory and Cauchy residue theorem. We begin with introducing a few notions. Let $\mathbb {N}_0:=\{0\}\cup \mathbb {N}:=\{1,2,\ldots \}$. For $n\in \mathbb {N}$, we set $\mathbb {Z}_n:=\{0\}\cup \mathbb {Z}_n^+$ with $\mathbb {Z}_n^+:=\{1,2,\ldots ,n\}$. Let $\overline{z}$ be the conjugate complex number for $z\in \mathbb {C}$. Let $L^2(I)$ denote the usual Hilbert space, equipped with the inner product $(\cdot ,\cdot )$ and the corresponding norm $\Vert \cdot \Vert$. For $r\in \mathbb {N}$, we denote by $C^r(I)$ the space of functions having a continuous r-th derivative ${\mathscr {D}}_x^rv$ on the interval I, where ${\mathscr {D}}_x^r$ is the r-th derivative operator about the variable x. For $\nu \in (0,+\infty )$, we use the symbol $C^{r,\nu }(I)$ to denote the space of functions $w\in C(I) \bigcap C^r(0,1]$ such that for $x\in (0,1]$ and $j\in \mathbb {Z}_{r}$,

$$\begin{aligned} |({\mathscr {D}}_x^jw)(x)|\le c \left\{ \begin{array}{ll}1,&{}j<\nu ,\\ 1+\log |x|,&{}j=\nu ,\\ 1+x^{\nu -j},&{}j>\nu . \end{array} \right. \end{aligned}$$

(2.1)

Obviously,

$$\begin{aligned} C^{r}(I)\subseteq C^{r,\nu }(I)\subseteq C(I),\ \ C^{r,\nu _1}(I)\subseteq C^{r,\nu _2}(I), \end{aligned}$$

where $v_1>v_2$. For simplicity, we let $C^{r,\infty }(I):=C^{r}(I).$ For $r_1,r_2\in \mathbb {N}_0$, we denote by $C^{r_1,r_2}(I^2)$ the space of functions $v(x,t),x,t\in I$ such that the hybrid derivative function ${\mathscr {D}}_x^{r_1}{\mathscr {D}}_t^{r_2}v$ is continuous on $I^2$. Following the notion in [5, 9], for any norm space X with the norm $\Vert \cdot \Vert _X$, we denote by $X_{\omega ,0}$ the non-$\omega$-oscillatory space, which means that the norm is independent of the wave number $\omega$.

Lemma 2.1

Suppose that $\nu _1,\nu _2>-1$ and $|a|,|b|\le \omega$. If $\phi$ is one analytic function on the complex plane ${\mathbb C}$ and there exists one positive constant c independent of $\phi$ such that

$$\begin{aligned} |\phi (z)|\le ce^{\varrho |z|}, \end{aligned}$$

(2.2)

where $\varrho$ is a positive constant such that $\varrho <\frac{\omega }{\sqrt{2}}.$ Then there holds

$$\begin{aligned}&\int _{a}^be^{i\omega x}(x-a)^{\nu _1}(b-x)^{\nu _2} \phi (x)dx \nonumber \\&=e^{i\omega a}\left( \frac{i}{\omega }\right) ^{1+\nu _1}\int _0^\infty e^{- y} y^{\nu _1}\left( b-a-i\frac{y}{\omega }\right) ^{\nu _2}\phi \left( a+i\frac{y}{\omega }\right) dy\nonumber \\ +&e^{i\omega b}\left( \frac{-i}{\omega }\right) ^{1+\nu _2}\int _0^\infty e^{- y}\left( b-a+i\frac{y}{\omega }\right) ^{\nu _1}y^{\nu _2} \phi \left( b+i\frac{y}{\omega }\right) dy. \end{aligned}$$

(2.3)

Proof

For $0<r<\frac{b-a}{4}$, we introduce six cures as follows

$$\begin{aligned}&\Gamma _1:=\{z=t: a+r\le t\le b-r\},\ \Gamma _2:=\left\{ z=b+re^{i\theta }:\frac{\pi }{2} \le \theta \le \pi \right\} ,\\&\Gamma _3:=\{z=b+iy: r\le y\le R\},\ \Gamma _4:=\left\{ z=t+iR: a\le t\le b\right\} ,\\&\Gamma _5:=\left\{ z=a+iy: r\le y\le R \right\} ,\ \Gamma _6:=\left\{ z=a+re^{i\theta }: 0\le \theta \le \frac{\pi }{2}\right\} , \end{aligned}$$

and then set

$$\begin{aligned} \Gamma :=\Gamma _1+\Gamma _2^-+\Gamma _3+\Gamma _4^-+\Gamma _5^-+\Gamma _6^-. \end{aligned}$$

Let

$$\begin{aligned} F(z):=e^{i\omega z}(z-a)^{\nu _1}(b-z)^{\nu _2}\phi (z),\ \ z\in \mathbb {D}, \end{aligned}$$

where $\mathbb {D}$ is the region bounded by $\Gamma$. Clearly, the function F is analytic in the region $\mathbb {D}$ and continuous on the domain $\mathbb {D}\cup \Gamma$. Let

$$\begin{aligned}&J_1:=\int _{a+r}^{b-r}e^{i\omega t}(t-a)^{\nu _1}(b-t)^{\nu _2}\phi (t)dt,\\&J_2:=ir^{1+\nu _2}e^{i\omega b}\int _\pi ^{\frac{\pi }{2}} e^{ire^{i\theta }}e^{i(1+\nu _2)\theta }(b+re^{i\theta }-a)^{\nu _1}\phi (b+re^{i\theta })d\theta ,\\&J_3:=(-1)^{\nu _2}i^{1+\nu _2}e^{i\omega b}\int _{r}^{R} e^{-\omega y}y^{\nu _2}(b+iy-a)^{\nu _1}\phi (b+iy) dy, \\&J_4:=e^{-\omega R}\int _b^a e^{i\omega t}(t+iR-a)^{\nu _1}(b-t-iR)^{\nu _2} \phi (t+iR)dt,\\&J_5:=-i^{1+\nu _1}e^{i\omega a}\int _r^R e^{-\omega y} y^{\nu _1}(b-a-iy)^{\nu _2}\phi (a+iy) dy,\\&J_6:=ir^{1+\nu _1}e^{i(1+\nu _1)}e^{i\omega a}\int _{0}^{\frac{\pi }{2}} e^{i\omega re^{i\theta }}e^{i\theta }(b-a-re^{i\theta })^{\nu _2}\phi (a+re^{i\theta })d\theta , \end{aligned}$$

then it follows from Cauchy integral theorem that

$$\begin{aligned} J_1+J_2+J_3+J_4+J_5+J_6=0. \end{aligned}$$

(2.4)

Applying $R\rightarrow \infty$ and $r\rightarrow 0$ to both sides of (2.4) and then using the next six estimates

$$\begin{aligned} \lim _{R\rightarrow +\infty ,r\rightarrow 0}J_1&=\int _0^xe^{-i\omega t}(x-t)^{\nu _1}t^{\nu _2}\phi (t)dt,\ \lim _{R\rightarrow +\infty ,r\rightarrow 0}J_2\\&=\lim _{R\rightarrow +\infty ,r\rightarrow 0}J_4 =\lim _{R\rightarrow +\infty ,r\rightarrow 0}J_6=0,\\ \lim _{R\rightarrow +\infty ,r\rightarrow 0}J_3&=(-1)^{\nu _2}i^{1+\nu _2}e^{i\omega b}\int _0^\infty e^{-\omega y}y^{\nu _2}(b+iy-a)^{\nu _1}\phi (b+iy) dy,\\ \lim _{R\rightarrow +\infty ,r\rightarrow 0}J_5&=-i^{1+\nu _1}e^{i\omega a}\int _0^\infty e^{-\omega y} y^{\nu _1}(b-a-iy)^{\nu _2}\phi (a+iy) dy, \end{aligned}$$

conclude that

$$\begin{aligned} \int _{a}^be^{i\omega x}(x-a)^{\nu _1}(b-x)^{\nu _2} \phi (x)dx =&\, i^{1+\nu _1}e^{i\omega a}\int _0^\infty e^{-\omega y} y^{\nu _1}(b-a-iy)^{\nu _2}\phi (a+iy) dy\nonumber \\ +&(-i)^{1+\nu _2}e^{i\omega b}\int _{0}^{\infty } e^{-\omega y}y^{\nu _2}(b+iy-a)^{\nu _1}\phi (b+iy) dy. \end{aligned}$$

(2.5)

Letting $x:=\omega y$ in the last result, we get the desired conclusion. $\square$

For $x\in I$, let

$$\begin{aligned} G_1(x;\omega ,\nu _1,\nu _2):&=(-i)^{1+\nu _2}\int _0^\infty e^{-\omega y} y^{\nu _2}(x+iy)^{\nu _1} dy, \\ G_2(x;\omega ,\nu _1,\nu _2):&=i^{1+\nu _1}\int _0^\infty e^{-\omega y}y^{\nu _1}(x-iy)^{\nu _2} dy. \end{aligned}$$

and then set for $x\in (-1,\infty )$

$$\begin{aligned} \sigma (x):=\left\{ \begin{array}{ll} \infty ,&{} x\in \mathbb {N}_0,\\ 1+x,&{} \text{ otherwise }. \end{array} \right. \end{aligned}$$

(2.6)

Lemma 2.2

Suppose that $\nu _1>-1$ and $\nu _2>0$. Then for any nonnegative integer r, $G_1\in C_{\omega ,0}^{r,\sigma (\nu _1)}(I)$ and $G_2\in C_{\omega ,0}^{r,\sigma (\nu _2)}(I)$.

Proof

We only prove the first result, the other is similar. In fact, when $\nu _1\in \mathbb {N}_0$, it is clear that $G_1\in C_{\omega ,0}^{r,\infty }(I)$. For $\nu _1\not \in \mathbb {N}_0$ and $j\in \mathbb {Z}_r$,

$$\begin{aligned} ({\mathscr {D}}_x^jG_1)(x;\omega ,\nu _1,\nu _2)=(-i)^{1+\nu _2}\int _0^\infty e^{-\omega y}y^{\nu _2}(x+iy)^{\nu _1-j}dy. \end{aligned}$$

Consequently,

$$\begin{aligned} |({\mathscr {D}}_x^jG_1)(x;\omega ,\nu _1,\nu _2)| \le \int _0^\infty e^{-\omega y}y^{\nu _2}(x^2+y^2)^{\frac{\nu _1-j}{2}} dy. \end{aligned}$$

(2.7)

When $j<\nu _1$, then

$$\begin{aligned} |({\mathscr {D}}_x^jG_1)(x;\omega ,\nu _1,\nu _2)|\le&2^{\frac{\nu _1-j}{2}}\int _0^1 e^{-\omega y}y^{\nu _2} dy+2^{\frac{\nu _1-j}{2}}\int _1^\infty e^{-\omega y}y^{\nu _2+\nu _1-j} dy, \nonumber \\ \le&\frac{ 2^{\frac{\nu _1-j}{2}}}{\nu _2+1}+2^{\frac{\nu _1-j}{2}}\omega ^{-1-\nu _2-\nu _1+j} \Gamma (\nu _2+\nu _1+1-j)={\mathscr {O}}(1). \end{aligned}$$

(2.8)

When $\nu _1<j-1<j$, for $y\in [0,\infty )$, there holds that $e^{-\omega y} y^{\nu _2}\le c$ for $\nu _2>0$. Then

$$\begin{aligned} |({\mathscr {D}}_x^jG_1)(x;\omega ,\nu _1,\nu _2)|\le cx^{1+\nu _1-j}\int _{0}^\infty (1+y^2)^{\frac{\nu _1-j}{2}}dy={\mathscr {O}}(1+x^{\sigma (\nu _1)-j}). \end{aligned}$$

(2.9)

When $j-1<\nu _1<j$, a direct observation yields the fact that $e^{-\omega y} y^{\nu _2} (x^2+y^2)^{\frac{1}{2}}\le c$ for $\nu _2>0$. Consequently,

$$\begin{aligned} |({\mathscr {D}}_x^jG_1)(x;\omega ,\nu _1,\nu _2)|={\mathscr {O}}(1+x^{\nu _1-j+1}). \end{aligned}$$

(2.10)

By using definition (2.1), a combination of (2.7)-(2.10) completes the proof. $\square$

Lemma 2.3

Suppose that the function $L\in C_{\omega ,0}^{r,r}(I^2)$ and define Volterra integral function by

$$\begin{aligned} S(x):=\int _0^xL(x,t)e^{-i\omega t}dt,\ \ x\in I. \end{aligned}$$

(2.11)

Then there exist two functions $S_1,S_2\in C_{\omega ,0}^r(I)$ such that

$$\begin{aligned} S(x)=S_1(x)+S_2(x)e^{-i\omega x},\ \ x\in I. \end{aligned}$$

Proof

This result is a consequence of the Lemma 5.2 in [9]. $\square$

Lemma 2.4

Suppose that $\nu _1>-1, \nu _2>0$ and $v\in C_{\omega ,0}^{2\,m,6\,m+1}(I^2)$. Then there exist one function $S\in C_{\omega ,0}^{m,m}(I^2)$ and some functions $c_k\in C_{\omega ,0}^{m}(I)$ for $k\in \mathbb {Z}_{2\,m}$, $d_j\in C_{\omega ,0}^m(I), j\in \mathbb {Z}_{m-1}$ such that

$$\begin{aligned} v(x,t)(x-t)^{\nu _1}t^{\nu _2}=S(x,t)+\sum _{k\in \mathbb {Z}_{2m}}c_{k}(x)(x-t)^{k+\nu _1}t^{\nu _2}+\sum _{j\in \mathbb {Z}_{m-1}}d_{j}(x)t^{j+\nu _2},\ \ x\in I, t\in [0,x]. \end{aligned}$$

(2.12)

Proof

A direct use of the 2m-order Taylor expansion to the function v about the variable t yields that

$$\begin{aligned} v(x,t)=\sum _{k\in \mathbb {Z}_{2m}}\frac{(-1)^k({\mathscr {D}}_t^kv)(x,x)}{k!}(x-t)^k+(x-t)^{2m+1}R(x,t), \end{aligned}$$

(2.13)

where the remainder term R(x, t) is given by

$$\begin{aligned} R(x,t):=-\frac{1}{(2m)!}\int _{0}^{1}({\mathscr {D}}_{t}^{2m+1}v)(x,x+y(t-x))y^{2m}dy. \end{aligned}$$

Again using the Taylor expansion to the above function R about the variable t yields that

$$\begin{aligned} R(x,t)=\sum _{k\in \mathbb {Z}_{m-1}}\frac{({\mathscr {D}}_t^kv)(x,0)}{k!}t^k+t^{m}Q(x,t), \end{aligned}$$

(2.14)

where the remainder term Q(x, t) is given by

$$\begin{aligned} Q(x,t):=\frac{1}{(m-1)!}\int _{0}^{1}({\mathscr {D}}_{t}^{m}R)(x,ts)(1-s)^{m-1}ds. \end{aligned}$$

It is clear that $Q\in C_{\omega ,0}^{m,m}(I^2).$ Substituting the results (2.13) and (2.14) into the left hand of (2.12) produces the desired conclusion with

$$\begin{aligned} S(x,t):=Q(x,t)(x-t)^{2m+1+\nu _1}t^{m+\nu _2},\ \ c_k(x):=\frac{(-1)^k({\mathscr {D}}_t^kv)(x,x)}{k!},\ \ d_j(x):=\frac{({\mathscr {D}}_t^kv)(x,0)}{k!}. \end{aligned}$$

This ends the proof. $\square$

Lemma 2.5

Suppose that the conditions in Lemma 2.4 hold. Let

$$\begin{aligned} {\mathscr {G}}(v;\nu _1,\nu _2)(x):=\int _{0}^x v(x,t)(x-t)^{\nu _1}t^{\nu _2}e^{-i\omega t}dt, \ \ x\in I. \end{aligned}$$

(2.15)

Then there exist two functions $G_1, G_2\in C_{\omega ,0}^{m,\nu }(I)$ with $\nu :=\min \{\sigma (\nu _1),\sigma (\nu _2)\}$ such that

$$\begin{aligned} {\mathscr {G}}(v;\nu _1,\nu _2)(x):=G_1(x)+e^{-i\omega x}G_2(x),\ \ x\in I. \end{aligned}$$

(2.16)

Proof

Substituting the estimate (2.12) into the right hand of (2.15) yields that

$$\begin{aligned} {\mathscr {G}}(v;\nu _1,\nu _2)(x)= & {} {\mathscr {G}}(S;0,0)(x)+\sum _{k\in \mathbb {Z}_{2m}}c_{k}(x){\mathscr {G}}(1;k+\nu _1,\nu _2)(x)\nonumber \\{} & {} +\sum _{j\in \mathbb {Z}_{m-1}}d_{j}(x){\mathscr {G}}(1;0,j+\nu _2)(x). \end{aligned}$$

(2.17)

Following Lemma 2.3, we concludes that there exist two functions $G_{11}, G_{12}\in C_{\omega ,0}^{m,\infty }(I)$ such that

$$\begin{aligned} {\mathscr {G}}(S;0,0)(x)=G_{11}(x)+e^{-i\omega x}G_{12}(x). \end{aligned}$$

(2.18)

On the other hand, making use of Lemma 2.1 with $\phi :=1$, $a:=0$ and $b:=x$, that

$$\begin{aligned} {\mathscr {G}}(1;k+\nu _1,\nu _2)(x) =&G_1(x;\omega ,k+\nu _1,\nu _2)+e^{-i\omega x}G_2(x;\omega ,k+\nu _1,\nu _2),\nonumber \\ {\mathscr {G}}(1;0,j+\nu _2)(x)=&G_1(x;\omega ,0,j+\nu _2)+e^{-i\omega x}G_2(x;\omega ,0,j+\nu _2). \end{aligned}$$

Let

$$\begin{aligned} G_{2,1,k}(x):&=c_{k}(x)G_1(x;\omega ,k+\nu _1,\nu _2),\ \ \ G_{2,2,k}(x):=c_{k}(x)G_2(x;\omega ,k+\nu _1,\nu _2),\\ G_{3,1,j}(x):&=d_{j}(x)G_1(x;\omega ,0,j+\nu _2),\ \ \ \ G_{3,2,j}(x):=d_{j}(x)G_2(x;\omega ,0,j+\nu _2). \end{aligned}$$

It follows from Lemma 2.2 that $G_{2,1,k}, G_{2,2,k}\in C_{\omega ,0}^{m,\sigma (k+\nu _1)}(I),$ $G_{3,1,j}, G_{3,2,j}\in C_{\omega ,0}^{m,\sigma (j+\nu _2)}(I)$, which completes the proof. $\square$

Next we introduce one finite-dimensional space ${V}_{\mu ,r}$ of fractional polynomials, defined by

$$\begin{aligned} V_{\mu ,r}:=\text{ span }\left\{ x^{j+k\mu }: (j,k)\in \mathbb {I}_{\mu ,r} \right\} ,\ \ \mathbb {I}_{\mu ,r}:=\{(j,k): j+k\mu <r, \ \ j+k\mu \not \in \mathbb {N}\}. \end{aligned}$$

Lemma 2.6

Suppose that the kernel function $B\in C_{\omega ,0}^{2\,m,6\,m+1}(I^2)$. If there exist some constants $c_{j,k}$ such that $f\in {V}_{\mu ,6\,m+1}\oplus C_{\omega ,0}^{6\,m+1}(I)$, i.e,

$$\begin{aligned} f(x):=\sum _{(j,k)\in \mathbb {I}_{\mu ,6m+1}}c_{j,k}x^{j+k\mu }+\widetilde{f}(x),\ \ \widetilde{f}\in C_{\omega ,0}^{6m+1}(I), \end{aligned}$$

(2.19)

then there exist two functions $\overline{u},\widetilde{u}\in C_{\omega ,0}^{m,\mu }(I)$ such that the solution u has the form

$$u(x):=\overline{u}(x)+e^{i\omega x}\widetilde{u}(x),\ \ x\in I.$$

Proof

Let $B_n(x,t)$ be the n-time iterative kernel of the kernel function $B_1(x,t):=B(x,t)$, given by

$$\begin{aligned} B_n(x,t):=\int _t^xB_1(x,s)B_{n-1}(s,t)ds,\ \ x,t\in I,\ \ n\ge 2, \end{aligned}$$

thus, the solution u of Eq. (1.1) has the expression

$$\begin{aligned} u(x)=f(x)+\sum _{n\in \mathbb {N}}\int _0^x(x-t)^{n\mu -1}e^{i\omega (x-t)}B_n(x,t)f(t)dt,\ \ x\in I. \end{aligned}$$

(2.20)

Clearly, there exists a positive integer N relative to the integer m such that

$$\begin{aligned} d(x,t):=\sum _{n=N+1}^\infty (x-t)^{n\mu -1}B_n(x,t)\in C_{\omega ,0}^{m,m}(I^2). \end{aligned}$$

If we set

$$\begin{aligned} G(x):=&{\mathscr {G}}(d\widetilde{f};0,0)(x)+\sum _{(j,k)\in \mathbb {I}_{\mu ,6m+1}}c_{j,k}{\mathscr {G}}(d;0,j+k\mu )(x)+\sum _{n\in \mathbb {Z}_N}{\mathscr {G}}(B_n\widetilde{f};n\mu -1,0)(x)\\ +&\sum _{n\in \mathbb {Z}_N}\sum _{(j,k)\in \mathbb {I}_{\mu ,6m+1}}c_{j,k}{\mathscr {G}}(B_n;n\mu -1,j+k\mu )(x),\ \ x\in I. \end{aligned}$$

then the solution u in (2.20) is rewritten as

$$\begin{aligned} u(x)=f(x)+e^{i\omega x}G(x),\ \ x\in I. \end{aligned}$$

(2.21)

It follows from Lemma 2.5 that there exist two functions $F_{11}, F_{12}\in C_{\omega ,0}^{m,\mu }(I)$ such that

$$\begin{aligned} G(x):=F_{11}(x)+e^{-i\omega x}F_{12}(x),\ \ x\in I, \end{aligned}$$

substituting the result above into the right hand of (2.21) with the aid of (2.19) produces the desired conclusion. $\square$

Theorem 2.1

Suppose that the kernel function $B\in C_{\omega ,0}^{2m,6m+1}(I^2)$. If the functions $\widetilde{f}_1,\widetilde{f}_2\in {V}_{6\,m+1,\mu }\oplus C_{\omega ,0}^{6\,m+1}(I)$,i.e,

$$\begin{aligned} f(x):=\widetilde{f}_1(x)+e^{i\omega x}\widetilde{f}_2(x), \ \ x\in I, \end{aligned}$$

(2.22)

where

$$\begin{aligned} \widetilde{f}_l(x):=\sum _{(j,k)\in \mathbb {I}_{\mu ,6m+1}}c_{l,j,k}x^{j+k\mu }+\hat{f}_l(x),\ \ \hat{f}_l\in C_{\omega ,0}^{6m+1}(I),\ \ l=1,2, \end{aligned}$$

then there exists two functions $\overline{u},\widetilde{u}\in C_{\omega ,0}^{m,\mu }(I)$ such that the solution u having the form

$$\begin{aligned} u(x):=\overline{u}(x)+e^{i\omega x}\widetilde{u}(x),\ \ x\in I. \end{aligned}$$

(2.23)

Proof

Let

$$\begin{aligned} v_1(x):=&\widetilde{f}_1(x)+\sum _{n\in \mathbb {N}}\int _0^x(x-t)^{n\mu -1}e^{i\omega (x-t)}B_n(x,t)\widetilde{f}_1(t)dt\\ v_2(x):=&e^{i\omega x}\widetilde{f}_2(x)+e^{i\omega x}\sum _{n\in \mathbb {N}}\int _0^x(x-t)^{n\mu -1}B_n(x,t)\widetilde{f}_2(t)dt. \end{aligned}$$

Clearly,

$$\begin{aligned} u(x)=v_1(x)+v_2(x). \end{aligned}$$

It follows from the classical result in [2] and Lemma 2.6 that $v_1, v_2\in C_{\omega ,0}^{m,\mu }(I)$. This ends the proof. $\square$

3 A Fully Discrete Numerical Method

In this section we are going to consider the spectral method. It is well known that the classical integer order spectral methods are essentially discretization methods for approximating solution of partial-differential equations. The most attractive property of spectral methods may be that when the solution of the problem is infinitely smooth and non- or low-oscillatory, the convergence of the spectral method is exponential. Due to this advantage, spectral methods have achieved great success and become popular in the scientific computing community (see [12,13,14,15,16,17,18,19,20]). But when the original solutions have the singularity, a direct spectral collocation method and a direct spectral Galerkin method are proposed in [17, 18] for solving (1.1) with non-smooth and non-oscillatory solutions, respectively. Although the approximate solution attains the optimal order, its accuracy is low because of a singularity property of the original solution. In order to obtain the exponential convergence of approximate solution for the non-smooth solution, Chen, Shen and Mao in[15] considered a class of generalized Jacobi functions related to fractional calculus, and proposed to use these functions to approximate the solutions of a class of fractional boundary value problems. Error estimates with convergence rate only depending on the smoothness of data were derived therein. In [19], they provide a fractional spectral method that is capable to handle a family of the aforementioned problems in a more efficient way, which achieve spectral convergence for the solution with limited regularity at the end points. In [21, 22], they consider the hp-version collocation method for solving Volterra integro-differential equations. In [12, 13], we propose the fractional spectral collocation method for solving linear and nonlinear VIEs with weakly singular kernels of the second kind. Motivated by the singularity and oscillation analysis in previous section, we are going to approximate two functions $\overline{u}$ and $\widetilde{u}$ in the solution (2.23) by using the fractional spectral-Galerkin method. To this end, for any integer $k\in \mathbb {I}:=\{0,1\}$, we denote by the vector

$$\begin{aligned} \textbf{v}_{n}:=[v_{j,k}: j\in \mathbb {I}, k\in \mathbb {Z}_n ]^T:=[v_{0,0},\ldots ,v_{0,n},v_{1,0},\ldots , v_{1,n}]^T, \end{aligned}$$

and

$$\begin{aligned} \textbf{v}_{n}^-:=[v_{j,k}: j\in \mathbb {I},k\in \mathbb {Z}_n ]^T:=[v_{0,0},\ldots ,v_{0,n},v_{-1,0},\ldots , v_{-1,n}]^T. \end{aligned}$$

For $\alpha ,\beta >-1$, we let $L_{w^{\alpha ,\beta }}^2(I)$ be the Hilbert space associated with the Jacobi weight function $w^{\alpha ,\beta }(x):=(1-x)^\alpha x^\beta$, equipped with the inner product and the corresponding norm

$$\begin{aligned} (\phi ,\psi )_{w^{\alpha ,\beta }}:=\int _{I}w^{\alpha ,\beta }(x)\phi (x)\overline{\psi (x)}dx, \ \ \Vert \phi \Vert _{\alpha ,\beta }:=(\phi ,\phi )_{\alpha ,\beta }^\frac{1}{2}. \end{aligned}$$

Let $J_n^{\alpha ,\beta }(x), n\in \mathbb {N}_0, x\in I$ be Jacobi orthnormal polynomials defined on the interval I with respect to the weight function $w^{\alpha ,\beta }$, which constitute the basis of $L_{w^{\alpha ,\beta }}^2(I)$. The special case $\alpha =\beta =0$ corresponds to the Legendre polynomials. Follow from [23], for any $k\in \mathbb {N}$,

$$\begin{aligned} {\mathscr {D}}_x^kJ_{n}^{\alpha ,\beta }(x)=\sqrt{\chi _{n,k}^{\alpha ,\beta }}J_{n-k}^{\alpha +k,\beta + k}(x),\ \ \ n\ge k\ge 1, \end{aligned}$$

(3.1)

where

$$\begin{aligned} \chi _{n,k}^{\alpha ,\beta }:=\frac{\Gamma (n+1)\Gamma (n+k+\alpha +\beta +1)}{\Gamma (n-k+1)\Gamma (n+\alpha +\beta +1)}={\mathscr {O}}(n^{2k}). \end{aligned}$$

(3.2)

In the second estimate of the equation above we have used the Stirling’s formula. Moreover, when $\alpha ,\beta >-\frac{1}{2}$, there holds

$$\begin{aligned} \Vert J_n^{\alpha ,\beta }\Vert _\infty ={\mathscr {O}}(n^{\max \{\alpha ,\beta \}}). \end{aligned}$$

(3.3)

Introducing a parameter $\lambda$

$$\begin{aligned} \lambda :=\frac{\mu }{m}, \end{aligned}$$

(3.4)

then from the analysis in Theorem 2.1, it is straightforward to approximate u(x) in the space ${\mathbb P}_n^\lambda \oplus e^{i\omega x}{\mathbb P}_n^\lambda$, where ${\mathbb P}_n^\lambda$ is given by

$${\mathbb P}_n^\lambda :=\text{ span }\{x^{\lambda i}: i\in \mathbb {Z}_{n}\}.$$

Now we define by the fractional orthonormal polynomial sequences ${T_n}$ of Legendre type,

$$T_n(x):=\sqrt{\lambda }J_n^{0,\frac{1}{\lambda }-1}(x^{\lambda }), x\in I,$$

which satisfies that condition

$$(T_p,T_q)=(J_p^{0,\frac{1}{\lambda }-1},J_q^{0,\frac{1}{\lambda }-1})_{w^{{0,\frac{1}{\lambda }-1}}}=\delta _{p,q}$$

where $\delta _{p,q}$ is the Kronecker Delta symbol. We also use Fa$\grave{a}$ di Bruno’s formula to $T_n$ and then obtain that there exists a constant c independent of n and x such that

$$\begin{aligned} |({\mathscr {D}}_x^kT_n)(x)|\le c n^{k+\frac{1}{\lambda }-1}x^{\lambda -k},\ \ x\in (0,1]. \end{aligned}$$

(3.5)

Moreover, the set $\{T_n\},n\in \mathbb {N}_0$ constitutes an orthnormal basis of the space $L^2(I)$. Based on this fact, we introduce the finite-dimensional subspace sequences $X_n$ of $L^2(I)$, defined by

$$\begin{aligned} X_{n}:=\text{ span }\{T_{j,p}: j\in \mathbb {I}, p\in \mathbb {Z}_n\},\ \ \ {T}_{j,p}(x):=e^{ij\omega x}T_p(x),\ \ x\in I. \end{aligned}$$

The efficient fractional spectral-Galerkin method for solving (1.1) is to seek a vector $\textbf{u}_n:=[{a}_{k,q}:q\in \mathbb {Z}_n,k\in \mathbb {I}]^T$ such that

$$\begin{aligned} u_n(x):=\sum _{k\in \mathbb {I}}\sum _{q\in \mathbb {Z}_n}a_{k,q}T_{k,q}(x),\ \ x\in I, \end{aligned}$$

satisfying the condition

$$\begin{aligned} (u_n,\phi )=({\mathscr {B}}u_n,\phi )+(f,\phi ),\ \ \text{ for }\ \ \ \text{ any }\ \ \ \phi \in X_{n}. \end{aligned}$$

If we denote by ${\mathscr {P}}_{n}$ the orthogonal projection operator from $L^2(I)$ to $X_{n}$ and set ${\mathscr {B}}_n:={\mathscr {P}}_n{\mathscr {B}}|_{X_n}$ and $f_n:={\mathscr {P}}_nf$, then the equation above is rewritten as

$$\begin{aligned} u_n={\mathscr {B}}_nu_n+f_n. \end{aligned}$$

(3.6)

In the following, we write the matrix form of (3.6). For $p,q\in \mathbb {Z}_n$ and $j,k\in \mathbb {I}$, we define

$$\begin{aligned} a_{j,k,p,q}:=\int _{I}e^{i\omega (k+j) x }T_{p}(x)T_q(x)dx, \end{aligned}$$

(3.7)

and then define matrices

$$\begin{aligned}\textbf{A}_{j,k,n}:=[a_{j,k,p,q}: p,q\in \mathbb {Z}_n],\ \ \ \ \textbf{A}_n:=\left[ \begin{array}{ccc} \textbf{A}_{0,0,n}&{}\textbf{A}_{0,1,n}\\ \textbf{A}_{-1,0,n}&{}\textbf{A}_{-1,1,n}\\ \end{array} \right] . \end{aligned}$$

On the other hand, we define

$$\begin{aligned} b_{j,k,p,q}:=\int _I\int _{0}^xe^{i\omega (1+j)x+i\omega (k-1)t}(x-t)^{\mu -1}B(x,t)T_p(x)T_q(t)dxdt, \end{aligned}$$

(3.8)

and

$$\begin{aligned}\textbf{B}_{j,k,n}:=[b_{j,k,p,q}: p,q\in \mathbb {Z}_n],\ \ \ \ \textbf{B}_{n}:=\left[ \begin{array}{ccc} \textbf{B}_{0,0,n}&{}\textbf{B}_{0,1,n}\\ \textbf{B}_{-1,0,n}&{}\textbf{B}_{-1,1,n}\\ \end{array} \right] . \end{aligned}$$

If we let

$$\begin{aligned} \textbf{f}_{n}^-:= & {} [f_{j,p}:j\in \mathbb {I},p\in \mathbb {Z}_n]^T,\ \ f_{j,p}:=\int _Ie^{i\omega j x} \widetilde{f}_1(x)T_p(x)dx \nonumber \\{} & {} +\int _Ie^{i\omega (j+1) x} \widetilde{f}_2(x)T_p(x)dx,\ \ j=0,-1, \end{aligned}$$

(3.9)

thus equation (3.6) has an equivalent matrix form

$$\begin{aligned} \textbf{A}_n\textbf{u}_n=\textbf{B}_{n}{} \textbf{u}_n+\textbf{f}_n^-. \end{aligned}$$

(3.10)

The exact fractional spectral Galerkin method could not always be used in practice because of the highly oscillatory or weakly singular integral in the matrices. From the computational point of view, we need a fully discrete scheme ready to use for numerical simulation. Thus the quadratures in the matrices will be approximated by general purpose methods in usual. However, these methods may not provide effective results because of the oscillation and singularity. To deal with these integrals efficiently, we design the simplest possible method to obtain the fully discrete form of (3.10), at the same time, the algorithm keeps the optimal convergence order. There are mainly four classes of approaches for calculating oscillatory integrals: asymptotic methods in [24, 25], Filon-type methods in [26, 27], Levin-type methods in [28,29,30,31] and the numerical steepest decent method in [32, 33]. Recently, a new method is presented in [34, 35], which combines the moment free Filon-type method with graded meshes. In this part, we shall first discretize the interval I using a graded meshes, then for each integrals on the subintervals, we use the conventional Gauss-Legendre numerical method and the steepest method to compute the non-oscillatory or low oscillatory and highly oscillatory integrals, respectively. To this end, for $j\in \mathbb {Z}_n$, let $\theta _{j,n}$ and ${\omega }_{j,n}$ be the set of $n+1$ Legendre-Gauss points and the corresponding weights with the Legendre weight function on the interval I. We also let $\widetilde{\theta }_{j,n}$ and $\widetilde{\omega }_{j,n}$ be the set of $n+1$ Laguerre-Gauss points and the corresponding weights with the Laguerre weight function $\widetilde{w}(x):=e^{-x}$ on the interval $[0,\infty )$. Let $\mathbb {P}_n$ be the set of all polynomials of degree not more than n. For $p\in \mathbb {P}_{2n+1}$, let

$$\begin{aligned} {\mathscr {Q}}(p;\omega ,n):=\int _Ie^{i\omega x}p(x)dx. \end{aligned}$$

It is clear that

$$\begin{aligned}&{\mathscr {Q}}(p;0,n)=\sum _{j\in \mathbb {Z}_n}{\omega }_{j,n}p({\theta }_{j,n}),\nonumber \\&{\mathscr {Q}}(p;\omega ,n)=\sum _{j\in \mathbb {Z}_n}\frac{i\widetilde{\omega }_{j,n}}{\omega }p\left( \frac{i\widetilde{\theta }_{j,n}}{\omega }\right) -\sum _{j\in \mathbb {Z}_n}\frac{i\widetilde{\omega }_{j,n}e^{i\omega }}{\omega }p\left( 1+\frac{i\widetilde{\theta }_{j,n}}{\omega }\right) ,\ \ \omega \not = 0. \end{aligned}$$

(3.11)

Suppose $\phi \in C^m(0,1]$ and there exist two constants $\delta \in (0,1)$ and $c_\phi$ depending on $\phi$ such that

$$\begin{aligned} |({\mathscr {D}}_x^m\phi )(x)|\le c_\phi x^{\delta -m},\ \ x\in (0,1]. \end{aligned}$$

(3.12)

Let

$$\begin{aligned} {\mathscr {I}}(\phi ;\omega ,\delta ,m):=\int _Ie^{i\omega x}\phi (x)dx. \end{aligned}$$

(3.13)

In the following we consider the numerical simulation for (3.13). Since $\phi$ may have a singularity at $x=0$, we consider a graded mesh in [36] here. For $M\in \mathbb {N}$, which will be determined in the next section, discretize the interval I by

$$\begin{aligned} 0=h_1<h_2\ldots<h_{M}<h_{M+1}=1,\ \ |I_k|:=h_{k+1}-h_k,\ \ h_k:=\left( \frac{k-1}{M}\right) ^{\frac{m}{\delta }},\ \ \end{aligned}$$

(3.14)

Let

$$\begin{aligned}&\phi _{k}(y):=|I_k|e^{i\omega h_{k}}\phi (|I_k|)y+h_{k}),\ \ \omega _{k}:=\omega |I_k|, \end{aligned}$$

and then set

$$\begin{aligned} \phi _{k}^*(y):=\left\{ \begin{array}{ll} e^{i\omega _{k}y}\phi _{k}(y),&{} |\omega _{k}|\le 1\\ \phi _{k}(y),&{} others,\\ \end{array} \right. \ \ \ \ \omega _k^*:=\left\{ \begin{array}{ll} 0,&{}|\omega _k|\le 1,\\ \omega _k,&{}others. \end{array}\right. \end{aligned}$$

then the integral (3.13) has the form

$$\begin{aligned} {\mathscr {I}}(\phi ;\omega ,\delta ,m)=\sum _{k=1}^{M}{\mathscr {I}}\left( \phi _{k}^*;\omega _{k}^*,\delta ,m\right) . \end{aligned}$$

(3.15)

In order to give the discrete form of ${\mathscr {I}}\left( \phi _{k}^*;\omega _{k}^*,\delta ,m\right)$ for $k=2,3,\ldots ,M$, we denote by ${\mathscr {L}}_r\phi$ the Lagrange interpolation polynomials for $\phi \in C(I)$, i.e,

$$\begin{aligned} ({\mathscr {L}}_r\phi )(x):=\sum _{p\in \mathbb {Z}_{r}}\phi (\theta _{p,r}){{l}}_{p,r}(x),\ \ \ x\in I, \end{aligned}$$

(3.16)

where ${{l}}_{p,n}$ is given by

$$\begin{aligned} l_{p,r}(x):=\frac{\Pi _{q=1,q\not =p}^{r+1}\left( x-\theta _{q,r}\right) }{\Pi _{q=1,q\not =p}^{r+1} \left( \theta _{p,r}-\theta _{q,r}\right) },\ \ x\in I. \end{aligned}$$

Replacing ${\mathscr {I}}\left( \phi _{1}^*;\omega _{1}^*,\delta ,m\right)$ by zero and ${\mathscr {I}}\left( \phi _{k}^*;\omega _{k}^*,\delta ,m\right)$ for $k=2,3,\ldots M$ by ${\mathscr {Q}}({\mathscr {L}}_{r}\phi _{k}^*;\omega _{k}^*,r)$ in (3.15) yields the approximation of ${\mathscr {I}}(\phi ;\omega ,\delta ,m)$ as follows

$$\begin{aligned} {\mathscr {Q}}(\phi ;\omega ,\delta ,M,r):=\sum _{k=2}^M{\mathscr {Q}}({\mathscr {L}}_{r}\phi _{k}^*;\omega _{k}^*,r). \end{aligned}$$

(3.17)

Thus, we can employ the approach (3.17) to estimate the integrals in $\textbf{A}_{n}$ and $\textbf{f}_{n}^-$, respectively. In fact, when $k=j=0$,

$$\begin{aligned} a_{0,0,p,q}=a_{-1,1,p,q}=\delta _{p,q}, \end{aligned}$$

when $j=0,k=1$, it is clear that

$$\begin{aligned} a_{0,1,p,q}={\mathscr {I}}(T_pT_q;\omega ,\lambda ,m),\ \ \ \ a_{-1,0,p,q}:=\overline{{\mathscr {I}}(T_pT_q;\omega ,\lambda ,m)}. \end{aligned}$$

By using (3.17), the fully discrete form of ${a}_{0,1,p,q}$ and ${a}_{-1,0,p,q}$ is obtained by,

$$\begin{aligned} \bar{a}_{0,1,p,q}={\mathscr {Q}}(T_pT_q;\omega ,\lambda ,m,M,n),\ \ \bar{a}_{-1,0,p,q}=\overline{{\mathscr {Q}}(T_pT_q;\omega ,\lambda ,m,M,n)}. \end{aligned}$$

On the other hand, for $j=0,-1$, by the definition (3.9),

$$\begin{aligned} f_{0,p}&={\mathscr {I}}(\widetilde{f}_1T_p;0,\mu ,m)+{\mathscr {I}}(\widetilde{f}_2T_p;\omega ,\mu ,m),\ \ f_{-1,p} \nonumber \\&=\overline{{\mathscr {I}}(\widetilde{f}_1T_p;\omega ,\mu ,m)}+{\mathscr {I}}(\widetilde{f}_2T_p;0,\mu ,m), \end{aligned}$$

(3.18)

similarly as before, using (3.17) yields that

$$\begin{aligned}&\bar{f}_{0,p}={\mathscr {Q}}(\widetilde{f}_1T_p;0,\mu ,m,M,n)+{\mathscr {Q}}(\widetilde{f}_2T_p;\omega ,\mu ,m,M,n),\end{aligned}$$

(3.19)

$$\begin{aligned}&\bar{f}_{-1,p}=\overline{{\mathscr {Q}}(\widetilde{f}_1T_p;\omega ,\mu ,m,M,n)}+{\mathscr {Q}}(\widetilde{f}_2T_p;0,\mu ,m,M,n), \end{aligned}$$

(3.20)

Next we present the fully discrete form of the entries in matrix $\textbf{B}_n$. Similarly as before, suppose that p(x, t) is a two-dimensional polynomial of degree not more than $2n_1+1$ about variable x and $2n_2+1$ about t, let

$$\begin{aligned} {\mathscr {Q}}(p;\omega ,n_1,n_2):=\int _{I^2}e^{i\omega _1 x}p(x,t)dxdt. \end{aligned}$$

Obviously, a use of Gauss quadrature twice yields that

$$\begin{aligned}&{\mathscr {Q}}(p;0,n_1,n_2)=\sum _{k_1\in \mathbb {Z}_{n_1}}\sum _{k_2\in \mathbb {Z}_{n_2}}{\omega }_{k_1,n_1}{\omega }_{k_2,n_2}p({\theta }_{k_1,n_1},{\theta }_{k_2,n_2}).\nonumber \\&{\mathscr {Q}}(p;\omega ,n_1,n_2). =\sum _{k_1\in \mathbb {Z}_{n_1}}\sum _{k_2\in \mathbb {Z}_{n_2}}\frac{i{\omega }_{k_1,n_1}{\omega }_{k_2,n_2}}{\omega }\left( p\left( \frac{i\widetilde{\theta }_{j,n}}{\omega },{\theta }_{k_2,n_2}\right) -e^{i\omega }p\left( 1+\frac{i\widetilde{\theta }_{j,n}}{\omega },{\theta }_{k_2,n_2}\right) \right) . \end{aligned}$$

the second result holds for $\omega \not =0$. Next for $\omega \in (-\infty ,\infty )$, let

$$\begin{aligned} {\mathscr {J}}(\psi ;\omega ,\delta ,m):=\int _{I^2}e^{i\omega x} \psi (x,t)dxdt, \end{aligned}$$

(3.21)

where the function $\psi (x,t)$ satisfies the condition that there exist constants ${\delta }\in (-1,0)$ and $c_\psi$ depending on the function $\phi$ such that

$$\begin{aligned} |{\mathscr {D}}_x^{m}{\mathscr {D}}_t^{m}\psi (x,t)|\le c_\psi \left( x^{\delta -m}+(1-x)^{\delta -m}\right) \left( t^{\delta -m}+(1-t)^{\delta -m}\right) . \end{aligned}$$

(3.22)

In order to give the numerical scheme of the integral above, we discretize the $I^2$ on a graded mesh. To this end, let

$$\begin{aligned}&0=\widetilde{h}_1<\widetilde{h}_2<\cdots<\widetilde{h}_{2M}<\widetilde{h}_{2M+1}=1,&|\widetilde{I}_j|:=\widetilde{h}_{j+1}-\widetilde{h}_j,\\ \end{aligned}$$

where

$$\begin{aligned}&\widetilde{h}_k:=\left\{ \begin{array}{ll}\frac{1}{2}\left( \frac{k-1}{M}\right) ^{\frac{m}{\lambda (\delta )}},&{}k=1,2,\ldots ,M+1,\\ 1-\frac{1}{2}\left( \frac{2M+1-k}{M}\right) ^{\frac{m}{\lambda (\delta )}},&{} k=M+2,M+3,\ldots ,2M+1. \end{array} \right. \end{aligned}$$

Let

$$\begin{aligned}&\psi _{j,k}(y):=|\widetilde{I}_j||\widetilde{I}_k|e^{i\omega \widetilde{h}_{j}}\psi (|\widetilde{I}_j|y+\widetilde{h}_{j},|\widetilde{I}_k|y+\widetilde{h}_{k}),\ \ \widetilde{\omega }_{j}:=\omega |\widetilde{I}_j|, \end{aligned}$$

and then set

$$\begin{aligned} \psi _{j,k}^*(y):=\left\{ \begin{array}{ll} e^{i\widetilde{\omega }_{j}y}\psi _{j,k}(y),&{} |\widetilde{\omega }_{j}|\le 1\\ \psi _{j,k}(y),&{} others,\\ \end{array} \right. \ \ \ \ \widetilde{\omega }_{j}^*:=\left\{ \begin{array}{ll} 0,&{}|\widetilde{\omega }_{j}|\le 1,\\ \widetilde{\omega }_{j},&{}others. \end{array}\right. \end{aligned}$$

then the integral (3.21) is decomposed into the next form

$$\begin{aligned} {\mathscr {J}}(\psi ;\omega ,\delta ,m)=&\sum _{j=1}^{2M}\sum _{k=1}^{2M}{\mathscr {J}}\left( \psi _{j,k}^*;\widetilde{\omega }_{j}^*,\delta ,m\right) . \end{aligned}$$

(3.23)

Let $({\mathscr {L}}_{r_1,r_2}\psi )(x,t)$ denote its two-dimensional interpolation polynomial about two variables x, t of $\psi$, i.e,

$$\begin{aligned} ({\mathscr {L}}_{r_1,r_2}\psi )(x,t):=\sum _{p\in \mathbb {Z}_{r_1}}\sum _{q\in \mathbb {Z}_{r_2}}\psi (\theta _{p,r_1},\theta _{q,r_2})l_{p,r_1}(x)l_{q,r_2}(t),\ \ (x,t)\in I^2. \end{aligned}$$

(3.24)

Next replacing ${\mathscr {J}}\left( \psi _{j,k}^*;\widetilde{\omega }_{j}^*,\delta ,m\right)$ by zero for $j=1,2\,M,k=1,2,\ldots ,2\,M$ and $k=1,2\,M, j=1,2,\ldots ,2\,M$ and others by ${\mathscr {Q}}\left( \psi _{j,k}^*;\widetilde{\omega }_{j}^*,r_1,r_2\right)$ and obtain the numerical scheme

$$\begin{aligned} {\mathscr {Q}}(\psi ;\omega ,\delta ,M,r_1,r_2):=\sum _{j=2}^{2M-1}\sum _{k=2}^{2M-1}{\mathscr {Q}}(\phi _{j,k}^*;\widetilde{\omega }_{j}^*,r_1,r_2). \end{aligned}$$

(3.25)

Next we use the scheme (3.25) to estimate $b_{j,k,p,q}$ in (3.8). For this purpose, let

$$\begin{aligned} B_{k}(x,t;p,q):=T_{p}(x)T_q(t)\left\{ \begin{array}{ll} x^{\mu -1}(1-x)B((1-x)t+x,(1-x)t;p,q),&{} k=1,\\ x^{\mu }(1-t)^{\mu -1}B(x,xt;p,q),&{}k=2,\\ (1-x)^{\mu }t^{\mu -1}B((1-x)t+x,x;p,q),&{}k=3,\\ \end{array} \right. \end{aligned}$$

(3.26)

then

$$\begin{aligned}&b_{0,0,p,q}={\mathscr {J}}(B_1;\omega ,\mu -1,m),&b_{0,1,p,q}={\mathscr {J}}(B_2;\omega ,\mu -1,m),\\&b_{-1,0,p,q}={\mathscr {J}}(B_3;-\omega ,\mu -1,m),&b_{-1,1,p,q}={\mathscr {J}}(B_1;0,\mu -1,m), \end{aligned}$$

Thus, a direct use of the quadrature (3.25) to the entries above yields their approximations

$$\begin{aligned}&\bar{b}_{0,0,p,q}={\mathscr {Q}}(B_1;\omega ,\mu -1,M, n,n),&\bar{b}_{p,q,0,1}={\mathscr {Q}}(B_2;\omega ,\mu -1,M,n,n),\\&\bar{b}_{p,q,-1,0}={\mathscr {Q}}(B_3;-\omega ,\mu -1,M,n,n),&\bar{b}_{p,q,-1,1}={\mathscr {Q}}(B_1;0,\mu -1,M,n,n). \end{aligned}$$

Replacing the entries $a_{j,k,p,q}$, $b_{j,k,p,q}$ and $f_{j,p}$ by the entries $\bar{a}_{j,k,p,q}$, $\widetilde{b}_{j,k,p,q}$ and $\bar{f}_{j,p}$ we likewise define the matrices $\bar{\textbf{A}}_{n}$, $\bar{\textbf{B}}_{n}$, $\bar{\textbf{f}}_n^-$ and its corresponding blocks. Thus, the fully discrete equation (3.10) had the form,

$$\begin{aligned} \bar{\textbf{A}}_n\bar{\textbf{u}}_n=\bar{\textbf{B}}_{n}\bar{\textbf{u}}_n+\bar{\textbf{f}}_n^-. \end{aligned}$$

(3.27)

where the vector $\bar{\textbf{u}}_{n}$ is given by,

$$\begin{aligned} \bar{\textbf{u}}_n:=[\bar{a}_{k,q}:q\in \mathbb {Z}_n, k\in \mathbb {I}]^T. \end{aligned}$$

If we denote by the linear operators $\bar{\mathscr {A}}_n$ and $\bar{\mathscr {B}}_{n}$ such that their matrix representations under the basis $X_{n}$ are ${\bar{\textbf{A}}_{n}}$ and $\bar{\textbf{B}}_{n}$, then Eq. (3.27) has the operator form

$$\begin{aligned} \bar{\mathscr {A}}_n\bar{u}_{n}=\bar{\mathscr {B}}_{n}\bar{u}_{n}+\bar{f}_{n}. \end{aligned}$$

(3.28)

where the functions $\bar{u}_{n}$ and $\bar{f}_{n}$ are given by

$$\begin{aligned} \bar{u}_{n}(x):=\sum _{k\in \mathbb {I}}\sum _{q\in \mathbb {Z}_{n}}\bar{a}_{k,q}L_{k,q}(x),\ \ \ \bar{f}_{n}(x):=\sum _{k\in \mathbb {I}}\sum _{q\in \mathbb {Z}_{n}}\bar{f}_{-k,q}L_{k,q}(x)\ x\in I. \end{aligned}$$

4 Convergence Analysis

This section presents some notations and lemmas and then employs them to establish the existence and uniqueness of the solution in (3.28). The approaches are similar as those in [11]. For the completeness the paper, we are going to give the whole proof process. We first introduce the non-uniformly weighted Sobolev space $H_{w^{\alpha ,\beta }}^r(I)$, given by

$$\begin{aligned} H_{w^{\alpha ,\beta }}^r(I):=\{\phi : {\mathscr {D}}_x^k\phi \in L_{w^{\alpha +k,\beta +k}}^2(I), k\in \mathbb {Z}_r\} \end{aligned}$$

with the norm

$$\begin{aligned} \Vert v\Vert _{w^{\alpha ,\beta },r}:=\sum _{k\in \mathbb {Z}_r}\Vert {\mathscr {D}}_x^k\phi \Vert _{w^{\alpha +k,\beta +k}}. \end{aligned}$$

Besides, we let ${\mathscr {R}}_n^{\alpha ,\beta }$ be the orthogonal projection operator from $L_{w^{\alpha ,\beta }}^2(I)$ to $P_n$. It follows from [23] that there exists a positive constant c such that for $v\in H_{w^{\alpha ,\beta }}^r(I)$,

$$\begin{aligned} \Vert v-{\mathscr {R}}_n^{\alpha ,\beta }v\Vert _{w^{\alpha ,\beta }}\le c \Vert {\mathscr {D}}_x^rv\Vert _{w^{\alpha +r,\beta +r}}n^{-r}. \end{aligned}$$

(4.1)

Moreover, following [23], for the Lagrange interpolation operator associated with the Legendre-Gauss points defined in (3.16), there exists a positive constant c such that for $v\in C^{r}(I)$,

$$\begin{aligned} \Vert v-{\mathscr {L}}_nv\Vert \le c \Vert {\mathscr {D}}_x^rv\Vert _{w^{r,r}} n^{-r}. \end{aligned}$$

(4.2)

We denote by another finite dimensional space $Z_n$,

$$\begin{aligned} {Z}_n:=\text{ span }\{T_p, p\in \mathbb {Z}_n\}, \end{aligned}$$

and then let $Q_n$ be the orthogonal projection operator from $L^2(I)$ to $Z_n$. It is clear that

$${Z}_n\subseteq X_n,$$

which implies that

$$\begin{aligned} {\mathscr {P}}_n{\mathscr {Q}}_n={\mathscr {Q}}_n. \end{aligned}$$

(4.3)

It is obvious that for $v\in C^{m,\mu }(0,1]$, then $v^{\star }(x):=v(x^{\frac{1}{\lambda }})\in C^m(I)$, which implies that

$$\begin{aligned} \Vert v-{\mathscr {Q}}_nv\Vert = \Vert v^{\star }-{\mathscr {R}}_n^{0,\frac{1}{\lambda }-1}v^{\star }\Vert _{w^{0,\frac{1}{\lambda }-1}}={\mathscr {O}}(n^{-m}). \end{aligned}$$

(4.4)

Following Theorem 2.1,

$$\begin{aligned} \Vert \overline{u}-{\mathscr {Q}}_n\overline{u}\Vert ={\mathscr {O}}(n^{-m}),\ \ \ \ \Vert \widetilde{u}-{\mathscr {Q}}_n\widetilde{u}\Vert ={\mathscr {O}}(n^{-m}). \end{aligned}$$

(4.5)

Moreover,

$$\begin{aligned}u(x)-({\mathscr {P}}_nu)(x)&=\overline{u}(x)+e^{i\omega x}\widetilde{u}(x)-({\mathscr {P}}_n)(\overline{u}(x)+e^{i\omega x}\widetilde{u}(x))\\&=\overline{u}(x)-({\mathscr {Q}}_n\overline{u})(x)+({\mathscr {Q}}_n\overline{u})(x)-({\mathscr {P}}_n{\mathscr {Q}}_n\overline{u})(x)\\&\quad +e^{i\omega x}\widetilde{u}(x)-e^{i\omega x}({\mathscr {Q}}_n\widetilde{u})(x)+e^{i\omega x}({\mathscr {Q}}_n\widetilde{u})(x)-({\mathscr {P}}_n(e^{i\omega x}{\mathscr {Q}}_n\widetilde{u}))(x), \end{aligned}$$

consequently,

$$\begin{aligned} \Vert u-{\mathscr {P}}_nu\Vert \le 2\Vert \overline{u}-{\mathscr {Q}}_n\overline{u}\Vert +2\Vert \widetilde{u}-{\mathscr {Q}}_n\widetilde{u}\Vert ={\mathscr {O}}(n^{-m}). \end{aligned}$$

(4.6)

Lemma 4.1

Suppose the condition (3.12) holds, then there exists a positive constant c independent of $\phi$ such that

$$\begin{aligned} |{\mathscr {I}}(\phi ;\omega ,\delta ,m)-{\mathscr {Q}}(\phi ;\omega ,\delta ,M,r)|\le c M^{-m}. \end{aligned}$$

(4.7)

Similarly, if (3.22) holds, then

$$\begin{aligned} |{\mathscr {J}}(\psi ;\omega ,\delta ,m)-{\mathscr {Q}}(\psi ;\omega ,\delta ,M,r_1,r_2)|\le c M^{-m}, \end{aligned}$$

(4.8)

Proof

We only prove the first result (4.7), the other is similar. Following (3.13) and (3.17),

$$\begin{aligned} {\mathscr {I}}(\phi ;\omega ,\delta ,m)-{\mathscr {Q}}(\phi ;\omega ,\delta ,M,r)&={\mathscr {I}}(\phi _{1};\omega _{1},\delta ,m) \nonumber \\&+\sum _{k=2}^{M}\left( {\mathscr {I}}\left( \phi _{k};\omega _{k},\delta ,m\right) -{\mathscr {Q}}({\mathscr {L}}_{r}\phi _{k}^*;\omega _{k}^*,r)\right) . \end{aligned}$$

(4.9)

The left thing is to estimate (4.9). Firstly,

$$\begin{aligned} |{\mathscr {I}}(\phi _{1};\omega _{1},\delta ,m)|=\int _{h_1}^{h_2}|\phi (x)|dx\le c M^{-m}. \end{aligned}$$

(4.10)

Secondly, using (4.2) yields that

$$\begin{aligned} | {\mathscr {I}}\left( \phi _{k};\omega _{k},\delta ,m\right) -{\mathscr {Q}}({\mathscr {L}}_{r}\phi _{k}^*;\omega _{k}^*,r)|&\le c r^{-m}\Vert {\mathscr {D}}_x^m\phi _{k}^*\Vert _{w^{m,m}}\nonumber \\&\le c r^{-m}|I_k|^{m+1} h_k^{\delta -m}\le c r^{-m}M^{-m-1}. \end{aligned}$$

(4.11)

In the last result we use the inequality of Theorem 2.1 in [36]. A combination of three results (4.9)–(4.11) yields the desired conclusion. $\square$

Following (3.5) and (3.26), there holds

$$\begin{aligned} |({\mathscr {D}}_x^m(T_pT_q))(x)|= |({\mathscr {D}}_x^m(\widetilde{f}_jT_p))(x)|={\mathscr {O}} (n^{m+\frac{1}{\lambda }-1}x^{\lambda -m}),\ \ x\in (0,1], \end{aligned}$$

and

$$\begin{aligned} |\left( {\mathscr {D}}_x^{m}{\mathscr {D}}_t^{m}B_k\right) (x)|= & {} {\mathscr {O}} (n^{2m+\frac{1}{\lambda }-1}(x^{\mu -1-m}\\{} & {} +(1-x)^{\mu -1-m}) (t^{\mu -1-m}+(1-t)^{\mu -1-m})),\ \ x,t\in (0,1], \end{aligned}$$

which confer that

$$\begin{aligned} |a_{j,k,p,q}-\bar{a}_{j,k,p,q}|= & {} |f_{j,p}-\bar{f}_{j,p}|={\mathscr {O}}(n^{m+\frac{1}{\lambda }-1}M^{-m}), \\{} & {} |b_{j,k,p,q}-\bar{b}_{j,k,p,q}|={\mathscr {O}}(n^{2m+\frac{1}{\lambda }-1}M^{-m}). \end{aligned}$$

Consequently,

$$\begin{aligned}&\Vert \textbf{A}_n-\bar{\textbf{A}}_n\Vert _1=\Vert \textbf{A}_n-\bar{\textbf{A}}_n\Vert _\infty ={\mathscr {O}}(n^{m+\frac{1}{\lambda }}M^{-m}), \\&|\textbf{B}_n-\bar{\textbf{B}}_n\Vert _1=|\textbf{B}_n-\bar{\textbf{B}}_n\Vert _\infty ={\mathscr {O}}(n^{2m+\frac{1}{\lambda }}M^{-m}). \end{aligned}$$

where the symbol $\Vert \textbf{G}\Vert _{k}$ is used to denote its k-norm, $k\in \{1,2,\infty \}$. From the well-known inequality that $\Vert \textbf{G}\Vert _2^2\le \Vert \textbf{G}\Vert _1\Vert \textbf{G}\Vert _\infty$, we conclude

$$\begin{aligned}&|\textbf{A}_n-\bar{\textbf{A}}_n\Vert _2={\mathscr {O}}(n^{m+\frac{1}{\lambda }}M^{-m}), \nonumber \\&|\textbf{B}_n-\bar{\textbf{B}}_n\Vert _2={\mathscr {O}}(n^{2m+\frac{1}{\lambda }}M^{-m}),\nonumber \\&|\textbf{f}_n-\bar{\textbf{f}}_n\Vert _2={\mathscr {O}}(n^{m+\frac{1}{\lambda }}M^{-m}). \end{aligned}$$

(4.12)

Lemma 4.2

Suppose that the conditions in Theorem 2.1 hold. If we choose M in (4.12) as follows

$$\begin{aligned} M:=n^{3+\frac{1}{\mu }}, \end{aligned}$$

(4.13)

then there exist a positive constant $\omega _0$ and a positive constant c such that $\omega \ge \omega _0$,

$$\begin{aligned} \Vert (\bar{\mathscr {A}}_{n}-{\mathscr {I}}){\mathscr {P}}_{n}v\Vert \le c n^{-m},\ \ \Vert (\bar{\mathscr {B}}_{n}-{\mathscr {B}}_n){\mathscr {P}}_{n}v\Vert \le c n^{-m}. \end{aligned}$$

(4.14)

Proof

We only prove the first result in (4.14), the other is similar. By the definition of norm,

$$\begin{aligned} \Vert (\bar{\mathscr {A}}_{n}-{\mathscr {I}}){\mathscr {P}}_{n}v\Vert&=\sup _{w\in X_{n}, \Vert w\Vert =1}\left| \left( (\bar{\mathscr {A}}_{n}-{\mathscr {I}}){\mathscr {P}}_{n}v, w\right) \right| \nonumber \\&=\sup _{w\in X_{n}, \Vert w\Vert =1}\left| \left( (\bar{\mathscr {A}}_{n}-{\mathscr {I}}){\mathscr {P}}_{n}v, {\mathscr {P}}_{n}w\right) \right| . \end{aligned}$$

(4.15)

For $w,v\in L^2(I)$, we express their projection onto $X_{n}$ as

$$\begin{aligned} ({\mathscr {P}}_{n}w)(x)=\sum _{k\in \mathbb {I}}\sum _{q\in \mathbb {Z}_{n}}w_{k,q}L_{k,q}(x),\ \ ({\mathscr {P}}_{n}v)(x)=\sum _{k\in \mathbb {I}}\sum _{q\in \mathbb {Z}_{n}}v_{k,q}L_{k,q}(x),\ \ x\in I. \end{aligned}$$

(4.16)

Two coefficient vectors in (4.16) are denoted by $\textbf{v}_{n}^-$ and $\textbf{w}_{n}$, respectively. From (4.16) and the definition of the operators $\textbf{A}_{n}$ and $\bar{\textbf{A}}_{n}$, we obtain that

$$\begin{aligned} (({\mathscr {I}}-\bar{\mathscr {A}}_{n}){\mathscr {P}}_{n}w, {\mathscr {P}}_{n}v)= & {} {\textbf{v}_{n}^{-}}^T(\textbf{A}_{n}-\bar{\textbf{A}}_{n})\textbf{w}_{n},\ \ \Vert {\mathscr {P}}_{n}w\Vert ^2 \nonumber \\= & {} \Vert {\textbf{w}_{n}^-}^T\textbf{A}_{n}{} \textbf{w}_{n}\Vert ,\ \ \ \Vert {\mathscr {P}}_{n}v\Vert _n^2=\Vert {\textbf{v}_{n}^-}^T\textbf{A}_{n}{} \textbf{v}_{n}\Vert . \end{aligned}$$

(4.17)

A direct application of the Lebesgue-Riemann theorem produces that

$$\begin{aligned} \lim _{\omega \rightarrow \infty }\int _I e^{i\omega x}\phi (x)dx=0,\ \ \phi \in C(I), \end{aligned}$$

(4.18)

which confers that

$$\begin{aligned} \lim _{\omega \rightarrow \infty }{} \textbf{A}_{n}=\textbf{I}_{4n+4}, \end{aligned}$$

(4.19)

where $\textbf{I}_{n+1}$ is the identity matrix of order $n+1$. Consequently, there exists a positive constant $\omega _0$ such that $\omega \ge \omega _0$,

$$\begin{aligned} \Vert \textbf{v}_{n}^-\Vert \le \Vert {\mathscr {P}}_{n}v\Vert ,\ \ \Vert \textbf{w}_{n}\Vert \le \Vert {\mathscr {P}}_{n}w\Vert . \end{aligned}$$

(4.20)

A combination of two estimates (4.17) and (4.20), we have that

$$\begin{aligned} \left| (({\mathscr {I}}-\bar{\mathscr {A}}_{n}){\mathscr {P}}_{n}v, {\mathscr {P}}_{n}w)\right| \le \Vert \textbf{A}_{n}-\bar{\textbf{A}}_{n}\Vert _2\Vert v\Vert \Vert w\Vert . \end{aligned}$$

(4.21)

which and the first result (4.12) with the choice of M in (4.13) yield the desired conclusion. $\square$

Next we observe that Theorem 2.1 means that there exists a positive constant $\rho$ such that for $v\in L^2(I)$,

$$\begin{aligned} \Vert ({\mathscr {I}}-{\mathscr {B}})v\Vert \ge \rho \Vert v\Vert . \end{aligned}$$

(4.22)

Theorem 4.1

Suppose that the conditions in Lemma 4.2 hold. Then there exists a positive integer $n_0$ and one constant $\omega _0$ such that for $n\ge n_0$, $\omega \ge \omega _0$ and $v\in X_n$

$$\begin{aligned} \Vert \bar{\mathscr {A}}_nv-\bar{\mathscr {B}}_{n}v\Vert \ge \frac{\rho }{2}\Vert v\Vert , \end{aligned}$$

(4.23)

where $\rho$ appears in (4.22). Moreover, the numerical solution $\bar{n}_n$ defined by (3.28) has the estimate

$$\begin{aligned} \Vert u-\bar{u}_n\Vert \le c n^{-m} . \end{aligned}$$

(4.24)

Proof

By using the compactness of the operator ${\mathscr {B}}$, there exists a positive constant $n_1$ such that $n\ge n_1$,

$$\begin{aligned} \Vert {\mathscr {B}}v-{\mathscr {B}}_nv\Vert \le \frac{\rho }{4}\Vert v\Vert . \end{aligned}$$

(4.25)

On the other hand, if follows from the result (4.14) that there exist a positive integer $n_2$ and one positive constant $\omega _0$ such that $n\ge n_2$ and $\omega \ge \omega _0,$

$$\begin{aligned} \Vert \tilde{\mathscr {A}}v-v\Vert +\Vert {\mathscr {B}}_nv-\bar{\mathscr {B}}_nv\Vert \le \frac{\rho }{4}\Vert v\Vert . \end{aligned}$$

(4.26)

A combination of (4.22), (4.25) and (4.26) and the next result

$$\begin{aligned} \Vert \bar{\mathscr {A}}_nv-\bar{\mathscr {B}}_nv\Vert \ge \Vert v-{\mathscr {B}}v\Vert -\Vert {\mathscr {B}}v-{\mathscr {B}}_nv\Vert - \Vert \tilde{\mathscr {A}}v-v\Vert +\Vert {\mathscr {B}}_nv-\bar{\mathscr {B}}_nv\Vert \end{aligned}$$

yields the first desired conclusion (4.23) with $n_0:=n_1+n_2$.

In order to estimate (4.24), we first observe that

$$\begin{aligned} \Vert u-\bar{u}_n\Vert \le \Vert u-{\mathscr {P}}_nu\Vert +\Vert {\mathscr {P}}_nu-\bar{u}_n\Vert . \end{aligned}$$

(4.27)

It follows from the estimate (4.6) that we were only required to estimate the second term of the right hand side of (4.27). In fact, employing both sides of (1.1) by ${\mathscr {P}}_n$ yields that

$$\begin{aligned} {\mathscr {P}}_nu={\mathscr {P}}_n{\mathscr {B}}u+{\mathscr {P}}_nf. \end{aligned}$$

(4.28)

A direct computation of (3.28) and (4.28) confirms that

$$\begin{aligned} \bar{\mathscr {A}}_n(\bar{u}_{n}-{\mathscr {P}}_nu)=\bar{\mathscr {B}}_{n}(\bar{u}_{n}-{\mathscr {P}}_nu)+({\mathscr {I}}-\bar{A}_n){\mathscr {P}}_nu+(\bar{\mathscr {B}}_n-{\mathscr {B}}_n){\mathscr {P}}_nu+{\bar{f}_n-f_n}+{\mathscr {P}}_n{\mathscr {B}}({\mathscr {P}}_nu-u). \end{aligned}$$

By Theorem 4.1, there exists a positive integer $n_0$ such that $n\ge n_0$,

$$\begin{aligned} \Vert {\mathscr {P}}_nu-\bar{u}_n\Vert \le c \Vert ({\mathscr {I}}-\bar{A}_n){\mathscr {P}}_nu\Vert +\Vert (\bar{\mathscr {B}}_n-{\mathscr {B}}_n){\mathscr {P}}_nu\Vert +\Vert {\bar{f}_n-f_n}\Vert +\Vert {\mathscr {P}}_n{\mathscr {B}}({\mathscr {P}}_nu-u)\Vert . \end{aligned}$$

(4.29)

It is clear that there exists a positive constant $\omega _0$ such that for $\omega \ge \omega _0$,

$$\begin{aligned} \Vert {\bar{f}_n-f_n}\Vert ^2\le \Vert ({\bar{\textbf{f}}_n-\textbf{f}_n})^T\textbf{A}_n({\bar{\textbf{f}}_n-\textbf{f}_n})^-\Vert \le cn^{-2m}. \end{aligned}$$

Substituting the results (4.6), (4.13) and the estimate above into the right hand side of Eq. (4.29) produces that

$$\begin{aligned} \Vert {\mathscr {P}}_nu-\bar{u}_n\Vert \le c n^{-m}. \end{aligned}$$

(4.30)

A combination of three estimates (4.27), (4.29) and (4.30) completes the proof. $\square$

Theorem 4.1 shows that the approximate equation (3.27) has a unique solution and the approximate solution reaches the optimal convergence order. Next we denote by $\textrm{cond}(\textbf{G}):=\Vert \textbf{G}\Vert \Vert \textbf{G}^{-1}\Vert$ its spectral condition number for any nonsingular square matrix $\textbf{G}$. Following Theorem 14.9 in [3], the stability of the corresponding linear system (3.27) is established in the next result.

Theorem 4.2

Suppose that the conditions in Theorem 4.1 hold. Then there exist a positive constant c and a positive integer $n_0$ and $\omega _0$ such that $n\ge n_0$ and $\omega \ge \omega _0$,

$$\begin{aligned} \textrm{cond}(\bar{\textbf{A}}_n-\bar{\textbf{B}}_n)\le c. \end{aligned}$$

5 Numerical Experiments

In this section, we present two examples to illustrate the effectiveness and accuracy of our proposed method. Here, we compute the Gauss-Jacobi quadrature rule nodes and weights by Theorem 3.4 and Theorem 3.6 discussed in [23]. All computer programs are compiled with the Matlab language. In the following example, the error $\Vert u-\bar{u}_n\Vert$ is computed by sampling at the points $\{\tau _j\}=0.01j$ for $j\in \mathbb {Z}_{100}$, i,e.,

$$\begin{aligned} \Vert u-\bar{u}_n\Vert \approx \frac{1}{100}\left( \sum _{j\in \mathbb {Z}_{100}}|u(\tau _j)-\bar{u}_n(\tau _j)|^2\right) ^\frac{1}{2}. \end{aligned}$$

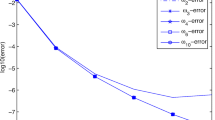
We also choose $n:=2,4,6,8,10,12$, and $\omega :=\omega _k:=10^{4k},\ \ k=1,2,3,4$ so as to show the efficiency of our hybrid fractional spectral Galerkin method. Following from the result (4.13) we let $M:=n^5$.

Example 5.1

In the first example, we suppose that the kernel function $B:=-1$ and $\mu :=\frac{1}{2}$. We choose the output function f so that the exact solution $u(x):=e^{i\omega x} x^{\frac{1}{2}},\ \ \ x\in I$. A direct computation produces that

$$\begin{aligned} f(x):=e^{i\omega x}\left( x^\frac{1}{2}+x\int _0^x(x-t)^{-\frac{1}{2}}t^\frac{1}{2}dt\right) =e^{i\omega x}\left( x^\frac{1}{2}+x\textbf{beta}\left( \frac{3}{2},\frac{1}{2}\right) \right) . \end{aligned}$$

By the definition of $\lambda$ in (3.4) we choose $\gamma :=0.5$ with $m:=1$, which implies that $\overline{u}(x^{0.5}), \widetilde{u}(x^{0.5})\in C^\infty (I)$. As expected, the errors show an exponential decay, since in this semi-log representation the error variations are essentially linear versus the degrees of the polynomial (Table 1).

Table 1 Our proposed efficient spectral method for Example 5.1

Example 5.2

In the second example, we also let the kernel function $B:=-1$ and $\mu :=\frac{1}{3}$. We choose the output function f so that the exact solution $u(x):= e^{i\omega x}x^{\frac{1}{3}},\ \ \ x\in I$. A direct computation produces that

$$\begin{aligned} f(x):=e^{i\omega x}\left( x^\frac{1}{3}+x\int _0^x(x-t)^{-\frac{2}{3}}t^\frac{1}{3}dt\right) =e^{i\omega x}\left( x^\frac{1}{3}+x^\frac{2}{3}\textbf{beta}\left( \frac{4}{3},\frac{1}{3}\right) \right) . \end{aligned}$$

By the definition of $\lambda$ in (3.4) we choose $\gamma :=1/3$ with $m:=1$, which implies that $\overline{u}(x^{1/3}), \widetilde{u}(x^{1/3})\in C^\infty (I)$. Hence, the theoretical results shows that the numerical errors will decay with an exponential rate. As expected, the numerical tests accord with the theoretical results since in this semi-log representation the error variations are essentially linear versus the degrees of the polynomial (Table 2) .

Table 2 Our proposed efficient spectral method for Example 5.2

6 Conclusion

The main purpose of this paper is to present the singularity and oscillation of the original of second kind classical Volterra integral equations with highly oscillatory and weakly singlar kernels. Then, based on this structure, we have developed an efficient numerical algorithm and then obtained the desired stability and convergence results in the space $L^2(I)$. In the future work, we will study the fast algorithm for this highly oscillatory problems.