Abstract
In this paper, we present a pressure-based semi-implicit numerical scheme for a first order hyperbolic formulation of compressible two-phase flow with surface tension and viscosity. The numerical method addresses several complexities presented by the PDE system in consideration: (i) The presence of involution constraints of curl type in the governing equations requires explicit enforcement of the zero-curl property of certain vector fields (an interface field and a distortion field); the problem is solved by adopting a set of compatible discrete curl and gradient operators on a staggered grid, allowing to preserve the Schwarz identity of cross-derivatives exactly at the discrete level. (ii) Since the complexity of the studied PDE system does not allow the explicit computation of its exact eigenvalues, reliable and precise analytical estimates are provided. (iii) The evolution equations feature highly nonlinear stiff algebraic source terms which are used for the description of viscous interactions as emergent behaviour of an elasto-plastic solid in the stiff strain relaxation limit; such source terms are reliably integrated with a novel and very efficient semi-analytical technique proposed for the first time in this paper. (iv) In the low-Mach number regime, standard explicit density-based Godunov-type schemes lose efficiency and accuracy; the issue is addressed by means of a simple semi-implicit, pressure-based, split treatment of acoustic and non-acoustic waves, again using staggered grids that recover the implicit solution for a single scalar field (the pressure) through a sequence of symmetric-positive definite linear systems that can be efficiently solved via the conjugate gradient method.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This work is part of a sequence of papers [26, 32, 42, 51, 52, 54, 62, 105, 120] dedicated to the extension and numerical solution of a first order hyperbolic Unified Model of Continuum Mechanics (UMCM), sometimes also called GPR model, in honor of the seminal works of Godunov and Romenski [67, 70, 73, 110] and Peshkov and Romenski [103] on the subject. Besides its first order hyperbolic character, the model in consideration has the notable feature of describing any continuum, ranging from elasto-plastic solids to viscous Newtonian, non-Newtonian and inviscid fluids, in a unified mathematical formulation (hence the designation of Unified Model of Continuum Mechanics), with only the material parameters and the characteristic strain relaxation time \(\tau \) mediating the distinction between solids and fluids within a single set of first order hyperbolic partial differential equations.
The model draws its origins in the seminal work of Godunov and Romenski [68,69,70, 73,74,75, 104, 113] on symmetric hyperbolic and thermodynamically compatible (SHTC) systems. In [103] Peshkov and Romenski advanced the key insight that the Godunov–Romenski model of nonlinear hyperelasticity in Eulerian coordinates [73] may be applied not only to elasto-plastic solids, but to fluid flows as well, up to then unexplored in this framework, with the notable exception of the early paper of Besseling [18], in which an equivalent formalism was introduced. The same modelling approach is employed in [14, 44, 58, 59, 66, 76, 97] for the study of elasto-plastic solids, and in [81, 82] with explicit reference to the fluid applications proposed by Peshkov and Romenski in [103]. SHTC systems have also been used to model the dynamics of compressible two-phase flows, see e.g. [91, 111, 112, 121].
In this paper, the Eulerian equations of nonlinear hyperelasticity of Godunov and Romenski [73] are employed for the purpose of introducing viscous-type forces in the hyperbolic two-phase flow model with surface tension of Gavrilyuk and collaborators [17, 116]. Furthermore, in [42] the authors have shown that the originally weakly hyperbolic model of surface tension given in [116] cannot be solved by means of general purpose Godunov-type schemes without explicitly accounting for the curl involution constraints that naturally arise in the model due to the direct evolution of gradient fields. In [42] it was shown that strong hyperbolicity can be restored by either adding appropriate nonconservative symmetrising Godunov–Powell-type [71, 107, 108] terms to the system, or by means of a new conservative generalized Lagrangian multiplier (GLM) curl-cleaning approach, which extends the seminal ideas of Munz et al. [46, 94] from classical hyperbolic divergence cleaning to the hyperbolic cleaning of curl constraints, see also [29, 55]. Such curl involutions also naturally appear in an alternative model for surface tension based on a first order hyperbolic reformulation of the Navier–Stokes–Korteweg equations [47] and in first order hyperbolic reformulations of the nonlinear Schrödinger equation of quantum hydrodynamics [48].
The governing PDE system solved in this paper belongs to the larger class of diffuse interface models for compressible multiphase flows. For a non-exhaustive overview of diffuse interface models, the reader is, for example, referred to [6, 9, 14, 28, 44, 45, 58, 59, 64, 83, 84, 97, 98, 109, 114] and references therein. Compared to [42] in the present work the problem of the curl involutions is tackled in a totally different manner by adopting a special combination of compatible discrete gradient and curl operators on a staggered grid like in [26, 105], so that curl involutions are by construction exactly preserved up to machine precision. As such, the method used here falls into the class of mimetic discretizations, see e.g. [10, 13, 80, 89, 92]. In this way (i.e. whenever the curl constraints are satisfied exactly), the GLM curl-cleaning and the Godunov–Powell formulations of the model given in [42] simply coincide exactly with the original weakly hyperbolic model [116] and viceversa, since only discrete zeros are introduced in either formulation. Compared to the structure-preserving semi-implicit method proposed in [26], besides the application to a new PDE system, the scheme presents several novel aspects aimed at improving its robustness and accuracy: in particular with regards to the implementation of momentum and energy updates due to the implicit pressure solver included in the method, while preserving the same semi-implicit split discretisation that enables the efficient application of the method to low Mach number flows.
The new scheme introduced in this paper employs a novel semi-analytical time integration method for the stiff strain relaxation source terms, which represent a rather challenging task, especially in the context of two-phase flows. This time integrator extends the ideas introduced in [27, 41, 120] to the full equations of the Unified Model of Continuum Mechanics in the fluid regime, thanks to a convenient polar decomposition of the stretch and rotation components of the distortion (or co-basis) field. Moreover, the numerical method is constructed in such a way that it can discretely preserve uniform pressure, uniform velocity multiphase flows, regardless of the distribution of density or volume fraction, i.e. it satisfies the Abgrall criterion [4].
The paper is structured as follows: in Sect. 2 we briefly introduce the first order hyperbolic model for compressible viscous two phase flows with surface tension considered in this work. In Sect. 3 we detail the numerical method developed for the solution of such a model, with particular attention given to the discretisation of involution constraints and the split treatment of convective and acoustic phenomena. We also provide a simple recipe for computing accurate analytical eigenvalue estimates for the PDE system here considered. In Sect. 4 we present a novel semi-analytical technique for the integration of the stiff strain relaxation sources that appear in the governing PDE system. Furthermore, we provide some details concerning the mathematical structure of the governing equations. In Sect. 5 we show an extensive selection of numerical experiments, including convergence results for the numerical method, an experimental verification of the uniform flow compatibility of the scheme, formally proven in Sect. 3, an experimental verification of the curl involution compatibility, and large scale simulations of colliding droplets and gravity-driven multiphase Rayleigh–Taylor instabilities. In Sect. 6 we summarise the conclusions that can be drawn from the results presented in the paper, and we point towards some possible future research directions.
2 First Order Hyperbolic Model for Two-Phase Viscous Flow with Surface Tension
The basis of the governing equations studied in this paper formally resembles the Kapila system [83] (sometimes called five-equation Baer–Nunziato [12] model) which describes two-phase flows under the pressure and velocity equilibrium hypothesis. In addition to the Kapila (sub)-system, a vector-valued equation for an interface field \({\varvec{\textrm{b}}}\) is employed in order to track interfaces and provide a hyperbolic description of surface tension [17, 42, 116]. Furthermore, another matrix-valued field \({\varvec{\textrm{A}}}\), called distortion field or cobasis, is used to model the deformation of the fluid in consideration, which is actually described as a visco-elastoplastic solid with stiff strain relaxation, that is, a stiff relaxation source is included in the governing equations such that the strain encoded in the components of the cobasis matrix \({\varvec{\textrm{A}}}\), see [103].
The first order hyperbolic system for single velocity, single-pressure, compressible two-phase flow with surface tension and hyperbolic viscosity then reads
where \(\rho _1\) and \(\rho _2\) are the mass densities of phase number 1 and 2, respectively, \(\alpha _1\) and \(\alpha _2\) their volume fractions; the velocity vector is denoted by \({\varvec{\textrm{u}}}\); \(\rho E\) is the total energy density, p is the mixture pressure and the mixture density is given by \(\rho = \alpha _1\,\rho _1 + \alpha _2\,\rho _2\).
The first two Eqs. (1a, 1b) state mass conservation for each phase, Eq. (1c) is the momentum balance for the mixture, with the source term accounting for constant gravitational acceleration \({\varvec{\textrm{g}}}\). The energy balance law is (1d) and Eq. (1e) governs the evolution of the volume fraction of the first phase, which due to the saturation constraint \(\alpha _1 + \alpha _2 = 1\) is sufficient to characterise the dynamics of both volume fractions.
The vector \({\varvec{\textrm{b}}}\) in (1f) is an interface field which represents the gradient of a scalar colour function c and its components are evolved independently as three separate state variables, rather than computed as the discrete gradient of c. Due to the field \({\varvec{\textrm{b}}}\) representing the gradient of a scalar, it must be curl-free, i.e. it is required to satisfy
It can easily be checked that if (2) holds at the initial time, then due to (1f) it remains curl-free for all times.
The vectors \({\varvec{\textrm{a}}}_{1}\), \({\varvec{\textrm{a}}}_{2}\), and \({\varvec{\textrm{a}}}_{3}\) are the rows of a three-by-three nonsymmetric matrix \({\varvec{\textrm{A}}}\), here called distortion, and \({\varvec{\textrm{Z}}}\) is a \(3 \times 3\) strain relaxation source term
where the deviator operator is defined as the trace-free part of a generic tensor \({\varvec{\textrm{T}}}\) as \({{\,\textrm{dev}\,}}({\varvec{\textrm{T}}}) = {\varvec{\textrm{T}}} - \frac{1}{3} {{\,\textrm{tr}\,}}({\varvec{\textrm{T}}})\,{\varvec{\textrm{I}}}\). The homogeneous part of (1g) shares exactly the same structure with Eq. (1f) and thus each one of the rows of \({\varvec{\textrm{A}}}\) can be discretised in the same manner. The presence of the source term, however, couples the three vector equations for the distortion matrix, which means that, unlike the spatial discretisation, the complete time integration of these equations cannot be carried out independently of each other.
The parameter \(\tau \) is called strain relaxation time for the mixture and is computed from a logarithmic interpolation \(\tau = \tau _1^{\alpha _1}\,\tau _2^{1 - \alpha _1}\), where the relaxation times of each phase are set as \(\tau _1 = 6\,\nu _1/c_\textrm{s}^2\) and \(\tau _2 = 6\,\nu _2/c_\textrm{s}^2\) to fit the kinematic viscosities \(\nu _1\) and \(\nu _2\) of the two fluids. For simplicity, in this work we take \(c_\textrm{s}\), a parameter representing the propagation speed of small-amplitude shear waves, to be common for both phases.
For each phase we assume that the equation of state has the following form
with \(\gamma _1\), \(\gamma _2\), \(\varPi _1\), \(\varPi _2\) given parameters of the equation of state and \(\rho \,e_1\) and \(\rho \,e_2\) the internal energy densities of the two phases. Due to the pressure equilibrium assumption \(p_1 = p_2 = p\), the mixture equation of state then reads
where \(\rho \,e\) is the internal energy density of the mixture. Furthermore, for this choice of closure relation, we have
with
According to [116] the capillary stress tensor is given by
where \(\sigma \) is a constant that characterizes surface tension. Furthermore, the total energy density reads in terms of the other state variables
with \(\rho \,e_\textrm{s} = \rho \,c_\textrm{s}^2\,{{\,\textrm{tr}\,}}{\left( {{\,\textrm{dev}\,}}{\varvec{\textrm{G}}}\,{{\,\textrm{dev}\,}}{{\varvec{\textrm{G}}}}\right) }/4\) the energy associated with elastic/shear stress, \(\rho \,e_\textrm{t} = \sigma \,\Vert {\varvec{\textrm{b}}}\Vert \) the surface energy density, and \(\rho \,e_\textrm{k} = \rho \,\Vert {\varvec{\textrm{u}}}\Vert ^2/2\) the kinetic energy density. For this choice of elastic energy potential, the elastic stress tensor reads
where \({\varvec{\textrm{G}}} = {\varvec{\textrm{A}}}^{\mathsf {{\tiny T}}}\,{\varvec{\textrm{A}}}\) is the metric tensor for the fluid mixture, which in the SHTC formalism is guaranteed to be symmetric and positive definite by construction at the discrete level, since it is computed from the distortion matrix \({\varvec{\textrm{A}}}\) rather than evolved directly. For an alternative equation of state in terms of \({\varvec{\textrm{A}}}\) with better mathematical properties, see [97].
3 Numerical Method
The scheme proposed in this work is based on a multiply staggered Cartesian discretisation introduced in [26] that employs special gradient and curl operators that can be used to evolve sensitive involution-constrained quantities such as the interface field that is used to track material interfaces and compute surface tension forces. This allows to solve the weakly hyperbolic surface tension model given in [116] without curl cleaning procedures, due to the fact that, if curl involutions are enforced exactly, the weakly hyperbolic model and its augmented hyperbolic variants collapse onto the same stable system.
The semi-discrete time discretization combined with a staggered grid allows to discretely recover a numerical scheme for the incompressible Navier–Stokes equations in the low Mach number limit, see also [1, 16, 23,24,25, 31, 37, 43, 49, 86,87,88, 95, 96, 102, 119, 122] for an incomplete overview of some semi-implicit all and low Mach number schemes for compressible gasdynamics. At the same time the new method proposed in this section eliminates the accuracy and efficiency issues of explicit density-based Godunov-type methods: the timestep restriction due to acoustic waves is lifted at the rather limited cost of solving a sequence of sparse symmetric-positive-definite systems for the scalar pressure at each timestep. Together with a suitable discretisation of the nonlinear convective fluxes with low dissipation, this enables the second-order spatially accurate method to achieve results that are comparable with schemes that formally feature a much higher order of accuracy, such as those forwarded in [42].
Finally, the method employs a semi-analytical integration technique for the strain relaxation sources of the unified model of continuum mechanics, introduced in Sect. 4, in order to robustly compute viscous forces in flows with high spatial and parametric variability.
3.1 Flux-Splitting Approach
The semi-implicit curl-preserving numerical method presented in this work is based on a three way split of the governing equations, such that convection, capillarity, strain, and acoustic effects are treated separately, each with an ad-hoc discretisation. In particular: (i) a MUSCL–Hancock scheme with primitive variable reconstruction and positivity preserving limiting is adopted for the solution of the convective part of the system; (ii) an implicit staggered conservative scheme is used to compute the unknown pressure field as the solution of a simple discrete wave equation leading to a well-behaved symmetric positive definite system of linear equations. This lifts timestep restrictions due to acoustic waves and preserves the accuracy of the method in the low-Mach regime; (iii) the evolution of geometric involution constrained fields associated with material distortion \({\varvec{\textrm{A}}}\) and material interfaces \({\varvec{\textrm{b}}}\) is carried out with ad-hoc discrete differential operators that can preserve the curl involutions of the governing equations exactly at the discrete level up to machine precision.
In sequence, at each timestep, first, the convective update of the conserved variable is computed via a path-conservative [34, 100] MUSCL–Hancock method, and at the same time the quantities \({\varvec{\textrm{A}}}\) and \({\varvec{\textrm{b}}}\), that are endowed with curl constraints, are evolved in time with a simple two-stage Runge–Kutta scheme, which adopts the semi-analytical solver introduced in Sect. 4 for strain relaxation. Following this, corner fluxes due to viscous forces and capillarity can be computed. Then, a discrete wave equation, derived from a staggered discretisation of the momentum-energy system, can be solved for the unknown scalar pressure and finally, since a robust predictor for all state variables has been obtained, momentum and energy interface fluxes can be computed and used to update the conserved variables to the next time level in a conservative fashion.
The system (1) can be written with matrix–vector notation as
with the state vector
a flux tensor \({\varvec{\textrm{F}}}({\varvec{\textrm{Q}}})\), a non-conservative product \({\varvec{\textrm{B}}}({\varvec{\textrm{Q}}}) \, \nabla {\varvec{\textrm{Q}}}\), and an algebraic source term \({\varvec{\textrm{S}}}({\varvec{\textrm{Q}}})\). As proposed in [26, 49, 53] the flux tensor is split into a pressure part, and a convective part, to be treated partially by means of a path-conservative MUSCL–Hancock scheme, partially with a special compatible and structure-preserving discretization using a vertex-based staggered grid. Hence, Eq. (10) is rewritten as
where \({\varvec{\textrm{F}}}_c({\varvec{\textrm{Q}}}) \) and \({\varvec{\textrm{B}}}_c({\varvec{\textrm{Q}}})\) contain the convective terms that will be discretized explicitly; \({\varvec{\textrm{F}}}_p({\varvec{\textrm{Q}}})\) are the pressure fluxes that will be discretized implicitly using an edge-based staggered grid. The resulting splitting into pressure and convective fluxes is identical to the flux-vector splitting scheme of Toro and Vázquez-Cendón recently forwarded in [124]. The terms \({\textbf{F}}_v({\varvec{\textrm{Q}}}) \), \(\nabla {\varvec{\textrm{K}}}_v({\varvec{\textrm{Q}}})\) and \({\varvec{\textrm{B}}}_v({\varvec{\textrm{Q}}}) \nabla {\varvec{\textrm{Q}}}\) are discretized in a structure-preserving manner using an explicit scheme on a vertex-based staggered mesh. The split fluxes read
The convective part of the non-conservative product is given by
The evolution of the curl-free vector field \({\textbf{b}}\) and the distortion matrix \({\varvec{\textrm{A}}}\) is governed by the terms \(\nabla {\varvec{\textrm{K}}}_v({\varvec{\textrm{Q}}})\), \({\varvec{\textrm{B}}}_v({\varvec{\textrm{Q}}}) \, \nabla {\varvec{\textrm{Q}}}\), and \({\varvec{\textrm{S}}}_v({\varvec{\textrm{Q}}})\), with
and
which accounts for the strain relaxation effects. For clarity, we specify that the tensor notation \(\left( \nabla {\varvec{\textrm{A}}} - \nabla {\varvec{\textrm{A}}}^{\mathsf {{\tiny T}}}\right) \,{\varvec{\textrm{u}}}\) yields a three by three matrix whose rows \({\varvec{\textrm{a}}}_k\) are the obtained by computing \(\left( \nabla {\varvec{\textrm{a}}}_k - \nabla {\varvec{\textrm{a}}}_k^{\mathsf {{\tiny T}}}\right) \,{\varvec{\textrm{u}}}\) for each row \({\varvec{\textrm{a}}}_k\) from \({\varvec{\textrm{a}}}_1\) to \({\varvec{\textrm{a}}}_3\), see [51] for a formulation in tensor index notation. The remaining source terms, corresponding to gravity forces, are included in the pressure sub-system as
As already mentioned before, the subsystem
will be discretized explicitly. The discretization method presented in the next section is a combination of a classical second order MUSCL–Hancock type [123, 125, 126] TVD finite volume scheme for the convective fluxes \({\varvec{\textrm{F}}}_c\) and the nonconservative term \({\varvec{\textrm{B}}}_c\,\nabla {\varvec{\textrm{Q}}}\), a curl-free discretization for the terms \({\varvec{\textrm{K}}}_v\), and \({\varvec{\textrm{B}}}_v \, \nabla {\varvec{\textrm{Q}}}\) using compatible gradient and curl operators, a semi-analytical integration technique for the relaxation source \({\varvec{\textrm{S}}}_v\), as well as a vertex-based discretization of the terms \({\varvec{\textrm{F}}}_v\). The pressure subsystem
is formally identical to the Toro–Vázquez pressure system [124], with the simple addition of gravity sources \({\varvec{\textrm{S}}}_p\) and is discretized implicitly.
3.2 Eigenvalue Estimates
Due to the large size of the hyperbolic PDE system coupling convective, acoustic, thermal, shear, and capillarity effects, it is at the present time impossible to explicitly compute the eigenstructure of the full system, that is, the eigenvalues and eigenvectors of the system matrix \({\varvec{\textrm{C}}}_1 = {\varvec{\textrm{C}}}\cdot \hat{{\varvec{\textrm{n}}}}\) in the direction specified by the unit vector \(\hat{{\varvec{\textrm{n}}}}\). Formally, \({\varvec{\textrm{C}}}\) is defined as
the quasi-linear form of the governing equations
recalling that the general first order balance law reads
As a matter of fact, even the eigenvalues of \({\varvec{\textrm{C}}}\) can be obtained in closed form only with several simplificative assumptions, such as setting the distortion matrix \({\varvec{\textrm{A}}}\) to the identity or the gradient field \({\varvec{\textrm{b}}}\) to null. Moreover, even the numerical computation of the eigenvalues of the system can become prohibitively expensive as the system matrix of the fully coupled system for two-phase flow with shear and surface tension is large enough that application of standard numerical eigenvalue methods whenever a Riemann solver of Rusanov of HLL type is evaluated is rather wasteful from a computational standpoint.
Since the Rusanov flux only requires an estimate of the maximum absolute eigenvalue \(\lambda _\textrm{max}\) of the system matrix, one might be tempted to employ a power iteration method (Von Mises iteration or Rayleigh quotient iteration) for the computation of the spectral radius of the matrix. However, even the evaluation of the Jacobian matrix for a given state vector is arithmetically very intensive and thus it is preferable to avoid the procedure entirely, favouring instead simpler estimates that can be computed directly from the state vector.
A practical and effective choice, which we found to be rather safe for the estimation of the spectral radius of the Jacobian matrix of the full system, while only leading to occasional mild overestimates, is setting
with
where \(\lambda _\textrm{ps}\) accounts for mixed pressure/shear waves, and \(\lambda _\textrm{t}\) is an estimate of the contribution due to capillarity waves only. In principle, the eigenvalues of the full model including two-phase flow, shear and surface tension appear to couple all effects in mixed shear-pressure-capillarity waves, and the same is true for the surface tension sub-system yielding acoustic-capillary waves, the shear sub-system yielding pressure-shear waves, thus it is impossible to rigorously assign a wavespeed to only one of the effects. Nonetheless, by means of numerical experimentations, we found that surprisingly robust and accurate estimates of the maximum absolute eigenvalue of the system can be achieved with appropriate choices of the two estimates \(\lambda _\textrm{ps}\), and \(\lambda _\textrm{t}\), which are given in the following paragraphs.
3.2.1 Wavespeed Estimate for Capillarity Waves
We begin discussing the eigenvalue estimates for the capillary sub-system, The full eigenstructure of the capillarity sub-system
can be computed analytically, as shown in [42]. A simple estimate for the speed associated with capillarity waves \(\lambda _\textrm{t}\) can therefore be computed analytically by recognising different velocities (i.e. the adiabatic sound speed) in the expression of the eigenvalues for the system of two-phase flow with surface tension, as already formally detailed in [42]. For clarity, we recall that the capillarity tensor has the form
and K is computed as \(K = \left( \rho _2\,a_2^2 - \rho _1\,a_1^2\right) \,\alpha _1\,\alpha _2/(\alpha _1\,\rho _2\,a_2^2 + \alpha _2\,\rho _1\,a_1^2)\). We generically denote with a the mixture speed of sound (adiabatic pressure waves), which, for Kapila-type models such as those considered in this section, is the Wood [127] speed of sound which reads
with the frozen soundspeeds \(a_1\) and \(a_2\) computed as
due to the stiffened gas equation of state being adopted for both phases. Note that for single phase flow, the Wood sound speed a simply coincides with the adiabatic soud speed.
The simplest estimate for the speed associated with capillarity waves \(\lambda _\textrm{t}\), is then given by
We refer to [42] for a detailed derivation of the eigenstructure of the capillarity sub-system.
3.2.2 Wavespeed of Large Amplitude Pressure-Shear Waves
The sub-system for two-phase flow with viscosity, which of course can also model hyperelastic solids by simply settings the relaxation time \(\tau \rightarrow \infty \), reads
By algebraic manipulation of the system matrix appearing in the quasilinear form of (30), one can find that the eigenvalues do not depend directly on the nine components of \({\varvec{\textrm{A}}}\), but only on the metric tensor \({\varvec{\textrm{G}}} = {\varvec{\textrm{A}}}^{\mathsf {{\tiny T}}}\,{\varvec{\textrm{A}}}\). In three space dimensions, i.e. for a general metric tensor of the form
one has that the three eigenvalues \(\lambda _1\), \(\lambda _2\), and \(\lambda _3\) associated with mixed pressure/shear waves are the square roots of the eigenvalues of the symmetric matrix
with
Note that the above expression for the components of \({\varvec{\textrm{M}}}\) is associated with the system matrix of the system projected along the x-axis direction, i.e. for \(\hat{{\varvec{\textrm{n}}}} = {(1,\ 0,\ 0)}^{\mathsf {{\tiny T}}}\). However, due to the rotational invariance of the governing equations, it is always possible to define a local reference frame in which the new x direction is that along which the directional eigenvalue estimate is sought, that would be along any of the outward normal vectors of the space-time faces when computing approximate Riemann fluxes. The characteristic polynomial (a cubic in terms of the square of \(\lambda \)) associated with \({\varvec{\textrm{M}}}\) then reads
and can be solved analytically for \(\lambda ^2\) by means of the Del Ferro–Tartaglia–Cardano procedure [33]. However, from a computational standpoint, it is much more efficient and accurate to apply the Jacobi method to the symmetric matrix \({\varvec{\textrm{M}}}\) directly. In any case we formally set the wavespeed estimate due to mixed pressure/shear waves to be \(\lambda _\textrm{ps} = \max \left( \lambda _1,\ \lambda _2,\ \lambda _3\right) \), with \(\lambda _1^2,\ \lambda _2^2,\ \lambda _3^2\) obtained by solving (34).
In two space dimensions, the \(G_{13}\) and \(G_{23}\) components of the metric tensor \({\varvec{\textrm{G}}}\) vanish, thus the eigenvalues of the system can be found as the square roots of the eigenvalues of a simplified matrix
for which closed form expression are easy to compute and write. In particular the components of (32) simplify to
and the eigenvalues of the sub-model for two-phase flow with shear, associated with pressure/shear waves are
with
For small deformations, i.e. when \({\varvec{\textrm{G}}}\rightarrow {\varvec{\textrm{I}}}\), it is easy to verify that the components of (36) further simplify to
and thus the linearised estimates for the eigenvalues are recovered
as given and employed in [51]. For simplicity, when adopting semi-implicit schemes, such as the one presented in this paper, the estimates for the eigenvalues used in the Rusanov dissipation and to define the timestep size, are taken to be the same used for explicit methods, but setting the adiabatic sound speed to \(a = 0\), reflecting the fact that the implicit solution of the pressure subsystem eliminates the timestep restrictions due to acoustic waves.
3.3 Validation of the Analytical Eigenvalue Estimates
The safety and sharpness of the proposed eigenvalue estimates can be assessed by carrying out an experimental comparison of such analytical estimates with the eigenvalues iteratively computed from the system Jacobian matrix associated with a given state, which can be assumed to be exact up to machine errors.
The novelties introduced here involve the explicit exact computation of the out-of-equilibrium eigenvalues of the shear subsystem, as opposed to the simple equilibrium estimates adopted in previous work in the literature [26, 51], as well as the combination of the estimates for separate subsystems.
In order to consider a representative sample of all possible configurations in the space spanned by the primitive variables \({\varvec{\textrm{V}}} = \left( {\rho _1,\ \rho _2,\ {\varvec{\textrm{u}}},\ p,\ \alpha _1,\ {\varvec{\textrm{b}}},\ {\varvec{\textrm{A}}}}\right) \) and the material parameters \({\varvec{\textrm{P}}} = {\left( \gamma _1,\ \gamma _2,\ \varPi _1, \varPi _2,\ c_\textrm{s},\ \sigma \right) }\), we choose 10 000 points according to the random sampling technique presented in the following paragraphs. The use of random exploration methods is due to the fact that the dimensionality of the state-space renders impractical its sampling with regular grids or in general without statistically based techniques.
Let \({\mathcal {U}}\left( x_1,\ x_2\right) \) be a random variable uniformly distributed in the interval \([x_1,\ x_2]\), and let \({\mathcal {L}}\left( x_1,\ x_2\right) \) be a second kind of random variable generating values ranging between \(x_1\) and \(x_2\) with uniformly distributed logarithms in the interval \([\log (x_1),\ \log (x_2)]\). The samples for the states \({\varvec{\textrm{V}}}\) and parameters \({\varvec{\textrm{P}}}\) will be generated with the aid of several instances of the random variables \({\mathcal {U}}\) and \({\mathcal {L}}\), each extracted independently. Hence the notation \(y_1 = {\mathcal {U}}\left( x_1,\ x_2\right) \), \(y_2 = {\mathcal {U}}\left( x_1,\ x_2\right) \) is to be read as: \(y_1\) is randomly picked with uniform probability in the interval \([x_1,\ x_2]\), and \(y_2\) is a second independent sample picked in the same way. For vectors, \({\mathcal {U}}_3\left( x_1,\ x_2\right) \) and \({\mathcal {L}}_3\left( x_1,\ x_2\right) \) collect three independent extractions of \({\mathcal {U}}\) and \({\mathcal {L}}\) respectively, one for each component of a vector. In the same way, for matrices, \({\mathcal {U}}_{3,3}\left( x_1,\ x_2\right) \) will generate nine independent components of a three-by-three matrix, uniformly distributed according to \({\mathcal {U}}\).
In our numerical experiments, a first subset of the state variables is chosen, with SI units, as
then we extract the material parameters
Finally, for each sample, the pressure p and surface tension coefficient \(\sigma \) are computed as
these choices being aimed at enforcing that the reference velocities for each subsystem, a for acoustics and \(a_\sigma \) for capillarity, be adequately sampled across a wide range of orders of magnitude and relative ratios. In particular, for the specific 10 000 samples shown in Fig. 1, the Mach number \(\Vert {\varvec{\textrm{u}}}\Vert /a\) is smoothly distributed (in log-scale) between \(1.3\times 10^{-6}\) and \(1.2\times 10^5\), and the same can be said for the ratios \(a_\sigma /a \in [2.2\times 10^{-6},\ 1.7\times 10^5]\) and \(c_\textrm{s}/a \in [1.3\times 10^{-6},\ 5.0\times 10^4]\), indicating that all possible flow configurations, from subsonic to strongly supersonic, surface tension dominated, shear dominated, acoustically dominated, and all in-between regimes have been adequately sampled.
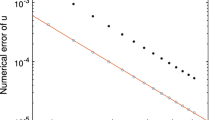
Validation of the proposed analytical eigenvalue estimates against reference eigenvalues computed numerically from the system Jacobian matrix (10 000 random points logarithmically distributed in phase space). In the top panels, on the left we compare the magnitude of the maximum eigenvalue \(\lambda _\textrm{max}\) with the estimates adopted in previous works in the literature (e.g. [26, 51] for the GPR model without surface tension), on the right we show the estimates proposed in this paper. In the bottom panels, we show a scatterplot of the relative error for the small-deformation estimates adopted in the literature and for the proposed estimates on the left and on the right respectively. Note that while the small-deformation estimates can produce error of large magnitude (80% less than the reference, meaning a fifth of the exact value), no underestimates are found with the proposed methodology
With reference to Fig. 1, the simple estimates adopted in past works (valid in the small deformation case, and thus referred to as equilibrium or small-deformation eigenvalues) gave underestimates below 99% of the exact value in 36% of the cases (3637 instances out of 10 000), with 21% of these (2098 samples) below 80% of the exact value and 7% yielding less than half of the exact value. About 1.6% of the samples (157) are overestimated by 20% or more and one sample exceeds the exact value by 40%.
On the other hand, the approach presented in this paper produces no underestimates (0 samples), with the maximum relative underestimate being \(3.9\times 10^{-10}\) (credibly due to machine errors). The top panels of Fig. 1 clearly show (note the logarithmic scaling of the y-axis) the magnitude of the errors of small-deformation-based estimates when applied in the regime of large deformations and the complete lack of such issues when the more accurate expressions presented in this work are used.
The number of overestimated samples (above 20% of the exact value) increases only mildly to 2.2% (223) (from 1.6%) and again only one sample exceeds the exact value by 40%. This occasional over-estimation of the eigenvalues of the system is due to the simple combination method, given in Eq. (24), for the wavespeeds of the separate sub-systems, since in absence of surface tension effects, Eqs. (34) and (37)–(38) for the multiphase flow system with shear are exact. See also the bottom panels of Fig. 1 for a visualisation of the distribution of the positive and negative errors for both approaches, highlighting the reliability of the analytical expressions presented in this work.
3.4 Explicit Discretisation of the Convective Subsystem
3.4.1 Data Reconstruction and Slope Limiting
In order to achieve second order spatial accuracy for the convective fluxes, a data reconstruction yielding a piecewise first-degree polynomial representation of the state variables, denoted by \({\varvec{\textrm{Q}}}^\textrm{r}_{ij}(x,\ y)\), must be carried out. For our PDE system, it is convenient to compute such a reconstruction in the primitive variable space, specified by choosing as a primitive state vector
which is related to the conserved state \({\varvec{\textrm{Q}}}\) by
Then we denote the primitive-variable reconstruction polynomial as \({\varvec{\textrm{V}}}^\textrm{r}(x,\ y) = {\mathcal {P}}\left[ {\varvec{\textrm{Q}}}^\textrm{r}(x,\ y)\right] \), and, complementarily, the conserved variable reconstruction polynomial is \({\varvec{\textrm{Q}}}^\textrm{r}(x,\ y) = {\mathcal {C}}\left[ {\varvec{\textrm{V}}}^\textrm{r}(x,\ y)\right] \). For the sake of clarity, we remark that the primitive-to-conserved operator \({\mathcal {C}}\) and conserved-to-primitive operator \({\mathcal {P}}\), due to their nonlinear nature, are to be read as pointwise operations, and the evaluation points will be explicitly stated in the following whenever conversion of state variables is necessary.
For each cell of index i, the left and right differences are computed in the primitive variable space as \(\varDelta {\varvec{\textrm{V}}}_L = {\varvec{\textrm{V}}}_{i} - {\varvec{\textrm{V}}}_{i-1}\) and \(\varDelta {\varvec{\textrm{V}}}_R = {\varvec{\textrm{V}}}_{i+1} - {\varvec{\textrm{V}}}_{i}\) respectively. They are then combined in a nonlinear fashion to ensure non-oscillatory property of the resulting scheme. In particular, we employ a simple slope limiter that can be computed as
where \(\epsilon = 10^{-14}\) is a small constant that avoids division by zero and all operations are to be taken componentwise.
The slope limiter (46) yields the minmod slope for \(\beta = 1\) and reduces to the MUSCL–Barth–Jespersen limiter for \(\beta = 3\). In all our numerical tests we set \(\beta = 2\).
The preliminary (undivided) slope \(\widetilde{\varDelta {\varvec{\textrm{V}}}}_i\) is then corrected to enforce the positivity of the reconstructed values of density and pressure, as well as the unit-sum constraints on the volume fractions \(\alpha _1\) and \(\alpha _2\). This is achieved by rescaling the slope with
having set
where, with reference to the primitive variable state vector (44), we have set the lower and upper bounds for each variable as
The values of H, \({\varvec{\textrm{h}}}\), and \({\varvec{\textrm{H}}}\) are set to a large arbitrary scalar, vector or matrix (like \(H = 10^{40}\)) to represent the absence of an upper or lower bound for the corresponding variable. The same sequence of operations is carried out in the y-direction to compute \(\varDelta {\varvec{\textrm{V}}}_j\). Then the primitive reconstruction polynomial can be evaluated at any point in space as
3.4.2 Computation of Convective Fluxes
The convective terms are explicitly integrated by means of a path-conservative MUSCL–Hancock scheme. The fully discrete one-step update formula reads
which is then applied to the convective subsystem and used to formally define a convective state \({\varvec{\textrm{Q}}}_{ij}^*= {\varvec{\textrm{Q}}}_{ij}^{n+1}\), which in particular is
For the computation of the conservative numerical fluxes we employ the simple Rusanov Riemann solver
where the signal speed estimates \(s_1^\textrm{max}\) and \(s_2^\textrm{max}\), i.e. the maximum absolute eigenvalues of the convective subsystem, in the first or second space direction, associated with a pair of states \({\varvec{\textrm{v}}}_L\) and \({\varvec{\textrm{v}}}_R\), are given by
An important consideration is that, in order to achieve a compatible discretisation of density, momentum, and kinetic energy in uniform flows, the jump of conserved variables \({\mathcal {C}}({\varvec{\textrm{v}}}_R) - {\mathcal {C}}({\varvec{\textrm{v}}}_L)\) must exclude the difference of internal energies. Thus, instead of \({\varDelta E = \rho \,E({\varvec{\textrm{v}}}_R) - \rho \,E({\varvec{\textrm{v}}}_L)}\), the jump in the energy conservation equation will be
where we recall \(e_\textrm{k} = \Vert {\varvec{\textrm{u}}}\Vert ^2/2\), \(e_\textrm{s} = c_\textrm{s}^2\,{{\,\textrm{tr}\,}}{\left( {{\,\textrm{dev}\,}}{{\varvec{\textrm{G}}}}\,{{\,\textrm{dev}\,}}{{\varvec{\textrm{G}}}}\right) }/4\), \(e_\textrm{t} = \sigma \,\Vert {\varvec{\textrm{b}}}\Vert /\rho \).
Nonconservative products are discretised within the path-conservative formalism [34, 100]. This means that, at each cell interface, generically indexed with \({i+1/2,j}\), in addition to numerical fluxes, two so-called fluctuations, denoted by \({{\varvec{\textrm{D}}}_{i+1/2,j}^-\left( {\varvec{\textrm{v}}}_L,\ {\varvec{\textrm{v}}}_R\right) }\) and \({{\varvec{\textrm{D}}}_{i+1/2,j}^+\left( {\varvec{\textrm{v}}}_L,\ {\varvec{\textrm{v}}}_R\right) }\), have to be computed. Our choice of for the discrete jump terms (fluctuations) is such that, the left and right fluctuations have the same value and may be denoted as \({\varvec{\textrm{D}}}_{i+1/2,j}\left( {\varvec{\textrm{v}}}_L,\ {\varvec{\textrm{v}}}_R\right) \). The same holds in the y-direction for \({\varvec{\textrm{D}}}_{i,j+1/2}^-\left( {\varvec{\textrm{v}}}_L,\ {\varvec{\textrm{v}}}_R\right) \) and \({\varvec{\textrm{D}}}_{i,j+1/2}^+\left( {\varvec{\textrm{v}}}_L,\ {\varvec{\textrm{v}}}_R\right) \). The fluctuations are computed with a three-point point quadrature rule over a segment path \({\varvec{\mathrm {\Psi }}}({\varvec{\textrm{v}}}_L,\ {\varvec{\textrm{v}}}_R,\ s) = (1 - s)\,{\varvec{\textrm{v}}}_L + s\,{\varvec{\textrm{v}}}_R\) in the primitive state space. Their discrete expressions read
where the nonconservative products for the convective subsystem are given by
with \(K = \left( \rho _2\,a_2^2 - \rho _1\,a_1^2\right) \,\alpha _1\,\alpha _2/(\alpha _1\,\rho _2\,a_2^2 + \alpha _2\,\rho _1\,a_1^2)\). For clarity, we explicitly give also the expressions for the fluxes of the convective subsystem
while the source term is simply \({\varvec{\textrm{S}}} = {\varvec{\textrm{0}}}\).
At each cell interface, of generic index \(i+\frac{1}{2}, j\) in the x-direction or \(i, j+\frac{1}{2}\) in the y-direction, the boundary-extrapolated states \({\varvec{\textrm{v}}}_L\) and \({\varvec{\textrm{v}}}_R\) are taken from a cell-local space-time predictor solution \({\varvec{\textrm{v}}}_{ij}(t,\ x,\ y)\). In particular, the space-time midpoint values for each face are
and they are explicitly computed as
where
For the sake of clarity, it should be pointed out that the primitive-to-conserved and conserved-to-primitive conversion operators in Eq. (60) are to be read as pointwise operations, or equivalently the formula can be taken as a projection between two different polynomial spaces, one in which the conserved variables are polynomials but the primitive ones are not, and viceversa, but it is not strictly satisfied in any point except those where the conversion of state variables has taken place, i.e. the space-time barycenters of each face.
3.5 Staggered Mesh and Discrete Divergence, Curl and Gradient Operators
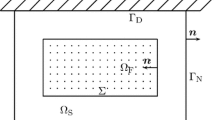
The numerical scheme is presented in a two-dimensional context. However, it is necessary and beneficial to retain all components of three-dimensional vectors to simplify the treatment of the relaxation source term, which acts on all components of the distortion matrix, regardless of whether derivatives in some direction vanish, or not. We consider a two-dimensional computational domain \( \varOmega \) covered by a set of uniformly sized and non-overlapping Cartesian control volumes \(\varOmega _{ij} = [x_{i-1/2},\ x_{i+1/2}] \times [y_{j-1/2},\ y_{j+1/2}]\) with mesh spacings \(\varDelta x = x_{i+1/2} - x_{i-1/2}\) and \(\varDelta y = y_{j+1/2} - y_{j-1/2}\) in x and y direction, respectively. The edges are located in \(x_{i \pm 1/2}=x_i \pm \varDelta x / 2\) and \(y_{j \pm 1/2} = y_j \pm \varDelta y /2\), while \(x_i\) and \(y_j\) denote the barycenter coordinates of the control volumes. We will furthermore use the notation \(\hat{{\varvec{\textrm{e}}}}_x = (1,\ 0,\ 0)\), \(\hat{{\varvec{\textrm{e}}}}_y = (0,\ 1,\ 0)\) and \(\hat{{\varvec{\textrm{e}}}}_z = (0,\ 0,\ 1)\) for the unit vectors pointing into the directions of the Cartesian coordinate axes. Then cell-center indices i and j run from \(i=1\) to \(i=N_x\) and from \(j=1\) to \(j=N_y\) respectively.
The set of discrete times will be denoted by \(t^n\). For a sketch of the employed staggered grid arrangement of the main quantities, see Figs. 2 and 3.
The main ingredients of the structure-preserving staggered semi-implicit scheme proposed in this paper are the definitions of appropriate discrete divergence, gradient and curl operators acting on quantities that are arranged in different and judiciously chosen locations on the staggered mesh. The discrete pressure field at time \(t^n\) is denoted by \(p^n\) and its degrees of freedom are located in the center of each control volume as \(p_{i,j}^n=p(t^n, x_i,\ y_j)\).
The discrete velocities \(u_1^{n}\) and \(u_2^{n}\) are arranged in an edge-based staggered fashion, i.e. \((u_{1})^n_{i+1/2,j} = u_1(t^n,\ x_{i+1/2},\ y_j)\) and \((u_{2})^n_{i,j+1/2} = u_2(t^n,\ x_{i},\ y_{j+1/2})\). The discrete vector field \({\varvec{\textrm{b}}}^{n}\) is defined on the vertices of each spatial control volume as \({\varvec{\textrm{b}}}^n_{i+1/2,j+1/2} = {\varvec{\textrm{b}}}(t^n,\ x_{i+1/2},\ y_{j+1/2})\). For clarity, see again Fig. 3.
The discrete divergence operator, \(\nabla _h\cdot \), acting on a discrete vector field \({\varvec{\textrm{u}}}^{n}\) is abbreviated by \(\nabla _h\cdot {\varvec{\textrm{u}}}^{n}\) and its degrees of freedom are given by
i.e. it is based on the edge-based staggered values of the field \({\varvec{\textrm{u}}}^{n}\). It defines a discrete divergence on the control volume \(\varOmega _{ij}\) via the Gauss theorem,
based on the mid-point rule for the computation of the integrals along each edge of \(\varOmega _{ij}\). In (63) the outward pointing unit normal vector to the boundary \(\partial \varOmega _{ij}\) of \(\varOmega _{ij}\) is denoted by \(\hat{{\varvec{\textrm{n}}}}\).
Staggered mesh configuration with a scalar field field \(\phi _{i}^{j}\) defined in the cell barycenters, and the interface field \({\varvec{\textrm{b}}}_{i+1/2,j+1/2}\) defined on the vertices of the main grid. The shaded control volumes indicate the stencil for the computation of the corner gradients \((\nabla _h \phi )_{i+1/2,j+1/2}\) and for the cell-centred curl operator \((\nabla _h \times {\varvec{\textrm{b}}})_{i,j}\)
In a similar manner, the z component of the discrete curl, \(\nabla _h\times \), of a discrete vector field \({\varvec{\textrm{b}}}^{n}\) (or \({\varvec{\textrm{a}}}_1^n = (1,\ 0,\ 0)\,{\varvec{\textrm{A}}}^n\) for example) is denoted by \( \hat{{\varvec{\textrm{e}}}}_z \cdot \nabla _h\times {\textbf{b}}^{n} \) and its degrees of freedom are naturally defined as
making use of the vertex based staggered values of the field \({\varvec{\textrm{b}}}^{n}\), see Fig. 3. In the present two-dimensional description of the scheme the first and second components of the discrete curl \((\nabla _h\times {\varvec{\textrm{b}}}^n)_{i,j}\) vanish identically. Equation (64) defines a discrete curl on the control volume \(\varOmega _{ij}\) via the Stokes theorem
based on the trapezoidal rule for the computation of the integrals along each edge of \(\varOmega _{ij}\).
Last but not least, we need to define a discrete gradient operator that is compatible with the discrete curl, so that the continuous identity
also holds on the discrete level. If we define a scalar field in the barycenters of the control volumes \(\varOmega _{ij}\) as \(\phi _{i,j}^{n}=\phi (t^n,\ x_i,\ y_j)\) then the corner gradient generates a natural discrete gradient operator \(\nabla _h\) of the discrete scalar field \(\phi ^{n}\) that defines a discrete gradient in all vertices of the mesh. The corresponding degrees of freedom generated by \(\nabla _h\phi ^{n}\) read (see Fig. 3)
It is then straightforward to verify that an immediate consequence of Eqs. (64) and (67) is
i.e. one obtains a discrete analogue of (66). This can be easily seen by computing
We furthermore define the following averaging operators from the edge-based staggered meshes to the cell barycenter \((x_i,\ y_j)\) and viceversa
Finally, we also introduce an interpolation operator to compute cell center approximations of the corner quantities like \({\varvec{\textrm{b}}}\) and \({\varvec{\textrm{a}}}_{k}\), which we write as
This equation represents a simple linear arithmetic averaging operator and introduces minimal numerical dissipation. However, when flow convection is particularly strong, we found beneficial to apply a partial upwinding to the interpolation operator for the interface field \({\varvec{\textrm{b}}}\), so to add additional numerical stabilisiation to the scheme. In this case, the interpolation from the corner values to the barycenter reads
The coefficients \(w_k\) are obtained by first constructing a set of preliminary weights by two-dimensional upwinding,
with \(\epsilon = 10^{-6}\), \({\varvec{\textrm{u}}}^+ = (u_1^+,\ u_2^+)^{\mathsf {{\tiny T}}}= \max \left( 0,\ {\varvec{\textrm{u}}}\right) /(\Vert {\varvec{\textrm{u}}}\Vert + \epsilon )\), and \({\varvec{\textrm{u}}}^- = (u_1^-,\ u_2^-)^{\mathsf {{\tiny T}}}= \max \left( 0,\ -{\varvec{\textrm{u}}}\right) /(\Vert {\varvec{\textrm{u}}}\Vert + \epsilon )\). Then the preliminary weights (73) are normalized in such a way that the upwind bias will be reduced for flows with weak convection. The final weights thus are computed as
3.6 Explicit Discretization of Involution Constrained Fields
The key ingredient of the numerical method proposed in this article is the curl-compatible discretization of the terms \(\nabla {\varvec{\textrm{G}}}_v({\varvec{\textrm{Q}}})\) and \({\varvec{\textrm{B}}}_v({\varvec{\textrm{Q}}}) \nabla {\varvec{\textrm{Q}}}\) present in (12). We propose the following compatible discretization for the interface field equation:
where the corner-averaged curl term is given by
It is easy to check that for an initially curl-free vector field \({\varvec{\textrm{b}}}^{n}\) that satisfies \(\nabla _h\times {\varvec{\textrm{b}}}^{n} = 0\) also \(\nabla _h\times {\varvec{\textrm{b}}}^{n+1} = 0\) holds. In order to see this, one needs to apply the discrete curl operator \(\nabla _h\times \) to Eq. (75). One realizes that the second row of (75), which contains the discrete curl of \({\varvec{\textrm{b}}}^{n}\) vanishes immediately, due to \(\nabla _h\times {\varvec{\textrm{b}}}^{n} = 0\). The curl of the first term on the right hand side in the first row of Eq. (75) is zero because of \(\nabla _h\times {\varvec{\textrm{b}}}^{n} = 0\) and the curl of the second term is zero because of \(\nabla _h\times \left( \nabla _h\phi ^{n}\right) = 0\), with the auxiliary scalar field \(\phi ^{n} = {\varvec{\textrm{b}}}^{n} \cdot {\varvec{\textrm{u}}}^{n}\), whose degrees of freedom are computed as \(\phi ^{n}_{i,j} = {\varvec{\textrm{b}}}^{n}_{i,j}\cdot {\varvec{\textrm{u}}}^{n}_{i,j}\) after interpolating the velocity vector and the gradient field \({\varvec{\textrm{b}}}\) into the barycenters of the control volumes \(\varOmega _{i,j}\). The key ingredient of our compatible discretization for the \({\varvec{\textrm{b}}}\) equation is indeed the use of a discrete gradient operator that is compatible with the discrete curl operator, see Eq. (69).
3.7 Compatible Numerical Viscosity
The discretization of the interface field \({\textbf{b}}\) presented in the previous section was central and thus did not contain any numerical viscosity. In order to add a compatible numerical viscosity operator, we first recall the definition of the vector Laplacian at the continuous level. It reads
Since we aim at constructing a compatible discrete analogue of (77) we first define another discrete divergence that is obtained from the definition of the discrete corner gradient (67)
It yields the degrees of freedom of the divergence of \({\varvec{\textrm{b}}}^n\) at the cell corner locations, starting from the cell center interpolated values of the vector field \({\varvec{\textrm{b}}}^n\). By shifting indices by a half step in both directions, the same operator can be used to obtain cell center values for \(\nabla _h\cdot {\varvec{\textrm{b}}}^n\) starting from the corner values of \({\varvec{\textrm{b}}}^n\). In this case, the operator reads
The corresponding discrete vector Laplacian is then obtained as follows,
i.e. it is composed of a grad-div contribution minus a curl-curl term. Making use of (80), a compatible discretization of the governing PDE of the interface field \({\textbf{b}}\) with numerical viscosity then reads
Here, \(h = \max ( \varDelta x, \varDelta y)\), is a characteristic mesh spacing and \(c_a\) is a characteristic velocity related to the artificial viscosity added to the scheme. In practice we take \(c_a = k_L\,\lambda \), with \(\lambda = \max _{\varOmega }\left( \Vert {\varvec{\textrm{u}}}\Vert \right) \) for the evolution of the distortion field \({\varvec{\textrm{A}}}\) and \(\lambda = \max _\varOmega \left( \Vert {\varvec{\textrm{u}}}\Vert + \sigma \Vert {\varvec{\textrm{b}}}\Vert /\rho \right) \) for the evolution of the interface field \({\varvec{\textrm{b}}}\). Unless otherwise specified, we take \(k_L = 0.1\). It is obvious that also (81) satisfies the curl-free property \(\nabla _h\times {\textbf{b}}^{n+1} = {\varvec{\textrm{0}}}\) if \(\nabla _h\times {\textbf{b}}^{n} = {\varvec{\textrm{0}}}\). In order to reduce the numerical dissipation, it is possible to employ a piecewise linear reconstruction and insert the barycenter extrapolated values into the discrete divergence operator under the discrete gradient. In two space dimensions, the curl-curl term in (81) simplifies to
denoting with \(\omega ^n_{i,j} = \left( \hat{{\varvec{\textrm{e}}}}_z \cdot \nabla _h\times {\varvec{\textrm{b}}} \right) ^n_{i,j}\) the third component of the discrete curl of \({\varvec{\textrm{b}}}^n\).
Due to the analogy of the evolution equations of the interface field \({\textbf{b}}\) and the distorsion field \({\textbf{A}}\), the evolution of each row vector of the distortion field is discretized in the same manner as the evolution of the vector \({\textbf{b}}\).
3.8 Implicit Solution of the Pressure Equation
The contribution of the pressure to the momentum and to the total energy conservation laws i.e. the pressure flux terms contained in \({\textbf{F}}_p\), have not yet been included in the scheme. The discrete momentum conservation law with the pressure term reads
Here, the pressure is taken implicitly, while the nonlinear convective terms have been discretized explicitly via the operators \({(\rho \,u_1^{*})}_{i+1/2}^{j} \) and \({(\rho \,u_2^{*})}_{i}^{j+1/2}\) given in (52) and after averaging of the obtained quantities back to the edge-based staggered dual grid. The contribution to momentum of the gravity source and the vertex fluxes, due to capillarity and viscosity, is computed using the discrete four-point divergence of the fluxes (79), as
where \({\varvec{\Omega }}_{1k}\) and \({\varvec{\Omega }}_{2k}\) indicate the first and the second row of the tensor \({\varvec{\Omega }} = -{\varvec{\Sigma }}_\textrm{t}({\varvec{\textrm{b}}}^{n+1}) - {\varvec{\Sigma }}_\textrm{s}({\varvec{\textrm{A}}}^{n+1},\ \rho ^{n+1})\) collecting the effects of the stress tensors associated with corner quantities \({\varvec{\textrm{b}}}\) and \({\varvec{\textrm{A}}}\), i.e. capillarity and viscous forces, respectively. Both components of the flux divergence are then interpolated onto the corresponding cell edges, yielding
The first component of \({\varvec{\textrm{f}}}^*\), \({(f_1)}^*_{i+1/2,j}\), will contribute to the momentum balance in the x-direction, and for this reason it is interpolated only at the \(u_1\)-velocity locations, while, the second component \({(f_2)}^*_{i,j+1/2}\) is part of the momentum balance in the y-direction and is interpolated at the \(u_2\)-velocity locations. The discrete total energy equation reads
with the term \((\rho \,{\tilde{w}}_\textrm{g})^{n+1}_{i,j} = \rho \,{\varvec{\textrm{u}}}_{i,j}^{n+1}\cdot {\varvec{\textrm{g}}}\) accounting for the work due to gravity forces. Inserting the discrete momentum Eq. (83) into the discrete energy equation (86) and making tilde symbols explicit via a simple Picard iteration (using the index r in the following), as suggested in [26, 49, 53], leads to the following discrete wave equation for the unknown pressure
with the known right hand side
The density at the new time \(\rho _{i,j}^{n+1} = \rho _{i,j}^{*} \) is already known from (52), and so are the energy contribution \((\rho \,e_{\textrm{s}})^{n+1}_{i,j}\) of the distortion field \({\varvec{\textrm{A}}}^{n+1}\) and the interface energy \((\rho \,e_{\textrm{t}})^{n+1}_{i,j}\) of the field \({\varvec{\textrm{b}}}^{n+1}\), after averaging onto the main grid of the staggered field components of \({\varvec{\textrm{b}}}\) and \({\varvec{\textrm{A}}}\) that have been evolved in the vertices via the compatible discretization (75).
Note that the definitions given in Eq. (85) are an important element of the scheme presented in this paper, aimed at improving its accuracy and robustess, with respect to simpler splitting techniques.
Concerning the kinetic energy contribution, it is updated explicitly via a Picard iteration, like the enthalpy \({\tilde{h}}^{n+1}\). It reads
and the same update strategy is applied for the work due to gravity forces
For general equations of state (EOS), the final pressure system (87) constitutes a mildly nonlinear system (see [49]) of the form
Its linear part is contained in \({\textbf{M}}\) and is symmetric and at least positive semi-definite.
If the assumptions on the nonlinearity detailed in [39] hold, it can be solved with the nested Newton method of Casulli and Zanolli [38, 39]. For our particular EOS (stiffened gas), the system is linear in the pressure and thus we can employ an even simpler Jacobi-preconditioned matrix free conjugate gradient method for its solution.
Note that in the incompressible limit \({\mathbb {M}}\textrm{a} \rightarrow 0\), following the asymptotic analysis performed in [86,87,88, 95, 96], the pressure tends to a constant and the contribution of the kinetic energy \(\rho \,{\tilde{e}}_\textrm{k}\) can be neglected with respect to the internal energy \(\rho \,e\). Therefore, in the incompressible limit the system (87) tends to the classic pressure Poisson equation used in incompressible flow solvers, see also [26]. In each Picard iteration, after the solution of the pressure system (87), the enthalpies are recomputed and the momentum is updated by
with \(g_x = {\varvec{\textrm{g}}}\cdot \hat{{\varvec{\textrm{e}}}}_x\) and \(g_y = {\varvec{\textrm{g}}}\cdot \hat{{\varvec{\textrm{e}}}}_y\). At the end of the Picard iterations, the total energy is updated as
While for the final main-grid update of the momentum variables we compute a set of interpolated cell-face values for the pressure field \(p_{i+1/2,j}^{n+1} = (p_{i,j}^{n+1} + p_{i+1,j}^{n+1})/2\) and \(p_{i,j+1/2}^{n+1} = (p_{i,j}^{n+1} + p_{i,j+1}^{n+1})/2\), and then update the momentum directly on the cell-centered main grid with
This approach further differentiates the method proposed in this paper from the one given in [26], and is preferred in this work as opposed to averaging the momentum from the cell-face grid to the cell center grid, in order to avoid the Lax–Friedrichs-type numerical diffusion that is generated when the final momentum is averaged back onto the main grid, see the detailed analysis provided in [53].
3.9 Boundary Conditions
In this paper, well-established practices for weakly prescribing simple boundary conditions by means of a layer of ghost cells, lying outside of the computational domain, i.e. where the cell center indices are \(i=0\), or \(i=N_x+1\), or \(j=0\), or \(j=N_y+1\). In particular: periodic boundary conditions are trivially set as
Similarly, at a boundary of wall type, in absence of viscous effects, for example at \(i = 1\), the corresponding ghost cell has index \(i = 0\) and we set
where \(\hat{{\varvec{\textrm{n}}}}\) is the unit vector normal to the boundary, pointing towards the interior of the domain, i.e. the normal component of the momentum vector \(\rho \,{\varvec{\textrm{u}}}\) is flipped in the ghost cell. In the same way, no-slip conditions are obtained by setting
switching the sign of all components of the momentum vector, leading to a zero velocity field on the boundary itself.
The cell-boundary values for the momentum components \((\rho \,u_1)_{i+1/2,j}\) and \((\rho \,u_2)_{i,j+1/2}\) are simply the averages of the corresponding boundary and ghost cells: we remark that in the scheme presented in this work, the momentum updates are carried out on the main grid (cell-centers) directly, in order to minimise numerical dissipation effects, unlike in previous works [26, 49], which made use of a genuinely staggered collocation of the quantities.
Nonetheless, the well-behaved structure of the implicit pressure system due to the staggered discretisation is unchanged with respect to [26, 49], since univocally defined auxiliary interface momenta \((\rho \,u_1)_{i+1/2,j}\) and \((\rho \,u_2)_{i,j+1/2}\) are computed by interpolation prior to its solution.
In addition, at each Picard iteration during the solution of the pressure system, the normal components of the auxiliary velocity field, for example \((u_1)_{1/2,j}\) at the left boundary, or \((u_2)_{i,1/2}\) at the bottom boundary, are explicitly set to zero if the boundary is of wall type. Finally, in presence of source terms associated with a gravity acceleration vector \({\varvec{\textrm{g}}} = (g_1,\ g_2,\ g_3)^{\mathsf {{\tiny T}}}\), the pressure values for the boundary ghost cells are adjusted according to a local hydrostatic equilibrium: instead of simply copying the pressure as
we account for the effects of gravity by setting
The treatment of static or dynamic contact angles by means of the interface field \({\varvec{\textrm{b}}}\) is a further nontrivial task left for future works. In the same spirit, it should be remarked that the simple ghost-cell approach adopted in this paper is a practical solution for the problem of boundary conditions in certain complex PDE systems such as the one here considered, but far from being a complete one.
3.10 Proof of the Abgrall Compatibility Condition
We provide here a simple proof that the proposed scheme respects the so-called Abgrall condition [4], that is, it preserves exactly those flows characterised by a constant velocity and constant pressure. In absence of other driving forces, such uniform flows should not be affected by spurious perturbations, regardless of the distribution of density or volume fraction as they do not affect the dynamics in these situations.
The starting point is showing that the velocity field produced by the convective step is kept uniform by the MUSCL–Hancock scheme applied to the convective subsystem. In one space dimension, the mixture density \(\rho \) obeys the update formula
with the Rusanov flux yielding explicitly
which is easily shown by direct sum of the equations for the phase densities \(\alpha _1\,\rho _1\) and \(\alpha _2\,\rho _2\). Since it is a fundamental assumption that the velocity field is constant at time level \(t^n\), in this proof we can denote \(u_1 = (u_1)_i = (\rho \,u_1)_i^n/\rho _i^n\) for any cell i, The update formula for the mixture momentum \(\rho \,u_1\) similarly reads
and exploiting the constant velocity assumption, the flux is
which means that (102) can be simplified to
from which, setting \((u_1)_i^{*} = (u_1)_i^n = u_1\) allows to factor out Eq. (100), showing that the constant velocity field is preserved by the scheme. The same formal proportionality argument can be applied also to the cell-local predictor of the MUSCL–Hancock scheme, showing that the velocity field generated by the predictor step is unaltered in the same way.
It remains to be shown that a constant pressure field \(p = p_i^n = p_i^{n+1}\) for any index i is a solution of the discrete wave equation resulting from the energy balance
together with the equivalences \((\rho \,e_\textrm{k})_{i}^{n+1} = (\rho \,e_\textrm{k})_{i}^{*}\) and \(\left( \rho \,u_1\right) _{i+1/2}^{n+1} = \left( \rho \,u_1\right) _{i+1/2}^{*}\) resulting from the constant-pressure assumption which means that momentum \(\rho \,u_1\) and kinetic energy \(\rho \,e_\textrm{k}\) at the new time level coincide with those resulting from the convective subsystem. Collecting the constant velocity \(u_1\) and plugging in a generic linear equation of state of the form \(\rho \,e = k_0 + k_1\,p\), which is the form of the stiffened gas EOS applied to our model when \(\alpha _1\) is constant throughout the domain, gives
which with the constant pressure assumption \(p_i^{n+1} = p_i = p\) yields a condition
highlighting that the enthalpy estimates \({\tilde{h}}_{i+1/2}^{n+1}\) must be chosen as
meaning that the density used for the computation of enthalpies must necessarily be the one produced by the convective step \(\rho _{i+1/2}^{*}\). Any interpolation scheme for computing \(p_{i+1/2}\) will clearly work in a constant pressure field, and we use a simple arithmetic average \(p_{i+1/2} = (p_i + p_{i+1})/2\), and the same average is employed for computing \(\rho _{i+1/2}^*\), but in this case it is important that the interpolation operator be the same applied for the computation of the momentum \((\rho \,u_1)_{i+1/2}^{*}\) from the cell-center quantities. Also, note that in order to be able to set \((\rho \,e_\textrm{k})_{i}^{n+1} = (\rho \,e_\textrm{k})_{i}^{*}\), the kinetic energy computed from averaging the (constant) velocities from the cell center to the edges and vice-versa, must be compatible with that obtained by the MUSCL–Hancock scheme itself, which is verified thanks again to the fact that a compatible numerical dissipation was chosen for density, momentum, and kinetic energy. Specifically, it is immediately apparent that, analogously to the momentum flux, we can write the kinetic energy flux as \(f_{i+1/2}^{\rho \,e_\textrm{k}} = e_\textrm{k}\,f_{i+1/2}^\rho \), thus the specific kinetic energy \(e_\textrm{k} = u_1^2/2\) is kept constant after the convective step.
Given the conditions above, one can immediately see that a constant pressure field, with \(\rho \,e_\textrm{k}^{n+1} = \rho \,e_\textrm{k}^{*}\) is solution to the discrete wave equation
A further condition on the scheme must be imposed whenever the volume fraction \(\alpha _1\) is not constant in space. In this case, the stiffened gas equation of state applied to each phase provides a more complex closure law of the type \(\rho \,e = \alpha _1\,\rho _1\,e_1 + \alpha _2\,\rho _2\,e_2\) or \(\rho \,e = \alpha _1\,k_{01} + \alpha _1\,k_{11}\,p + \alpha _2\,k_{02} + \alpha _2\,k_{12}\,p\). Applied to the discrete wave equation, the mixture equation of state gives
that is, at least when the velocity field \(u_1\) is a constant, the scheme for the update of \(\alpha _1\) must coincide with one in flux form, for some appropriate choice of \((\alpha _1)_{i+1/2}^*\).
For a constant velocity field, the nonconservative products not associated with pure convection of the volume fraction vanish and, the update scheme reads
with the path-conservative fluctuations as well as the numerical dissipation from the Rusanov flux collected in
This automatically gives rise to an upwind discretisation that suggests the interpolated values of \(\alpha _{i+1/2}^*\) should be computed with the same upwinding rule
for any left and right states \((\alpha _1)_L\) and \((\alpha _1)_R\) obtained from the predictor step of the MUSCL–Hancock scheme. Then it can be verified that for any distribution of volume fraction \(\alpha _1\) and density \(\rho \) the discrete wave equation will indeed preserve constant-pressure, constant-velocity solutions exactly.
4 Semi-Analytic Integration of Strain Relaxations Sources
A necessary element for the successful solution of the unified model of continuum mechanics is the accurate integration of the distortion matrix \({\varvec{\textrm{A}}}\).
The evolution dynamics of the distortion matrix \({\varvec{\textrm{A}}}\) and of the metric tensor \({\textbf{G}}= {\varvec{\textrm{A}}}^{\mathsf {{\tiny T}}}\,{\varvec{\textrm{A}}}\) take place on a wide span of timescales: given a fixed evolution speed of the kinematics of distortion (due to flow convection and velocity gradients), one can find anything from infinitely slow strain relaxation in elastic solids, to infinitely fast shear dissipation in perfect fluids, with viscous fluids also being a nontrivial example of fast-acting (stiff) strain relaxation.
From the mathematical standpoint, such timescales can be quantified by means of a relaxation time \(\tau \) in the evolution equation of the distortion matrix
and in the corresponding equation for the metric tensor
The relaxation time \(\tau \), in principle a function of the state variables, but often a fixed constant, is what defines the stiff nature of the algebraic source terms governing the relaxation towards an equilibrium state of the material strain. To highlight the connection between the distortion matrix \({\varvec{\textrm{A}}}\), the metric tensor \({\varvec{\textrm{G}}}\) and what we generically call strain, it should be recalled that, in a purely elastic context, for small deformations, the linear strain \({\varvec{\mathrm {\epsilon }}}\) can be directly expressed as \({\varvec{\mathrm {\epsilon }}} = \left( {\varvec{\textrm{I}}} - {\varvec{\textrm{G}}}\right) /2\), for this reason we refer to the above right hand side terms as strain relaxation sources.
One of the major difficulties in the solution of the unified model of continuum mechanics is indeed the presence of these nonlinear source terms. In the past, the locally implicit ADER treatment of source terms [50] has proven to be effective [51], as well as the splitting or fractional step approach, in conjunction with the implicit Euler scheme for stable time integration used in [26]. However, we found that a new approach has to be adopted for certain choices of the material parameters, for example for extremely fast relaxation times in complex flows, or for the nonlinearly stress-dependent timescales encountered in the application of the model to material failure dynamics or non-Newtonian flows, see [105, 120].
A final major step forward in the development of a robust solver for the strain relaxation system (114), in particular allowing to accurately capture the Navier–Stokes limits regardless of the timestep size, is based on three key observations:
-
1.
The splitting approach is not always adequate
-
2.
The structure of the problem can be significantly simplified by choosing the appropriate reference frames
-
3.
Equilibrium states can be computed algebraically without time integration
The details regarding the semi-analytical solution strategy adopted in this work are given in the following paragraphs.
4.1 Limits of the Splitting Approach
In previously discussed techniques [41, 120] for the solution of relaxation processes we have adopted the fractional step (or splitting) approach. The technique is very useful, as it allows to separate the solution of the relaxation source from all other dynamics, and attack the resulting ordinary differential equation system with ad hoc techniques. However, the relaxation processes in the unified model of continuum mechanics, besides complex nonlinear dynamics, also feature nontrivial equilibrium states that must be reliably captured and preserved. If not, important properties of the continuum model, like the convergence to the Navier–Stokes–Fourier system [51], may be lost in its discrete version. For that reason, the development of asymptotic preserving (AP) schemes [26] is very important.
To quantitatively argue the point, we highlight the problem with regards to a simpler example, namely given by the thermal impulse equation [26], in the simple case of a vanishing velocity field, which is
and assume to dispose of a generic numerical scheme by which one can compute for each cell/degree of freedom an update \({\varvec{\textrm{P}}}_*= ({\varvec{\mathrm {J^*}}} - {\varvec{\textrm{J}}}^n)/\varDelta t\) such that \({\varvec{\mathrm {J^*}}}\) is the solution to the update of the left hand side of (116), i.e. the homogeneous system that is solved by application of the splitting approach. In this particular case \({\varvec{\textrm{P}}}_*\) can be seen as a discretisation of \(-\nabla T\). Then, a straightforward application of the splitting method would find the solution at time \(t^{n+1} = t^n + \varDelta t\) of the initial value problem
If Eq. (117) is integrated via the implicit Euler method, then one can prove that the final value of \({\varvec{\textrm{J}}}^{n+1}\) will indeed yield an asymptotic preserving discretization of the PDE (provided obviously that the discretisation of the left hand side is compatible). However, it is easy to see that, isolated from the left hand side of (116), the ordinary differential problem (117) asymptotically relaxes \({\varvec{\textrm{J}}}\) to zero if the relaxation time is sufficiently small with respect to the timestep size, regardless of the value of the initial condition \({\varvec{\textrm{J}}}^*\). This implies that if one were to integrate (117) exactly, then the updated value of the thermal impulse \({\varvec{\textrm{J}}}\) would be \({\varvec{\textrm{J}}}^{n+1} = {\varvec{\textrm{0}}}\) instead of \({\varvec{\textrm{J}}}^{n+1} = -\tau _\textsc {h}\,\nabla T\), highlighting a very clear issue in a naive application of the splitting approach.
In order to overcome this issue, a simple modification to the ordinary differential problem (117) allows to account for the left hand side of (116) and thus converge to the correct asymptotic state \({\varvec{\textrm{J}}} = -\tau _\textsc {h}\,\nabla T\) in the stiff limit \(\tau _h \rightarrow 0\).
An alternative ordinary differential problem to be solved is then
where, as stated, \({\varvec{\textrm{P}}}_*\) accounts for the discrete update from the left hand side of (116). Again, (118) can be seen as a system of three uncoupled first order linear ordinary differential equations (ODEs) and an exact solution is indeed found thanks to the linearity and independence of the three equations. Explicitly, the solution is
The only degenerate case to be considered is that if \(\varDelta t/\tau _\textsc {h}\) is very small (of the order of \(10^{-8}\)), i.e. if the source term is not stiff at all, then (119) might yield inaccurate results, due to floating point representation issues. In this case, one may simply opt to to switch to explicit Euler integration, which for such mild (vanishing) sources yields perfectly valid solutions.
4.2 Simplification of the Problem by Polar Decomposition and Principal Axes Coordinates
The nine components of the distortion matrix/basis triad \({\varvec{\textrm{A}}}\) encode two different kinds of information: six degrees of freedom are directly linked to the stress tensor \({\varvec{\mathrm {\sigma }}} = -\rho \,c_\textrm{s}^2\,{\varvec{\textrm{G}}}\,{{\,\textrm{dev}\,}}{\varvec{\textrm{G}}}\), while the remaining three are associated with an angular orientation which does not influence stresses or energies but are nonetheless part of the structure of the governing equations. This can be formalized by means of the polar decomposition of \({\varvec{\textrm{A}}}\), by which we can highlight the six stress-inducing components of \({\varvec{\textrm{A}}}\), identifying them as the square root \({\varvec{\textrm{G}}}^{1/2}\) of the metric tensor \({\varvec{\textrm{G}}}\). Moreover, one can easily see that, if an appropriate fixed transformation of the reference frame is applied to (114) (a polar decomposition followed by a spectral decomposition), such that at time \(t = t^n\) one has \({\varvec{\textrm{A}}}\) in diagonal form, and if the convection/production term on the left hand side of (114) is null (if the flow field is uniform, i.e. \(\nabla {\varvec{\textrm{u}}} = {\varvec{\textrm{0}}}\), or if formally we want to study the invariance properties of the strain relaxation source), then the diagonality of \({\varvec{\textrm{A}}}\) is maintained for all \(t \ge t^n\). This means that the relaxation source on the right hand side of (114) does not alter the rotational component of \({\varvec{\textrm{A}}}\). In the following we establish the notation for the polar decomposition procedure enabling separate treatment of rotational degrees of freedom of \({\varvec{\textrm{A}}}\) and volumetric/shear/relaxation effects and provide some formal justification of the validity of the approach.
4.2.1 Polar Decomposition of the Distortion Matrix
Given the definition of the metric tensor \({\varvec{\textrm{G}}} = {\varvec{\textrm{A}}}^{\mathsf {{\tiny T}}}\,{\varvec{\textrm{A}}}\), the distortion matrix \({\varvec{\textrm{A}}}\) can always be expressed as
and where \({\varvec{\textrm{R}}}\) is an orthogonal transformation with positive unitary determinant, i.e. a rotation matrix. Numerically, the matrix square root \({\varvec{\textrm{G}}}^{1/2}\) can be evaluated by means of the Denman–Beavers algorithm, or alternatively, thanks to the symmetry of \({\varvec{\textrm{G}}}\), one can reliably and accurately compute the eigenvectors \({\varvec{\textrm{E}}}\) and diagonal form \(\hat{{\varvec{\textrm{G}}}}\) from the eigen-decomposition of the metric tensor
with the Jacobi eigenvalue algorithm. In the work reported in the present paper, the latter is indeed the method of choice for the task. This allows, for any given state \({\varvec{\textrm{A}}}\), to compute a rotation matrix
which allows to apply any operation to \({\varvec{\textrm{G}}}={\varvec{\textrm{A}}}^{\mathsf {{\tiny T}}}\,{\varvec{\textrm{A}}}\), or its square root \({\varvec{\textrm{G}}}^{-1/2}\), exploiting their symmetric and positive definite properties, or, temporarily in the solution procedure and locally in space, adopting a simpler form of the governing equations, written in terms of \({\varvec{\textrm{G}}}\) instead of \({\varvec{\textrm{A}}}\). Then the effects of such operations can be mapped onto \({\varvec{\textrm{A}}}\) directly via the rotation \({\varvec{\textrm{A}}} = {\varvec{\textrm{R}}}_{*}\,{\varvec{\textrm{G}}}^{-1/2}\), with \({\varvec{\textrm{R}}}_*\) a rotation matrix that can be computed independently from the nonlinear source terms as \({\varvec{\textrm{R}}}_*= {\varvec{\textrm{A}}}_*\,{\varvec{\textrm{G}}}^{-1/2}_*\), having defined \({\varvec{\textrm{A}}}_*\) the distortion matrix obtained from the left hand side of the evolution equation as customarily done per the fractional step method. To summarize, one may first compute \({\varvec{\textrm{R}}}_n = {\varvec{\textrm{A}}}_n\,{\varvec{\textrm{G}}}^{-1/2}_n\), use it to map to an auxiliary frame in which one can easily integrate the source term as applied to the symmetric positive definite metric tensor \({\varvec{\textrm{G}}}\), and then map back to \({\varvec{\textrm{A}}}\) by means of a different rotation matrix \({\varvec{\textrm{R}}}_*= {\varvec{\textrm{A}}}_*\,{\varvec{\textrm{G}}}^{-1/2}_*\), already obtained as a function of the left hand side only.
4.2.2 Invariance Under Strain Relaxation of the Rotational Component of the Distortion Matrix
We can study the effects of the relaxation source on the distortion matrix \({\varvec{\textrm{A}}}\) and the metric tensor \({\varvec{\textrm{G}}}\) in isolation from those of flow gradients by formally setting \(\nabla {\varvec{\textrm{u}}} = {\varvec{\textrm{0}}}\) obtaining the uniform flow equations
with, \(k = 3\,\tau ^{-1}\,\left( \det {\varvec{\textrm{G}}}\right) ^{5/6}\), or, in the co-moving reference, equivalently
where \({{\,\mathrm{d\!}\,}}/{{\,\mathrm{d\!}\,}}t\) is the customary notation for the total/convective/Lagrangian derivative. In the following paragraphs we derive a set of evolution equations, valid in uniform flow, where only strain relaxation effects can be observed, which are provided as an argument for the separate computation of rotations and volumetric/shear effects in the proposed semi-analytical solver.
Evolution equation for the square root of the metric tensor. The metric tensor Eq. (126) can be mapped to a principal reference frame, by setting \({\varvec{\textrm{G}}} = {\varvec{\textrm{E}}}\,\hat{{\varvec{\textrm{G}}}}\,{\varvec{\textrm{E}}}^{-1}\), with \({\varvec{\textrm{E}}}\) the matrix of eigenvectors of \({\varvec{\textrm{G}}}\) computed at a fixed time \(t = t_*\) and \(\hat{{\varvec{\textrm{G}}}}\) a diagonal matrix defined at any time t by \(\hat{{\varvec{\textrm{G}}}}(t) = {\varvec{\textrm{E}}}^{-1}\,{\varvec{\textrm{G}}}(t)\,{\varvec{\textrm{E}}}\). Then (126) can be rewritten as
and, since \({\varvec{\textrm{E}}}\) is fixed at time \(t = t_*\), we obtain
which implies that for a fixed orthonormal transformation \({\varvec{\textrm{E}}}\) such that at a given time \(t_*\) one has a diagonal \(\hat{{\varvec{\textrm{G}}}}(t_*) = {\varvec{\textrm{E}}}^{-1}\,{\varvec{\textrm{G}}}(t_*)\,{\varvec{\textrm{E}}}\), the matrix \(\hat{{\varvec{\textrm{G}}}}\) will remain diagonal for all times, implying that the strain relaxation source does not affect the eigenvectors of \({\varvec{\textrm{G}}}\) but only its eigenvalues. Moreover, since in the fixed principal axes reference frame \(\hat{{\varvec{\textrm{G}}}}\) and its square root are guaranteed to be diagonal at any time t, then one can write
since, in this specific reference frame, all matrices involved are diagonal and products are commutative. Therefore the evolution equation for the square root of \(\hat{{\varvec{\textrm{G}}}}\), under the effects of strain relaxation only, and in the principal frame reads
Evolution equation for the rotational component of the distortion matrix. A simple governing equation for the rotational component \({\varvec{\textrm{R}}}\) of the distortion matrix \({\varvec{\textrm{A}}}\) can be derived, in uniform flow \(\nabla {\varvec{\textrm{u}}} = {\varvec{\textrm{0}}}\), or equivalently under the effect of the strain relaxation source only, by substituting the polar decomposition
in (125), obtaining
Then, expanding the derivative, we have
and by substituting (130) in (133) we recover
and hence the simple (non)-evolution law for the rotations of \({\varvec{\textrm{A}}}\) reads
which means that the rotational component \({\varvec{\textrm{R}}}\) is not affected by the relaxation source and can only change due to non-uniformity of the flow, unlike the principal components of the metric tensor \({\varvec{\textrm{G}}}\), accounting for volumetric and shear effects. In [72], Godunov and Peshkov recognised that the structure of the governing equations of the cobasis \({\varvec{\textrm{A}}}\) could be exploited to simplify the relaxation procedure. Similarly, in [81, 82], Jackson and Nikiforakis develop and employ an approximate semi-analytical integration technique for the relaxation source of the GPR model, which however is tied to a periodic reset procedure for the cobasis \({\varvec{\textrm{A}}}\) and for strain energy, restoring a new local small deformations configuration whenever necessary. Hence this clarifies the motivation for developing a novel integration methodology capable of handling arbitrary deformations and extreme parameter choices potentially varying between \(\tau = 10^{20}\) and \(\tau = 10^{-14}\) as a function of stress as in [27], without modification to the structure of the PDE system.
4.3 Direct Solution of Strain Equilibrium States
A final welcome fact about the particular structure of the strain production/relaxation Eqs. (114) and (115) is that, if the source term is very stiff, one may easily compute the asymptotic solution without necessarily resolving the stiff dynamics: the asymptotic state does not depend on the initial conditions and can be computed by means of a simple and quickly convergent fixed point iteration scheme. Moreover, from the numerical standpoint, time-dependent closed form solutions of the strain relaxation equations can be less accurate than expected for certain initial conditions, parameter choices, or flow configurations. In such cases, the availability of the solution for the sought equilibrium state is not only a matter of efficiency, but also of accuracy and robustness of the computations. Additionally, the fixed point iteration allows to prove that the integration scheme for the relaxation source will indeed provide, in the Navier–Stokes limit of the model, the correct unique asymptotic stress tensor, reflecting the convergence limit of the continuum model to the Navier–Stokes equations. The details for a direct and efficient calculation of equilibrium states and the transients leading to them will be given in the following paragraphs.
4.4 Integration of the Strain Relaxation Equations with Finite Relaxation Time Without Operator Splitting
The solver for the strain relaxation source is based on the exponential integrator developed in [120] for the computation of diffuse interface fractures and material failure, but exploits in a deeper manner the particular structure of the equation being solved, following the technique presented in [41] for finite-rate pressure relaxation.
We recall that the solver employed in [120] required, in general, the solution of a sequence of a nonhomogeneous nine-by-nine systems of linear ordinary differential equations for the nine independent components of the distortion matrix \({\textbf{A}}\), which involves the numerical computation of matrix exponentials and the inversion of the Jacobian matrix of the ODE system. Both these operations constitute delicate tasks in linear algebra that require special care to be carried out in an efficient and accurate manner.
The approach used in this work entirely foregoes the solution of such nine-by-nine systems (six-by-six, in the case of the symmetric tensor \({\textbf{G}}\)) and the associated linear algebra intricacies. Instead, we compute the analytical solution to one of several different linearised equations that approximate the nonlinear ordinary differential equation
while admitting simple solutions that can be computed in a robust fashion. Here with \({\textbf{L}}_*\) we denote a constant convective/productive forcing term to be given in the following paragraphs, in analogy to the previously defined term \({\varvec{\textrm{P}}}_*\), representing a discrete time derivative of the thermal impulse \({\textbf{J}}\).
An important aspect of the scheme is that it avoids fractional-step-type splitting, so that the Navier–Stokes stress tensor can be recovered regardless of the ratio between the computational timestep size and the relaxation timescales. This means that the global timestep size does not need to be adjusted to accommodate for the fast dynamics of the relaxation sources. This is achieved by first computing, cell by cell, the update to \({\textbf{G}}\) associated with the left hand side of (115), and then including its effects in (136), in the form of the constant forcing term \({\textbf{L}}_*\). Formally, the first step amounts to computing the solution \({\textbf{G}}_*= {\textbf{G}}(t^{n+1})\) to the initial value problem
In our case, instead of Eq. (137), we solve the more general equation for the distortion matrix
with the compatible scheme (81) illustrated for the interface field \({\textbf{b}}\) and which is applied in the same manner to the time evolution of the left hand side of \({\varvec{\textrm{A}}}\), from which we obtain a pointwise update to the cell averages or degrees of freedom, which is in turn used to define the constant convective/productive forcing term
Then a sub-timestepping loop with adaptive step size \(\delta t^m\) is entered in order to approximate the solution of (136) with a sequence of solutions of linearised ODEs. Such a sub-timestepping loop is useful for ensuring the robustness and accuracy of the solver in complex flow configurations, but generally in our computations the solver achieves convergence in one single sub-timestep \(\delta t^m = \varDelta t\). We refer to [41, 120] for more details on the sub-timestepping approach, and we carry on our presentation of the method by listing three possible approximation choices for the solution of (136).
4.5 Approximate Analytical Solution for Strain, Approach 1
When dealing with fluid flows (that is, when the source term acts on fast timescales), rather often one may assume that \({\textbf{G}}\) be a perturbation of a spherical tensor, that is, \({{\,\textrm{dev}\,}}{{\textbf{G}}}\) can be assumed small. Then, it is advantageous to rewrite (136) as
with \(k = {6}\,{\det ({\textbf{G}})}^{5/6}/\tau \) taken constant for the sub-timestep. This splits the source in four pieces. The first is the constant \({\textbf{L}}_*\), associated with convection which, by definition, cannot be stiff as its size is limited by the CFL constraint of the global timestepping scheme. The second is a (small by hypothesis) quadratic term in \({{\,\textrm{dev}\,}}{{\textbf{G}}}\) which can be safely approximated as constant. The third is a function of \({{\,\textrm{tr}\,}}{\textbf{G}}\) only, again formally taken constant. This assumption can be justified by writing the evolution equation for the trace of \({\textbf{G}}\)
which shows that either \({{\,\textrm{tr}\,}}{{\textbf{G}}}\) varies on a timescale associated with convection (by definition, slow), or as a quadratic function of \({{\,\textrm{dev}\,}}{{\textbf{G}}}\) (small by assumption). The approximate Eq. (140) then admits the simple exact solution
with
We should remark that nowhere in this approximate solution we neglected the contributions due to \({{\,\textrm{dev}\,}}{{\textbf{G}}}\), they only have taken to be constant for a sub-timestep. Specifically, our constant approximations are initially set to \({{\,\textrm{tr}\,}}{\textbf{G}}= {{\,\textrm{tr}\,}}{\textbf{G}}_m\) and \({{\,\textrm{dev}\,}}{\textbf{G}}= {{\,\textrm{dev}\,}}{\textbf{G}}_m\) and then updated within a fixed point iteration as \({{\,\textrm{tr}\,}}{\textbf{G}}= {{\,\textrm{tr}\,}}({\textbf{G}}_m + {\textbf{G}}_{m+1})/2\) and \({{\,\textrm{dev}\,}}{\textbf{G}}= {{\,\textrm{dev}\,}}({\textbf{G}}_m + {\textbf{G}}_{m+1})/2\).
4.6 Approximate Analytical Solution for Strain, Approach 2
Whenever the deviatoric part of \({\textbf{G}}\) cannot be assumed small, i.e. in practice when
better accuracy in the approximation of (136) can be obtained by observing that it is possible to switch the order of the operands of the matrix product \({\textbf{G}}\,{{\,\textrm{dev}\,}}{({\textbf{G}})}\) appearing in (136). Thus we rewrite (136) as
where we will take \({\textbf{L}}_*\), \(k = {6}\,{(\det {{\textbf{G}}})}^{5/6}/\tau \), and \({{\,\textrm{dev}\,}}{({\textbf{G}})}\) to be constant at each sub-timestep. In order to simplify the solution of (145), we work in the principal reference frame which diagonalizes \({\textbf{G}}\) and \({{\,\textrm{dev}\,}}{({\textbf{G}})}\), i.e. we compute the orthonormal matrix \({\textbf{E}}\) such that \({\hat{{\textbf{G}}}} = {\textbf{E}}^{-1}\,{{\textbf{G}}}\,{\textbf{E}}\)
is a diagonal matrix and apply the associated change of basis to all vectors and tensors in our equation. This way the exact solution to Eq. (145) is
The three-by-three matrix \({\textbf{E}}\) having for columns the eigenvectors of \({\textbf{G}}\) can be quickly and robustly computed to arbitrary precision by means of Jacobi’s method for the eigenstructure of symmetric matrices, and its inverse is simply given by \({\textbf{E}}^{-1} = {\textbf{E}}^{{\mathsf {{\tiny T}}}}\). Furthermore, \({{\,\textrm{dev}\,}}{{\hat{{\textbf{G}}}}}\) can be inverted trivially in the principal reference frame by just taking the reciprocal of each diagonal entry. Like for the previous solution we iteratively update the estimate \({{\,\textrm{dev}\,}}{\hat{{\textbf{G}}}} = {{\,\textrm{dev}\,}}({\hat{{\textbf{G}}}}_m + {\hat{{\textbf{G}}}}_{m+1})/2\).
Determinant constraint. In the solution of the equation for the metric tensor \({\textbf{G}}\), specifically when the computation involves fluid-type behaviour, special care must be paid to preserve the nonlinear algebraic constraint \(\det {{\textbf{G}}}(t,\ {\varvec{\textrm{x}}}) = \left[ \rho (t,\ {\varvec{\textrm{x}}})/\rho _0\right] ^2 = D(t,\ {\varvec{\textrm{x}}})\). The constraint must be actively enforced since the discretisation scheme may in principle introduce significant errors that over time could let the solution drift away from a compatible state in which \(\det {\varvec{\textrm{A}}} \ne \rho /\rho _0\). A simple approach to the problem constitutes in uniformly multiplying all components of \({\textbf{G}}\) by \((D/\det {\textbf{G}})^{1/3}\) so that the resulting determinant is D.
The specific numerical value of the determinant D is clearly known (from density) at the time levels \(t^n\) and \(t^{n+1}\), however it must be somehow approximated for all the in-between times during which we operate our sub-timestepping procedure. In this work we impose that for a given sub-timestep indexed by m, connecting \(t^m\) and \(t^{m+1}\) the determinant D be computed as
where we define \(D_s = \det \left[ {\textbf{G}}+ (t^m + \delta t^m - t^n)\,{\textbf{L}}_*\right] \) to be the value that the determinant would have following a linear segment path connecting the two states \({\textbf{G}}\) and \({\textbf{G}}_*\), that is, the value that would allow preserve exact integration of the (zero) source term in the solid case. Instead, \(D_f = \det {{\textbf{G}}} + (t^m + \delta t^m - t^n)\,(\det {{\textbf{G}}_*} - \det {\textbf{G}}_{n})\) is a second order approximation of the determinant in the fluid limit. The mixing ratio \(\beta _s\) for the two approximations \(D_s\) and \(D_f\) is an heuristic measure of how close to a solid can the material be considered and its expression is
with \(||{\textbf{A}}||_2^2\) denoting the square of the Frobenius norm of a given tensor \({\textbf{A}}\).
4.7 Approximate Analytical Solution for Strain, Approach 3: Fixed Point Iteration for the Navier–Stokes Equilibrium State
Oftentimes the timescale \(\tau \) of strain relaxation is so fast that one may decide to just compute the strain state for which the forcing term due to convection \({\textbf{L}}_*\) and the relaxation source are balanced yielding an equilibrium state corresponding to the Navier–Stokes limit of the GPR model. Such an equilibrium state can be easily computed by means of a fixed point iteration in the form
with D the target determinant as defined in (147) and i the iteration index in the fixed point procedure. We found that the fixed point iteration (149) is always convergent regardless of the initial guess, but nonetheless we care to provide a simple and efficient choice in the form
Details on the derivation of this fixed point iteration scheme, as well as a proof of convergence are given in [40].
4.8 Summary of the Selection Procedure for the Approximation Method
At each sub-timestep between \(t^m\) and \(t^{m+1}\), our solver for the equation of the elastic metric tensor \({\textbf{G}}\) has to select the optimal approximation method for the specific distortion configuration at hand. The selection procedure is carried out as follows:
-
1.
If the source is not stiff, i.e. if \(\beta _s > 1 - 10^{-14}\), then we use explicit Euler integration and compute the solution at the next time sub-level \({\textbf{G}}_{m+1} = {\textbf{G}}_m + \varDelta t\,\left( {\textbf{L}}_*- \dfrac{6}{\tau \,\det {({\textbf{G}}_m)}^{5/6}\,{\textbf{G}}\,{{\,\textrm{dev}\,}}{{\textbf{G}}}}\right) \).
-
2.
Else define the indicator matrix \({\varvec{\Lambda }} = {{\,\textrm{abs}\,}}{\left( {\textbf{G}}_m^{-1}\,{\textbf{L}}_*- k\,{{\,\textrm{dev}\,}}{{\textbf{G}}_m}\right) }\) and if the sum of the off-diagonal components of \({\varvec{\Lambda }}\) is less than \({{\,\textrm{tr}\,}}{{\varvec{\Lambda }}}/5\) and \(\delta t^m > \tau \) then the scheme selects the fixed point iteration (149).
-
3.
Else if \(\sqrt{{{\,\textrm{tr}\,}}{({{\,\textrm{dev}\,}}{{\textbf{G}}_m}\,{{\,\textrm{dev}\,}}{{\textbf{G}}_m})}} < (\det {{\textbf{G}}_m})^{1/3}/5\) or if any of the diagonal entries of \({{\,\textrm{dev}\,}}{{\hat{{\textbf{G}}}}_m}\) has magnitude smaller than \({{\,\textrm{tr}\,}}{{\hat{{\textbf{G}}}}_m}/1000\) then the scheme uses (140).
-
4.
If none of the above, then we apply approximation (145).
Regardless of the chosen approximation method, at the end of each sub-timestep, the result \({\textbf{G}}_{m+1} = {\textbf{G}}(t^{m+1})\) must be multiplied by \({(D/\det {{\textbf{G}}_{m+1}})}^{1/3}\) so that the determinant constraint is satisfied.
5 Numerical Results
5.1 Experimental Verification of the Abgrall Condition
We begin the validation of the proposed numerical method by showing that the implementation of the numerical scheme does indeed satisfy the Abgrall condition [4], i.e. it preserves uniformity of the velocity and pressure fields regardless of the distribution of density or volume fraction. The test is carried out on a domain \(\varOmega = [-1,\ 1]\times [-1,\ 1]\), where we set up a circular jump in \(\rho _1,\) \(\rho _2\), and \(\alpha _1\). Precisely, if \(r = \Vert {\varvec{\textrm{x}}}\Vert < 1/2\) we set \(\rho _1 = 1\), \(\rho _2 = 1/2\), and \(\alpha _1 = 0.3\) and otherwise if \(r \ge 1/2\) we have \(\rho _1 = 1/2\), \(\rho _2 = 1\), and \(\alpha _1 = 0.7\). The uniform pressure is \(p = 1\) and a constant velocity field \({\varvec{\textrm{u}}} = (1,\ 1,\ 0)^{\mathsf {{\tiny T}}}\) are initially imposed, so that the solution will consist in simple advection (and numerical diffusion) of the initially circular density and volume fraction jumps. Surface tension, shear, and gravity effects are not present, hence we set \(\sigma = 0\) and \({\varvec{\textrm{A}}} = {\varvec{\textrm{I}}}\), \({\varvec{\textrm{b}}} = {\varvec{\textrm{0}}}\), \({\varvec{\textrm{g}}} = {\varvec{\textrm{0}}}\), \(\tau = 10^{-14}\), \(c_\textrm{s}=0\), and the governing equations reduce to Kapila’s model. The material parameters for this test are \(\gamma _1 = 4.0\), \(\gamma _2 = 1.4\), \(\varPi _1 = 2.0\), \(\varPi _2 = 0\). Throughout this section, unless explicitly noted, we adopt SI units for all quantities.
In Fig. 4 we report the time evolution of errors (in the \(L_1\) norm) for both nonzero components of the velocity field and for pressure with regard to simulations carried out on two different uniform Cartesian grids of \(250^2\) and \(500^2\) elements. For both meshes, the errors are of order \(10^{-14}\) to \(10^{-13}\) and present no exponential or linear growth, thus they can perfectly be explained as accumulation of roundoff errors due to floating point arithmetic and small errors due to the iterative solution of the discrete wave equation for the pressure field.
5.2 Numerical Convergence Study for a Steady Droplet in Equilibrium
A numerical convergence study is carried out in order to assess the order of accuracy of the proposed semi-implicit curl-preserving method. The problem setup consists of the uniform convective transport of a diffuse droplet initialised according to the exact solution derived in [42].
In detail, with reference to [42], the initial condition for the liquid volume fraction \(\alpha _1\) is given according to the chosen colour function profile, but bounding it between the two values \(\alpha _\textrm{min} = 0.01\) and \(\alpha _\textrm{max} = 0.99\), so that we have
The density fields are set to the constant values of \(\rho _1 = 1000\) and \(\rho _2 = 1\).
The remaining numerical constants for the test are \(u_0 = v_0 = 1\,\mathrm {m\,s^{-1}}\), \(R = 1\,\textrm{m}\), \(k_\epsilon = 0.3\), \(\sigma = 1\,\mathrm {N\,m^{-1}}\), \(p_\textrm{atm} = 1\,\textrm{Pa}\), \(\overline{\rho _1} = 1000\,\mathrm {kg\,m^{-3}}\), \(\overline{\rho _2} = 1\,\mathrm {kg\,m^{-3}}\), \(\delta = 0.1\), \(\omega = \pi /3\,\mathrm {m^{-1}}\), \(\varPi _1 = 20\,\textrm{Pa}\), \(\varPi _2 = 0\,\textrm{Pa}\), \(\gamma _1 = 4\), \(\gamma _2 = 1.4\).
The computational domain is the square \(\varOmega = [-3\,\textrm{m},\ 3\,\textrm{m}]\times [-3\,\textrm{m},\ 3\,\textrm{m}]\) so that at \(t = 12\,\textrm{s}\) we expect the water column to have completed two full advection cycles.
Here we carry out an additional second test with a stationary droplet in order to assess the convergence rates both in steady and unsteady problems. The order is theoretically expected to be 2 for steady solutions, since all fluxes are integrated separately with second order accurate discretisations. In the unsteady case, due to the first order splitting of convection, pressure, and capillarity effects, we expect that the scheme be first order accurate. Error norms and convergence rates, with respect to the variables \(\alpha _1\,\rho _1\), \(\rho \,{\varvec{\textrm{u}}}\), \(\rho \,E\), \(\alpha _1\), and \(b_1\), are given in Table 1 for the steady case and in Table 2 for the unsteady one. Both sets of simulations experimentally confirm the expected order of accuracy.
5.3 Validation of the Viscosity Model and Algorithms
First problem of Stokes. In the context of this paper, the test serves the dual purpose of showing that the GPR model of continuum mechanics does indeed include the Navier–Stokes equations as a special case, and that the semi-analytical integration scheme can capture the same limit. An important benchmark for viscous flow solvers is the first problem of Stokes: for this test the computational domain is \(\varOmega = [0,\ 1]\times [0,\ 0.1]\), with periodic boundary conditions in y direction and no-slip boundaries in the x direction. The initial condition of the problem is given by uniform density \(\rho =1\) and pressure \(p = 1/\gamma \), with \(\gamma = \gamma _1 = \gamma _2 = 1.4\) since this is a single-phase problem, albeit solved in a two-phase framework. The x-component of the velocity field is initialized as \(u_1=0\), the distortion field is initially set to \({\varvec{\textrm{A}}}={\varvec{\textrm{I}}}\), while the y-velocity component \(u_2\) is \(u_2=-(u_2)_0\) for \(x<1/2\) and \(u_2=(u_2)_0\) for \(x\ge 1/2\). The parametric quantities for this test are given as \((u_2)_0 = 0.1\), \(\gamma _1 = \gamma _2=1.4\), \(\varPi _1 = \varPi _2 = 0\), \(\rho _0=1\), \(c_\textrm{s}=1\).
Numerical solutions of the first problem of Stokes, for three different values of the kinematic viscosity \(\nu \). The simulations are carried out with the semi-implicit structure-preserving Finite Volume scheme employing the semi-analytical integrator for strain relaxation. The right panel is a zoomed-in view about the location of the shear interface, showing perfect agreement of the GPR model with the analytical solution of the Navier–Stokes equations
The simulations are performed with the structure preserving semi-implicit finite volume scheme on a grid composed of 500 by 50 square control volumes up to a final time of \(t=0.4\). The exact solution of the incompressible Navier–Stokes equations for this test case is expressed in terms of the y-velocity component \(u_2\) as
see also [115], with \(\nu = \mu / \rho _0\). The test is repeated for three different values of kinematic viscosity \(\nu =10^{-2}\), \(\nu =10^{-3}\), \(\nu =10^{-4}\). The comparison between the Navier–Stokes reference solution (152) and the numerical results obtained with the new scheme for the unified model of continuum mechanics are presented in Fig. 5, where one can observe an excellent agreement between the two for various kinematic viscosities \(\nu \). This proves that the proposed numerical algorithm can accurately capture the Navier–Stokes regime of the governing equations.
Double shear layer problem Here we solve the double shear layer test problem [15, 26, 32, 51, 118]. The computational domain is \(\varOmega =[0,\ 1]^2\) with periodic boundary conditions everywhere. The x-component of the velocity field is initialised as
and the y-component is \(u_2= \delta \,\sin (2\,\pi \,x)\), the density is initially uniform \(\rho = \rho _0 = 1\) and the pressure is \(p = 100/\gamma _1\). Since the test problem is usually adopted in a single-phase context, we set the volume fraction function is \(\alpha = 0.5\) throughout the computational domain to emulate the single-phase equations: both phases compute the exact same solution, and one simply obtains the mixture (single-phase) density by direct sum of the two partial densities.
For this test case we set the parameters that determine the shape of the velocity field to \(\delta =0.05\) and \({\tilde{\rho }}=30\). The viscosity coefficient is set to \(\nu = \mu / \rho _0 = 2 \times 10^{-4}\) and \(\nu = \mu / \rho _0 = 2 \times 10^{-3}\) in two separate runs of the test problem. The other parameters of the model are \(\gamma _1 = \gamma _2 = 1.4\), \(\varPi _1 = \varPi _2 = 0\), \(\rho _0=1\), \(c_\textrm{s}=8\). The initial condition for the distortion field is \({\varvec{\textrm{A}}}={\textbf{I}}\) and surface tension effects are not to be accounted for in this test, which means that we set \({\varvec{\textrm{b}}} = {\varvec{\textrm{0}}}\). Simulations are carried out with the new structure-preserving semi-implicit finite volume scheme up to a final time of \(t=1.8\). The computational mesh is composed of \(5120 \times 5120\) control volumes. In Fig. 6 we show the temporal evolution of the distortion field component \(A_{12}\). The results, highlighting the incredibly rich structure found in the rotational component \({\varvec{\textrm{R}}}\) of the distortion field \({\varvec{\textrm{A}}}\), are in excellent agreement with those obtained in [32] using a thermodynamically compatible scheme on the same fine uniform grid.
5.4 Riemann Problems and Circular Explosion Problem
We continue the validation of the semi-implict scheme with two one-dimensional Riemann Problems showing that the semi-implicit numerical method can reproduce the correct wave structure of the Kapila model [83] of two-phase flow: in these tests, surface tension, shear, and gravity effects are not present, hence we set \(\sigma = 0\) and \({\varvec{\textrm{A}}} = {\varvec{\textrm{I}}}\), \({\varvec{\textrm{b}}} = {\varvec{\textrm{0}}}\), \({\varvec{\textrm{g}}} = {\varvec{\textrm{0}}}\), \(\tau = 10^{-14}\), \(c_\textrm{s}=0\), and the governing equations reduce to Kapila’s model exactly.
Filled contours of the \(A_{12}\) component of the distortion field \({\varvec{\textrm{A}}}\) in the double shear layer problem for two values of kinematic viscosity \(\nu =2\!\times \!10^{-3}\,\mathrm {m^2\,s^{-1}}\) (\({\mathbb {R}}\textrm{e}\simeq 1000\)) and \(\nu =2\!\times \!10^{-4}\,\mathrm {m^2\,s^{-1}}\) (\({\mathbb {R}}\textrm{e}\simeq 10000\))
Numerical solution of the multiphase Riemann problem RP1 obtained with the semi-implict curl-preserving scheme on a uniform Cartesian grid with mesh size \(\varDelta x = 1/4000\), compared with a reference solution obtained with a standard explicit path-conservative second order TVD MUSCL–Hancock scheme on a mesh of \(40\,000\) cells
Numerical solution of the multiphase Riemann problem RP2 obtained with the semi-implicit curl-preserving scheme on a uniform Cartesian grid with mesh size \(\varDelta x = 1/4000\), compared with a reference solution obtained with a standard explicit path-conservative second order TVD MUSCL–Hancock scheme on a mesh of \(40\,000\) cells
Filled contour plots for the two-phase inviscid circular explosion problem with the curl-preserving semi-implicit scheme for viscous two-phase flow on a fine uniform Cartesian grid counting \(4096^2\) cells. In the lower left quadrant of each panel, we show a reference solution computed with an explicit path-conservative second order method on the same fine uniform mesh of \(4096^2\) elements
First, we set up two simple planar Riemann problems RP1 and RP2 by partitioning the computational domain in two regions with constant state separated by a discontinuity normal to the x-direction, i.e. for RP1 we set \(\rho _1 = 1\), \(\rho _2 = 1\), \({\varvec{\textrm{u}}} = 0\), \(p = 1\), \(\alpha _1 = 0.5\), if \(x \le 0.5\), and \(\rho _1 = 1\), \(\rho _2 = 0.1\), \({\varvec{\textrm{u}}} = 0\), \(p = 0.1\), \(\alpha _1 = 0.5\) otherwise.
In Figs. 7 and 8, we show the one-dimensional profiles of the partial densities \(\alpha _1\,\rho _1\) and \(\alpha _2\,\rho _2\), of the x-component of the velocity field \(u_1\), and of the pressure p, obtained by applying the semi-implicit scheme on a mesh of 4000 by 400 square cells over the domain \(\varOmega =[0,\ 1]\times [0,\ 0.1]\). The results are compared with a reference solutions computed by a second order explicit path-conservative TVD MUSCL–Hancock method on a fine one-dimensional grid composed of \(40\,000\) uniform control volumes. The results match up to some minor artifacts observed in the solution obtained from the semi-implicit method, in this regard, it is important to note that such a semi-implicit scheme is designed specifically for low Mach number flows, rather than for the treatment of shock waves. The observed artifacts are not a hinderance for large scale simulations lying within the design regime of the method.
Then, a two-dimensional explosion problem is set up in a similar fashion, with the discontinuity now representing an inner and outer state rather than a left and right one. The computational domain is the square \(\varOmega = [-0.8,\ 0.8]\times [-0.8,\ 0.8]\) and is disctretised with a mesh of \(4096^2\) uniform Cartesian control volumes. The inner state is given by \(\rho _1^\textrm{i} = 1000\), \(\rho _2^\textrm{i} = 1000\), \({\varvec{\textrm{u}}}^\textrm{i} = {\varvec{\textrm{0}}}\), \(p^\textrm{i} = 10^{10}\), \(\alpha _1^\textrm{i} = 0.5\). The outer state is \(\rho _1^\textrm{o} = 1000\), \(\rho _2^\textrm{o} = 1\), \({\varvec{\textrm{u}}}^\textrm{o} = {\varvec{\textrm{0}}}\), \(p^\textrm{o} = 10^{5}\), \(\alpha _1^\textrm{0} = 0.5\). The discontinuity is initially located at \(r = \Vert {\varvec{\textrm{x}}}\Vert = 1/2\), and the final simulation time is \(t_\textrm{end} = 6\times 10^{-5}\). The parameters of the stiffened gas equation of state are \(\gamma _1 = 4.4\), \(\gamma _2 = 1.4\), \(\varPi _1 = 6\times 10^8\), \(\varPi _2 = 0\).
In Fig. 9 we show the filled contour plots for the mixture density \(\rho \), for the pressure p, for the volume fraction \(\alpha _1\), and for the x-component of the velocity field \(u_1\). The results correctly preserve symmetries and are in agreement with the reference solutions obtained by means of an explicit path-conservative second order TVD MUSCL–Hancock method on the same mesh of \(4096^2\) cells.
5.5 Long-Time Evolution of an Oscillating Droplet at Low Mach Number
In this Section, we reproduce the numerical experiments shown in [42] and based on high order ADER Discontinuous Galerkin \({\mathbb {P}}_{N}{\mathbb {P}}_{N}\) schemes with a posteriori Finite Volume subcell limiting, now using instead the novel semi-implicit curl-preserving scheme introduced in this work.
Time evolution of the total kinetic energy \(E_\textrm{k}\) for the elliptical droplet oscillation problem. On the left: solution obtained with the a second order semi-implicit Finite Volume scheme with GLM curl cleaning on a uniform Cartesian mesh composed of \(384\times 384\) elements. On the right: solution obtained on the same mesh with the curl-preserving variant of the same semi-implicit scheme. In both cases it is apparent that the numerical diffusion is much lower than that of standard second order TVD schemes (see [42]): the oscillation amplitude shows only mild decay for the full 15 oscillation cycles simulated in the numerical experiment. For comparison, without involution enforcement, the weakly hyperbolic model (WH) produces chaotic results before the end of the first oscillation cycle. The parameter \(c_h\) refers to the cleaning speed adopted in the GLM curl-cleaning formulation of the governing equations as in [42]
Three-dimensional view of the second component of the velocity field \(u_2\) for the elliptical droplet oscillation problem at time \(t = 6.91\times \!10^{-4}\,\textrm{s}\) (half of the first oscillation cycle). In the top row the uniform Cartesian mesh counts \(384^2\) elements, in the bottom row the mesh is refined to \(512^2\) elements. On the left, curl constraints are enforced with GLM curl-cleaning and the equations solved with the semi-implicit Finite Volume scheme presented in this work (without curlfree discretisation of the interface field), while on the right the results are computed with the curlfree structure-preserving semi-implicit method. The difference in the quality of the results obtained with the two different approaches is immediately apparent by comparing the specular highlights in the plots on the left column (from GLM curl cleaning, rough surface), with those on the right column (from the exactly curlfree scheme, smooth surface). Moreover, note that the smoothness of the curlfree solution is not due to numerical diffusion (peak heights are the same) and that the observations are the same for different meshes. The parameter \(c_h\) refers to the cleaning speed adopted in the GLM curl-cleaning formulation of the governing equations as in [42]
Time evolution of curl errors for the oscillating droplet test problem. In each panel of the top row, we compare the curl errors given by the GLM curl cleaning variant of the model with cleaning speed \(c_h\) ranging from \(5\,\mathrm {m\,s^{-1}}\) to \(40\,\mathrm {m\,s^{-1}}\), and those given by the curl-preserving semi-implicit method. The errors are computed in the \(L_1\) (left panel) and the \(L_2\) (right panel) norms, and are relative to a common uniform Cartesian mesh counting \(192^2\) elements. The curl-preserving semi-implicit method produces errors more than nine orders of magnitude smaller than those obtained with GLM curl cleaning in the same semi-implicit framework. If involutions are not enforced (WH) curl errors grow uncontrollably and appear to decrease but the effect is only due to the complete breakdown of the simulation. In the bottom row, we show, for a variety of uniform Cartesian meshes, that the errors of the curl-preserving semi-implicit Finite Volume scheme are due to statistical accumulation of roundoff errors: as expected from random-walk/Brownian [56, 60] processes, they grow in time proportionally to \(\sqrt{t}\), and they grow faster for finer meshes which require more floating point operations in order to integrate the solution up to a given time
Snapshots of the interface energy \(\sigma \,\Vert {\varvec{\textrm{b}}}\Vert \) for the droplet oscillation problem with different mesh resolutions and for different schemes. WH is the unconstrained weakly hyperbolic model, GLM refers to the curl cleaning method (with cleaning speed \(c_h\)), SP indicates the curl-free semi-implicit scheme
While we refer to [42] for a detailed exposition of the computational setup, we list here the parameters of the problem: the density fields are set to the uniform values \(\rho _1^0\) and \(\rho _2^0\) throughout the computational domain, as is the velocity field for which we set \({\varvec{\textrm{u}}} = {(0,\ 0,\ 0)}^{\mathsf {{\tiny T}}}\). The numerical values employed for this test problem are: \(\rho _1^0 = 1000\,\mathrm {kg\,m^{-3}}\), \(\rho _2^0 = 1\,\mathrm {kg\,m^{-3}}\), \(p_\textrm{atm} = 100\,\textrm{kPa}\), \(R_x = 3\,\textrm{mm}\), \(R_y = 2\,\textrm{mm}\), \(\alpha _\textrm{min} = 0.01\), \(\alpha _\textrm{max} = 0.99\), \(\sigma = 60\,\mathrm {N\,m^{-1}}\). The parameters for the stiffened gas equation of state are: \(\varPi _1 = 1\,\textrm{MPa}\), \(\varPi _2 = 0\), \(\gamma _1 = 4\), \(\gamma _2 = 1.4\). The domain is the square \(\varOmega = [-6\,\textrm{mm},\ 6\,\textrm{mm}]\times [-6\,\textrm{mm},\ 6\,\textrm{mm}]\) and additionally, the initial condition is rotated counter-clockwise by 30 degrees, in order to avoid mesh alignment. In a first batch of tests, we set \(\epsilon = 0.5\,\textrm{mm}\) and discretise the computational domain with \(384^2\) square cells, which yields the same number of degrees of freedom previously employed for the same test with the ADER-DG \({\mathbb {P}}_{5}{\mathbb {P}}_{5}\) scheme in [42]. These simulations are intended to test the capability of the method in a dynamical setting where the interface deforms significantly under the effect of strong surface tension, and show that the curl-preserving semi-implicit scheme, when applied to such low Mach problems, can be competitive even with very high order methods and in particular that that new curl-free scheme is clearly competitive or superior to the GLM curl cleaning approach proposed in [42].
In Fig. 10, we show the time evolution of the total kinetic energy and compare the results obtained without any enforcement of curl involutions (which we recall, as shown in [42], are totally unstable and quickly lead to the breakdown of computations), with those from GLM curl cleaning formulation of the governing equations, with the results from the structure preserving methodology. Both curl-control solutions yield stable results, but higher accuracy is achieved with the exactly curlfree scheme. Note that the results relative to the GLM curl cleaning formulation [42] of the PDE system have been produced with a the same second-order semi-implicit code presented in this work, switching off the curl-preserving discretisation of course, including the evolution of the \({\varvec{\textrm{b}}}\), \({\varvec{\textrm{A}}}\), and curl-cleaning fields in the convective sub-system directly, so that important experimental variables (numerical dissipation, timestep size) are eliminated and the differences observed can be understood to be due to the choice of curl-preserving operators or GLM cleaning only.
The same can be observed in Fig. 11, where we plot a three-dimensional view of the second component of the velocity field \(u_2\) for the at time \(t = 6.91\times \!10^{-4}\,\textrm{s}\) (half of the first oscillation cycle), computed on two different meshes of size \(384^2\) and \(512^2\), and for both the GLM variant of the method and for the exactly curlfree method. The difference in the quality of the results obtained with the two different approaches is immediately apparent by comparing the specular highlights in the plots on the left column, obtained with GLM curl cleaning (the surface is rough), with those on the right column, obtained with the exactly curlfree scheme (the surface is perfectly smooth). Moreover, note that the smoothness of the curlfree solution is not due to numerical diffusion (peak heights are the same) and that the observations are the same for different meshes.
In Fig. 12 we show the time evolution of curl errors. Specifically, we compare the curl errors given by the GLM curl cleaning variant of the model with cleaning speed \(c_h\) ranging from \(5\,\mathrm {m\,s^{-1}}\) to \(40\,\mathrm {m\,s^{-1}}\), and those given by the curl-preserving semi-implicit method. The errors are computed in the \(L_1\) and the \(L_2\) norms and are relative to a common uniform Cartesian mesh counting \(192^2\) elements. The curl-preserving semi-implicit method produces errors more than nine orders of magnitude smaller (less than \(\sim 10^{-13}\) instead of more than \(\sim 10^{-4}\)) than those obtained with GLM curl cleaning in the same semi-implicit framework. If involutions are not enforced (WH) curl errors grow uncontrollably and appear to decrease but the effect is only due to the complete breakdown of the simulation and the disappearance of all physical flow features. Additionally, in order to argue that the curl errors produced by the exactly curlfree method originate from statistical accumulation of roundoff error, we plot their time evolution as a function of the square root of time \(\sqrt{t}\) (essentially proportional to the square root of the number of timesteps as well). This scaling law shows that curl errors are growing in a perfectly linear fashion as a function of \(\sqrt{t}\), as expected from a process of random-walk, of Brownian origin [56, 60]. Moreover the growth rate is higher on finer meshes, since more operations are required to integrate the solution up to a given time t. Nonetheless, this does not constitute an issue since the order of magnitude of the errors is that of machine-epsilon accumulated roundoff.
Finally, in Fig. 13 we collect several snapshots of the global dynamics of the droplet oscillation problem, which clearly show that both the exactly curlfree methodology, and the GLM curl-cleaning method yield stable computations, counter to the unconstrained (weakly hyperbolic) variant of the model for hyperbolic surface tension, which catastrophically deteriorates within short times.
5.6 Binary Droplet Collision With High Density Ratio
Next, we continue our validation of the semi-implicit curl-preserving scheme for viscous two-phase flow with surface tension with an application to binary droplet collisions, motivated by [79, 106].
Early stages of the binary droplet collision simulation for three different values of the Weber number. The effects of surface tension penalising the formation of sharp features is evident: the lower the Weber number (corresponding to higher strength of capillarity forces), the stronger the tendency towards minimizing the interface curvature
Late stages of the binary droplet collision simulation for three different values of the Weber number. At low Weber number (\({\mathbb {W}}\textrm{e}\simeq 80\)) the collision results in stretching and separation of the two droplets. At all values of Weber number the effects of Rayleigh–Plateau instability are evident and in particular for the higher Weber numbers they result in the formation of multiple small secondary droplets
Two circular droplets are initialised according to the equilibrium solution derived in [42], with the centers of the droplets being
Their radii are \(R_\textrm{l} = R_\textrm{r} = 5\times 10^{-4}\), and the interface thickness is \(\epsilon = 10^{-5}\). The initial volume fractions are \(\alpha _1 = \alpha _\textrm{min} = 10^{-4}\) for the gas phase and \(\alpha _1 = \alpha _\textrm{max} = 1 - 10^{-4}\) for the liquid phase. The atmospheric pressure is \(p_\textrm{atm} = 10^5\) and gravity effects are not present (\({\varvec{\textrm{g}}} = {\varvec{\textrm{0}}}\)). The droplets are set on an off-center collision path by superimposing, to each droplet, a diffuse circular region in which the velocity field is \({\varvec{\textrm{u}}} = (1,\ 0,\ 0)^{\mathsf {{\tiny T}}}\) for the left droplet and \({\varvec{\textrm{u}}} = (-1,\ 0,\ 0)^{\mathsf {{\tiny T}}}\) for the right droplet, while the surrounding fluid is at rest. These circular regions are defined by the same smooth profile used for the droplets but with radius larger by a factor \(k=1.1\) with respect the droplet itself, and with interface thickness \(\epsilon =5\times 10^{-5}\). The strain relaxation times are \(\tau _\textrm{w} = 9.3750\times 10^{-8}\) and \(\tau _\textrm{a} = 1.4064\times 10^{-6}\) for the liquid and the gas respectively, which translates to kinematic viscosities \(\nu _\textrm{w} = 10^{-6}\) and \(\nu _\textrm{a} = 1.5\times 10^{-5}\). The densities are \(\rho _1 = 10^{3}\) for the liquid phase and \(\rho _2 = 1\) for the gas phase. The remaining material parameters are \(\gamma _1 = 8.0\), \(\gamma _2 = 1.4\), \(\varPi _1 = 10^6\), \(\varPi _2 = 0\) for the stiffened gas equation of state and \(c_\textrm{s}=8\) for the mesoscale strain energy closure. Three separate numerical experiments are carried out with different values of the Weber number \({\mathbb {W}}\textrm{e}\), defined by changing the surface tension coefficient from \(\sigma = 0.2\times 10^{-3}\) (corresponding to \({\mathbb {W}}\textrm{e}\simeq 80\)), to \(\sigma = 0.1\times 10^{-3}\) (i.e. \({\mathbb {W}}\textrm{e}\simeq 160\)), to \(\sigma = 0.05\times 10^{-3}\) (\({\mathbb {W}}\textrm{e}\simeq 320\)). The computational domain is \(\varOmega = [-4\times 10^{-3},\ 4\,\times 10^{-3}]\times [-3\,\times 10^{-3},\ 3\,\times 10^{-3}]\) and the mesh is of Cartesian type with 2048 and 1536 cells in the x and y directions respectively.
The qualitative behaviour is in agreement with experimental findings [8, 61, 117] about collision regimes in liquid droplets. In particular in Fig. 15 one can clearly distinguish different separation modes taking place following the collision: at low Weber number (\({\mathbb {W}}\textrm{e}\simeq 80\)) the collision results in stretching and separation of the two droplets. At all values of Weber number, the effects of Rayleigh–Plateau instability are evident and in particular for the higher Weber numbers they result in the formation of multiple small secondary droplets. In the early stages of the simulations (Fig. 14) one can also clearly see how sharp interfacial features are penalized by surface tension, which tends to reduce the curvature of interfaces, the more the stronger the capillarity forces with respect to convective effects.
Strong scaling results (computational times and speedup efficiency) from 64 CPU cores to 65 536 CPU cores (512 nodes) of the HPE-Hawk supercomputer at HLRS in Stuttgart. The semi-implicit structure-preserving scheme for hyperbolic viscous two-phase flow with surface tension achieves excellent scaling performance (\(>\sim 95\%\)) up to about 16k CPU cores, also thanks to cache effects mitigating the main bottleneck of the scheme which is the solution of the pressure system via matrix-free conjugate gradient method. On 65k CPU cores, the strong scaling efficiency drops to about \(50\%\). The computational grid is composed of 33.5 million Cartesian cells
The same test, with \({\mathbb {W}}\textrm{e}\simeq 80\) and a smaller domain \(\varOmega = [-3\times 10^{-3},\ 3\,\times 10^{-3}]\times [-1.5\,\times 10^{-3},\ 1.5\,\times 10^{-3}]\) is employed for a study of the strong scaling performance of the computational code. In this case the grid counts 8192 by 4096 cells and the simulations have been carried out with the aid of the HPE–Hawk supercomputer at the HLRS in Stuttgart, Germany, in order to test the scaling capabilities of our semi-implicit computational code on massively parallel distributed memory supercomputer architectures. The results of this latter test are summarised in Fig. 16: the strong scaling tests starts from 64 CPU cores (half node) and extends up to 65 536 CPU cores (512 nodes) of the HPE–Hawk supercomputer at HLRS in Stuttgart. Our semi-implicit scheme achieves excellent scaling performance (more than \(\sim 95\%\)) up to about 16k CPU cores, also thanks to cache effects mitigating the main bottleneck of the scheme which is the solution of the pressure system via matrix-free conjugate gradient method and only on 65k CPU cores, we see the speedup efficiency starting to drop significantly to about \(50\%\).
Mesh convergence test for the Rayleigh–Taylor instability problem: the rightmost panels show that mesh convergence has been achieved with a uniform Cartesian mesh counting 1024 by 3072 cells, since no new flow features appear if the mesh resolution is doubled. In the left panels we show the effects of choosing a different reduction coefficient \(k_L\) for the compatible vector Laplacian diffusion operator applied to the distortion matrix \({\varvec{\textrm{A}}}\). By comparing the top and bottom rows one can see that increasing \(k_L\) has a visible effect on the finer features of the distortion field, but this does not translate to comparably visible effects in the volume fraction contours on the right
Development of the Rayleigh–Taylor instability at time \(t=12.5\,\textrm{s}\), with varying viscosity and surface tension. From left to right: the first panel shows the solution with Weber number \({\mathbb {W}}\textrm{e}\simeq 1200\) in inviscid flow; the second panel shows how the solution changes if mild viscosity is introduced (\({\mathbb {R}}\textrm{e}\simeq 8000\)); the third panels is relative to a simulation with increased viscosity (\({\mathbb {R}}\textrm{e}\simeq 2000\)); the fourth and last panel depicts the results of a simulation of viscous flow without surface tension. The curl-preserving semi-implicit scheme with grid size 4096 by \(12\,288\) has been employed for all simulations
Volume fraction plots for the inviscid two-phase Rayleigh–Taylor instability solved with the Structure Preserving Semi-Implicit Finite Volume scheme applied to the unified model of continuum mechanics in the inviscid limit \((\tau =10^{-14})\), at different mesh resolutions (\(4096\!\times \!12\,288\) and \(10\,080\!\times \!30\,240\))
5.7 Multiphase Rayleigh–Taylor Instability
Finally, we put all elements of the scheme to the test at the same time, by simulating a low Mach, genuinely two-phase, Rayleigh–Taylor instability with viscosity and surface tension. The setup follows [90], but with the notable modification that, instead of initialising a single fluid with two different densities (one above a horizontal material interface, one below), we define two separate density fields, each one with constant phase densities \(\rho _1 = \rho _\textrm{t}\) and \(\rho _2 = \rho _\textrm{b}\), then distinguishing the two fluids by means of a jump from \(\alpha _1 = \alpha _\textrm{min} = 10^{-4}\) to \(\alpha _1 = \alpha _\textrm{max} = 1 - 10^{-4}\) in the volume fraction field. This renders the problem much more challenging because near-vacuum states of one of the two phases are introduced almost throughout the computational domain. The curved material interface location is
and we impose the transition between the two states by means of a smooth switch function
with interface thickness \(\delta = \max (0.004,\ 6\,\varDelta x)\). This is intended to suppress spurious instabilities that would be triggered by inaccurate representation of the initial condition on a discrete Cartesian grid (stairstepping), thus allowing only the physical instabilities to develop. The volume fraction field is then \(\alpha _1 = s\,\alpha _\textrm{min} + (1 - s)\,\alpha _\textrm{max}\), while the top and bottom pressures are
and, just like the volume fraction \(\alpha _1\), the pressure field is given by \(p = s\,p_\textrm{t} + (1 - s)\,p_\textrm{b}\). We initially set \({\varvec{\textrm{A}}} = {\varvec{\textrm{I}}}\), \({\varvec{\textrm{u}}} = {\varvec{\textrm{0}}}\), and the remaining parameters common to all simulations carried out with regard to this test problem are \(\rho _\textrm{t} = 2\), \(\rho _\textrm{b} = 1\), the gravity vector is \({\varvec{\textrm{g}}} = (0,\ -0.1,\ 0)^{\mathsf {{\tiny T}}}\), and finally \({\varvec{\textrm{b}}}\) is initialised as a compatible discrete gradient of an auxiliary colour function field \(s_c\) given by \(s_c = 1/2 + \textrm{erf}\left[ (y - y_I)/(2\,\delta )\right] /2\). boundary conditions are preiodic in the x-direction and no-slip in the y-direction. With this setup, we carry out a parametric study of the behaviour of the instability.
First, in order to verify mesh convergence of the solution algorithm, we set the Reynolds number \({\mathbb {R}}\textrm{e}\simeq 2000\) (which translates to \(c_\textrm{s}=0.3\) and \(\tau = 2\times 10^{-3}\)) and \({\mathbb {W}}\textrm{e}\simeq \infty \) (i.e. we neglect surface tension), and we carry out two simulation on two different meshes, one composed of \(1024 \times 3072\) elements, and one of \(2048 \times 6144\) elements, and show, in Fig. 17, that indeed the structure of the solution does not depend on mesh effects. Furthermore, again in Fig. 17, we also show that the method is robust with respect to the choice of the scaling factor for the compatible numerical viscosity \(k_L\): by varying such a factor from \(k_L = 0.01\) to \(k_L = 0.2\) we see that some of the fine scale structures in the distortion field \({\varvec{\textrm{A}}}\) are lost to numerical dissipation. However, this does not translate into a visible effect in the shape of the interface separating the two fluids. This can be explained by the fact that the rotational component \({\varvec{\textrm{R}}}\) of the distortion field \({\varvec{\textrm{A}}}\) is significantly affected by numerical viscosity, but instead this is not the case for the stress \({\varvec{\mathrm {\sigma }}}_\textrm{s} = -\rho \,c_\textrm{s}^2\,{\varvec{\textrm{G}}}\,{{\,\textrm{dev}\,}}{{\varvec{\textrm{G}}}}\), which does not depend on these rotations, thus leading to the same global dynamics for both choices of the numerical viscosity coefficient \(k_L\).
In Fig. 18 we report a variety of snapshots for this test problem at different times between \(t = 7\,\textrm{s}\) and \(t = 8\,\textrm{s}\), at different values of the Weber number \({\mathbb {W}}\textrm{e}= \rho \,U^2\,L/\sigma \) and at different values of the Reynolds number \({\mathbb {R}}\textrm{e}= U\,L/\nu \). These runs employ a uniform Cartesian grid counting 4096 by \(12\,288\) elements. With \({\mathbb {W}}\textrm{e}\simeq 1200\) we indicate simulations carried out with \(\sigma = 2 \times 10^{-5}\), and \({\mathbb {W}}\textrm{e}\simeq \infty \) corresponds to \(\sigma = 0\). With \({\mathbb {R}}\textrm{e}\simeq 2000\) we indicate simulations carried out with \(c_\textrm{s}=0.3\) and \(\tau = 2\times 10^{-3}\), and the label \({\mathbb {R}}\textrm{e}\simeq 8000\) corresponds to \(c_\textrm{s}=0.3\) and \(\tau = 5\times 10^{-4}\), while the inviscid limit \({\mathbb {R}}\textrm{e}\simeq \infty \) is given by \(c_\textrm{s}=0.3\) and \(\tau = 10^{-14}\). The results show the stabilising effects of surface tension and viscosity and the characteristic morphology they regulate. See [99] for striking experimental results on the Richtmyer–Meshkov instability, featuring similar flow structures.
In Fig. 19, we plot the results of the same battery of simulations at a later time \(t = 12.5\,\textrm{s}\). Again, the distinctive features determined by the presence of viscosity and surface tension, as well as Rayleigh–Plateau secondary instabilities, can be clearly identified.
In a final set of runs we study the \({\mathbb {R}}\textrm{e}\rightarrow \infty \), \({\mathbb {W}}\textrm{e}\rightarrow \infty \) limit of the governing equations, by setting \(\tau = 10^{-14}\), \(\sigma = 0\), \(c_\textrm{s}= 0.1\). With this test we intend to verify the applicability of our MPI-parallel computational code to large scale simulations, its resolution properties, and its robustness in turbulent multiphase flows. We report, in Fig. 20, the results of a large scale simulation of turbulent multiphase flow, run on \(32\textrm{k}\) CPU cores of the HPE–Hawk supercomputer at the HLRS in Stuttgart, with a grid counting \(10\,080\) by \(30\,240\) uniform Cartesian elements. For comparison, in the same Figure are also plotted the results of the same setup on a coarser grid of 4096 by \(12\,288\) cells.
6 Conclusion
In this paper, we have presented a novel semi-implicit pressure-based scheme for the solution of compressible two-phase flows with surface tension and viscous effects. Both, surface tension and viscosity are modelled within the framework of Symmetric Hyperbolic and Thermodynamically Compatible (SHTC) systems. Thus the governing equations are of first order in space and time and have hyperbolic character.
The scheme makes use of a multiply-staggered Cartesian grid, featuring traditional Finite Volume cell average quantities which can be interpreted (up to second order errors) as collocated cell center values, as well as edge-based quantities (momentum components) that are used for the discretisation of pressure forces (the acoustic subsystem), making the scheme well suited for simulating low Mach number flows, since such a staggered configuration allows the computation of the pressure field, along with its associated forces and work terms, as the solution of a sequence of symmetric positive definite linear systems, as in traditional staggered pressure-based schemes for incompressible and low Mach number flows, see [15, 35,36,37, 77, 93, 102]. Additionally, since the governing equations must obey a set of curl-type involutions (notably the interface field \({\varvec{\textrm{b}}}\) must remain curl-free for all times if initially curl-free), several corner quantities are employed in order to achieve a curl-free discretisation of the distortion field \({\varvec{\textrm{A}}}\) (also called co-basis in solid mechanics), like in [26], and in this work the same discretisation is also applied to an interface field \({\varvec{\textrm{b}}}\) that tracks interfaces and is used for the computation of surface tension forces.
A major result of this paper is that our new curl-free discretisation can be used to solve the surface tension model of Gavrilyuk and collaborators [17, 116] for the first time in its original weakly hyperbolic formulation, without any GLM curl-cleaning or Godunov–Powell symmetrising terms [42]. In other words: thanks to the compatible curl-free discretization adopted in this paper, the interface field \({\varvec{\textrm{b}}}\) can be evolved directly by means of the original weakly hyperbolic formulation proposed in [116], without the generation of spurious instabilities associated with weak hyperbolicity. In [42] these instabilities were highlighted and studied and were subsequently solved by providing several alternative strongly hyperbolic reformulations of the governing equations, while in the present paper the instabilities associated with weak hyperbolicity can be avoided ab initio thanks to a special compatible (mimetic) discretization. It is worth noting that, if the constraint \(\nabla \times {\varvec{\textrm{b}}} = {\varvec{\textrm{0}}}\) is satisfied exactly, all formulations of the hyperbolic surface tension model of Gavrilyuk collapse onto the same set of partial differential equations, since the non-conservative Godunov–Powell terms vanish, and so does the auxiliary GLM curl cleaning field introduced in [42].
Several computational experiments, including very high resolution simulations of Rayleigh–Taylor instabilities at different Weber and Reynolds numbers, have been carried out and employed to highlight the efficacy of the new numerical scheme forwarded in this paper.
Future work will include the extension of the method to uniform high order in space and time, by means of IMEX timestepping [11, 19,20,21,22, 85, 101], as well as an implicit discretization of shear waves, similar to the three-split for the MHD equations proposed in [57], aiming at eliminating the timestep restriction associated with the shear wavespeed \(c_\textrm{s}\), which can be very high in certain fluids, for example when the model is applied to lava flows. In the future we will also consider a provably thermodynamically compatible discretization of the model, similar to the schemes recently forwarded in [2, 3, 5, 7, 30, 32, 63, 78], as well as an extension to moving unstructured meshes with topology changes [65].
Data Availability
The data can be obtained from the authors on reasonable request.
References
Abbate, E., Iollo, A., Puppo, G.: An asymptotic-preserving all-speed scheme for fluid dynamics and nonlinear elasticity. SIAM J. Sci. Comput. 41, A2850–A2879 (2019)
Abgrall, R., Busto, S., Dumbser, M.: A simple and general framework for the construction of thermodynamically compatible schemes for computational fluid and solid mechanics. Appl. Math. Comput. (2022)
Abgrall, R., Nordström, R., Öffner, P., Tokareva, S.: Analysis of the SBP-SAT stabilization for finite element methods part II: entropy stability. Commun. Appl. Math. Comput (2021)
Abgrall, R.: How to prevent pressure oscillations in multicomponent flow calculations: a quasi conservative approach. J. Comput. Phys. 125(1), 150–160 (1996)
Abgrall, R.: A general framework to construct schemes satisfying additional conservation relations. Application to entropy conservative and entropy dissipative schemes. J. Comput. Phys. 372, 640–666 (2018)
Abgrall, R., Saurel, R.: Discrete equations for physical and numerical compressible multiphase mixtures. J. Comput. Phys. 186, 361–396 (2003)
Abgrall, R., Nordström, J., Öffner, P., Tokareva, S.: Analysis of the SBP-SAT stabilization for finite element methods. I: Linear problems. J. Sci. Comput. 85(2), 28 (2020)
Al-Dirawi, K.H., Bayly, A.E.: An experimental study of binary collisions of miscible droplets with non-identical viscosities. Exp. Fluids 61 (2020)
Andrianov, N., Warnecke, G.: The Riemann problem for the Baer-Nunziato two-phase flow model. J. Comput. Phys. 212, 434–464 (2004)
Arnold, D., Falk, R., Winther, R.: Finite element exterior calculus, homological techniques, and applications. Acta Numer. 15, 1–155 (2006)
Ascher, U.M., Ruuth, S.J., Spiteri, R.J.: Implicit-explicit Runge-Kutta methods for time-dependent partial differential equations. Appl. Numer. Math. 25(2), 151–167 (1997). (Special Issue on Time Integration)
Baer, M.R., Nunziato, J.W.: A two-phase mixture theory for the deflagration-to-detonation transition (DDT) in reactive granular materials. J. Multiphase Flow 12, 861–889 (1986)
Balsara, D., Käppeli, R., Boscheri, W., Dumbser, M.: Curl constraint-preserving reconstruction and the guidance it gives for mimetic scheme design. Commun. Appl. Math. Comput. Sci. (2021)
Barton, P.: An interface-capturing Godunov method for the simulation of compressible solid-fluid problems. J. Comput. Phys. 390, 25–50 (2019)
Bell, J., Colella, P., Glaz, H.: A second-order projection method for the incompressible Navier–Stokes equations. J. Comput. Phys. 85, 257–283 (1989)
Bermúdez, A., Busto, S., Dumbser, M., Ferrín, J., Saavedra, L., Vázquez-Cendón, M.: A staggered semi-implicit hybrid FV/FE projection method for weakly compressible flows. J. Comput. Phys. 421, 109743 (2020)
Berry, R., Saurel, R., Petitpas, F., Daniel, E., Le Métayer, O., Gavrilyuk, S.: Progress in the development of compressible. Multiphase flow modeling capability for nuclear reactor flow applications. Idaho National Laboratory (2008)
Besseling, J.: A thermodynamic approach to rheology. In: H. Parkus, L. Sedov (eds.) Irreversible Aspects of Continuum Mechanics and Transfer of Physical Characteristics in Moving Fluids, IUTAM Symposia, pp. 16–53. Springer Vienna (1968)
Boscarino, S.: Error analysis of IMEX Runge-Kutta methods derived from differential-algebraic systems. SIAM J. Numer. Anal. 45(4), 1600–1621 (2007)
Boscarino, S.: On an accurate third order implicit-explicit Runge-Kutta method for stiff problems. Appl. Numer. Math. 59(7), 1515–1528 (2009)
Boscarino, S., Russo, G.: On a class of uniformly accurate IMEX Runge-Kutta schemes and applications to hyperbolic systems with relaxation. SIAM J. Sci. Comput. 31(3), 1926–1945 (2009)
Boscarino, S., Pareschi, L., Russo, G.: Implicit-explicit Runge-Kutta schemes for hyperbolic systems and kinetic equations in the diffusion limit. SIAM J. Sci. Comput. 35(1), A22–A51 (2013)
Boscarino, S., Russo, G., Scandurra, L.: All Mach number second order semi-implicit scheme for the Euler equations of gasdynamics. J. Sci. Comput. 77, 850–884 (2018)
Boscheri, W., Pareschi, L.: High order pressure-based semi-implicit IMEX schemes for the 3D Navier-Stokes equations at all Mach numbers. J. Comput. Phys. 434, 110206 (2021)
Boscheri, W., Dimarco, G., Tavelli, M.: An efficient second order all Mach finite volume solver for the compressible Navier-Stokes equations. Comput. Methods Appl. Mech. Eng. 374, 113602 (2021)
Boscheri, W., Dumbser, M., Ioriatti, M., Peshkov, I., Romenski, E.: A structure-preserving staggered semi-implicit finite volume scheme for continuum mechanics. J. Comput. Phys. 424, 109866 (2021)
Boscheri, W., Chiocchetti, S., Peshkov, I.: A cell-centered implicit-explicit Lagrangian scheme for a unified model of nonlinear continuum mechanics on unstructured meshes. J. Comput. Phys. 451, 110852 (2022)
Busto, S., Chiocchetti, S., Dumbser, M., Gaburro, E., Peshkov, I.: High order ADER schemes for continuum mechanics. Front. Phys. 8, 32 (2020)
Busto, S., Dumbser, M., Escalante, C., Gavrilyuk, S., Favrie, N.: On high order ADER discontinuous Galerkin schemes for first order hyperbolic reformulations of nonlinear dispersive systems. J. Sci. Comput. 87, 48 (2021)
Busto, S., Dumbser, M., Gavrilyuk, S., Ivanova, K.: On thermodynamically compatible finite volume methods and path-conservative ADER discontinuous Galerkin schemes for turbulent shallow water flows. J. Sci. Comput. 88, 28 (2021)
Busto, S., Rio, L.D., Vázquez-Cendón, M., Dumbser, M.: A semi-implicit hybrid finite volume / finite element scheme for all Mach number flows on staggered unstructured meshes. Appl. Math. Comput. 402, 126117 (2021)
Busto, S., Dumbser, M., Peshkov, I., Romenski, E.: On thermodynamically compatible finite volume schemes for continuum mechanics. SIAM J. Sci. Comput. 44(3), A1723–A1751 (2022)
Cardano, G.: Artis magnae sive de regulis algebraicis liber unus. Petreius, Nürnberg (1545)
Castro, M.J., Gallardo, J.M., Parés, C.: High-order finite volume schemes based on reconstruction of states for solving hyperbolic systems with nonconservative products. Applications to shallow-water systems. Math. Comput. 75, 1103–1134 (2006)
Casulli, V.: Semi-implicit finite difference methods for the two-dimensional shallow water equations. J. Comput. Phys. 86, 56–74 (1990)
Casulli, V.: A semi-implicit finite difference method for non-hydrostatic free-surface flows. Int. J. Numer. Meth. Fluids 30, 425–440 (1999)
Casulli, V., Greenspan, D.: Pressure method for the numerical solution of transient, compressible fluid flows. Int. J. Numer. Meth. Fluids 4(11), 1001–1012 (1984)
Casulli, V., Zanolli, P.: A nested Newton-type algorithm for finite volume methods solving Richards’ equation in mixed form. SIAM J. Sci. Comput. 32, 2255–2273 (2009)
Casulli, V., Zanolli, P.: Iterative solutions of mildly nonlinear systems. J. Comput. Appl. Math. 236, 3937–3947 (2012)
Chiocchetti, S.: High order numerical methods for a unified theory of fluid and solid mechanics, PhD thesis (2022)
Chiocchetti, S., Müller, C.: A Solver for Stiff Finite-Rate Relaxation in Baer-Nunziato Two-Phase Flow Models. Fluid Mech. Appl. 121, 31–44 (2020)
Chiocchetti, S., Peshkov, I., Gavrilyuk, S., Dumbser, M.: High order ADER schemes and GLM curl cleaning for a first order hyperbolic formulation of compressible flow with surface tension. J. Comput. Phys. 426, 109898 (2021)
Cordier, F., Degond, P., Kumbaro, A.: An Asymptotic-Preserving all-speed scheme for the Euler and Navier-Stokes equations. J. Comput. Phys. 231, 5685–5704 (2012)
de Brauer, A., Iollo, A., Milcent, T.: A cartesian scheme for compressible multimaterial hyperelastic models with plasticity. Commun. Comput. Phys. 22, 1362–1384 (2017)
De Lorenzo, M., Pelanti, M., Lafon, P.: HLLC-type and path-conservative schemes for a single-velocity six-equation two-phase flow model: a comparative study. Appl. Math. Comput. 333, 95–117 (2018)
Dedner, A., Kemm, F., Kröner, D., Munz, C.D., Schnitzer, T., Wesenberg, M.: Hyperbolic divergence cleaning for the MHD equations. J. Comput. Phys. 175, 645–673 (2002)
Dhaouadi, F., Dumbser, M.: A first order hyperbolic reformulation of the Navier–Stokes–Korteweg system based on the GPR model and an augmented Lagrangian approach. J. Comput. Phys. 470, 111544 (2022)
Dhaouadi, F., Favrie, N., Gavrilyuk, S.: Extended Lagrangian approach for the defocusing nonlinear Schrödinger equation. Stud. Appl. Math. 142, 336–358 (2019)
Dumbser, M., Casulli, V.: A conservative, weakly nonlinear semi-implicit finite volume method for the compressible Navier–Stokes equations with general equation of state. Appl. Math. Comput. 272, 479–497 (2016)
Dumbser, M., Enaux, C., Toro, E.F.: Finite volume schemes of very high order of accuracy for stiff hyperbolic balance laws. J. Comput. Phys. 227, 3971–4001 (2008)
Dumbser, M., Peshkov, I., Romenski, E., Zanotti, O.: High order ADER schemes for a unified first order hyperbolic formulation of continuum mechanics: viscous heat-conducting fluids and elastic solids. J. Comput. Phys. 314, 824–862 (2016)
Dumbser, M., Peshkov, I., Romenski, E., Zanotti, O.: High order ADER schemes for a unified first order hyperbolic formulation of Newtonian continuum mechanics coupled with electro-dynamics. J. Comput. Phys. 348, 298–342 (2017)
Dumbser, M., Balsara, D., Tavelli, M., Fambri, F.: A divergence-free semi-implicit finite volume scheme for ideal, viscous and resistive magnetohydrodynamics. Int. J. Numer. Meth. Fluids 89, 16–42 (2019)
Dumbser, M., Chiocchetti, S., Peshkov, I.: On Numerical Methods for Hyperbolic PDE with Curl Involutions, pp. 125–134. Springer International Publishing, Cham (2020)
Dumbser, M., Fambri, F., Gaburro, E., Reinarz, A.: On GLM curl cleaning for a first order reduction of the CCZ4 formulation of the Einstein field equations. J. Comput. Phys. 404, 109088 (2020)
Einstein, A.: Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 322(8), 549–560 (1905)
Fambri, F.: A novel structure preserving semi-implicit finite volume method for viscous and resistive magnetohydrodynamics. Int. J. Numer. Meth. Fluids 93, 3447–3489 (2021)
Favrie, N., Gavrilyuk, S.: Diffuse interface model for compressible fluid: compressible elastic-plastic solid interaction. J. Comput. Phys. 231, 2695–2723 (2012)
Favrie, N., Gavrilyuk, S., Saurel, R.: Solid-fluid diffuse interface model in cases of extreme deformations. J. Comput. Phys. 228, 6037–6077 (2009)
Feynman, R.P.: The Feynman lectures on physics. Addison-Wesley Pub. Co., Reading (1963)
Finotello, G., Kooiman, R.F., Padding, J.T., Buist, K.A., Jongsma, A., Innings, F., Kuipers, J.A.M.: The dynamics of milk droplet-droplet collisions. Exp. Fluids 59 (2017)
Gabriel, A.A., Li, D., Chiocchetti, S., Tavelli, M., Peshkov, I., Romenski, E., Dumbser, M.: A unified first-order hyperbolic model for nonlinear dynamic rupture processes in diffuse fracture zones. Philos. Trans. Royal Soc. A 379 (2021)
Gaburro, E., Öffner, P., Ricchiuto, M., Torlo, D.: High order entropy preserving ADER-DG schemes. Appl. Math. Comput. (2022)
Gaburro, E., Castro, M.J., Dumbser, M.: A well balanced diffuse interface method for complex nonhydrostatic free surface flows. Comput. Fluids 175, 180–198 (2018)
Gaburro, E., Boscheri, W., Chiocchetti, S., Klingenberg, C., Springel, V., Dumbser, M.: High order direct Arbitrary–Lagrangian–Eulerian schemes on moving Voronoi meshes with topology changes. J. Comput. Phys. 407, 109167 (2020)
Gavrilyuk, S., Favrie, N., Saurel, R.: Modelling wave dynamics of compressible elastic materials. J. Comput. Phys. 227, 2941–2969 (2008)
Godunov, S.K., Romenski, E.I.: Elements of Continuum Mechanics and Conservation Laws. Kluwer Academic/ Plenum Publishers (2003)
Godunov, S.K., Romenski, E.: Elements of Mechanics of Continuous Media. Nauchnaya Kniga (1998)
Godunov, S.K.: Elements of mechanics of continuous media. Nauka (1978)
Godunov, S.: An interesting class of quasilinear systems. Dokl. Akad. Nauk SSSR 139(3), 521–523 (1961)
Godunov, S.: Symmetric form of the magnetohydrodynamic equation. Numer. Methods Mech. Contin. Med. 3(1), 26–34 (1972)
Godunov, S.K., Peshkov, I.: Thermodynamically consistent nonlinear model of elastoplastic maxwell medium. Comput. Math. Math. Phys. 50(8), 1409–1426 (2010)
Godunov, S.K., Romenski, E.I.: Nonstationary equations of the nonlinear theory of elasticity in Euler coordinates. J. Appl. Mech. Tech. Phys. 13, 868–885 (1972)
Godunov, S.K., Romenski, E.: Elements of Continuum Mechanics and Conservation Laws. Kluwer Academic/Plenum Publishers, New York (2003)
Godunov, S.K., Mikhaîlova, T.Y., Romenskiî, E.I.: Systems of thermodynamically coordinated laws of conservation invariant under rotations. Sib. Math. J. 37(4), 690–705 (1996)
Hank, S., Gavrilyuk, S., Favrie, N., Massoni, J.: Impact simulation by an Eulerian model for interaction of multiple elastic-plastic solids and fluids. Int. J. Impact Eng 109, 104–111 (2017)
Harlow, F., Welch, J.: Numerical calculation of time-dependent viscous incompressible flow of fluid with a free surface. Phys. Fluids 8, 2182–2189 (1965)
Hennemann, S., Rueda-Ramírez, A., Hindenlang, F., Gassner, G.: A provably entropy stable subcell shock capturing approach for high order split form DG for the compressible Euler equations. J. Comput. Phys. 426 (2021)
Hinterbichler, H., Planchette, C., Brenn, G.: Ternary drop collisions. Exp. Fluids 56, 190/1-190/12 (2015)
Hyman, J., Shashkov, M.: Natural discretizations for the divergence, gradient, and curl on logically rectangular grids. Comput. Math. Appl. 33, 81–104 (1997)
Jackson, H., Nikiforakis, N.: A numerical scheme for non-Newtonian fluids and plastic solids under the GPR model. J. Comput. Phys. 387, 410–429 (2019)
Jackson, H., Nikiforakis, N.: A unified Eulerian framework for multimaterial continuum mechanics. J. Comput. Phys. 401, 109022 (2019)
Kapila, A.K., Menikoff, R., Bdzil, J.B., Son, S.F., Stewart, D.S.: Two-phase modelling of deflagration-to-detonation in granular materials: reduced equations. Phys. Fluids 13, 3002–3024 (2001)
Kemm, F., Gaburro, E., Thein, F., Dumbser, M.: A simple diffuse interface approach for compressible flows around moving solids of arbitrary shape based on a reduced Baer-Nunziato model. Comput. Fluids 204, 104536 (2020)
Kennedy, C.A., Carpenter, M.H.: Additive Runge-Kutta schemes for convection-diffusion-reaction equations. Appl. Numer. Math. 44(1), 139–181 (2003)
Klainermann, S., Majda, A.: Singular Limits of Quasilinear Hyperbolic Systems with Large Parameters and the Incompressible Limit of Compressible Fluid. Commun. Pure Appl. Math. 34, 481–524 (1981)
Klainermann, S., Majda, A.: Compressible and incompressible fluids. Commun. Pure Appl. Math. 35, 629–651 (1982)
Klein, R., Botta, N., Schneider, T., Munz, C., Roller, S., Meister, A., Hoffmann, L., Sonar, T.: Asymptotic adaptive methods for multi-scale problems in fluid mechanics. J. Eng. Math. 39, 261–343 (2001)
Lipnikov, K., Manzini, G., Shashkov, M.: Mimetic finite difference method. J. Comput. Phys. 257, 1163–1227 (2014)
Loubère, R., Maire, P.H., Shashkov, M., Breil, J., Galera, S.: ReALE: a reconnection-based arbitrary-Lagrangian–Eulerian method. J. Comput. Phys. 229, 4724–4761 (2010)
Lukácová-Medvidóvá, M., Puppo, G., Thomann, A.: An all Mach number finite volume method for isentropic two-phase flow. J. Numer. Math. (2022). https://doi.org/10.1515/jnma-2022-0015
Margolin, G., Shashkov, M., Smolarkiewicz, P.: A discrete operator calculus for finite difference approximations. Comput. Methods Appl. Mech. Eng. 187, 365–383 (2000)
Munz, C., Klein, R., Roller, S., Geratz, K.: The extension of incompressible flow solvers to the weakly compressible regime. Comput. Fluids (2003)
Munz, C., Omnes, P., Schneider, R., Sonnendrücker, E., Voss, U.: Divergence correction techniques for Maxwell solvers based on a hyperbolic model. J. Comput. Phys. 161, 484–511 (2000)
Munz, C., Roller, S., Klein, R., Geratz, K.: The extension of incompressible flow solvers to the weakly compressible regime. Comput. Fluids 32, 173–196 (2003)
Munz, C., Dumbser, M., Roller, S.: Linearized acoustic perturbation equations for low Mach number flow with variable density and temperature. J. Comput. Phys. 224, 352–364 (2007)
Ndanou, S., Favrie, N., Gavrilyuk, S.: Criterion of hyperbolicity in hyperelasticity in the case of the stored energy in separable form. J. Elast. 115, 1–25 (2014)
Ndanou, S., Favrie, N., Gavrilyuk, S.: Multi-solid and multi-fluid diffuse interface model: applications to dynamic fracture and fragmentation. J. Comput. Phys. 295, 523–555 (2015)
Niederhaus, C.E., Jacobs, J.W.: Experimental study of the Richtmyer–Meshkov instability of incompressible fluids. J. Fluid Mech. 485, 243–277 (2003)
Parés, C.: Numerical methods for nonconservative hyperbolic systems: a theoretical framework. SIAM J. Numer. Anal. 44, 300–321 (2006)
Pareschi, L., Russo, G.: Implicit-explicit Runge-Kutta schemes and applications to hyperbolic systems with relaxation. J. Sci. Comput. 25(1), 129–155 (2005)
Park, J., Munz, C.: Multiple pressure variables methods for fluid flow at all mach numbers. Int. J. Numer. Meth. Fluids 49, 905–931 (2005)
Peshkov, I., Romenski, E.: A hyperbolic model for viscous Newtonian flows. Continuum Mech. Thermodyn. 28, 85–104 (2016)
Peshkov, I., Pavelka, M., Romenski, E., Grmela, M.: Continuum mechanics and thermodynamics in the Hamilton and the Godunov-type formulations. Continuum Mech. Thermodyn. 30(6), 1343–1378 (2018)
Peshkov, I., Dumbser, M., Boscheri, W., Romenski, E., Chiocchetti, S., Ioriatti, M.: Simulation of non-Newtonian viscoplastic flows with a unified first order hyperbolic model and a structure-preserving semi-implicit scheme. Comput. Fluids 224, 104963 (2021)
Planchette, C., Hinterbichler, H., Liu, M., Bothe, D., Brenn, G.: Colliding drops as coalescing and fragmenting liquid springs. J. Fluid Mech. 814, 277–300 (2017)
Powell, K.: An Approximate Riemann Solver for Magnetohydrodynamics. In: v.L.B. M.Y., V.R. J. (eds.) Upwind and High-Resolution Schemes, pp. 570–583. Springer, Berlin (1997)
Powell, K., Roe, P., Linde, T., Gombosi, T., Zeeuw, D.D.: A solution-adaptive upwind scheme for ideal magnetohydrodynamics. J. Comput. Phys. 154(2), 284–309 (1999)
Re, B., Abgrall, R.: A pressure-based method for weakly compressible two-phase flows under a Baer-Nunziato type model with generic equations of state and pressure and velocity disequilibrium. Int. J. Numer. Methods Fluids 94, 1183–1232 (2022)
Romenski, E.: Hyperbolic systems of thermodynamically compatible conservation laws in continuum mechanics. Math. Comput. Model. 28(10), 115–130 (1998)
Romenski, E., Resnyansky, A., Toro, E.: Conservative hyperbolic formulation for compressible two-phase flow with different phase pressures and temperatures. Q. Appl. Math. 65, 259–279 (2007)
Romenski, E., Drikakis, D., Toro, E.: Conservative models and numerical methods for compressible two-phase flow. J. Sci. Comput. 42, 68–95 (2010)
Romensky, E.I.: Thermodynamics and hyperbolic systems of balance laws in continuum mechanics. In: Toro, E. (ed.) Godunov Methods: Theory and Applications, pp. 745–761. Springer, New York (2001)
Saurel, R., Abgrall, R.: A multiphase Godunov method for compressible multifluid and multiphase flows. J. Comput. Phys. 150, 425–467 (1999)
Schlichting, H., Gersten, K.: Grenzschichttheorie. Springer, New York (2005)
Schmidmayer, K., Petitpas, F., Daniel, E., Favrie, N., Gavrilyuk, S.: A model and numerical method for compressible flows with capillary effects. J. Comput. Phys. 334, 468–496 (2017)
Sommerfeld, M., Pasternak, L.: Advances in modelling of binary droplet collision outcomes in sprays: a review of available knowledge. Int. J. Multiph. Flow 117, 182–205 (2019)
Tavelli, M., Dumbser, M.: A staggered space-time discontinuous Galerkin method for the incompressible Navier–Stokes equations on two-dimensional triangular meshes. Comput. Fluids 119, 235–249 (2015)
Tavelli, M., Dumbser, M.: A pressure-based semi-implicit space-time discontinuous Galerkin method on staggered unstructured meshes for the solution of the compressible Navier–Stokes equations at all Mach numbers. J. Comput. Phys. 341, 341–376 (2017)
Tavelli, M., Chiocchetti, S., Romenski, E., Gabriel, A.A., Dumbser, M.: Space-time adaptive ADER discontinuous Galerkin schemes for nonlinear hyperelasticity with material failure. J. Comput. Phys. 422, 109758 (2020)
Thein, F., Romenski, E., Dumbser, M.: Exact and numerical solutions of the Riemann problem for a conservative model of compressible two-phase flows. J. Sci. Comput. 93, 83 (2022)
Thomann, A., Puppo, G., Klingenberg, C.: An all speed second order well-balanced IMEX relaxation scheme for the Euler equations with gravity. J. Comput. Phys. 420, 109723 (2020)
Toro, E.F.: Riemann Solvers and Numerical Methods for Fluid Dynamics. A Practical Introduction, 3rd edn. Springer, Berlin (2009)
Toro, E., Vázquez-Cendón, M.: Flux splitting schemes for the Euler equations. Comput. Fluids 70, 1–12 (2012)
van Leer, B.: Towards the ultimate conservative difference scheme. II. Monotonicity and conservation combined in a second-order scheme. J. Comput. Phys. 14, 361–370 (1974)
van Leer, B.: Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 32, 101–136 (1979)
Wood, A.: A Textbook of Sound. B. Bell and Sons LTD, London (1930)
Acknowledgements
The research presented in this paper has been funded by the Italian Ministry of Education, University and Research (MIUR) in the frame of the Departments of Excellence Initiative 2018–2022 attributed to DICAM of the University of Trento (grant L. 232/2016) and in the frame of the PRIN 2017 project Innovative numerical methods for evolutionary partial differential equations and applications. The research was also funded by the Deutsche Forschungsgemeinschaft (DFG) via the project DROPIT, grant no. GRK 2160/2. Furthermore, S. C. has also received funding within Project HPC-EUROPA3 (INFRAIA-2016-1-730897), with the support of the EC Research Innovation Action under the H2020 Programme. In particular, S. C. gratefully acknowledges the support of Prof. Dr. rer. nat. Claus-Dieter Munz at IAG and the computer resources and technical support provided by HLRS in Stuttgart. M. D. and S. C. are both members of the INdAM GNCS group.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Chiocchetti, S., Dumbser, M. An Exactly Curl-Free Staggered Semi-Implicit Finite Volume Scheme for a First Order Hyperbolic Model of Viscous Two-Phase Flows with Surface Tension. J Sci Comput 94, 24 (2023). https://doi.org/10.1007/s10915-022-02077-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-022-02077-2