A Lowest-Degree Conservative Finite Element Scheme for Incompressible Stokes Problems on General Triangulations

Abstract

In this study, we investigate how low the degree of polynomials can be to construct a stable conservative pair for incompressible Stokes problems that works on general triangulations. We propose a finite element pair that uses a slightly enriched piecewise linear polynomial space for velocity and piecewise constant space for pressure. The pair is illustrated to be a lowest-degree stable conservative pair for Stokes problems on general triangulations.

1 Introduction

For the Stokes problem, if a stable finite element pair can inherit mass conservation, the approximation of the velocity can be independent of the pressure, and the method does not suffer from the locking effect with respect to a high Reynolds number (cf., e.g., [6]). Over the past decade, conservative schemes have been recognized more clearly as pressure robustness and widely studied and surveyed in, for example, [13, 15, 22, 29]. This conservation is also connected to other key features such as “viscosity-independence” [33] and “gradient-robustness” [23] for numerical schemes. Conservative schemes are also significant in nonlinear mechanics [4, 5] and magnetohydrodynamics [18,19,20]. The construction of conservative schemes has thus been drawing wide interests.

Various conservative finite element pairs have been designed for the Stokes problem. Conforming examples include conforming elements designed for special meshes, such as $\varvec{P}_{k}$–$P_{k-1}$ triangular elements for $k\ge 4$ on singular-vertex-free meshes [30], smaller k constructed on composite grids [3, 28, 30, 36, 41], and the pairs given in [12, 15], which work for general triangulations and with extra smoothness requirements. An alternative method is to use $\varvec{H}{}({\mathrm{div}})$-conforming but $\varvec{H}{}^1$-nonconforming space for the velocity. A systematic approach for finite element methods is to add bubble-like functions onto $\varvec{H}{}({\mathrm{div}})$ finite element spaces for tangential weak continuity for the velocity. Examples along this line can be found in [14, 25, 32] and [35]. Generally, to construct a conservative pair that works on general triangulations without special structures, cubic and higher-degree polynomials are used for the velocity field.

Recently, a new $\varvec{P}{}_2$–$P_1$ finite element pair was proposed on general triangulations [37]; for the velocity field, this pair uses piecewise quadratic $\varvec{H}{}({\mathrm{div}})$ functions with enhanced tangential continuity in addition to using discontinuous piecewise linear functions for pressure. The pair is stable and immediately strictly conservative on general triangulations, and is of the lowest degree ever known. As the tangential component of the velocity function is continuous only in the average sense, the convergence rate of the pair is proved to be of $\mathscr {O}(h)$ order. However, due to its strict conservativeness on general triangulations, it plays superior to some $\mathscr {O}(h^2)$ schemes numerically in robustness with respect to triangulations and with respect to small parameters. As pointed out in [37], this $\varvec{P}{}_2$–$P_1$ pair can be viewed as a smoothened reduction from the famous second-order Brezzi–Douglas–Marini pair, and this idea can be applied to other $\varvec{H}{}({\mathrm{div}})$ pairs so that the degrees of finite element pairs may be reduced further.

In this work, we study how low the degree of polynomials can be to construct a stable conservative pair that works on general triangulations. We begin with the reduction of the second-order Brezzi–Douglas–Fortin–Marini(BDFM) element pair to construct an auxiliary finite element pair $\varvec{V}{}_{h0}^\mathrm{sBDFM}$–$\mathbb {P}^{1}_{h0}$ (with $\mathscr {O}(h)$ convergence rate), and then a further reduction of the $\varvec{V}{}_{h0}^\mathrm{sBDFM}$–$\mathbb {P}^{1}_{h0}$ pair leads to a $\varvec{V}{}_{h0}^\mathrm{el}$–$\mathbb {P}^0_{h0}$ pair. The finally proposed pair, as the centerpiece of this study, uses a slightly enriched piecewise linear polynomial space for the velocity and piecewise constant for the pressure, and is stable and conservative. A further reduction of this pair leads to a $\varvec{P}{}_1$–$P_0$ pair, which is constructed naturally but not stable on general triangulations. Accordingly, we find that the newly designed $\varvec{V}{}_{h0}^\mathrm{el}$–$\mathbb {P}^0_{h0}$ pair is of a lowest-degree conservative pair. We remark that the $\varvec{V}{}_{h0}^{\mathrm{el}}$–$\mathbb {P}^0_{h0}$ pair is of the type “nonconforming spline” and cannot be represented by Ciarlet’s triple. However, the velocity space does admit a set of basis functions with local supports, which are clearly stated in Sect. 5. This makes the pair embedded in the standard framework for programming.

The technical ingredients of this study are twofold. One is to determine the locally supported basis functions of $\varvec{V}{}_{h0}^\mathrm{el}$. The supports are considerably different from those of existing finite elements. However, the explicit formulations of the basis functions make the scheme easy to implement. Another ingredient is to prove the stability of the pair (specifically the inf-sup condition), where we mainly utilize a two-step argument. We first prove the stability of the auxiliary pair $\varvec{V}{}_{h0}^\mathrm{sBDFM}$–$\mathbb {P}^{1}_{h0}$, and then the stability of the pair $\varvec{V}{}_{h0}^{\mathrm{el}}$–$\mathbb {P}^0_{h0}$, which is a sub-pair of $\varvec{V}{}_{h0}^{\mathrm{sBDFM}}$–$\mathbb {P}^{1}_{h0}$, is proved simply by inheriting the stability of $\varvec{V}{}_{h0}^\mathrm{sBDFM}$–$\mathbb {P}^{1}_{h0}$. This “reduce-and-inherit” procedure can be found in [46, 47], where some low-degree optimal schemes were designed for other problems. Furthermore, for the velocity space of the auxiliary pair $\varvec{V}{}_{h0}^{\mathrm{sBDFM}}$–$\mathbb {P}^{1}_{h0}$, all the degrees of freedom are located on the edges of the triangulation, and it is thus impossible to construct a commutative nodal interpolator with respect to a non-constant pressure space. We adopt Stenberg’s macroelement technique [31]. Unlike in the general macroelement argument, on every macroelement, the surjection property of the divergence operator is confirmed by figuring out the kernel space. This technique used to be applied in [38] to show the stability of the Stokes finite element pair. It is natural to generalize all these technical ingredients to other applications.

As a structure of the discretized Stokes complex is given on local macroelements, similar to the study of conservative pairs in [12, 15] and the study of biharmonic finite elements in [11, 39, 45, 46], the proposed global space is embedded in a discretized Stokes complex on the whole triangulation. This global Stokes complex is established in Sect. 4 with a new finite element scheme constructed for the biharmonic equation.

Finally, there have been various schemes constructed for the Stokes problem in the category of discontinuous Galerkin (DG) methods, weak Galerkin (WG) methods, and virtual element methods (VEMs), where extra stabilizations are generally used. They can be found in various studies, such as in [9, 10, 24, 27, 34, 48]. In the present study, we do not discuss such methods in depth and instead focus on methods without stabilization terms.

The rest of the paper is organized as follows. In the remainder of this section, we present some standard notations. Some preliminaries on finite elements are collected in Sect. 2. In Sect. 3, a smoothened BDFM(sBDFM) element and an auxiliary stable conservative pair $\varvec{V}{}_{h0}^\mathrm{sBDFM}$–$\mathbb {P}^{1}_{h0}$ are established. In Sect. 4, a low-degree continuous nonconforming scheme for the biharmonic equation is presented, together with a discretized Stokes complex. In Sect. 5, a lower-degree stable conservative pair $\varvec{V}{}_{h0}^{\mathrm{el}}$–$\mathbb {P}^0_{h0}$ is constructed. In Sect. 6, some numerical experiments are reported to demonstrate the effect of the schemes given in the present paper. In Sect. 7, some concluding remarks are given. Finally, it is verified numerically in Appendix A that the most natural $\varvec{P}{}_1$–$P_0$ pair, generated by the patch test, is not stable on general shape-regular triangulations. This illustrates that the $\varvec{V}{}_{h0}^{\mathrm{el}}$–$\mathbb {P}^0_{h0}$ pair is a lowest-degree conservative stable pair on general triangulations.

1.1 Notations

In this paper, we use $\varOmega$ to denote a simply connected polygonal domain. We use $\nabla$, $\mathrm{curl}$, $\mathrm{div}$, $\mathrm{rot}$, and $\nabla ^2$ to denote the gradient operator, curl operator, divergence operator, rot operator, and Hessian operator, respectively. Specifically, $\mathrm{curl}\, v(x,y) = (\frac{\partial v}{\partial y}, -\frac{\partial v}{\partial x})$ and $\mathrm{rot}\, (v_1,v_2) = \frac{\partial v_1}{\partial y}-\frac{\partial v_2}{\partial x}$. Generally, we use $H^1(\varOmega )$, $H^1_0(\varOmega )$, $H^2(\varOmega )$, $H^2_0(\varOmega )$, $\varvec{H}{}(\mathrm{div},\varOmega )$, $\varvec{H}{}_0(\mathrm{div},\varOmega )$, $H(\mathrm{rot},\varOmega )$, $H_0(\mathrm{rot},\varOmega )$, and $L^2(\varOmega )$ to denote certain Sobolev spaces, and denote $\displaystyle L^2_0(\varOmega ):=\{w\in L^2(\varOmega ):\int _\varOmega w dx=0\}$, $\varvec{H}{}{}^1_0(\varOmega ):=(H^1_0(\varOmega ))^2$. A space written in boldface denotes a two-vector valued analogue of the corresponding scalar space, and naturally, a function written in boldface denotes a two-vector valued analogue of the corresponding scalar function. We use $(\cdot ,\cdot )$ to represent the $L^2$ inner product, and $\langle \cdot ,\cdot \rangle$ to denote the duality between a space and its dual. To avoid ambiguity, we use the same notation $\langle \cdot ,\cdot \rangle$ for different dualities, and it can occasionally be treated as the $L^2$ inner product for certain functions. We use the subscript $``\cdot _h''$ to denote the dependence on triangulation. In particular, an operator with the subscript $``\cdot _h''$ indicates that the operation is performed cell by cell. In addition, $\Vert \cdot \Vert _{1,h}$ denotes the piecewise $\varvec{H}{}^1$-norm $\Vert \varvec{v}{}\Vert _{1,h}^2=\sum _{T\in \mathscr {T}_h} \Vert \varvec{v}{}\Vert _{1,T}^2$. Finally, denotes equality up to a constant. The hidden constants depend on the domain, and when triangulation is involved, they also depend on the shape regularity of the triangulation, but not on h or any other mesh parameter.

The two complexes below are well known:

$$\begin{aligned}&\{0\} \xrightarrow {{\mathrm{inc}}} H^1_0(\varOmega ) \xrightarrow {{\mathrm{curl}}} \varvec{H}{}_0(\mathrm{div},\varOmega ) \xrightarrow {{\mathrm{div}}} L^2_0(\varOmega ) \xrightarrow {\int _\varOmega \cdot } \{0\}, \end{aligned}$$

(1.1)

$$\begin{aligned}&\{0\} \xrightarrow {{\mathrm{inc}}} H^2_0(\varOmega ) \xrightarrow {{\mathrm{curl}}} \varvec{H}{}_0^1(\varOmega ) \xrightarrow {{\mathrm{div}}} L^2_0(\varOmega ) \xrightarrow {\int _\varOmega \cdot } \{0\}. \end{aligned}$$

(1.2)

We refer to [1, 2] for related discussion on more complexes and finite elements.

The fundamental incompressible Stokes problem is

$$\begin{aligned} \left\{ \begin{aligned} -\varepsilon ^{2} \varDelta \,\varvec{u}{}+ \nabla \, p&= \varvec{f}{}, \quad \text{ in } \ \varOmega , \\ \mathrm{div}\, \varvec{u}{}&= 0, \quad \text{ in } \ \varOmega , \\ \varvec{u}{}&= 0, \quad \text{ on } \ \partial \varOmega . \end{aligned} \right. \end{aligned}$$

(1.3)

Here, $\varvec{u}{}$ is the velocity field, p is the pressure field of the incompressible flow, and $\varepsilon ^2$ is the inverse of the Reynolds number, which can be small. The equation’s variational formulation is to find $(\varvec{u}{},p)\in \varvec{H}{}_0^1(\varOmega )\times L^2_0(\varOmega )$ such that

$$\begin{aligned} \left\{ \begin{aligned}&\varepsilon ^{2}\big (\nabla \,\varvec{u}{}, \nabla \,\varvec{v}{}\big ) -( \mathrm{div}\,\varvec{v}{}, p)&= ( \varvec{f}{},\varvec{v}{}),&\forall \, \varvec{v}{}\in \varvec{H}{}_0^1(\varOmega ), \\&(\mathrm{div}\,\varvec{u}{}, q )&= 0,&\forall \, q\in L^2_0(\varOmega ). \end{aligned} \right. \end{aligned}$$

(1.4)

2 Preliminaries

2.1 Triangulations

Let $\mathscr {T}_h$ be a shape-regular triangular subdivision of $\varOmega$ with the mesh size h such that $\overline{\varOmega }=\cup _{T\in \mathscr {T}_h}{\overline{T}}$. Denote $\mathscr {X}_h$, $\mathscr {X}_h^i$, $\mathscr {X}_h^b$, $\mathscr {E}_h$, $\mathscr {E}_h^i$, $\mathscr {E}_h^b$, $\mathscr {T}_h$, and $\mathscr {T}^i_h$ as the set of vertices, interior vertices, boundary vertices, edges, interior edges, boundary edges, cells, and cells with three interior edges, respectively. For any edge $e\in \mathscr {E}_h$, denote ${\textbf {n}}_e$ and ${\textbf {t}}_e$ as the globally defined unit normal and tangential vectors of e, respectively. The subscript ${\cdot }_e$ can be dropped when there is no ambiguity.

Denote (see Fig. 1a)

$$\begin{aligned} \mathscr {X}_h^{b,+1}:=\{a\in \mathscr {X}_h^i,\ a\ \text{ is } \text{ connected } \text{ to }\ \mathscr {X}_h^b\ \text{ by } \ e\in \mathscr {E}_h^i\},\ \text{ and }\ \ \mathscr {X}_h^{i,-1}:=\mathscr {X}_h^i\setminus \mathscr {X}_h^{b,+1}; \end{aligned}$$

further, denote with $\mathscr {X}^{i,-(k-1)}_h\ne \emptyset$,

$$\begin{aligned} \mathscr {X}_h^{b,+k}:=\{a\in \mathscr {X}_h^{i,-(k-1)},\ a\ \text{ is } \text{ connected } \text{ to }\ \mathscr {X}_h^{b,+(k-1)}\ \text{ by }\ e\in \mathscr {E}_h^i\} \end{aligned}$$

and

$$\begin{aligned} \mathscr {X}_h^{i,-k}:=\mathscr {X}_h^{i,-(k-1)}\setminus \mathscr {X}_h^{b,+k}. \end{aligned}$$

The smallest k such that $\mathscr {X}_h^{i,-(k-1)}=\mathscr {X}_h^{b,+k}$ is called the number of layers of the triangulation.

We call $\mathscr {X}_h^{b,+k}$ the k-layer boundary vertices and particularly $\mathscr {X}_h^{b}:=\mathscr {X}_h^{b,+0}$ the 0-layer boundary vertices. Consequently, the $\displaystyle \mathscr {X}_h^{i,-k}=\mathscr {X}_h \backslash \mathop {\cup }\limits _{s=0:k}\mathscr {X}_h^{b,+s}$ is a collection of all vertices except vertices from the 0-layer to k-layer.

On the triangle T with vertices $\{a_1,a_2,a_3\}$ and edges $\{e_1,e_2,e_3\}$, we denote local unit outward normal vectors by $\{{\textbf {n}}_{T,e_1}, {\textbf {n}}_{T,e_2}, {\textbf {n}}_{T,e_3}\}$ and local unit tangential vectors $\{{\textbf {t}}_{T,e_1}, {\textbf {t}}_{T,e_2}, {\textbf {t}}_{T,e_3}\}$ such that ${\textbf {n}}_{T,e_i} \times {\textbf {t}}_{T,e_i} >0,i\in \{1,2,3\}$; see Fig. 1(b) for an illustration. In addition $\{\lambda _1, \lambda _2, \lambda _3\}$ are the barycentric coordinates with respect to the three corners of T. Also, we denote the lengths of edges by $\{d_1,d_2,d_3\}$, the area of T is $S_T$, and we drop the subscript when no ambiguity exists. Particularly, $\tilde{S}_{\triangle (A_i,A_j,A_k)}$ represents the directed area of an triangle of corners $A_i,A_j, \text{ and } A_k$ sequentially, that is, $\tilde{S}_{\triangle (A_i,A_j,A_k)}=\overrightarrow{A_iA_j}\times \overrightarrow{A_iA_k}.$

Fig. 1

A grid with vertices labeled differently, as positions, and a reference cell

Fig. 2

Illustration of the supports of two types of patches

Next, we figure out two types of patches: combinations of cells.

Interior vertex patch::

For the interior vertex A, the cells that connect to A form a (closed) interior vertex patch, denoted by $P_A$ (see Fig. 2a);

Interior cell patch::

For the interior cell T, three neighbored cells and T form an interior cell patch, denoted by $P_{T}$ (see Fig. 2b).

The number of interior vertex patches is $\# \mathscr {X}_h^i$, and the number of interior cell patches is $\# \mathscr {T}^i_h (=2 \# \mathscr {X}_h^i-2)$.

In the sequel, we make a mild assumption about the grid.

Assumption 2.1

Every boundary vertex is connected to at least one interior vertex.

This assumption assures that every cell is covered by at least one interior vertex patch.

2.2 Polynomial Spaces on a Triangle

For the triangle T, we use $P_k(T)$ to denote the set of polynomials on the T of degrees not higher than k. In a similar manner, $P_k(e)$ is defined on the edge e. We define $\varvec{P}{}_k(T)=(P_k(T))^2$, and similarly, $\varvec{P}{}_k(e)$ is defined.

Following [25], we introduce the shape function space as

$$\begin{aligned} \varvec{P}{}^{\mathrm{MTW}}(T):=\{\varvec{v}{}\in \varvec{P}{}_3(T):\varvec{v}{}\cdot {\textbf {n}}|_{e_i}\in P_1(e_i),\ i=1:3,\ \mathrm{div}\, \varvec{v}{}\ \text{ is } \text{ a } \text{ constant } \text{ on }\ T\}. \end{aligned}$$

It can be verified (cf. [14]) that

$$\begin{aligned} \varvec{P}{}^{\mathrm{MTW}}(T)=\varvec{P}{}_1(T)\oplus \mathrm{span}\{\mathrm{curl}(\lambda _i^2\lambda _j\lambda _k)\}_{\{i,j,k\}=\{1,2,3\}}. \end{aligned}$$

Following [14], we introduce the shape functions space as

$$\begin{aligned} \varvec{P}{}^{\mathrm{GN-1}}(T)=\varvec{P}{}_1(T)\oplus \mathrm{span}\{\mathrm{curl}(\lambda _i^2\lambda _j^2\lambda _k)\}_{\{i,j,k\}=\{1,2,3\}}. \end{aligned}$$

We further denote that

$$\begin{aligned} \varvec{P}{}^{2-}(T):= & {} \varvec{P}{}_1(T)\oplus {\mathrm{span}}\{\lambda _i\lambda _j{\textbf {t}}_k\}_{\{i,j,k\}=\{1,2,3\}},\ \ \ \text{ and }\ \ \ \\ \varvec{P}{}^{1+}(T):= & {} \varvec{P}{}_1(T)\oplus {\mathrm{span}}\{\mathrm{curl}(\lambda _1\lambda _2\lambda _3)\}. \end{aligned}$$

It can be verified that $\varvec{P}{}^{1+}(T)\subset \varvec{P}{}^{2-}(T)$,

$$\begin{aligned} \varvec{P}{}^{2-}(T)=\{\varvec{v}{}\in \varvec{P}{}_2(T):\varvec{v}{}\cdot {\textbf {n}}|_{e_i}\in P_1(e_i),\ i=1:3\}, \end{aligned}$$

and

$$\begin{aligned} \varvec{P}{}^{1+}(T)=\{\varvec{v}{}\in \varvec{P}{}^{2-}(T):\mathrm{div}\,\varvec{v}{}\ \text{ is } \text{ a } \text{ constant } \text{ on }\ T\}. \end{aligned}$$

Further we denote that

$$\begin{aligned} P^{2+}(T):=P_2(T)\oplus {\mathrm{span}}\{\lambda _1\lambda _2\lambda _3\}. \end{aligned}$$

Lemma 2.1

The two exact sequences hold:

$$\begin{aligned} \mathbb {R} \xrightarrow {\mathrm{inc}} P^{2+}(T) \xrightarrow {{\mathrm{curl}}} \varvec{P}{}^{2-}(T) \xrightarrow {{\mathrm{div}}} P_1(T), \end{aligned}$$

(2.1)

and

$$\begin{aligned} \mathbb {R} \xrightarrow {\mathrm{inc}} P^{2+}(T) \xrightarrow {{\mathrm{curl}}} \varvec{P}{}^{1+}(T) \xrightarrow {{\mathrm{div}}} P_0(T). \end{aligned}$$

(2.2)

Proof

Noting that $\varvec{P}{}^{2-}(T)$ is exactly the local shape functions space of the quadratic ${\mathrm{BDFM}}$ element, $\mathrm{div}\,\varvec{P}{}^{2-}(T)=P_1(T)$ is well known. Evidently, $\mathrm{curl}\, P^{2+}(T)\subset \{\varvec{v}{}\in \varvec{P}{}^{2-}(T):\mathrm{div}\,\varvec{v}{}=0\}$ and $\dim (\mathrm{curl}\, P^{2+}(T))=\dim (P^{2+}(T))-1=\dim (\varvec{P}{}^{2-}(T))-\dim (P_1(T))=\dim (\{\varvec{v}{}\in \varvec{P}{}^{2-}(T):\mathrm{div}\,\varvec{v}{}=0\})$, thus $\mathrm{curl}\, P^{2+}(T)= \{\varvec{v}{}\in \varvec{P}{}^{2-}(T):\mathrm{div}\,\varvec{v}{}=0\}$. The proof of (2.1) is completed. Similarly, $\mathrm{div}\,\varvec{P}{}^{1+}(T) = P_0(T)$ follows the definition of $\varvec{P}{}^{1+}(T)$, and (2.2) can be proved the same way.$\square$

Next, we introduce some functions on a cell, and we call them atom basis functions. Defined for $i=1:3,\,\varvec{w}{}_{T,e_i} := \mathrm{curl}(\lambda _j \lambda _k (3\lambda _i-1))$, $\varvec{w}{}_{T,e_j,e_k} := \mathrm{curl}(\lambda _i^2)$ and $\varvec{\eta }{}_{T,e_j,e_k} := -\frac{2}{d_i} \lambda _i {\textbf {n}}_{T,e_i}$. It holds immediately that $\mathrm{div}\, \varvec{w}{}_{T,e_i} = 0$, $\mathrm{div}\, \varvec{w}{}_{T,e_j,e_k} = 0$ and $\mathrm{div}\, \varvec{\eta }{}_{T,e_j,e_k} = \frac{1}{S}$. This also indicates that $\varvec{w}{}_{T,e_i}$ is a function with vanishing normal components and tangential integral on the edges $e_j \text{ and } e_k$, and $\varvec{w}{}_{T,e_j,e_k}$ on the edge $e_i$ is similar. For instance, refer to Fig. 3 for an illustration of supports of $\varvec{w}{}_{T,e_1}$, $\varvec{w}{}_{T,e_2,e_3}$ and $\varvec{\eta }{}_{T,e_2,e_3}$.

Fig. 3

Illustration of the supports of atom basis functions; degrees of freedom vanish on dotted edges

Then,

$$\begin{aligned}&\varvec{Z}{}{}_T:=\{\varvec{v}{}\in \varvec{P}{}{}^{2-}(T):\mathrm{div}\,\varvec{v}{}=0\}=\{\varvec{v}{}\in \varvec{P}{}{}^{1+}(T):\mathrm{div}\,\varvec{v}{}=0\} \\&\quad ={{\mathrm{span}}}\{\varvec{w}{}{}_{T,e_1},\varvec{w}{}{}_{T,e_2},\varvec{w}{}{}_{T,e_3}, \varvec{w}{}{}_{T,e_2,e_3},\varvec{w}{}{}_{T,e_3,e_1},\varvec{w}{}{}_{T,e_1,e_2} \}\qquad \end{aligned}$$

and

$$\begin{aligned} \varvec{P}{}^{1+}(T)={{\mathrm{span}}}\{\varvec{w}{}{}_{T,e_1},\varvec{w}{}{}_{T,e_2},\varvec{w}{}{}_{T,e_3}, \varvec{w}{}{}_{T,e_2,e_3},\varvec{w}{}{}_{T,e_3,e_1},\varvec{w}{}{}_{T,e_1,e_2}, \varvec{\eta }{}{}_{T,e_2,e_3},\varvec{\eta }{}{}_{T,e_3,e_1},\varvec{\eta }{}{}_{T,e_1,e_2}\}.\quad \nonumber \\ \end{aligned}$$

(2.3)

Indeed, the functions of the set in (2.3) are not linearly independent. Any one among $\{ \varvec{\eta }{}{}_{T,e_2,e_3},\varvec{\eta }{}{}_{T,e_3,e_1},\varvec{\eta }{}{}_{T,e_1,e_2} \}$ together with $\{\varvec{w}{}{}_{T,e_1},\varvec{w}{}{}_{T,e_2},\varvec{w}{}{}_{T,e_3}, \varvec{w}{}{}_{T,e_2,e_3},\varvec{w}{}{}_{T,e_3,e_1},\varvec{w}{}{}_{T,e_1,e_2}\}$ forms a set of independent bases of $\varvec{P}{}{}^{1+}(T)$.

2.3 Some Known Finite Elements

The Madal–Tai–Winther element (see [25]) is defined as

• (1) T is a triangle;

• (2) $P_T=\varvec{P}{}{}^{MTW}(T)$;

• (3) for any $\varvec{v}{}\in (H^1(T))^2$, the nodal functionals on T, denoted by $D_T$, are .

Following [25], we introduce

$$\begin{aligned} \varvec{V}{}{}_h^{{\mathrm{MTW}}} = \{\varvec{v}{}{}_h\in \varvec{H}{}(\mathrm{div},\varOmega ):\varvec{v}{}{}_h|_{T}\in \varvec{P}{}^{{\mathrm{MTW}}}(T),\, \int _{e}\varvec{v}{}\cdot {\textbf {t}}\ \text{ is } \text{ continuous } \text{ across } \text{ interior } \text{ edge }\ e\}, \end{aligned}$$

and

$$\begin{aligned} \varvec{V}{}{}_{h0}^{{\mathrm{MTW}}}:=\{\varvec{v}{}{}_h\in \varvec{V}{}{}_h^{{\mathrm{MTW}}}\cap \varvec{H}{}_0(\mathrm{div},\varOmega ):\ \int _{e}\varvec{v}{}\cdot {\textbf {t}}=0\ \text{ on } \text{ boundary } \text{ edge }\ e\}. \end{aligned}$$

The lowest-degree Guzman–Neilan element (see [14]) is defined as

• (1) T is a triangle;

• (2) $P_T=\varvec{P}{}{}^{{\mathrm{GN-1}}}(T)$;

• (3) for any $\varvec{v}{}\in (H^1(T))^2$, the nodal functionals on T, denoted by $D_T$, are .

Following [14], we introduce

$$\begin{aligned} \varvec{V}{}{}_h^{{\mathrm{GN-1}}}:=\{\varvec{v}{}{}_h\in \varvec{H}{}(\mathrm{div},\varOmega ):\varvec{v}{}{}_h|_{T}\in P^{{\mathrm{GN-1}}}(T),\ \int _{e}\varvec{v}{}\cdot {\textbf {t}}\ \text{ is } \text{ continuous } \text{ across } \text{ interior } \text{ edge }\ e\}, \end{aligned}$$

and

$$\begin{aligned} \varvec{V}{}{}_{h0}^{{\mathrm{GN-1}}}:=\{\varvec{v}{}{}_h\in \varvec{V}{}{}_h^{{\mathrm{GN-1}}}\cap \varvec{H}{}_0(\mathrm{div},\varOmega ):\ \int _{e}\varvec{v}{}\cdot {\textbf {t}}=0\ \text{ on } \text{ boundary } \text{ edge }\ e\}. \end{aligned}$$

Following Zeng-Zhang-Zhang [37], introduce

$$\begin{aligned} \varvec{V}{}{}_h^{{\mathrm{ZZZ}}}:=\{\varvec{v}{}{}_h\in \varvec{H}{}(\mathrm{div},\varOmega ):\varvec{v}{}{}_h|_{T}\in \varvec{P}{}{}_2(T),\ \int _{e}\varvec{v}{}\cdot {\textbf {t}}\ \text{ is } \text{ continuous } \text{ across } \text{ interior } \text{ edge }\ e\}, \end{aligned}$$

and

$$\begin{aligned} \varvec{V}{}{}_{h0}^{{\mathrm{ZZZ}}}:=\{\varvec{v}{}{}_h\in \varvec{V}{}{}_h^{\mathrm{ZZZ}}\cap \varvec{H}{}_0(\mathrm{div},\varOmega ):\ \int _{e}\varvec{v}{}\cdot {\textbf {t}}=0\ \text{ on } \text{ boundary } \text{ edge }\ e\}. \end{aligned}$$

As revealed by [37], the space can be viewed as a reduced second-order Brezzi–Douglas–Marini element space with enhanced smoothness.

2.4 Stenberg’s Macroelement Technique for the Inf-sup Condition (cf. [31])

A macro-element partition of $\mathscr {T}_h$, denoted by $\mathscr {M}_h$, is a set of macroelements satisfying that each triangle of $\mathscr {T}_h$ is covered by at least one macroelement in $\mathscr {M}_h$.

Definition 2.1

Two macroelements $M_1$ and $M_2$ are said to be equivalent if there exists a continuous one-to-one mapping $G:M_1 \rightarrow M_2$, such that

• (a) $G(M_1) = M_2$;

• (b) if $M_1=\bigcup _{i=1:m}^m T_i^1$, then $T_i^2=G(T_i^1)$ with $i=1:m$ are the cells of $M_2$;

• (c) $G|_{T_i^1} = F_{T_i^2}\circ F_{T_i^1}^{-1}, i=1:m,$ where $F_{T_i^1}$ and $F_{T_i^2}$ are the mappings from a reference element $\hat{T}$ onto $T_i^1$ and $T_i^2$, respectively.

In addition, a class of equivalent macroelements is a set in which any two macroelements are equivalent to each other.

Next, we introduce some spaces defined on the macroelement M locally. As a subspace of $\varvec{V}{}{}_h$, $\varvec{V}{}_{h0,M}$ consists of functions in $\varvec{V}{}{}_h$ that are equal to zero outside M; for any $\varvec{v}{}_h\in \varvec{V}{}_{h0,M}$, continuity constraints of $\varvec{V}{}{}_h$ enable its corresponding nodal functionals on $\partial M$ to be zero. Similarly, $Q_{h,M}$ is a subspace of $Q_h$, and it consists of functions that are equal to zero outside M. Denote

$$\begin{aligned} N_M:=\{q_h \in Q_{h,M}:\int _M \mathrm{div}\, \varvec{v}{}{}_h \ q_h \,dM=0, \forall \, \varvec{v}{}{}_h \in \varvec{V}{}{}_{h0,M}\}. \end{aligned}$$

(2.4)

Stenberg’s macroelement technique can be summarized as the following proposition:

Proposition 2.1

Suppose there exists the macroelement partitioning $\mathscr {M}_h$ with the fixed set of equivalence classes $\mathbb {E}_i$ of macroelements, $i=1,2,...,n$, a positive integer N (n and N are independent of h), and an operator $\varPi :\varvec{H}{}{}_0^1(\varOmega ) \rightarrow \varvec{V}{}{}_{h0}$ such that

($C_1$):

for each $M\in \mathbb {E}_i,i=1,2,...,n$, the space $N_M$ defined in (2.4) is one-dimensional, which consists of functions that are constant on M;

($C_2$):

each $M\in \mathscr {M}_h$ belongs to one of the classes $\mathbb {E}_i, i=1,2,...,n$;

($C_3$):

each $e \in \mathscr {E}_h^i$ is an interior edge of at least one and no more than N macroelements;

($C_4$):

for any $\varvec{w}{}\in \varvec{H}{}{}_0^1(\varOmega )$, it holds that

$$\begin{aligned} \sum _{T\in \mathscr {T}_h} h_T^{-2} \Vert \varvec{w}{}- \varPi \varvec{w}{}\Vert _{0,T}^2 + \sum _{e\in \mathscr {E}_h^i} h_e^{-1} \Vert \varvec{w}{}- \varPi \varvec{w}{}\Vert _{0,e}^2 \leqslant C \Vert \varvec{w}{}\Vert _{1,\varOmega }^2 \quad and \quad \Vert \varPi \varvec{w}{}\Vert _{1,h} \leqslant C \Vert \varvec{w}{}\Vert _{1,\varOmega }. \end{aligned}$$

Then, the uniform inf-sup condition holds for the finite element pair.

3 An Auxiliary Stable Pair for the Stokes Problem

3.1 An sBDFM Element

We define the sBDFM element by

• (1) T is a triangle;

• (2) $P_T=\varvec{P}{}{}^{2-}(T)$;

• (3) for any $\varvec{v}{}\in (H^1(T))^2$, the nodal functionals on T, denoted by $D_T$, are .

The above triple is $P_T-$unisolvent. We use $\varvec{\varphi }{}_{{\textbf {n}}_{T,e_i},0}$, $\varvec{\varphi }{}_{{\textbf {n}}_{T,e_i},1}$, and $\varvec{\varphi }{}_{{\textbf {t}}_{T,e_i},0}$ to represent the corresponding nodal basis functions, and then

$$\begin{aligned} \left\{ \begin{aligned}&\varvec{\varphi }{}_{{\textbf {n}}_{T,e_i},0} = \lambda _j (3 \lambda _j - 2) \frac{{\textbf {t}}_{T,e_k}}{({\textbf {n}}_{T,e_i},{\textbf {t}}_{T,e_k})} + \lambda _k (3 \lambda _k - 2) \frac{{\textbf {t}}_{T,e_j}}{({\textbf {n}}_{T,e_i},{\textbf {t}}_{T,e_j})} + 6 \lambda _j \lambda _k {\textbf {n}}_{T,e_i};\\&\varvec{\varphi }{}_{{\textbf {n}}_{T,e_i},1} = 3\lambda _j (3 \lambda _j - 2) \frac{{\textbf {t}}_{T,e_k}}{({\textbf {n}}_{T,e_i},{\textbf {t}}_{T,e_k})} - 3\lambda _k (3 \lambda _k - 2) \frac{{\textbf {t}}_{T,e_j}}{({\textbf {n}}_{T,e_i},{\textbf {t}}_{T,e_j})};\\&\varvec{\varphi }{}_{{\textbf {t}}_{T,e_i},0} = 6 \lambda _j \lambda _k {\textbf {t}}_{T,e_i}. \end{aligned} \right. \end{aligned}$$

(3.1)

We use $\varvec{V}{}{}_h^{{\mathrm{sBDFM}}}$ and $\varvec{V}{}{}_{h0}^{{\mathrm{sBDFM}}}$ for the corresponding finite element spaces, where the subscript $\cdot _{h0}$ implies that the nodal functionals along the boundary of the domain are all zero.

(3.2)

(3.3)

Evidently, it holds that

$$\begin{aligned} \varvec{\varphi }{}\cdot {\textbf {n}}_{T,e_j}|_{e_j}\in P_1(e_j),\,j=1:3,\, \forall \, \varvec{\varphi }{}\in \{\varvec{\varphi }{}_{{\textbf {n}}_{T,e_i},0},\, \varvec{\varphi }{}_{{\textbf {n}}_{T,e_i},1}, \varvec{\varphi }{}_{{\textbf {t}}_{T,e_i},0}\},\,i=1:3. \end{aligned}$$

Therefore, $\varvec{V}{}{}_h^{{\mathrm{sBDFM}}}$ is a smoothened subspace of the famous second-order BDFM element space. Indeed, $\varvec{V}{}{}_h^{{\mathrm{sBDFM}}} \subset \varvec{H}{}(div,\varOmega )$ but , and $\varvec{V}{}{}_{h0}^{\mathrm{sBDFM}}$ is similar.

We define a nodal interpolation operator $\varPi _h:\varvec{H}{}^1(\varOmega )\rightarrow \varvec{V}{}{}_h^{\mathrm{sBDFM}}$ such that for any $e \subset \mathscr {E}_h$,

The operator $\varPi _h$ is locally defined on each triangle, and it preserves linear functions locally. Furthermore, the local space $\varvec{P}{}^{2-}(T)$ is invariant under the Piola’s transformation; that is, it maps $\varvec{P}{}^{2-}(T)$ onto $\varvec{P}{}^{2-}(\hat{T})$. Therefore, approximation estimates of $\varPi _h$ can be derived from Lemma 2.1.5 and Remark 2.1.8 in [6], along with standard scaling arguments and the Bramble–Hilbert lemma.

Proposition 3.1

It holds for $k \le s, 1 < s \le 2$ that

$$\begin{aligned} |\varvec{v}{}- \varPi _h \varvec{v}{}|_{k,h}\leqslant C h^{s-k} |\varvec{v}{}|_{s,\varOmega }, \quad \forall \, \varvec{v}{}\in \varvec{H}{}^s(\varOmega ). \end{aligned}$$

3.2 Structure of the Kernel of $\mathrm{div}$ on a Closed Patch

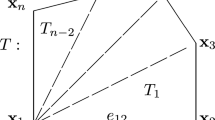
For the $m-$cell interior vertex patch $P_A$, we label cells of it sequentially as $T_i,i=1:m$, and label $e_i = \overline{T_i}\cap \overline{T_{i+1}}\,(i=1:m-1), e_m = \overline{T_m}\cap \overline{T_{1}}$. Also, we label $e_{m+i}\,(i=1:m)$ as the edge opposite to A in $T_i$; we refer to Fig. 4a for an illustration.

Viewing $P_A$ as a special grid, we can construct $\varvec{V}{}{}^\mathrm{sBDFM}_{h0}(P_A)$ as follows:

(3.4)

Denote

$$\begin{aligned} \varvec{Z}{}{}_{A}:=\{\varvec{v}{}\in \varvec{V}{}{}^{{\mathrm{sBDFM}}}_{h0}(P_A):\mathrm{div}\,\varvec{v}{}=0\}. \end{aligned}$$

Fig. 4

Illustration of the patch around A and its part amplification

Lemma 3.1

$\dim (\varvec{Z}{}{}_{A})=1$.

Proof

Assume $\varvec{\psi }{}{}_h\in \varvec{Z}{}{}_{A}$, then $\varvec{\psi }{}{}_h|_{T_i}\subset \varvec{Z}{}{}_{T_i}$, $i=1:m$. By the boundary conditions, it follows that

$$\begin{aligned} \left\{ \begin{aligned}&\varvec{\psi }{}{}_h|_{T_1}=\gamma _{T_1}^m\varvec{w}{}{}_{T_1,e_m}+\gamma _{T_1}^{1}\varvec{w}{}{}_{T_1,e_{1}}+\gamma _{T_1}^{m,1}\varvec{w}{}{}_{T_1,e_{m},e_1},\\&\varvec{\psi }{}{}_h|_{T_i}=\gamma _{T_i}^{i-1}\varvec{w}{}{}_{T_i,e_{i-1}}+\gamma _{T_i}^{i}\varvec{w}{}{}_{T_i,e_{i}}+\gamma _{T_i}^{i-1,i}\varvec{w}{}{}_{T_i,e_{i-1},e_i},\ (i=2:m-1)\\&\varvec{\psi }{}{}_h|_{T_m}=\gamma _{T_m}^{m-1}\varvec{w}{}{}_{T_m,e_{m-1}}+\gamma _{T_m}^{m}\varvec{w}{}{}_{T_m,e_{m}}+\gamma _{T_m}^{m-1,m}\varvec{w}{}{}_{T_m,e_{m-1},e_m}, \end{aligned} \right. \end{aligned}$$

(3.5)

with $\gamma _{T_1}^m,\,\gamma _{T_1}^{1},\,\gamma _{T_1}^{m,1},\,\gamma _{T_m}^{m-1},\,\gamma _{T_m}^{m},\,\gamma _{T_m}^{m-1,m}$ and $\gamma _{T_i}^{i-1},\,\gamma _{T_i}^{i},\,\gamma _{T_i}^{i-1,i}\ (i=2:m-1)$ determined such that $\varvec{\psi }{}{}_h$ satisfies the continuity restriction of $\varvec{V}{}{}^{{\mathrm{sBDFM}}}_{h}$.

For an arbitrary edge $e_i$, $1\leqslant i\leqslant m$, across it, the normal component of $\varvec{\psi }{}{}_h$ and integration of the tangential component of $\varvec{\psi }{}{}_h$ are continuous; see Fig. 4b for an illustration. Based on the continuity conditions, a direct calculation shows that

$$\begin{aligned} \begin{aligned}&\gamma ^{i-1,i}_{T_i}=\gamma _{T_{i+1}}^{i,i+1} \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \left\{ \begin{aligned}&\gamma _{T_i}^{i} = \frac{\tilde{S}_{\triangle (A_i,A_{i+1},A_{i-1})}}{S_i+S_{i+1}} \gamma ^{i-1,i}_{T_i},\\&\gamma _{T_{i+1}}^{i} = \frac{\tilde{S}_{\triangle (A_i,A_{i+1},A_{i-1})}}{S_i+S_{i+1}} \gamma _{T_{i+1}}^{i,i+1}. \end{aligned} \right. \end{aligned}$$

(3.6)

By checking weak tangential continuity conditions of $\varvec{V}{}_h^\mathrm{sBDFM}$ on all edges $e_i$, $i=1:m$, we have

$$\begin{aligned} \gamma ^{m,1}_{T_1}=\gamma ^{1,2}_{T_2}=...=\gamma ^{m-1,m}_{T_m}. \end{aligned}$$

(3.7)

Now, we choose $\gamma ^{m,1}_{T_1}=1$ in (3.7) and it follows that

$$\begin{aligned} \gamma ^{m,1}_{T_1}=\gamma ^{1,2}_{T_2}=...=\gamma ^{m-1,m}_{T_m}=1. \end{aligned}$$

(3.8)

Substituting (3.8) into the counterparts of (3.6) on every cell $T_i,\ i=1:m$, we have

$$\begin{aligned} \left\{ \begin{aligned}&\gamma _{T_1}^{m} = \frac{\tilde{S}_{\triangle (A_m,A_{1},A_{m-1})}}{S_{m}+S_1} , \ \gamma _{T_1}^{1}= \frac{\tilde{S}_{\triangle (A_1,A_{2},A_{m})}}{S_1+S_{2}}, \\&\gamma _{T_i}^{i-1} = \frac{\tilde{S}_{\triangle (A_{i-1},A_{i},A_{i-2})}}{S_{i-1}+S_i}, \ \gamma _{T_i}^{i}= \frac{\tilde{S}_{\triangle (A_i,A_{i+1},A_{i-1})}}{S_i+S_{i+1}}, \ (i=2:m-2) \\&\gamma _{T_m}^{m-1} = \frac{\tilde{S}_{\triangle (A_{m-1},A_{m},A_{m-2})}}{S_{m-1}+S_m}, \ \gamma _{T_m}^{m}= \frac{\tilde{S}_{\triangle (A_m,A_{1},A_{m-1})}}{S_m+S_1}. \end{aligned} \right. \end{aligned}$$

(3.9)

Then, bringing (3.9) back to (3.5) gives

$$\begin{aligned} \left\{ \begin{aligned}&\varvec{\psi }{}{}_h|_{T_1}= \frac{\tilde{S}_{\triangle (A_m,A_{1},A_{m-1})}}{S_{m}+S_1} \varvec{w}{}{}_{T_1,e_{m}} + \frac{\tilde{S}_{\triangle (A_1,A_2,A_m)}}{S_1+S_2} \varvec{w}{}{}_{T_1,e_{1}} + \varvec{w}{}{}_{T_1,e_{m},e_1},\\&\varvec{\psi }{}{}_h|_{T_i} = \frac{\tilde{S}_{\triangle (A_{i-1},A_{i},A_{i-2})}}{S_{i-1}+S_i} \varvec{w}{}{}_{T_i,e_{i-1}} + \frac{\tilde{S}_{\triangle (A_i,A_{i+1},A_{i-1})}}{S_i+S_{i+1}} \varvec{w}{}{}_{T_i,e_{i}} + \varvec{w}{}{}_{T_i,e_{i-1},e_i}, \ (i=2:m-1)\\&\varvec{\psi }{}{}_h|_{T_m} = \frac{\tilde{S}_{\triangle (A_{m-1},A_{m},A_{m-2})}}{S_{m-1}+S_m} \varvec{w}{}{}_{T_m,e_{m-1}} + \frac{\tilde{S}_{\triangle (A_m,A_{m+1},A_{m-1})}}{S_m+S_1} \varvec{w}{}{}_{T_m,e_{m}} + \varvec{w}{}{}_{T_m,e_{m-1},e_m}. \end{aligned} \right. \end{aligned}$$

Now, it is evident that $\varvec{\psi }{}{}_h\in \varvec{Z}{}{}_A$ and further $\varvec{Z}{}{}_A={{\mathrm{span}}}\{\varvec{\psi }{}{}_h\}$. The proof is completed. $\square$

3.3 A Stable Conservative Pair for the Stokes Problem

Denote

$$\begin{aligned} \mathbb {P}{}^1_h(\mathscr {T}_h):=\{q_h\in L^2(\varOmega ):q_h|_T\in P_1(T), \forall \, T \in \mathscr {T}_h\} \ \text{ and }\ \ \mathbb {P}^1_{h0}(\mathscr {T}_h):=\mathbb {P}{}^1_h(\mathscr {T}_h)\cap L^2_0(\varOmega ). \end{aligned}$$

Then, $\varvec{V}{}{}_{h0}^{{\mathrm{sBDFM}}}\times \mathbb {P}^1_{h0}$ forms a stable pair for the Stokes problem.

Theorem 3.1

(Stability of $\varvec{V}{}{}_{h0}^\mathrm{sBDFM}$–$\mathbb {P}^1_{h0}$) Let $\{\mathscr {T}_h\}$ be a family of triangulations of $\varOmega$ satisfying Assumption 2.1. Then it holds that

$$\begin{aligned} \sup _{\varvec{v}{}{}_h \in \varvec{V}{}{}_{h0}^\mathrm{sBDFM}} \frac{( div \ \varvec{v}{}{}_h , q_h )}{\Vert \varvec{v}{}{}_h\Vert _{1,h}} \geqslant C \Vert q_h\Vert _{0,\varOmega },\forall \, q_h\in \mathbb {P}^1_{h0}(\mathscr {T}_h). \end{aligned}$$

(3.10)

Proof

First, for any interior vertex A and its patch $P_A$, we can construct $\varvec{V}{}{}_{h0}^\mathrm{sBDFM}(P_A)$ as (3.4) and $\mathbb {P}^1_{h0}(P_A)=\{q_h\in L^2(P_A): q_h|_T \in P_1(T), \forall \, T \in P_A \} \cap L_0^2(P_A)$. Obviously, $\mathrm{div}\, \varvec{V}{}{}_{h0}^\mathrm{sBDFM}(P_A)\subset \mathbb {P}^1_{h0}(P_A)$. Thus, counting the dimension, we obtain $\mathrm{div}\, \varvec{V}{}{}_{h0}^\mathrm{sBDFM}(P_A)=\mathbb {P}^1_{h0}(P_A)$ by Lemma 3.1. This verifies the condition (C${}_1$) of Proposition 2.1. The other conditions of Proposition 2.1 are direct, and the inf-sup condition (3.10) holds by Proposition 2.1. The proof is completed.$\square$

Now consider the finite element discretization: Find $(\varvec{\varphi }{}{}_h,p_h)\in \varvec{V}{}{}_{h0}^\mathrm{sBDFM}\times \mathbb {P}^1_{h0}$, such that

$$\begin{aligned} \left\{ \begin{array}{lcll} \varepsilon ^2(\nabla _h \, \varvec{\varphi }{}{}_h,\nabla _h\, \varvec{\psi }{}{}_h)-(\mathrm{div}\,\varvec{\psi }{}{}_h,p_h)&{}=&{}(\varvec{f}{},\varvec{\psi }{}{}_h),&{}\forall \,\varvec{\psi }{}{}_h\in \varvec{V}{}{}_{h0}^\mathrm{sBDFM}, \\ (\mathrm{div}\,\varvec{\varphi }{}{}_h,q_h)&{}=&{}0,&{}\forall \,q_h\in \mathbb {P}^1_{h0}. \end{array} \right. \end{aligned}$$

(3.11)

The well-posedness of (3.11) is immediate.

Lemma 3.2

Given $\varvec{\varphi }{}\in \varvec{H}{}{}_0^1(\varOmega )\cap \varvec{H}{}^2(\varOmega )$ such that $\mathrm{div}\,\varvec{\varphi }{}=0$, it holds that

$$\begin{aligned} \inf _{\varvec{\psi }{}{}_h\in \varvec{V}{}{}_{h0}^\mathrm{sBDFM},\,\mathrm{div}\,\varvec{\psi }{}{}_h=0}\Vert \varvec{\varphi }{}-\varvec{\psi }{}{}_h\Vert _{1,h} \leqslant C h \Vert \varvec{\varphi }{}\Vert _{2,\varOmega }. \end{aligned}$$

Proof

Let $(\varvec{\varphi }{}^*,p^*)\in \varvec{H}{}{}_0^1(\varOmega )\times L^2_0(\varOmega )$ be such that

$$\begin{aligned} \left\{ \begin{array}{lcll} (\nabla \, \varvec{\varphi }{}^*,\nabla \,\varvec{\psi }{})-(\mathrm{div}\,\varvec{\psi }{},p^*)&{}=&{}(\mathrm{curl}\,\mathrm{rot}\,\varvec{\varphi }{},\varvec{\psi }{}),&{}\forall \,\varvec{\psi }{}\in \varvec{H}{}{}^1_0(\varOmega ), \\ (\mathrm{div}\,\varvec{\varphi }{}^*,q)&{}=&{}0,&{}\forall \,q\in L^2_0(\varOmega ). \end{array} \right. \end{aligned}$$

Then $\varvec{\varphi }{}^*=\varvec{\varphi }{}$ and $p^*=0$. Now let $(\varvec{\varphi }{}{}_h^*,p^*_h)\in \varvec{V}{}{}^\mathrm{sBDFM}_{h0}\times \mathbb {P}^1_{h0}$ be such that

$$\begin{aligned} \left\{ \begin{array}{lcll} (\nabla _h \, \varvec{\varphi }{}{}_h^*,\nabla _h\,\varvec{\psi }{}{}_h)-(\mathrm{div}\,\varvec{\psi }{}{}_h,p^*_h)&{}=&{}(\mathrm{curl}\,\mathrm{rot}\,\varvec{\varphi }{},\varvec{\psi }{}{}_h),&{}\forall \,\varvec{\psi }{}{}_h\in \varvec{V}{}{}^\mathrm{sBDFM}_{h0}, \\ (\mathrm{div}\,\varvec{\varphi }{}{}_h^*,q_h)&{}=&{}0,&{}\forall \,q_h\in \mathbb {P}^1_{h0}. \end{array} \right. \end{aligned}$$

(3.12)

Then the second equation of (3.12) together with $\mathrm{div}\varvec{\varphi }{}{}_h^* \in \mathbb {P}^1_{h0}$ gives $\mathrm{div}\,\varvec{\varphi }{}{}_h^*=0$, and further it holds that $\Vert \varvec{\varphi }{}^*-\varvec{\varphi }{}{}_h^*\Vert _{1,h} \leqslant C h\Vert \varvec{\varphi }{}\Vert _{2,\varOmega }$. The proof is completed.$\square$

The convergence estimate robustness in $\varepsilon$ can be obtained in a standard way (cf. [7]).

Theorem 3.2

Let $(\varvec{\varphi }{},p)$ and $(\varvec{\varphi }{}{}_h,p_h)$ be the solutions of (1.4) and (3.11), respectively. If $(\varvec{\varphi }{},p)\in \varvec{H}{}^2(\varOmega )\times H^1(\varOmega )$, then

$$\begin{aligned} |\varvec{u}{}- \varvec{u}{}{}_{h}|_{1,h} \leqslant C h|\varvec{u}{}|_{2,\varOmega },\ \ \ \text{ and }\ \ \ \Vert p-p_{h}\Vert _{0,\varOmega } \leqslant C (h|p|_{1,\varOmega } + \varepsilon ^{2} h|\varvec{u}{}|_{2,\varOmega }). \end{aligned}$$

4 A Continuous Nonconforming Finite Element Scheme for the Biharmonic Equation

4.1 A Finite Element Stokes Complex

We define

$$\begin{aligned} V_h^{2+}:=\left\{ v_h\in H^1(\varOmega ):v_h|_T\in P^{2+}(T),\ \forall \,T\in \mathscr {T}_h;\ \int _e\frac{\partial v_h}{\partial {\textbf {n}}}\ \text{ is } \text{ continuous } \text{ across } \text{ interior } \text{ edge }\ e\right\} , \end{aligned}$$

and

$$\begin{aligned} V^{2+}_{h0}:=\left\{ v_h\in V_h^{2+}\cap H^1_0(\varOmega ):\int _e\frac{\partial v_h}{\partial {\textbf {n}}}=0 \ \text{ on } \text{ boundary } \text{ edge }\ e\right\} . \end{aligned}$$

Lemma 4.1

The exact sequence holds as

$$\begin{aligned} \{0\} \xrightarrow {{\mathrm{inc}}} V^{2+}_{h0} \xrightarrow {{\mathrm{curl}}} \varvec{V}{}{}^{{\mathrm{sBDFM}}}_{h0} \xrightarrow {{\mathrm{div}}} \mathbb {P}^1_{h0} \xrightarrow {\int _\varOmega \cdot } \{0\}. \end{aligned}$$

Proof

Regarding Theorem 3.1, we only have to show that

$$\begin{aligned} \{\varvec{v}{}_h\in \varvec{V}{}^\mathrm{sBDFM}_{h0}:\mathrm{div}\,\varvec{v}{}_h=0\}=\mathrm{curl}\, V^{2+}_{h0}. \end{aligned}$$

Denote $V^{2+,C}_{h0}:=\{v_h\in H^1_0(\varOmega ):v_h|_T\in P^{2+}(T),\ \forall \,T\in \mathscr {T}_h\}$. Given $\varvec{v}{}{}_h\in \varvec{V}{}{}^\mathrm{sBDFM}_{h0}\subset \varvec{H}{}_0(\mathrm{div},\varOmega )$ such that $\mathrm{div}\,\varvec{v}{}{}_h=0$, by the local exact sequence Lemma 2.1 and the de Rham complex (1.1), there exists a $w_h\in V^{2+,C}_{h0}$, such that $\mathrm{curl}\, w_h=\varvec{v}{}{}_h$. Further, by the tangential continuity restriction on $\varvec{v}{}{}_h$, it follows that $w_h\in V^{2+}_{h0}$. The proof is completed.$\square$

4.2 A Low-Degree Scheme for the Biharmonic Equation

We consider the following biharmonic equation: given $g\in H^{-1}(\varOmega )$, find $u\in H^2_0(\varOmega )$, such that

$$\begin{aligned} (\nabla ^2\,u,\nabla ^2\,v)=\langle g,v\rangle ,\quad \forall \,v\in H^2_0(\varOmega ). \end{aligned}$$

(4.1)

A finite element discretization is to find $u_h\in V^{2+}_{h0}$, such that

$$\begin{aligned} (\nabla _h^2\,u_h,\nabla _h^2\,v_h)=\langle g,v_h\rangle ,\quad \forall \,v_h\in V^{2+}_{h0}. \end{aligned}$$

(4.2)

Remark 4.1

Note that $V^{2+}_{h0}\subset H^1_0(\varOmega )$. For the right hand side $g\in H^{-1}(\varOmega )$, no extra interpolation to $H^1$ functions is needed.

The lemma below is an immediate consequence of Lemmas 3.2 and 4.1:

Lemma 4.2

It holds for $w\in H^3(\varOmega )\cap H^2_0(\varOmega )$ that

$$\begin{aligned} \inf _{v_h\in V^{2+}_{h0}}\Vert w-v_h\Vert _{2,h}\leqslant C h\Vert w\Vert _{3,\varOmega }. \end{aligned}$$

Proof

By Lemmas 3.2 and 4.1,

$$\begin{aligned}&\inf _{v_h\in V^{2+}_{h0}}|w-v_h|_{2,h}=\inf _{v_h\in V^{2+}_{h0}}|\mathrm{curl}\, w-\mathrm{curl}\, v_h|_{1,h} \\&\quad =\inf _{\varvec{\psi }{}{}_h\in \varvec{V}{}{}_{h0}^\mathrm{sBDFM},\,\mathrm{div}\,\varvec{\psi }{}{}_h=0}|\mathrm{curl}\, w-\varvec{\psi }{}{}_h|_{1,h}\leqslant C h|\mathrm{curl}\, w|_{2,\varOmega }\leqslant C h\Vert w\Vert _{3,\varOmega }.\qquad \end{aligned}$$

This completes the proof.$\square$

Theorem 4.1

Let u and $u_h$ be the solutions of (4.1) and (4.2), respectively, and assume $u\in H^3(\varOmega )\cap H^2_0(\varOmega )$. Then it holds that

$$\begin{aligned} \Vert u-u_h\Vert _{2,h}\leqslant C h\Vert u\Vert _{3,\varOmega }. \end{aligned}$$

The proof of the theorem follows from standard arguments, and we omit it here.

4.3 Basis Functions of $V^{2+}_{h0}$

For the implementation of the finite element schemes, we present the explicit formulation of the basis functions of certain finite element spaces in this section.

4.3.1 Basis Functions of the Kernel Subspace of the sBDFM Element

Denote the kernel subspace of sBDFM element as

$$\begin{aligned} \varvec{Z}{}{}_{h0}:=\{\varvec{v}{}{}_h\in \varvec{V}{}{}_{h0}^\mathrm{sBDFM}:\mathrm{div}\,\varvec{v}{}{}_h=0\}. \end{aligned}$$

Fig. 5

Illustration of an interior vertex patch and an interior cell patch

First, associated with the interior vertex patch around interior vertex A, denote $\varvec{\psi }{}^A$ as (see Fig. 5a)

$$\begin{aligned} \varvec{\psi }{}^A= \left\{ \begin{aligned}&\frac{\tilde{S}_{\triangle (A_1,A_{2},A_{m})}}{S_1 + S_2} \varvec{w}{}{}_{T_1,e_1} + \frac{\tilde{S}_{\triangle (A_m,A_{1},A_{m-1})}}{S_1 + S_m} \varvec{w}{}{}_{T_1,e_m} + \varvec{w}{}{}_{T_1,e_1,e_m}, \ in \ T_1,\\&\frac{\tilde{S}_{\triangle (A_i,A_{i+1},A_{i-1})}}{S_i + S_{i+1}} \varvec{w}{}{}_{T_i,e_i} + \frac{\tilde{S}_{\triangle (A_{i-1},A_{i},A_{i-2})}}{S_i + S_{i-1}} \varvec{w}{}{}_{T_i,e_{i-1}} + \varvec{w}{}{}_{T_i,e_i,e_{i-1}}, in \ T_i \ (i=2:m-1),\\&\frac{\tilde{S}_{\triangle (A_m,A_{1},A_{m-1})}}{S_m + S_1} \varvec{w}{}{}_{T_m,e_m} + \frac{\tilde{S}_{\triangle (A_{m-1},A_{m},A_{m-2})}}{S_m+S_{m-1}} \varvec{w}{}{}_{T_m,e_{m-1}} + \varvec{w}{}{}_{T_m,e_m,e_{m-1}}, \ in \ T_m. \end{aligned} \right. \nonumber \\ \end{aligned}$$

(4.3)

Second, associated with the interior cell patch around interior cell T, denote $\varvec{\psi }{}{}_{T}$ as (see Fig. 5b)

$$\begin{aligned} \varvec{\psi }{}{}_{T} \!=\! \left\{ \begin{aligned}&\frac{S_1}{S_1+S} \varvec{w}{}_{T_1, e_1}, \ in \ T_1,\\&\frac{S_2}{S_2+S} \varvec{w}{}_{T_2, e_2}, \ in \ T_2,\\&\frac{S_3}{S_3+S} \varvec{w}{}_{T_3, e_3}, \ in \ T_3,\\&\frac{1}{3}( \frac{S_1-2S}{S_1+S} \varvec{w}{}_{T,e_1} + \frac{S_2-2S}{S_2+S} \varvec{w}{}_{T,e_2} + \frac{S_3-2S}{S_3+S} \varvec{w}{}_{T,e_3} + \varvec{w}{}_{T,e_2,e_3}\\&\quad + \varvec{w}{}_{T,e_3,e_1} + \varvec{w}{}_{T,e_1,e_2} ), \ in \ T. \end{aligned} \right. \end{aligned}$$

(4.4)

Lemma 4.3

The functions of $\varPhi _h(\mathscr {T}_h):=\{\varvec{\psi }{}^A,\ A\in \mathscr {X}_h^i;\ \varvec{\psi }{}{}_T,\ T\in \mathscr {T}_h^i\}$ form a basis of $\varvec{Z}{}{}_{h0}$.

The proof is given in Appendix B.1.

4.3.2 Basis functions of $V^{2+}_{h0}$

Note that the $\mathrm{curl}$ operator is a bijection from $V^{2+}_{h0}$ onto $\varvec{Z}{}{}_{h0}$. Therefore, the basis functions of $V^{2+}_{h0}$ are $\{\zeta ^A,\ A\in \mathscr {X}_h^i;\ \zeta _T,\ T\in \mathscr {T}_h^i\}$, such that $\mathrm{curl}\,\zeta ^A=\varvec{\psi }{}^A$ and $\mathrm{curl}\, \zeta _T=\varvec{\psi }{}{}_T$. More precisely (cf. Fig. 5),

$$\begin{aligned} \zeta ^{A} = \left\{ \begin{aligned}&\lambda ^2 + \frac{\tilde{S}_{\triangle (A_1,A_{2},A_{m})}}{S_1+S_2} \lambda \lambda _1(3\lambda _m-1) + \frac{\tilde{S}_{\triangle (A_m,A_{1},A_{m-1})}}{S_1+S_m} \lambda \lambda _m(3\lambda _1-1),\ in \ T_1,\\&\lambda ^2 + \frac{\tilde{S}_{\triangle (A_i,A_{i+1},A_{i-1})}}{S_i+S_{i+1}} \lambda \lambda _i(3\lambda _{i-1}-1) + \frac{\tilde{S}_{\triangle (A_{i-1},A_{i},A_{i-2})}}{S_i+S_{i-1}} \lambda \lambda _{i-1}(3\lambda _i-1),\ in \ T_i, \, (i=2:m-1)\\&\lambda ^2 + \frac{\tilde{S}_{\triangle (A_m,A_{1},A_{m-1})}}{S_m+S_1} \lambda \lambda _m(3\lambda _{m-1}-1) + \frac{\tilde{S}_{\triangle (A_{m-1},A_{m},A_{m-2})}}{S_m+S_{m-1}} \lambda \lambda _{m-1}(3\lambda _m-1),\ in \ T_m,\\ \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \zeta _{T}= \left\{ \begin{aligned}&\frac{S_1}{S_1+S} \lambda _2\lambda _3(3\lambda _4-1),\ in \ T_1,\\&\frac{S_2}{S_1+S} \lambda _1\lambda _3(3\lambda _5-1),\ in \ T_2,\\&\frac{S_3}{S_1+S} \lambda _1\lambda _2(3\lambda _6-1),\ in \ T_3,\\&\frac{S_1}{S_1+S} \lambda _2\lambda _3(3\lambda _1-1) + \frac{S_2}{S_1+S} \lambda _1\lambda _3(3\lambda _2-1) + \frac{S_3}{S_1+S} \lambda _1\lambda _2(3\lambda _3-1) - 6 \lambda _1\lambda _2\lambda _3,\ in \ T. \end{aligned} \right. \end{aligned}$$

5 An Enriched Linear–Constant Finite Element Scheme for Incompressible Flows

5.1 An Enriched Linear Element Space

We define

$$\begin{aligned} \varvec{V}{}{}_h^\mathrm{el}:=\left\{ \varvec{v}{}{}_h\in \varvec{H}{}(\mathrm{div},\varOmega ):\varvec{v}{}{}_h|_T\in \varvec{P}{}^{1+}(T),\ \int _e\varvec{v}{}{}_h\cdot {\textbf {t}}\ \text{ is } \text{ continuous } \text{ across } \text{ interior } \text{ edge }\ e\right\} , \end{aligned}$$

and

$$\begin{aligned} \varvec{V}{}{}_{h0}^\mathrm{el}:=\left\{ \varvec{v}{}{}_h\in \varvec{V}{}{}_h^\mathrm{el}\cap \varvec{H}{}_0(\mathrm{div},\varOmega ): \int _e\varvec{v}{}{}_h\cdot {\textbf {t}}\ \text{ vanishes } \text{ on } \text{ boundary } \text{ edge }\ e\right\} . \end{aligned}$$

Remark 5.1

Evidently, $\varvec{V}{}{}_h^\mathrm{el}=\{\varvec{v}{}{}_h\in \varvec{V}{}{}_h^\mathrm{sBDFM}:\mathrm{div}\,\varvec{v}{}{}_h\in \mathbb {P}^0_{h0}\}$, and $\varvec{V}{}{}_{h0}^\mathrm{el}=\{\varvec{v}{}{}_h\in \varvec{V}{}{}_{h0}^\mathrm{sBDFM}:\mathrm{div}\,\varvec{v}{}{}_h\in \mathbb {P}^0_{h0}\}$. Particularly, $\{\varvec{v}{}{}_h\in \varvec{V}{}{}_{h0}^\mathrm{el}:\mathrm{div}\,\varvec{v}{}{}_h=0\}=\{\varvec{v}{}{}_h\in \varvec{V}{}{}_{h0}^\mathrm{sBDFM}:\mathrm{div}\,\varvec{v}{}{}_h=0\}$.

The next lemma is an immediate result of Lemma 4.1 and Remark 5.1:

Lemma 5.1

The exact sequence holds as

$$\begin{aligned} \{0\} \xrightarrow {\mathrm{inc}} V^{2+}_{h0} \xrightarrow {{\mathrm{curl}}} \varvec{V}{}{}^\mathrm{el}_{h0} \xrightarrow {{\mathrm{div}}} \mathbb {P}^0_{h0} \xrightarrow {\int _\varOmega \cdot } \{0\}. \end{aligned}$$

Lemma 5.2

$\varvec{V}{}{}_{h0}^\mathrm{el}=\varvec{V}{}{}_{h0}^\mathrm{ZZZ}\cap \varvec{V}{}{}_{h0}^\mathrm{MTW}$.

Proof

On on hand, by definition, it holds that $\varvec{V}{}{}_{h0}^\mathrm{el}\subset \varvec{V}{}{}_{h0}^\mathrm{sBDFM}\subset \varvec{V}{}{}_{h0}^\mathrm{ZZZ}$ and $\varvec{V}{}{}_{h0}^\mathrm{el}\subset \varvec{V}{}{}_{h0}^\mathrm{MTW}$, which implies that $\varvec{V}{}{}_{h0}^\mathrm{el}\subset \varvec{V}{}{}_{h0}^\mathrm{ZZZ}\cap \varvec{V}{}{}_{h0}^\mathrm{MTW}$. On the other hand, given $\varvec{v}{}{}_h\in \varvec{V}{}{}_{h0}^\mathrm{ZZZ}\cap \varvec{V}{}{}_{h0}^\mathrm{MTW}$, $\varvec{v}{}{}_h|_T\in \varvec{P}{}{}_2(T)$, the normal component of $\varvec{v}{}{}_h|_T$ is piecewise linear, and $\mathrm{div}\,\varvec{v}{}{}_h|_T$ is a constant on T for any $T\in \mathscr {T}_h$; namely, $\varvec{v}{}{}_h|_T\in \varvec{P}{}^{1+}(T)$. Since all these spaces $\varvec{V}{}{}_{h0}^\mathrm{el}$, $\varvec{V}{}{}_{h0}^\mathrm{ZZZ}$ and $\varvec{V}{}{}_{h0}^\mathrm{MTW}$ possess the same continuity, it holds that $\varvec{V}{}{}_{h0}^\mathrm{el}\supset \varvec{V}{}{}_{h0}^\mathrm{ZZZ}\cap \varvec{V}{}{}_{h0}^\mathrm{MTW}$.$\square$

5.1.1 Basis functions

First, we present a locally supported function $\varvec{\psi }{}{}_e$ that is associated with the edge $e\in \mathscr {E}_h^i$. Given $e\in \mathscr {E}_h^i$, both ends of e could be interior or one end of e could be on the boundary.

If e has a boundary vertex (see Fig. 6a), denote $\varvec{\psi }{}{}_e$ as

$$\begin{aligned} \varvec{\psi }{}{}_e:= \left\{ \begin{aligned}&\frac{S_3}{S_3+S_1} \varvec{w}{}{}_{T_3,e_1}, \ in \ T_3, \\&\varvec{\eta }{}{}_{T_1,e_1,e} + \frac{d_1 \cos {\alpha _2}}{d_2}\varvec{w}{}{}_{T_1,e_1,e} + \frac{S_3}{S_3+S_1}\varvec{w}{}{}_{T_1,e_1} - \frac{\tilde{S}_{\triangle (A_1,A_{2},A_{4})}}{S_1+S_2} \varvec{w}{}{}_{T_1,e}, \ in \ T_1, \\&- \varvec{\eta }{}{}_{T_2,e_4,e} + \frac{d_4 \cos {\alpha _4}}{d_3}\varvec{w}{}{}_{T_2,e_4,e} + \frac{S_4}{S_4+S_2}\varvec{w}{}{}_{T_2,e_4} - \frac{\tilde{S}_{\triangle (A_1,A_{2},A_{4})}}{S_1+S_2} \varvec{w}{}{}_{T_2,e}, \ in \ T_2, \\&\frac{S_4}{S_4+S_2} \varvec{w}{}{}_{T_4,e_4},\ in \ T_4. \end{aligned} \right. \end{aligned}$$

(5.1)

If both of the ends of e are interior vertices (see Fig. 6b), $\varvec{\psi }{}{}_e$ is denoted by

$$\begin{aligned} \varvec{\psi }{}{}_e:= \left\{ \begin{aligned}&\frac{S_3}{2(S_3+S_1)} \varvec{w}{}{}_{T_3,e_1}, \ in \ T_3, \\&\frac{S_4}{2(S_4+S_2)} \varvec{w}{}{}_{T_4,e_4},\ in \ T_4, \\&( \frac{S_3}{2(S_3+S_1)} -1 ) \varvec{w}{}{}_{T_1,e_1} + (1 - \frac{S_6}{2(S_6+S_1)} ) \varvec{w}{}{}_{T_1,e_2} + \frac{\tilde{S}_{\triangle (A3,A4,A2)}- \tilde{S}_{\triangle (A1,A2,A4)}}{2(S_1+S_2)} \varvec{w}{}{}_{T_1,e} \\&\qquad \qquad \qquad \quad + ( \frac{d_2 \cos {\beta _3}}{d} - \frac{1}{2} ) \varvec{w}{}{}_{T_1,e_1,e_2} + \frac{1}{2} \varvec{w}{}{}_{T_1,e_1,e} - \frac{1}{2} \varvec{w}{}{}_{T_1,e_2,e} + \varvec{\eta }{}{}_{T_1,e_1,e_2} , \ in \ T_1, \\&( \frac{S_4}{2(S_4+S_2)} -1 ) \varvec{w}{}{}_{T_2,e_4} + (1 - \frac{S_5}{2(S_5+S_2)} ) \varvec{w}{}{}_{T_2,e_3} + \frac{\tilde{S}_{\triangle (A3,A4,A2)}- \tilde{S}_{\triangle (A1,A2,A4)}}{2(S_1+S_2)} \varvec{w}{}{}_{T_2,e} \\&\qquad \qquad \qquad \quad + ( \frac{1}{2} - \frac{d_4 \cos {\beta _1}}{d} ) \varvec{w}{}{}_{T_2,e_3,e_4} + \frac{1}{2} \varvec{w}{}{}_{T_2,e_4,e} - \frac{1}{2} \varvec{w}{}{}_{T_2,e_3,e} - \varvec{\eta }{}{}_{T_2,e_3,e_4} , \ in \ T_2, \\&- \frac{S_5}{2(S_5+S_2)} \varvec{w}{}{}_{T_5,e_3}, \ in \ T_5, \\&- \frac{S_6}{2(S_6+S_1)} \varvec{w}{}{}_{T_6,e_2}, \ in \ T_6. \end{aligned} \right. \end{aligned}$$

(5.2)

Fig. 6

Illustration of the supports of basis functions associated with interior edges

Fig. 7

Two cases of degeneration; see Remark 5.2

Remark 5.2

It is still possible that the support of a basis function associated with an interior edge can cover exactly three or five cells. These can be viewed as the degenerated cases, and the function $\varvec{\psi }{}{}_e$ can be defined the same way. Specifically, when $T_3$ and $T_4$ coincide, the pattern in Fig. 6a degenerates to a patch with three cells, as shown in Fig. 7a; moreover, $\varvec{\psi }{}{}_{e}|_{T_3}=\frac{S_3}{S_3+S_1} \varvec{w}{}{}_{T_3,e_1} + \frac{S_3}{S_3+S_2} \varvec{w}{}{}_{T_3,e_4}$ and $\varvec{\psi }{}{}_{e}|_{T_i}(i=1,2)$ are the same as their counterparts in (5.1). Correspondingly, the pattern in Fig. 6b degenerates to a set of five cells, as shown in Fig. 7b; $\varvec{\psi }{}{}_{e}|_{T_3}=\frac{S_3}{(2S_3+S_1)} \varvec{w}{}{}_{T_3,e_1} + \frac{S_3}{2(S_3+S_2)} \varvec{w}{}{}_{T_3,e_4}$ and $\varvec{\psi }{}{}_{e}|_{T_i}(i=1,2,5,6)$ have the same counterparts as (5.2).

Lemma 5.3

$\varvec{V}{}{}_{h0}^\mathrm{el}=\mathrm{span}\{\varvec{\psi }{}{}_e,\ e\in \mathscr {E}_h^i;\ \varvec{\psi }{}{}_T,\ T\in \mathscr {T}_h^i\}$.

For completeness, we provide the proof of Lemma 5.3 in Appendix B.2.

5.2 A lowest-degree conservative scheme for the Stokes equation

We denote

$$\begin{aligned} \mathbb {P}{}^0_h(\mathscr {T}_h):=\{q_h\in L^2(\varOmega ):q_h|_T\in P_0(T), \forall \, T \in \mathscr {T}_h\}, \ \text{ and }\ \ \mathbb {P}^0_{h0}(\mathscr {T}_h):=\mathbb {P}{}^0_h(\mathscr {T}_h)\cap L^2_0(\varOmega ). \end{aligned}$$

Based on the new finite element, the discretization scheme of (1.3) is: Find $(\varvec{u}{}{}_{h},p_{h})\in \varvec{V}{}{}_{h0}^\mathrm{el}\times \mathbb {P}^0_{h0}$, such that

$$\begin{aligned} \left\{ \begin{aligned}&\varepsilon ^{2}\big (\nabla _{h}\,\varvec{u}{}{}_{h}, \nabla _{h}\,\varvec{v}{}{}_{h}\big ) -( \mathrm{div}\,\varvec{v}{}{}_{h}, p_{h})&= ( \varvec{f}{},\varvec{v}{}{}_{h} ),&\forall \, \varvec{v}{}{}_{h}\in \varvec{V}{}{}_{h0}^\mathrm{el}, \\&(\mathrm{div}\,\varvec{u}{}{}_{h}, q_{h} )&= 0,&\forall \, q_{h}\in \mathbb {P}_{h0}^0. \end{aligned} \right. \end{aligned}$$

(5.3)

Lemma 5.4

(Stability of $\varvec{V}{}{}_{h0}^\mathrm{el}$–$\mathbb {P}^0_{h0}$) It holds uniformly that

$$\begin{aligned} \inf _{q_h\in \mathbb {P}^0_{h0}}\sup _{\varvec{v}{}{}_h\in \varvec{V}{}{}_{h0}^\mathrm{el}}\frac{(\mathrm{div}\,\varvec{v}{}{}_h,q_h)}{\Vert q_h\Vert _{0,\varOmega }\Vert \varvec{v}{}{}_h\Vert _{1,h}}\geqslant C>0. \end{aligned}$$

Proof

Given $q_h\in \mathbb {P}^0_{h0}\subset \mathbb {P}^1_{h0}$, there exists a $\varvec{v}{}{}_h\in \varvec{V}{}{}_{h0}^\mathrm{sBDFM}$, such that $\Vert \varvec{v}{}{}_h\Vert _{1,h}\leqslant C\Vert q_h\Vert _{0,\varOmega }$ and $\mathrm{div}\,\varvec{v}{}{}_h=q_h$, which implies $\varvec{v}{}{}_h\in \varvec{V}{}{}_{h0}^\mathrm{el}$. The proof is completed.$\square$

Lemma 5.5

Given $\varvec{w}{}\in \varvec{H}{}^2(\varOmega )$, it holds that

$$\begin{aligned} \inf _{\varvec{v}{}{}_h\in \varvec{V}{}{}_h^\mathrm{el}}\Vert \varvec{w}{}-\varvec{v}{}{}_h\Vert _{1,h}\leqslant Ch\Vert \varvec{w}{}\Vert _{2,\varOmega }. \end{aligned}$$

(5.4)

Given $\varvec{w}{}\in \varvec{H}{}^2(\varOmega )\cap \varvec{H}{}{}_0^1(\varOmega )$, such that $\mathrm{div}\,\varvec{w}{}=0$, it holds that

$$\begin{aligned} \inf _{\varvec{v}{}{}_h\in \varvec{V}{}{}_{h0}^\mathrm{sBDFM},\,\mathrm{div}\,\varvec{v}{}{}_h=0}\Vert \varvec{w}{}-\varvec{v}{}{}_h\Vert _{1,h}\leqslant Ch\Vert \varvec{w}{}\Vert _{2,\varOmega }. \end{aligned}$$

(5.5)

Proof

Since linear element space is contained in $\varvec{V}{}{}_{h0}^\mathrm{el}$, the estimation (5.4) holds directly. Also, (5.5) follows from Lemma 3.2 and Remark 5.1. The proof is completed.$\square$

The system (5.3) is uniformly well-posed by Brezzi’s theory.

Lemma 5.6

The problem (5.3) admits a unique solution pair $(\varvec{u}{}{}_h,p_h)$, and it holds that

where $\Vert \varvec{f}{}\Vert _{-1,h}:=\sup _{\varvec{v}{}{}_h\in \varvec{V}{}{}_{h0}^\mathrm{el}}\frac{(\varvec{f}{},\varvec{v}{}{}_h)}{\Vert \varvec{v}{}{}_h\Vert _{1,h}}$.

Theorem 5.1

Let $(\varvec{u}{},p)$ and $(\varvec{u}{}{}_{h},p_{h})$ be the solutions of (1.4) and (5.3), respectively. If $\varvec{u}{}\in \varvec{H}{}^2(\varOmega )$ and $p\in H^1(\varOmega )$, then

$$\begin{aligned} \Vert \varvec{u}{}-\varvec{u}{}{}_h\Vert _{1,h}\leqslant Ch\Vert \varvec{u}{}\Vert _{2,\varOmega },\,\ \ \ \Vert p-p_h\Vert _{0,\varOmega }\leqslant Ch(\varepsilon ^2\Vert \varvec{u}{}\Vert _{2,\varOmega }+\Vert p\Vert _{1,\varOmega }). \end{aligned}$$

Here, the constant C does not depend on the parameter $\varepsilon$.

Proof

The argument is standard, so we omit the details here. We only note that, as the scheme is strictly conservative, the velocity solution $\varvec{u}{}$ can be completely separated from the pressure p, and Lemma 5.5 works here.$\square$

Remark 5.3

A further reduction of $\varvec{V}{}{}_h^\mathrm{el}$ leads to the spaces:

$$\begin{aligned} \varvec{V}{}{}_{h}^1:=\left\{ \varvec{v}{}{}_h\in \varvec{H}{}(\mathrm{div},\varOmega ):\ \varvec{v}{}{}_h|_T\in \varvec{P}{}{}_1(T),\ \forall \,T\in \mathscr {T},\ \int _e\varvec{v}{}{}_h\cdot {\textbf {t}}\ \text{ is } \text{ continuous } \text{ across }\ e\in \mathscr {E}_h^i\right\} , \end{aligned}$$

and

$$\begin{aligned} \varvec{V}{}{}_{h0}^1:=\left\{ \varvec{v}{}{}_h\in \varvec{V}{}{}_h^1\cap \varvec{H}{}_0(\mathrm{div},\varOmega ),\ \int _e\varvec{v}{}{}_h\cdot {\textbf {t}}=0\ \text{ on } \text{ boundary } \text{ edges }\ e\in \mathscr {E}_h^b\right\} . \end{aligned}$$

As it passes the patch test, the pair $\varvec{V}{}{}_{h0}^1$–$\mathbb {P}^0_{h0}$ may be viewed as the most natural, if not the only, $\varvec{P}{}{}_1$–$P_0$ pair for the Stokes problem. Generally, this pair is not stable; refer to Appendix A for a numerical verification. Accordingly, we recognize the $\varvec{V}{}{}_{h0}^\mathrm{el}$–$\mathbb {P}^0_{h0}$ pair as a lowest-degree stable conservative pair for the Stokes problem on general triangulations.

6 Numerical Examples

In this section, we investigate the numerical properties of $\varvec{V}{}{}_{h0}^\mathrm{el}$–$\mathbb {P}^0_{h0}$. In theory, the pairs $\varvec{V}{}{}_{h0}^\mathrm{sBDFM}$–$\mathbb {P}^1_{h0}$ and $\varvec{V}{}{}_{h0}^\mathrm{el}$–$\mathbb {P}^0_{h0}$ lead to same numerical velocity solutions on the same grids, and numerical experiments validate it. Thus we do not present separate experiments with respect to $\varvec{V}{}{}_{h0}^\mathrm{sBDFM}$–$\mathbb {P}^1_{h0}$. All simulations are performed on uniformly refined grids.

It has been revealed that $\varvec{V}{}{}_{h0}^\mathrm{el}$ does not correspond to a Ciarlet’s triple. However, it does admit a set of tightly supported basis functions. This makes the $\varvec{V}{}{}_{h0}^\mathrm{el}$–$\mathbb {P}^0_{h0}$ embedded in the standard framework of programming. Precisely, on every cell, only a fixed small number (no more than 13) of basis functions contribute to the cell-wise stiffness matrix, and the assembly of cell-wise stiffness matrices into a global stiffness matrix follows the standard procedure. The numerical experiments given verify the implementability of the scheme.

6.1 On the pressure robustness with respect to parameter Ra

This example was introduced in [22]. Here, we utilize it to show that the pair $\varvec{P}{}^{1+}$–$P_0$ is of pressure robustness. Consider the Stokes Eq. (1.3) in $\varOmega = (0,1) \times (0,1)$ with $\varepsilon =1$ and $\varvec{f}{}= (0,Ra(1-y+3y^2))^T$, where $Ra>0$ is a parameter. The exact solution pair is $\varvec{u}{}= 0$ and $p=Ra(y^3 - 2/y^2+y-7/12)$. For the continuous problem, changing the parameter Ra in the right-hand side changes only the pressure. It was suggested in [22] that for standard finite elements, the discrete velocity is far from being equal to zero even for $Ra=1$. However, as is shown in Fig. 8, for the new pair $\varvec{V}{}{}_{h0}^\mathrm{el}$–$\mathbb {P}^0_{h0}$, the numerical velocities are close to zero for different values of Ra, which implies the pair’s pressure robustness with respect to the parameter Ra.

Fig. 8

Velocity errors in the no-flow Stokes equations by the $\varvec{P}{}{}^{1+} - P_0$ pair

6.2 On the $\varepsilon -$robustness

This example is designed to test $\varepsilon$ robustness with fixed $\varvec{f}{}$. Consider the Stokes problem (1.3) in $\varOmega =(0,1)\times (0,1)$. Assume $\varepsilon =1$ and the exact solution pair $(\varvec{u}{}, p)=(\varvec{u}{}^{\varepsilon =1}, p^{\varepsilon =1})$ with $\varvec{u}{}^{\varepsilon =1} = \mathrm{curl}(\frac{1}{2} x^2y^2(x-1)^2(y-1)^2)$ and $p^{\varepsilon =1}=3x^2+3y^2-2$. Consequently we obtain $\varvec{f}{}^{\varepsilon =1}$. Now, for the continuous problem (1.3) with $p=p^{\varepsilon =1}$ and $\varvec{f}{}= \varvec{f}{}^{\varepsilon =1}$ fixed, changing $\varepsilon$ only changes the true velocity solution to $\frac{1}{\varepsilon ^2} \, \varvec{u}{}^{\varepsilon =1}=:\varvec{u}{}^{\varepsilon }$, while $p^{\varepsilon }=p^{\varepsilon =1}$. For the discrete problem (5.3), we still hope to find this law. We denote $(\varvec{u}{}{}_h^{\varepsilon =1},p_h^{\varepsilon =1})$ and $(\varvec{u}{}{}_h^{\varepsilon },p_h^{\varepsilon })$ as numerical solutions associated with $(\varvec{u}{}^{\varepsilon =1},p^{\varepsilon =1})$ and $(\varvec{u}{}^{\varepsilon },p^{\varepsilon })$, respectively. Numerical tests show that $\varvec{u}{}{}_h^{\varepsilon }=\frac{1}{\varepsilon ^2} \, \varvec{u}{}{}_h^{\varepsilon =1}$ and $p_h^{\varepsilon }=p_h^{\varepsilon =1}$. For the convenience of display, we present the errors of velocity below:

Table 1 Errors of velocity in the $L^2$-norm by the $\varvec{P}{}{}^{1+}-P_0$ pair

Table 2 Errors of velocity in the $H^1$-norm by the $\varvec{P}{}{}^{1+}-P_0$ pair

It can be observed that

• (i) when the mesh level is fixed, both $\Vert \varvec{u}{}^\varepsilon -\varvec{u}{}{}_h^\varepsilon \Vert _{0,h}$ and $|\varvec{u}{}^\varepsilon -\varvec{u}{}{}_h^\varepsilon |_{1,h}$ are of the $\mathscr {O}((\frac{1}{\varepsilon })^2)$ order, while $\Vert p^\varepsilon -p_h^\varepsilon \Vert _{0,h}$ is of the $\mathscr {O}((\frac{1}{\varepsilon })^0)$ order; this corresponds to our expectation;

• (ii) when $\varepsilon$ is fixed, velocity errors in the $L^2$-norm and $H^1$-norm are of the $\mathscr {O}(h^2)$ and $\mathscr {O}(h)$ order, respectively, and pressure errors are of the $\mathscr {O}(h)$ order.

6.3 On the convergence in polygon regions (with unstructured subdivisions)

In this subsection, simulations for Stokes problems are performed in various domains with general triangulations to verify the convergence rate results in Theorem 5.1 for finite element approximation $\varvec{V}{}{}_{h0}^\mathrm{el}$–$\mathbb {P}^0_{h0}$.

Consider the Stokes problem (1.3) in the two-dimensional domain $\varOmega$, which is sequentially a rectangle, a hexagon, a pentagon, an L-shaped area, and a star-shaped area.

For each domain, we denote $\displaystyle \partial \varOmega = \cup _i \varGamma _i$. Also, we define $\displaystyle \phi =C_\phi \prod _{\varGamma _i \subset \partial \varOmega } (r(\varGamma _i))^2$, with $r(\varGamma _i)=0$ representing the equation of $\varGamma _i$; for the precise expression of $r(\varGamma _i)$, refer to each example’s caption. Assume $\varepsilon =1$, and the right-hand side $\varvec{f}{}$ is chosen such that the exact solution pair is $\varvec{u}{}=\mathrm{curl}\, \phi$ and $p=3x^2+3y^2+C_p$, where $C_p$ satisfies $\int _\varOmega p \, dx = 0$.

For every test, we display the domains with the initial grid in the left, and corresponding error convergence figures are given on the right (Figs. 9, 10, 11, 12 and 13).

Fig. 9

Example 1. Left: An initially divisioned unit square domain, with $\partial \varOmega =\cup _{i=1}^4 \varGamma _i$, $A_1(0,0)$, $A_2(1,0)$, $A_3(1,1)$, and $A_4(0,1)$; Right: Velocity errors in the $L^2$- and $H^1$-norm and pressure errors in the $L^2$-norm by the $\varvec{P}{}{}^{1+}-P_0$ pair, with $r(\varGamma _1)=y$, $r(\varGamma _2)=x-1$, $r(\varGamma _3)=y-1$, $r(\varGamma _4)=x$, $C_p=-2$, and $C_\phi =1/2$

Fig. 10

Example 2. Left: An initially divisioned hexagon domain, with $\partial \varOmega =\cup _{i=1}^6 \varGamma _i$, $A_1(0,0)$, $A_2(0.5,0)$, $A_3(1,0.5)$, $A_4(1,1)$, $A_5(0.5,1)$, and $A_6(0,0.5)$; Right: Velocity errors in the $L^2$- and $H^1$-norm and pressure errors in the $L^2$-norm by the $\varvec{P}{}{}^{1+}-P_0$ pair, with $r(\varGamma _1)=y$, $r(\varGamma _2)=2x-2y-1$, $r(\varGamma _3)=x-1$, $r(\varGamma _4)=y-1$, $r(\varGamma _5)=2x-2y+1$, $r(\varGamma _6)=x$, $C_p=-23/12$, and $C_\phi =1/16$

Fig. 11

Example 3. Left: An initially divisioned pentagon domain, with $\partial \varOmega =\cup _{i=1}^5 \varGamma _i$, $A_1(-0.1,-0.8)$, $A_2(0.9,-0.15)$, $A_3(1,1)$, $A_4(-0.6,0.8)$, and $A_5(-1,0)$; Right: Velocity errors in the $L^2$- and $H^1$-norm and pressure errors in the $L^2$-norm by the $\varvec{P}{}{}^{1+}-P_0$ pair, with $r(\varGamma _1)=130x-200y-147$, $r(\varGamma _2)=23x-2y-21$, $r(\varGamma _3)=x-8y+7$, $r(\varGamma _4)=2x-y+2$, $r(\varGamma _5)=8x+9y+8$, $C_p=- 205333/153120$, and $C_\phi =10^{-13}$

Fig. 12

Example 4. Left: An initially divisioned L-shaped domain with $\partial \varOmega =\cup _{i=1}^6 \varGamma _i$, $A_1(0,0)$, $A_2(2,0)$, $A_3(2,1)$, $A_4(1,1)$, $A_5(1,2)$, and $A_6(0,2)$; Right: Velocity errors in the $L^2$- and $H^1$-norm and pressure errors in the $L^2$-norm by the $\varvec{P}{}{}^{1+}-P_0$ pair, with $r(\varGamma _1)=y$, $r(\varGamma _2)=x-2$, $r(\varGamma _3)=y-1$, $r(\varGamma _4)=x-1$, $r(\varGamma _5)=y-2$, $r(\varGamma _6)=x$, $C_p=-6$, and $C_\phi =10^{-2}$

Fig. 13

Example 5. Left: An initially divisioned star-shape domain, with $\partial \varOmega =\cup _{i=1}^{10} \varGamma _i$, $A_1(-1,-1.2)$, $A_2(-0.1,-0.8)$, $A_3(0.7,-1.1)$, $A_4(0.6,-0.3)$, $A_5(0.8,0.35)$, $A_6(0.4,0.4)$, $A_7(0,1.1)$, $A_8(-0.5,0.5)$, $A_9(-1.2,0.25)$, and $A_{10}(-0.8,-0.3)$; Right: Velocity errors in the $L^2$- and $H^1$-norm and pressure errors in the $L^2$-norm by the $\varvec{P}{}{}^{1+}-P_0$ pair, with $r(\varGamma _1)=20x-45y-34$, $r(\varGamma _2)=30x+80y+67$, $r(\varGamma _3)=16x+2y-9$, $r(\varGamma _4)=13x-4y-9$, $r(\varGamma _5)=5x+40y-18$, $r(\varGamma _6)=35x+20y-22$, $r(\varGamma _7)=12x-10y+11$, $r(\varGamma _8)=10x-28y+19$, $r(\varGamma _9)=55x+40y+56$, $r(\varGamma _{10})=45x-10y+33$, $C_p=-243923/163680$, and $C_\phi =10^{-30}$

From these examples, the convergence rate of the velocity is approximately two with respect to the $L^2$-norm and one to $H^1$-norm; the convergence rate of the pressure is approximately one with respect to the $L^2$-norm; these are consistent with the analysis in Theorem 5.1.

7 Concluding Remarks

In this study, a new conservative pair, $\varvec{V}{}{}_{h0}^\mathrm{el}$–$\mathbb {P}^0_{h0}$, is established and shown to be stable for the incompressible Stokes problem, and a numerical verification (see Appendix A) illustrates that the $\varvec{V}{}{}_{h0}^\mathrm{el}$–$\mathbb {P}^0_{h0}$ pair is the lowest-degree one that is stable and conservative on general triangulations. The velocity component, in a generalized sense, can also be viewed as the $H(\mathrm{div})$ element functions added with piecewise divergence-free normal-bubble functions, and is thus comparable with ones given in, for example, [14, 25, 35]. However, the finite element space for velocity does not correspond to a Ciarlet’s triple, and the construction and theoretical analysis cannot be carried out in the usual way. The main technical ingredient is thus to use an indirect approach by constructing and utilizing the auxiliary pair $\varvec{V}{}{}_{h0}^\mathrm{sBDFM}$–$\mathbb {P}^1_{h0}$.

The auxiliary pair $\varvec{V}{}{}_{h0}^\mathrm{sBDFM}$–$\mathbb {P}^1_{h0}$ is constructed by reducing $H(\mathrm{div})$ finite element spaces, as adopted in [37]. Note that the sBDFM element has the same nodal functionals as ones given in [25, 35] and [14] (the lowest-degree one of each), but it uses the lowest-degree polynomials among these four, and only the sBDFM element space can accompany the piecewise linear polynomial space to form a stable pair. The other three can only accompany the piecewise constant space.

As for conservative pairs in three-dimension, we refer to [16, 40, 44], where composite grids were required, as well as [17] and [43], where high-degree local polynomials were utilized. We refer to [8, 21, 42] for pairs on rectangular grids and [26] for ones on cubic grids, where full advantage was taken of the geometric symmetry of the cells. The approaches given in [37] and the present paper can be generalized to higher dimensions and non-simplicial grids. This will be discussed in the future.

Appendices

Appendix

A The Most Natural Linear–Constant Pair is not Stable: A Numerical Verification

In this section, we show by numerics the pair, $\varvec{V}{}{}_{h0}^1$–$\mathbb {P}^0_{h0}$, defined in Remark 5.3, is not stable on general triangulations, whereas

$$\begin{aligned} \displaystyle \inf _{q_h\in \mathrm{div}\,\varvec{V}{}{}_{h0}^1}\sup _{\varvec{v}{}{}_h\in \varvec{V}{}{}_{h0}^1}\frac{(\mathrm{div}\,\varvec{v}{}{}_h,q_h)}{\Vert q_h\Vert _{0,\varOmega }|\varvec{v}{}{}_h|_{1,h}}= \mathscr {O}(h) \end{aligned}$$

(A.1)

on a specific kind of triangulations.

1.1 A.1 A special triangulation and finite element space

We consider the computational domain $\varOmega = (0,1)\times (0,1) \setminus ( \{(x,y) : 0 \leqslant x \leqslant \frac{1}{2}, x + \frac{1}{2} \leqslant y \leqslant 1\} \cup \{ (x,y) : \frac{1}{2} \leqslant x \leqslant 1, 0 \leqslant y \leqslant x - \frac{1}{2} \})$. The initial triangulation is shown in Fig. 14a, and a sequence of triangulations is obtained by refining it uniformly (cf. Fig. 14b).

Fig. 14

An initially divisioned grid and its sketch map after uniform refinements

Given a patch $P_A$ as shown in Fig. 14a, we denote $\varvec{V}{}{}_{h0}^1(P_A) = \mathrm{span} \{ \varvec{\varphi }{}{}_1^A, \varvec{\varphi }{}{}_2^A, \varvec{\varphi }{}{}_3^A \}$, and for $i=1:6, \ \varvec{V}{}{}_{h0}^1(T_i) = \mathrm{span} \{ \varvec{\varphi }{}{}_{T_i}^1, \varvec{\varphi }{}{}_{T_i}^2, \varvec{\varphi }{}{}_{T_i}^3 \}$. Specifically, for $s=1:2, \ i=1:6, \, \varvec{\varphi }{}{}_s^A|_{T_i}=\varvec{\varphi }{}{}_{T_i}^s$, and for $s=3$,

$$\begin{aligned} \varvec{\varphi }{}{}_3^A = \left\{ \begin{aligned}&\varvec{\varphi }{}{}_{T_1}^1 - 2 \varvec{\varphi }{}{}_{T_1}^2 + \varvec{\varphi }{}{}_{T_1}^3 , \ in \ T_1;&\varvec{\varphi }{}{}_{T_2}^1 - \varvec{\varphi }{}{}_{T_2}^2 - \varvec{\varphi }{}{}_{T_2}^3 , \ in \ T_2;\\&2 \varvec{\varphi }{}{}_{T_3}^1 - \varvec{\varphi }{}{}_{T_3}^2 + \varvec{\varphi }{}{}_{T_3}^3 , \ in \ T_3;&\varvec{\varphi }{}{}_{T_4}^1 - 2 \varvec{\varphi }{}{}_{T_4}^2 + \varvec{\varphi }{}{}_{T_4}^3 , \ in \ T_4;\\&\varvec{\varphi }{}{}_{T_5}^1 - \varvec{\varphi }{}{}_{T_5}^2 - \varvec{\varphi }{}{}_{T_5}^3 , \ in \ T_5;&2 \varvec{\varphi }{}{}_{T_6}^1 - \varvec{\varphi }{}{}_{T_6}^2 + \varvec{\varphi }{}{}_{T_6}^3 , \ in \ T_6;\\ \end{aligned} \right. \end{aligned}$$

where for $i=1:6$, $\varvec{\varphi }{}{}_{T_i}^1= \left( \begin{array}{c} \lambda \\ 0 \\ \end{array} \right)$, $\varvec{\varphi }{}{}_{T_i}^2= \left( \begin{array}{c} 0 \\ \lambda \\ \end{array} \right)$, and $\varvec{\varphi }{}{}_{T_1}^3= \left( \begin{array}{c} \lambda _6-\lambda _1\\ 0 \end{array} \right)$, $\varvec{\varphi }{}{}_{T_2}^3= \left( \begin{array}{c} \lambda _1-\lambda _2\\ \lambda _1-\lambda _2 \end{array} \right)$, $\varvec{\varphi }{}{}_{T_3}^3= \left( \begin{array}{c} 0\\ \lambda _2-\lambda _3 \end{array} \right)$, $\varvec{\varphi }{}{}_{T_4}^3= \left( \begin{array}{c} \lambda _3-\lambda _4\\ 0 \end{array} \right)$, $\varvec{\varphi }{}{}_{T_5}^3= \left( \begin{array}{c} \lambda _4-\lambda _5\\ \lambda _4-\lambda _5 \end{array} \right)$, $\varvec{\varphi }{}{}_{T_6}^3= \left( \begin{array}{c} 0\\ \lambda _5-\lambda _6 \end{array} \right)$.

Similarly to Lemma 4.3, we can show the lemma below:

Lemma A.1

$dim(\varvec{V}{}{}_{h0}^{1})=3 \# \mathscr {X}_h^i$ and $\varvec{V}{}{}_{h0}^1=\mathrm{span}\{ \varvec{\varphi }{}{}_1^A, \varvec{\varphi }{}{}_2^A, \varvec{\varphi }{}{}_3^A, A \in \mathscr {X}_h^i \}$.

1.2 A.2 Numerical Verification of the Inf-sup Constant

By the Courant’s min-max theorem, it is easy to show the lemma below:

Lemma A.2

With respect to any set of basis functions of $\varvec{V}{}{}_{h0}^1$ and $\mathbb {P}^0_h$, denote by A the stiffness matrix of $(\nabla _h\,\cdot ,\nabla _h\,\cdot )$ on $\varvec{V}{}{}_{h0}^1$, by M the mass matrix of $(\cdot ,\cdot )$ on $\varvec{V}{}{}_{h0}^1$, and by B the stiffness matrix of $(\mathrm{div}\,\cdot ,\cdot )$ on $\varvec{V}{}{}_{h0}^1\times \mathbb {P}^0_h$. Then

$$\begin{aligned} \inf _{q_h\in \mathrm{div}\,\varvec{V}{}{}_{h0}^1}\sup _{\varvec{v}{}{}_h\in \varvec{V}{}{}_{h0}^1}\frac{(\mathrm{div}\,\varvec{v}{}{}_h,q_h)}{\Vert q_h\Vert _{0,\varOmega }|\varvec{v}{}{}_h|_{1,h}}= \lambda ^+_{\min }, \end{aligned}$$

where $\lambda ^+_{\min }$ is the smallest positive eigenvalue of the matrix eigenvalue problem

$$\begin{aligned} BA^{-1}B^{T} \mathrm{v} = {\lambda } M \mathrm{v}. \end{aligned}$$

(A.2)

The maximum eigenvalue of the eigenvalue problem (A.2) is denoted by $\lambda _{\max }$. Table 3 displays the computed values of $\lambda ^+_{\min }$ and $\lambda _{\max }$ on a series of refined grids. Figure 15 illustrates that $\lambda ^+_{\min }$ degenerates in the rate of $\mathscr {O}(h)$. This verifies (A.1) numerically.

Table 3 Computed values of $\lambda _{\min }^+$ and $\lambda _{\max }$

Fig. 15

$\lambda _{min}^+$ decays along with mesh refinements

B Proofs of Lemmas 4.3 and  5.3

1.1 B.1 Proof of Lemma 4.3

In this subsection, we provide the proof of Lemma 4.3, which establishes a basis of $\varvec{Z}{}_{h0}$. To this end, we need to analyze $\varvec{Z}{}_{h0}|_T$ with $T\in \mathscr {T}_h$ firstly.

For the interior cell $T\in \mathscr {T}_h^i$ with vertices $A_i$, $i=1:3$, and neighboring cells $T_j$, $j=1:3$, it is covered by functions of the set $\varvec{\Psi }{}_h(T)=\{\varvec{\psi }{}^{A_1}|_T,\varvec{\psi }{}^{A_2}|_T,\varvec{\psi }{}^{A_3}|_T,\varvec{\psi }{}_{T}|_T,\varvec{\psi }{}_{T_1}|_T,\varvec{\psi }{}_{T_2}|_T,\varvec{\psi }{}_{T_3}|_T\}$;see Fig. 16 for an illustration. It is clear that the seven functions in $\varvec{\Psi }{}_h(T)$ are linearly dependent; however, any six of them are linearly independent. For conciseness, a particular case is stated in the following lemma, which also serves Lemma 4.3.

Lemma B.1

For the interior cell $T\in \mathscr {T}_h^i$, with vertices $A_i,\ i=1:3$ and neighboring cells $T_j,\ j=1:3$ (see Fig. 16 for an illustration), the functions in $\{ \varvec{\psi }{}^{A_2}|_{T}, \varvec{\psi }{}^{A_3}|_{T}, \varvec{\psi }{}{}_{T}|_{T}, \varvec{\psi }{}{}_{T_1}|_{T}, \varvec{\psi }{}{}_{T_2}|_{T}, \varvec{\psi }{}{}_{T_3}|_{T}\}$ are linearly independent.

Fig. 16

Illustration of the supports of all kernel basis functions upon one cell

Proof

With the help of (4.3) and (4.4), a direct calculation leads to

$$\begin{aligned}&\left( \varvec{\psi }{}^{A_2}|_{T}, \varvec{\psi }{}^{A_3}|_{T}, \varvec{\psi }{}{}_{T}|_{T}, \varvec{\psi }{}{}_{T_1}|_{T}, \varvec{\psi }{}{}_{T_2}|_{T}, \varvec{\psi }{}{}_{T_3}|_{T} \right) ^\top \nonumber \\&\quad ={\textbf {A}} \left( \varvec{w}{}{}_{T,e_2,e_3}, \varvec{w}{}{}_{T,e_3,e_1}, \varvec{w}{}{}_{T,e_1,e_2}, \varvec{w}{}{}_{T,e_1}, \varvec{w}{}{}_{T,e_2}, \varvec{w}{}{}_{T,e_3}\right) ^\top ,\nonumber \\&\qquad \text{ with }\ \ {\textbf {A}}= \left[ \begin{array}{cccccc} 0 &{} 1 &{} 0 &{} \frac{d_2 d_5 \sin {(\alpha _3+\gamma _3)}}{2(S_1+S)} &{} 0 &{} \frac{d_2 d_8 \sin {(\alpha _1+\beta _1)}}{2(S_3+S)} \\ 0 &{} 0 &{} 1 &{} \frac{d_3 d_4 \sin {(\alpha _2+\beta _2)}}{2(S_1+S)} &{} \frac{d_3 d_7 \sin {(\alpha _1+\gamma _1)}}{2(S_2+S)} &{} 0 \\ \frac{1}{3} &{} \frac{1}{3} &{} \frac{1}{3} &{} \frac{S_1-2S}{3(S_1+S)} &{} \frac{S_2-2S}{3(S_2+S)} &{} \frac{S_3-2S}{3(S_3+S)} \\ 0 &{} 0 &{} 0 &{} \frac{S}{S_1+S} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \frac{S}{S_2+S} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \frac{S}{S_3+S} \end{array}\right] . \end{aligned}$$

As $\displaystyle \det ({\textbf {A}})=\frac{1}{3} \prod _{i=1:3} \frac{S}{S+S_i}\ne 0$ and $\left\{ \varvec{w}{}{}_{T,e_2,e_3}, \varvec{w}{}{}_{T,e_3,e_1}, \varvec{w}{}{}_{T,e_1,e_2}, \varvec{w}{}{}_{T,e_1}, \varvec{w}{}{}_{T,e_2}, \varvec{w}{}{}_{T,e_3}\right\}$ are linearly independent, it concludes that $\left\{ \varvec{\psi }{}^{A_2}|_{T}, \varvec{\psi }{}^{A_3}|_{T}, \varvec{\psi }{}{}_{T}|_{T}, \varvec{\psi }{}{}_{T_1}|_{T}, \varvec{\psi }{}{}_{T_2}|_{T}, \varvec{\psi }{}{}_{T_3}|_{T} \right\}$ are linearly independent.$\square$

Remark B.1

If a cell $T\in \mathscr {T}_h$ has one (or more) vertices aligned on the boundary, then it is covered by no more than two interior vertex patches and contained in the supports of no more than six vertex- or cell-related kernel basis functions; the restriction of these six functions on T is linearly independent.

Proof of Lemma 4.3

We only have to prove that the functions of $\varPhi _h(\mathscr {T}_h)$ are linearly independent. Indeed, provided that the set $\varPhi _h(\mathscr {T}_h)$ is linearly independent, $\dim (\mathrm{span}(\varPhi _h(\mathscr {T}_h))) = \# \mathscr {X}^i_h + \# \mathscr {T}^i_h = 3 \# \mathscr {X}^i_h -2 = 3\# \mathscr {E}^i_h - (3 \# \mathscr {T}_h - 1) =\dim (\varvec{V}{}{}_{h0}^\mathrm{sBDFM})-\dim (\mathbb {P}^1_{h0})=\dim (\varvec{V}{}{}_{h0}^\mathrm{sBDFM})-\dim (\mathrm{div}\,\varvec{V}{}{}_{h0}^\mathrm{sBDFM})=\dim (\varvec{Z}{}{}_{h0})$, and thus $\varvec{Z}{}{}_{h0}=\mathrm{span}\left( \varPhi _h(\mathscr {T}_h)\right)$.

Now, given $\displaystyle \varvec{\psi }{}{}_h=\sum _{A\in \mathscr {X}_h^i}c_A\varvec{\psi }{}^A+\sum _{T\in \mathscr {T}_h^i}c_T\varvec{\psi }{}{}_T=0$, we show that all $c_A$ and $c_T$ are zero. Similar to [46], we adopt a sweeping process here. Given $a\in \mathscr {X}_h^b$, let T be such that a is a vertex of T. Then,

$$\begin{aligned} \varvec{\psi }{}{}_h|_T=\sum _{A\in \mathscr {X}_h^i\cap \overline{T}}c_A\varvec{\psi }{}^A|_T+\sum _{T'\in \mathscr {T}_h^i,T'\ \text{ and }\ T\ \text{ share } \text{ a } \text{ common } \text{ edge }}c_{T'}\varvec{\psi }{}{}_{T'}|_T=0. \end{aligned}$$

By Lemma B.1 and Remark B.1, $c_A=0$ for $A\in \mathscr {X}_h^i\cap \overline{T}$ and $c_{T'}=0$ for $T'\in \mathscr {T}_h^i$, where $T'$ and T share a common edge. Therefore, $c_A=0$ for any vertex $A\in \mathscr {X}_h^i$ that is connected to one boundary vertex $a\in \mathscr {X}_h^b$, and $c_T=0$ for any $T\in \mathscr {T}_h^i$ that connects to a boundary vertex $a\in \mathscr {X}^b_h$. Similarly, we can show

$$\begin{aligned} c_A=0\ \forall \,A\in \mathscr {X}_h^{b,+2},\ \ \ c_T=0\ \forall \,T\in \mathscr {T}_h\ \text{ that } \text{ connects } \text{ to } \mathscr {X}_h^{b,+1}. \end{aligned}$$

Repeating the procedure recursively, finally, we obtain

$$\begin{aligned} c_A=0 \ \forall \, A \in \mathscr {X}_h^{b,+k},\ \ \ c_T=0\ \forall \,T\in \mathscr {T}_h\ \text{ that } \text{ connects } \text{ to } \mathscr {X}_h^{b,+(k-1)} \end{aligned}$$

where k is the number of levels of the triangulation $\mathscr {T}_h$. Therefore, $c_A$ and $c_T$ are all zero, and the functions of $\varPhi _h(\mathscr {T}_h)$ are linearly independent. The proof is completed. $\square$

1.2 B.2 Proof of Lemma 5.3

In this subsection, we provide the proof of Lemma 5.3, which establishes a basis of $\varvec{V}{}_{h0}^\mathrm{el}$.

Proof of Lemma 5.3

Evidently, $\varvec{V}{}{}_{h0}^\mathrm{el}\supset \mathrm{span}\{\varvec{\psi }{}{}_e,\ e\in \mathscr {E}_h^i;\ \varvec{\psi }{}{}_T,\ T\in \mathscr {T}_h^i\}$. So we turn to the other direction.

First, we show $\mathrm{span}\{\mathrm{div}\,\varvec{\psi }{}{}_e,\ e\in \mathscr {E}_h^i\}=\mathbb {P}^0_{h0}.$ For both cases, as in Fig. 6, $\mathrm{div}\, \varvec{\psi }{}{}_e=\frac{1}{S_1}$ on $T_1$ and $-\frac{1}{S_2}$ on $T_2$, and vanishes on all the other cells. A simple algebraic argument leads to this assertion.

Second, all functions of $\varvec{Z}{}{}_{h0}$ can be represented by these functions. We only have to verify it for any kernel function, which is supported in a vertex patch. $\square$

Fig. 17

Illustration of the support of $\varvec{\psi }{}{}_{e_i}$. Left: $e_i$ has one interior vertex; Right: $e_i$ has two interior vertices

In fact, for an interior vertex A, $P_A=\cup _{i=1:m}T_i$, $\overline{T}_{i}\cap \overline{T}_{i+1}=e_i$, $T_{m+1}=T_1$ and $e_i$ connects A and $A_i$. Denote for $i=1:m$ (see Fig. 17)

$$\begin{aligned} \varvec{\psi }{}{}_{e_i}^* = \left\{ \begin{aligned}&\varvec{\psi }{}{}_{e_i}, \ A_i \in \mathscr {X}_h^b, \\&\varvec{\psi }{}{}_{e_i} + \frac{1}{2} \varvec{\psi }{}{}_{T_i} + \frac{1}{2} \varvec{\psi }{}{}_{T_{i+1}}, \ A_i \in \mathscr {X}_h^i. \end{aligned} \right. \end{aligned}$$

We refer to (4.3), (4.4), (5.1), (5.2) for the expressions of $\varvec{\psi }{}^A$, $\varvec{\psi }{}{}_{T_i}$ and $\varvec{\psi }{}{}_{e_i}$(cf Figs. 5, 6 and 7). Then, in any event $\mathrm{supp}(\varvec{\psi }{}{}_{e_i}^*)=T_{i-1} \cup T_{i} \cup T_{i+1} \cup T_{i+2} \subset P_A$, and $\mathrm{div}\,\sum _{i=1:m}\varvec{\psi }{}{}_{e_i}^*=0$. Thus $\sum _{i=1:m}\varvec{\psi }{}{}_{e_i}^*\in \varvec{Z}{}{}_A=\mathrm{span}\{\varvec{\psi }{}^A\}$. A further calculation gives $\sum _{i=1:m}\varvec{\psi }{}{}_{e_i}^*=\varvec{\psi }{}^A$, which thus leads to

$$\begin{aligned} \displaystyle \varvec{\psi }{}^{A}= \sum _{i=1:m} \varvec{\psi }{}{}_{e_i} + \frac{1}{2}\sum _{i=1:m, \ A_i \in \mathscr {X}_h^i} ( \varvec{\psi }{}{}_{T_i} + \varvec{\psi }{}{}_{T_{i+1}} ). \end{aligned}$$

Now, $\varvec{V}{}{}_{h0}^\mathrm{el}$ and $\mathrm{span}\{\varvec{\psi }{}{}_e,\ e\in \mathscr {E}_h^i;\ \varvec{\psi }{}{}_T,\ T\in \mathscr {T}_h^i\}$ have the same range under the operator $\mathrm{div}$. It also holds that $\varvec{Z}{}{}_{h0}\subset \mathrm{span}\{\varvec{\psi }{}{}_e,\ e\in \mathscr {E}_h^i;\ \varvec{\psi }{}{}_T,\ T\in \mathscr {T}_h^i\}$. Thus, $\varvec{V}{}{}_{h0}^\mathrm{el}=\mathrm{span}\{\varvec{\psi }{}{}_e,\ e\in \mathscr {E}_h^i;\ \varvec{\psi }{}{}_T,\ T\in \mathscr {T}_h^i\}$.

Further, $\dim (\mathrm{span}\{\varvec{\psi }{}{}_e,\ e\in \mathscr {E}_h^i;\ \varvec{\psi }{}{}_T,\ T\in \mathscr {T}_h^i\})=\dim (\varvec{V}{}{}_{h0}^\mathrm{el})=\dim (\varvec{Z}{}{}_{h0}) + \dim (\mathbb {P}{}_{h0}^0) = \# \mathscr {X}^i_h + \# \mathscr {T}^i_h + \# \mathscr {T}_h - 1 = \# \mathscr {T}^i_h + \# \mathscr {E}^i_h=\#(\{\varvec{\psi }{}{}_e,\ e\in \mathscr {E}_h^i;\ \varvec{\psi }{}{}_T,\ T\in \mathscr {T}_h^i\})$. Therefore, the functions $\{\varvec{\psi }{}{}_e,\ e\in \mathscr {E}_h^i;\ \varvec{\psi }{}{}_T,\ T\in \mathscr {T}_h^i\}$ are linearly independent, and they form a basis of $\varvec{V}{}{}_{h0}^\mathrm{el}$. The proof is completed. $\square$