Generalized Bernoulli Polynomials: Solving Nonlinear 2D Fractional Optimal Control Problems

Abstract

This work develops an optimization method based on a new class of basis function, namely the generalized Bernoulli polynomials (GBP), to solve a class of nonlinear 2-dim fractional optimal control problems. The problem is generated by nonlinear fractional dynamical systems with fractional derivative in the Caputo type and the Goursat–Darboux conditions. First, we use the GBP to approximate the state and control variables with unknown coefficients and parameters. Afterwards, we substitute the obtained values for the variables and parameters in the objective function, nonlinear fractional dynamical system and Goursat–Darboux conditions. The 2-dim Gauss–Legendre quadrature rule together with a fractional operational matrix construct a constrained problem, that is solved by the Lagrange multipliers method. The convergence of the GBP method is proved and its efficiency is demonstrated by several examples.

1 Introduction

Fractional calculus, a generalized form of the classical calculus, is an important tool the for modeling physical problems in various branches of science [1,2,3]. The modeling in these fields requires the use of ordinary and partial fractional differential equations. It is well know that the analytic and exact solutions of such equations are not available in most cases, motivating researchers to develop accurate approximation numerical methods [4, 5]. Fu et al. [6] implemented the Radial basis functions and Muntz polynomials basis for solving multi-term variable order time fractional partial differential equations. Chen et al. [7] developed a discrete numerical scheme using the finite difference method for solving a multi-term time-space variable order fractional advection–diffusion model. Hajipour et al. [8] proposed a discretization technique using a compact finite difference operator to solve a class of variable order fractional reaction-diffusion problems. Hassani et al. [9] introduced an optimization method based on transcendental Bernstein series for solving nonlinear variable order fractional functional boundary value problems. In recent years, several approximate methods have been applied to solve this type of differential equations [10,11,12,13,14,15,16,17,18].

Optimal control problems (OCP) has a wide range of applications [19,20,21]. In the OCP, the dynamical system and/or the performance index (cost functional) may involve variable order fractional operators. Recently, some researchers focused on numerical methods for this problem. Heydari [22] used the shifted Chebyshev polynomials and their operational matrices (OM) to solve 2-dim variable order fractional optimal control problems. Mohammadi and Hassani [23] applied generalized polynomials for solving the 2-dim variable order fractional optimal control problems. Li and Zhou [24] investigated the fractional spectral collocation discretization of OCP governed by a space-fractional diffusion equation. Salati et al. [25] presented three methods based on the Grünwald–Letnikov, trapezoidal and Simpson fractional integral formulas to solve fractional OCP. Zhang and Zhou [26] provided a spectral Galerkin approximation of OCP governed by a Riesz fractional differential equation with control integral constraint. Zaky and Machado [27] proposed the pseudo-spectral method and the Jacobi–Gauss–Lobatto integration algorithm for distributed fractional OCP. Some numerical approximation methods are investigated in [28,29,30,31,32,33,34,35,36,37,38,39,40,41] for solving the OCP.

It is well known that the Bernoulli polynomials (BP) play a vital role as basis functions in numerical techniques for solving various types of differential equations. Zeghdane [42] proposed a computational method based on the stochastic OM for the integration of BP in the case of the nonlinear Volterra–Fredholm–Hammerstein stochastic integral equations. Singh et al. [43] used OM of integration and differentiation of BP to find the approximate solution of second order two-dimensional telegraph equations with the Dirichlet boundary conditions. Ren and Tian [44] obtained an approximate solution of a boundary value problem for fourth order nonlinear integro-differential equation of Kirchhoff type based on the BP approximation. Loh and Phang [45] derived a BP based on OM of the right-sided Caputo’s fractional derivative to solve fractional integro-differential equation of Fredholm type. Golbabai and Panjeh Ali Beik [46] presented the OM of integration and the product based on the shifted BP for solving a class of linear matrix differential equations. Several other studies on BP can be found in [47,48,49,50,51].

In this paper, we consider nonlinear 2-dim fractional OCP including a fractional derivative in the Caputo type of the form:

$$\begin{aligned} \min \,{\mathcal {J}}[\mu , y]=\int _{0}^{1}\int _{0}^{1}{\mathcal {Q}}\left( x,t,\mu (x,t),y(x,t)\right) dxdt, \end{aligned}$$

(1.1)

subject to the nonlinear fractional dynamical system

$$\begin{aligned} {{}^{C}_{0}}{D_{t}^{\eta }}\mu (x,t)&={\mathcal {S}}\left( x,t,\mu (x,t),\mu _{x}(x,t),\mu _{xx}(x,t),y(x,t)\right) ,\quad \nonumber \\&\quad 0< \eta \le 1,\quad (x,t)\in [0,1]\times [0,1], \end{aligned}$$

(1.2)

and the Goursat–Darboux conditions [52, 53]

$$\begin{aligned} \mu (x,0)=e_{0}(x),\quad \quad \mu (0,t)=e_{1}(t). \end{aligned}$$

(1.3)

In the above relations, $\mu$ and y are the state and control variables, respectively, that are assumed to be continuous. It is supposed that the nonlinear operators ${\mathcal {Q}}$ and ${\mathcal {S}}$ are differentiable. Moreover, the given functions $e_{0}$ and $e_{1}$ are assumed to be continuous.

Here, ${}^{C}_{0}\!{D_{t}^{\eta }}$ denotes the fractional derivative operator of order $\eta \in (0,1]$ in the Caputo type and is defined as [1, 2]

$$\begin{aligned} ^{C}_{0}{D_{t}^{\eta }}\mu (x,t)= \displaystyle \left\{ \begin{array}{ll} \displaystyle \frac{1}{\Gamma \left( 1-\eta \right) }\int _{0}^{t}\left( t-s\right) ^{-\eta }\frac{\partial \mu (x,s)}{\partial s}ds,&{}\quad \eta \in (0, 1),\\ \frac{\partial \mu (x,t)}{\partial t}, &{} \quad \eta =1, \end{array} \right. \end{aligned}$$

(1.4)

where $\Gamma (\cdot )$ denotes the gamma function.

From the definitions of the fractional derivative of the Caputo type, it is straightforward to conclude that

$$\begin{aligned} ^C_0{D_{t}^{\eta }}t^{\zeta }= \displaystyle \left\{ \begin{array}{ll} \displaystyle \frac{\Gamma (\zeta +1)}{\Gamma (\zeta -\eta +1)}\,t^{\zeta -\eta }, &{}\quad n\le \zeta \in {\mathbb {N}}, \\ 0, &{}\quad \text {otherwise}, \end{array} \right. \end{aligned}$$

(1.5)

where $n-1<\eta \le n$.

The proposed method transforms the solution of the above fractional model into an algebraic system of nonlinear equations. To this end, the functions $\mu$ and y are approximated by the GBP with unknown coefficients and parameters. By inserting these approximations into the objective function and employing the Gauss–Legendre quadrature rule for computing the double integral, a nonlinear algebraic equation including the unknown coefficients and parameters is obtained. Besides, by substituting these approximations in the nonlinear fractional dynamical systems and the Goursat–Darboux conditions, and by adopting the OM of fractional derivative of the GBP, a set of nonlinear algebraic equations is extracted. The method of constrained extremum is employed for the problem generated by jointing the algebraic equations (extracted of the dynamical system) and the Goursat–Darboux conditions to the algebraic equation (obtained of the objective function) by using Lagrange multipliers. As an immediate result, the optimal solution of the problem is obtained by means an algebraic system of nonlinear equations.

The rest of the paper is organized as follows. Section 2 introduces the BP, the GBP and the approximation of a given function. Section 3 describes the OM of fractional derivative and function approximation. Section 4 applies the fractional derivative of the GBP and the Lagrange multipliers method to obtain an approximate solution of (1.1). Section 5 is devoted to the convergence analysis and error estimation. Section 6 provides the numerical results. Section 7 outlines the key conclusions and discusses future works.

2 Bernoulli Polynomials and Generalizes Bernoulli Polynomials

This section introduces the main concepts concerning the BP and GBP and derives the approximation of a given function by means of the BP and GBP.

2.1 Bernoulli Polynomials

The classical BP of degree w, ${\mathcal {B}}_{w}(\tau )$, is defined by [42,43,44]

$$\begin{aligned} {\mathcal {B}}_{w}(\tau )=\sum _{i=0}^{w}\left( {\begin{array}{c}w\\ i\end{array}}\right) {\mathcal {B}}_{w-i}(0) \tau ^{i},\quad w=1,2,\ldots , \end{aligned}$$

(2.1)

where ${\mathcal {B}}_{i}:={\mathcal {B}}_{i}(0)$, $i=0,1,\ldots ,w$, are rational numbers, called Bernoulli numbers, that are obtained by the expansion:

$$\begin{aligned} \frac{\tau }{e^{\tau }-1}=\sum _{i=0}^{\infty }{\mathcal {B}}_{i}(0)\frac{\tau ^i}{i!}. \end{aligned}$$

The first Bernoulli numbers are given by:

$$\begin{aligned} {\mathcal {B}}_{0}=1,\quad {\mathcal {B}}_{1}=\frac{-1}{2},\quad {\mathcal {B}}_{2}=\frac{1}{6},\quad {\mathcal {B}}_{4}=\frac{-1}{30}, \end{aligned}$$

with ${\mathcal {B}}_{2i+1}=0,~i=1, 2,3,\ldots$.

The first BP can be written as:

$$\begin{aligned} \begin{array}{ll} {\mathcal {B}}_{0}(\tau )=1,\\ {\mathcal {B}}_{1}(\tau )=\tau -\frac{1}{2},\\ {\mathcal {B}}_{2}(\tau )=\tau ^2-\tau +\frac{1}{6},\\ {\mathcal {B}}_{3}(\tau )=\tau ^3-\frac{3}{2}\tau ^2+\frac{1}{2}\tau ,\\ {\mathcal {B}}_{4}(\tau )=\tau ^4-2\tau ^3+\tau ^2-\frac{1}{30}. \end{array} \end{aligned}$$

Using the above polynomial basis functions, we can expand any function f(x, t) as follows

$$\begin{aligned} f(x,t)={\mathcal {B}}_{w_1,w_2}(x,t)\simeq \daleth _{w_{1}}(x)^{T}\,{\mathcal {O}}\,\beth _{w_{2}}(t), \end{aligned}$$

(2.2)

where

$$\begin{aligned} \daleth _{w_{1}}(x)= & {} {\mathcal {U}}\,\Phi _{w_{1}}(x),\quad \quad \beth _{w_{2}}(t)={\mathcal {V}}\,\Psi _{w_{2}}(t), \end{aligned}$$

(2.3)

$$\begin{aligned} {\mathcal {O}}= & {} \begin{pmatrix} o_{0,0}&{}\quad o_{0,1}&{}\quad \cdots &{}\quad o_{0,w_{2}}\\ o_{1,0}&{}\quad o_{1,1}&{}\quad \cdots &{}\quad o_{1,w_{2}} \\ \vdots &{}\quad \vdots &{}\quad \cdots &{}\quad \vdots \\ o_{w_{1},0} &{}\quad o_{w_{1},1}&{}\quad \cdots &{}\quad o_{w_{1},w_{2}} \\ \end{pmatrix},\quad {\mathcal {U}}= \begin{pmatrix} u_{0,0} &{}\quad u_{0,1}&{}\quad \cdots &{}\quad u_{0,w_{1}} \\ u_{1,0} &{}\quad u_{1,1}&{}\quad \cdots &{}\quad u_{1,w_{1}} \\ \vdots &{}\quad \vdots &{}\quad \cdots &{}\quad \vdots \\ u_{w_{1},0} &{}\quad u_{w_{1},1}&{}\quad \cdots &{}\quad u_{w_{1},w_{1}} \\ \end{pmatrix},\nonumber \\ \quad {\mathcal {V}}= & {} \begin{pmatrix} v_{0,0} &{}\quad v_{0,1}&{}\quad \cdots &{}\quad v_{0,w_{2}} \\ v_{1,0} &{}\quad v_{1,1}&{}\quad \cdots &{}\quad v_{1,w_{2}} \\ \vdots &{}\quad \vdots &{}\quad \cdots &{}\quad \vdots \\ v_{w_{2},0} &{}\quad v_{w_{2},1}&{}\quad \cdots &{}\quad v_{w_{2},w_{2}} \\ \end{pmatrix}, \nonumber \\ u_{ij}= & {} \displaystyle \left\{ \begin{array}{ll} \displaystyle \left( {\begin{array}{c}i\\ j\end{array}}\right) {\mathcal {B}}_{i-j}, &{}\quad i\ge j, \\ 0, &{}\quad i<j, \end{array} \right. \quad i,j=0,1,\ldots , w_{1}, \end{aligned}$$

(2.4)

$$\begin{aligned} v_{ij}= & {} \displaystyle \left\{ \begin{array}{ll} \displaystyle \left( {\begin{array}{c}i\\ j\end{array}}\right) {\mathcal {B}}_{i-j}, &{}\quad i\ge j, \\ 0, &{}\quad i<j, \end{array} \right. \quad i,j=0,1,\ldots , w_{2}, \end{aligned}$$

(2.5)

and

$$\begin{aligned} \Phi _{w_{1}}(x)\triangleq [\varphi _{0}(x)\,\,\,\varphi _{1}(x)\,\,\,\ldots \,\,\,\varphi _{w_{1}}(x)]^{T},\quad \Psi _{w_{2}}(t)\triangleq [\psi _{0}(t)\,\,\,\psi _{1}(t)\,\,\,\ldots \,\,\,\psi _{w_{2}}(t)]^{T}, \end{aligned}$$

(2.6)

so that

$$\begin{aligned} \varphi _{i}(x)= x^{i},\quad i=0,1,\ldots , w_{1},\quad \quad \psi _{j}(t)=t^{j},\quad j=0,1,\ldots , w_{2}. \end{aligned}$$

(2.7)

2.2 Generalized Bernoulli Polynomials

The GBP, ${\mathscr {B}}_{m}(t)$, are constructed by change of variable $t^{i}$ to $t^{i+\varrho _{i}}$, $(i+\varrho _{i} > 0)$, on the BP and are defined by

$$\begin{aligned} {\mathscr {B}}_{m}(t)=\sum _{i=0}^{m}\left( {\begin{array}{c}m\\ i\end{array}}\right) {\mathcal {B}}_{m-i}(0) t^{i+\varrho _{i}}, \end{aligned}$$

(2.8)

where the symbols $\varrho _{i}$ correspond to the control parameters. In particular, if $\varrho _{i}=0$ then the GBP coincide with the classical BP.

The expansions of a given functions $\mu (x,t)$ and y(x, t) in the terms of GBP can be represented in the following matrices form

$$\begin{aligned} \begin{array}{ll} \mu (x,t)={\mathscr {B}}_{m_1,m_2}(x,t)\simeq {\mathcal {F}}_{m_{1}}(x)^{T}\,{\mathcal {A}}\,{\mathcal {G}}_{m_{2}}(t),\\ y(x,t)={\mathscr {B}}_{n_1,n_2}(x,t)\simeq {\mathcal {H}}_{n_{1}}(x)^{T}\,{\mathcal {B}}\,{\mathcal {Z}}_{n_{2}}(t), \end{array} \end{aligned}$$

(2.9)

where

$$\begin{aligned} {\mathcal {A}}= & {} \begin{pmatrix} a_{0,0}&{}\quad a_{0,1}&{}\quad \cdots &{}\quad a_{0,m_{2}}\\ a_{1,0}&{}\quad a_{1,1}&{}\quad \cdots &{}\quad a_{1,m_{2}} \\ \vdots &{}\quad \vdots &{}\quad \cdots &{}\quad \vdots \\ a_{m_{1},0} &{}\quad a_{m_{1},1}&{}\quad \cdots &{}\quad a_{m_{1},m_{2}} \\ \end{pmatrix},\quad {\mathcal {B}}= \begin{pmatrix} b_{0,0}&{}\quad b_{0,1}&{}\quad \cdots &{}\quad b_{0,n_{2}}\\ b_{1,0}&{}\quad b_{1,1}&{}\quad \cdots &{}\quad b_{1,n_{2}} \\ \vdots &{}\quad \vdots &{}\quad \cdots &{}\quad \vdots \\ b_{n_{1},0} &{}\quad b_{n_{1},1}&{}\quad \cdots &{}\quad b_{n_{1},n_{2}} \\ \end{pmatrix}, \nonumber \\\end{aligned}$$

(2.10)

$$\begin{aligned} {\mathcal {F}}_{m_{1}}(x)= & {} {\mathcal {C}}\,\Theta _{m_{1}}(x),\quad {\mathcal {G}}_{m_{2}}(t)={\mathcal {D}}\,\Xi _{m_{2}}(t),\quad {\mathcal {H}}_{n_{1}}(x)={\mathcal {P}}\,\Upsilon _{n_{1}}(x),\quad \nonumber \\ {\mathcal {Z}}_{n_{2}}(t)= & {} {\mathcal {Q}}\,\Omega _{n_{2}}(t), \nonumber \\ \Theta _{m_{1}}(x)= & {} [\theta _{0}(x)\,\,\,\theta _{1}(x)\,\ldots \,\theta _{m_{1}}(x)]^{T},\quad \quad \nonumber \\ \Xi _{m_{2}}(t)= & {} [\xi _{0}(t)\,\,\,\xi _{1}(t)\,\ldots \,\xi _{m_{2}}(t)]^{T},\nonumber \\ \Upsilon _{n_{1}}(x)= & {} [\upsilon _{0}(x)\,\,\,\upsilon _{1}(x)\,\ldots \,\upsilon _{n_{1}}(x)]^{T},\nonumber \\ \Omega _{n_{2}}(t)= & {} [\omega _{0}(t)\,\,\,\omega _{1}(t)\,\ldots \,\omega _{n_{2}}(t)]^{T}, \end{aligned}$$

(2.11)

$$\begin{aligned} {\mathcal {C}}= & {} \begin{pmatrix} 1 &{}\quad 0&{}\quad 0&{}\quad \cdots &{}\quad 0 \\ 0 &{}\quad 1&{}\quad 0&{}\quad \cdots &{}\quad 0 \\ c_{2,0} &{}\quad c_{2,1}&{}\quad c_{2,2}&{}\quad \cdots &{}\quad c_{2,m_{1}} \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \cdots &{}\quad \vdots \\ c_{m_{1},0} &{}\quad c_{m_{1},1}&{}\quad c_{m_{1},2}&{}\quad \cdots &{}\quad c_{m_{1},m_{1}} \\ \end{pmatrix},\quad \nonumber \\ {\mathcal {D}}= & {} \begin{pmatrix} 1 &{}\quad 0&{}\quad 0&{}\quad \cdots &{}\quad 0 \\ d_{1,0} &{}\quad d_{1,1}&{}\quad d_{1,2}&{}\quad \cdots &{}\quad d_{1,m_{2}} \\ d_{2,0} &{}\quad d_{2,1}&{}\quad d_{2,2}&{}\quad \cdots &{}\quad d_{2,m_{2}} \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \cdots &{}\quad \vdots \\ d_{m_{2},0} &{}\quad d_{m_{2},1}&{}\quad d_{m_{2},2}&{}\quad \cdots &{}\quad d_{m_{2},m_{2}} \\ \end{pmatrix}, \nonumber \\ {\mathcal {P}}= & {} \begin{pmatrix} 1 &{}\quad 0&{}\quad 0&{}\quad \cdots &{}\quad 0 \\ p_{1,0} &{}\quad p_{1,1}&{}\quad p_{1,2}&{}\quad \cdots &{}\quad p_{1,n_{1}} \\ p_{2,0} &{}\quad p_{2,1}&{}\quad p_{2,2}&{}\quad \cdots &{}\quad p_{2,n_{1}} \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \cdots &{}\quad \vdots \\ p_{n_{1},0} &{}\quad p_{n_{1},1}&{}\quad p_{n_{1},2}&{}\quad \cdots &{}\quad p_{n_{1},n_{1}} \\ \end{pmatrix},\quad \nonumber \\ {\mathcal {Q}}= & {} \begin{pmatrix} 1 &{}\quad 0&{}\quad 0&{}\quad \cdots &{}\quad 0 \\ q_{1,0} &{}\quad q_{1,1}&{}\quad q_{1,2}&{}\quad \cdots &{}\quad q_{1,n_{2}} \\ q_{2,0} &{}\quad q_{2,1}&{}\quad q_{2,2}&{}\quad \cdots &{}\quad q_{2,n_{2}} \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \cdots &{}\quad \vdots \\ q_{n_{2},0} &{}\quad q_{n_{2},1}&{}\quad q_{n_{2},2}&{}\quad \cdots &{}\quad q_{n_{2},n_{2}} \\ \end{pmatrix}, \nonumber \\ c_{ij}= & {} \displaystyle \left\{ \begin{array}{ll} \displaystyle \left( {\begin{array}{c}i\\ j\end{array}}\right) {\mathcal {B}}_{i-j}, &{}\quad i\ge j, \\ 0, &{}\quad i<j, \end{array} \right. \quad i=2,3,\ldots , m_{1},\quad j=0,1,\ldots , m_{1}, \end{aligned}$$

(2.12)

$$\begin{aligned} d_{ij}= & {} \displaystyle \left\{ \begin{array}{ll} \displaystyle \left( {\begin{array}{c}i\\ j\end{array}}\right) {\mathcal {B}}_{i-j}, &{}\quad i\ge j, \\ 0, &{}\quad i<j, \end{array} \right. \quad i=1,2,\ldots , m_{2},\quad j=0,1,\ldots , m_{2}, \end{aligned}$$

(2.13)

$$\begin{aligned} p_{ij}= & {} \displaystyle \left\{ \begin{array}{ll} \displaystyle \left( {\begin{array}{c}i\\ j\end{array}}\right) {\mathcal {B}}_{i-j}, &{}\quad i\ge j, \\ 0, &{}\quad i<j, \end{array} \right. \quad i=1,2,\ldots , n_{1},\quad j=0,1,\ldots , n_{1}, \end{aligned}$$

(2.14)

$$\begin{aligned} q_{ij}= & {} \displaystyle \left\{ \begin{array}{ll} \displaystyle \left( {\begin{array}{c}i\\ j\end{array}}\right) {\mathcal {B}}_{i-j}, &{}\quad i\ge j, \\ 0, &{}\quad i<j, \end{array} \right. \quad i=1,2,\ldots , n_{2},\quad j=0,1,\ldots , n_{2}, \end{aligned}$$

(2.15)

$$\begin{aligned} \theta _{i}(x)= & {} \left\{ \begin{array}{lll} x^{i},&{}&{}i=0,1, \\ x^{i+k_{i}},&{}&{}i=2,3,\ldots ,m_{1}, \end{array} \right. \quad \xi _{j}(t)=\left\{ \begin{array}{lll} t^{j},&{}&{}j=0,\\ t^{j+l_{j}},&{}&{}j=1,2,\ldots ,m_{2}, \end{array} \right. \end{aligned}$$

(2.16)

$$\begin{aligned} \upsilon _{i}(x)= & {} \left\{ \begin{array}{lll} x^{i},&{}&{}i=0,\\ x^{i+r_{i}},&{}&{}i=1,2,\ldots , n_{1}, \end{array} \right. \quad \omega _{j}(t)=\left\{ \begin{array}{lll} t^{j},&{}&{}j=0,\\ t^{j+s_{j}},&{}&{}j=1,2,\ldots , n_{2}, \end{array} \right. \end{aligned}$$

(2.17)

where $k_{i}$, $l_{j}$, $r_{i}$ and $s_{j}$ are the control parameters.

3 The Operational Matrices and Function Approximation

In this section, we derive the OM for the GBP.

The fractional derivative of order $\eta$ in the Caputo type can be represented by

$$\begin{aligned} {}^{C}_{0}\!{D_{t}^{\eta }}\Xi _{m_{2}}(t)={\mathscr {D}}^{(\eta )}_{t}\Xi _{m_{2}}(t), \end{aligned}$$

(3.1)

where ${\mathscr {D}}^{(\eta )}_{t}$ denotes the $(m_{2}+1)\times (m_{2}+1)$ OM of fractional derivative defined by:

$$\begin{aligned} {\mathscr {D}}^{(\eta )}_{t}=t^{-\eta } \begin{pmatrix} 0 &{}\quad 0&{}\quad 0&{}\quad \cdots &{}\quad 0\\ 0 &{}\quad \frac{\Gamma \left( 2+l_{2}\right) }{\Gamma \left( 2-\eta +l_{2}\right) }&{}\quad 0&{}\quad \cdots &{}\quad 0 \\ 0 &{}\quad 0&{}\quad \frac{\Gamma \left( 3+l_{3}\right) }{\Gamma \left( 3-\eta +l_{3}\right) }&{}\quad \cdots &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 0 &{}\quad 0&{}\quad 0&{}\quad \cdots &{}\quad \frac{\Gamma \left( m_{2}+1+l_{m_{2}}\right) }{\Gamma \left( m_{2}+1-\eta +l_{m_{2}}\right) } \\ \end{pmatrix}. \end{aligned}$$

(3.2)

The first and second order derivatives of $\Theta _{m_{1}}(x)$ are given by:

$$\begin{aligned} \frac{d\Theta _{m_{1}}(x)}{dx}={\mathscr {D}}^{(1)}_{x}\,\Theta _{m_{1}}(x),\quad \frac{d^{2}\Theta _{m_{1}}(x)}{dx^{2}}={\mathscr {D}}^{(2)}_{x}\,\Theta _{m_{1}}(x), \end{aligned}$$

(3.3)

where ${\mathscr {D}}^{(1)}_{x}$ and ${\mathscr {D}}^{(2)}_{x}$ denote the $(m_{1}+1)\times (m_{1}+1)$ OM of derivatives, respectively, so that we can write:

$$\begin{aligned}&{\mathscr {D}}^{(1)}_{x}= \begin{pmatrix} 0 &{}\quad 0&{}\quad 0&{}\quad \cdots &{}\quad 0\\ 0 &{}\quad \frac{1}{x}&{}\quad 0&{}\quad \cdots &{}\quad 0 \\ 0 &{}\quad 0&{}\quad \frac{2+k_{2}}{x}&{}\quad \cdots &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 0 &{}\quad 0&{}\quad 0&{}\quad \cdots &{}\quad \frac{m_{1}+k_{m_{1}}}{x} \\ \end{pmatrix},\quad \nonumber \\&{\mathscr {D}}^{(2)}_{x}= \begin{pmatrix} 0&{}\quad 0&{}\quad 0&{}\quad \cdots &{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad \cdots &{}\quad 0 \\ 0&{}\quad 0&{}\quad \frac{(2+k_{2})(1+k_{2})}{x^{2}}&{}\quad \cdots &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ 0&{}\quad 0&{}\quad 0&{}\quad \cdots &{}\quad \frac{(m_{1}+k_{m_{1}})(m_{1}-1+k_{m_{1}})}{x^{2}} \\ \end{pmatrix}. \end{aligned}$$

(3.4)

3.1 Function Approximation

Let ${\mathbb {X}}=L^{2}[0,1]\times [0,1]$ and ${\mathbb {Y}}=\left\langle x^{k_{i}}t^{l_{j}};\,\ 0\le i\le m_{1},\,\ 0\le j\le m_2\right\rangle$. Then, ${\mathbb {Y}}$ is a finite dimensional vector subspace of ${\mathbb {X}}\,\left( dim {\mathbb {Y}} \le (m_1+1)(m_2+1)<\infty \right)$ and each ${\tilde{\mu }}={\tilde{\mu }}(x,t)\in X$ has a unique best approximation $\mu _0=\mu _0(x,t)\in {\mathbb {Y}}$, given by:

$$\begin{aligned} \forall ~{\hat{\mu }}\in {\mathbb {Y}},~~~\parallel {\tilde{\mu }}-\mu _{0}\parallel _2\le \parallel {\tilde{\mu }}-{\hat{\mu }}\parallel _2. \end{aligned}$$

For more details, see Theorem 6.1-1 of [54]. Since $\mu _0\in {\mathbb {Y}}$ and ${\mathbb {Y}}$ is a finite dimensional vector subspace of ${\mathbb {X}}$, by an elementary argument in linear algebra, we have unique coefficients $a_{ij} \in {\mathbb {R}}$ such that the dependent variable $\mu _0(x,t)$ may be expanded in terms of the GP as

$$\begin{aligned} \mu _0(x,t)\simeq {\mathcal {F}}_{m_{1}}(x)^{T}\,{\mathcal {A}}\,{\mathcal {G}}_{m_{2}}(t), \end{aligned}$$

where ${\mathcal {F}}_{m_{1}}(x)$ and ${\mathcal {G}}_{m_{2}}(t)$ are defined in Eq. (2.11).

4 Explanation of the Proposed Method

This section describes the implementation details of the GBP and OM of derivatives for the nonlinear 2-dim fractional OCP in Eqs. (1.1)–(1.3). Firstly, we approximate the state and control variables $\mu (x,t)$ and y(x, t) by the GBP as

$$\begin{aligned} \begin{array}{ll} \mu (x,t)\simeq {\mathcal {F}}_{m_{1}}(x)^{T}\,{\mathcal {A}}\,{\mathcal {G}}_{m_{2}}(t)=\left( {\mathcal {C}}\,\Theta _{m_{1}}(x)\right) ^{T}\,{\mathcal {A}}\,\left( {\mathcal {D}}\,\Xi _{m_{2}}(t)\right) ,\\ y(x,t)\simeq {\mathcal {H}}_{n_{1}}(x)^{T}\,{\mathcal {B}}\,{\mathcal {Z}}_{n_{2}}(t)=\left( {\mathcal {P}}\,\Upsilon _{n_{1}}(x)\right) ^{T}\,{\mathcal {B}}\,\left( {\mathcal {Q}}\,\Omega _{n_{2}}(t)\right) , \end{array} \end{aligned}$$

(4.1)

where ${\mathcal {A}}_{(m_{1}+1)\times (m_{2}+1)}$ and ${\mathcal {B}}_{(n_{1}+1)\times (n_{2}+1)}$ unknown matrices to be found, and the vectors ${\mathcal {F}}_{m_{1}}(x)$, ${\mathcal {G}}_{m_{2}}(t)$, ${\mathcal {H}}_{n_{1}}(x)$ and ${\mathcal {Z}}_{n_{2}}(t)$ are formulated in (2.11). Then, we apply the OM of derivatives for $\mu (x,t)$ in the following form:

$$\begin{aligned} \begin{array}{lllllll} {}^{C}_{0}\!{D_{t}^{\eta }}\mu (x,t)\simeq \left( {\mathcal {C}}\,\Theta _{m_{1}}(x)\right) ^{T}\,{\mathcal {A}}\,\left( {\mathcal {D}}\,{\mathscr {D}}^{(\eta )}_{t}\,\Xi _{m_{2}}(t)\right) ,\\ \mu _{x}(x,t)\simeq \left( {\mathcal {C}}\,{\mathscr {D}}^{(1)}_{x}\,\Theta _{m_{1}}(x)\right) ^{T}\,{\mathcal {A}}\,\left( {\mathcal {D}}\,\Xi _{m_{2}}(t)\right) ,\\ \mu _{xx}(x,t)\simeq \left( {\mathcal {C}}\,{\mathscr {D}}^{(2)}_{x}\,\Theta _{m_{1}}(x)\right) ^{T}\,{\mathcal {A}}\,\left( {\mathcal {D}}\,\Xi _{m_{2}}(t)\right) . \end{array} \end{aligned}$$

(4.2)

The functions $e_{0}(x)$ and $e_{1}(t)$ are expressed by utilizing the GBP as follows

$$\begin{aligned} e_{0}(x)\simeq \left( {\mathcal {C}}\,\Theta _{m_{1}}(x)\right) ^{T}\,{\mathscr {E}}_{0},\quad e_{1}(t)\simeq {\mathscr {E}}_{1}\,\left( {\mathcal {D}}\,\Xi _{m_{2}}(t)\right) , \end{aligned}$$

(4.3)

where ${\mathscr {E}}_{0}=[e_0^0\,\,e_1^0\,\,\cdots \,\,e_{m_{1}}^0]^T$ and ${\mathscr {E}}_{1}=[e_0^1\,\,e_1^1\,\,\cdots \,\,e_{m_{2}}^1]$ are unknown vectors to be found.

Regarding to relations (4.1), (4.3) and (1.3), we have

$$\begin{aligned}&{\hat{Z}}_{1}\triangleq \left( {\mathcal {C}}\,\Theta _{m_{1}}(x)\right) ^{T}\,\left( {\mathcal {A}}\,\left( {\mathcal {D}}\,\Xi _{m_{2}}(0)\right) -{\mathscr {E}}_{0}\right) \simeq 0,\nonumber \\&{\hat{Z}}_{2}\triangleq \left( \left( {\mathcal {C}}\,\Theta _{m_{1}}(0)\right) ^{T}\,{\mathcal {A}}-{\mathscr {E}}_{1}\right) \,\left( {\mathcal {D}}\,\Xi _{m_{2}}(t)\right) . \end{aligned}$$

(4.4)

Substituting Eq. (4.1) into Eq. (1.1), the objective function can be expressed as follows

$$\begin{aligned}&\min \,{\mathcal {J}}[{\mathcal {A}},{\mathcal {B}},{\mathcal {K}},{\mathcal {L}},{\mathcal {R}},{\mathcal {S}}]\nonumber \\&\quad =\int _{0}^{1}\int _{0}^{1}{\mathcal {Q}}\left( x,t,\left( {\mathcal {C}}\,\Theta _{m_{1}}(x)\right) ^{T}\,{\mathcal {A}}\,\left( {\mathcal {D}}\,\Xi _{m_{2}}(t)\right) ,\left( {\mathcal {P}}\,\Upsilon _{n_{1}}(x)\right) ^{T}\,{\mathcal {B}}\,\left( {\mathcal {Q}}\,\Omega _{n_{2}}(t)\right) \right) dxdt,\nonumber \\ \end{aligned}$$

(4.5)

where ${\mathcal {K}}$, ${\mathcal {L}}$, ${\mathcal {R}}$ and ${\mathcal {S}}$ are unknown control vectors that can be represented as

$$\begin{aligned} \begin{array}{lllllll} {\mathcal {K}}=\left[ k_{2}\,\ k_{3}\,\,\ldots \,\ k_{m_{1}}\right] ,\quad &{}{\mathcal {L}}=\left[ l_{1}\,\ l_{2}\,\,\ldots \,\ l_{m_{2}}\right] ,\\ {\mathcal {R}}=\left[ r_{1}\,\ r_{2}\,\,\ldots \,\ r_{n_{1}}\right] ,\quad &{}{\mathcal {S}}=\left[ s_{1}\,\ s_{2}\,\,\ldots \,\ s_{n_{2}}\right] . \end{array} \end{aligned}$$

(4.6)

The double integral in Eq. (4.5) can be approximately calculated by using an M-point Gauss–Legendre quadrature rule [55] with the nodal points $\rho _{i}$ shifted on the unit interval and corresponding weights $\varpi _{i}$. Therefore, we have

$$\begin{aligned}&{\mathcal {J}}[{\mathcal {A}},{\mathcal {B}},{\mathcal {K}},{\mathcal {L}},{\mathcal {R}},{\mathcal {S}}]\nonumber \\&\quad \simeq \frac{1}{4}\sum _{i=1}^{M}\sum _{j=1}^{M}\varpi _{i}\varpi _{j}{\mathcal {Q}}\left( \rho _{i},\rho _{j},\left( {\mathcal {C}}\,\Theta _{m_{1}}(\rho _{i})\right) ^{T}\,{\mathcal {A}}\,\left( {\mathcal {D}}\,\Xi _{m_{2}}(\rho _{j})\right) ,\right. \nonumber \\&\quad \left. \left( {\mathcal {P}}\,\Upsilon _{n_{1}}(\rho _{i})\right) ^{T}\,{\mathcal {B}}\,\left( {\mathcal {Q}}\,\Omega _{n_{2}}(\rho _{j})\right) \right) . \end{aligned}$$

(4.7)

Furthermore, substituting Eqs. (4.1) and (4.2) into Eq. (1.2) yields

$$\begin{aligned}&\left( {\mathcal {C}}\,\Theta _{m_{1}}(x)\right) ^{T}\,{\mathcal {A}}\,\left( {\mathcal {D}}\,{\mathscr {D}}^{(\eta )}_{t}\,\Xi _{m_{2}}(t)\right) \nonumber \\&\quad -{\mathcal {S}}\Bigg (x,t,\left( {\mathcal {C}}\,\Theta _{m_{1}}(x)\right) ^{T}\,{\mathcal {A}}\,\left( {\mathcal {D}}\,\Xi _{m_{2}}(t)\right) ,\left( {\mathcal {C}}\,{\mathscr {D}}^{(1)}_{x}\,\Theta _{m_{1}}(x)\right) ^{T}\,{\mathcal {A}}\,\left( {\mathcal {D}}\,\Xi _{m_{2}}(t)\right) ,\nonumber \\&\left( {\mathcal {C}}\,{\mathscr {D}}^{(2)}_{x}\,\Theta _{m_{1}}(x)\right) ^{T}\,{\mathcal {A}}\,\left( {\mathcal {D}}\,\Xi _{m_{2}}(t)\right) ,\left( {\mathcal {P}}\,\Upsilon _{n_{1}}(x)\right) ^{T}\,{\mathcal {B}}\,\left( {\mathcal {Q}}\,\Omega _{n_{2}}(t)\right) \Bigg )\triangleq {\mathscr {R}}(x,t,{\mathcal {A}},{\mathcal {B}},{\mathcal {K}},{\mathcal {L}},{\mathcal {R}},{\mathcal {S}})\nonumber \\&\quad \simeq 0. \end{aligned}$$

(4.8)

Taking the collocation points $(x_{i},t_{j})=(\frac{i}{{\hat{m}}},\frac{j}{{\hat{m}}})$ for $i=1,2,\ldots , {\hat{m}},\,\,\,j=1,2,\ldots , {\hat{m}}$, where $m=\min (m_{1},m_{2})$, $n=\min (n_{1},n_{2})$ and ${\hat{m}}=\min (m,n),$ into Eq. (4.8), we obtain the algebraic equations

$$\begin{aligned} Z_{ij}\triangleq {\mathscr {R}}\left( x_{i},t_{j},{\mathcal {A}},{\mathcal {B}},{\mathcal {K}},{\mathcal {L}},{\mathcal {R}},{\mathcal {S}}\right) =0,\quad i=1,2,\ldots , {\hat{m}},\quad j=1,2,\ldots , {\hat{m}}. \end{aligned}$$

(4.9)

From Eq. (4.4) we obtain the following algebraic equations

$$\begin{aligned}&{\hat{Z}}_{1}(x_i)\triangleq \left( {\mathcal {C}}\,\Theta _{m_{1}}(x_i)\right) ^{T}\,\left( {\mathcal {A}}\,\left( {\mathcal {D}}\,\Xi _{m_{2}}(0)\right) -{\mathscr {E}}_{0}\right) ,i=2,3,\ldots ,{\hat{m}}+1,\nonumber \\&{\hat{Z}}_{2}(t_j)\triangleq \left( \left( {\mathcal {C}}\,\Theta _{m_{1}}(0)\right) ^{T}\,{\mathcal {A}}-{\mathscr {E}}_{1}\right) \,\left( {\mathcal {D}}\,\Xi _{m_{2}}(t_j)\right) ,j=1,2,\ldots ,{\hat{m}}+1. \end{aligned}$$

(4.10)

Let

$$\begin{aligned} {\mathcal {J}}^{*}[{\mathcal {A}},{\mathcal {B}},{\mathcal {K}},{\mathcal {L}},{\mathcal {R}},{\mathcal {S}},\Lambda ]={\mathcal {J}}[{\mathcal {A}},{\mathcal {B}},{\mathcal {K}},{\mathcal {L}},{\mathcal {R}},{\mathcal {S}}]+Z\,\Lambda , \end{aligned}$$

(4.11)

where

$$\begin{aligned} Z=\Bigg [Z_{1,1}\,Z_{1,2}\,\ldots Z_{1,{\hat{m}}}|Z_{2,1}\,Z_{2,2}\ldots Z_{2,{\hat{m}}}|\ldots |Z_{{\hat{m}},1}\,Z_{{\hat{m}},2}\ldots Z_{{\hat{m}},{\hat{m}}}|{\hat{Z}}_{1}|{\hat{Z}}_{2}\Bigg ], \end{aligned}$$

(4.12)

and

$$\begin{aligned} \Lambda =\Bigg [\lambda _{1}\,\lambda _{2}\,\ldots \,\lambda _{{\hat{m}}^{2}+2{\hat{m}}+1}\Bigg ]^{T}. \end{aligned}$$

(4.13)

We remind that $\Lambda$ is the Lagrange multipliers vector. The necessary and sufficient conditions of the optimality are obtained as follows [56, 57]

$$\begin{aligned} \begin{array}{lllllll} \displaystyle \frac{\partial {\mathcal {J}}^{*}}{\partial {\mathcal {A}}}=0,&\displaystyle \frac{\partial {\mathcal {J}}^{*}}{\partial {\mathcal {B}}}=0,&\displaystyle \frac{\partial {\mathcal {J}}^{*}}{\partial {\mathcal {K}}}=0,&\displaystyle \frac{\partial {\mathcal {J}}^{*}}{\partial {\mathcal {L}}}=0,&\displaystyle \frac{\partial {\mathcal {J}}^{*}}{\partial {\mathcal {R}}}=0,&\displaystyle \frac{\partial {\mathcal {J}}^{*}}{\partial {\mathcal {S}}}=0,&\displaystyle \frac{\partial {\mathcal {J}}^{*}}{\partial \Lambda }=0. \end{array} \end{aligned}$$

(4.14)

By solving the above system and computing ${\mathcal {A}}$, ${\mathcal {B}}$, ${\mathcal {K}}$, ${\mathcal {L}}$, ${\mathcal {R}}$ and ${\mathcal {S}}$, the approximate solutions $\mu (x,t)$ and y(x, t) are obtained respectively from Eq. (4.1).

5 Convergence Analysis and Error Estimate of the Proposed Method

In this section, we investigate the convergence of the proposed method. We first prove the following convergence theorem for approximating an arbitrarily continuous function.

Theorem 1

Let $f:[0,1]\times [0,1]\rightarrow {\mathbb {R}}$ be a continuous function. Then, for every $x,t\in [0,1]$ and $\epsilon >0$, there exists a GBP, $\mu (x,t)$, such that

$$\begin{aligned} |f(x,t)-\mu (x,t)|<\epsilon . \end{aligned}$$

Proof

Let $\epsilon >0$ be arbitrarily chosen. In view of Weierstrass theorem [54], there exists a polynomial $P_{m_1,m_2}(x,t)=\sum ^{m_1}_{i=0}\sum ^{m_1}_{j=0}\sum ^{m_2}_{q=0}\sum ^{m_2}_{p=0}b_{j,i}e_{q,p}x^jt^p$, with $x,t\in [0,1]$ and $b_{j,i},e_{q,p}\in {\mathbb {R}}$ such that

$$\begin{aligned} \Vert f-P_{m_1,m_2}\Vert =\sup _{x,t\in [0,1]}|f(x,t)-P_{m_1,m_2}(x,t)|<\frac{\epsilon }{2}. \end{aligned}$$

We construct a GBP, $\mu (x,t)$, as follows:

If $x=0$ or $t=0$, then by setting $k_0=0$, $l_0=0$ and $\mu (x,t)=\sum ^{m_1}_{i=0}\sum ^{m_1}_{j=0}\sum ^{m_2}_{q=0}\sum ^{m_2}_{p=0}b_{j,i}e_{q,p}$, we get the desired conclusion. Assume now that $x\ne 0$ and $t\ne 0$. Letting

$$\begin{aligned} c_{j,i}=\left\{ \begin{array}{ll} \left( \begin{array}{c} j \\ i \\ \end{array} \right) \beta _{j-i},\quad j\ge i,\quad j,i=0,1,\ldots ,m_1,\\ 0,\quad j<i, \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} d_{q,p}=\left\{ \begin{array}{ll} \left( \begin{array}{c} q \\ p \\ \end{array} \right) \beta _{q-p},\quad q\ge p,\quad q,p=0,1,\ldots ,m_2,\\ 0,\quad q<p, \end{array}\right. \end{aligned}$$

for all $i=0,1,\ldots ,m_1$, $j=0,1,2,\ldots ,m_1$, $q=0,1,\ldots ,m_2$ and $p=0,1,\ldots ,m_2$, we can find two sequences $\{k_{i,j,q,n}\}_{n\in {\mathbb {N}}}$ and $\{s_{q,p,n}\}_{n\in {\mathbb {N}}}$ of real numbers such that $k_{i,j,q,n}\rightarrow \frac{-\ln (|c_{j,i}a_{i,q}|)}{\ln (x)}$ and $l_{q,p,n}\rightarrow \frac{-\ln (|d_{q,p}|)}{\ln (t)}$, where $\beta _{j-i}$ are Bernoulli numbers. This implies that $x^{k_{i,j,q,n}}\rightarrow \frac{1}{|c_{j,i}a_{i,q}|}$ and $t^{l_{q,p,n}}\rightarrow \frac{1}{|d_{l,p}|}$. Hence, for every $\epsilon >0$, there exist $N_{0,j},N_{1,j},\ldots ,N_{m_1,j}$ and $N_{0,p},N_{1,p},\ldots ,N_{m_2,p}$ in ${\mathbb {N}}$, such that, for any $n\ge N:=\max \{N_{i,j},N_{q,p}:i,j=0,1,\ldots , m_1,~q,p=0,1,\ldots ,m_2\}$, for all $i,j=0,1,\ldots ,m_1$ and $q,p=0,1,\ldots ,m_2$, we deduce that

$$\begin{aligned}&|1-c_{j,i}a_{i,q}d_{q,p}x^{k_{i,j,q,n}}t^{l_{q,p,n}}|\\&\quad <\frac{\epsilon }{2\max \{|b_{j,i}e_{q,p}|:i,j=0,1,2,\ldots ,m_1 ,~q,p=0,1,2,\ldots ,m_2\}(m_1+1)^{2}(m_2+1)^{2}}. \end{aligned}$$

By setting

$$\begin{aligned} \mu (x,t)=\sum ^{m_1}_{i=0}\sum ^{m_1}_{j=0}\sum ^{m_2}_{q=0}\sum ^{m_2}_{p=0} b_{i,j}c_{j,i}a_{i,q}e_{q,p}d_{q,p}x^{j+k_{i,j,q,N}}t^{p+l_{q,p,N}}, \end{aligned}$$

we conclude that

$$\begin{aligned} |P_{m_1,m_2}(x,t)-\mu (x,t)|<\frac{\epsilon }{2}. \end{aligned}$$

This implies that

$$\begin{aligned} |f(x,t)-\mu (x,t)|\le |f(x,t)-P_{m_1,m_2}(x,t)|+|P_{m_1,m_2}(x,t)-\mu (x,t)|<\frac{\epsilon }{2}+\frac{\epsilon }{2}=\epsilon , \end{aligned}$$

completing the proof. $\square$

We show in the follow-up (Theorem 2) that with an increase in the number of the GBP basis $m_1$ and $m_2$ in (2.9), the approximate optimum value in (4.5) tends to the exact value. We apply the fractional derivative OM, to compute the fractional derivatives. Therefore, the error of the OM is defined by the following expression:

$$\begin{aligned} E^{\eta }_{m_1,m_2}(t):={}^{C}_{0}\!{D^{\eta }_{t}}(\Xi _{m_2}(t)) -{{{\mathscr {D}}}^{(\eta )}_{t}}({\mathcal {D}}\Xi _{m_2}(t))= \left( \begin{array}{c} e^{\eta }_{m_1,0}(t) \\ e^{\eta }_{m_1,1}(t) \\ . \\ . \\ . \\ e^{\eta }_{m_1,m_2}(t) \\ \end{array} \right) . \end{aligned}$$

(5.1)

Let us discuss the convergence of the method for the variable t and the vector ${\mathcal {D}}\Xi _{m_2}$. A similar argument can be applied for the case of ${\mathcal {Q}}{\Omega }_{n_2}$ and, therefore, the details are omitted. If $0\le j\le m_2$, then we obtain

$$\begin{aligned} \frac{\partial }{\partial t} {}^{C}_{0}\!{D^{\eta }_{t}}(\xi _j(t))={}^{C}_{0}\!{D^{\eta +1}_{t}}(\xi _j(t)). \end{aligned}$$

This shows that $^C_0D^{\eta }_{t}(\xi _j)$ is continuously differentiable. Employing (3.1), (3.3) and Theorem 1, for $j=0,1,\dots , m_2$, we conclude that

$$\begin{aligned} \lim _{m_1\rightarrow \infty }\left\| e^{{\eta }}_{m_1,j}(t)\right\| =\lim _{m_1\rightarrow \infty }\left\| ^C_0D^{\eta }_{t}(\xi _j(t)) -{{{\mathscr {D}}}^{(\eta )}_{t}}(d_{m_1,j}\xi _j(t))\right\| =0. \end{aligned}$$

Let ${GBP}_{m_2}([0,1])$ be the space of all GBP functions of degree less than or equal to $m_1m_2$ on the interval [0, 1]. The following lemma shows that for $m_1,m_2\in \mathbb {N}$, increasing the number of approximations $m_1$, the two sides of (3.1), that is, the functional and the OM of fractional Caputo derivatives, representing two operators on the space ${GBP}_{m_2}([0,1])$, get close to each other with respect to the operator norm.

Lemma 1

Let $T_{m_2}$ and $S_{m_1,m_2}$ be two linear operators defined by

$$\begin{aligned}&T_{m_2}:({GBP}_{m_2}([0,1])),\Vert \cdot \Vert _{\infty })\rightarrow (C([0,1]),\Vert \cdot \Vert _{\infty }),\quad T_{m_2}\left( \sum _{j=0}^{m_2}c_j\xi _j(t)\right) \\&\quad =\sum _{j=0}^{m_2}c_j\,{^C_0D^{\eta }_{t}}(\xi _j(t)) \end{aligned}$$

and

$$\begin{aligned}&S_{m_1,m_2}:({GBP}_{m_2}([0,1])),\Vert \cdot \Vert _{\infty })\rightarrow (C([0,1]),\Vert \cdot \Vert _{\infty }),\quad S_{m_2,m_2}\left( \sum _{j=0}^{m_2}c_j\xi _j(t)\right) \\&\quad =\sum _{i=0}^{m_1} \sum _{j=0}^{m_2}c_j{{{\mathscr {D}}}^{(\eta )}_{t}}({d_{i,j}}\xi _j(t)). \end{aligned}$$

Then, $T_{m_2}$ and $S_{m_1,m_2}$ are bounded and

$$\begin{aligned} \lim _{m_1\rightarrow \infty }\Vert T_{m_2}-S_{m_1,m_2}\Vert =0, \end{aligned}$$

where $c_j\in \mathbb {R}$, $j=0,1,\ldots ,m_2$.

Proof

By the definition of $T_{m_2}$, we deduce that

$$\begin{aligned} \Vert T_{m_2}\Vert _{\infty }=\sup \left\{ \left\| \sum _{j=0}^{m_2}c_j{^C_0D^{\eta }_{t}}(\xi _j)\right\| _{\infty }: \left\| \sum _{j=0}^{m_2}c_j\xi _j\right\| _{\infty }\le 1\right\} . \end{aligned}$$

If $\Vert \sum _{j=0}^{m_2}c_j\xi _j \Vert _{\infty }\le 1$, then we obtain

$$\begin{aligned} {^C_0D^{\eta }_{t}}\left( \sum _{j=0}^{m_2}c_j\xi _j(t)\right)= & {} \frac{1}{\Gamma (2-\eta )}\int _{0}^t (t-s)^{1-\eta }\frac{\partial }{\partial s}\left( \sum _{j=0}^{m_2}c_j\xi _j(s)\right) ds. \end{aligned}$$

(5.2)

Since $m_1$ and $m_2$ are fixed numbers and the Caputo derivative is a linear operator defined on the finite dimensional normed space ${GBP}_{m_2}([0,1])$, then it is a bounded linear operator (see more details [54]) and, therefore, there exists a constant $L_{{m_2,\eta }}$ such that

$$\begin{aligned} \left\| \frac{\partial }{{\partial s}}\sum _{j=0}^{m_2}c_j\xi _j(s)\right\| _{\infty }\le L_{{m_2,\eta }}\left\| \sum _{j=0}^{m_2}c_j\xi _j\right\| _{\infty }. \end{aligned}$$

(5.3)

This implies that

$$\begin{aligned} \left\| {^C_0D^{\eta }_{t}}\left( \sum _{j=0}^{m_2}c_j\xi _j\right) \right\| _{\infty }= & {} \max _{t\in [0,1]}\left| \frac{1}{\Gamma (2-\eta )}\int _{0}^t (t-s)^{1-\eta }\frac{\partial }{\partial s}\left( \sum _{j=0}^{m_2}c_j\xi _j(s)\right) ds\right| \\ {}\le & {} \max _{t\in [0,1]}\left| \int _{0}^t (t-s)^{1-\eta }\left\| \frac{\partial }{\partial s}\left( \sum _{j=0}^{m_2}c_j\xi _j\right) \right\| _{\infty }ds\right| \\ {}\le & {} L_{{m_2,\eta }}. \end{aligned}$$

This proves that $T_{m_2}$ is a bounded linear operator. On the other hand, in view of (1.1), we conclude that

$$\begin{aligned} (T_{m_2}-S_{m_1,m_2})\left( \sum _{j=0}^{m_2}c_j\xi _j(t)\right) =\sum _{j=0}^{m_2}c_je^{\eta }_{m_1,j}. \end{aligned}$$

This entails to

$$\begin{aligned} \left\| T_{m_2}-S_{m_1,m_2}\right\| _{\infty }=\sup \left\{ \left\| \sum _{j=0}^{m_2}c_je^{\eta }_{m_1,j}\right\| _{\infty }: \left\| \sum _{j=0}^{m_2}c_j\xi _j\right\| _{\infty }\le 1\right\} . \end{aligned}$$

Now, if we suppose that $\epsilon >0$, then we have

$$\begin{aligned} \left\| \sum _{j=0}^{m_2}c_j\xi _j\right\| _2\le 1. \end{aligned}$$

We may assume that $|c_j|\le 1$. In view of (1.1) we can select $m_1$ large enough such that

$$\begin{aligned} \left\| e^{\eta }_{m_1,j}\right\| _{\infty }\le \frac{1}{m_2+1}, \end{aligned}$$

from which we conclude that

$$\begin{aligned} \left\| \sum _{j=0}^{m_2}c_je^{\eta }_{m_1,j}\right\| _{\infty }\le \sum _{j=0}^{m_2}|c_j|\Vert e^{\eta }_{m_1,j}\Vert _{\infty }\le \epsilon . \end{aligned}$$

This completes the proof. $\square$

Let $\Delta =[0,1]\times [0,1]$ and $(C^2(\Delta ,\Vert \cdot \Vert ))$ be the normed space of all order two differentiable continuous functions where $\Vert \cdot \Vert$ is defined by

$$\begin{aligned} \Vert \mu \Vert =\Vert \mu \Vert _{\infty }+\left\| \frac{\partial \mu }{\partial t}\right\| _{\infty }+\left\| \frac{\partial \mu }{\partial x}\right\| _{\infty }+\left\| \frac{\partial ^2\mu }{\partial x^2}\right\| _{\infty }. \end{aligned}$$

Now we prove the following lemma that plays an important role in the convergence analysis.

Lemma 2

Let $\Delta =[0,1]\times [0,1]$. Then, the functional $J:C^2(\Delta )\rightarrow \mathbb {R}$ defined by (1.1) is uniformly continuous on the spaces $(C^2(\Delta ),\Vert \cdot \Vert )$.

Proof

In view of the definition of Caputo derivative, we obtain

$$\begin{aligned} {^C_0D^{\eta }_{t}}\xi (x,t)=\frac{1}{\Gamma (2-\eta )}\int _{0}^t (t-s)^{1-\eta }\frac{{\partial }\xi }{{\partial } s}(x,t)ds \end{aligned}$$

(5.4)

and, hence, we can write:

$$\begin{aligned} \left\| {^C_0D^{\eta }_{t}}\right\| \le \max _{t\in [0,1]} \left| \int _{0}^t (t-s)^{1-\eta }\left\| \frac{{\partial }\xi }{{\partial } s}\right\| _{\infty }ds\right| \le \left\| \frac{{\partial \xi }}{{\partial } s}\right\| _{\infty }. \end{aligned}$$

Let $\epsilon >0$, $\mu (x,t)\in C^2(\Delta )$ and $\delta >0$ be arbitrarily chosen. Then, there exists $h(x,t)\in C^2(\Delta )$ such that

$$\begin{aligned} \Vert \mu -h\Vert =\Vert \mu -h\Vert _{\infty }+\left\| \frac{\partial }{\partial x}(\mu -h)\right\| _{\infty }+\left\| \frac{\partial ^2}{\partial x^2}(\mu -h)\right\| _{\infty }<\delta . \end{aligned}$$

This, together with (1.1)–(1.4), implies that

$$\begin{aligned} \left\| {^C_0D^{\eta }_{t}}\mu -{^C_0D^{\eta }_{t}}h\right\| _{\infty } =\left\| {^C_0D^{\eta }_{t}}(\mu -h)\right\| _{\infty } \le \left\| \frac{{\partial }}{{\partial } s}\mu -\frac{{\partial }}{{\partial } s}h\right\| _{\infty }. \end{aligned}$$

By the assumption on the nonlinear fractional dynamical system (1.2), ${\mathcal {S}}(x,t,\mu ,\mu _x,\mu _{xx},y)$, is a continuous function. Thus, for sufficiently small valued of $\delta >0$ with $\Vert \mu -h\Vert <\delta$ we conclude that $\Vert {\mathcal {Q}}\left( x,t,\mu ,y\right) -{\mathcal {Q}}\left( x,t,h,y\right) \Vert _{\infty }<\epsilon$ and

$$\begin{aligned} \Vert {\mathcal {S}}(x,t,\mu ,\mu _x,\mu _{xx},y)-{\mathcal {S}}(x,t,h,h_x,h_{xx},y)\Vert _{\infty } <\epsilon . \end{aligned}$$

This ensures that

$$\begin{aligned} J[\mu (x,t)]-J[h(x,t)]<\epsilon . \end{aligned}$$

$\square$

Theorem 2

Let $\sigma$ be the optimum of the functional J of $C^2(\Delta )$. If ${\sigma }_{m_1,m_2}$ is the optimum of J on $C^2(\Delta )\cap GBP_{m_1,m_2}([0,1])$, then

$$\begin{aligned} {\sigma }_{m_1,m_2}\rightarrow \sigma . \end{aligned}$$

Let $\epsilon >0$ be fixed. In view of the definition of J, there exists $\mu _0\in C^2(\Delta )$ such that

$$\begin{aligned} J[\mu _0]<\sigma +\epsilon . \end{aligned}$$

Using Lemmas 1 and 2, and the continuity of J, for $h(x,t)\in C^2(\Delta )$ with $\Vert h-\mu _0\Vert <\delta$, we conclude that

$$\begin{aligned} |J[h]-J[\mu _0]|<\epsilon . \end{aligned}$$

Using Theorem 1, for $m_1$ and $m_2$ large enough, we can find $\nu _{m_1,m_2}\in C^2(\Delta )\cap {GBP}_{m_1,m_2}([0,1])$ such that

$$\begin{aligned} \Vert \nu _{m_1,m_2}-\mu _0\Vert <\delta . \end{aligned}$$

Setting $\sigma _{m_1,m_2}:=J[\nu _{m_1,m_2}]$, we obtain

$$\begin{aligned} \sigma \le \sigma _{m_1,m_2}=J[\nu _{m_1,m_2}]-J[\mu _0]+J[\mu _0]\le |J[\nu _{m_1,m_2}]-J[\mu _0]|+|J[\mu _0]|\le \sigma +2\epsilon . \end{aligned}$$

If $\epsilon \rightarrow 0$, then we arrive at

$$\begin{aligned} {\sigma }_{m_1,m_2}\rightarrow \sigma . \end{aligned}$$

This completes the proof.

Now, we investigate the error estimate of the GBP expansion in two dimensions by means of the following theorem. We first mention the polynomial interpolation formula from [58].

Interpolation formula 1. Let P(x, t) be any two variables polynomial in x and t. Then, we have

$$\begin{aligned} P(x,t)=\sum _{i=0}^{m_1}\sum _{j=0}^{m_2}f(x_0,x_1,\ldots ,x_{m_1};t_0,t_1,\ldots ,t_{m_2})\prod _{k=0}^{i-1}(x-x_k)\prod _{s=0}^{j-1}(t-t_s). \end{aligned}$$

The remainder formula can be derived as follows. For any smooth function f, there exist values $\zeta ,\zeta ',\gamma$ and $\gamma '$ such that

$$\begin{aligned} R(x,t)= & {} \frac{{\partial }^{{m_1}+1}f(\zeta ,t)}{{\partial }x^{{m_1}+1}} \frac{\prod _{k=0}^{i-1}(x-x_k)}{({m_1}+1)!}+\frac{{\partial }^{{m_2}+1}f(x,\gamma )}{{\partial }t^{{m_2}+1}} \frac{\prod _{s=0}^{j-1}(t-t_s)}{({m_2}+1)!}\\&-\frac{{\partial }^{{m_1}+{m_2}+2}f(\zeta ',\gamma ')}{{\partial }x^{{m_1}+1}{\partial }t^{{m_2}+1}} \frac{\prod _{k=0}^{i-1}(x-x_k)}{({m_1}+1)!}\frac{\prod _{s=0}^{j-1}(t-t_s)}{({m_2}+1)!}, \end{aligned}$$

where $x_k$, $k=0,1,2,\ldots , m_1$ and $t_s$, $s=0,1,2,\ldots , m_2$, are the roots of the $(m_1+1)$-degree and $(m_2+1)$-degree GBP, respectively.

Theorem 3

Let $\mathbb {X}=L^2([0,1]\times [0,1])$ and $\mathbb {Y}=\langle x^{k_i}t^{l_j}:0\le i\le m_1,0\le j\le m_2\rangle$. Suppose that $\mu _0=\mu _0(x,t)\in \mathbb {Y}$ is the unique best approximation of ${\tilde{\mu }}={\tilde{\mu }}(x,t)\in \mathbb {X}$. Let ${\tilde{\mu }}:[0,1]\times [0,1]\rightarrow {\mathbb {R}}$ be a continuous function. Then, we have

$$\begin{aligned} \Vert {\tilde{\mu }}-\mu _0\Vert _{\infty }\le \Vert {\tilde{\mu }}-{\hat{\mu }}\Vert _{\infty },~~\forall {\hat{\mu }}={\hat{\mu }}(x,t)\in \mathbb {Y}. \end{aligned}$$

Proof

We first notice that if ${\hat{\mu }}={\hat{\mu }}(x,t)$ is the interpolation polynomial for ${\tilde{\mu }}$ at the points $(x^i,t^j)$ and $(x^{i+k_i},t^{j+l_j})$, where $x^i$, $t^j$, $x^{i+k_i}$ and $t^{j+l_j}$ are defined in (2.16) and (2.17), respectively, then we get from the above inequality that

$$\begin{aligned} {\tilde{\mu }}(x,t)-{\hat{\mu }}(x,t)= & {} \frac{{\partial }^{m_1+1}{\tilde{\mu }}(\zeta ,t)}{{\partial }x^{m_1+1}} \frac{\prod _{k=0}^{i-1}(x-x_k)}{(m_1+1)!}+\frac{{\partial }^{m_2+1}{\tilde{\mu }}(x,\gamma )}{{\partial }t^{m_2+1}} \frac{\prod _{s=0}^{j-1}(t-t_s)}{(m_2+1)!}\\&-\frac{{\partial }^{m_1+m_2+2}{\tilde{\mu }}(\zeta ',\gamma ')}{{\partial }x^{m_1+1}{\partial }t^{m_2+1}} \frac{\prod _{k=0}^{i-1}(x-x_k)}{(m_1+1)!}\frac{\prod _{s=0}^{j-1}(t-t_s)}{(m_2+1)!}, \end{aligned}$$

where $\zeta ,\zeta '\in [0,1]$ and $\gamma ,\gamma '\in [0,1]$. This implies that

$$\begin{aligned}&\Vert {\tilde{\mu }}(x,t)-{\hat{\mu }}(x,t)\Vert _{\infty }\le \frac{1}{(m_1+1)!}\max _{(x,t)\in [0,1]\times [0,1]}\left| \frac{{\partial }^{m_1+1}{\tilde{\mu }}(\zeta ,t)}{{\partial }x^{m_1+1}}\right| \left\| \prod _{k=0}^{i-1}(x-x_k)\right\| _{\infty }\\&\quad +\frac{1}{(m_2+1)!}\max _{(x,t)\in [0,1]\times [0,1]}\left| \frac{{\partial }^{m_2+1}{\tilde{\mu }}(x,\gamma )}{{\partial }t^{m_2+1}}\right| \left\| \prod _{s=0}^{j-1}(t-t_s)\right\| _{\infty }\\&\quad +\frac{1}{(m_1+1)!}\frac{1}{(m_2+1)!}\max _{(x,t)\in [0,1]\times [0,1]}\left| \frac{{\partial }^{m_1+m_2+2} {\tilde{\mu }}(\zeta ',\gamma ')}{{\partial }x^{m_1+1}{\partial }t^{m_2+1}}\right| \left\| \prod _{k=0}^{i-1}(x-x_k)\right\| \left\| \prod _{s=0}^{j-1}(t-t_s)\right\| . \end{aligned}$$

Since $[0,1]\times [0,1]$ is a compact set and ${\tilde{\mu }}$ is continuous on $[0,1]\times [0,1]$, we have

$$\begin{aligned}&\chi :=\max \left\{ \max _{(x,t)\in [0,1]\times [0,1]}\left| \frac{{\partial }^{m_1+1}{\tilde{\mu }}(\zeta ,t)}{{\partial }x^{m_1+1}}\right| ,\max _{(x,t)\in [0,1]\times [0,1]}\left| \frac{{\partial }^{m_2+1}{\tilde{\mu }}(x,\gamma )}{{\partial }t^{m_2+1}}\right| ,\right. \\&\left. \max _{(x,t)\in [0,1]\times [0,1]}\left| \frac{{\partial }^{m_1+m_2+2} {\tilde{\mu }}(\zeta ',\gamma ')}{{\partial }x^{m_1+1}{\partial }t^{m_2+1}}\right| \right\} <\infty . \end{aligned}$$

Now, knowing that $(x^i,t^j),(x^{i+k_i},t^{j+l_j})\in [0,1]\times [0,1]$, we are led to

$$\begin{aligned} \Vert {\tilde{\mu }}-{\hat{\mu }}\Vert _{\infty }\le \frac{\chi }{(m_1+1)!}+\frac{\chi }{(m_2+1)!}+\frac{\chi }{(m_1+1)!(m_2+1)!}. \end{aligned}$$

This completes the proof. $\square$

6 Numerical Examples

In this section two test problems are solved with the method presented in the previous sections. To confirm the accuracy and efficiency of the method, the approximations are compared with the exact solutions. All numerical calculations were performed using Maple 17 via 30 digits precision. Also, an 30-point Gauss–Legendre quadrature rule is employed for the numerical purposes. The absolute errors for the state variable ($\varepsilon _{\mu }(x_{i},t_{i})$) and the control variable ($\varepsilon _y(x_{i},t_{i})$) in various points $(x_{i},t_{i})\in [0,1]\times [0,1]$ are obtained as

$$\begin{aligned} \varepsilon _{\mu }(x_{i},t_{i})=\left| \left( {\mathcal {C}}\,\Theta _{m_{1}}(x_{i})\right) ^{T}\,{\mathcal {A}}\,\left( {\mathcal {D}}\,\Xi _{m_{2}}(t_{i})\right) -\mu (x_{i},t_{i})\right| , \end{aligned}$$

(6.1)

and

$$\begin{aligned} \varepsilon _y(x_{i},t_{i})=\left| \left( {\mathcal {P}}\,\Upsilon _{n_{1}}(x_{i})\right) ^{T}\,{\mathcal {B}}\,\left( {\mathcal {Q}}\,\Omega _{n_{2}}(t_{i})\right) -y(x_{i},t_{i})\right| . \end{aligned}$$

(6.2)

The convergence order of the proposed scheme is computed as follows

$$\begin{aligned} \Xi =\left| \frac{\log \left( \varepsilon _{2}\right) }{\log \left( \varepsilon _{1}\right) }\right| , \end{aligned}$$

(6.3)

where $\varepsilon _{1}$ and $\varepsilon _{2}$ are the first and the second values of the absolute error respectively. For more details on the order convergence, we refer the readers to [59, 60].

Example 1

Consider the objective function

$$\begin{aligned} \min \,{\mathcal {J}}[\mu , y]=\int _{0}^{1}\int _{0}^{1}\Bigg [\left( \mu (x,t)-x^{2.5}\,t^{2.1}\right) ^{2}+\left( y(x,t)-x^{1.8}\,t^{2.3}\right) ^{2}\Bigg ]dxdt, \end{aligned}$$

(6.4)

subject to the nonlinear fractional dynamical system

$$\begin{aligned}&{}^{C}_{0}\!{D_{t}^{\eta }}\mu (x,t)=e^{\mu (x,t)}+\mu _{x}(x,t)\,\mu _{xx}(x,t)+y^{2}(x,t)-\left( e^{x^{2.5}\,t^{2.1}}+9.375\,x^{2}\,t^{4.2}+x^{3.6}\,t^{4.6}\right) \\&\quad +\frac{\Gamma {\left( 3.1\right) }\,x^{2.5}\,t^{2.1-\eta }}{\Gamma {\left( 3.1-\eta \right) }}, \end{aligned}$$

and the Goursat–Darboux conditions

$$\begin{aligned} \mu (x,0)=0,\quad \quad \mu (0,t)=0. \end{aligned}$$

The analytical optimal solution of this example is $\left<\mu (x,t),y(x,t)\right>=\left<x^{2.5}\,t^{2.1},x^{1.8}\,t^{2.3}\right>$. The method introduced in Sect. 4 is used for solving this example using the GBP and BP with some values of $m_{1}$, $m_{2}$, $n_{1}$, $n_{2}$ and $\eta$. The approximate values of the objective function ${\mathcal {J}}$ are summarized in Tables 1 and 2, respectively. The resulting values of the absolute errors for the state and control variables and the value of $\Xi$ for the case 5 with $\eta =0.50$ are summarized in Table 3. The approximate solution and the absolute error for the state and control variables for the case 5 with $\eta =0.50$ are shown in Figs. 1 and 2, respectively. The results depicted in Tables 1 and 2 imply that the proposed method is more accurate than the method based on the BP. The results confirm the presented method is highly efficient when solving this problem. Moreover, the results show that applying more terms of the GBP provides numerical results with high accuracy.

Table 1 The values of ${\mathcal {J}}$ (the exact optimal value equals zero) at different choices of $m_{1}$, $m_{2}$, $n_{1}$, $n_{2}$ and $\eta$ using GBP for Example 1

Table 2 The values of ${\mathcal {J}}$ (the exact optimal value equals zero) at different choices of $m_{1}$, $m_{2}$, $n_{1}$, $n_{2}$ and $\eta$ using BP for Example 1

Table 3 The values of the absolute errors $\varepsilon _{\mu }(x_{i},t_{i})$, $\varepsilon _y(x_{i},t_{i})$ and convergence order $\Xi$ of the proposed scheme for case 5 ($m_{1}=m_{2}=n_{1}=n_{2}=5$ and $\eta =0.50$) in Example 1

Fig. 1

The approximate solution $\mu (x,t)$ (left side) and the absolute error function $\varepsilon _{\mu }$ (right side) for case 5 ($m_{1}=m_{2}=n_{1}=n_{2}=5$ and $\eta =0.50$) in Example 1

Fig. 2

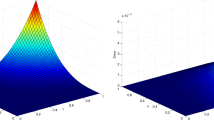
The approximate solution y(x, t) (left side) and the absolute error function $\varepsilon _y$ (right side) for case 5 ($m_{1}=m_{2}=n_{1}=n_{2}=5$ and $\eta =0.50$) in Example 1

Example 2

Consider the objective function

$$\begin{aligned} \min \,{\mathcal {J}}[\mu , y]=\int _{0}^{1}\int _{0}^{1}\Bigg [\left( \mu (x,t)-t^{4}\sin (x)\right) ^{2}+\left( y(x,t)-t^{3}\cos (x)\right) ^{2}\Bigg ]dxdt, \end{aligned}$$

(6.5)

subject to the nonlinear fractional dynamical system

$$\begin{aligned} {}^{C}_{0}\!{D_{t}^{\eta }}\mu (x,t)&=\cos (\mu (x,t))+2\sin (x)\mu _{x}(x,t)+\mu _{xx}(x,t)+6\sin (x)y(x,t)\\&\quad -\left( \cos (t^{4}\sin (x))+t^{3}\left( t\sin (2x)-t\sin (x)+3\sin (2x)\right) \right) +\frac{\Gamma {\left( 5\right) }\,\sin (x)\,t^{4-\eta }}{\Gamma {\left( 5-\eta \right) }},\ \end{aligned}$$

and the Goursat–Darboux conditions

$$\begin{aligned} \mu (x,0)=0,\quad \quad \mu (0,t)=0. \end{aligned}$$

The analytical optimal solution of this example is $\left<\mu (x,t),y(x,t)\right>=\left<t^{4}\sin (x),t^{3}\cos (x)\right>$. The presented and the standard BP methods with some values of $m_{1}$, $m_{2}$, $n_{1}$, $n_{2}$ and $\eta$ are used for solving this example. The approximate values of the objective function ${\mathcal {J}}$ are summarized in Tables 4 and 5, respectively. The resulting values of the absolute error for the state and control variables and and the value of $\Xi$ for the case 5 with $\eta =0.80$ are summarized in Table 6. The approximate solution and the absolute error for the state and control variables for the case 5 with $\eta =0.80$ are shown in Figs. 3 and 4, respectively. The results confirm the proposed method is convergent and perform very accurate for Problem (6.5). The results listed in Tables 4 and 5 imply that the method using the GBP is more accurate than the one based on BP. Moreover, from Tables 4 and 6 and also Figs. 3 and 4, we can conclude that our numerical solutions are in high agreement with the exact solution.

Table 4 The values of ${\mathcal {J}}$ (the exact optimal value equals zero) at different choices of $m_{1}$, $m_{2}$, $n_{1}$, $n_{2}$ and $\eta$ using GBP for Example 2

Table 5 The values of ${\mathcal {J}}$ (the exact optimal value equals zero) at different choices of $m_{1}$, $m_{2}$, $n_{1}$, $n_{2}$ and $\eta$ using BP for Example 2

Table 6 The values of the absolute errors $\varepsilon _{\mu }(x_{i},t_{i})$, $\varepsilon _y(x_{i},t_{i})$ and convergence order $\Xi$ of the proposed scheme for case 5 ($m_{1}=n_{1}=7$, $m_{2}=n_{2}=5$ and $\eta =0.80$) in Example 2

Fig. 3

The approximate solution $\mu (x,t)$ (left side) and the absolute error function $\varepsilon _{\mu }$ (right side) for case 5 ($m_{1}=n_{1}=7$, $m_{2}=n_{2}=5$ and $\eta =0.80$) in Example 2

Fig. 4

The approximate solution y(x, t) (left side) and the absolute error function $\varepsilon _y$ (right side) for case 5 ($m_{1}=n_{1}=7$, $m_{2}=n_{2}=5$ and $\eta =0.80$) in Example 2

7 Conclusion

In this work, an optimization algorithm based on the OM of derivatives for GBP together with the Gauss–Legendre quadrature rule is used to solve the nonlinear 2-dim fractional optimal control problems. The OM derived and the use of Gauss–Legendre quadrature rule and Lagrange multipliers methods for reduce the problem into a system of nonlinear algebraic equations. The proposed method provides very accurate solution even for small number of basis function. The error analyses of the method discussed show that this proposed technique will be an effective approach to solve the problem under study. The method can also be extended for higher order nonlinear PDEs which is a topic of our future study.