A Deuflhard-Type Exponential Integrator Fourier Pseudo-Spectral Method for the “Good” Boussinesq Equation

Abstract

We propose a Deuflhard-type exponential integrator Fourier pseudo-spectral (DEI-FP) method for solving the “Good” Boussinesq (GB) equation. The numerical scheme is based on a Deuflhard-type exponential integrator and a Fourier pseudo-spectral method for temporal and spatial discretizations, respectively. The scheme is fully explicit and efficient due to the fast Fourier transform. Rigorous error estimates are established for the method without any CFL-type condition constraint. In more details, the method converges quadratically and spectrally in time and space, respectively. Extensive numerical experiments are reported to confirm the theoretical analysis and to demonstrate rich dynamics of the GB equation.

1 Introduction

Similar to the Korteweg–de Vries (KdV) equation or cubic Schrödinger equation, the “Good” Boussinesq (GB) equation [1] also gives rise to solitons:

$$\begin{aligned} z_{tt}-z_{xx}+z_{xxxx}-(z^2)_{xx}=0. \end{aligned}$$

(1.1)

However, the GB equation possesses some remarkable features which make it different from the KdV equation, e.g., two solitary waves can merge into a single wave or develop into the so-called antisolitons [2]. The GB equation was originally introduced to model one-dimensional weakly nonlinear dispersive waves in shallow water [1]. Furthermore, it was extended by replacing the quadratic nonlinearity with a general function of z to model small oscillations of nonlinear beams [3] or the two-way propagation of water waves in a channel [4].

There have been extensive studies for the GB equation in recent decades. For the local well-posedness of the initial value problem, we refer to [5,6,7]. Specifically, the GB equation is locally well posed for initial data in $H^s({\mathbb {R}})\times H^{s-2}({\mathbb {R}})$ with $s>-1/2$. In the periodic setting, we refer to [8,9,10,11] for the local well-posedness. More precisely, it was shown in [10] that the initial value problem in $H^s({\mathbb {T}})\times H^{s-2}({\mathbb {T}})$ is locally well-posed for $s\ge -1/2$ and ill-posed for $s<-1/2$. For the numerical and analytical study of the GB equation, it can be traced back to [12], where the soliton interaction mechanism was investigated and some numerical experiments were reported while little analysis was given on the stability and convergence of the methods employed. Since then numerous numerical methods were developed for solving the GB equation. Finite difference methods (FDM) have been developed in [13,14,15]. Particularly, in [15], the nonlinear stability and convergence was shown for a family of explicit finite difference schemes for solving the GB equation under a severe Courant–Friedrichs–Lewy (CFL) condition: $\varDelta t=O(\varDelta x^2)$ where $\varDelta t$ and $\varDelta x$ represent the discretization parameters in time and space, respectively. More competitive Fourier spectral methods were also proposed and analyzed for the GB equation [16,17,18,19]. A second order temporal pseudo-spectral discretization was proposed in [18] and the full order convergence was proved in a weak energy norm: the $L^2$ norm in z combined with the $H^{-2}$ norm in $z_t$ under a similar time step constraint $\varDelta t=O(\varDelta x^2)$. Such a constraint becomes very restrictive and leads to a high computational cost. The energy norm was improved in [16] with the help of aliasing error control techniques in the Fourier pseudo-spectral space, where a second order temporal scheme was proved to converge unconditionally in a stronger energy norm: the $H^2$ norm in z combined with the $L^2$ norm in $z_t$. However, it requires the solution to be regular enough: $z\in H^4([0,T];L^2)\cap L^\infty ([0,T];H^{m+4})\cap H^2([0,T];H^4)$ to get an error of $O(\varDelta t^2+\varDelta x^m)$. An alternative second order (in time) scheme was proposed and analyzed by applying the operator splitting technique in a more recent article [20], and the convergence in the stronger energy norm (given by [16]) was established. There are some other methods in the literatures for solving the GB equation, such as Petrov–Galerkin methods [12], meshless methods [21], integral equation preconditioned deferred correction methods [22], energy-preserving methods [19, 23,24,25] and Runge–Kutta exponential integrators [26].

Nowadays, exponential time integrators have been widely applied for parabolic and hyperbolic equations [26,27,28,29]. Particularly, several efficient schemes were proposed for solving the GB equation [26] based on fourth-order exponential integrators of Runge–Kutta type. However, nothing concerning the stability and convergence results was involved. Very recently, two low regularity exponential-type integrators were proposed and analyzed for the GB equation [28] based on a technique of twisting variable. The advantage of the low regularity exponential-type integrators is that it requires less regularities on the solution to obtain the same accuracy, compared to the classical exponential integrators. However, the design of low regularity integrators depends strongly on the particular form of the nonlinearity. Such an integrator can hardly be extended to more general equations, e.g., the GB equation with a general nonlinearity.

In the present work, we consider a second-order Deuflhard-type exponential integrator for solving the GB equation. Our work differs from the existing studies in the literatures in the following two aspects: (i) we consider the GB equation with a general nonlinearity; (ii) an unconditional convergence is proved in a general energy norm: the $H^m$ norm in z combined with the $H^{m-2}$ norm in $z_t$ for $m>1/2$.

The rest of this paper is organized as follows. In Sect. 2, we propose the Deuflhard-type exponential integrator Fourier pseudo-spectral (DEI-FP) method for the GB equation. The main error estimate is given and proved in Sect. 3. Numerical results are reported in Sect. 4 to illustrate the proved convergence results and to demonstrate the complicated dynamics of the GB equation. Finally, some concluding remarks are drawn in Sect. 5.

2 A Deuflhard-Type Exponential Integrator Fourier Pseudo-Spectral Method

In this section, we present the exponential integrator Fourier pseudo-spectral (DEI-FP) method for the GB equation, based on a Deuflhard-type time integrator in combination with a Fourier pseudo-spectral discretization in space.

For implementation issues, we consider the GB equation with a general nonlinearity with periodic boundary conditions imposed:

$$\begin{aligned} \left\{ \begin{array}{l} z_{tt}-z_{xx}+z_{xxxx}-(f(z))_{xx}=0, \quad x \in \varOmega ,\quad t>0,\\ z(x,0)=z_0(x),\quad \partial _t z(x,0)=z_1(x),\quad x\in \overline{\varOmega }, \end{array}\right. \end{aligned}$$

(2.1)

where $f(\cdot )$ is a smooth functional. For integer $m>0$, $\varOmega =[a, b]$, we denote by $H^m(\varOmega )$ the standard Sobolev space with norm

$$\begin{aligned} \Vert f\Vert _m^2=\sum \limits _{l} (1+|\mu _l|^2)^m|\widehat{f}_l|^2, \quad \mathrm {for}\quad f(x)=\sum \limits _{l\in {\mathbb {Z}}} \widehat{f}_l e^{i\mu _l(x-a)},\quad \mu _l=\frac{2l\pi }{b-a}. \end{aligned}$$

(2.2)

For $m=0$, the space is exactly $L^2(\varOmega )$ and the corresponding norm is denoted as $\Vert \cdot \Vert$. Furthermore, we denote by $H_{\mathrm p}^m(\varOmega )$ the subspace of $H^m(\varOmega )$ which consists of functions with derivatives of order up to $m-1$ being $(b-a)$-periodic. We see that the space $H^m(\varOmega )$ with fractional m is also well-defined which consists of functions such that $\Vert \cdot \Vert _m$ is finite.

For the full discretization of (1.1), we introduce some discrete spaces. Choose a mesh size $h:=(b-a)/M$ with M a positive integer, and a time step $\tau >0$. Denote the grid points and time steps as

$$\begin{aligned} x_j:=a+jh,\quad j=0,1,\ldots ,M;\quad t_k:=k\tau ,\quad k=0,1,2,\ldots . \end{aligned}$$

Denote

$$\begin{aligned}&X_M:=\left\{ v=\left( v_0,v_1,\ldots ,v_M\right) ^T\ | \ v_0=v_M\right\} \subseteq {\mathbb {C}}^{M+1},\\&Y_M:=\mathrm {span}\left\{ e^{i\mu _l(x-a)},\quad l=-M/2,\ldots , M/2-1\right\} . \end{aligned}$$

For any function $\psi (x)\in L^2(\varOmega )$ and $\phi (x)\in C_0(\overline{\varOmega })$ or vector $\phi =(\phi _0,\phi _1,\ldots ,\phi _M)^T\in X_M$, let ${\mathcal {P}}_M: L^2(\varOmega )\rightarrow Y_M$ be the standard $L^2$-projection operator, and $I_M: C_0(\overline{\varOmega })\rightarrow Y_M$ or $I_M: X_M\rightarrow Y_M$ be the standard interpolation operator as

$$\begin{aligned} (P_M \psi )(x)=\sum \limits _{l=-M/2}^{M/2-1} \widehat{\psi }_le^{i\mu _l(x-a)}, \quad (I_M \phi )(x)=\sum \limits _{l=-M/2}^{M/2-1} \widetilde{\phi }_le^{i\mu _l(x-a)}, \end{aligned}$$

(2.3)

where $\widehat{\psi }_l$ and $\widetilde{\phi }_l$ are the Fourier and discrete Fourier transform coefficients of the function $\psi (x)$ and vector $\phi$ (with $\phi _j=\phi (x_j)$ when involved), respectively, defined as

$$\begin{aligned} \widehat{\psi }_l=\frac{1}{b-a}\int _a^b \psi (x)e^{-i\mu _l(x-a)}dx, \quad \widetilde{\phi }_l=\frac{1}{M}\sum \limits _{j=0}^{M-1}\phi _j e^{-i\mu _l(x_j-a)},\quad l=-\frac{M}{2},\ldots , \frac{M}{2}-1. \end{aligned}$$

(2.4)

Concerning the projection and interpolation operators, we review the standard estimates for the errors.

Lemma 2.1

[30] For any $0 \le \mu \le k$, we have

$$\begin{aligned} \Vert v-P_M(v)\Vert _\mu \le Ch^{k-\mu }\Vert v\Vert _{k},\quad \Vert P_N(v)\Vert _k \le C\Vert v\Vert _k,\quad \forall v\in H_\mathrm{p}^k(\varOmega ). \end{aligned}$$

(2.5)

Moreover, if $k>1/2$, we have

$$\begin{aligned} \Vert v-I_M(v)\Vert _{\mu } \le C h^{k-\mu }\Vert v\Vert _{k},\quad \Vert I_M(v)\Vert _k \le C\Vert v\Vert _k,\quad \forall v\in H_\mathrm{p}^k(\varOmega ). \end{aligned}$$

(2.6)

Here $C>0$ is a generic constant independent of h and v.

A Fourier pseudo-spectral method for discretizing (2.1) is to find

$$\begin{aligned} z_{_M}(x,t)=\sum \limits _{l=-M/2}^{M/2-1} \widehat{z}_l(t)e^{i\mu _l(x-a)}, \end{aligned}$$

(2.7)

such that

$$\begin{aligned} \partial _{tt} z_{_M}-\partial _x^2 z_{_M}+\partial _x^4z_{_M} -\partial _{xx} P_M(f(z_{_M}))=0, \quad x \in \varOmega ,\quad t>0. \end{aligned}$$

(2.8)

Substituting (2.7) into (2.8) and noticing the orthogonality of $\{e^{i\mu _l(x-a)}: -M/2\le l<M/2\}$, we obtain around time $t_k=k\tau \ (k\ge 0)$

$$\begin{aligned} \frac{d^2}{ds^2} \widehat{z}_l(t_k+s)+\theta _l^2\widehat{z}_l(t_k+s) +\mu _l^2\widehat{\rho }_l(t_k+s)=0, \end{aligned}$$

(2.9)

where $\rho =f(z_{_M})$ and $\theta _l=\sqrt{\mu _l^2+\mu _l^4}$. Applying the variation-of-constants formula [29] for $k\ge 0$ and $s\in {\mathbb {R}}$, the general solution of (2.9) can be written as follows for any $s\in {\mathbb {R}}$,

$$\begin{aligned} \widehat{z}_0(t_k+s)= & {} \widehat{z}_0(t_k)+s\widehat{z}'_0(t_k),\nonumber \\ \widehat{z}_l(t_k+s)= & {} \cos {(\theta _l s)}\widehat{z}_l(t_k)+\frac{\sin (\theta _l s)}{\theta _l}\widehat{z}'_l(t_k)- \frac{\mu _l^2}{\theta _l}\int _0^s\widehat{\rho }_l(t_k+\omega ) \sin {(\theta _l(s-\omega ))}d\omega ,\,\,\,\, l\ne 0.\nonumber \\ \end{aligned}$$

(2.10)

Differentiating (2.10) with respect to s, we obtain

$$\begin{aligned} \widehat{z}_0'(t_k+s)= & {} \widehat{z}_0'(t_k),\nonumber \\ \widehat{z}_l'(t_k+s)= & {} -\theta _l \sin {(\theta _l s)} \widehat{z}_l(t_k)+\cos (\theta _l s)\widehat{z}'_l(t_k) -\mu _l^2\int _0^s\widehat{\rho }_l(t_k+\omega )\cos {(\theta _l(s-\omega ))}d\omega ,\quad l\ne 0.\nonumber \\ \end{aligned}$$

(2.11)

Evaluating (2.10) and (2.11) with $s=\tau$ and approximating the integral by the trapezoid rule or the Deuflhard-type quadrature [29, 31], we immediately get

$$\begin{aligned}&\widehat{z}_0(t_{k+1})=\widehat{z}_0(t_k)+\tau \widehat{z}'_0(t_k), \quad \widehat{z}_0'(t_{k+1})=\widehat{z}_0'(t_k),\\&\widehat{z}_l(t_{k+1})\approx \cos {(\theta _l \tau )}\widehat{z}_l(t_k) +\frac{\sin (\theta _l \tau )}{\theta _l}\widehat{z}'_l(t_k) -\frac{\tau \mu _l^2}{2\theta _l}\widehat{\rho }_l(t_k),\quad l\ne 0,\\&\widehat{z}_l'(t_{k+1})\approx -\theta _l \sin {(\theta _l \tau )} \widehat{z}_l(t_k)+\cos (\theta _l \tau )\widehat{z}'_l(t_k) -\frac{\tau \mu _l^2}{2} \left[ \cos (\theta _l\tau )\widehat{\rho }_l(t_{k}) +\widehat{\rho }_l(t_{k+1})\right] ,\quad l\ne 0. \end{aligned}$$

For implementation, the integrals for computing the Fourier transform coefficients are usually approximated by the numerical quadratures of (2.4). Let $z_j^k$ and $\dot{z}_j^k$ be the approximations of $z(x_j,t_k)$ and $\partial _t z(x_j,t_k)$, respectively, for $0\le j<M$ and $k\ge 0$; and denote $z^k$ and $\dot{z}^k$ as the vectors with components $z_j^k$ and $\dot{z}_j^k$, respectively. Choosing $z_j^0=z_0(x_j)$, $\dot{z}_j^0=z_1(x_j)$ for $0\le j<M$, a Fourier pseudo-spectral discretization for the problem (2.1) reads

$$\begin{aligned} z_j^{k+1}=\sum \limits _{l=-M/2}^{M/2-1} \widetilde{z^{k+1}_l}e^{i\mu _l(x_j-a)}, \quad \dot{z}_j^{k+1}=\sum \limits _{l=-M/2}^{M/2-1} \widetilde{\dot{z}^{k+1}_l} e^{i\mu _l(x_j-a)}, \end{aligned}$$

(2.12)

where

$$\begin{aligned} \widetilde{z^{k+1}_0}= & {} \widetilde{z^{k}_0}+\tau \widetilde{\dot{z}^k_0}, \quad \widetilde{\dot{z}^{k+1}_0}=\widetilde{\dot{z}^{k}_0},\nonumber \\ \widetilde{z^{k+1}_l}= & {} \cos {(\theta _l \tau )}\widetilde{z^k_l} +\frac{\sin (\theta _l \tau )}{\theta _l}\widetilde{\dot{z}^k_l} -\frac{\tau \mu _l^2}{2\theta _l}\sin {(\theta _l \tau )} \widetilde{(f(z^k))}_l,\quad l\ne 0,\nonumber \\ \widetilde{\dot{z}^{k+1}_l}= & {} -\theta _l \sin {(\theta _l \tau )} \widetilde{z^k_l}+\cos (\theta _l \tau )\widetilde{\dot{z}^k_l} -\frac{\tau \mu _l^2}{2}\left[ \cos (\theta _l\tau )\widetilde{(f(z^k))}_l +\widetilde{(f(z^{k+1}))}_l\right] , \quad l\ne 0.\nonumber \\ \end{aligned}$$

(2.13)

The above scheme is clearly explicit and very efficient due to the fast discrete Fourier transform. The memory cost is O(M) and the computational cost per time step is $O(M\ln (M))$.

3 Convergence Analysis

For simplicity of notation, we denote the trigonometric interpolations of numerical solutions of (2.12) as

$$\begin{aligned} z_I^k(x):=I_M(z^k)(x),\quad \dot{z}_I^k(x):=I_M(\dot{z}^k)(x), \quad x\in \varOmega . \end{aligned}$$

Define the error functions as

$$\begin{aligned} e^k(x):=z(x,t_k)-z_I^k(x),\quad \dot{e}^k(x) :=\partial _t z(x,t_k)-\dot{z}_I^k(x),\quad x\in \varOmega ,\quad k=0, 1, \ldots . \end{aligned}$$

Then we have the following error estimates for (2.12) with (2.13).

Theorem 3.1

Suppose $m>1/2$ and $\sigma \ge 4$. Let the solution of the GB equation (2.1) satisfies the regularity properties $z\in C([0,T]; H^{m+\sigma }_{\mathrm{p}})\bigcap C^1([0,T]; H^{m+\sigma -2}_{\mathrm{p}})\cap C^2([0,T]; H^{m}_{\mathrm{p}})$. There exist $\tau _0>0$, $h_0>0$ sufficiently small such that when $\tau \le \tau _0$ and $h\le h_0$, we have the following error estimate for the numerical scheme (2.12) with (2.13):

$$\begin{aligned} \Vert {e}^n\Vert _{m}+\Vert \dot{e}^n\Vert _{m-2}\le K (\tau ^2+h^{\sigma }), \quad 0\le n\le T/\tau . \end{aligned}$$

(3.1)

Furthermore, we have

$$\begin{aligned} \Vert z_I^n\Vert _{m}\le K_1+1,\quad \Vert \dot{z}_I^n\Vert _{m-2}\le K_2+1, \end{aligned}$$

(3.2)

where $K_1:=\Vert z\Vert _{L^\infty ([0,T]; H^m)}$ and $K_2:=\Vert \partial _t z\Vert _{L^\infty ([0,T]; H^{m-2})}$.

It is well-known that the existence of aliasing error in the nonlinear term brings a serious challenge in the numerical analysis of Fourier pseudo-spectral approximation. Some aliasing error control techniques have been developed for the Fourier pseudo-spectral method in recent years for the Navier–Stokes equations [32], the viscous Burgers’ equation [33], the Cahn–Hilliard equation [34] and the GB equation [16]. Here we present an alternative proposition established in [35], which allows us to bound the aliasing error for the nonlinear term and will be critical to our analysis.

Proposition 1

[35] For any function $g\in C^\infty ({\mathbb {C}}, {\mathbb {C}})$ and $s >1/2$, there exists a nondecreasing function $\chi _g: {\mathbb {R}}^+\rightarrow {\mathbb {R}}^+$ such that

$$\begin{aligned} \Vert g(u)\Vert _s \le \Vert g(0)\Vert _s+\chi _g(\Vert u\Vert _{L^\infty })\Vert u\Vert _s, \quad \forall u\in H^s. \end{aligned}$$

(3.3)

For all $v, w\in B_R^s:=\{u\in H^s: \Vert u\Vert _s\le R\}$, we have

$$\begin{aligned} \Vert g(v)-g(w)\Vert _s\le \alpha (g, R)\Vert v-w\Vert _s, \end{aligned}$$

(3.4)

where $\alpha (g, R)=\Vert g'(0)\Vert _s+R\chi _{g'}(cR)$ is nondecreasing with respect to R, with $c>0$ being the constant for the Sobolev imbedding $\Vert \cdot \Vert _{L^\infty }\le c\Vert \cdot \Vert _s$.

Proof of Theorem 3.1

We deduce (3.1) and (3.2) by induction. For $n=0$, (3.1) is obvious by noticing

$$\begin{aligned} \Vert e^0\Vert _m=\Vert z_0-I_M(z_0)\Vert _m\le Ch^\sigma \Vert z_0\Vert _{m+\sigma }, \quad \Vert \dot{e}^0\Vert _{m-2}=\Vert z_1-I_M(z_1)\Vert _{m-2}\le Ch^\sigma \Vert z_1\Vert _{m+\sigma -2}. \end{aligned}$$

Furthermore, (3.2) can be obtained by the triangle inequality when $\tau$ and h are small enough.

Now assume (3.1) and (3.2) are valid for $n=0, \ldots , k<T/\tau$, next we show (3.1) and (3.2) are true for $k+1$. To precede, denote the projected error functions as

$$\begin{aligned} e_M^n(x):=P_M(e^n)(x)=\sum \limits _{l=-M/2}^{M/2-1} \widehat{e^n_l} e^{i\mu _l(x-a)},\quad \dot{e}_M^n(x):=P_M(\dot{e}^n)(x) =\sum \limits _{l=-M/2}^{M/2-1}\widehat{\dot{e}^n_l}e^{i\mu _l(x-a)}, \end{aligned}$$

where the corresponding coefficients satisfy

$$\begin{aligned} \widehat{e^n_l}=\widehat{z}_l(t_n)-\widetilde{z^n_l}, \quad \widehat{\dot{e}^n_l} =\widehat{ z}'_l(t_n)-\widetilde{\dot{z}^n_l},\quad l=-M/2,\ldots ,M/2-1. \end{aligned}$$

Applying the triangle inequality and Lemma 2.1, we have

$$\begin{aligned}&\Vert e^n\Vert _m\le \Vert e_M^n\Vert _m+\Vert P_M(z(\cdot , t_n))-z(\cdot , t_n)\Vert _m \le \Vert e_M^n\Vert _m+Ch^\sigma \Vert z(\cdot , t_n)\Vert _{m+\sigma },\\&\Vert \dot{e}^n\Vert _{m-2}\le \Vert \dot{e}_M^n\Vert _{m-2}+\Vert P_M(\partial _tz(\cdot , t_n)) -\partial _tz(\cdot , t_n)\Vert _{m-2}\le \Vert \dot{e}_M^n\Vert _{m-2}+Ch^\sigma \Vert \partial _t z(\cdot , t_n)\Vert _{m+\sigma -2}, \end{aligned}$$

thus it suffices to show (3.2) and

$$\begin{aligned} \Vert e_M^n\Vert _m+\Vert \dot{e}_M^n\Vert _{m-2}\le K (\tau ^2+h^{\sigma }) . \end{aligned}$$

(3.5)

Define the local truncation errors as

$$\begin{aligned} \xi ^n(x):=\sum \limits _{l=-M/2}^{M/2-1}\widehat{\xi ^n_l}e^{i\mu _l(x-a)}, \quad \dot{\xi }^n(x):=\sum \limits _{l=-M/2}^{M/2-1} \widehat{\dot{\xi }^n_l} e^{i\mu _l(x-a)}, \end{aligned}$$

where $\widehat{\xi ^n_0}=\widehat{\dot{\xi }^n_0}=0$, and for $l\ne 0$,

$$\begin{aligned} \widehat{\xi ^n_l}&=\widehat{z}_l(t_{n+1})-\widehat{z}_l(t_n)\cos (\theta _l\tau ) -\frac{\sin (\theta _l\tau )}{\theta _l}\widehat{z}_l'(t_n)+\frac{\tau \mu _l^2}{2\theta _l} \sin (\theta _l\tau )\widehat{\rho }_l(t_n),\\ \widehat{\dot{\xi }^n_l}&=\widehat{z}'_l(t_{n+1})+\theta _l\sin (\theta _l\tau ) \widehat{z}_l(t_n)-\cos (\theta _l\tau )\widehat{z}_l'(t_n)+\frac{\tau \mu _l^2}{2} \left[ \cos (\theta _l\tau )\widehat{\rho }_l(t_n)+\widehat{\rho }_l(t_{n+1})\right] , \end{aligned}$$

with $\rho (x,s)=f(z(x,s))$. Adding the local truncation errors from the scheme, we are led to the error equations as

$$\begin{aligned} \widehat{e^{n+1}_0}= & {} \widehat{e^n_0}+\tau \widehat{\dot{e}^n_0}, \quad \widehat{\dot{e}^{n+1}_0}=\widehat{\dot{e}^{n}_0},\nonumber \\ \widehat{e^{n+1}_l}= & {} \cos (\theta _l\tau )\widehat{e^n_l} +\frac{\sin (\theta _l\tau )}{\theta _l}\widehat{\dot{e}^n_l} +\widehat{\xi ^n_l}-\frac{\tau \mu _l^2}{2\theta _l}\sin (\tau \theta _l) \widehat{\eta ^n_l},\quad l\ne 0,\nonumber \\ \widehat{\dot{e}^{n+1}_l}= & {} -\theta _l\sin (\theta _l\tau )\widehat{e^n_l} +\cos (\theta _l\tau )\widehat{\dot{e}^n_l}+\widehat{\dot{\xi }^n_l} -\frac{\tau \mu _l^2}{2}\left[ \cos (\theta _l\tau )\widehat{\eta ^n_l} +\widehat{\eta ^{n+1}_l}\right] , \quad l\ne 0,\nonumber \\ \end{aligned}$$

(3.6)

where

$$\begin{aligned} \widehat{\eta ^n_l}=\widehat{\rho }_l(t_n)-\widetilde{\rho ^n_l} , \quad l\ne 0,\quad \rho ^n=f(z^n). \end{aligned}$$

It follows from (3.6) that

$$\begin{aligned} |\widehat{e^{n+1}_l}|^2&\le (1+\tau )\left| \cos (\theta _l\tau )\widehat{e^n_l} +\frac{\sin (\theta _l\tau )}{\theta _l}\widehat{\dot{e}^n_l}\right| ^2+\left( 1+\frac{1}{\tau }\right) \left| \widehat{\xi ^n_l}+\frac{\tau \mu _l^2}{2\theta _l}\sin (\tau \theta _l) \widehat{\eta ^n_l}\right| ^2,\\ |\widehat{\dot{e}^{n+1}_l}|^2&\le (1+\tau )\left| \theta _l\sin (\theta _l\tau ) \widehat{e^n_l}-\cos (\theta _l\tau )\widehat{\dot{e}^n_l}\right| ^2\\&\quad +\left( 1+\frac{1}{\tau }\right) \left| \widehat{\dot{\xi }^n_l}+\frac{\tau \mu _l^2}{2} \left[ \cos (\theta _l\tau )\widehat{\eta ^n_l}+\widehat{\eta ^{n+1}_l}\right] \right| ^2, \quad l\ne 0, \end{aligned}$$

which yields for $l\ne 0$,

$$\begin{aligned} \theta _l^2|\widehat{e^{n+1}_l}|^2+|\widehat{\dot{e}^{n+1}_l}|^2&\le (1+\tau )\left[ \theta _l^2|\widehat{e^{n}_l}|^2+|\widehat{\dot{e}^{n}_l}|^2\right] +\left( 1+\frac{1}{\tau }\right) \left[ \theta _l^2\left| \widehat{\xi ^n_l}+\frac{\tau \mu _l^2}{2\theta _l} \sin (\tau \theta _l)\widehat{\eta ^n_l}\right| ^2\right. \nonumber \\&\quad \left. +\left| \widehat{\dot{\xi }^n_l}+\frac{\tau \mu _l^2}{2} \left[ \cos (\theta _l\tau )\widehat{\eta ^n_l}+\widehat{\eta ^{n+1}_l}\right] \right| ^2\right] \nonumber \\&\le (1+\tau )\left[ \theta _l^2|\widehat{e^{n}_l}|^2+|\widehat{\dot{e}^{n}_l}|^2\right] +\left( 1+\frac{1}{\tau }\right) \Big [2\theta _l^2|\widehat{\xi ^n_l}|^2+\tau ^2\mu _l^4 |\widehat{\eta ^n_l}|^2\Big .\nonumber \\&\quad \Big .+2|\widehat{\dot{\xi }^n_l}|^2+\tau ^2\mu _l^4 \Big (|\widehat{\eta ^n_l}|^2+|\widehat{\eta ^{n+1}_l}|^2\Big )\Big ]. \end{aligned}$$

(3.7)

Denote

$$\begin{aligned} {\mathcal {E}}^n=|\widehat{e^n_0}|^2+|\widehat{\dot{e}^n_0}|^2 +\sum \limits _{-\frac{M}{2}\le l<\frac{M}{2},\,\, l\ne 0}(1+|\mu _l|^2)^{m-2} (\theta _l^2|\widehat{e^n_l}|^2+|\widehat{\dot{e}^n_l}|^2). \end{aligned}$$

By definition (2.2), we have

$$\begin{aligned} {\mathcal {E}}^n\sim \Vert e_M^n\Vert _m^2+\Vert \dot{e}_M^n\Vert _{m-2}^2, \end{aligned}$$

(3.8)

where $p \lesssim q$ means there exist a constant $C>0$ such that $p\le C q$ and $p\sim q$ represents $q\lesssim p\lesssim q$. Noticing that

$$\begin{aligned} |\widehat{e^{n+1}_0}|^2\le (1+\tau )|\widehat{e^n_0}|^2 +\left( 1+\frac{1}{\tau }\right) \tau ^2|\widehat{\dot{e}^n_0}|^2, \quad |\widehat{\dot{e}^{n+1}_0}|^2=|\widehat{\dot{e}^{n}_0}|^2, \end{aligned}$$

this together with (3.7) derives that

$$\begin{aligned} {\mathcal {E}}^{n+1}-{\mathcal {E}}^n \lesssim \tau {\mathcal {E}}^n+\frac{1}{\tau } \left( \Vert \xi ^n\Vert _m^2+\Vert \dot{\xi }^n\Vert _{m-2}^2\right) +\tau \left( \Vert \eta ^n\Vert _m^2+\Vert \eta ^{n+1}\Vert _m^2\right) . \end{aligned}$$

(3.9)

Next we estimate the local error and the error for the nonlinear term, respectively.

Local error. Applying the quadrature error

$$\begin{aligned} \int _0^\tau g(s)ds-\frac{\tau }{2}(g(0)+g(\tau )) =-\frac{1}{2}\int _0^\tau g''(s)s(\tau -s)ds, \end{aligned}$$

we get for $l\ne 0$,

$$\begin{aligned} \widehat{\xi ^n_l}&=\frac{\mu _l^2}{2\theta _l}\int _0^\tau s(\tau -s)[\sin (\theta _l(\tau -s))\widehat{\rho }_l(t_k+s)]''ds =\frac{\mu _l^2}{2\theta _l}\int _0^\tau s(\tau -s)P_l^n(s)ds,\\ \widehat{\dot{\xi }^n_l}&=\frac{\mu _l^2}{2}\int _0^\tau s(\tau -s)[\cos (\theta _l(\tau -s))\widehat{\rho }_l(t_k+s)]''ds =\frac{\mu _l^2}{2}\int _0^\tau s(\tau -s)Q_l^n(s)ds, \end{aligned}$$

where

$$\begin{aligned} P_l^n(s)&=-\theta _l^2\sin (\theta _l(\tau -s))\widehat{\rho }_l(t_n+s) -2\theta _l\cos (\theta _l(\tau -s))\widehat{\rho }_l'(t_n+s)+\sin (\theta _l(\tau -s)) \widehat{\rho }''_l(t_n+s),\\ Q_l^n(s)&=-\theta _l^2\cos (\theta _l(\tau -s))\widehat{\rho }_l(t_n+s) -2\theta _l\sin (\theta _l(\tau -s))\widehat{\rho }'_l(t_n+s)+\cos (\theta _l(\tau -s)) \widehat{\rho }''_l(t_n+s). \end{aligned}$$

Applying the Hölder’s inequality, we get for $l\ne 0$,

$$\begin{aligned} |\widehat{\xi ^n_l}|&\le \frac{\mu _l^2}{2\theta _l}\left( \int _0^\tau s^2(\tau -s)^2ds\right) ^{1/2}\left( \int _0^\tau |P_l^n(s)|^2ds\right) ^{1/2} \le \frac{\tau ^{5/2}}{2}\left( \int _0^\tau |P_l^n(s)|^2ds\right) ^{1/2},\\ |\widehat{\dot{\xi }^n_l}|&\le \frac{\mu _l^2}{2}\left( \int _0^\tau s^2(\tau -s)^2ds\right) ^{1/2}\left( \int _0^\tau |Q_l^n(s)|^2ds\right) ^{1/2} \le \frac{\mu _l^2\tau ^{5/2}}{2}\left( \int _0^\tau |Q_l^n(s)|^2ds\right) ^{1/2}. \end{aligned}$$

Thus

$$\begin{aligned} \Vert \xi ^n\Vert ^2_m&= \sum \limits _{l=-M/2}^{M/2-1}(1+|\mu _l|^2)^m|\widehat{\xi ^n_l}|^2\\&\lesssim \tau ^5 \sum \limits _{-\frac{M}{2}\le l<\frac{M}{2},\,\, l\ne 0}(1+|\mu _l|^2)^m \int _0^\tau |P_l^n(s)|^2ds\\&\lesssim \tau ^5 \sum \limits _{-\frac{M}{2}\le l<\frac{M}{2},\,\, l\ne 0}(1+|\mu _l|^2)^m \left[ \theta _l^4\int _0^\tau |\widehat{\rho }_l(t_n+s)|^2ds+\theta _l^2\int _0^\tau | \widehat{\rho }'_l(t_n+s)|^2ds\right. \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \left. +\int _0^\tau | \widehat{\rho }''_l(t_n+s)|^2ds\right] \\&\lesssim \tau ^{5}\int _0^\tau \left[ \Vert \rho (\cdot ,t_n+s)\Vert _{m+4}^2 +\Vert \partial _t\rho (\cdot , t_n+s)\Vert _{m+2}^2+\Vert \partial _t^2\rho (\cdot ,t_n+s)\Vert _{m}^2\right] ds. \end{aligned}$$

Noticing that

$$\begin{aligned} \partial _t \rho =f'(z)\partial _tz,\quad \partial _t^2\rho =f''(z)(\partial _tz)^2+f'(z)\partial _t^2z, \end{aligned}$$

recalling $m>1/2$, using the bilinear estimate [36]

$$\begin{aligned} \Vert f g\Vert _{r}\le C_r \Vert f\Vert _r\Vert g\Vert _r,\quad r>1/2, \end{aligned}$$

(3.10)

and Proposition 1, we yield that

$$\begin{aligned}&\Vert \rho (\cdot ,t)\Vert _{m+4}\le \Vert f(0)\Vert _{m+4}+\chi _f(\Vert z(\cdot ,t) \Vert _{L^\infty })\Vert z(\cdot , t)\Vert _{m+4}\le \Vert f(0)\Vert _{m+4}+\chi _f(L)\Vert z(\cdot , t)\Vert _{m+4},\\&\Vert \partial _t\rho (\cdot , t)\Vert _{m+2}\le C_m(\Vert f'(0)\Vert _{m+2}+\chi _{f'}(L)\Vert z(\cdot , t) \Vert _{m+2})\Vert \partial _tz(\cdot ,t)\Vert _{m+2},\\&\Vert \partial _t^2\rho (\cdot , t)\Vert _{m}\le C_m(\Vert f'(0)\Vert _{m}+\chi _{f'}(L)\Vert z(\cdot , t) \Vert _{m})\Vert \partial _t^2z(\cdot ,t)\Vert _{m}\\&\qquad \qquad \qquad \qquad + C_m^2 (\Vert f''(0)\Vert _{m}+\chi _{f''}(L)\Vert z(\cdot ,t)\Vert _{m}) \Vert \partial _tz(\cdot ,t)\Vert ^2_{m}, \end{aligned}$$

where $L=\Vert z\Vert _{L^\infty ([0,T]; L^\infty )}$, which is finite by recalling that $z\in C([0,T]; H^{m+\sigma }_{\mathrm{p}})$. By the assumptions on the regularities of z, we get that

$$\begin{aligned} \Vert \xi ^n\Vert _m^2\lesssim \tau ^6. \end{aligned}$$

Similar approach leads to that

$$\begin{aligned} \Vert \dot{\xi }^n\Vert _{m-2}^2&= \sum \limits _{l=-M/2}^{M/2-1} (1+|\mu _l|^2)^{m-2}| \widehat{\dot{\xi }^n_l}|^2\\&\lesssim \tau ^5 \sum \limits _{-\frac{M}{2}\le l<\frac{M}{2},\,\, l\ne 0} \mu _l^4(1+|\mu _l|^2)^{m-2} \int _0^\tau |Q_l^n(s)|^2ds\\&\lesssim \tau ^5 \sum \limits _{-\frac{M}{2}\le l<\frac{M}{2},\,\, l\ne 0} (1+|\mu _l|^2)^{m}\left[ \theta _l^4\int _0^\tau |\widehat{\rho }_l(t_n+s)|^2ds +\theta _l^2\int _0^\tau |\widehat{\rho }'_l(t_n+s)|^2ds\right. \\&\quad \left. +\int _0^\tau |\widehat{\rho }''_l(t_n+s)|^2ds\right] \lesssim \tau ^{6}. \end{aligned}$$

Hence we get the estimate on the local errors

$$\begin{aligned} \Vert \xi ^n\Vert ^2_m+\Vert \dot{\xi }^n\Vert _{m-2}^2\le M_1\tau ^6, \end{aligned}$$

(3.11)

where $M_1$ depends on m, f, $\Vert z\Vert _{L^\infty ([0,T]; H^{m+4})}$, $\Vert \partial _tz\Vert _{L^\infty ([0,T]; H^{m+2})}$ and $\Vert \partial _t^2z\Vert _{L^\infty ([0,T]; H^{m})}$.

Error of nonlinear terms. By definition, we have

$$\begin{aligned} \Vert \eta ^n\Vert _m&=\Vert I_M(\rho ^n)-P_M(\rho (\cdot ,t_n))\Vert _{m}\nonumber \\&\le \Vert I_M(f(z_I^n))-I_M(\rho (\cdot ,t_n))\Vert _{m}+\Vert I_M(\rho (\cdot ,t_n)) -P_M(\rho (\cdot ,t_n))\Vert _m\nonumber \\&\lesssim \Vert f(z_I^n)-f(z(\cdot ,t_n))\Vert _m+h^{\sigma }\Vert \rho (\cdot ,t_n) \Vert _{m+\sigma }\nonumber \\&\le \alpha (f, \max \{\Vert z_I^n\Vert _m, \Vert z(\cdot ,t_n)\Vert _m\})\Vert z_I^n -z(\cdot ,t_n)\Vert _m+h^{\sigma } (\Vert f(0)\Vert _{m+\sigma }+\chi _f(L)\Vert z(\cdot ,t_n)\Vert _{m+\sigma })\nonumber \\&\lesssim \alpha (f, \max \{\Vert z_I^n\Vert _m, \Vert z(\cdot ,t_n)\Vert _m\}) (\Vert e_M^n\Vert _m+h^\sigma \Vert z(\cdot ,t_n)\Vert _{m+\sigma })+h^{\sigma }. \end{aligned}$$

(3.12)

Similar approach yields that

$$\begin{aligned} \Vert \eta ^{n+1}\Vert _m\lesssim \alpha (f, \max \{\Vert z_I^{n+1}\Vert _m, \Vert z(\cdot ,t_{n+1})\Vert _m\})(\Vert e_M^{n+1}\Vert _m+h^\sigma \Vert z(\cdot ,t_{n+1})\Vert _{m+\sigma })+h^{\sigma }. \end{aligned}$$

(3.13)

To estimate this, we need an a prior bound for $\Vert z_I^{n+1}\Vert _m$. It follows from the scheme that

$$\begin{aligned} \Vert z_I^{n+1}\Vert _m&=\left( \sum \limits _{l=-M/2}^{M/2-1} (1+|\mu _l|^2)^m|\widetilde{z^{n+1}_l}|^2\right) ^{1/2}\nonumber \\&\le \left| \widetilde{z^{n}_0}+\tau \widetilde{\dot{z}^n_0}\right| +\Vert z_I^n\Vert _m+\left( \sum \limits _{-M/2\le l<M/2, l\ne 0} (1+|\mu _l|^2)^m\theta _l^{-2}|\widetilde{\dot{z}^n_l}|^2\right) ^{1/2} +\frac{\tau }{2}\Vert f(z_I^n)\Vert _m\nonumber \\&\le 2\Vert z_I^n\Vert _m+\tau \left| \widetilde{\dot{z}^n_0}\right| +c_1\Vert \dot{z}_I^n\Vert _{m-2}+\frac{\tau }{2}\left( \Vert f(0)\Vert _m+\chi _f(\Vert z_I^n\Vert _{L^\infty }) \Vert z_I^n\Vert _m\right) \nonumber \\&\le 2(K_1+1)+c_1(K_2+1)+\Vert f(0)\Vert _m+\chi _f(c(K_1+1))(K_1+1) +\left| \widetilde{\dot{z}^0_0}\right| , \end{aligned}$$

(3.14)

when $\tau \le 1$. Here we have used the property (3.10), $\widetilde{\dot{z}^n_0}=\widetilde{\dot{z}^{k-1}_0}=\ldots =\widetilde{\dot{z}^0_0}$, the induction and the inequality

$$\begin{aligned} \theta _l^{-2}\le c_1^2(1+|\mu _l|^2)^{-2},\quad l\ne 1, \end{aligned}$$

with $c_1^2=1+\frac{(b-a)^2}{4\pi ^2}$. Hence combining (3.12), (3.13) and (3.14), we get

$$\begin{aligned} \Vert \eta ^n\Vert _m^2+\Vert \eta ^{n+1}\Vert _m^2\le C(f, K_1){\mathcal {E}}^n +C(f, K_1, K_2){\mathcal {E}}^{n+1}+C(f, K_1, K_2, K_\sigma )h^{2\sigma }. \end{aligned}$$

(3.15)

Combining (3.9), (3.11) and (3.15), we derive that

$$\begin{aligned} {\mathcal {E}}^{n+1}-{\mathcal {E}}^n \lesssim \tau ^5+\tau h^{2\sigma } +\tau \left( {\mathcal {E}}^n+{\mathcal {E}}^{n+1}\right) . \end{aligned}$$

Summing the above inequality for $n=0, 1, \ldots , k$, one gets

$$\begin{aligned} {\mathcal {E}}^{k+1}-{\mathcal {E}}^{0}\lesssim \tau \sum \limits _{n=0}^{k+1} {\mathcal {E}}^n+\tau ^4+h^{2\sigma }. \end{aligned}$$

Applying the discrete Gronwall’s inequality, when $\tau$ is sufficiently small, we have

$$\begin{aligned} {\mathcal {E}}^{k+1}\lesssim \tau ^4+h^{2\sigma }, \end{aligned}$$

which immediately gives (3.5) by recalling (3.8). Finally (3.2) can be obtained by (3.1) and the triangle inequality. $\square$

4 Numerical Experiments

In this section, we first test the order of accuracy of the DEI-FP scheme (2.12) with (2.13). Then we apply this method to investigate some long time dynamics of the GB equation. For all the numerical experiments, we choose the commonly used nonlinearity $f(z)=z^2$.

4.1 Accuracy Test

In the first experiment, we test the convergence of the Deuflhard-type exponential integrator Fourier pseudo-spectral scheme (2.12) with (2.13) for the solitary wave solution.

Example 1

The well-known soliton solution of the GB equation (1.1) is given by [22, 28]

$$\begin{aligned} z(x,t)=-A\,\mathrm{sech}^2\left( \sqrt{A/6}(x-vt-x_0)\right) ,\quad v=\pm \sqrt{1-2A/3}, \end{aligned}$$

(4.1)

where A, $x_0$ and v represent the amplitude, the initial location and the velocity of the soliton, respectively.

Noticing that the solitary wave decays exponentially in the far field, this enables us to consider the GB equation on a bounded interval $[-a, a]$ with periodic boundary conditions when a is large enough such that the artificial boundaries are located far out enough for the theoretical solution to satisfy the periodic boundary conditions except for a negligible remainder. Here we choose $A=3/8$, $x_0=0$ and the torus $\varOmega =(-60,60)$. Denote $z^{\tau ,h}$ and $\dot{z}^{\tau ,h}$ as the numerical solutions obtained by the DEI-FP method with mesh size h and time step $\tau$ for approximating the exact solutions $z(\cdot ,t)$ and $\partial _tz(\cdot ,t)$. To quantify the numerical error, we define the error function as

$$\begin{aligned} e_m^{\tau ,h}:=\Vert I_M(z^{\tau ,h})-z(\cdot ,t)\Vert _m+\Vert I_M(\dot{z}^{\tau ,h}) -\partial _t z(\cdot ,t)\Vert _{m-2}. \end{aligned}$$

Figure 1 displays the spatial and temporal errors of the DEI-FP method (2.12)–(2.13) and the second-order low-regularity exponential integrator (LEI) proposed in [28] for the solitary wave solution at $T=2$ under various values of $\tau$ and h. The errors are quantified in several norms with $m=1,2,3$. For spatial error analysis, we take a tiny time step $\tau =10^{-6}$ such that the temporal error is negligible; for temporal error, we set the mesh size $h=1/8$ such that the spatial error can be ignorable. It can be clearly observed that the scheme converges spectrally and quadratically in space and time, respectively, which confirms the theoretical result in Theorem 3.1. Moreover, for solitary solutions, Fig. 1 also suggests that the LEI in [28] is more accurate than the DEI-FP for the same time step size. For a numerical comparison between the second-order DEI-FP method and the LEI method in [28] for rough initial datum, we refer to [28], where extensive experiments show the superiority of LEI since it requires less regularity on the solution to obtain the same second-order convergence rate. However, as explained in Sect. 1, the DEI-FP method works for general nonlinearities, for which the LEI in [28] is hardly applicable.

Fig. 1

Spatial (left) and temporal (right) errors of the DEI-FP scheme as well as the LEI method proposed in [28] for the soliton solution under different mesh size and time step size

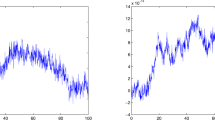
Next we investigate the long time behavior of the DEI-FP method. Noticing that for the soliton solution (4.1), $\int _\varOmega \partial _t z(x, 0)dx=0$, this implies that the mass is conserved:

$$\begin{aligned} M(t):=\int _\varOmega z(x,t)dx. \end{aligned}$$

Figure 2 shows the conservation law of mass for the numerical solitary wave solution (left) and the long time error of the DEI-FP scheme (right). Here the solution is obtained on a bounded interval $\varOmega =[-300, 300]$ under $h=1/8$ and $\tau =0.001$. We clearly see that the DEI-FP method is reliable and excellent for long time simulations.

Fig. 2

Conservation of mass (left) and long-time errors of the DEI-FP method (right)

4.2 Birth of Solitons

Example 2

In this experiment, we still use the initial data for the solitary wave solution (4.1):

$$\begin{aligned} z_0(x)= & {} -A\,\mathrm{sech}^2\left( \sqrt{A/6}\,x\right) ,\nonumber \\ z_1(x)= & {} -A\sqrt{1-2A/3}\sqrt{2A/3}\,\mathrm{sech}^2(\sqrt{A/6}\,x)\tanh (\sqrt{A/6}\,x). \end{aligned}$$

(4.2)

Fig. 3

Evolution of the solitary wave for initial data (4.2) with different A: $A=1.1, 1.3, 1.4, 1.5$ (from top to bottom)

Computations are done for $h=1/8$ and $\tau =0.001$ on the interval $\varOmega =[-400, 400]$. We find that for small A, the numerical solution agrees with the exact solution well. However, for larger A, the soliton fails to preserve its shape and splits into two pulses as time evolves. Figure 3 shows the evolution of the soliton for different amplitudes $A=1.1, 1.3, 1.4, 1.5$. It can be observed that for smaller A, the soliton preserves its shape and velocity well, which coincides with the exact solitary wave solution (4.1). However, for the initial soliton with larger amplitude, the initial pulse is preserved for a period and then splits into two solitons moving in the opposite directions. This suggests an instability occurs around this kind of initial condition. Furthermore, the larger A is, the smaller the difference between the amplitudes of the two solitons is. Particularly, for $A=1.5$ which corresponds to null initial velocity $z_1(x)=0$, the soliton finally splits into two identical solitons with equal amplitudes and equal velocities traveling in opposite directions.

For comparison, we also investigate the evolution of arbitrary pulse with zero initial velocity:

$$\begin{aligned} z_0(x)=-A\,\mathrm{sech}^2(\sqrt{A/6}\,x),\quad z_1(x)=0, \end{aligned}$$

(4.3)

which has been studied in the literature [25]. Figure 4 displays the dynamics of the soliton with null initial velocity and different amplitudes $A=0.6, 1.4$. Different from the case with non-zero initial velocity, the soliton always splits into two pulses with equal amplitudes and equal velocities propagating in opposite directions. Besides the two main solitons, some dispersive oscillations are emitted in front of the main solitons after splitting as long as $A<1.5$. This is different from that of the improved Boussinesq equation where the emitting oscillations are between the main solitons [37]. Furthermore, the smaller the amplitude is, the stronger the additional emitting wave is.

Fig. 4

Evolution of the solitary wave with zero initial velocity (4.3) for different A : $A=0.6, 1.4$ (from top to bottom)

4.3 Interaction of Two Solitons

In this section, we apply the DEI-FP method to investigate the interaction of two solitary waves traveling in the opposite/same directions. The initial data is chosen as

$$\begin{aligned} z_0(x)= & {} -\sum _{k=1}^2 A_k\,\mathrm{sech}^2\Big (\sqrt{\frac{A_k}{6}}(x-x_k)\Big ), \quad v_k=\pm \sqrt{1-\frac{2}{3}A_k},\nonumber \\ z_1(x)= & {} -\sum _{k=1}^2 A_k v_k\sqrt{\frac{2A_k}{3}} \,\mathrm{sech}^2 \Big (\sqrt{\frac{A_k}{6}}(x-x_k)\Big )\tanh \Big (\sqrt{\frac{A_k}{6}}(x-x_k)\Big ). \end{aligned}$$

(4.4)

It represents two solitary waves located initially at the positions $x=x_1$ and $x=x_2$, respectively, moving to the right or left depending on the sign of the velocity $v_k$. Computations are done for $h=1/8$ and $\tau =0.001$ on the interval $\varOmega =[-400, 400]$. We test the following cases:

• (1) Elastic collision:

  • (i). $x_2=-x_1=50$, $A_1=0.2$, $A_2=0.3$, $v_1>0$, $v_2<0$;

  • (ii). $x_2=-x_1=10$, $A_1=0.2$, $A_2=0.5$, $v_1>0$, $v_2<0$;

• (2) Blow-up phenomenon:

  • (iii). $x_2=-x_1=50$, $A_1=0.37$, $A_2=0.37$, $v_1>0$, $v_2<0$;

  • (iv). $x_2=-x_1=50$, $A_1=0.38$, $A_2=0.38$, $v_1>0$, $v_2<0$;

  • (v). $x_2=-x_1=50$, $A_1=0.3$, $A_2=0.45$, $v_1>0$, $v_2<0$;

  • (vi). $x_2=-x_1=50$, $A_1=0.3$, $A_2=0.46$, $v_1>0$, $v_2<0$;

• (3) Interaction with static solitons:

  • (vii). $x_2=-x_1=50$, $A_1=0.37$, $A_2=1.5$, $v_1>0$, $v_2=0$;

  • (viii). $x_2=-x_1=50$, $A_1=0.38$, $A_2=1.5$, $v_1>0$, $v_2=0$;

  • (ix). $x_2=-x_1=30$, $A_1=A_2=1.5$, $v_1=v_2=0$;

  • (x). $x_2=-x_1=20$, $A_1=A_2=1.5$, $v_1=v_2=0$;

• (4) Overtaking interaction:

  • (xi). $x_1=-50$, $x_2=-80$, $A_1=0.2$, $A_2=1$, $v_1>0$, $v_2>0$.

Fig. 5

Elastic collision of two solitons for Cases (i)–(ii) (from top to bottom)

Fig. 6

Collision of two solitons for Cases (iii)–(vi) (from top to bottom, from left to right)

Figure 5 shows the evolution of $-z(x,t)$ at different time for elastic collision (Cases (i)–(ii)). We see that the two solitons which are initially located at the positions $x_1=-50$ and $x_2=50$ moving towards each other with velocities $v_1$ and $v_2$, respectively. As time progresses they collide, stick together and split after collision without changing their shape and velocities. It can be clearly seen that the collision is elastic and no radiation is generated. Similar phenomena occurs for Case (ii) where the two solitons contact each other initially. This is different from the inelastic collision for the improved Boussinesq equation, where small rediation is created after the interaction between the solitons [37].

Figure 6 investigates the blow-up phenomenon for the head-on collision. For $A_1=A_2=0.38$, the solution blows up quickly after $t=68$. Similar blow-up occurs for $A_1=0.3$, $A_2=0.46$ after $t=70$. We see that for $A_1=A_2$, there exists $A_c\in (0.37, 0.38)$ such that the solution blows up in finite time when $A_1=A_2>A_c$. Similarly, for fixed $A_1=0.3$, there exists $A_c\in (0.45, 0.46)$ such that the solution blows up in finite time when $A_2>A_c$. This blow-up phenomenon was revealed in [38] for two solitons with the same initial amplitude.

Fig. 7

Collision of two solitons for Cases (vii)–(viii) (from top to bottom)

Figure 7 shows the interaction of two solitons, one of which has initial amplitude $A=1.5$ and null initial velocity. As time evolves, the static soliton splits into two identical pulses propagating in different directions. Then one of the splitting solitons collides with the pulse moving towards it. When the amplitude is not large enough, they collide and split again without changing their shape and velocities (cf. Fig. 7 top). While if the amplitude is large enough, blow-up occurs quickly after the collision (cf. Fig. 7 bottom).

Fig. 8

Evolution of two static solitons for Cases (ix)–(x) (from top to bottom)

Fig. 9

Overtaking interaction of two solitons traveling in the same direction

Figure 8 displays the evolution of two solitons with initial amplitudes $A_1=A_2=1.5$ and zero initial velocities. When the two solitons are well-separated initially (Case (ix)), each pulse splits into two solitons spreading towards opposite directions. Then the two head-on pulses collide and recover as one solitary wave with amplitude $A=1.5$. The recovered soliton keeps static for a period of time and finally splits into two equal pulses moving in the opposite directions. However, when the two solitons are not initially well-separated (Case (x)), the recovered solitary wave blows up quickly after $t=95$. As far as we know, this phenomena of recovering as a static soliton after collision has not been found in the existing literature.

Figure 9 displays the overtaking interaction of two solitons moving in the same direction with different velocities. The faster wave catches up with the slower one and leaves it behind as time evolves. Both solitons recover their shape and velocities after interaction. Noticing that the amplitude decreases during the interaction, which is completely different from the head-on interaction case, where the amplitude is strengthened during the collision (cf. Fig. 5). In addition, the overtaking interaction is also elastic, which is different from the case for the improved Boussinesq equation, where some small waves are emitted during the overtaking process [37].

5 Conclusions

A Deuflhard-type exponential integrator was proposed and analyzed for the “Good” Boussinesq (GB) equation with a general nonlinearity. The method was proved to converge unconditionally at the second order in time and spectrally in space, respectively, in a generic energy norm. Specifically, it requires four additional orders of regularities in space on the solution to attain the quadratic convergence rate in time. Numerical results confirm our analytical results. Extensive numerical experiments reveal rich and complicated dynamical phenomena for the GB equation, such as elastic interaction, blow-up phenomena, recovering as a static soliton and so forth.