Nonoverlapping Localized Exponential Time Differencing Methods for Diffusion Problems

Abstract

In this paper, we propose nonoverlapping localized exponential time differencing (ETD) methods for diffusion problems. The model time-dependent diffusion equation is first reformulated on subdomains based on the nonoverlapping domain decomposition, in which Neumann boundary conditions are imposed on the interfaces for the subdomain problems and Dirichlet type conditions are enforced to form a space-time interface problem. After spatial discretization by standard central finite differences and temporal integration with the first or second order ETD methods, the fully discrete interface problem is obtained. Such an interface problem is then solved iteratively either at each time step or over the whole time interval: the former involves the solution of stationary problems in each subdomain at each iteration while the latter involves the solution of time-dependent subdomain problems at each iteration. For both approaches, we prove that localized ETD solutions conserve mass exactly and converge in time to the exact space semidiscrete solution. Numerical experiments in two dimensions are also presented to illustrate the performance of the proposed methods.

1 Introduction

A common approach to solve evolution partial differential equations is to first discretize the equations in space, which results in a system of differential equations of the general form:

$$\begin{aligned} \frac{d\pmb {u}}{dt} = \pmb {G}(t, \pmb {u}), \quad \pmb {u}(0)=\pmb {u}_{0}. \end{aligned}$$

This system is then solved either explicitly or implicitly in time. We are interested in cases where the system is stiff in the sense that the explicit Euler method only works under a very restrictive condition on the time step size. In particular, one may encounter stiff problems when dealing with linear parabolic equations, $\pmb {G}(t,\pmb {u})=\pmb {A}\pmb {u}+ \pmb {F}(t)$ or semilinear parabolic equations, $\pmb {G}(t,\pmb {u})=\pmb {A}\pmb {u}+ \pmb {F}(t, \pmb {u})$. Instead of using implicit integrators, we consider exponential integrators for the time integration of stiff problems since implicit schemes can be expensive in the presence of nonlinear terms. Exponential integrators were first introduced in 1960 in [3] based on the variation-of-constants formula. This approach involves evaluations of some exponential functions, thus, could become impractical due to the high computational cost. Over the last three decades, thanks to the improvements in computer technology and matrix exponential algorithms [13, 19, 32, 35, 36], exponential integrators have revived strongly and attracted great interests in designing and improving exponential integrator-based methods [4, 5, 8, 20, 21, 24,25,26,27, 31, 38]. Among them, the exponential time differencing (ETD) methods [4, 8, 21, 26, 38] evaluate the time integration of nonlinearity in the variation-of-constants form by explicit multistep or Runge–Kutta approaches. Indeed, they approximate $\pmb {F}$ by its polynomial interpolation and then integrate the product of exponential integrating factor and the polynomials exactly. Comparing with other approaches such as the implicit integration factor that applies quadrature rules directly to the integrals, the ETD is able to provide a better solution to problems whose exponential integrator has components of highly different decaying rates. A nice review and additional references on the exponential integrator-based methods can be found in [22]. The costs of ETD methods are obviously dominated by the computing of matrix exponentials and their products with vectors. One possibility to overcome this challenge is to further improve the efficiency of the matrix exponential approximations as in these very recent publications [6, 15, 39, 40]. Another approach is to use domain decomposition techniques to reduce the size of the problem by solving instead a sequence of smaller-sized subdomain problems, in which the matrix exponentials are computed locally and thus much less expensively.

Domain decomposition methods (see [7, 30, 34, 37] and the references therein) have become a powerful tool for parallel computing of large scale problems. Although domain decomposition methods have been well established for many classic time integration methods, no enough attention and work have been devoted to accelerate exponential integrators. In [41] a highly scalable compact localized ETD method based on overlapping domain decomposition was proposed for extreme-scale parallel phase field simulations of 3D coarsening dynamics. Note that the parallelism of this approach is domain decomposition-based, which is completely different from the parallel adaptive-Krylov exponential solver proposed in [29]. The convergence analysis of Schwarz iterations combined with ETD methods, namely overlapping, localized ETD methods, was first carried out in our work [18], which was concerned with scalar diffusion problems with a finite difference discretization in space. As in the classical Schwarz methods, the localized ETD algorithms require the subdomains to overlap. Their convergence rate strictly depends on the overlapping size and, in general, cannot conserve mass up to machine precision.

In this work we design and analyze localized ETD algorithms based on nonoverlapping domain decomposition, which conserve mass exactly. Our model problem is the scalar time-dependent diffusion equation with no-flux boundary conditions. Different from the case of overlapping subdomains, the transmission conditions on the space-time interface between subdomains include not only Dirichlet conditions but also Neumann conditions. Thus one may impose either Dirichlet conditions or Neumann conditions on the interface as boundary conditions for solving the subdomain problems. The former corresponds to a primal formulation with the time-dependent Steklov–Poincaré operator [1, 33] and the latter corresponds to a dual formulation. For stationary problems, the dual formulation was first proposed for mixed finite elements [16] and later on widely studied for finite elements in finite element tearing and interconnecting (FETI) methods [10,11,12]. Since the Dirichlet boundary conditions may not guarantee mass conservation as in the case of overlapping localize-ETD methods, we use the dual approach by imposing Neumann boundary conditions for subdomain problems and then enforcing Dirichlet conditions to obtain a space-time interface problem. Such an interface problem is solved iteratively either at each time step or over the whole time interval, and we demonstrate that the resulting localized ETD algorithms satisfy exact mass conservation. It should be noted that, as in the case of overlapping subdomains [18], the nonoverlapping, localized ETD solutions are not exactly the same as the global ETD solution of the corresponding problem on the whole domain. However, it will be proved that the localized ETD solutions converge to the exact solution as the time step size tends to zero. Numerical experiments for many subdomains having cross points produced by two-direction domain decompositions are carried out to investigate the convergence (GMRES is used for solving the interface problem iteratively) and accuracy in time of the proposed algorithms.

The outline of the paper is as follows: in Sect. 2, we consider the continuous model problem and derive a space-time interface problem for a decomposition into two nonoverlapping subdomains. In Sect. 3, we discretize the monodomain and subdomain problems in space using central finite difference approximations and obtain a corresponding semidiscrete interface problem. Semidiscrete formulations for the case of multiple subdomains having cross points are also discussed. To derive a fully discrete interface problem, in Sect. 4, we use the first and second order ETD schemes for time marching and consider two approaches: the first method involves solving the interface problem at each time step sequentially and the second solving the interface problem for the whole time interval. In Sect. 7.3, it is proved that the global and localized ETD solutions satisfy discrete mass conservation. The convergence in time of the localized ETD solutions to the exact space semidiscrete solution is shown in Sect. 6. Some numerical experiments in two dimensions are presented to verify the theoretical results in Sect. 7. Finally some concluding remarks are drawn in Sect. 8.

2 The Model Problem and Nonoverlapping Domain Decomposition

For an open and bounded domain $\varOmega$ of ${\mathbb {R}}^{d} \; (d=1,2,3)$ with Lipschitz boundary $\partial \varOmega$ and some $T >0$, we consider the time-dependent diffusion equation with no-flux boundary conditions:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial u}{\partial t} =\; \nu \varDelta u + f, &{}\quad \text {in} \; \varOmega \times (0,T), \\ \nabla u \cdot \pmb {n}=\; 0, &{}\quad \text {on} \; \partial \varOmega \times (0,T),\\ u(\cdot ,0)=\;u_{0}, &{}\quad \text {in} \; \varOmega , \end{array} \right. \end{aligned}$$

(2.1)

where $\nu$ is a positive constant diffusion coefficient, $f(\pmb {x},t)$ is a source/sink term independent of the exact solution $u(\pmb {x},t)$, and $\pmb {n}$ is the unit outward normal vector on $\partial \varOmega .$ Assume the data is sufficiently smooth so that there exists a classical solution $u \in C^{1}(0,T; C^{2}(\varOmega ))$.

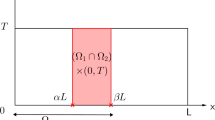
Let us decompose the domain $\varOmega$ into two nonoverlapping subdomains $\varOmega _{1}$ and $\varOmega _{2}$ and denote by $\varGamma =\partial \varOmega _{1}\cap \partial \varOmega _{2}$ the interface between the two subdomains, see Fig. 1. For $l= 1, 2,$ let $\pmb {n}_{l}$ denote the unit outward pointing vector field on $\partial \varOmega _{l}$, and for any function g defined on $\varOmega$, let $g_{l}$ denote the restriction of g onto $\varOmega _{l}$. We also make use of the notation $\pmb {n}_{\varGamma }$ for the normal vector on the interface pointing outward from $\varOmega _{1}$. A multidomain problem equivalent to (2.1) consists of solving in the following coupled subdomains problems:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial u_{l}}{\partial t} =\; \nu \varDelta u_{l} + f, &{}\quad \text {in} \; \varOmega _{l} \times (0,T),\\ \nabla u_{l} \cdot \pmb {n}_{l}=\; 0, &{}\quad \text {on} \; \left( \partial \varOmega _{l} \cap \partial \varOmega \right) \times (0,T),\\ u_{l}(\cdot ,0) =\;u_{0} \vert _{\varOmega _{l}}, &{}\quad \text {in} \; \varOmega _{l}, \end{array}\right. \end{aligned}$$

(2.2)

for $l=1,2,$ together with the transmission conditions on the space-time interface:

$$\begin{aligned} \left\{ \begin{array}{rl} u_{1} &{}=\;u_{2} , \\ \nabla u_{1} \cdot \pmb {n}_{\varGamma }&{}=\;\nabla u_{2} \cdot \pmb {n}_{\varGamma }, \end{array}\right. \quad \text {on} \; \varGamma \times (0,T). \end{aligned}$$

(2.3)

Fig. 1

A decomposition into two nonoverlapping subdomains with a space-time interface $\varGamma \times (0,T)$

Since the transmission conditions include not only the continuity of the solution but also the continuity of the normal flux, one may impose either Dirichlet conditions or Neumann conditions on the interface as boundary conditions for solving the subdomain problems. The former corresponds to a primal formulation and the latter corresponds to a dual formulation. As described in Sect. 1, in order to conserve the mass exactly, we will use the dual approach by imposing Neumann boundary conditions for subdomain problems and then enforcing Dirichlet conditions to obtain an interface problem for the coupling. Let $\xi$ be the interface unknown representing the normal flux across the interface

$$\begin{aligned} \xi = \nabla \pmb {u}_{1} \cdot \pmb {n}_{\varGamma } = \nabla \pmb {u}_{2} \cdot \pmb {n}_{\varGamma }, \qquad \text {on} \; \varGamma \times (0,T), \end{aligned}$$

and denote by $u_{l}(\xi , f, u_{0}), \; l=1,2,$ the solution to the following subdomain initial and Neumann boundary value problem:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial u_{l}}{\partial t} =\; \nu \varDelta u_{l} + f, &{}\quad \text {in} \; \varOmega _{l} \times (0,T),\\ \nabla u_{l} \cdot \pmb {n}_{l} =\;0, &{}\quad \text {on} \; \left( \partial \varOmega _{l} \cap \partial \varOmega \right) \times (0,T),\\ \nabla u_{l} \cdot \pmb {n}_{\varGamma }=\;\xi , &{}\quad \text {on} \; \varGamma \times (0,T), \\ u_{l}(\cdot ,0)=u_{0}\vert _{\varOmega _{l}}, &{}\quad \text {in} \; \varOmega _{l}, \end{array}\right. \end{aligned}$$

(2.4)

Clearly, $\left( u_{1}(\xi ,f, u_{0}), u_{2}(\xi , f, u_{0})\right)$ is the solution to the multidomain problem (2.2)–(2.3) if and only if

$$\begin{aligned} u_{1}(\xi ,f, u_{0}) = u_{2}(\xi ,f, u_{0}), \quad \text {on} \; \varGamma \times (0,T), \end{aligned}$$

or equivalently, the following interface condition

$$\begin{aligned} u_{1}(\xi ,0,0)-u_{2}(\xi ,0,0) = - \left( u_{1}(0,f,u_{0})-u_{2}(0,f, u_{0})\right) , \quad \text {on} \; \varGamma \times (0,T), \end{aligned}$$

(2.5)

holds. Denote by ${\mathcal {S}}$ an interface operator representing the jump of the subdomain solutions across the interface

$$\begin{aligned} {\mathcal {S}}\xi = {\mathcal {S}}_{1}\xi - {\mathcal {S}}_{2}\xi , \; \; \end{aligned}$$

with ${\mathcal {S}}_{l}\xi =u_{l}(\xi ,0,0)$ for $l=1,2$. It is easy to verify that ${\mathcal {S}}$ is a linear operator. Define

$$\begin{aligned} \chi (f,u_{0})= \chi _{1}(f,u_{0}) - \chi _{2}(f,u_{0}), \end{aligned}$$

with $\chi _{l}(f,u_{0})=-u_{l}(0,f,u_{0})$ for $l=1,2$. Then the resulting interface problem (2.5) can be rewritten as

$$\begin{aligned} {\mathcal {S}}\xi = \chi (f, u_{0}), \quad \text {on} \; \varGamma \times (0,T), \end{aligned}$$

(2.6)

in which the left-hand side only depends on the interface unknown, $\xi$, and the right-hand side is known from the the original problem (2.1). This linear problem (2.6) is to be solved by any effective iterative approach. Next we will discuss the semidiscretizations in space of the problems using finite difference on a regular mesh that matches on the interface between the subdomains. We approximate the interface normal flux $\xi$ in such a way that the semidiscrete subdomain problems give the same solution as the semidiscrete problem on the whole domain.

3 Semidiscrete (in Space) Problems

For simplicity of presentation, we consider a square domain in ${\mathbb {R}}^{2}$, $\varOmega =(0,L)^{2}$ for some $L>0$, and a uniform partition in space with a mesh size $h=L\big / (N-1)$. Denote by

$$\begin{aligned} u_{i,j}(t)= u((i-1)h, (j-1)h,t), \qquad f_{i,j}(t)=f((i-1)h, (j-1)h,t), \end{aligned}$$

the values of u and f, respectively, at the node (ih, jh) for all $i,j=1, \ldots , N$ at the time t. Using the standard central difference scheme for Neumann boundary conditions, we obtain the following system of linear ordinary differential equations (ODEs) for the semidiscrete monodomain problem (2.1):

$$\begin{aligned} \left\{ \begin{array}{l} \frac{d \pmb {u}}{d t} = \pmb {A}\pmb {u}+ \pmb {f}(t), \quad 0< t< T, \\ \pmb {u}(0) = \pmb {u}_{0}, \end{array} \right. \end{aligned}$$

(3.1)

where $\pmb {u}_{0}=\left( u_{0}(ih,jh)\right) _{i,j=0, \ldots , N-1}$, $\pmb {u}(t) =(u_{1,1}(t), \ldots ,u_{1,N}(t),\ldots , u_{N,N}(t))^{\top },$$\pmb {f}(t) =(f_{1,1}(t), \ldots ,f_{1,N}(t), \ldots , f_{N,N}(t))^{\top },$ and $\pmb {A}$ is a block tridiagonal matrix of size $N^{2}$, with each of the blocks a square matrix of size N:

$$\begin{aligned} \pmb {A}= \frac{\nu }{h^2} \left[ \begin{array}{cccccc} \pmb {B}&{} \quad 2\pmb {I}&{}\quad \pmb {0}&{} \quad \cdots &{} \quad \cdots &{} \quad \pmb {0}\\ \pmb {I}&{} \quad \pmb {B}&{} \quad \pmb {I}&{} \quad \pmb {0}&{} \quad \cdots &{} \quad \pmb {0}\\ \pmb {0}&{}\quad \pmb {I}&{} \quad \pmb {B}&{} \quad \pmb {I}&{} \quad \pmb {0}&{} \quad \pmb {0}\\ \cdots &{} \quad \cdots &{} \quad \cdots &{} \quad \cdots &{} \quad \cdots &{} \quad \cdots \\ \pmb {0}&{} \quad \cdots &{} \quad \pmb {0}&{} \quad \pmb {I}&{} \quad \pmb {B}&{} \quad \pmb {I}\\ \pmb {0}&{} \quad \cdots &{} \quad \cdots &{} \quad \pmb {0}&{} \quad 2\pmb {I}&{} \quad \pmb {B}\end{array} \right] , \end{aligned}$$

(3.2)

with $\pmb {I}$ being the identity matrix of size N and

$$\begin{aligned} \pmb {B}=\left[ \begin{array}{cccccc} -\,4 &{} \quad 2 &{} \quad 0 &{} \quad \cdots &{} \quad \cdots &{} \quad 0 \\ 1 &{} \quad -\,4 &{} \quad 1 &{} \quad 0&{} \quad \cdots &{} \quad 0 \\ 0&{}\quad 1 &{} \quad -\,4&{} \quad 1 &{} \quad 0&{} \quad 0\\ \cdots &{} \quad \cdots &{} \quad \cdots &{} \quad \cdots &{} \quad \cdots &{} \quad \cdots \\ 0 &{} \quad \cdots &{} \quad 0 &{} \quad 1 &{} \quad -\,4 &{}\quad 1 \\ 0 &{} \quad \cdots &{} \quad \cdots &{} \quad 0 &{} \quad 2 &{} \quad -\,4 \end{array} \right] . \end{aligned}$$

(3.3)

Correspondingly assume that the rectangle $\varOmega$ is divided into two subdomains with an interface

$$\begin{aligned} \varGamma =\left\{ x=(N_{\varGamma }-1)h \right\} , \quad \text {for some positive integer }N_{\varGamma }<N. \end{aligned}$$

Hence, the partition of each subdomain is a subset of the partition of $\varOmega$. Denote by $N_{1}=N_{\varGamma }$ and $N_{2}=N-N_{\varGamma }+1$ the numbers of grid points in the horizontal direction of $\varOmega _{1}$ and $\varOmega _{2}$, respectively. To derive the semidiscrete subdomain problems, let $\pmb {\xi }_{h}(t)$ be an approximation of $\xi (t)$ in space. An explicit formula for $\pmb {\xi }_{h}(t)$ will be specified in the following. Using ghost points to treat Neumann boundary conditions on the interface (as done for the boundary $\partial \varOmega$):

$$\begin{aligned} \nabla _{h} u_{1, N_{\varGamma },j} \cdot \pmb {n}_{x}= & {} \frac{u_{1, N_{\varGamma }+1,j}-u_{1, N_{\varGamma }-1,j}}{2h} = \xi _{h,j},\nonumber \\ \nabla _{h} u_{2, N_{\varGamma },j} \cdot \pmb {n}_{x}= & {} \frac{u_{2, N_{\varGamma }+1,j}-u_{2, N_{\varGamma }-1,j}}{2h}= \xi _{h,j}, \end{aligned}$$

(3.4)

for $j=1, \ldots , N$ and $\pmb {n}_{x}$ the unit vector in the x-direction, we obtain the following ODE system for the semidiscrete subdomain problem:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{d \pmb {u}_{l}}{d t} = \pmb {A}_{l} \pmb {u}_{l} + \pmb {F}_{l}(\pmb {\xi }_{h}(t), \pmb {f}(t)), \quad 0< t< T, \\ \pmb {u}_{l} (0) = \pmb {u}_{0}, \; \end{array} \right. \end{aligned}$$

(3.5)

where $\pmb {A}_{l}$ is a block matrix of size $NN_{l}$ (each of the blocks is a square matrix of size N), $l=1,2,$ that has the same structure as $\pmb {A}$ in (3.2), and

$$\begin{aligned}&\pmb {u}_{1}(t)=(u_{1,i,j}(t))_{i=1,\ldots , N_{\varGamma }, j=1, \ldots , N}\\&\pmb {u}_{2}(t)= (u_{2,i,j}(t))_{i=N_{\varGamma }, \ldots , N, j=1, \ldots , N},\\&\pmb {F}_{1}(\pmb {\xi }_{h}(t),\pmb {f}(t))=\big ( f_{1,1}(t), \ldots , f_{1,N}(t), \ldots , f_{N_{\varGamma }-1,1}(t), \ldots , f_{N_{\varGamma }-1,N}(t),\\&\quad f_{N_{\varGamma },1}(t) + 2\frac{\nu }{h} \xi _{h,1}(t), f_{N_{\varGamma },2}(t) + 2\frac{\nu }{h} \xi _{h,2}(t),\ldots , f_{N_{\varGamma },N}(t) + 2\frac{\nu }{h} \xi _{h,N}(t)\big )^{\top },\\&\pmb {F}_{2}(\pmb {\xi }_{h}(t), \pmb {f}(t)) =\;\big (f_{N_{\varGamma },1}(t) - 2\frac{\nu }{h} \xi _{h,1}(t), f_{N_{\varGamma },2}(t) - 2\frac{\nu }{h} \xi _{h,2}(t), \ldots ,\\&\quad f_{N_{\varGamma },N}(t) -2\frac{\nu }{h} \xi _{h,N}(t), f_{N_{\varGamma }+1,1}(t), \ldots , f_{N_{\varGamma }+1,N}(t), \ldots , f_{N,1}(t),\ldots , f_{N,N}(t)\big )^{\top }. \end{aligned}$$

We denote by $\pmb {u}_{l}(\pmb {\xi }_{h}(t), \pmb {f}(t), \pmb {u}_{0})$ the solution of (3.5). Next, we establish the condition under which the semidiscrete multidomain problem (3.5) is equivalent to the semidiscrete monodomain problem (3.1). If $\pmb {u}$ is the solution of the semidiscrete monodomain problem (3.1) and define

$$\begin{aligned} \pmb {u}_{1}= & {} \pmb {u}\vert _{\varOmega _{1}} = (u_{i,j})_{i=1,\ldots , N_{\varGamma }, j=1, \ldots , N},\nonumber \\ \pmb {u}_{2}= & {} \pmb {u}\vert _{\varOmega _{2}} = (u_{i,j})_{i=N_{\varGamma }, \ldots , N, j=1, \ldots , N}, \end{aligned}$$

(3.6)

then $\pmb {u}_{1}$ and $\pmb {u}_{2}$ match on the space-time interface; moreover, they are solutions of the semidiscrete subdomain problems (3.5) if and only if

$$\begin{aligned} \pmb {\xi }_{h}(t) = \left( \xi _{h,j}(t)\right) _{j=1, \ldots , N}, \qquad \xi _{h,j}(t):=\frac{u_{N_{\varGamma }+1,j}(t)-u_{N_{\varGamma }-1, j}(t)}{2h}, \end{aligned}$$

(3.7)

for all $j=1, \ldots , N, \; t \in (0,T)$. On the contrary, let $\pmb {u}(\pmb {\xi }_{h}(t), \pmb {f}(t), \pmb {u}_{0})$ be defined as

$$\begin{aligned} \pmb {u}(\pmb {\xi }_{h}(t), \pmb {f}(t), \pmb {u}_{0})\vert _{\varOmega _{1}}= & {} \pmb {u}_{1}(\pmb {\xi }_{h}(t), \pmb {f}(t), \pmb {u}_{0}),\nonumber \\ \pmb {u}(\pmb {\xi }_{h}(t), \pmb {f}(t), \pmb {u}_{0})\vert _{\varOmega _{2}}= & {} \pmb {u}_{2}(\pmb {\xi }_{h}(t), \pmb {f}(t), \pmb {u}_{0}), \end{aligned}$$

(3.8)

where $\pmb {u}_{1}(\pmb {\xi }_{h}(t), \pmb {f}(t), \pmb {u}_{0})$ and $\pmb {u}_{2}(\pmb {\xi }_{h}(t), \pmb {f}(t), \pmb {u}_{0})$ are the solution to (3.5). Then, as in the continuous case, $\pmb {u}(\pmb {\xi }_{h}(t), \pmb {f}(t), \pmb {u}_{0})$ is the solution of the semidiscrete monodomain problem (3.1) if and only if

$$\begin{aligned} \pmb {u}_{1, N_{\varGamma },j}(\pmb {\xi }_{h}(t), \pmb {f}(t), \pmb {u}_{0}) = \pmb {u}_{2, N_{\varGamma },j}(\pmb {\xi }_{h}(t), \pmb {f}(t), \pmb {u}_{0}), \end{aligned}$$

(3.9)

for $j=1, \ldots , N$ and $t \in (0,T)$. In the context of central finite difference approximations, one can prove that equation (3.9) is equivalent to have $\pmb {\xi }_{h}(t)$ defined as

$$\begin{aligned} \xi _{h,j}(t):=\frac{u_{2, N_{\varGamma }+1,j}(t)-u_{1,N_{\varGamma }-1, j}(t)}{2h}, \quad \forall \, j=1, \ldots , N, \; t \in (0,T). \end{aligned}$$

(3.10)

The matching condition (3.9) defines the semidiscrete counterpart of the interface problem (2.6):

$$\begin{aligned} {\mathcal {S}}_{h} \pmb {\xi }_{h}(t) = \chi _{h}(\pmb {f}(t),\pmb {u}_{0}), \quad \forall \, t \in (0,T), \end{aligned}$$

(3.11)

where

$$\begin{aligned} {\mathcal {S}}_{h} \pmb {\xi }_{h}(t)= & {} {\mathcal {S}}_{1,h} \pmb {\xi }_{h}(t) -{\mathcal {S}}_{2,h} \pmb {\xi }_{h}(t),\\ \chi _{h} (\pmb {f}(t), \pmb {u}_{0})= & {} \chi _{1,h} (\pmb {f}(t), \pmb {u}_{0}) -\chi _{2,h}(\pmb {f}(t), \pmb {u}_{0}), \end{aligned}$$

with

$$\begin{aligned} {\mathcal {S}}_{l,h} \pmb {\xi }_{h}(t)&= \left( u_{l,N_{\varGamma },j}(\pmb {\xi }_{h}(t), \pmb {0},\pmb {0})\right) _{j=1,\ldots , N}, \\ \chi _{l,h} (\pmb {f}(t), \pmb {u}_{0})&= \left( -\,u_{l,N_{\varGamma },j}(\pmb {0},\pmb {f}(t),\pmb {u}_{0})\right) _{j=1,\ldots , N}. \end{aligned}$$

Remark 3.1

The above domain decomposition approach and corresponding spatial discretizations can be extended straightforwardly to the case of a strip decomposition of the domain into multiple subdomains (see Fig. 2a). For the case of domain decomposition in both spatial directions with cross points as depicted in Fig. 2b, some treatments have to be specially done at these cross points, while interface points shared by only two subdomains can be treated in the same way as the case of strip decomposition.

Fig. 2

Illustrations of domain decomposition into multiple subdomains

The key idea is to impose Neumann and Dirichlet conditions at the cross points in a way such that the resulting semidiscrete multidomain problem is equivalent to the semidiscrete monodomain problem (3.1). In particular, at each cross point P, two unknowns $\xi _{x, i_{P}, j_{P}}(t)$ and $\xi _{y, i_{P}, j_{P}}(t)$ representing the flux in the x-direction and y-direction respectively are introduced and the continuity of the solution at the cross point is imposed in each direction with a use of some average operator. For the decomposition in Fig. 2b, the semidiscrete transmission conditions at the cross point P are as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \xi _{x,i_{P},j_{P}}=\nabla _{h}u_{1,i_{P},j_{P}}\cdot \pmb {n}_{x} =\nabla _{h}u_{3,i_{P},j_{P}}\cdot \pmb {n}_{x} =\nabla _{h}u_{2,i_{P},j_{P}}\cdot \pmb {n}_{x} =\nabla _{h}u_{4,i_{P},j_{P}}\cdot \pmb {n}_{x}, \\ \xi _{y,i_{P},j_{P}}=\nabla _{h}u_{1,i_{P},j_{P}} \cdot \pmb {n}_{y} =\nabla _{h}u_{2,i_{P},j_{P}}\cdot \pmb {n}_{y} =\nabla _{h}u_{3,i_{P},j_{P}}\cdot \pmb {n}_{y} =\nabla _{h}u_{4,i_{P},j_{P}}\cdot \pmb {n}_{y}, \\ \frac{1}{2}\left( u_{1,i_{P},j_{P}} + u_{3,i_{P},j_{P}}\right) =\frac{1}{2}\left( u_{2,i_{P},j_{P}} + u_{4,i_{P},j_{P}}\right) , \\ \frac{1}{2}\left( u_{1,i_{P},j_{P}} + u_{2,i_{P},j_{P}}\right) =\frac{1}{2}\left( u_{3,i_{P},j_{P}} + u_{4,i_{P},j_{P}}\right) , \end{array}\right. \end{aligned}$$

(3.12)

where $\pmb {n}_{x}$ and $\pmb {n}_{y}$ are unit vectors in x-direction and y-direction respectively. We remark that the conditions (3.12) ensure not only the continuity of the flux but also the continuity of the subdomain solutions at the cross point, i.e.:

$$\begin{aligned} u_{1,i_{P},j_{P}} =u_{2,i_{P},j_{P}}=u_{3,i_{P},j_{P}} =u_{4,i_{P},j_{P}}. \end{aligned}$$

(3.13)

Indeed, it is implied from (3.12)$_{3}$–(3.12)$_{4}$ that

$$\begin{aligned} u_{1,i_{P},j_{P}} =u_{4,i_{P},j_{P}}, \quad \mathrm{and} \quad u_{2,i_{P},j_{P}}=u_{3,i_{P},j_{P}}. \end{aligned}$$

(3.14)

In addition, by using Neumann conditions at the cross point (3.12)$_{1}$–(3.12)$_{2}$, we obtain:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{d u_{1, i_{P}, j_{P}}}{dt}=\frac{\nu }{h^{2}} \left( 2u_{1,i_{P}-1, j_{P}}+ 2u_{1,i_{P}, j_{P}-1} - 4u_{1,i_{P},j_{P}}\right) + \frac{2\nu }{h} \left( \xi _{x,i_{P}, j_{P}}+\xi _{y,i_{P}, j_{P}}\right) + f_{i_{P}, j_{P}}, \\ \frac{d u_{2, i_{P}, j_{P}}}{dt}=\frac{\nu }{h^{2}} \left( 2u_{2,i_{P}+1, j_{P}}+ 2u_{2,i_{P}, j_{P}-1} - 4u_{2,i_{P},j_{P}}\right) + \frac{2\nu }{h} \left( -\xi _{x,i_{P}, j_{P}}+\xi _{y,i_{P}, j_{P}}\right) + f_{i_{P}, j_{P}},\\ \frac{d u_{3, i_{P}, j_{P}}}{dt}=\frac{\nu }{h^{2}} \left( 2u_{3,i_{P}-1, j_{P}}+ 2u_{3,i_{P}, j_{P}+1} - 4u_{3,i_{P},j_{P}}\right) + \frac{2\nu }{h} \left( \xi _{x,i_{P}, j_{P}}- \xi _{y,i_{P}, j_{P}}\right) + f_{i_{P}, j_{P}}, \\ \frac{d u_{4, i_{P}, j_{P}}}{dt}=\frac{\nu }{h^{2}} \left( 2u_{4,i_{P}+1, j_{P}}+ 2u_{4,i_{P}, j_{P}+1}- 4u_{4,i_{P},j_{P}}\right) + \frac{2\nu }{h} \left( -\xi _{x,i_{P}, j_{P}}-\xi _{y,i_{P}, j_{P}}\right) + f_{i_{P}, j_{P}}. \end{array}\right. \end{aligned}$$

(3.15)

This together with (3.14) leads to

$$\begin{aligned} \left\{ \begin{array}{ll} 0&{}=\frac{d u_{1, i_{P}, j_{P}}}{dt}-\frac{d u_{4, i_{P}, j_{P}}}{dt} = \frac{\nu }{h^{2}} \left( 2u_{1,i_{P}-1, j_{P}}+ 2u_{1,i_{P}, j_{P}-1}\right) \\ &{} \quad -\frac{\nu }{h^{2}} \left( 2u_{4,i_{P}+1, j_{P}} + 2u_{4,i_{P}, j_{P}+1}\right) + \frac{4\nu }{h} \xi _{x,i_{P}, j_{P}}+\frac{4\nu }{h} \xi _{y,i_{P}, j_{P}}, \\ 0&{}=\frac{d u_{2, i_{P}, j_{P}}}{dt}-\frac{d u_{3, i_{P}, j_{P}}}{dt} = \frac{\nu }{h^{2}} \left( 2u_{2,i_{P}+1, j_{P}}+ 2u_{2,i_{P}, j_{P}-1}\right) \\ &{} \quad - \frac{\nu }{h^{2}} \left( 2u_{3,i_{P}-1, j_{P}}+ 2u_{3,i_{P}, j_{P}+1}\right) - \frac{4\nu }{h} \xi _{x,i_{P}, j_{P}}+\frac{4\nu }{h} \xi _{y,i_{P}, j_{P}}. \end{array} \right. \end{aligned}$$

(3.16)

Note that the solutions match at interface points $(i_{P},j)$ (with $j\ne j_{P}$) or $(i,j_{P})$ (with $i \ne i_{P}$) shared by any two subdomains $\varOmega _{l}$ and $\varOmega _{k}$, hence we write:

$$\begin{aligned} u_{l,i_{P}, j}=u_{k,i_{P}, j}:=u_{lk, i_{P},j}, \quad \forall j \ne j_{P}, \end{aligned}$$

and

$$\begin{aligned} u_{l,i,j_{P}}=u_{k,i,j_{P}}:=u_{lk, i, j_{P}}, \quad \forall i \ne i_{P}. \end{aligned}$$

Using this continuity and by adding and subtracting the two equations of (3.16) we obtain:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\nu }{h^{2}}\left( 4u_{13,i_{P}-1, j_{P}}-\,4u_{24,i_{P}+1, j_{P}}\right) + \frac{8\nu }{h} \xi _{x,i_{P}, j_{P}}=0, \\ \frac{\nu }{h^{2}}\left( 4u_{12,i_{P}, j_{P}-1}-\,4u_{34,i_{P}, j_{P}+1}\right) + \frac{8\nu }{h} \xi _{y,i_{P}, j_{P}}=0, \end{array}\right. \end{aligned}$$

(3.17)

or equivalently,

$$\begin{aligned} \left\{ \begin{array}{l} \xi _{x,i_{P}, j_{P}}=\frac{u_{24,i_{P}+1, j_{P}}-u_{13,i_{P}-1, j_{P}}}{2h}, \\ \xi _{y,i_{P}, j_{P}}=\frac{u_{34,i_{P}, j_{P}+1}-u_{12,i_{P}, j_{P}-1}}{2h}. \end{array} \right. \end{aligned}$$

(3.18)

Substituting this into (3.15)$_{1}$ and (3.15)$_{2}$ and subtracting the resulting equations we find that:

$$\begin{aligned} \frac{d}{dt}\left( u_{1, i_{P}, j_{P}}-u_{2, i_{P}, j_{P}}\right) = -\,4\frac{\nu }{h^{2}}\left( u_{1, i_{P}, j_{P}}-u_{2, i_{P}, j_{P}}\right) . \end{aligned}$$

This along with the fact that $u_{1, i_{P}, j_{P}}(t=0)-u_{2, i_{P}, j_{P}}(t=0)=0$ implies that

$$\begin{aligned} u_{1, i_{P}, j_{P}}(t)=u_{2, i_{P}, j_{P}}(t), \quad t \in (0,T). \end{aligned}$$

Similarly, we have $u_{3, i_{P}, j_{P}}(t)=u_{4, i_{P}, j_{P}}(t)$. From these two equations and (3.14), we conclude that (3.13) holds.

Note that for three dimensional problems with seven-point finite difference discretization, a similar treatment can be applied: at each cross point, the unknowns for the flux in the x-, y- and z-directions are introduced and the continuity of the solution at the cross point is imposed in each direction using some average operator. As a consequence, there are six semi-discrete transmission conditions at each cross point. Further developments of nonoverlapping domain decomposition methods based on ETD time discretization for three dimensional problems will be studied in our future work.

4 Localized ETD Methods

In this section, we will use the first and second order ETD schemes to further obtain temporal approximations of the semidiscrete subdomain problems (3.5) on respective nonoverlapping subdomains and derive the corresponding fully discrete interface problem for (3.11). We remark that other ETD schemes [4] can be similarly used to construct the localized ETD methods. It should be noted that for classic implicit schemes such as the backward Euler method, the fully discrete coupled subdomain problems are equivalent to the fully discrete monodomain problems. However, for ETD methods, the solutions of the couple subdomain problems and of the monodomain problem are not the same due to the presence of matrix exponentials. We shall demonstrate later (cf. Sect. 6) that the global and localized ETD solutions are related to each other in the sense that they both converge to the exact semidiscrete solution as the time step size tends to zero.

4.1 Monodomain ETD Solution

For simplicity, consider a uniform partition of the time interval [0, T]:

$$\begin{aligned} 0= t_{0}< t_{1}< \ldots < t_{M} = T, \quad \text {with a time step size} \; \varDelta t~=~T\big / M. \end{aligned}$$

The exact (in time) solution to the semidiscrete monodomain problem (3.1) at each time level is given by the variation-of-constants formula:

$$\begin{aligned} \pmb {u}(t_{m+1}) = \text {e}^{\varDelta t \pmb {A}} \pmb {u}(t_{m}) + \int _{0}^{\varDelta t} \text {e}^{(\varDelta t-s) \pmb {A}} \pmb {f}\left( t_{m}+s\right) \, ds, \quad \text {for} \; m=0, \ldots , M-1. \end{aligned}$$

The first order (monodomain) ETD scheme, ETD1, is obtained after approximating $\pmb {f}(t)$ on each time interval $[t_{m}, t_{m+1}]$ by a constant:

$$\begin{aligned} \pmb {u}^{m+1} = \text {e}^{\varDelta t \pmb {A}} \pmb {u}^{m} + \int _{0}^{\varDelta t} \text {e}^{(\varDelta t-s) \pmb {A}} \pmb {f}\left( t_{m+1} \right) \, ds. \end{aligned}$$

(4.1)

Better approximations can be obtained by using linear interpolation of $\pmb {f}(t)$ on each time interval $[t_{m}, t_{m+1}]$, which results in the second order ETD scheme, ETD2, as follows:

$$\begin{aligned} \pmb {u}^{m+1} = \text {e}^{\varDelta t \pmb {A}} \pmb {u}^{m} + \int _{0}^{\varDelta t} \text {e}^{(\varDelta t-s) \pmb {A}} \left[ \pmb {f}\left( t_{m} \right) +\frac{\pmb {f}\left( t_{m+1} \right) - \pmb {f}\left( t_{m} \right) }{\varDelta t} s \right] \, ds. \end{aligned}$$

(4.2)

Define the matrix exponential functions

$$\begin{aligned} \varphi _{1}(z)=\int _{0}^{1} \text {e}^{(1-\theta )z} d\,\theta = \frac{\text {e}^{z}-1}{z}, \qquad \varphi _{2}(z)=\int _{0}^{1} \text {e}^{(1-\theta )z} \theta d\,\theta = \frac{\varphi _{1}(z)-1}{z}. \end{aligned}$$

Then the formulations for ETD1 and ETD2 methods (Equations (4.1) and (4.2)) can be rewritten as

$$\begin{aligned} \pmb {u}^{m+1} = \text {e}^{\varDelta t \pmb {A}} \pmb {u}^{m} + \varDelta t \varphi _{1}(\varDelta t \pmb {A}) \pmb {f}\left( t_{m+1}\right) , \end{aligned}$$

(4.3)

if using ETD1 and

$$\begin{aligned} \pmb {u}^{m+1} = \text {e}^{\varDelta t \pmb {A}} \pmb {u}^{m} + \varDelta t \varphi _{1}(\varDelta t \pmb {A}) \pmb {f}\left( t_{m}\right) + \varDelta t \varphi _{2}(\varDelta t \pmb {A}) \left( \pmb {f}(t_{m+1}) - \pmb {f}(t_{m})\right) , \end{aligned}$$

(4.4)

if using ETD2. The cost of ETD methods thus is dominated by the computations of products of the $\varphi$-functions and vectors.

Next we derive our localized ETD methods in which the semidiscrete subdomain problems (3.5) are solved by either ETD1 or ETD2. Since the sizes of the local matrices $\{\pmb {A}_{l}\}_{l=1}^2$ are only about half of the global matrix $\pmb {A}$ for the case of two subdomains, the computations of the products of matrix exponentials with vectors are much less expensive than that in the monodomain problem. This advantage clearly becomes more obvious as the number of subdomains gets larger in practical simulations.

4.2 Nonoverlapping, Localized ETD1

We first derive the fully discrete interface problem by ETD1 associated with (3.11). Denote by $\pmb {{\widetilde{\xi }}}_{h}^{m+1}$, an approximation in time of $\pmb {\xi }_{h}(t_{m+1})$ which will be specified later. Applying ETD1 to the subdomain problems (3.5), we obtain:

$$\begin{aligned} \pmb {u}^{m+1}_{l}= & {} u_{l}^{m+1}(\pmb {{\widetilde{\xi }}}_{h}^{m+1}, \pmb {f}(t_{m+1})),\pmb {u}^{m}_{l}) = \text {e}^{\varDelta t \pmb {A}_{l}} \pmb {u}^{m}_{l} + \varDelta t \varphi _{1}(\varDelta t \pmb {A}_{l}) \pmb {F}_{l} \left( \pmb {{\widetilde{\xi }}}_{h}^{m+1}, \pmb {f}(t_{m})\right) ,\nonumber \\ \end{aligned}$$

(4.5)

for $l=1,2,$ and $m=0,\ldots , M-1$, with the initial condition $\pmb {u}_{l}^{0}=\pmb {u}_{0}$. The interface unknown $\pmb {{\widetilde{\xi }}}_{h}^{m+1}$ is the solution to the fully discrete counterpart of the interface problem (3.11):

$$\begin{aligned} u_{1,N_{\varGamma },j}^{m+1}(\pmb {{\widetilde{\xi }}}_{h}^{m+1}, \pmb {f}(t_{m+1})),\pmb {u}^{m}_{1}) = u_{2,N_{\varGamma },j}^{m+1}(\pmb {{\widetilde{\xi }}}_{h}^{m+1},\pmb {f}(t_{m+1})),\pmb {u}^{m}_{2}), \end{aligned}$$

(4.6)

or equivalently, according to (4.5),

$$\begin{aligned}&\left( \varDelta t \varphi _{1} (\varDelta t \pmb {A}_{1}) \pmb {F}_{1}(\pmb {{\widetilde{\xi }}}_{h}^{m+1}, \pmb {0})\right) _{N_{\varGamma }, j} -\left( \varDelta t \varphi _{1} (\varDelta t \pmb {A}_{2}) \pmb {F}_{2}(\pmb {{\widetilde{\xi }}}_{h}^{m+1}, \pmb {0})\right) _{N_{\varGamma }, j} \nonumber \\&\quad = \sum _{l=1}^{2} (-1)^{l} \left[ \text {e}^{\varDelta t \pmb {A}_{l}} \pmb {u}_{l}^{m} + \varDelta t \varphi _{1} (\varDelta t \pmb {A}_{l}) \pmb {F}_{l} (\pmb {0}, \pmb {f}(t_{m+1})) \right] _{N_{\varGamma },j}, \end{aligned}$$

(4.7)

for $j=1, \ldots , N,\; m=0,\ldots , M-1$. Therefore, $\pmb {{\widetilde{\xi }}}_{h}^{m+1}=({\widetilde{\xi }}_{h,j}^{m+1})_{j=1, \ldots , N}$ can be expressed (formally) as a linear function in $\pmb {u}_{1}^{m}, \pmb {u}_{2}^{m},\pmb {f}(t_{m+1})$. Alternatively, we can compute $\pmb {{\widetilde{\xi }}}_{h} = (\pmb {{\widetilde{\xi }}}_{h}^{m})_{m=1, \ldots , M}$ by solving (4.6) iteratively either at each time step sequentially or over the whole time interval. The former corresponds to space, localized ETD1 in which each iteration involves the solution of stationary problems in the subdomains, and the latter corresponds to space-time localized ETD1 wherein each iteration involves the solution of time-dependent subdomain problems.

4.3 Space Localized ETD1

Assume that the solutions and interface values at $t_{m}$, $\pmb {u}_{1}^{m}$, $\pmb {u}_{2}^{m}$ and $\pmb {{\widetilde{\xi }}}_{h}^{m}$, are given, we aim to find the interface values at the next time level $\pmb {{\widetilde{\xi }}}_{h}^{m+1}$. For $l=1,2,$ and for $m=0, \ldots , M-1$, let ${\mathcal {E}}_{l,h}^{m+1}$ be the interface operator that maps the interface boundary data, the right-hand side function at $t_{m+1}$ and the solution at $t_{m}$, $(\pmb {{\widetilde{\xi }}}_{h}^{m+1},\pmb {f}(t_{m+1}),\pmb {u}_{l}^{m})$, to the solution $\pmb {u}_{l}^{m+1}$ given by (4.5) on the interface:

$$\begin{aligned} \begin{array}{lccc} {\mathcal {E}}_{l,h}^{m+1}\,:&{} {\mathbb {R}}^{N} \times {\mathbb {R}}^{N_{l}N} \times {\mathbb {R}}^{N_{l}N} &{} \longrightarrow &{} {\mathbb {R}}^{N} \\ &{}(\pmb {{\widetilde{\xi }}}_{h}^{m+1},\pmb {f}(t_{m+1}), \pmb {u}_{l}^{m})&{} \mapsto &{} \left( \pmb {u}_{l, N_{\varGamma },j}^{m+1}\right) _{j=1, \ldots , N}. \end{array} \end{aligned}$$

The discrete interface problem for $\pmb {{\widetilde{\xi }}}_{h}^{m+1}$ is given by:

$$\begin{aligned} {\overline{{\mathcal {S}}}}_{h}^{m+1} \pmb {{\widetilde{\xi }}}_{h}^{m+1} = {\overline{\chi }}_{h}^{m+1}(\pmb {f}(t_{m+1}), \pmb {u}_{1}^{m},\pmb {u}_{2}^{m}), \end{aligned}$$

(4.8)

where

$$\begin{aligned}&{\overline{{\mathcal {S}}}}_{h}^{m+1}\pmb {{\widetilde{\xi }}}_{h}^{m+1} = {\mathcal {E}}_{1,h}^{m+1}(\pmb {{\widetilde{\xi }}}_{h}^{m+1},\pmb {0},\pmb {0},)-{\mathcal {E}}_{2,h}^{m+1}(\pmb {{\widetilde{\xi }}}_{h}^{m+1},\pmb {0},\pmb {0}), \\&{\overline{\chi }}_{h}^{m+1}(\pmb {f}(t_{m+1}), \pmb {u}_{1}^{m}, \pmb {u}_{2}^{m})=-({\mathcal {E}}_{1,h}^{m+1}(\pmb {0}, \pmb {f}(t_{m+1}),\pmb {u}_{1}^{m})-{\mathcal {E}}_{2,h}^{m+1}(\pmb {0},\pmb {f}(t_{m+1}), \pmb {u}_{2}^{m})). \end{aligned}$$

We solve (4.8) iteratively to determine $\pmb {{\widetilde{\xi }}}_{h}^{m+1}$. Once it converges, we calculate $\pmb {u}_{1}^{m+1}$ and $\pmb {u}_{2}^{m+1}$, and advance to the next time level.

4.4 Space-Time Localized ETD1

Different from the approach above, here we find the interface unknown globally in time. Denote by $\pmb {{\widetilde{\xi }}}_{h}=(\pmb {{\widetilde{\xi }}}^m_{h})_{1\le m \le M}$ the interface space vector over all time steps. For $l=1,2,$ let ${\mathcal {G}}_{l,h}$ be the interface operator that maps the interface vector, the right-hand side function and initial data $(\pmb {{\widetilde{\xi }}}_{h}, \pmb {f}, \pmb {u}_{0})$, to the solution $(\pmb {u}_{l}^{m+1})_{m=0, \ldots ,M-1}$ given by (4.5) on the interface:

$$\begin{aligned} \begin{array}{lccc} {\mathcal {G}}_{l,h}\,:&{} {\mathbb {R}}^{NM} \times {\mathbb {R}}^{N_{l}NM} \times {\mathbb {R}}^{N_{l}N} &{} \longrightarrow &{} {\mathbb {R}}^{NM} \\ &{}(\pmb {{\widetilde{\xi }}}_{h}, \pmb {f}, \pmb {u}_{0})&{} \mapsto &{} \left( \pmb {u}_{l, N_{\varGamma },j}^{m}\right) _{j=1, \ldots , N, \; m=1, \ldots , M}. \end{array} \end{aligned}$$

In this case, the discrete interface problem is defined globally in time:

$$\begin{aligned} {\widehat{S}}_{h} \pmb {\xi }_{h}= {\widehat{\chi }}_{h}(\pmb {f},\pmb {u}_{0}), \end{aligned}$$

(4.9)

where

$$\begin{aligned} {\widehat{{\mathcal {S}}}}_{h} \pmb {\xi }_{h}&= {\mathcal {G}}_{1,h}(\pmb {{\widetilde{\xi }}}_{h}, \pmb {0}, \pmb {0})-{\mathcal {G}}_{2,h}(\pmb {{\widetilde{\xi }}}_{h}, \pmb {0}, \pmb {0}), \\ {\widehat{\chi }}_{h}(\pmb {f},\pmb {u}_{0})&= -({\mathcal {G}}_{1,h}(\pmb {0},\pmb {f},\pmb {u}_{0})-{\mathcal {G}}_{2,h}(\pmb {0},\pmb {f},\pmb {u}_{0})). \end{aligned}$$

Again, this problem is solved iteratively to find the interface space-time vector $\pmb {{\widetilde{\xi }}}_{h}$.

Remark 4.1

As in the case of localized ETD methods with overlapping subdomains [18], the nonoverlapping localized ETD solution (4.5) is not exactly the same as the one (4.3) by the corresponding monodomain ETD method. This feature is typical of exponential integrators.

4.5 Nonoverlapping, Localized ETD2

We now derive the localized ETD methods of second order accuracy in time by following the quite similar procedure as in the first order case. Applying ETD2 to the subdomain problems (3.5), we obtain:

$$\begin{aligned} \pmb {u}^{m+1}_{l}= & {} u_{l}^{m+1}(\pmb {{\widetilde{\xi }}}_{h}^{m+1}, \pmb {{\widetilde{\xi }}}_{h}^{m}, \pmb {f}(t_{m+1}), \pmb {f}(t_{m}),\pmb {u}^{m}_{l}) = \text {e}^{\varDelta t \pmb {A}_{l}} \pmb {u}^{m}_{l} + \varDelta t \varphi _{1}(\varDelta t \pmb {A}_{l}) \pmb {F}_{l} \left( \pmb {{\widetilde{\xi }}}_{h}^{m}, \pmb {f}(t_{m})\right) \nonumber \\&+ \,\varDelta t \varphi _{2}(\varDelta t \pmb {A}_{l}) \left( \pmb {F}_{l}\left( \pmb {{\widetilde{\xi }}}_{h}^{m+1}, \pmb {f}(t_{m+1})\right) - \pmb {F}_{l}\left( \pmb {{\widetilde{\xi }}}_{h}^{m}, \pmb {f}(t_{m})\right) \right) , \end{aligned}$$

(4.10)

for $l=1,2,$ and $m=0,\ldots , M-1$, in which the initial interface values are given by

$$\begin{aligned} \pmb {{\widetilde{\xi }}}_{h}(0)=\pmb {\xi }_{h}(0)=\left( \frac{u_{2,N_{\varGamma }+1,j}^{0}-u_{1,N_{\varGamma }-1,j}^{0}}{2h}\right) _{j=1, \ldots , N}. \end{aligned}$$

As in the case of localized ETD1, the interface unknown $\pmb {{\widetilde{\xi }}}_{h}^{m+1}$ is the solution to the fully discrete counterpart of the interface problem (3.11):

$$\begin{aligned} u_{1,N_{\varGamma },j}^{m+1}(\pmb {{\widetilde{\xi }}}_{h}^{m+1}, \pmb {{\widetilde{\xi }}}_{h}^{m}, \pmb {f}(t_{m+1}), \pmb {f}(t_{m}),\pmb {u}^{m}_{1}) = u_{2,N_{\varGamma },j}^{m+1}(\pmb {{\widetilde{\xi }}}_{h}^{m+1}, \pmb {{\widetilde{\xi }}}_{h}^{m}, \pmb {f}(t_{m+1}), \pmb {f}(t_{m}),\pmb {u}^{m}_{2}), \end{aligned}$$

(4.11)

or equivalently, due to (4.10),

$$\begin{aligned}&\left( \varDelta t \varphi _{2} (\varDelta t \pmb {A}_{1}) \pmb {F}_{1}(\pmb {{\widetilde{\xi }}}_{h}^{m+1}, \pmb {0})\right) _{N_{\varGamma }, j} -\left( \varDelta t \varphi _{2} (\varDelta t \pmb {A}_{2}) \pmb {F}_{2}(\pmb {{\widetilde{\xi }}}_{h}^{m+1}, \pmb {0})\right) _{N_{\varGamma }, j} \nonumber \\&\quad = \sum _{l=1}^{2} (-1)^{l} \bigg [\text {e}^{\varDelta t \pmb {A}_{l}} \pmb {u}_{l}^{m} + \varDelta t \varphi _{1} (\varDelta t \pmb {A}_{l}) \pmb {F}_{l} (\pmb {{\widetilde{\xi }}}_{h}^{m}, \pmb {f}(t_{m})) \nonumber \\&\qquad +\, \varDelta t \varphi _{2} (\varDelta t \pmb {A}_{l}) \left( \pmb {F}_{l}\left( \pmb {0}, \pmb {f}(t_{m+1})\right) - \pmb {F}_{l}\left( \pmb {{\widetilde{\xi }}}_{h}^{m}, \pmb {f}(t_{m})\right) \right) \bigg ]_{N_{\varGamma },j}, \end{aligned}$$

(4.12)

for $j=1, \ldots , N,\; m=0,\ldots , M-1$. Hence, $\pmb {{\widetilde{\xi }}}_{h}^{m+1}=({\widetilde{\xi }}_{h,j}^{m+1})_{j=1, \ldots , N}$ can be expressed as a linear function in $\pmb {{\widetilde{\xi }}}_{h}^{m}, \pmb {u}_{1}^{m}, \pmb {u}_{2}^{m}, \pmb {f}(t_{m}), \pmb {f}(t_{m+1})$. Similarly to the case of localized ETD1, we compute $\pmb {{\widetilde{\xi }}}_{h} = (\pmb {{\widetilde{\xi }}}_{h}^{m})_{m=1, \ldots , M}$ by solving (4.11) iteratively either at each time step sequentially or over the whole time interval.

4.6 Space Localized ETD2

Assume that the solutions and interface values at $t_{m}$, $\pmb {u}_{1}^{m}$, $\pmb {u}_{2}^{m}$ and $\pmb {{\widetilde{\xi }}}_{h}^{m}$, are given, we aim to find the interface values at the next time level $\pmb {{\widetilde{\xi }}}_{h}^{m+1}$. For $l=1,2,$ and for $m=0, \ldots , M-1$, let ${\mathcal {E}}_{l,h}^{m+1}$ be the interface operator that maps the interface boundary data, the right-hand side function at $t_{m}$ and $t_{m+1}$, and the solution at $t_{m}$, $(\pmb {{\widetilde{\xi }}}_{h}^{m+1},\pmb {{\widetilde{\xi }}}_{h}^{m}, \pmb {f}(t_{m+1}), \pmb {f}(t_{m}),\pmb {u}_{l}^{m})$, to the solution $\pmb {u}_{l}^{m+1}$ given by (4.10) on the interface:

$$\begin{aligned} \begin{array}{lccc} {\mathcal {E}}_{l,h}^{m+1}\,:&{} {\mathbb {R}}^{N} \times {\mathbb {R}}^{N} \times {\mathbb {R}}^{N_{l}N} \times {\mathbb {R}}^{N_{l}N} \times {\mathbb {R}}^{N_{l}N} &{} \longrightarrow &{} {\mathbb {R}}^{N} \\ &{}(\pmb {{\widetilde{\xi }}}_{h}^{m+1},\pmb {{\widetilde{\xi }}}_{h}^{m}, \pmb {f}(t_{m+1}), \pmb {f}(t_{m}),\pmb {u}_{l}^{m})&{} \mapsto &{} \left( \pmb {u}_{l, N_{\varGamma },j}^{m+1}\right) _{j=1, \ldots , N}. \end{array} \end{aligned}$$

The discrete interface problem for $\pmb {{\widetilde{\xi }}}_{h}^{m+1}$ is given by:

$$\begin{aligned} {\overline{{\mathcal {S}}}}_{h}^{m+1} \pmb {{\widetilde{\xi }}}_{h}^{m+1} = {\overline{\chi }}_{h}^{m+1}(\pmb {{\widetilde{\xi }}}_{h}^{m}, \pmb {f}(t_{m+1}), \pmb {f}(t_{m}),\pmb {u}_{1}^{m},\pmb {u}_{2}^{m}), \end{aligned}$$

(4.13)

where

$$\begin{aligned}&{\overline{{\mathcal {S}}}}_{h}^{m+1}\pmb {{\widetilde{\xi }}}_{h}^{m+1} = {\mathcal {E}}_{1,h}^{m+1}(\pmb {{\widetilde{\xi }}}_{h}^{m+1},\pmb {0},\pmb {0},\pmb {0},\pmb {0})-{\mathcal {E}}_{2,h}^{m+1}(\pmb {{\widetilde{\xi }}}_{h}^{m+1},\pmb {0},\pmb {0},\pmb {0},\pmb {0}),\\&{\overline{\chi }}_{h}^{m+1}(\pmb {{\widetilde{\xi }}}_{h}^{m}, \pmb {f}(t_{m+1}), \pmb {f}(t_{m}),\pmb {u}_{1}^{m}, \pmb {u}_{2}^{m})=-({\mathcal {E}}_{1,h}^{m+1}(\pmb {0},\pmb {{\widetilde{\xi }}}_{h}^{m}, \pmb {f}(t_{m+1}), \pmb {f}(t_{m}),\pmb {u}_{1}^{m})\\&\quad -{\mathcal {E}}_{2,h}^{m+1}(\pmb {0},\pmb {{\widetilde{\xi }}}_{h}^{m}, \pmb {f}(t_{m+1}), \pmb {f}(t_{m}),\pmb {u}_{2}^{m})). \end{aligned}$$

We solve (4.13) iteratively to determine $\pmb {{\widetilde{\xi }}}_{h}^{m+1}$. Once it converges, we calculate $\pmb {u}_{1}^{m+1}$ and $\pmb {u}_{2}^{m+1}$, and advance to the next time level.

4.7 Space-Time Localized ETD2

Denote by $\pmb {{\widetilde{\xi }}}_{h}=(\pmb {{\widetilde{\xi }}}^m_{h})_{1\le m \le M}$ the interface space vector over all time steps. For $l=1,2,$ let ${\mathcal {G}}_{l,h}$ be the interface operator that maps the interface vector, the right-hand side function and initial data $(\pmb {{\widetilde{\xi }}}_{h}, \pmb {f}, \pmb {u}_{0})$, to the solution $(\pmb {u}_{l}^{m+1})_{m=0, \ldots ,M-1}$ given by (4.10) on the interface:

$$\begin{aligned} \begin{array}{lccc} {\mathcal {G}}_{l,h}\,:&{} {\mathbb {R}}^{NM} \times {\mathbb {R}}^{N_{l}NM} \times {\mathbb {R}}^{N_{l}N} &{} \longrightarrow &{} {\mathbb {R}}^{NM} \\ &{}(\pmb {{\widetilde{\xi }}}_{h}, \pmb {f}, \pmb {u}_{0})&{} \mapsto &{} \left( \pmb {u}_{l, N_{\varGamma },j}^{m}\right) _{j=1, \ldots , N, \; m=1, \ldots , M}. \end{array} \end{aligned}$$

In this case, the discrete interface problem is defined globally in time:

$$\begin{aligned} {\widehat{S}}_{h} \pmb {\xi }_{h}= {\widehat{\chi }}_{h}(\pmb {f},\pmb {u}_{0}), \end{aligned}$$

(4.14)

where

$$\begin{aligned} {\widehat{{\mathcal {S}}}}_{h} \pmb {\xi }_{h}&= {\mathcal {G}}_{1,h}(\pmb {{\widetilde{\xi }}}_{h}, \pmb {0}, \pmb {0})-{\mathcal {G}}_{2,h}(\pmb {{\widetilde{\xi }}}_{h}, \pmb {0}, \pmb {0}), \\ {\widehat{\chi }}_{h}(\pmb {f},\pmb {u}_{0})&= -({\mathcal {G}}_{1,h}(\pmb {0},\pmb {f},\pmb {u}_{0})-{\mathcal {G}}_{2,h}(\pmb {0},\pmb {f},\pmb {u}_{0})). \end{aligned}$$

Again, this problem is solved iteratively to find the interface space-time vector $\pmb {{\widetilde{\xi }}}_{h}$.

5 Mass Conservation

For backward Euler or Crank–Nicolson time-stepping techniques, it is well-known that the resulting schemes naturally conserve mass exactly. Now we will show that the monodomain ETD solution and the localized ETD solution also possess such important property.

Theorem 5.1

The monodomain ETD solution (4.4) with $f\equiv 0$ is conservative for all time steps:

$$\begin{aligned} \int _{\varOmega } \pmb {u}^{m}=\int _{\varOmega } \pmb {u}^{m-1}, \quad \forall \, 1\le m \le M. \end{aligned}$$

Proof

Conservation of mass in discrete setting is equivalent to taking a Riemann sum with values of u at the grid points:

$$\begin{aligned} \begin{aligned} \int _{\varOmega } \pmb {u}^{m}&= h^{2} \sum _{i,j=2}^{N-1}u_{i,j}^{m} +\frac{h^{2}}{4} \left( u_{1,1}^{m} +u_{1,N}^{m}+u_{N,1}^{m}+u_{N,N}^{m} \right) \\&\quad + \frac{h^{2}}{2} \left( \sum _{i=2}^{N-1} (u_{i,1}^{m}+u_{i,N}^{m})+\sum _{j=2}^{N-1} (u_{1,j}^{m}+u_{N,j}^{m}) \right) \\&= h^{2} \; \pmb {\iota }^{\top }\pmb {u}^{m}, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \pmb {\iota } = \left( \frac{1}{2} \pmb {b}, \underbrace{\pmb {b}, \pmb {b}, \ldots , \pmb {b}}_{(N-2) \text { times}}, \frac{1}{2} \pmb {b}\right) ^{\top } \in {\mathbb {R}}^{N^{2}}, \qquad \pmb {b}=\left( \frac{1}{2}, \underbrace{1,1, \ldots , 1}_{(N-2)\text { times}}, \frac{1}{2}\right) \in {\mathbb {R}}^{N}. \end{aligned}$$

Using this notation and (4.4), we have

$$\begin{aligned} \begin{aligned} \int _{\varOmega } \pmb {u}^{m}= \int _{\varOmega } e^{\varDelta t \pmb {A}} \pmb {u}^{m-1}&= \int _{\varOmega } \sum _{l=0}^{\infty } \frac{(\varDelta t)^{l} \pmb {A}^{l}}{l!} \pmb {u}^{m-1} \\&= h^{2} \; \pmb {\iota }^{\top } \left( \pmb {I} + \varDelta t \pmb {A}+ \frac{(\varDelta t)^{2} \pmb {A}^{2}}{2!} + \ldots \right) \pmb {u}^{m-1}. \end{aligned} \end{aligned}$$

Since $\pmb {\iota }^{\top } \pmb {A}= \pmb {0}$, only the first term with the identity remains and consequently

$$\begin{aligned} \int _{\varOmega } \pmb {u}^{m} = h^{2} \; \pmb {\iota }^{\top } \pmb {u}^{m-1}= \int _{\varOmega } \pmb {u}^{m-1}. \end{aligned}$$

The proof is completed. $\square$

Theorem 5.2

The nonoverlapping localized ETD1 and ETD2 solutions, (4.5) and (4.10) respectively, with $f\equiv 0$ are conservative for all time steps:

$$\begin{aligned} \int _{\varOmega _{1}} \pmb {u}_{1}^{m}+\int _{\varOmega _{2}} \pmb {u}_{2}^{m}=\int _{\varOmega _{1}} \pmb {u}_{1}^{m-1}+\int _{\varOmega _{2}} \pmb {u}_{2}^{m-1}, \qquad \forall \, 1\le m \le M. \end{aligned}$$

Proof

Similarly to the global ETD solution, we have

$$\begin{aligned} \int _{\varOmega _{1}} \pmb {u}_{1}^{m}+\int _{\varOmega _{2}} \pmb {u}_{2}^{m}=h^{2} \left( \pmb {\iota _{1}}^{\top } \pmb {u}_{1}^{m} + \pmb {\iota _{2}}^{\top }\pmb {u}_{2}^{m}\right) , \end{aligned}$$

(5.1)

where

$$\begin{aligned} \pmb {\iota }_{l} = \left( \frac{1}{2} \pmb {b}, \underbrace{\pmb {b}, \pmb {b}, \ldots , \pmb {b}}_{(N_{l}-2)\text { times}}, \frac{1}{2} \pmb {b}\right) ^{\top } \in {\mathbb {R}}^{NN_{l}}, \quad \text {for }l=1,2. \end{aligned}$$

In addition, as $\pmb {\iota }_{l}^{\top } \pmb {A}_{l} = 0$, we deduce that

$$\begin{aligned} \pmb {\iota }_{l}^{\top } \text {e}^{\varDelta t \pmb {A}_{l}} = \pmb {\iota }_{l}^{\top } \pmb {I}= \pmb {\iota }_{l}^{\top } \varphi _{1}(\varDelta t \pmb {A}_{l}), \quad \pmb {\iota }_{l}^{\top } \varphi _{2}(\varDelta t \pmb {A}_{l}) = \frac{1}{2}\pmb {\iota }_{l}^{\top } \pmb {I}, \quad \text {for l=1,2.} \end{aligned}$$

(5.2)

For the localized ETD1 solution (4.5), we have:

$$\begin{aligned} \pmb {\iota }_{1}^{\top } \pmb {u}_{1}^{m} =&\; \pmb {\iota }_{1}^{\top } \pmb {u}_{1}^{m-1}+ \varDelta t \, \pmb {\iota }_{1}^{\top } \pmb {F}_{1}\left( \pmb {{\widetilde{\xi }}}_h^{m},0\right) \nonumber \\ =&\;\pmb {\iota }_{1}^{\top } \pmb {u}_{1}^{m-1} + \varDelta t \, \frac{\nu }{h} \left[ \frac{1}{2} \left( {\widetilde{\xi }}^{m-1}_{h,1}+{\widetilde{\xi }}^{m-1}_{h,N}\right) + \sum _{j=2}^{N-1} {\widetilde{\xi }}^{m-1}_{h,j} \right] \end{aligned}$$

(5.3)

Similarly, we also have

$$\begin{aligned} \pmb {\iota }_{2}^{\top } \pmb {u}_{2}^{m}= & {} \pmb {\iota }_{2}^{\top } \pmb {u}_{2}^{m-1} - \varDelta t \, \frac{\nu }{h} \left[ \frac{1}{2} \left( {\widetilde{\xi }}^{m-1}_{h,1}+{\widetilde{\xi }}^{m-1}_{h,N}\right) + \sum _{j=2}^{N-1} {\widetilde{\xi }}^{m-1}_{h,j} \right] . \end{aligned}$$

(5.4)

Substituting (5.3) and (5.4) into (5.1), we obtain

$$\begin{aligned} \int _{\varOmega _{1}} \pmb {u}_{1}^{m}+\int _{\varOmega _{2}} \pmb {u}_{2}^{m} = h^{2} \left( \pmb {\iota }_{1}^{\top } \pmb {u}_{1}^{m-1} +\pmb {\iota }_{2}^{\top } \pmb {u}_{1}^{m-1} \right) =\int _{\varOmega _{1}} \pmb {u}_{1}^{m-1}+\int _{\varOmega _{2}} \pmb {u}_{2}^{m-1}, \end{aligned}$$

which completes the proof for the localized ETD1.

Similar results can be shown for the localized ETD2 solution (4.10):

$$\begin{aligned} \pmb {\iota }_{1}^{\top } \pmb {u}_{1}^{m} =&\; \pmb {\iota }_{1}^{\top } \pmb {u}_{1}^{m-1}+ \varDelta t \pmb {\iota }_{1}^{\top } \pmb {F}_{1}\left( \pmb {{\widetilde{\xi }}}_h^{m-1},0\right) + \frac{\varDelta t}{2} \pmb {\iota }_{1}^{\top } \left( \pmb {F}_{1}\left( \pmb {{\widetilde{\xi }}}_h^{m}, 0\right) - \pmb {F}_{1}\left( \pmb {{\widetilde{\xi }}}_h^{m-1},0\right) \right) \\ =&\;\pmb {\iota }_{1}^{\top } \pmb {u}_{1}^{m-1} + \varDelta t \, \frac{\nu }{h} \left[ \frac{1}{2} \left( {\widetilde{\xi }}^{m-1}_{h,1}+{\widetilde{\xi }}^{m-1}_{h,N}\right) + \sum _{j=2}^{N-1} {\widetilde{\xi }}^{m-1}_{h,j} \right] \\&+\frac{\varDelta t}{2} \, \frac{\nu }{h} \left[ \frac{1}{2} \left( {\widetilde{\xi }}^{m}_{h,1}-{\widetilde{\xi }}^{m-1}_{h,1}+{\widetilde{\xi }}^{m}_{h,N}-{\widetilde{\xi }}^{m-1}_{h,N}\right) + \sum _{j=2}^{N-1} \left( {\widetilde{\xi }}^{m}_{h,j}-{\widetilde{\xi }}^{m-1}_{h,j}\right) \right] , \end{aligned}$$

or equivalently,

$$\begin{aligned} \pmb {\iota }_{1}^{\top } \pmb {u}_{1}^{m}= & {} \pmb {\iota }_{1}^{\top } \pmb {u}_{1}^{m-1} + \frac{\varDelta t}{2} \, \frac{\nu }{h} \left[ \frac{1}{2} \left( {\widetilde{\xi }}^{m}_{h,1}+{\widetilde{\xi }}^{m-1}_{h,1}+{\widetilde{\xi }}^{m}_{h,N}+{\widetilde{\xi }}^{m-1}_{h,N}\right) +\sum _{j=2}^{N-1} \left( {\widetilde{\xi }}^{m}_{h,j}+{\widetilde{\xi }}^{m-1}_{h,j}\right) \right] . \end{aligned}$$

Similarly,

$$\begin{aligned} \begin{array}{rcl} \pmb {\iota }_{2}^{\top } \pmb {u}_{2}^{m}= & {} \pmb {\iota }_{2}^{\top } \pmb {u}_{2}^{m-1} - \frac{\varDelta t}{2} \, \frac{\nu }{h} \left[ \frac{1}{2} \left( {\widetilde{\xi }}^{m}_{h,1}+{\widetilde{\xi }}^{m-1}_{h,1}+{\widetilde{\xi }}^{m}_{h,N}+{\widetilde{\xi }}^{m-1}_{h,N}\right) + \sum _{j=2}^{N-1} \left( {\widetilde{\xi }}^{m}_{h,j}+{\widetilde{\xi }}^{m-1}_{h,j}\right) \right] . \end{array} \end{aligned}$$

Thus the localized ETD2 solution also conserves mass over all time steps. $\square$

6 Convergence Analysis

We now prove that the localized ETD1 and ETD2 solutions $\{(\pmb {u}_{1}^{m}, \pmb {u}_{2}^{m})\}_{m=0}^M$ defined by (4.5) and (4.10) respectively converge to the exact solution $(\pmb {u}_{1}, \pmb {u}_{2})$ of the semidiscrete subdomain problems (3.5) as $\varDelta t$ tends to zero. Denote by $\pmb {e}_{l}^{m} = \pmb {u}_{l}(t_{m})- \pmb {u}_{l}^{m},$ for $l=1,2,$ the error between the exact (in time) solution and the fully discrete localized ETD solution.

Theorem 6.1

For sufficiently smooth data, the nonoverlapping localized ETD1 solution converges as $\varDelta t$ tends to 0. In particular, the error bound

$$\begin{aligned} \Vert \pmb {e}_{l}^{m} \Vert _{\infty } \le CT\, \varDelta t, \qquad l=1,2, \end{aligned}$$

(6.1)

holds uniformly for $m=1, \ldots , M$ with a constant C depending on $\nu , h, \sup _{t\in (0,T), i,j} \vert f_{i,j}^{\prime }(t) \vert$ and $\sup _{t \in (0,T), j} \vert \xi _{h,j}^{\prime }(t) \vert$, and independent of $\varDelta t$.

Proof

The proof is mostly based on the variation-of-constants formula by which the exact (in time) solution of (3.5) is obtained as follows:

$$\begin{aligned} \pmb {u}_{l}(t_{m+1})= & {} \text {e}^{\varDelta t \pmb {A}_{l}} \pmb {u}_{l}(t_{m}) + \int _{0}^{\varDelta t} \text {e}^{(\varDelta t-s) \pmb {A}_{l}} \pmb {F}_{l}(\pmb {\xi }_{h}(t_{m}+s), \pmb {f}(t_{m}+s)) ds\nonumber \\= & {} \text {e}^{\varDelta t \pmb {A}_{l}} \pmb {u}_{l}(t_{m}) + \int _{0}^{\varDelta t} \text {e}^{(\varDelta t-s) \pmb {A}_{l}} \pmb {F}_{l}(\pmb {\xi }_{h}(t_{m}+s), \pmb {0}) ds \nonumber \\&+ \int _{0}^{\varDelta t} \text {e}^{(\varDelta t-s) \pmb {A}_{l}} \pmb {F}_{l}(\pmb {0}, \pmb {f}(t_{m}+s)) ds, \end{aligned}$$

(6.2)

for $l=1,2,$ and for $m=0, \ldots , M-1$ with the initial condition as given in (3.5). Let us expand the space vector function $\pmb {\xi }_{h}(t)$ in a Taylor series with the remainder in integral form:

$$\begin{aligned} \pmb {\xi }_{h}(t_{m}+s) = \pmb {\xi }_{h}(t_{m+1})+\int _{\varDelta t}^{s} \pmb {\xi }_{h}^{\prime }(t_{m}+\tau ) d\tau . \end{aligned}$$

(6.3)

A similar expansion can be obtained for $\pmb {f}(t_{m}+s)$. Substituting these expansions in (6.2) and note that $\pmb {F}_{l}$ is linear in each argument, we have that

$$\begin{aligned} \pmb {u}_{l}(t_{m+1})&= \,\text {e}^{\varDelta t \pmb {A}_{l}} \pmb {u}_{l}(t_{m}) + \int _{0}^{\varDelta t} \text {e}^{(\varDelta t-s) \pmb {A}_{l}} \pmb {F}_{l}(\pmb {\xi }_{h}(t_{m+1}), \pmb {0}) ds \nonumber \\&\quad + \int _{0}^{\varDelta t} \text {e}^{(\varDelta t-s) \pmb {A}_{l}} \pmb {F}_{l}(\pmb {0}, \pmb {f}(t_{m+1})) ds + \gamma _{l,m+1}, \end{aligned}$$

or equivalently,

$$\begin{aligned} \pmb {u}_{l}(t_{m+1}) =&\;\text {e}^{\varDelta t \pmb {A}_{l}} \pmb {u}_{l}(t_{m}) + \varDelta t \varphi _{1}(\varDelta t \pmb {A}_{l}) \pmb {F}_{l}(\pmb {\xi }_{h}(t_{m+1}), \pmb {f}(t_{m+1})) + \gamma _{l,m+1}, \end{aligned}$$

(6.4)

where $\gamma _{l,m+1}$ is the defect given by

$$\begin{aligned} \gamma _{l,m+1}=&\int _{0}^{\varDelta t} \text {e}^{(\varDelta t-s)\pmb {A}_{l}} \int _{\varDelta t}^{s} \pmb {F}_{l}(\pmb {\xi }_{h}^{\prime }(t_{m}+\tau ), \pmb {f}^{\prime }(t_{m}+\tau )) d\tau \,ds. \end{aligned}$$

(6.5)

The error equation is derived by subtracting (4.5) from (6.4):

$$\begin{aligned} \begin{aligned}&\pmb {e}_{l}^{m+1}=\;\text {e}^{\varDelta t \pmb {A}_{l}} \pmb {e}_{l}^{m}+ \varDelta t \varphi _{1}(\varDelta t \pmb {A}_{l}) \pmb {F}_{l}(\pmb {e}_{\xi }^{m+1}, \pmb {0}) + \gamma _{l,m+1}, \end{aligned} \end{aligned}$$

(6.6)

where $\pmb {e}_{l}^{m} = \pmb {u}_{l}(t_{m+1}) - \pmb {u}^{m+1}$, for $l=1,2,$ and $\pmb {e}_{\xi }^{m}=\pmb {\xi }_{h}(t_{m}) - \pmb {{\widetilde{\xi }}}_{h}^{m}$, for $m=0, \ldots , M$. We solve the error Eq. (6.6) recursively and obtain

$$\begin{aligned} \pmb {e}_{l}^{m+1}&= \varDelta t \sum _{p=0}^{m} \text {e}^{(m-p)\varDelta t \pmb {A}_{l}} \varphi _{1}(\varDelta t \pmb {A}_{l}) \pmb {F}_{l}(\pmb {e}_{\xi }^{p+1}, \pmb {0}) + \sum _{p=0}^{m} \text {e}^{p\varDelta t \pmb {A}_{l}} \gamma _{l,m+1-p}. \end{aligned}$$

(6.7)

To derive the estimate for the terms on the right-hand side, we notice that the subdomain solutions match on the interface:

$$\begin{aligned} \pmb {e}^{m+1}_{1, N_{\varGamma },j} = \pmb {e}^{m+1}_{2, N_{\varGamma },j}. \end{aligned}$$

(6.8)

Note that the entries of $\text {e}^{t \pmb {A}_{l}}$ (and thus those of $\varphi _{1}(t\pmb {A}_{l})$) are nonnegative for $t\ge 0$ (see, for instance, [18]) and

$$\begin{aligned} \pmb {F}_{1}(\pmb {e}_{\xi }^{m+1}, \pmb {0})&= \left( 0, \ldots , 0, 2\frac{\nu }{h}e_{\xi ,1}^{m+1}, \ldots , 2\frac{\nu }{h}e_{\xi ,N}^{m+1}\right) , \\ \pmb {F}_{2}(\pmb {e}_{\xi }^{m+1}, \pmb {0})&= \left( -2\frac{\nu }{h}e_{\xi ,1}^{m+1}, \ldots , -2\frac{\nu }{h}e_{\xi ,N}^{m+1}, 0, \ldots , 0\right) . \end{aligned}$$

Using these facts and substituting (6.8) into (6.6) yields

$$\begin{aligned} \vert \varDelta t \varphi _{1}(\varDelta t \pmb {A}_{l}) \pmb {F}_{l}(\pmb {e}_{\xi }^{m+1}, \pmb {0}) \vert _{N_{\varGamma },j}&\le \vert \text {e}^{\varDelta t \pmb {A}_{1}} \pmb {e}_{1}^{m} - \text {e}^{\varDelta t \pmb {A}_{2}} \pmb {e}_{2}^{m} \vert _{N_{\varGamma }, j} + \vert \gamma _{1,m+1} - \gamma _{2,m+1}\vert _{N_{\varGamma },j}. \end{aligned}$$

(6.9)

Since most of the entries of $\pmb {F}_{l}(\pmb {e}_{\xi }^{m+1}, \pmb {0})$ are zeros except those on the interface, $\pmb {A}_{l}$ is diagonally dominant and by the fact that the exponential of a banded matrix has elements decaying rapidly away from the diagonal [23], it is implied that

$$\begin{aligned} \Vert \varphi _{1}(\varDelta t \pmb {A}_{l}) \pmb {F}_{l}(\pmb {e}_{\xi }^{m+1}, \pmb {0}) \Vert _{\infty }&\le \max _{j}\vert \varphi _{1}(\varDelta t \pmb {A}_{l}) \pmb {F}_{l}(\pmb {e}_{\xi }^{m+1}, \pmb {0}) \vert _{N_{\varGamma },j}. \end{aligned}$$

(6.10)

On the other hand, according to Theorem 2 in [28] (or Lemma 3.2 in [9]), it holds that

$$\begin{aligned} \Vert \text {e}^{t\pmb {A}_{l}} \Vert _{\infty } \le 1,\quad \forall \, t>0. \end{aligned}$$

Using this results and by definition of the defect $\gamma _{l, m+1}$ in (6.5), we deduce that

$$\begin{aligned} \Vert \gamma _{1,m+1} - \gamma _{2,m+1} \Vert _{\infty }&\le \left( \sup _{t\in (0,T), i,j} \vert f_{i,j}^{\prime }(t) \vert + 2\frac{\nu }{h} \sup _{t \in (0,T), j} \vert \xi _{h,j}^{\prime }(t) \vert \right) \frac{(\varDelta t)^{2}}{2} \\&\le C (\varDelta t)^{2}, \end{aligned}$$

and consequently,

$$\begin{aligned} \left\| \sum _{p=0}^{m} \text {e}^{p\varDelta t \pmb {A}_{l}} \gamma _{l,m+1-p} \right\| _{\infty } \le \sum _{p=0}^{m} C(\varDelta t)^{2} \le CT \varDelta t, \end{aligned}$$

(6.11)

where C denotes a generic constant independent of $\varDelta t$ and T. Combining the results in (6.9)–(6.11), we arrive at

$$\begin{aligned} \Vert \varDelta t \varphi _{1}(\varDelta t \pmb {A}_{l}) \pmb {F}_{l}(\pmb {e}_{\xi }^{m+1}, \pmb {0}) \Vert _{\infty } \le \max _{j} \vert \text {e}^{\varDelta t \pmb {A}_{1}} \pmb {e}_{1}^{m} - \text {e}^{\varDelta t \pmb {A}_{2}} \pmb {e}_{2}^{m} \vert _{N_{\varGamma }, j} +C (\varDelta t)^{2}. \end{aligned}$$

(6.12)

As we consider the convergence when $\varDelta t$ goes to zero, we can approximate

$$\begin{aligned} \text {e}^{\varDelta t \pmb {A}_{l}} \pmb {e}_{l}^{m} = (\pmb {I}+ \varDelta t \pmb {A}_{l}) \pmb {e}_{l}^{m} + C(\varDelta t)^{2}, \end{aligned}$$

(6.13)

and so

$$\begin{aligned} \vert \text {e}^{\varDelta t \pmb {A}_{1}} \pmb {e}_{1}^{m} - \text {e}^{\varDelta t \pmb {A}_{2}} \pmb {e}_{2}^{m} \vert _{N_{\varGamma }, j}&= \left| \varDelta t \pmb {A}_{1} \pmb {e}_{1}^{m} - \varDelta t \pmb {A}_{2} \pmb {e}_{2}^{m} \right| _{N_{\varGamma },j} + C(\varDelta t)^{2}. \end{aligned}$$

(6.14)

Note that the solutions match on the interface at all m, i.e. $e^{m}_{1, N_{\varGamma },j} = e^{m}_{2, N_{\varGamma },j}$ for $j=1, \ldots , N$. Thus by the definition of $\pmb {A}_{l}$, we rewrite (6.14) as

$$\begin{aligned} \vert \text {e}^{\varDelta t \pmb {A}_{1}} \pmb {e}_{1}^{m} - \text {e}^{\varDelta t \pmb {A}_{2}} \pmb {e}_{2}^{m} \vert _{N_{\varGamma }, j} = \varDelta t\frac{2\nu }{h^{2}}\vert e^{m}_{1, N_{\varGamma }-1,j} - e^{m}_{2, N_{\varGamma }+1,j} \vert + C(\varDelta t)^{2}. \end{aligned}$$

Plug this back to (6.15) we obtain

$$\begin{aligned} \Vert \varDelta t \varphi _{1}(\varDelta t \pmb {A}_{l}) \pmb {F}_{l}(\pmb {e}_{\xi }^{m+1}, \pmb {0}) \Vert _{\infty } \le \varDelta t\frac{2\nu }{h^{2}} \left( \Vert \pmb {e}^{m}_{1}\Vert _{\infty } + \Vert \pmb {e}^{m}_{2} \Vert _{\infty }\right) + C(\varDelta t)^{2}. \end{aligned}$$

(6.15)

Using this and (6.11), we can deduce from (6.7) that

$$\begin{aligned} \Vert \pmb {e}_{l}^{m+1} \Vert _{\infty } \le \varDelta t \frac{2\nu }{h^{2}} \sum _{p=0}^{m} \left( \Vert \pmb {e}^{m}_{1}\Vert _{\infty } + \Vert \pmb {e}^{m}_{2} \Vert _{\infty }\right) + CT \varDelta t. \end{aligned}$$

(6.16)

The application of the discrete Gronwall lemma to

$$\begin{aligned} \Vert \pmb {e}_{1}^{m+1} \Vert _{\infty } + \Vert \pmb {e}_{2}^{m+1} \Vert _{\infty } \le \varDelta t \frac{4\nu }{h^{2}} \sum _{p=0}^{m} \left( \Vert \pmb {e}^{m}_{1}\Vert _{\infty } + \Vert \pmb {e}^{m}_{2} \Vert _{\infty }\right) + CT \varDelta t, \end{aligned}$$

(6.17)

completes the Proof of Theorem 6.1. $\square$

Theorem 6.2

For sufficiently smooth data, the nonoverlapping localized ETD2 solution converges as $\varDelta t$ tends to 0. In particular, the error bound

$$\begin{aligned} \Vert \pmb {e}_{l}^{m} \Vert _{\infty } \le CT\, (\varDelta t)^{2}, \quad l=1,2, \end{aligned}$$

(6.18)

holds uniformly for $m=1, \ldots , M$ with a constant C depending on $\nu , h, \sup _{t\in (0,T), i,j} \vert f_{i,j}^{\prime \prime }(t) \vert$ and $\sup _{t \in (0,T), j} \vert \xi _{h,j}^{\prime \prime }(t) \vert$, and independent of $\varDelta t$.

Proof

Theorem 6.2 can be proved in a similar manner as Theorem 6.1. For the ease of representation, same notation is used for the second order in time approximate solution, error and the defect. Using again the variation-of-constants formula (6.2) but perform higher-order Taylor expansion of the space vector function $\pmb {\xi }_{h}(t)$:

$$\begin{aligned} \pmb {\xi }_{h}(t_{m}+s) = \pmb {\xi }_{h}(t_{m})+s\pmb {\xi }_{h}^{\prime }(t_{m}) + \int _{0}^{s} (s-\tau ) \pmb {\xi }_{h}^{\prime \prime }(t_{m}+\tau ) d\tau . \end{aligned}$$

(6.19)

For $s=\varDelta t$, we have

$$\begin{aligned} \pmb {\xi }_{h}(t_{m+1}) = \pmb {\xi }_{h}(t_{m})+\varDelta t \pmb {\xi }_{h}^{\prime }(t_{m}) + \int _{0}^{\varDelta t} (\varDelta t-\tau ) \pmb {\xi }_{h}^{\prime \prime }(t_{m}+\tau ) d\tau , \end{aligned}$$

i.e.,

$$\begin{aligned} \pmb {\xi }_{h}^{\prime }(t_{m}) = \frac{\pmb {\xi }_{h}(t_{m+1})-\pmb {\xi }_{h}(t_{m})}{\varDelta t} +\frac{1}{\varDelta t}\int _{0}^{\varDelta t} (\tau -\varDelta t) \pmb {\xi }_{h}^{\prime \prime }(t_{m}+\tau ) d\tau . \end{aligned}$$

Substitution of this to (6.19) yields:

$$\begin{aligned} \pmb {\xi }_{h}(t_{m}+s)&= \pmb {\xi }_{h}(t_{m})+s \left[ \frac{\pmb {\xi }_{h}(t_{m+1})-\pmb {\xi }_{h}(t_{m})}{\varDelta t} + \frac{1}{\varDelta t}\int _{0}^{\varDelta t} (\tau -\varDelta t) \pmb {\xi }_{h}^{\prime \prime }(t_{m}+\tau ) d\tau \right] \\&\quad + \int _{0}^{s} (s-\tau ) \pmb {\xi }_{h}^{\prime \prime }(t_{m}+\tau ) d\tau . \end{aligned}$$

A similar expansion can be obtained for $\pmb {f}(t_{m}+s)$, then by substitution of these expansions in (6.2), we have that

$$\begin{aligned} \pmb {u}_{l}(t_{m+1})&= \text {e}^{\varDelta t \pmb {A}_{l}} \pmb {u}_{l}(t_{m}) + \int _{0}^{\varDelta t} \text {e}^{(\varDelta t-s) \pmb {A}_{l}} [\pmb {F}_{l}(\pmb {\xi }_{h}(t_{m}), \pmb {0}) + \pmb {F}_{l}(\pmb {0}, \pmb {f}(t_{m}))] ds \nonumber \\&\quad + \int _{0}^{\varDelta t} \text {e}^{(\varDelta t-s) \pmb {A}_{l}} \left[ \frac{\pmb {F}_{l}(\pmb {\xi }_{h}(t_{m+1}), \pmb {0})-\pmb {F}_{l}(\pmb {\xi }_{h}(t_{m}), \pmb {0})}{\varDelta t}\right] s \, ds \nonumber \\&\quad + \int _{0}^{\varDelta t} \text {e}^{(\varDelta t-s) \pmb {A}_{l}} \left[ \frac{\pmb {F}_{l}(\pmb {0}, \pmb {f}(t_{m+1}))-\pmb {F}_{l}(\pmb {0}, \pmb {f}(t_{m}))}{\varDelta t}\right] s \, ds + \gamma _{l,m+1}, \end{aligned}$$

or equivalently,

$$\begin{aligned} \pmb {u}_{l}(t_{m+1}) =&\;\text {e}^{\varDelta t \pmb {A}_{l}} \pmb {u}_{l}(t_{m}) + \varDelta t \varphi _{1}(\varDelta t \pmb {A}_{l}) \pmb {F}_{l}(\pmb {\xi }_{h}(t_{m}), \pmb {f}(t_{m})) \nonumber \\&+ \varDelta t \varphi _{2}(\varDelta t \pmb {A}_{l}) \left[ \pmb {F}_{l}(\pmb {\xi }_{h}(t_{m+1}), \pmb {f}(t_{m+1}))-\pmb {F}_{l}(\pmb {\xi }_{h}(t_{m}), \pmb {f}(t_{m}))\right] + \gamma _{l,m+1}, \end{aligned}$$

(6.20)

where $\gamma _{l,m+1}$ is the defect given by

$$\begin{aligned} \gamma _{l,m+1}=&\int _{0}^{\varDelta t} \text {e}^{(\varDelta t-s)\pmb {A}_{l}} \left( \frac{1}{\varDelta t}\int _{0}^{\varDelta t} (\tau -\varDelta t) \pmb {F}_{l}(\pmb {\xi }_{h}^{\prime \prime }(t_{m}+\tau ), \pmb {f}^{\prime \prime }(t_{m}+\tau )) d\tau \right) s \, ds \\&\ + \int _{0}^{\varDelta t} \text {e}^{(\varDelta t-s)\pmb {A}_{l}} \int _{0}^{s} (s-\tau ) \pmb {F}_{l}(\pmb {\xi }_{h}^{\prime \prime }(t_{m}+\tau ), \pmb {f}^{\prime \prime }(t_{m}+\tau )) d\tau \, ds. \end{aligned}$$

By comparing (6.20) and (4.10), we obtain:

$$\begin{aligned} \begin{aligned}&\pmb {e}_{l}^{m+1}=\;\text {e}^{\varDelta t \pmb {A}_{l}} \pmb {e}_{l}^{m}+ \varDelta t \varphi _{1}(\varDelta t \pmb {A}_{l}) \pmb {F}_{l}(\pmb {e}_{\pmb {\xi }}^{m}, \pmb {0}) \\&\quad + \varDelta t \varphi _{2}(\varDelta t \pmb {A}_{l}) \left[ \pmb {F}_{l}(\pmb {e}_{\pmb {\xi }}^{m+1}, \pmb {0})-\pmb {F}_{l}(\pmb {e}_{\pmb {\xi }}^{m}, \pmb {0})\right] + \gamma _{l,m+1}, \end{aligned} \end{aligned}$$

(6.21)

and hence

$$\begin{aligned} \begin{aligned} \pmb {e}_{l}^{m+1}&=\varDelta t \sum _{p=0}^{m} \text {e}^{(m-p) \varDelta t \pmb {A}_{l}} \left( \varphi _{1}(\varDelta t \pmb {A}_{l}) \pmb {F}_{l}(\pmb {e}_{\xi }^{p}, \pmb {0})+ \varphi _{2}(\varDelta t \pmb {A}_{l}) \left[ \pmb {F}_{l}(\pmb {e}_{\xi }^{p+1}, \pmb {0}) -\pmb {F}_{l}(\pmb {e}_{\xi }^{p}, \pmb {0}) \right] \right) \\&\quad + \sum _{p=0}^{m} \text {e}^{p\varDelta t \pmb {A}_{l}} \gamma _{l,m+1-p}. \end{aligned} \end{aligned}$$

(6.22)

by recursion. Using the same argument as in the localized ETD1 case, we obtain a bound for the defect as follows:

$$\begin{aligned} \begin{aligned} \Vert \gamma _{l,m} \Vert _{\infty }&\le \left( \sup _{t\in (0,T), i,j} \vert f_{i,j}^{\prime \prime }(t) \vert + 2\frac{\nu }{h} \sup _{t \in (0,T), j} \vert \xi _{h,j}^{\prime \prime }(t) \vert \right) \\&\quad \cdot \left( \left| \int _{0}^{\varDelta t} s \frac{1}{\varDelta t} \int _{0}^{\varDelta t} (\tau -\varDelta t) d\tau ds \right| + \left| \int _{0}^{\varDelta t} \int _{0}^{s} (s-\tau ) d\tau ds \right| \right) \\&\le C (\varDelta t)^{3}. \end{aligned} \end{aligned}$$

(6.23)

As the subdomain solutions match on the interface, as in the proof of Theorem 6.1, we deduce that

$$\begin{aligned} \begin{aligned}&\left\| \varDelta t \left( \varphi _{1}(\varDelta t \pmb {A}_{l}) \pmb {F}_{l}(\pmb {e}_{\xi }^{p}, \pmb {0})+ \varphi _{2}(\varDelta t \pmb {A}_{l}) \left[ \pmb {F}_{l}(\pmb {e}_{\xi }^{p+1}, \pmb {0}) -\pmb {F}_{l}(\pmb {e}_{\xi }^{p}, \pmb {0}) \right] \right) \right\| _{\infty } \\&\quad \le \vert \text {e}^{\varDelta t \pmb {A}_{1}} \pmb {e}_{1}^{m} - \text {e}^{\varDelta t \pmb {A}_{2}} \pmb {e}_{2}^{m} \vert _{N_{\varGamma }, j} +C (\varDelta t)^{3}. \end{aligned} \end{aligned}$$

(6.24)

Different from the case of localized ETD1, here we use higher-order approximation for the matrix exponential vector products:

$$\begin{aligned} \text {e}^{\varDelta t \pmb {A}_{l}} \pmb {e}_{l}^{m} = \left( \pmb {I}+ \varDelta t \pmb {A}_{l}+ \frac{(\varDelta t)^2}{2} \pmb {A}_{l}^{2}\right) \pmb {e}_{l}^{m} + C(\varDelta t)^{3}. \end{aligned}$$

(6.25)

By definition of $\pmb {A}_{l}$ and as the solutions match on the interface, after some calculations, we have that

$$\begin{aligned}&\left( \pmb {A}_{1}^{2} \pmb {e}_{1}^{m} - \pmb {A}_{2}^{2} \pmb {e}_{2}^{m}\right) _{N_{\varGamma }, j} = \left( \pmb {A}_{1} (\pmb {A}_{1}\pmb {e}_{1}^{m}) - \pmb {A}_{2} (\pmb {A}_{2} \pmb {e}_{2}^{m})\right) _{N_{\varGamma }, j} =\left( \frac{\nu }{h^{2}}\right) ^{2} \\&\quad \cdot \left\{ \begin{array}{l} \big \vert (2e_{1,N_{\varGamma }-2, j}+8e_{1, N_{\varGamma }-1, j+1}-16 e_{1,N_{\varGamma }-1,1}) \\ \quad - (2e_{2,N_{\varGamma }+2, j}+8e_{2, N_{\varGamma }+1, j+1}-16 e_{2,N_{\varGamma }+1,1}) \big \vert , \quad \text {if} \; j=1,\\ \big \vert (2e_{1,N_{\varGamma }-2, j}+4e_{1, N_{\varGamma }-1, j+1}+4e_{1, N_{\varGamma }-1, j-1}-16 e_{1,N_{\varGamma }-1,1}) \\ \quad - (2e_{2,N_{\varGamma }+2, j}+4e_{2, N_{\varGamma }+1, j+1}+4e_{2, N_{\varGamma }+1, j-1}-16 e_{2,N_{\varGamma }+1,1}) \big \vert , \quad \text {if} \; 1< j < N, \\ \big \vert (2e_{1,N_{\varGamma }-2, j}+8e_{1, N_{\varGamma }-1, j-1}-16 e_{1,N_{\varGamma }-1,1}) \\ \quad - (2e_{2,N_{\varGamma }+2, j}+8e_{2, N_{\varGamma }+1, j-1}-16 e_{2,N_{\varGamma }+1,1}) \big \vert , \quad \text {if} \; j = N. \end{array} \right. \end{aligned}$$

Thus

$$\begin{aligned} \vert \text {e}^{\varDelta t \pmb {A}_{1}} \pmb {e}_{1}^{m} - \text {e}^{\varDelta t \pmb {A}_{2}} \pmb {e}_{2}^{m} \vert _{N_{\varGamma }, j} \le \left( \varDelta t\frac{2\nu }{h^{2}}+ \frac{(\varDelta t)^2}{2} 26 \left( \frac{\nu }{h^{2}}\right) ^{2} \right) \left( \Vert \pmb {e}^{m}_{1}\Vert _{\infty } + \Vert \pmb {e}^{m}_{2} \Vert _{\infty }\right) + C(\varDelta t)^{3}. \end{aligned}$$

Substituting this in (6.22), we arrive at

$$\begin{aligned} \Vert \pmb {e}_{l}^{m+1} \Vert _{\infty } \le \varDelta t \left( \frac{2\nu }{h^{2}}+ 13 \varDelta t \frac{\nu ^{2}}{h^{4}} \right) \sum _{p=0}^{m} \left( \Vert \pmb {e}^{m}_{1}\Vert _{\infty } + \Vert \pmb {e}^{m}_{2} \Vert _{\infty }\right) + CT (\varDelta t)^{2}. \end{aligned}$$

(6.26)

Again, we use the discrete Gronwall lemma to conclude the proof. $\square$

7 Numerical Experiments

We perform numerical experiments in two dimensions to study the convergence behavior, the accuracy in time and the mass conservation property of the proposed algorithms. The case of multiple subdomains having cross points produced by two-direction domain decomposition is more common and useful in practice and thus will be considered in the following. Though it is not presented, the convergence behavior for the strip decomposition is similar to the multiple subdomain case with cross points. Three test cases are considered: the error equation with zero solution, a test case with a known analytical solution and a test case with mass conservation. In all the experiments except the one in Sect. 7.3, we set the diffusion coefficient $\nu =1$.

7.1 The Error Equation

We consider the error equation on $\varOmega =(0,1)^{2}$ and start the iteration for the interface problems with a random initial guess. Denote by $\text {NPX}$ and $\text {NPY}$ the numbers of subdomains in x- and y-directions respectively. The mesh size is fixed, $h=1/64$, while the time step size $\varDelta t$ and the final time T are varying. We investigate the convergence of the space localized ETD (S-LETD) method with respect to the time step size $\varDelta t$ and the convergence of the space-time localized ETD (ST-LETD) method with respect to the time horizon T. We decompose the domain into four subdomains having one cross point, $\text {NPX}=\text {NPY}=2$.

For S-LETD, we compute the the normalized error in $L^{\infty }(\varOmega )$ at the first time level $t=\varDelta t$ as a function of the number of iterations. Figure 3 shows the error curves of the first and second order S-LETD schemes for different $\varDelta t \in \{0.5, 0.25, 0.125, 0.0625\}$. We observe superconvergence at the first few iterations then the convergence becomes slower. The performance for the first and second order ETD methods is quite similar. Recall that for overlapping localized ETD methods [18], the convergence is faster when the time step size is smaller. However, here the convergence rate is almost independent of the time step size, so that large time step sizes can be used without affecting the convergence speed.

Fig. 3

First order (left) and second order (right) S-LETD schemes: Errors at $t=\varDelta t$ in $L^{\infty }(\varOmega )$-norm for different time step sizes $\varDelta t$. Four subdomains with a cross point are considered: $\text {NPX}=\text {NPY}=2$

For ST-LETD, we fix the time step size $\varDelta t=0.125$ but vary T. Figure 4 shows the error curves of the first and second order ST-LETD schemes for different $T \in \{0.25, 0.5, 1, 2\}$. We also observe superconvergence for initial few iterations, and as the error reduction becomes larger, the effect of T on the convergence speed is more noticeable. In particular, for sufficiently small errors, the larger T, the larger number of iterations needed to reach the same error. Again, the first and second order ETD schemes have comparable convergence behaviors. Note that the cost per iteration for S-LETD and ST-LETD methods is different. Thus, for the same time step size and time horizon, it is implied from Figs. 3 and 4 that S-LETD methods are more efficient than ST-LETD methods in terms of total subdomain solves for the whole time interval.

Fig. 4

First order (left) and second order (right) ST-LETD schemes: Errors at $t=T$ in $L^{\infty }(\varOmega )$-norm for different final times T. Four subdomains with a cross point are considered: $\text {NPX}=\text {NPY}=2$

Next, we study the effect of the number of subdomains on the convergence speed. We consider the multiple subdomains with cross points $\text {NPX}=\text {NPY} \in \{2,3,4\}$. The time step size and the final time are fixed with $\varDelta t=0.125$ and $T=1$. In Fig. 5, the error curves of the first and second order S-LETD schemes at the first time step $t=\varDelta t$ are shown. Similar results for the first and second order ST-LETD schemes are obtained and plotted in Fig. 6. It is expected that the convergence speed declines as the number of subdomains increases. For S-LETD, it is just a slightly slower convergence speed, while for ST-LETD (especially ST-LETD1), the convergence is quite slower for large numbers of subdomains.

Fig. 5

First order (left) and second order (right) S-LETD schemes: Errors at $t=\varDelta t$ with $\varDelta t= 0.125$ in $L^{\infty }(\varOmega )$-norm for different numbers of subdomains (with cross points)

Fig. 6

First order (left) and second order (right) ST-LETD schemes: Errors at $t=T$ with $T=1$ in $L^{\infty }(\varOmega )$-norm for different numbers of subdomains

7.2 A Test Case with Known Analytical Solution

Next, we study the accuracy in time of the localized ETD schemes. We consider a test case with the exact solution given by

$$\begin{aligned} u(x,y,t)= \exp (-\,4t) \sin \left( x-\frac{1}{4}\right) \sin \left( 2y-\frac{1}{4}\right) . \end{aligned}$$

on $\varOmega =(0,\pi )^{2}$. In space, we use a Cartesian grid with a fixed mesh size $h=\pi /256$. In time, uniform time partitions are considered with different $\varDelta t$. We decompose $\varOmega$ into square subdomains of equal sizes, $\text {NPX}=\text {NPY} \in \{2,3,4\}$. The “converged” localized ETD solutions are computed after some fixed number of GMRES iterations and compared with the exact solution. Tables 1 and 2 show the errors in $L^{\infty }(\varOmega )$-norm at $t=T$ with $T=0.5$ between the first and second order global/localized ETD solutions and the exact solution. The corresponding numbers of iterations are listed in brackets. Note that the localized ETD solutions and the global ETD solutions are not equivalent but they all converge to the exact solution as $\varDelta t$ tends to zero. Thus, the errors by localized and global ETD solutions are not exactly the same. Importantly, we observe numerically that the temporal accuracy of the localized ETD solutions are well maintained.

S-LETD schemes converge after a few iterations despite the number of subdomains and reaches the accuracy of the monodomain ETD solution (this is consistent with the results for the error equation, cf. Fig. 5). However, for ST-LETD schemes, the convergence is slower: with the same number of iterations, the numerical errors by S-LETD are nearly the same as those by the monodomain ETD solution while the numerical errors by ST-LETD are much larger. ST-LETD methods take more iterations to achieve the desired accuracy, especially when the time step sizes are small. Finally, Fig. 7 confirms the first and second order of convergence in time of the global and converged localized ETD solutions. As the errors for different decomposition are quite the same (cf. Tables 1 and 2), we only display the errors of the localized ETD solutions for the case of $4 \times 4$ subdomains.

Table 1 $L^{\infty }(\varOmega )$-errors between the localized ETD1 solutions and the exact solution at the final time $T=0.5$. Numbers of GMRES iterations are shown in square brackets

Table 2 $L^{\infty }(\varOmega )$-errors between the localized ETD2 solutions and the exact solution at the final time $T=0.5$. Numbers of GMRES iterations are shown in square brackets

Fig. 7

$L^{\infty }(\varOmega )$-norm errors in logarithmic scales at $T=0.5$ of the global ETD solutions and the localized ETD solutions for the case of $4 \times 4$ subdomains. Both first and second order accuracy is shown

7.3 A Test Case with Mass Conservation

To verify that the proposed localized ETD methods satisfy exact mass conservation, we consider a test case with no-flux boundary conditions and a zero right-hand side function. The initial condition is given by

$$\begin{aligned} u_{0}(x,y)=xy(x-1)(y-1)e^{-100((x-0.5)^2+(y-0.5)^2)}, \quad (x,y) \in (0,1)^{2}, \end{aligned}$$

and the diffusion coefficient is $\nu =0.1$. The solution is approximated on the mesh of size $h=1/64$ with a time step size $\varDelta t=1/64$. We consider both strip and cross decomposition with $4 \times 1$ and $4 \times 4$ subdomains respectively. The “converged” localized ETD solutions are obtained by solving the interface problems iteratively by GMRES with a tolerance of $10^{-6}$. The relative changes of the total mass by the first and second order global and localized ETD solutions as a function of time are plotted in Fig. 8, which confirms that the localized ETD methods conserve mass exactly as the global ETD methods.

Fig. 8

Evolution of the relative changes of total mass by the first and second order global and localized ETD schemes for the cases of $4 \times 1$ and $4 \times 4$ subdomains

8 Conclusions

We have proposed space and space-time localized ETD methods based on nonoverlapping subdomains for solving diffusion problems discretized in space by finite differences. The first approach involves at each iteration the solution of stationary problems in the subdomains while the second approach involves at each iteration the solution of time-dependent subdomain problems. The proposed localized ETD schemes of first and second order in time all conserve mass exactly and their solution converges to the exact space semidiscrete solution as $\varDelta t$ tends to zero. We have carried out numerical experiments for multiple subdomains having cross points on different test cases. Numerical results confirm that the proposed methods converge as the number of iterations increases and compare quite well with the global ETD methods with respect to accuracy in time. It takes only few iterations for the space localized ETD method to reach similar errors as the global ETD method, while for the space-time localized ETD method, the convergence of the iterations is slower. For heterogeneous problems, it could be necessary to construct an efficient preconditioner for the interface problems to make the convergence independent of the jumps in the coefficients. This will be an important topic of our future work, in addition to developing localized ETD methods based on Robin transmission conditions with optimized parameters (see, e.g., [2, 14, 17]). Moreover, though not yet explored in this paper, as space-time localized ETD methods are global in time, it makes possible the use of different time step sizes in different subdomains with some suitable $L^{2}$ projection to exchange information between nonconforming time grids. This feature can be very useful when a nonuniform mesh is employed for the spatial discretization.