Abstract
We construct a family of compact fourth order accurate finite difference schemes for the three dimensional scalar wave (d’Alembert) equation with constant or variable propagation speed. High order accuracy is of key importance for the numerical simulation of waves as it reduces the dispersion error (i.e., the pollution effect). The schemes that we propose are built on a stencil that has only three nodes in any coordinate direction or in time, which eliminates the need for auxiliary initial or boundary conditions. These schemes are implicit in time and conditionally stable. A particular scheme with the maximum Courant number can be chosen within the proposed class. The inversion at the upper time level is done by FFT for constant coefficients and multigrid for variable coefficients, which keeps the overall complexity of time marching comparable to that of a typical explicit scheme.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, we consider an initial boundary value problem the three dimensional wave (d’Alembert) equation:
where \(\varOmega \subset \mathbb {R}^3\), the wave speed c may vary in space, and the source term F is given. Equation (1a) provides a simple yet relevant model for a broad range of unsteady wave propagation phenomena in acoustics and electromagnetism. The excitation \(F( \varvec{x}, t)\) in acoustics works via altering the balance of mass and/or momentum of the fluid, see [19, Section 4.1]. In electromagnetism, \(F( \varvec{x}, t)\) can be interpreted as density of the extraneous electric current differentiated in time.
We are interested in approximating problem (1) by finite differences with high order accuracy. It is particularly important because of numerical dispersion. For any given frequency \(\omega \) and wavenumber \(k = {\omega }/{c}\), the error of a pth order accurate scheme is proportional to \(k^{p+1} h^{p}\), where h is the discretization size (see [3]). Thus, to maintain a fixed discretization error the number of points per wavelength \(\sim (kh)^{-1}\) must grow as \(k^{1/p}\). This phenomenon is known as pollution [2, 3, 12]. The error growth \({\mathcal {O}}(k^{1/p})\) decreases as the order of the scheme p increases. Therefore, a natural way of reducing the pollution effect is to increase the order of accuracy of the scheme.
Furthermore, we are interested in building a finite difference approximation on a compact stencil in both space and time. In [9], we have derived a scheme for the two-dimensional wave equation; it uses three consecutive time levels and a \(3\times 3\) stencil in space. In 3D, our goal is to construct a compact scheme that would also have no more than three nodes in each spatial direction or time. Compact finite difference approximations require no additional initial or boundary conditions beyond those needed for the differential equation itself (see conditions (1b)–(1d) for Eq. (1a)). This is an important advantage compared to the more traditional high order schemes that employ wider stencils. Previously, compact high order accurate finite difference schemes have been developed for various models, including the Helmholtz equation [8, 16, 25] and Navier–Stokes equations [1, 13, 29].
Compact finite difference schemes for the wave equation (1a) have to be implicit in time. Otherwise, the discretization will require more than three time levels. Therefore, to compute the solution at the upper time level one needs to solve a system of linear algebraic equations. For the schemes that we are proposing, this system is obtained as a finite difference counterpart to the modified Helmholtz equation \(\varDelta u - \kappa ^2 u =f\), which is elliptic and symmetric negative definite. The coefficient \(\kappa ^2\) in this equation is constant if the propagation speed c is constant; otherwise, \(\kappa ^2\) also varies. In the case of a constant \(\kappa ^2\), the inversion at the upper time level is done by FFT at a log-linear cost with respect of the grid dimension in space. This yields the overall complexity of time marching comparable to that of a typical explicit scheme. In the case of a variable \(\kappa ^2\), we do not want the complexity to deteriorate. Therefore, we choose multigrid iterations to do the inversion at the upper time level. Indeed, their convergence rate does not depend on the condition number of the matrix [6]. For finite difference approximations of second order elliptic operators, the latter is usually \({\mathcal {O}}(h^{-2})\).
The main objective of this paper is do derive and test the fourth order compact scheme for Eq. (1a) per se, while leaving the discussion of its applications to future publications. Therefore, it is sufficient to choose an otherwise simple setting for the initial boundary value problem (1). The fourth order compact scheme (i.e., family of schemes) will be built on a uniform Cartesian grid, and the domain \(\varOmega \) will be a Cartesian parallelepiped. The boundary condition (1d) is homogeneous Dirichlet, i.e., the simplest possible. We realize, of course, that for the analysis of practical problems more capabilities will need to be added. Therefore, we will later incorporate the currently proposed scheme into a broader framework that includes the method of difference potentials (MDP) by Ryaben’kii [23] and lacunae-based time marching [22]. It will allow us to compute the solutions with various types of boundary conditions, not only simple ones, such as the Dirichlet or Neumann boundary conditions, but also Robin (i.e., impedance), Zaremba (i.e., mixed), nonlocal, etc. It will also allow us to accommodate the non-conforming boundaries with no loss of accuracy (e.g., the scattering shapes). Note that in [10], the MDP was applied to the 2D wave equation. We also plan to develop a PML closure [4] at the artificial outer boundary to enable the simulation of exterior problems.
The rest of the paper is organized as follows. In Sect. 2, we describe the implicit fourth order accurate finite difference scheme in time. In Sect. 3, we build a family of fourth order accurate compact schemes in space for the modified Helmholtz equation that appears on the upper time level of the time discretization. In Sect. 4, we analyze the stability of time marching. In Sect. 5, we describe the multigrid iterations at the upper time level and analyze their convergence rate. In Sects. 6 and 7, we present the numerical results for the modified Helmholtz equation and the full time marching algorithm, respectively. In Sect. 8, we draw the conclusions and outline the directions for subsequent work.
2 Implicit Time Discretization
Let \(\tau \) be the uniform time step and define \(t_n = n \tau \)\( (\forall n \in \mathbb {N})\). Let \(\delta _t^2\) denote the second order central difference formula, \(\delta _t^2 u^n = (u^{n+1} - 2 u^n + u^{n-1})/\tau ^2\). Consider the semi-discrete approximation to the wave equation centered at time \(t_n\):
The above is referred to as the \(\theta \)-scheme [11, 18]. Rearranging (2) yields:
We define the auxiliary variable \(f^{n+1} =\varDelta u^{n+1} - \frac{1}{\theta \tau ^2 c^2} u^{n+1}\), and rewrite (3) as
where \(G^{n+1} = \frac{1}{\theta c^2} F^n + \frac{1}{c^2} \tau ^2 \delta _t^2 F^n = \frac{1}{\theta c^2} F^n + \frac{1}{c^2} \tau ^4 F_{tt}^n\). If \(\theta = \frac{1}{12}\), the semi-discrete approximation (4) is implicit, fourth order accurate in time, and conditionally stable [9]. Therefore, advancing the time marching scheme simply amounts to solving the modified Helmholtz equation
where \(\kappa ^2 = \frac{1}{\theta \tau ^2 c^2 }\) and the right hand side \(f^{n+1}\) depends on the inhomogeneous term of (1a) and the previously computed solutions \(u^{n}\) and \(u^{n-1}\). For constant speed of propagation, the discrete modified Helmholtz equation can be solved efficiently by FFT. In the case of a variable propagation speed, the most efficient solution methodology is multigrid iterations, because the equation is elliptic and symmetric negative definite.
To initialize the time marching scheme we will compute the functions \(u^0, u^1, f^0,\) and \(f^1\) analytically or approximately with at least fourth order accuracy in space and time. The variable \(u^0\) is obtained from (1b) and the variable \(u^1\) is obtained from the Taylor expansion:
where the high order terms are found by differentiating (1a). A similar approach can be taken to compute \(f^0\) and \(f^1\) too. In Sect. 3, we describe how to discretize the modified Helmholtz equation using only a \(3 \times 3 \times 3\) stencil in space.
3 Fourth Order Compact (FOC) Schemes
A conventional approach to constructing fourth order accurate schemes would require fourth order central differences or, equivalently, a stencil that extends at least five nodes in each coordinate direction. However, we will see that an equally accurate compact scheme can be built on a \(3 \times 3 \times 3\) stencil in space. Hence, the conventional approach necessitates additional modification near the boundary due to the width of the stencil, while compact finite difference schemes need no additional treatment near the boundary. For some examples of compact finite difference schemes applied to the original Helmholtz equation see [14, 16, 26, 28].
Given the bounded domain \(\varOmega \subset \mathbb {R}^3\), let \(\varOmega _h\) denote a uniform discretization of \(\varOmega \) with a step size h. Given the node \((x_i, y_j, z_k) \in \varOmega _h\) we group the adjacent nodes as shown in Fig. 1. The node \((\circ )\) is at the center of the stencil \((x_i, y_j, z_k)\). We will refer to the \((\blacksquare )\), \((\bullet )\), and  as the side–side, side-corner, and corner-corner nodes, respectively. In order to write the FOC economically, let \(u_{i,j,k} = u(x_i, y_j, z_k)\) and define the quantities:
as the side–side, side-corner, and corner-corner nodes, respectively. In order to write the FOC economically, let \(u_{i,j,k} = u(x_i, y_j, z_k)\) and define the quantities:
where the subscripts ss, sc, and cc refer to the side–side, side–corner, and corner–corner stencils, respectively. Let \(\delta _{x}^2, \delta _{y}^2\), and \(\delta _z^2\) denote the second order central difference operators for \( \frac{\partial ^2}{\partial x^2}, \frac{\partial ^2}{\partial y^2}\) and \(\frac{\partial ^2}{\partial z^2}\). Introduce three additional operators: \(\varDelta _h := \delta _x^2 + \delta _y^2 + \delta _z^2,\)\(\mathcal {A}_h := \delta _x^2 \delta _y^2+ \delta _x^2 \delta _z^2 + \delta _y^2 \delta _z^2,\) and \( \mathcal {B}_h := \delta _x^2 \delta _y^2 \delta _z^2 \). Then,
We will derive two FOC schemes for the modified Helmholtz equation (5a). Both schemes will have the general form:
where the weights \(\alpha ^0, \alpha ^{ss}, \alpha ^{sc}, \alpha ^{cc}, \cdots , \gamma ^{cc}\) are nonnegative real numbers that satisfy:
The resulting linear system is \( \varvec{Q}_h(\kappa ^2) u_h = h^2 \varvec{P}_h f_h \), where the matrix \(\varvec{P}_h\) is symmetric positive definite and strictly diagonally dominant because of (8f), and the matrix \(\varvec{Q}_h(\kappa ^2)\) is diagonally dominant for sufficiently small \(h > 0\) because of (8d) and (8e). For the purposes of analysis, the linear system can be written \( \frac{1}{h^2} \varvec{L}_h(\kappa ^2) u_h = f_h\), where \(\varvec{L}_h(\kappa ^2) = \varvec{P}_{h}^{-1} \varvec{Q}_h(\kappa ^2)\).
3.1 Padé Based FOC Scheme
Assuming u is smooth, Taylor’s theorem states that
After combining like terms and applying the formal inverse \((1 + \frac{h^2}{12} \delta _{x}^2 )^{-1}\), the fourth order accurate approximation of the second derivative with respect to x is
Substituting (9) (and the analogous derivatives with respect to y and z) into the modified Helmholtz equation, we have:
Multiplying (10) by
implies that
where the truncation error is
Finally, rescaling (11) by a factor of \(h^2\), dropping the truncation error term, and replacing the difference operators with (6), yields the Padé based FOC scheme:
3.2 Equation Based FOC Scheme
The key idea behind equation based schemes is to explicitly remove one or several leading terms in the expansion of the truncation error, while computing the higher order derivatives of the solution in those terms by differentiating the governing differential equation itself, see [26] or [7]. In the case of a fourth order compact scheme obtained from the baseline second order central difference scheme, the resulting expression will usually consist of mixed partial derivatives of u and f with at most two derivatives taken in any given variable. As a result, we can approximate the required high order derivatives with second order accuracy using only nodes in the \(3 \times 3 \times 3\) stencil shown in Fig. 1.
In this section, we construct a family of fourth order accurate equation based schemes. From this family, we can choose specific schemes with most favorable properties, e.g., those with the smallest stencil or those with the largest stability region. In Sect. 3.2.1, we derive a particular scheme from the family in great detail. In Sect. 3.2.2, we derive the entire parametric family of schemes by slightly modifying the results of Sect. 3.2.1.
3.2.1 Canonical Equation Based Scheme
For sufficiently smooth u, the Taylor expansion of the Laplacian is
Applying the derivatives \(\frac{\partial ^2}{\partial x^2}, \frac{\partial ^2}{\partial y^2}\), and \(\frac{\partial ^2}{\partial z^2}\) separately to the modified Helmholtz equation (5a), we have:
Combining Eqs. (13a)–(13c), we can write:
Then, substituting (14) into (12) we arrive at
At this point, we could have replaced the derivatives in the \(\sim \frac{h^2}{6}\) term on the right-hand side of (15) with \(\mathcal {A}_h\) of (6), which would preserve fourth order accuracy, and then continue similarly to (9)–(11). However, the resulting discrete modified Helmholtz equation appears deficient. Its right-hand side operator \(\varvec{P}_h\) is positive but only semidefinite, which does not allow one to apply the stability analysis of Sect. 4. Moreover, we observed difficulties with convergence of the time marching scheme. To remedy those, we have developed the following approach.
The fourth order derivatives \(\frac{\partial ^4}{\partial x^2 \partial y^2}, \frac{\partial ^4}{\partial x^2 \partial z^2}\), and \(\frac{\partial ^4}{\partial y^2 \partial z^2}\) of the modified Helmholtz equation (5a) are
The sum of Eqs. (16a)–(16c) can be written as
Next, the Taylor formula yields:
and
Substituting (17) into (19), we have:
Combining (15), (18), and (20) with the modified Helmholtz equation (5a), we obtain:
where the remainder is
Note that, we keep the \(\sim \frac{h^4}{72}\) term on the right-hand side of (21) separate from the remainder R to enable energy estimates for the analysis of stability, see Sect. 4. To approximate the RHS terms of (21) with fourth order accuracy, we first differentiate (13a), (13b), and (13c) twice with respect to x, y, and z, respectively, which yields:
Then,
Combining (21) and (22), we have:
where the truncation error is
Finally, rescaling (23) by a factor of \(h^2\), dropping the truncation error (24), and replacing the difference operators with (6), yields the canonical FOC Equation Based scheme:
3.2.2 Family of Equation Based FOC Scheme
We derive a one parameter family of equation based schemes by extending the analysis of Sect. 3.2.1. Let EB\((\rho )\) denote the equation based scheme, where the parameter \(\rho \in \mathbb {R}\). First consider the finite difference operator
Using the multivariate Taylor’s formula, we can write:
Next, for any \(\rho \in \mathbb {R}\) define the new finite difference operator
Consequently,
If we repeat the same steps as (15)–(22), but replace \(\mathcal {A}_h\) with \(\tilde{\mathcal {A}^{\rho }_h}\) and use (26) whenever we utilize \(\tilde{\mathcal {A}_h^p}\), then we obtain the family of equation based schemes:
where the corresponding truncation error is
Our family of equation based schemes (27) partitions into four distinct categories:
If \(\rho = 1\), we recover the canonical equation based scheme (25). The 19-point stencil contains only the nodes \((\circ )\), \((\blacksquare )\), and (\(\bullet \)), as shown in Fig. 1.
If \(\rho = 0\), the 15-point stencil contains only the nodes \((\circ )\),
 , and \((\blacksquare )\), as shown in Fig. 1.
, and \((\blacksquare )\), as shown in Fig. 1.If \(\rho = 2\), the 21-point stencil contains only the nodes \((\circ )\), \((\bullet )\), and
 , as shown in Fig. 1.
, as shown in Fig. 1.If \(\rho \not \in \{ 0 ,1, 2 \}\), the equation based scheme uses the full 27-node stencil.
In Sect. 4, we will show how the parameter \(\rho \) in Eq. (27) affects the stability of the scheme. The corresponding analysis requires that the right-hand side operator \(\varvec{P}_h\) be strictly diagonally dominant. The strict diagonal dominance holds provided that \(\frac{|11 + \rho |}{18} > \frac{|2 - \rho |}{6} + \frac{|\rho |}{6} + \frac{|1 - \rho |}{18}\) or \( \rho \in (- \frac{1}{2}, 3)\). Similarly, the matrix \(\varvec{Q}_h(\kappa ^2)\) is diagonally dominant for sufficiently small \(h > 0\) and for any \(\rho \in (- \frac{1}{2}, 3)\).
4 Stability Criteria
Let \(\lambda =\lambda (\varvec{x})\) denote the CFL number:
where h is the grid size in space and \(\tau \) is the time step. Let \( \varvec{L}_h(0) \) denote the left-hand side operator of the FOC scheme applied to the Laplace equation (i.e., Eq. (5a) for \(\kappa ^2 = 0\)). In [9], stability of this scheme was studied using the energy estimates. Specifically, the energy was taken as \(\Vert u^{n} - u^{n-1} \Vert ^2 + \Vert u^n + u^{n-1} \Vert ^2\), which is equivalent to \(\Vert u^n \Vert ^2 + \Vert u^{n-1}\Vert ^2\) if and only if \(1/\lambda (\varvec{x})^2 - (1/4 - \theta ) L_{\text {upper}} \geqslant 0\), where \(0 < (-\varvec{L}_h(0) u, u) \leqslant L_{\text {upper}} \Vert u\Vert ^2\) for all u. As the fourth order accuracy is achieved for \(\theta = \frac{1}{12}\), the fourth order time marching scheme is stable provided that
To compute the quantity \(L_{ \text {upper} }\), assume that the FOC scheme (7) has periodic boundary conditions and a constant wave speed. Then, we can take the Fourier transform (in space) and apply the Parseval equality to conduct the analysis in the frequency domain. As \( \frac{1}{h^2} \varvec{L}_h(0) = \varvec{P}_h^{-1} \varvec{Q}_h(0) \), the Fourier transform of \(-\varvec{L}_h(0)\) is given by
where \((\xi , \eta , \zeta ) \in [-\pi , \pi ]^3\) and
For both the Padé scheme and equation based scheme, the denominator of (29) is never zero since \(\varvec{P}_h\) is strictly diagonally dominant. Using the maximize subroutine of Mathematica, we can find:
In Fig. 2, we show the effect that the parameter \(\rho \) has on the quantity \(L_{\text {upper}}^{ \text {EB}(\rho )}\). As \(\rho \) increases, \(L_{ \text {upper} }^{ \text {EB}(\rho )}\) monotonically decreases until is reaches the minimum value of 48 / 5. We observe that for all \(\rho > 3/4\) we have \(L_{\text {upper}}^{\text {EB}(\rho )} = 48/5\).
We also see from Fig. 2 that for all \(\rho < \frac{2}{5}\), \(L_{\text {upper}}^{ \text {EB}(\rho )} > L_{\text {upper}}^{ \text {Pade} }\). In this case, both schemes utilize the full \(3 \times 3 \times 3\) stencil (27 nodes), but the Padé based scheme has a larger CFL number and smaller truncation error. However, if \(\rho > \frac{2}{5}\) we have \(L_{\text {upper}}^{ \text {EB}(\rho )} \leqslant L_{\text {upper}}^{ \text {Pade}}\) and the CFL number produced by the equation based scheme is larger. If our objective is to maximize the CFL number, then we can choose any value of \(\rho > \frac{3}{4}\) which yields \(L_{\text {upper}} = 48/5\). However, \(\rho = 1\) and \(\rho = 2\) are the only equation based schemes in this scenario that do not utilize the full 27-node stencil. Consequently, if our goal is to maximize the CFL number while minimizing the number of non-zero coefficients on the \(3 \times 3 \times 3\) stencil (the latter may affect multigrid performance, see Sect. 5), then EB(1) and EB(2) are the best candidates.
The CFL numbers for periodic boundary conditions and a constant wave speed are given by
There are several other factors we could consider when trying to determine the “optimal” parameter \(\rho \). For example, one can take into account anisotropy and the dispersion error along individual coordinate directions, spurious reflections, and other criteria, see, e.g., [16].
If we allow \(L_{\text {upper}}\) to depend on the boundary conditions and \(\kappa \), then the time step must satisfy
where \(\varepsilon \in (0,1]\) is a “safety factor” to accommodate the additional considerations. Note that, the role of Eqs. (20) and (21) in the derivation of the equation based scheme is to make it amenable to the foregoing stability analysis. If we omit (20) and (21), the RHS operator \(\varvec{P}_h\) remains symmetric but becomes only positive semidefinite. Therefore, the denominator of (29) vanishes at the point \((-\pi ,-\pi ,-\pi )\).
We emphasize, that while the proposed scheme is implicit, its stability is only conditional. Indeed, the implicitness of the scheme is an implication of its fourth order accuracy and compactness in time. It corresponds to \(\theta =\frac{1}{12}\) in Eq. (4), and the choice of \(\theta \) (along with the spectral properties of the spatial operator \(\varvec{L}_h\)) determines the stability characteristics of the scheme. For other values of \(\theta \), one can construct the unconditionally stable schemes of type (2), but their accuracy will not be as high as fourth order. Note also that as the problem we are studying is linear, the stability of the scheme combined with its consistency imply convergence. The grid convergence with the design rate (fourth order) is demonstrated experimentally in numerical simulations of Sect. 7.
5 Multigrid
Multigrid methods are a family of fast iterative methods for solving systems of linear algebraic equations derived from discretizations of elliptic PDEs. Unlike other iterative methods, such as Krylov subspaces or conjugate gradients, multigrid methods theoretically achieve the rates of convergence that are independent of the condition number (i.e., the grid size). Hence, multigrid methods can solve problems for a constant amount of work per unknown regardless of the dimension N of the problem. Computational complexity of multigrid methods scales similarly to that of FFT. Namely, reducing the initial error by a prescribed factor requires \({\mathcal {O}}(N\ln N)\) arithmetic operations. The constants that characterize multigrid methods are usually larger than those for FFT, but multigrid methods apply to a much broader class of formulations including, in particular, equations with variable coefficients. Moreover, by carefully choosing and arranging the discretization variables, the constant in the \({\mathcal {O}}(N\ln N)\) estimate can be made fairly modest.
The main principle of multigrid methods is to write the error as a linear combination of high frequency modes and low frequency modes. Then, the error is attenuated using several nested grids. More specifically, the high frequency components of the error on a given grid are damped by a smoother, while the low frequency components of the error are damped by a combination of the coarse grid correction and recursion. For a complete introduction to multigrid methods see the texts [6, 24]. For a more advanced treatment of multigrid methods see [27].
In Sect. 5.1, we give a short introduction to multigrid methods. Specifically, we list the main components of multigrid iterations and illustrate the above concepts using the simplest multigrid method, the two-grid cycle. We also illustrate the V, W, and F cycles, and explain how we plan on adapting multigrid methods to the time marching scheme.
In Sect. 5.2, we estimate the rate of convergence of multigrid methods as applied to the modified Helmholtz equation (5a). We use local Fourier analysis to obtain theoretical predictions and compare those against the convergence factors evaluated numerically for several different examples.
5.1 Multigrid Methods
Suppose that we have \(\ell \) nested grids: \(\varOmega _{h} \supset \varOmega _{2h} \supset \cdots \supset \varOmega _{ 2^{\ell - 1} h}\). Then, standard multigrid methods require the following components:
Coarse grid operator \(\varvec{L}_{2^{i-1}h}: \varOmega _{2^{i-1} h} \rightarrow \varOmega _{2^{i-1} h}\) is the operator of the linear system that corresponds to the grid \(\varOmega _{2^{i-1} h}\). In this paper, \(\varvec{L}_{2^{i-1}h}\) is the operator derived from the scheme (7) on the grid with size of \(2^{i-1}h\).
Smoother \(\varvec{S}_i: \varOmega _{2^{i-1} h} \rightarrow \varOmega _{2^{i-1} h}\) is an iterative solver that damps the high frequency components of the error while leaving the low frequency components largely unaffected. Jacobi iterations, Gauss–Seidel iterations, or successive overrelaxation (SOR) are commonly used as smoothers. Hereafter, “\(\text {smooth}^{\nu }( \varvec{L}_{2^{i-1} h}, v_{2^{i-1} h}, f_{2^{i-1}h})\)” will indicate that the smoother is applied \(\nu \) times to the linear system with the operator \(\varvec{L}_{2^{i-1} h}\), solution \({v}_{2^{i-1} h}\), and RHS \(f_{ 2^{i-1} h}\).
Restriction operator \(\mathcal {R}_{i}^{i+1}: \varOmega _{2^{i-1} h} \rightarrow \varOmega _{ 2^{i} h}\) takes a coarse grid node and assigns its value as a weighted average of neighboring nodes of the fine grid. The injection and full weighting operators are commonly used.
Prolongation operator \(\mathcal {P}_{i+1}^{i}: \varOmega _{ 2^{i} h} \rightarrow \varOmega _{2 ^{i-1} h}\) takes a node in \(\varOmega _{2^{i-1}h} {\setminus } \varOmega _{2^{i} h}\) and uses polynomial interpolation from the neighboring nodes of the coarse grid to define the grid function at this node. If the node belongs to \(\varOmega _{2^{i-1}h} \bigcap \varOmega _{2^{i} h}\), then the value of the grid function is unmodified. Otherwise, linear interpolation along each axis (tri-linear interpolation) or cubic interpolation along each axis (tri-cubic interpolation) are commonly used for prolongation.
The two-grid method \((\ell = 2)\) schematically shown in Fig. 3 is the simplest multigrid method. It provides a convenient framework for showing how the foregoing components interact. Given the \(m^{th}\) iterate, the smoother is applied \(\nu _1\) times to damp the high frequency components of the error on the fine grid. To attenuate the low frequency components of the error, one uses a process called coarse grid correction. Let \(\varvec{L}_h u_h = f_h\) and assume that the current iterate is \(v_h\). Then, the error \(e_h = u_h - v_h\) must satisfy \(\varvec{L}_h e_h = f_h - \varvec{L}_h v_h = r_{h}\). Coarse grid correction approximates the error using a coarse grid. Specifically, one computes the residual on the fine grid, maps it onto the coarse grid with the restriction operator, solves the analogous coarse grid linear system \(\varvec{L}_{2h} e_{2h} = r_{2h}\), and then uses prolongation to map the coarse grid error \(e_{2h}\) to the fine grid. Once the prolongated coarse grid error is combined with the fine grid approximation of the solution, the coarse grid correction is completed. The last step is to apply the smoother \(\nu _2\) times to damp any remaining error. That concludes one iteration of the two-grid cycle.
In practice, we do not employ the two-grid cycle per se. We rather use it to construct more advanced multigrid methods. Consider the coarse grid system \(\varvec{L}_{2h} e_{2h} = r_{2h}\) as shown in Fig. 3. The two-grid method requires that we solve the linear system on the coarse grid. If we treat the residual \(r_{2h}\) as a generic RHS vector, we can apply the two-grid method once more as a solver. Thus, more advanced multigrid methods can be obtained by applying the two-grid cycle recursively. Examples are provided by the V, F, and W cycles that are schematically shown in Fig. 4 in the case of a total of four nested grids. We generally refer to this family of multigrid methods as multigrid cycles (MGCYC). Algorithm 1 explicitly states the details of the V cycle. It can easily be extended to perform F and W cycles as well.
Schematic of the three commonly used multigrid cycles (MGCYC) in the case of four nested grids, \(\varOmega _h\), \(\varOmega _{2h}\), \(\varOmega _{4h}\), and \(\varOmega _{8h}\), and standard coarsening. The symbols \((\bullet )\) denote pre-smoothing steps, \((\circ )\)—post-smoothing steps, \((\blacksquare )\)—direct solver or fast iterative solver, \((\searrow )\)—restriction, and \((\nearrow )\)—prolongation

The computational complexity of multigrid iterations \(O(N \ln N)\) arithmetic operations since the rate of reduction in the error is constant (does not depend on N). However, the actual cost also depends on the initial guess because it is the initial guess that determines the initial error, from which the multigrid reduction starts off. The time marching scheme has access to two solutions on the previous time levels. These two approximations can be used to generate a very good initial iterate and obtain a cost reduction compared, say, to simply setting the initial guess to zero. Suppose we want to solve the discrete modified Helmholtz equation (5a) on the upper time level \(t_{n+1}\). The Taylor formula yields:
where \(\varDelta _h\) is the central difference second order discrete Laplacian. Consequently, equation
provides a fourth order initial guess for the modified Helmholtz equation on the upper time level \(t_{n+1}\). On the right-hand side of (30), \(u^{n}\) and \(u^{n-1}\) are known with fourth order accuracy, the term \(F^{n}\) can be evaluated on the grid up to machine precision, and \(\varDelta _h u^n\) can be computed by a sparse matrix vector product.
Another way to provide a good initial guess to MGCYC is to employ the procedure called nested iteration. It provides an initial iterate to the fine grid problem by solving the analogous linear system on a coarse grid and using a high order prolongation operator. The output of high order prolongation will serve as the initial guess on the fine grid. Of course, this idea can be applied using several nested grids. Nested iteration combined with multigrid cycles yields the full multigrid method (FMG). Algorithm 2 depicts the full multigrid method in detail. The FMG requires that the RHS vector is assembled on every level. Therefore, we need to do that using (4) for each auxiliary grid. In addition to that, when applying several consecutive multigrid cycles (\(\nu _3\) in the construct of Algorithm 2), it is the solution from the previous cycle that provides the initial guess to the next one.

The most common smoothers used for standard multigrid iterations are the damped Jacobi method, lexicographic Gauss–Seidel [17], or SOR. In [9], the rate of convergence was estimated by performing an eigenvalue analysis of the damped Jacobi method. This is possible since the eigenvectors of the linear system \(\varvec{L}_h\) and the damped Jacobi method coincide. Yet it is no longer true if Gauss–Seidel is used as the smoother. Generally, the Gauss–Seidel method is known to have better smoothing properties than damped Jacobi iterations [27].
In Sect. 5.2, we estimate numerically the multigrid convergence rate when Gauss–Seidel is used as the smoother and compare the results against the theoretical predictions by local Fourier analysis [6, 27].
According to Trottenberg et al. [27], the order of the restriction operator plus that of the prolongation operator should exceed the order of the differential operator to achieve multigrid convergence. Therefore, injection (zeroth order) plus tri-cubic interpolation (fourth order) or full weighting (second order) plus tri-linear interpolation (second order) are both sufficient combinations of restriction and prolongation operators. We chose full weighting and tri-cubic interpolation as our particular combination. However, we empirically observed that any of the above combinations produces similar results. Finally, we chose tri-quartic interpolation as our high order interpolation operator for FMG, since the finite difference scheme is fourth order accurate.
To summarize, in our simulations that involve multigrid iterations (Sects. 6 and 7) we choose the following components:
Smoother—Gauss–Seidel,
Restriction operator—full weighting,
Prolongation operator—tri-cubic interpolation,
High order (FMG) interpolation operator—tri-quartic interpolation.
5.2 Multigrid Convergence Rate
Local Fourier analysis (LFA) provides sharp estimates of the multigrid convergence rate for a large class of linear elliptic PDEs [5]. A detailed account of LFA can be found, e.g., in [6, 27].
Let \(\omega \) denote the amplification factor of the Gauss–Seidel smoother \(\varvec{S}_h\) applied to the compact scheme (7). It depends on the frequency \(\varvec{\theta } = (\theta _1, \theta _2, \theta _3) \in [- \pi , \pi ]^3\) on the grid and on the quantity \(h^2\kappa ^2\). In the context of time marching, \(\kappa ^2\) is inversely proportional to the square of the time step \(\tau \), see the definition given right after Eq. (5b). Hence, the quantity \(h^2\kappa ^2\) is inversely proportional to the CFL number (28) squared, as follows from the discussion of stability in Sect. 4. In the case of a variable \(\kappa ^2=\kappa ^2(\varvec{x})\), the amplification factor is introduced by freezing the coefficient \(\kappa ^2(\varvec{x})\) and thus, in addition to \(\varvec{\theta }\), it depends on the location \(\varvec{x}\) where the coefficient \(\kappa ^2\) is frozen.
The smoothing factor is commonly defined as
where \(\varvec{\varTheta }_{H} = [-\pi , \pi ]^{3} {\setminus } [ - \frac{\pi }{2}, \frac{\pi }{2} )^3\) is the subset of high frequencies on the grid. In the simplest case of a constant \(\kappa ^2\) where \(\mu \) of (31) does not depend on \(\varvec{x}\), the smoothing factor immediately provides an estimate of how slowly the high frequency modes on the grid may decay when damped by \(\varvec{S}_h\). This, in turn, allows one to estimate the multigrid convergence rate. For example, if we perform a \(V(\nu _1, \nu _2)\) cycle, then the error should be expected to decrease by a factor of approximately \(\mu ^{\nu _1 + \nu _2}\). In the case of a variable \(\kappa ^2\) where \(\mu \) of (31) depends on the location \(\varvec{x}\) at which \(\kappa ^2(\varvec{x})\) is frozen, the slowest decay (i.e., the worst case scenario) corresponds to the maximum value of \(\mu \) across all \(\varvec{x}\). For the Gauss–Seidel smoother applied to the FOC scheme (7), this translates into \(\mu =\mu (h^2\kappa ^2_{\min })\), where \(\kappa ^{2}_{\min } = \min _{\varvec{x}} \kappa ^2( \varvec{x})\).
Figure 5 shows the LFA produced smoothing factor (31) as a function of \(h^2 \kappa ^2\). Clearly, \(\mu (h^2 \kappa ^2)\) decreases as \(h^2 \kappa ^2\) increases for both the equation based and Padé scheme, which implies faster convergence. In the time-dependent framework, we have \(h^2\kappa ^2=\frac{1}{\theta \lambda ^2}\), where \(\theta =\frac{1}{12}\) enables fourth order accuracy in time (see Sect. 2), and the Courant number \(\lambda \) of (28) has a scheme-dependent upper bound that guarantees the stability of time marching (see Sect. 4).
Another way to estimate the rate of multigrid convergence is to evaluate the convergence factor \( \displaystyle \rho = \lim _{m \rightarrow \infty } \Vert r_h^{( m )} \Vert /\Vert r_{h}^{( m-1)} \Vert \) numerically, where \(r_h^{(m)}\) is the residual of the \(m^{th}\) iterate: \(r_h^{(m)} = \ \varvec{P}_h f_h - \frac{1}{h^2} \varvec{Q}_h(\kappa ^2) v_h^{(m)}\). To do so, we compute the two quantities:
where \(m_0\) and m are sufficiently large to observe the asymptotic rate of convergence. A convenient setting for this numerical evaluation is the homogeneous counterpart of problem (5a)–(5b), for which the right-hand side of the modified Helmholtz equation is zero, discretized on a cube \(\varOmega = \Big [- \frac{\pi }{2}, \frac{\pi }{2}\Big ]^3\).
Table 1 compares the numerically computed convergence factors (32a) and (32b) to the LFA predicted convergence rate for several different functions \(\kappa ^2(\varvec{x})\). When the total number of smoothing steps \(\nu _1+\nu _2\) is less than or equal to two, the convergence factors (32a) and (32b) agree with the LFA prediction for both the Padé and equation based scheme. However, once more than three (two) total smoothing steps for the Padé (equation based) scheme are performed, the LFA tends to over-predict the convergence rate. A similar observation was made in [27, Remark 2.5.4] as well. Note that, the value of \(\kappa ^2=0\) that transforms the modified Helmholtz equation into the Laplace (Poisson) equation is included in Table 1 only for comparison purposes. It does not correspond to any time marching scheme.
6 Numerical Results for the Modified Helmholtz Equation
6.1 Constant Coefficients
Consider a homogeneous Dirichlet problem for the modified Helmholtz equation on a cubic domain \(\varOmega \) [cf. (5)]:
For Test Problem 1, define the analytic solution as \(u(x,y,z) = \sin (\pi x) \sin (2 \pi y) \sin (3 \pi z)\). The corresponding RHS f in (33) is generated by substituting u under the modified Helmholtz operator for a specified \(\kappa ^2\), which is constant in space.
Let \(u^{(h)}\) denote the analytic solution evaluated on the appropriate uniform Cartesian grid with size h and \(u_h\) denote the solution to the discretized problem (33) on the corresponding grid domain \(\varOmega _h\). We measure the error in all of our experiments with the discrete \(\ell _2\)-norm:
The quantity \(\Vert u^{(h)} - u_h \Vert _{\ell _2}\) is the discretization error.
In Fig. 6, we show the error as a function of h when solving Test Problem 1 for \(\kappa ^2 = 1, 100\), and 1000 by means of the FFT. Since the error graphs are parallel to the reference line that represents the dependence \(\sim h^4\), fourth order convergence is achieved. We also observe that as the quantity \(\kappa ^2\) increases, the error decreases.
Table 2 shows the run time for the simulations depicted in Fig. 6. When the grid size is reduced by a factor of two, the total number of grid points increases eight times, and the run time increases approximately 8–10 times. This matches our expectations as the computational complexity of FFT is \(O(N \log N)\).
6.2 Variable Coefficients
We consider the same homogeneous Dirichlet problem (33) for the modified Helmholtz equation, but let the quantity \(\kappa ^2\) vary. For Test Problem 2, we take \( \kappa ^2(x,y,z) = 1 + x^2 + y^2 + z^2\) and define the analytic solution as \(u(x,y,z) = \sin (\pi x) \sin (2 \pi y) \sin (3 \pi z)\). For Test Problem 3, we take \( \kappa ^2(x,y,z) = 2 + \cos ( e^{3x}) \cos ( e^{2y}) \cos ( e^{3z})\) in (33) and define the analytic solution as \(u(x,y,z) = \sin (5 \pi x) \sin (7\pi y) \sin (5 \pi z)\). The corresponding RHS f in (33) is generated by substituting a given u under the modified Helmholtz operator for a given \(\kappa ^2\).
In the case of variable coefficients, we also redefine the error. Let \(u^{(h)}\) denote the analytic solution evaluated on the appropriate grid, \(u_h\) denote the exact solution to the discrete modified Helmholtz equation on \(\varOmega _h\), and \(v_h\) denote the approximate solution computed on \(\varOmega _h\) by multigrid iterations. The overall error is the error of our approximate solution \(v_h\): \(\Vert u^{(h)} - v_h \Vert _{\ell _2}\). We want it to be as close as possible to the discretization error: \(\Vert u^{(h)} - v_{h} \Vert _{\ell _2} \approx \Vert u^{(h)} - u_h\Vert _{\ell _2}\).
Figures 7 and 8 show the error history for Test Problem 2 and Test Problem 3 when applying several consecutive W(1, 1) cycles. The first W(1, 1) cycle is initiated with the initial guess \(v_h^{(0)} = \varvec{0}\), while for all subsequent cycles the solution on the previous one initiates the next one. We notice that the error levels off as the number of cycles increases. This implies that the error of the approximate solution approaches the discretization error. We also see that the graphs from the first to second cycle (and the second to third cycle as well) are roughly parallel on each grid. This indicates that the rate of reduction in the error is roughly the same on every grid once the approximate solution is sufficiently close to the true solution. Finally, we observe that fourth order convergence is attained. The distance between the tick marks on the y axis and the distance between the horizontal portions of each graph are roughly the same. Since the y axis has a base 2 scale, each tick mark represents a factor of 16.
Table 3 presents mean run times for several V and W cycles. Note that, as we reduce the step size in half we increase the total number of grid points by a factor of about eight. We observe that the run time also increases by a factor of about eight when cutting the step size in half. Comparing the data in Tables 2 and 3 we see that while the multigrid execution times are acceptable, the FFT still computes the solution much faster on the grid of equivalent dimension. It will remain considerably faster even if the corresponding multigrid execution times are cut in half, because as Figs. 7 and 8 show, we do not need as many multigrid cycles for reaching the level of the discretization error.
Next, we apply the FMG method (see Algorithm 2) to Test Problem 2 and Test Problem 3. Tables 4 and 5 compare the discretization error to the error of the approximate solution for Test Problems 2 and 3, respectively. If two cycles are used on every grid (the FMG(1,1,2) method), the discretization error is achieved on every level regardless of the cycle type. However, with only one cycle per grid (the FMG(1,1,1) method) the approximate solution does not quite reach the discretization error level. For solving the modified Helmholtz equation per se this may be acceptable. However, the recursively defined right-hand side (4) is a function of the approximate solutions on previous time levels. If the discretization error is not achieved, the error may accumulate for the RHS vectors on subsequent time levels. Most likely, this is the reason for the disruption of convergence that we report in Sect. 7.2 in the case where FMG with insufficiently many cycles is applied to the time marching scheme.
7 Numerical Results for the Time Marching Scheme
7.1 Constant Coefficients
We consider problem (1a)–(1d) on the domain \(\varOmega = \left( - \frac{\pi }{2}, \frac{\pi }{2} \right) ^3\) with constant wave speed and analytic solution \(u(x,y,z,t) = \cos (x) \cos (y) \cos (z) \cos (t)\). The terminal time is \(T = 2\). The right-hand side F is generated by substituting u under the d’Alembert operator. This formulation will be referred to as Test Problem 4. Given the size h on the finest grid, we utilize the largest possible time step of \(\tau = \frac{ h \lambda }{ c }\), where the CFL number \(\lambda \) is defined by (28).
If \(e^{n}_{h} = u^{(h),n} - u_{h}^{n}\) is the error on the \(n^{th}\) time level, then the overall error of the time marching scheme is given by
and order of convergence is given by
Figure 9 shows that the time marching scheme is fourth order accurate. Indeed, the graph of the error \(\sup _{n} \Vert e_h^n \Vert _{\ell _2}\) as a function of the grid size h is parallel to the reference line, which has a slope of four on a log–log scale. The same conclusion was made in Sect. 6.1. Since time marching relies on solving the modified Helmholtz equation at every step, the fourth order convergence in the time domain is expected.
Table 6 shows that increasing the wave speed from one to three triples the run time. When the size h is fixed and the wave speed triples, the Courant number decreases by a factor of three. Therefore, the number of time steps triples.
7.2 Variable Coefficients
We consider the same formulation as in Sect. 7.1 except that the wave speed varies in space: \(c^2(x,y,z) = 1 + \frac{1}{8} x^2\). The analytic solution is also the same as in Sect. 7.1: \(u(x,y,z,t) = \cos (x) \cos (y) \cos (z) \cos (t)\). This formulation will be referred to as Test Problem 5. Given the size h of the finest grid, we use a time step of \(\tau = .98 h \lambda /(1 + \frac{\pi ^2}{8})\), where the CFL number \(\lambda \) is defined by (28).
We employ two solvers on the upper time level of the time marching scheme. Time marching solver 1 (TMS1) uses W(1,2) cycles with (30) as the initial guess to solve the modified Helmholtz equation at every time level. Time marching solver 2 (TMS2) uses FMG(1,2,2) with W cycles on each level. The total error is defined similarly to how it is done in Sect. 6.2. At every time level, it is the difference between the exact solution on the grid and the solution of the corresponding modified Helmholtz equation obtained by multigrid iterations.
In Fig. 10, we show the error history for Test Problem 5 and both the Padé and equation based scheme when applying TMS1. A sharp increase of the error in the beginning of time marching is not surprising since \(u^0\) is accurate to machine precision and \(u^1\) is fifth order accurate in time. At the same time, we see that once we go past the first few time levels, the distance between the graphs remains approximately constant for both schemes. We observed a similar behavior in Figs. 7 and 8, which indicates that the discretization error is achieved. The error of the equation based scheme exceeds that of the Padé scheme for the same grid dimension in space. However, both schemes demonstrate fourth order convergence. In particular, if we examine the error history for either scheme at the terminal time, the distance between the graphs and the tick marks is almost identical. As the distance between the tick marks represents a factor of 16, fourth order convergence is attained.
Next, we compare TMS1 and TMS2 for Test Problem 5. Figure 11 shows the error of the initial guess as a function of time for the Padé scheme. For TMS1, the initial guess refers to (30) and for TMS2 the initial guess is the output of nested iteration prolongated to the finest grid. One can clearly see from Fig. 11 that the initial guesses for both approaches are comparable. In addition, Table 7 demonstrates that both schemes are fourth order convergent. However, the run time for TMS2 is about twice as large as that for TMS1. We can attribute this to TMS1 only using one cycle while TMS2 using two cycles on each level. To reduce the computational cost of TMS2 and thus make both schemes comparable, we tried to use FMG(1,2,1) instead of FMG(1,2,2). However, the method did not converge. Most likely, the reason is that FMG with fewer cycles does not drive the error of the approximate solution all the way down to discretization error (see Sect. 6.2). We also attempted to use FMG with one pre-relaxation sweep and two post relaxation sweeps where two cycles are performed on the auxiliary grids and one cycle on the finest grid. Unfortunately, that led to a reduction of accuracy by roughly one order of magnitude. The conclusion therefore is that FMG is not beneficial for the type of problems we are investigating, and that the use of consecutive W cycles is more efficient.
The error of the initial guess as a function of time for the Padé approximation in space. Left panel: initial guess (30) for TMS1. Right panel: output of nested iteration prolongated to the finest grid for TMS2
8 Conclusions and Future Work
We solve the three dimensional wave equation subject to homogeneous Dirichlet boundary conditions with fourth order accuracy using only three levels in time and three nodes along each coordinate axis (i.e., compactly in time and space). The approximation in time is implicit and requires solving the modified Helmholtz equation on the upper time level at every step. The modified Helmholtz is discretized in space with two compact fourth order accurate finite difference schemes. Since the equation is symmetric negative definite elliptic, one can efficiently solve it by multigrid in the case of variable coefficients. For constant coefficients, it is solved by FFT. In both cases, we compare the CFL numbers, multigrid convergence factors, and run times induced by each compact discretization in space. Finally, we provide numerical examples to demonstrate that fourth order accuracy is achieved for the modified Helmholtz equation alone, as well as in the course of time marching.
The simple geometry of the domain \(\varOmega \) (a Cartesian cube) and simple boundary conditions do not present a limitation because our next step will be to combine the proposed fourth order accurate compact scheme with the method of difference potentials [23]. It will allow us to accommodate non-conforming boundary shapes and a variety of boundary conditions with no deterioration of accuracy while still using a Cartesian grid, see [10] for a 2D implementation with fourth order accuracy and [22] for a 3D implementation with second order accuracy.
Also in the future, we will adopt a perfectly matched layer (PML) approach for the simulation of the three dimensional wave equation on unbounded regions. Our present work will provide a foundation for constructing a fourth order accurate compact approximation for the PML formulation of the wave equation. For examples of the PML applied to the wave equation see [4, 15, 20, 21].
References
Abide, S., Binous, M.S., Zeghmati, B.: An efficient parallel high-order compact scheme for the 3D incompressible Navier–Stokes equations. Int. J. Comput. Fluid Dyn. 31(4–5), 214–229 (2017). https://doi.org/10.1080/10618562.2017.1326592
Babuška, I.M., Sauter, S.A.: Is the pollution effect of the FEM avoidable for the Helmholtz equation considering high wave numbers? SIAM Rev. 42(3), 451–484 (electronic) (2000). Reprint of SIAM J. Numer. Anal. 34 (1997), no. 6, 2392–2423 [MR1480387 (99b:65135)]
Bayliss, A., Goldstein, C.I., Turkel, E.: On accuracy conditions for the numerical computation of waves. J. Comput. Phys. 59(3), 396–404 (1985)
Bérenger, J.P.: Perfectly Matched Layer (PML) for Computational Electromagnetics. Synthesis Lectures on Computational Electromagnetics. Morgan and Claypool Publishers, San Rafael, CA (2007)
Brandt, A.: Rigorous quantitative analysis of multigrid. I. Constant coefficients two-level cycle with \(L_2\)-norm. SIAM J. Numer. Anal. 31(6), 1695–1730 (1994). https://doi.org/10.1137/0731087
Briggs, W.L., Henson, V.E., McCormick, S.F.: A Multigrid Tutorial, 2nd edn. Society for Industrial and Applied Mathematics (SIAM), Philadelphia (2000)
Britt, S., Tsynkov, S., Turkel, E.: A compact fourth order scheme for the Helmholtz equation in polar coordinates. J. Sci. Comput. 45(1–3), 26–47 (2010). https://doi.org/10.1007/s10915-010-9348-3
Britt, S., Tsynkov, S., Turkel, E.: Numerical simulation of time-harmonic waves in inhomogeneous media using compact high order schemes. Commun. Comput. Phys. 9(3), 520–541 (2011)
Britt, S., Tsynkov, S., Turkel, E.: A high order compact time/space finite difference scheme for the wave equation with variable speed of sound. J. Sci. Comput. 76, 777–811 (2018). https://doi.org/10.1007/s10915-017-0639-9
Britt, S., Tsynkov, S., Turkel, E.: Numerical solution of the wave equation with variable wave speed on nonconforming domains by high-order difference potentials. J. Comput. Phys. 354, 26–42 (2018)
Chabassier, J., Imperiale, S.: Introduction and study of fourth order theta schemes for linear wave equations. J. Comput. Appl. Math. 245, 194–212 (2013). https://doi.org/10.1016/j.cam.2012.12.023
Deraemaeker, A., Babuška, I.M., Bouillard, P.: Dispersion and pollution of the FEM solution for the Helmholtz equation in one, two and three dimensions. Int. J. Numer. Methods Eng. 46, 471–499 (1999)
Fishelov, D.: A new fourth-order compact scheme for the Navier–Stokes equations in irregular domains. Comput. Math. Appl. 74(1), 6–25 (2017). https://doi.org/10.1016/j.camwa.2016.10.020
Fu, Y.: Compact fourth-order finite difference schemes for Helmholtz equation with high wave numbers. J. Comput. Math. 26(1), 98–111 (2008)
Grote, M.J., Sim, I.: Efficient PML for the wave equation (2010). arXiv:1001.0319
Harari, I., Turkel, E.: Accurate finite difference methods for time-harmonic wave propagation. J. Comput. Phys. 119(2), 252–270 (1995)
Hocking, L.R., Greif, C.: Closed-form multigrid smoothing factors for lexicographic Gauss–Seidel. IMA J. Numer. Anal. 32(3), 795–812 (2012). https://doi.org/10.1093/imanum/drr037
Liang, H., Liu, M.Z., Lv, W.: Stability of \(\theta \)-schemes in the numerical solution of a partial differential equation with piecewise continuous arguments. Appl. Math. Lett. 23(2), 198–206 (2010). https://doi.org/10.1016/j.aml.2009.09.012
Lončarić, J., Tsynkov, S.V.: Optimization of acoustic source strength in the problems of active noise control. SIAM J. Appl. Math. 63(4), 1141–1183 (2003)
Ma, Y., Yu, J., Wang, Y.: An efficient complex-frequency shifted-perfectly matched layer for second-order acoustic wave equation. Int. J. Numer. Methods Eng. 97(2), 130–148 (2014). https://doi.org/10.1002/nme.4594
Ma, Y., Yu, J., Wang, Y.: A novel unsplit perfectly matched layer for the second-order acoustic wave equation. Ultrasonics 54(6), 1568–1574 (2014). https://doi.org/10.1016/j.ultras.2014.03.016
Petropavlovsky, S., Tsynkov, S., Turkel, E.: A method of boundary equations for unsteady hyperbolic problems in 3D. J. Comput. Phys. 365, 294–323 (2018). https://doi.org/10.1016/j.jcp.2018.03.039
Ryaben’kii, V.S.: Method of Difference Potentials and Its Applications, Springer Series in Computational Mathematics, vol. 30. Springer, Berlin (2002)
Saad, Y.: Iterative Methods for Sparse Linear Systems, 2nd edn. Society for Industrial and Applied Mathematics, Philadelphia (2003). https://doi.org/10.1137/1.9780898718003
Singer, I., Turkel, E.: High-order finite difference methods for the Helmholtz equation. Comput. Methods Appl. Mech. Eng. 163(1–4), 343–358 (1998)
Singer, I., Turkel, E.: High-order finite difference methods for the Helmholtz equation. Comput. Methods Appl. Mech. Eng. 163(1–4), 343–358 (1998). https://doi.org/10.1016/S0045-7825(98)00023-1
Trottenberg, U., Oosterlee, C.W., Schüller, A.: Multigrid. Academic Press Inc., San Diego (2001). With contributions by A. Brandt, P. Oswald and K. Stüben
Turkel, E., Gordon, D., Gordon, R., Tsynkov, S.: Compact 2D and 3D sixth order schemes for the Helmholtz equation with variable wave number. J. Comput. Phys. 232(1), 272–287 (2013). https://doi.org/10.1016/j.jcp.2012.08.016
Zhou, L., Armfield, S.: A compact fourth-order spatial discretisation applied to the Navier–Stokes equations. ANZIAM Journal 56, 481–501 (2016)
Author information
Authors and Affiliations
Corresponding author
Additional information
We dedicate this paper to the memory of Professor Saul (Shalom) Abarbanel who provided mentorship and inspiration to a whole generation of students and colleagues.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Work supported by the US Army Research Office (ARO) under Grant No. W911NF-16-1-0115 and the US–Israel Binational Science Foundation (BSF) under Grant No. 2014048.
Rights and permissions
About this article
Cite this article
Smith, F., Tsynkov, S. & Turkel, E. Compact High Order Accurate Schemes for the Three Dimensional Wave Equation. J Sci Comput 81, 1181–1209 (2019). https://doi.org/10.1007/s10915-019-00970-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-019-00970-x
Keywords
- Unsteady wave propagation
- Fourth order accurate approximation
- Small stencil
- Cartesian grid
- Implicit scheme
- Multigrid methods


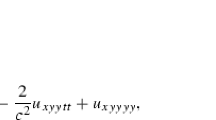


 )
) , and
, and  , as shown in Fig.
, as shown in Fig. 








