Abstract
We develop in this paper highly efficient, second order and unconditionally energy stable schemes for the epitaxial thin film growth models by using the scalar auxiliary variable (SAV) approach. A main difficulty here is that the nonlinear potential for the model without slope selection is not bounded from below so the SAV approach can not be directly applied. We overcome this difficulty with a suitable splitting of the total free energy density into two parts such that the integral of the part involving the nonlinear potential becomes bounded from below so that the SAV approach can be applied. We then construct a set of linear, second-order and unconditionally energy stable schemes for the reformulated systems. These schemes lead to decoupled linear equations with constant coefficients at each time step so that they can be implemented easily and very efficiently. We present ample numerical results to demonstrate the stability and accuracy of our SAV schemes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Epitaxy is referred to the deposition of a crystalline overlayer on a substrate. The technique of epitaxy thin film growth is usually used in nanotechnology or semiconductor fabrication. It is an affordable way to obtain high quality crystal for many multilayer structures and semiconductor materials. To understand the mechanisms of thin film growth behind its technological applications, many theoretical models have been developed and numerical simulations based on these models were carried out. In summary, there are mainly three types of mathematical models to simulate the thin film epitaxial growth process, including atomistic models (cf. [4, 8]), continuum models (cf. [9, 18]) and hybrid models (cf.[1, 7]). In this paper, we focus on the numerical approximations for the continuum models, which are obtained by minimizing a given total free energy where the nonlinear potential is either a fourth order Ginzburg–Landau double well potential (with slope selection) or a nonlinear logarithmic potential (without slope selection). Both are in terms of the gradient of a scalar height function.
There have been many attempts on developing efficient numerical schemes for solving the continuum thin film growth models. Examples include the stabilized semi-implicit method (see, for instance, [20], the convex splitting method (see, for instance, [2, 3, 14, 19], and the Invariant Energy Quadratization (IEQ) method (cf. [22]). The stabilized semi-implicit schemes [15] are easy to implement and very efficient, but it is in general difficult to construct truly unconditionally energy stable second-order schemes, and the stability proof and error analysis usually rely on a uniform Lipschitz condition on the derivative of the nonlinear potential (cf. [15]). However, for the MBE model without slope selection, by introducing an auxiliary variable, second-order energy stable schemes are constructed in [13]. The convex splitting approach [5, 6] can be applied to a large class of gradient flows to construct unconditionally energy stable first-order schemes, but it is also generally difficult to construct second-order schemes for complicated nonlinear potentials, although for the MBE model, second-order convex splitting schemes are constructed in [14]. A drawback of the convex splitting approach is that it requires solving a nonlinear system at each time step. The IEQ method [21] enables one to construct linear, second-order, unconditionally energy stable schemes for a large class of gradient flows, but it requires solving an elliptic system with complicated variable coefficients at each time step. It is shown to be successful for the model with slope selection [22] since the fourth order polynomial type Ginzburg–Landau potential is bounded from below naturally, but it is problematic for the model without slope selection since the nonlinear logarithmic potential is not bounded from below.
Recently, a new approach, termed as scalar auxiliary variable (SAV) approach, was proposed in [17] (see also [16]). This approach is inspired by the IEQ approach but fixes most, if not all, its shortcomings. In particular, it does not require the nonlinear potential (integrand) to be bounded from below, but only requires the integral of the part of the total free energy involving the nonlinear potential to be bounded from below. Furthermore, it leads to much simplified numerical schemes.
The purpose of this paper is to apply the SAV approach to develop new efficient and accurate schemes for the epitaxial thin film growth models. A main difficulty is that the nonlinear potential for the model without slope selection is not bounded from below so the SAV approach can not be directly applied. We overcome this difficulty by introducing a suitable splitting of the total free energy density into two parts such that the integral of the part involving the nonlinear potential becomes bounded from below. Then, we can reformulate the epitaxial thin film growth models with and without slope selection into equivalent PDE systems by introducing a scalar auxiliary variable. We can then develop efficient and accurate schemes for the reformulated PDE systems. More precisely, we shall construct second-order schemes based on BDF and Crank–Nicolson in which the nonlinear terms are all treated explicitly. We shall show that these schemes are unconditionally energy stable, and at each time step, they can be decoupled into two bi-Laplacian equations. Furthermore, each of the bi-Laplacian equation can be reduced to two decoupled Poisson type equations [23]. Thus, these schemes are second-order accurate and extremely efficient, especially when coupled with a suitable adaptive time stepping (see, for instance, [12]). Note that all previous unconditionally energy stable schemes by convex splitting or IEQ approaches lead to nonlinear systems or fourth-order equations with variable coefficients to solve at each time step. Hence, these new schemes appear to be more efficient than existing schemes. We must emphasize that the unconditional energy stability is for a modified energy, not for the original energy. While we can not prove that the original energy of our SAV schemes is dissipative as in the continuous case, we can show that they are uniformly bounded (see Remark 4.2).
The rest of the paper is organized as follows. In Sect. 2, we describe the thin film growth models with and without slope selections. In Sect. 3, we reformulate the thin film growth models into equivalent PDE systems by introducing a scalar auxiliary variable. Then we develop in Sect. 4 a set of schemes using the SAV approach for the reformulated systems, and show that they can be decoupled into two linear equations of fourth-order with only constant coefficients and are unconditionally energy stable. In Sect. 5, we present several numerical results to validate the accuracy and stability of the proposed schemes. Some concluding remarks are presented in Sect. 6.
2 Thin Film Epitaxy Growth Models
We first introduce some notations. We denote by \((f,g)=\int _\Omega f(\varvec{x})g(\varvec{x})d\varvec{x}\) the \(L^2\) inner product between functions \(f(\varvec{x})\) and \(g(\varvec{x})\), by \(\Vert f\Vert =(f,f)^{\frac{1}{2}}\) the \(L^2\) norm of a function \(f(\varvec{x})\).
We now introduce the thin film epitaxy growth models. Let \(\phi (\varvec{x})\): \(\Omega \rightarrow R\) represents the height of the thin film, the total phenomenological free energy is
where \(F(\varvec{y})\) is a smooth function, \(\epsilon \) is the gradient energy coefficient [10, 19]. The first term \(\int _{\Omega }F(\nabla \phi )d\varvec{x}\) represents a continuum description of the Ehrlich–Schwoebel effect, while the second term \(\int _{\Omega }\frac{\epsilon ^2}{2}(\Delta \phi )^2dx\) represents the surface diffusion effect.
There are two popular choices for the nonlinear potential \(F(\nabla \phi )\):
-
(i)
Double well potential for the model with slope selection
$$\begin{aligned} F(\nabla \phi )=\frac{1}{4}(|\nabla \phi |^2-1)^2. \end{aligned}$$(2.2) -
(ii)
Logarithmic potential for the model without slope selection
$$\begin{aligned} F(\nabla \phi )=-\frac{1}{2}\mathrm{ln}(1+|\nabla \phi |^2). \end{aligned}$$(2.3)
The evolution equation for the height function \(\phi \) is governed by the gradient flow:
where M is the mobility constant, and
The boundary conditions can be either the periodic boundary condition or the no-flux boundary condition, where \(\varvec{n}\) is the outward normal on the domain boundary \(\partial \Omega \):
One can easily obtain the energy dissipation property for the two models mentioned above by taking the \(L^2\) inner product of (2.4) with \(\phi _t\) and performing integration by parts:
By taking the \(L^2\) inner product with 1 for (2.4), we obtain the mass conservation property:
Hence, without loss of generality, we can assume \(\int _\Omega \phi (\varvec{x})d\varvec{x}=0\) so that the Poincaré inequality holds, i.e., there exists a positive constant \(c_0\) such that
3 Equivalent PDE Systems with the SAV Approach
In this section, we reformulate the thin film models into equivalent PDE systems by introducing a scalar auxiliary variable (SAV). We shall construct efficient numerical schemes based on these reformulated systems in the next section.
3.1 Model with Slope Selection
Since the free energy (2.2) for the model with slope selection is non-negative, the SAV (or IEQ) approach can be directly applied. Indeed, we introduce a non-local, time-dependent SAV:
where \(A_1\) can be any positive constant, \(A_1\) is used to avoid the denominator of \(H(\phi )\) being zero. The total energy for the model with slope selection becomes
Correspondingly, we rewrite the PDE system (2.4) for the model with slope selection as follows,
where
The above system is subjected to the boundary conditions (2.6), and initial conditions
Taking the \(L^2\) inner product of (3.3) with \(M^{-1}\phi _t\), and multiplying (3.4) with 2u, then performing integration by parts and summing up both equalities, we obtain the energy law for (3.3), (3.4):
It is easy to see that the transformed system (3.3), (3.4) is equivalent to the original PDE system (2.4) for the model with slope selection. Indeed, if \(\phi \) is a solution of (2.4) for the model with slope selection, then by the definition (3.1), we find immediately \((\phi ,u)\) is a solution of (3.3), (3.4). On the other hand, if \((\phi ,u)\) is a solution of (3.3), (3.4), we can integrate (3.4) to obtain (3.1), which, together with (3.3), implies \(\phi \) is a solution of (2.4) for the model with slope selection.
3.2 Model Without Slope Selection
On the other hand, the free energy (2.3) is unbounded from below so one can not apply the IEQ nor SAV approaches directly. However, inspired from [19], we shall show below, by adding part of the surface diffusion energy in (2.1) to the free energy (2.2), we can still apply the SAV (but not IEQ) approach.
Lemma 3.1
where \(c_0\) is the constant in (2.9).
Proof
For any \(\gamma >0\), the function \(G(t):=\frac{\gamma }{2}t-\frac{1}{2}\mathrm{ln}(1+t)\) is always convex (\(G''(t)> 0\)), and at \(t^\star =\frac{1}{\gamma }-1\), \(G(t^\star )\) reaches its minimum, i.e.,
Setting \(t=|\nabla \phi |^2\) in the above and integrating over \(\Omega \), we obtain
By using the Poincaré inequality, we derive
which implies that for any \(\gamma >0\),
Taking \(\gamma =\frac{\epsilon ^2}{2c_0^2}\) in the above, along with (3.10), we obtain
\(\square \)
Hence, we can define a non-local, time-dependent SAV:
where \(A_2\) is a positive constant to ensure the term under square root is positive, for example, we can choose \(A_2=-\frac{1}{2}(\mathrm{ln}(\frac{\epsilon ^2}{2c_0^2})-\frac{\epsilon ^2}{2c_0^2}+1 )|\Omega |+1\) thanks to Lemma 3.1.
We can then rewrite the total energy for the model without slope selection as
and reformulate the PDE system (2.4) as
where
The above system is subjected to the boundary conditions (2.6), and initial conditions
Taking the \(L^2\) inner product of (3.16) with \(M^{-1}\phi _t\) and multiplying (3.17) with 2v, then performing integration by parts and summing up both equalities, we obtain an equivalent dissipative law:
It is easy to see that the transformed system (3.16), (3.17) is equivalent to the original PDE system (2.4) for the model without slope selection. Indeed, if \(\phi \) is a solution of (2.4) for the model without slope selection, then by the definition (3.14), we find immediately \((\phi ,v)\) is a solution of (3.16), (3.17). On the other hand, if \((\phi ,v)\) is a solution of (3.16), (3.17), we can integrate (3.17) to obtain (3.14), which, together with (3.16), implies \(\phi \) is a solution of (2.4) for the model without slope selection.
Note that even with Lemma 3.1, we can not apply the IEQ approach to reformulate the PDE system (2.4) for the model without slope selection, since the integrand in (3.8) is not bounded from below.
4 Numerical Schemes by the SAV Approach
We now develop a set of very efficient unconditionally energy stable second order schemes to solve the new system (3.3), (3.4) and (3.16), (3.17). To simplify the presentation, we consider only semi-discretized schemes in time, but the stability results carry over in a straightforward fashion to fully discretized versions with any consistent finite dimensional Galerkin type approximations since the proofs are all based on variational formulations with all test functions in the same space as the space of the trial functions.
Let \(\delta t >0\) be a time step size and set \(t^n=n \delta t\) for \(0\le n \le N=[T/\delta t]\), let \(U^n\) denotes the numerical approximation to \(U(\cdot ,t)|_{t=t^n}\), and \(U^{n+\frac{1}{2} }=\frac{U^{n+1}+U^n}{2}\) for any function U. We use \((\cdot ,\cdot )\) to denote the inner product in \(L^2(\Omega )\) and set \(\Vert v\Vert ^2=(v,v)\).
4.1 SAV Schemes for the Model with Slope Selection
We firstly construct a second order scheme for solving the model with slope selection (3.3), (3.4) based on the second order backward differentiation formula (BDF2).
Scheme 1
(SAV-BDF2 scheme for the model with slope selection). Assuming that \(\phi ^{n-1}\), \(\phi ^{n}\) and \(u^{n-1}\), \(u^{n}\) are known, we solve \(\phi ^{n+1}\), \(u^{n+1}\) as follows:
where \(H^{\star ,n+1}=2H(\phi ^n)-H(\phi ^{n-1})\).
Note that the above scheme for \((\phi ^{n+1},u^{n+1})\) is linear but coupled. However, as in the IEQ approach, the system can be decoupled. Furthermore, as pointed in [17], a main advantage of the SAV approach is that the decoupled system only involves linear equations with constant coefficients. We now describe how to decouple the above system.
We first rewrite (4.2) as
with \(g^n=\frac{4u^n-u^{n-1}}{3}-\frac{1}{2} \int _\Omega H^{\star ,n+1} \frac{4\phi ^n-\phi ^{n-1}}{3}d\varvec{x}\). Then we can eliminate \(u^{n+1}\) from (4.1) to get
with \(f^n=\frac{4\phi ^n-\phi ^{n-1}}{2\delta t} - MH^{\star , n+1} g^n.\)
Next, we shall derive an explicit formula for computing \(\int _\Omega H^{\star , n+1}\phi ^{n+1}d\varvec{x}\). Define an linear operator \(\chi ^{-1}(\cdot )\), such that for any \(\phi \in L^2(\Omega )\), \(\psi =\chi ^{-1}(\phi )\) is defined as the solution of
with the boundary conditions (2.6). Applying the operator \(\chi ^{-1}\) to (4.4), we obtain
Taking the \(L^2\) inner product with \(H^{\star ,n+1}\), we find
To summarize, to obtain \(\phi ^{n+1}\) through (4.6), we only need to compute \(\psi _1=\chi ^{-1}(f^n)\) and \(\psi _2=\chi ^{-1}(H^{\star ,n+1})\), which amount to solving two decoupled equations
and
with the boundary conditions (2.6). As shown in [23], each of the above equations can be further reduced to two decoupled Poisson type equations so that they can be solved very efficiently. Once \(\phi ^{n+1}\) is known, one can obtain \(u^{n+1}\) from (4.3) using (4.7).
Remark 4.1
The authors in [22] applied the IEQ approach for solving the model (2.4) with slope selection. The resultant scheme can also be decoupled but leads to a PDE system with non-constant coefficients, which is much more expensive and complicated to solve numerically.
In addition to its remarkable simplicity, the scheme (4.1), (4.2) is also unconditionally energy stable as we show below.
Theorem 4.1
The scheme (4.1), (4.2) admits a unique solution, and is unconditionally energy stable in the sense that it satisfies the following discrete energy dissipation law:
where \(E_A^{n+1,n}=\frac{\epsilon ^2}{4}(\Vert \Delta \phi ^{n+1}\Vert ^2+\Vert \Delta (2\phi ^{n+1}-\phi ^n)\Vert ^2)+ \frac{1}{2}\big ((u^{n+1})^2+(2u^{n+1}-u^n)^2\big )\).
Proof
Taking the \(L^2\) inner product of (4.1) with \(\frac{1}{2M}(3\phi ^{n+1}-4\phi ^n+\phi ^{n-1})\), and applying the following identity
we obtain
Multiplying \(u^{n+1}\) to (4.2), we find
Combining (4.12) and (4.13), we arrive at
which implies the desired result after dropping some positive terms above. \(\square \)
Similarly, one can also construct a second order SAV Crank–Nicolson scheme.
Scheme 2
(SAV-CN scheme for the model with slope selection) Assuming that \(\phi ^{n-1}\), \(\phi ^{n}\) and \(u^{n-1}\), \(u^{n}\) are known, we solve \(\phi ^{n+1}\), \(U^{n+1}\) as follows:
where \(H^{\star ,n+\frac{1}{2}}=\frac{3}{2}H(\phi ^n)-\frac{1}{2}H(\phi ^{n-1})\).
Using the similar process as for the SAV-BDF2 scheme, the SAV-CN scheme can also be decoupled into two linear equations of the form
with the boundary conditions (2.6). Thus the SAV-CN scheme is as efficient as the SAV-BDF2 scheme, it has smaller truncation error but could be prone to numerical oscillations if the initial error has highly oscillatory part.
Theorem 4.2
The scheme (4.15)–(4.16) admits a unique solution, and is unconditionally energy stable in the sense that it satisfies the following discrete energy dissipation law:
where \(E_A^{n+1}=\frac{\epsilon ^2}{2}\Vert \Delta \phi ^{n+1}\Vert ^2+ (u^{n+1})^2\).
Proof
Taking the \(L^2\) inner product of (4.15) with \(\frac{1}{M}(\phi ^{n+1}-\phi ^n)\), we obtain
Taking the \(L^2\) inner product of (4.16) with \(u^{n+1}+u^n\), we find
Combining (4.19) and (4.20), we obtain
Then proof is complete. \(\square \)
4.2 SAV Schemes for the Model Without Slope Selection
Similar to the model with slope selection, we can construct efficient SAV schemes for the reformulated system (3.16), (3.17). Since the construction, the solution process and the proof of stability follow essentially the same procedure as in the model with slope selection, we shall only state the results below.
Scheme 3
(SAV-BDF2 scheme for the model without slope selection). Assuming that \(\phi ^{n-1}\), \(\phi ^{n}\) and \(v^{n-1}\), \(v^{n}\) are known, we solve \(\phi ^{n+1}\) and \(v^{n+1}\) as follows:
where \(S^{\star , n+1}=2S(\phi ^n)-S(\phi ^{n-1})\) and function \(S(\phi )\) is defined as equation (3.18).
As in the model with slope selection, one can eliminate \(v^{n+1}\) from above and decouple it into two linear systems of the form
with the boundary conditions (2.6), and establish the following result.
Theorem 4.3
The scheme (4.22), (4.23) is unconditionally energy stable in the sense that it satisfies the following discrete energy dissipation law:
where \(E_B^{n+1,n}=\frac{\epsilon ^2}{8}(\Vert \Delta \phi ^{n+1}\Vert ^2+\Vert \Delta (2\phi ^{n+1}-\phi ^n)\Vert ^2)+ \frac{1}{2}\big ((v^{n+1})^2+(2v^{n+1}-v^n)^2\big )\).
One can also construct the SAV-CN scheme for the model without slope selection as follows:
Scheme 4
(SAV-CN scheme for the model without slope selection) Assuming that \(\phi ^{n-1}\), \(\phi ^{n}\) and \(v^{n-1}\), \(v^{n}\) are known, we solve \(\phi ^{n+1}\), \(v^{n+1}\) as follows:
where \(S^{\star ,n+\frac{1}{2}}=\frac{3}{2}S(\phi ^n)-\frac{1}{2}S(\phi ^{n-1})\).
One can also eliminate \(v^{n+1}\) from above and decouple it into two linear systems of the form
with the boundary conditions (2.6), and establish the following result.
Theorem 4.4
The scheme (4.26), (4.27) is unconditionally energy stable in the sense that it satisfies the following discrete energy dissipation law:
where \(E_B^{n+1}=\frac{\epsilon ^2}{4}\Vert \Delta \phi ^{n+1}\Vert ^2+(v^{n+1})^2\).
Remark 4.2
Note that the SAV schemes only guarantee that the modified energy is unconditionally energy stable. While the original energy may not be unconditionally energy stable, it is easy to show that the original energy is uniformly bounded. Indeed, thanks to the boundary condition (2.6) and the assumption that \(\int _\Omega \phi dx=0\), the uniform bound on \(\Vert \Delta \phi ^n\Vert \) derived in Theorems 4.1–4.4 implies that \(\Vert \phi ^n\Vert _{H^2}\) is uniformly bounded for all n. On the other hand, we derive from the Sobolev inequality
that the original energy of the SAV schemes for the MBE model with slope selection is uniformly bounded. As for the MBE model without slope selection, thanks to Lemma 3.1, the original energy of the SAV schemes is also uniformly bounded.
4.3 Adaptive Time Stepping
In most practical problems, energy evolution may undergo large variations initially and at some time intervals, but may change very little in some other time intervals (see, e.g., simulations in the next subsection). One main advantage of unconditionally energy stable schemes is that it can be easily combined with an adaptive strategy which chooses time step based on the accuracy requirement only. So small time steps are only used when the energy variation is large while lager time steps can be used when the energy variation is small. We shall adapt the following strategy (cf. [12]):
where \(\Delta t_{min},\; \Delta t_{max}\) are predetermined minimum and maximum time steps, and \(\alpha \) is a suitable parameter.
5 Numerical Simulations
We now present several numerical simulations to validate the theoretical results derived in the previous section and demonstrate the efficiency, the stability and the accuracy of the new SAV schemes.
In all examples, \(\Omega =(0,L)^d, d=2,3\), and the boundary conditions are periodic. If not explicitly specified, the default values of parameters \(\epsilon \) and M are \(\epsilon ^2= 0.1,\; M=1\) so as to be consistent with the numerical examples performed in the literature [10, 12, 19, 20, 22].
5.1 Convergence Tests
We first test convergence rates of the four new schemes. We denote by S-BDF, S-CN, n-S-BDF and n-S-CN, respectively, the SAV-BDF2 scheme for the the model with slope selection (Scheme 1),
the SAV-CN scheme for the model with slope selection (Scheme 2), the SAV-BDF2 scheme for the model without slope selection (Scheme 3), and the SAV-CN scheme for the model without slope selection (Scheme 4).
5.1.1 Case with a Given Exact Solution
In this test, we take the exact solution to be
The computational domain is \([0, 2\pi )^2\) and we use \(129\times 129\) Fourier modes.
In Tables 1 and 2, we present the absolute \(L^2\) error of the height function \(\phi \) at time \(t=1\) with various time steps. We observe that all four schemes yield the expected second-order convergence rate.
Evolution of the total energy using the schemes S-CN and n-S-CN for the models with and without slope selection, respectively. a Energy evolution for the model with slope selection when \(t\in (0, 0.04)\) and \(t\in (0,30)\) and b energy evolution for the model without slope selection when \(t\in (0, 0.04)\) and \(t\in (0,30)\)
The evolution of the roughness W(t) using the schemes S-CN and n-S-CN for the models with and without slope selection, respectively: with the initial condition (5.2) and the time step \(\delta t=0.001\). a The roughness W(t) when \(t\in (0,4)\) (left) and \(t\in (0,30)\) (right) for the model with slope selection and b the roughness W(t) when \(t\in (0,4)\) (left) and \(t\in (0,30)\) (right) for the model without slope selection
5.1.2 Case with a Given Initial Condition
In this test, we take the initial condition to be
which has also been used in [10, 12, 19, 20, 22]. The computational domain is again \([0, 2\pi )^2\) and we use \(129\times 129\) Fourier modes. Since no exact solution is available, we use the numerical solution by the S-BDF and n-S-BDF schemes with the smallest time step size of \(\delta t=\)1e−5 as the reference solution.
We present in Tables 3 and 4, the \(L^2\) errors at \(t=1\) with different time step sizes for the models with and without slope selection, respectively. We observe that all four schemes achieve the expected second-order convergence rate.
To quantify the deviation of the height function, we define the roughness function \(R(\phi )\) (cf. [10, 12, 19, 20, 22]):
where \(\bar{\phi }(t)=\frac{1}{|\Omega |}\int _{\Omega }\phi (\varvec{x},t)d\varvec{x}\).
We plot the evolution of energy curves and the roughness for the models with and without slope selection in Figs. 1 and 2, respectively. We observe that initially the energy and the roughness decay rapidly. After a relatively long period of time, the roughness starts to grow. These results are quantitatively identical to those obtained in [10, 19, 22].
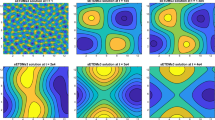
The isolines of the numerical solutions of the height function \(\phi \) and its Laplacian \(\Delta \phi \) for the model with slope selection with random initial condition. For each subfigure, the left is \(\phi \) and the right is \(\Delta \phi \) . Snapshots are taken at \(t = 0 , 1 , 10 , 50 , 100 , 500\), respectively. a\(t=0\), b\(t=1\), c\(t=10\), d\(t=50\), e\(t=100\) and f\(t=500\)
The isolines of the numerical solutions of the height function \(\phi \) and its Laplacian \(\Delta \phi \) for the model without slope selection with random initial condition. For each subfigure, the left is \(\phi \) and the right is \(\Delta \phi \) . Snapshots are taken at \(t = 0 , 1 , 10 , 50 , 100 , 500\), respectively. a\(t=0\), b\(t=1\), c\(t=10\), d\(t=50\), e\(t=100\) and f\(t=500\)
It is shown in the last sections that the modified energy of all SAV schemes is dissipative, but we do not have a theoretical proof of this property for the original energy. Thus, we plot the original energy and the modified energy for both models in Fig. 3. We observe that the modified energy and the original energy for both models are almost indistinguishable.
5.2 Coarsening Dynamics
To simulate the coarsening dynamics, we choose a random initial condition varying from \(-0.001\) to 0.001. The parameters are
The computational domain is \(\Omega =[0,12.8)^2\), and we use \(513\times 513\) Fourier modes so that the errors from the spatial discretization are negligibly small compared with the time discretization error. We use the adaptive time strategy (4.30) to determine the time steps with \(\Delta t_{min}=10^{-5}\), \(\Delta t_{max}=10^{-2}\) and \(\alpha =10^5\).
In Figs. 4 and 5, we show snapshots of numerical solutions of the height function \(\phi \) and its Laplacian \(\Delta \phi \) at different time for both models, respectively.
In the left of Figs. 6 and 7, we plot the evolution of the roughness and the energy for the model with slope section, respectively. We observe that the former grows like \(t^{\frac{1}{3}}\) while the latter decays like \(t^{-\frac{1}{3}}\), as found in [11] (see also [12, 14, 19]).
In the right of Figs. 6 and 7, we plot the evolution of the roughness and the energy for the model without slope section, respectively. We observe that the former grows like \(t^{\frac{1}{2}}\) while the latter decays like \(-\log _{10}(t)\) for the model without slope selection, shown in Fig. 7, the energy decays rather rapidly like \(-\log _{10}(t)\), as found in [10].
As the last example, we perform numerical simulations of the coarsening dynamics in 3D with a random initial state ranging from \(-\,0.001\) to 0.001. Simulations are carried out in the domain \(\Omega =[0,2\pi )^3\) with \(129\times 129 \times 129\) Fourier modes and the time step \(\delta t=\)2.5e−4. In Figs. 8 and 9, we plot three iso-surfaces for \(\phi =0.3\) for the model with slope selection and the model without slope selection, respectively. We observe similar coarsening dynamics as in the 2D case.
In Figs. 10 and 11, we plot evolutions of free energy and roughness for both models. We observe that the decay rates of the free energy and growth rates of the roughness are qualitatively similar as in the 2D case but with quantitatively different rates.
6 Concluding Remarks
We developed in this paper a set of time discretization schemes using the SAV approach for the epitaxial thin film models with slope selection and without slope selection. These schemes enjoy the following advantages:
-
second order accurate in time;
-
unconditional energy stable;
-
can be decoupled into two linear fourth-order equations with constant coefficients (in fact two bi-Laplacian equations) at each time step. As shown in [23], each of the bi-Laplacian equation with the boundary condition (2.6) can be further reduced to two decoupled Poisson type equations.
Thus, these schemes are easy to implement and extremely efficient when coupled with an adaptive time stepping.
Although we considered only semi-discretized schemes in time in this paper, the stability results here can be carried over to any consistent finite dimensional Galerkin type approximations since the proofs are all based on a variational formulation with all test functions in the same space as the space of the trial functions.
References
Caflisch, R.E., Gyure, M.F., Merriman, B., Osher, S.J., Ratsch, C., Vvedensky, D.D., Zinck, J.J.: Island dynamics and the level set method for epitaxial growth. Appl. Math. Lett. 12(4), 13–22 (1999)
Chen, W., Conde, S., Wang, C., Wang, X., Wise, S.: A linear energy stable scheme for a thin film model without slope selection. J. Sci. Comput. 52, 546–562 (2012)
Chen, Wenbin, Wang, Cheng, Wang, Xiaoming, Wise, Steven M.: A linear iteration algorithm for a second-order energy stable scheme for a thin film model without slope selection. J. Sci. Comput. 59(3), 574–601 (2014)
Clarke, S., Vvedensky, D.D.: Origin of reflection high-energy electron-diffraction intensity oscillations during molecular-beam epitaxy: a computational modeling approach. Phys. Rev. Lett. 58(21), 2235 (1987)
Elliott, C.M., Stuart, A.M.: The global dynamics of discrete semilinear parabolic equations. SIAM J. Numer. Anal. 30, 1622–1663 (1993)
Eyre, D.J.: Unconditionally gradient stable time marching the Cahn–Hilliard equation. In: Computational and Mathematical Models of Microstructural Evolution, San Francisco, CA, 1998, Volume 529 of Materials Research Society Symposia Proceedings, pp. 39–46. MRS, Warrendale, PA (1998)
Gyure, M.F., Ratsch, C., Merriman, B., Caflisch, R.E., Osher, S.T., Zinck, J.J., Vvedensky, D.D.: Level-set methods for the simulation of epitaxial phenomena. Phys. Rev. E 58(6), R6927 (1998)
Kang, H.C., Weinberg, W.H.: Dynamic Monte Carlo with a proper energy barrier: surface diffusion and two-dimensional domain ordering. J. Chem. Phys. 90(5), 2824–2830 (1989)
Krug, J.: Origins of scale invariance in growth processes. Adv. Phys. 46(2), 139–282 (1997)
Li, B., Liu, J.G.: Epitaxial growth without slope selection: energetics, coarsening, and dynamic scaling. J. Nonlinear Sci. 14(5), 429–451 (2004)
Moldovan, D., Golubovic, L.: Interfacial coarsening dynamics in epitaxial growth with slope selection. Phys. Rev. E 61(6), 6190 (2000)
Qiao, Z., Zhang, Z., Tang, T.: An adaptive time-stepping strategy for the molecular beam epitaxy models. SIAM J. Sci. Comput. 33(3), 1395–1414 (2011)
Qiao, Z., Sun, Z.-Z., Zhang, Z.: Stability and convergence of second-order schemes for the nonlinear epitaxial growth model without slope selection. Math. Comput. 84(292), 653–674 (2015)
Shen, J., Wang, C., Wang, X., Wise, S.M.: Second-order convex splitting schemes for gradient flows with Ehrlich–Schwoebel type energy: application to thin film epitaxy. SIAM J. Numer. Anal. 50(1), 105–125 (2012)
Shen, J., Yang, X.: Numerical approximations of Allen–Cahn and Cahn–Hilliard equations. Discrete Contin. Dyn. Syst. A 28, 1669–1691 (2010)
Shen, J., Xu, J., Yang, J.: A new class of efficient and robust energy stable schemes for gradient flows. Submitted to SIAM Rev.
Shen, J., Jie, X., Yang, J.: The scalar auxiliary variable (SAV) approach for gradient flows. J. Comput. Phys. 352, 407–417 (2018)
Villain, J.: Continuum models of crystal growth from atomic beams with and without desorption. Journal de physique I 1(1), 19–42 (1991)
Wang, C., Wang, X., Wise, S.M.: Unconditionally stable schemes for equations of thin film epitaxy. Discrete Contin. Dyn. Syst. 28(1), 405–423 (2010)
Xu, C., Tang, T.: Stability analysis of large time-stepping methods for epitaxial growth models. SIAM J. Numer. Anal. 44(4), 1759–1779 (2006)
Yang, X.: Linear, first and second order and unconditionally energy stable numerical schemes for the phase field model of homopolymer blends. J. Comput. Phys. 327, 294–316 (2016)
Yang, X., Zhao, J., Wang, Q.: Numerical approximations for the molecular beam epitaxial growth model based on the invariant energy quadratization method. J. Comput. Phys. 333, 104–127 (2017)
Yue, P., Feng, J.J., Liu, C., Shen, J.: A diffuse-interface method for simulating two-phase flows of complex fluids. J. Fluid Mech. 515, 293–317 (2004)
Acknowledgements
This work is supported in part by NSFC Grants 91630204, 11421110001 and 51661135011, and NSF Grants DMS-1720442 and DMS-1720212.
Funding
Funding was provided by Directorate for Mathematical and Physical Sciences (Grant No. DMS-1620262).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Cheng, Q., Shen, J. & Yang, X. Highly Efficient and Accurate Numerical Schemes for the Epitaxial Thin Film Growth Models by Using the SAV Approach. J Sci Comput 78, 1467–1487 (2019). https://doi.org/10.1007/s10915-018-0832-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-018-0832-5