Efficient Parallelization of a Shock Capturing for Discontinuous Galerkin Methods using Finite Volume Sub-cells

Abstract

We present a shock capturing procedure for high order Discontinuous Galerkin methods, by which shock regions are refined in sub-cells and treated by finite volume techniques. Hence, our approach combines the good properties of the Discontinuous Galerkin method in smooth parts of the flow with the perfect properties of a total variation diminishing finite volume method for resolving shocks without spurious oscillations. Due to the sub-cell approach the interior resolution on the Discontinuous Galerkin grid cell is nearly preserved and the number of degrees of freedom remains the same. This structure allows the interpretation of the data either as DG solution or as finite volume solution on the subgrid. In this paper we explain the efficient implementation of this coupled method on massively parallel computers and show some numerical results.

1 Introduction

Discontinuous Galerkin methods of high order accuracy have the problem that transient shock waves or under-resolved strong gradients travelling may introduce instabilities. The high order polynomial in the coarse grid cell generates spurious oscillations when such an inner element jump has to be resolved. There exist different methods to circumvent these problems. One is the use of explicit artificial viscosity [6, 27, 28], which adds locally viscosity to the original equations to smear the discontinuities in such a way that it can be resolved by the numerical approximation continuous in the grid cell. The artificial viscosity was originally proposed by von Neumann and Richtmyer [41] for finite difference schemes. Persson and Peraire [27] adapted this to high order Discontinuous Galerkin (DG) methods to eliminate the high frequencies without widening the shock over a couple of cells.

There exists a lot of work in which WENO approaches are combined with the Discontinuous Galerkin method to limited the solution in a presence of a shock. Qiu and Shu [29] introduced the idea of using Hermite WENO schemes as limiters fo Runge–Kutta Discontinuous Galerkin schemes. Balsara et al. [4] extended this approach to hybrid RKDG+HWENO schemes, where they used indicators on sub-cells to detect the troubled zones.

Another technique to capture shocks in a DG framework, which is inspired by the finite volume methodology, is the approach of refining the grid in shock regions, while reducing the degree of the polynomials [7, 8], often called hp-adaption. Huerta et al. [20] had this idea in mind, when they proposed a Discontinuous Galerkin method, where the polynomial ansatz space is extended by piecewise constant functions in sub-cells of the original DG elements. In general the reduction of the polynomial degree decreases the oscillations, while the resolution has to be preserved by h-refinement.

In this paper we investigate the latter approach. But, we use an inherent refinement of the Discontinuous Galerkin elements into several finite volume sub-cells with a lower order approximation without changing the degrees of freedom or the general data structure. The outline of this paper is as follows. First we summarize the basic concepts of our DG method and define the degrees of freedom (DOF) of an element. In Sect. 3 we then derive a finite volume method, where each sub-cell is associated with one degree of freedom within the DG grid cell. The interior FV method is capable to capture strong shocks due to its total variation diminishing character. The following section shows numerical examples to illustrate the effectiveness of our approach to handle shocks on high performance computing (HPC) systems.

2 The Discontinuous Galerkin Spectral Element Method

The Discontinuous Galerkin method was originally introduced by Reed and Hill [31] to solve the hyperbolic neutron transport equation in the early 1970’s. The first theoretical considerations were done by Lasaint and Raviart [24]. Later around 1990 Cockburn and Shu developed in a series of papers [9, 11–13, 15] a solid theoretical framework for the DG method to apply it to nonlinear hyperbolic systems of conservation laws. The Discontinuous Galerkin method is based on the finite volume and the Finite Element methods. While the solution inside the elements is approximated by a high order polynomial (FE), the solution is discontinuous across element interfaces. These discontinuities are resolved by numerical fluxes computed with approximative Riemann solvers (FV).

In the following we shortly introduce the Discontinuous Galerkin method on spectral elements [22] to keep the paper self-consistent. This DG method is the basis of our CFD solver FLEXI. A detailed description of the basic approach in three space dimensions can be found in Hindelang et al. [19]. To keep the notation simple we confine ourselves to the two-dimensional case in the following, even so the implementation is 3D only. All derivations can be easily extended to a higher dimensional space.

2.1 Weak Formulation

The general system of conservation laws in physical space is given by

$$\begin{aligned} \mathbf {u}_t(x) + \nabla \cdot F(\mathbf {u}(x)) = 0 \quad \forall x \in \varOmega , \end{aligned}$$

(1)

where $\mathbf {u}$ is the vector of conservative variables, $F= \left( F^1,F^2 \right)$ are the physical fluxes and $\varOmega$ is the computational domain, which is subdivided into hexahedral elements. Each of this element is mapped onto the reference $E = [-1,1]^2$ yielding

$$\begin{aligned} J(\xi ) \mathbf {u}_t(t, \xi ) + \nabla _\xi \cdot \mathcal {F}(\mathbf {u}(t,\xi )) = 0, \end{aligned}$$

(2)

where $J(\xi )$ is the Jacobian of the mapping, $\mathcal {F}= \left(\mathcal {F}^1, \mathcal {F}^2 \right)$ are the transformed fluxes and $\xi = (\xi ^1, \xi ^2)^{\top }$ are the coordinates in the reference space. Multiplying the transformed conservation law (2) with a test function $\varPhi$ and integration over the reference element E gives, after partial integration of the second integral, the weak formulation

$$\begin{aligned} \int _E J \mathbf {u}_t \varPhi \,\hbox {d}\xi + \int _{\partial E} \left(\mathcal {F}\cdot n \right)^* \varPhi \,\hbox {d}S_\xi - \int _E \mathcal {F}\cdot \nabla _\xi \varPhi \,\hbox {d}\xi = 0 \quad \forall \varPhi , \end{aligned}$$

(3)

where n is the normal vector of the reference element E. Since the solution is allowed to be discontinuous along element interfaces we also introduce the numerical flux $(\mathcal {F}\cdot n)^*$, which is later evaluated by use of a Riemann solver, see [38].

2.2 Approximation of the Solution and Face Fluxes

The solution in the reference element is approximated by a polynomial tensor product basis of degree N in each space direction

$$\begin{aligned} \mathbf {u}(\xi ) = \sum _{i,j=0}^N {\hat{\mathbf{u}}}_{ij} \psi _{ij}(\xi ) \quad \text {with } \psi _{ij} = l_i\left( \xi ^1\right) l_j\left( \xi ^2\right) , \end{aligned}$$

(4)

where ${\hat{\mathbf{u}}}_{ij}$ are the nodal degrees of freedom and $l_i(\xi )$ are the one-dimensional Lagrange interpolation polynomials defined by the Gauss nodes $\lbrace \xi _i \rbrace _{i=0}^N$. The Lagrange interpolation polynomials have the nice Lagrange property

$$\begin{aligned} \delta _{ij} = l_i(\xi _j) \quad \forall i,j = 0, \ldots , N. \end{aligned}$$

(5)

With $\lbrace \omega _i\rbrace _{i=0}^N$ we denote the weights of the Gauss quadrature corresponding to the nodes $\lbrace \xi _i \rbrace _{i=0}^N$. The numerical flux $(\mathcal {F}\cdot n)^*$ at the faces of the reference element is discretized in the same way. In the $\xi ^1$ direction at $\xi ^1=\pm 1$ we get

$$\begin{aligned} \left(\mathcal {F}(\mathbf {u}^-, \mathbf {u}^+) \cdot n\right)^* = \sum _{m=0}^N f_m^{*,\xi ^1}(\mathbf {u}^-,\mathbf {u}^+, n) l_m(\xi ^2), \end{aligned}$$

(6)

where $\mathbf {u}^-$ denotes the extrapolated face state of the actual element, $\mathbf {u}^+$ the face state of the corresponding neighbor element and $f_m^{*,\xi ^1}$ the numerical flux evaluated at $\xi ^2_m$. To distinguish between fluxes in $\xi ^1$ and $\xi ^2$ direction we added the superscript $\xi ^1$ and write for the fluxes in $\xi ^2$ direction $f_m^{*,\xi ^2}(\mathbf {u}^-,\mathbf {u}^+, n)$ respectively.

2.3 Time Derivative Integral

In our spectral element approach we use collocation of interpolation and integration and since we build a Galerkin method we choose test functions to be identical to the basis functions $\varPhi = \psi _{ij}$. Inserting the approximation of the state and an auxiliary test function the first integral of (3) reads as

$$\begin{aligned} \frac{\partial }{\partial t} \int _E J \mathbf {u}\varPhi \,\hbox {d}\xi = \frac{\partial }{\partial t}\int _{-1}^1 \int _{-1}^1 J(\xi ) \left(\sum _{mn=0}^N {\hat{\mathbf{u}}}_{mn} \psi _{mn}(\xi )\right) \psi _{ij}(\xi ) \,\hbox {d}\xi _1 \,\hbox {d}\xi _2, \end{aligned}$$

(7)

where we already split the integration over the reference element E into the coordinate directions $\xi _1$ and $\xi _2$. Approximating these integrals by the Gauss–Legendre quadrature and inserting the definition of the basis function $\psi _{mn}$ and the test function $\psi _{ij}$ in the second step yields

$$\begin{aligned} \begin{aligned} \frac{\partial }{\partial t} \int _E J \mathbf {u}\varPhi \,\hbox {d}\xi&= \frac{\partial }{\partial t}\sum _{\lambda , \mu =0}^{N} J(\xi _{\lambda \mu }) \left(\sum _{mn=0}^N {\hat{\mathbf{u}}}_{mn} \underbrace{l_m(\xi ^1_\lambda )}_{\delta _{m\lambda }} \underbrace{l_n(\xi ^2_\mu )}_{\delta _{n \mu }} \right) \psi _{ij}(\xi _{\lambda \mu }) \omega _\lambda \omega _\mu \\&= \frac{\partial }{\partial t}\sum _{\lambda , \mu =0}^{N} J(\xi _{\lambda \mu }) {\hat{\mathbf{u}}}_{\lambda \mu } \underbrace{l_i(\xi ^1_\lambda )}_{\delta _{i\lambda }} \underbrace{l_j(\xi ^2_\mu )}_{\delta _{j \mu }} \omega _\lambda \omega _\mu \\&= J(\xi _{ij}) \frac{\partial {\hat{\mathbf{u}}}_{ij}}{\partial t} \omega _i \omega _j. \end{aligned} \end{aligned}$$

(8)

2.4 Surface Integral

The surface integral of the weak formulation (3) can be split into four integrals from $-1$ to 1 at $\xi ^1=\pm 1$ and $\xi ^2=\pm 1$. Inserting the approximation of the test function and the fluxes we get

$$\begin{aligned} \begin{aligned} \int _{\partial E} \left(\mathcal {F}\cdot n \right) \varPhi \,\hbox {d}S_\xi&= \left[ \int _{-1}^{1} \left( \sum _{m=0}^N f_m^{*,\xi ^1}(\mathbf {u}^-, \mathbf {u}^+, n) l_m(\xi ^2) \right) l_i(\xi ^1) l_j(\xi ^2) \,\hbox {d}S_{\xi ^2} \right]_{\xi ^1=-1}^1 \\&\quad + \left[ \int _{-1}^{1} \left( \sum _{m=0}^N f_m^{*,\xi ^2}(\mathbf {u}^-, \mathbf {u}^+, n) l_m(\xi ^1) \right) l_i(\xi ^1) l_j(\xi ^2) \,\hbox {d}S_{\xi ^1} \right]_{\xi ^2=-1}^1. \end{aligned} \end{aligned}$$

(9)

Again we replace the integration by Gauss-Legendre quadrature and use the Lagrange property (5) to obtain in the end

$$\begin{aligned} \begin{aligned} \int _{\partial E} \left(\mathcal {F}\cdot n \right) \varPhi \,\hbox {d}S_\xi&= \left[ f_j^{*,\xi ^1}(\mathbf {u}^-, \mathbf {u}^+, n) l_i(\xi ^1) \omega _j \right]_{\xi ^1=-1}^1 \\&\quad + \left[ f_i^{*,\xi ^2}(\mathbf {u}^-, \mathbf {u}^+, n) l_j(\xi ^2) \omega _i \right]_{\xi ^2=-1}^1 . \end{aligned} \end{aligned}$$

(10)

For a more detailed view on this deduction and also the discretization of the volume integral we refer the reader to [19].

2.5 Volume Integral

Using the same discretization for the fluxes $\mathcal {F}$ as for the solution $\mathbf {u}$

$$\begin{aligned} \mathcal {F}^d(\mathbf {u}(\xi )) = \sum _{i,j=0}^N \hat{\mathcal {F}}^d_{ij} \psi _{ij}(\xi ) \end{aligned}$$

(11)

and inserting the approximation of the test function into the volume integral of the weak formulation (3) yields

$$\begin{aligned} -\int _E \mathcal {F}\cdot \nabla _\xi \varPhi \,\hbox {d}\xi = \sum _{d=1}^2 \int _E \mathcal {F}^d \frac{\partial \varPhi }{\partial \xi ^d} \,\hbox {d}\xi = \sum _{d=1}^2 \int _E \sum _{m,n=0}^N \hat{\mathcal {F}}^d_{mn} \psi _{mn} \frac{\partial \psi _{ij}}{\partial \xi ^d} \,\hbox {d}\xi . \end{aligned}$$

(12)

Substituting the integration by the Gauss-Legendre quadrature and the Lagrange property simplify this expression to

$$\begin{aligned} -\int _E \mathcal {F}\cdot \nabla _\xi \varPhi \,\hbox {d}\xi = - \omega _j \sum _{\lambda =0}^N D_{i\lambda } \hat{\mathcal {F}}^1_{\lambda j} \omega _\lambda - \omega _i \sum _{\mu =0}^N D_{j \mu } \hat{\mathcal {F}}^2_{i \mu } \omega _\mu , \end{aligned}$$

(13)

where $D_{ij}$ is the differentation matrix defined by

$$\begin{aligned} D_{ij} = \left.\frac{\partial l_j(\xi )}{\partial \xi }\right|_{\xi =\xi _i}, \quad i,j=0,\ldots ,N. \end{aligned}$$

(14)

All the details can be found in [19].

2.6 Semi-Discrete Discontinuous Galerkin Formulation

Putting all these components of the weak formulation (3) together we get the following semi-discrete Discontinuous Galerkin formulation

$$\begin{aligned} \begin{aligned} J(\xi _{ij}) \frac{\partial {\hat{\mathbf{u}}}_{ij}}{\partial t} \omega _i \omega _j&= -\left[ f_j^{*,\xi ^1}(\mathbf {u}^-, \mathbf {u}^+, n) l_i(\xi ^1) \omega _j \right]_{\xi ^1=-1}^1 \\&\,\quad -\left[ f_i^{*,\xi ^2}(\mathbf {u}^-, \mathbf {u}^+, n) l_j(\xi ^2) \omega _i \right]_{\xi ^2=-1}^1 \\&\,\quad + \omega _j \sum _{\lambda =0}^N D_{i\lambda } \hat{\mathcal {F}}^1_{\lambda j} \omega _\lambda + \omega _i \sum _{\mu =0}^N D_{j \mu } \hat{\mathcal {F}}^2_{i \mu } \omega _\mu , \end{aligned} \end{aligned}$$

(15)

which is integrated in time by an explicit Runge Kutta time integration. An alternative possibility would be to use the ADER approach to integration in time. A comparison between Runge Kutta and the ADER approach in terms of computational efficiency can be found in [5]. In this work we restrict ourselves to explicit Runge Kutta time integration.

2.7 Discontinuous Galerkin Algorithm

In this subsection we will explain shortly the main sequence of our parallel implementation of the DG operator. We use an explicit Runge Kutta time integration to integrate (15) in time. Let us assume the solution at time t is denoted by $\mathbf {u}$. To compute the time derivate $\frac{\partial \mathbf {u}_{ij}}{\partial t}$ of each DOF we have to evaluate the right hand side of (15). Therefore we compute on each element the volume and on each face the surface integral. Since the nodal solution is given at Gauss points we have to extrapolate it on each element to the faces of the element. On the reference element this is a evaluation of $\mathbf {u}(\xi )$ at $\xi = (\pm 1, \xi ^2_j)$ and $\xi = (\xi ^1_i, \pm 1)$, which correspondes to 1D operations at all $\xi ^2_j$-lines in $\xi ^1$ direction and $\xi ^1_i$-lines in $\xi ^2$ direction respectively, see Fig. 1. Since the states at the interfaces between elements are doubly defined we have to distinguish between left and right, your and mine values at the faces. In the flow chart of Fig. 2 we use the notation from an elemental point of view. With $\mathbf {u}^-$ we label the extrapolated values of this element, whereas $\mathbf {u}^+$ denotes the values at the face extrapolated from the adjacent element. Our code is parallelized with the MPI framework, where MPI interfaces are located at element interfaces. To keep the amount of operations independent of the number of processors, the fluxes at MPI interface must not be computed twice. Therefore we label the two adjacent elements of each face as master and slave element of this face. Since always only the master element is computing the flux, we have to send the extrapolated face values on each slave face to the master element. This data communication is hidden by the computation of the volume integral for each element, which is an absolutely local operation, without any data from neighboring elements. After this we receive the face values from the slave side and compute the fluxes in a first step only on the MPI faces to send them back from the master to the slave element of all MPI faces as early as possible. While this communication is going on we calculate the remaining inner fluxes and boundary condition fluxes. The last step is then to evaluate the surface integrals.

Fig. 1

DG reference element E with Gauss points

and locations of the boundary fluxes

at the DG interface for $N=3$ in 2D

Fig. 2

Flow chart of DG operator

3 Shock Capturing with Finite Volume Sub-cells

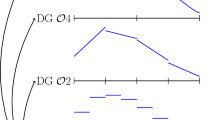
Numerical schemes of high order accuracy often have difficulties resolving shocks without generating new extrema or oscillations in the solution. In Fig. 3 we used the DG method of polynomial degree $N=5$ to compute an advected density jump with four elements in 1D. The right travelling shock immediately forces the DG polynomial to start oscillating. To handle this problem of higher order polynomials oscillating at discontinuities an often used technique is to reduce the polynomial degree in the region of the shock and at the same time combine it with a local mesh refinement to avoid a loss in resolution.

Fig. 3

Oscillations of a DG solution with polynomial degree 5

In this section we present a natural way of shock capturing by constructing a refinement of the high order Discontinuous Galerkin element into several internal finite volume elements without introducing new degrees of freedom. The fixed number of DOFs helps us to keep the method as simple as possible and to reach a high computational performance in the actual implementation.

3.1 First Order Finite Volume Sub-cell Method

In Sect. 2 we formulated the Discontinuous Galerkin spectral element method for a polynomial degree N, where we used in a tensor product ansatz, the $N+1$ Gauss points of the Gauss–Legendre quadrature for interpolation and integration in each space direction.

Fig. 4

DG reference element split into FV sub-cells

with Gauss points

, Gauss weights $\omega _i$ and locations of the inner

and the interface

boundary fluxes

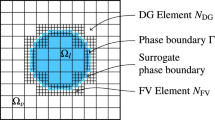
In 2D we subdivide the DG reference element into $(N+1)^2$ finite volume sub-cells, where each of the $(N+1)^2$ Gauss points $\lbrace \xi _{ij} \rbrace _{i,j=0}^N$ is a node of a finite volume sub-cell $\kappa _{ij}$. The size of the ij-th finite volume sub-cell is chosen to correspond to the weights of the 1D quadrature rule in each space dimension and becomes $\omega _i \times \omega _j$, see Fig. 4. Remember, this is all in reference space.

Remark 1

(Why exactly $(N+1)^d$ FV sub-cells?) Mainly there are two reasons for choosing exactly $(N+1)^d$, where d is the dimension. The first reason is, that using the same number of FV sub-cells as the number of DOFs of a DG element enables the use of the same data structures for both methods. From an implementation point of view on can use the same arrays to store the DG solution and the FV sub-cells solution. The use of this technique is mandatory to achieve a efficient implementation in a massive parallel environment. The second reason is also related to the efficiency of the shock capturing. Performing computations in parallel requires a evenly distributed load among the processors. Thinking of a shock that travels through the domain, it is clear, that there should not be a big difference in the computational time to update an element with the two different schemes. Otherwise this would introduce strong load imbalances, which would require a redistribution of the load among the processors leading to a big loss in the overall performance. In Sect. 4 we show, that the use of the same number of finite volume sub-cells as the number of DOFs leads to a scheme, where the shock capturing nearly takes the same time as the Discontinuous Galerkin method. This directly means that there is only a very small load inbalance, which does not require the extra costs of a load balancing.

We now formulate the finite volume method for the transformed conservation law (2) on the reference element of the Discontinuous Galerkin method E. Each sub-cell $\kappa _{ij}$ of E is now a control volume in the finite volume context and the corresponding equation reads

$$\begin{aligned} \int _{\kappa _{ij}} J \mathbf {u}_t \,\hbox {d}\xi + \int _{\kappa _{ij}} \nabla _\xi \cdot \mathcal {F}(\mathbf {u}) \,\hbox {d}\xi = 0 \quad \forall {\kappa _{ij} \in E}. \end{aligned}$$

(16)

Applying the divergence theorem to the second integral yields

$$\begin{aligned} \int _{\kappa _{ij}} J \mathbf {u}_t \,\hbox {d}\xi + \int _{\partial \kappa _{ij}} \mathcal {F}(\mathbf {u}) \cdot n \,\hbox {d}S_\xi = 0. \end{aligned}$$

(17)

Since we do not introduce new DOFs, every finite volume sub-cell $\kappa _{ij}$ contains exactly one Gauss point $\xi _{ij}$ of the Discontinuous Galerkin discretization. To enforce the same integral mean value of the solution inside each DG element, regardless the approximation by DG or FV sub-cells, we choose each Gauss point $\xi _{ij}$ as “center” of the respective finite volume sub-cell and the nodal value ${\hat{\mathbf{u}}}_{ij}$ of the DG approximation (4) as the constant mean value inside this FV sub-cell. Inserting the DG approximation of the state and replacing the integral by the Gauss-Legendre quadrature yields

$$\begin{aligned} \int _E \mathbf {u} \,\hbox {d}\xi = \int _E \sum _{i,j}^N {\hat{\mathbf{u}}}_{ij} \psi _{ij}(\xi ) \,\hbox {d}\xi = \sum _{\lambda ,\mu =0}^N \sum _{i,j}^N {\hat{\mathbf{u}}}_{ij} \underbrace{l_i(\xi ^1_\lambda )}_{\delta _{i \lambda }} \underbrace{l_j(\xi ^2_\mu )}_{\delta _{j \mu }} \omega _\lambda \omega _\mu = \sum _{i,j}^N {\hat{\mathbf{u}}}_{ij} \omega _i \omega _j. \end{aligned}$$

(18)

On the other hand, if the DG element is subdivided into finite volume sub-cells the following equation holds

$$\begin{aligned} \int _E \mathbf {u} \,\hbox {d}\xi = \sum _{i,j=0}^N \int _{\kappa _{ij}} {\hat{\mathbf{u}}}_{ij} \,\hbox {d}\xi = \sum _{i,j=0}^N {\hat{\mathbf{u}}}_{ij} \omega _i \omega _j, \end{aligned}$$

(19)

since we assume the state to be constant inside each finite volume sub-cell. Comparing equations (18) and (19) it is clear, that the nodal representation $\lbrace {\hat{\mathbf{u}}}_{ij} \rbrace _{i,j=0}^N$ can be interpreted as DG and as FV sub-cell solution at the same time.

Inserting this discretization into the finite volume formulation (17) we get for the volume integral

$$\begin{aligned} \int _{\kappa _{ij}} J \mathbf {u}_t \,\hbox {d}\xi = \omega _i \omega _j J_{ij} \, \frac{\partial \hat{\mathbf {u}}_{ij}}{\partial t}, \end{aligned}$$

(20)

where $J_{ij}$ is the average of the Jacobian in the ij-th subelement. Since the state in a FV sub-cell is constant, we can replace the boundary integral of (17) by the midpoint rule

$$\begin{aligned} \begin{aligned} \int _{\partial \kappa _{ij}} \mathcal {F}(\mathbf {u}) \cdot n \,\hbox {d}S_\xi&= \omega _j \left( f_{i-\frac{1}{2},j}(\mathbf {u}^-,\mathbf {u}^+,n) + f_{i+\frac{1}{2},j}(\mathbf {u}^-,\mathbf {u}^+,n)\right) \\&\quad +\omega _i \left( f_{i,j-\frac{1}{2}}(\mathbf {u}^-,\mathbf {u}^+,n) + f_{i,j+\frac{1}{2}}(\mathbf {u}^-,\mathbf {u}^+,n)\right), \end{aligned} \end{aligned}$$

(21)

where $f(\mathbf {u}^-,\mathbf {u}^+,n)_{i-\frac{1}{2},j}$ denotes the flux at the left edge of the ij-th sub-cell and $\omega _i$ and $\omega _j$ are the lengths of the corresponding edges. As in the DG method the numerical flux is computed by a Riemann solver involving the state $\mathbf {u}^+$ of the neighboring sub-cells. In total the finite volume method for the ij-th sub-cell reads as

$$\begin{aligned} \begin{aligned} J_{ij} \frac{\partial \hat{\mathbf {u}}_{ij}}{\partial t} \omega _i \omega _j&= - \omega _j \left( f_{i-\frac{1}{2},j}(\mathbf {u}^-,\mathbf {u}^+,n) + f_{i+\frac{1}{2},j}(\mathbf {u}^-,\mathbf {u}^+,n)\right) \\&\,\quad - \omega _i \left( f_{i,j-\frac{1}{2}}(\mathbf {u}^-,\mathbf {u}^+,n) + f_{i,j+\frac{1}{2}}(\mathbf {u}^-,\mathbf {u}^+,n)\right). \end{aligned} \end{aligned}$$

(22)

This expression gives the time derivative of all DOFs located in a single DG element and can directly be interchanged with the respective expression of the DG method (15) within each stage of the Runge Kutta time integration.

Remark 2

(Block unstructured FV method) Using finite volume sub-cells in in every DG element may be interpreted as a blockwise finite volume method on unstructured curved hexahedral blocks, where the blocks are coupled through Riemann solvers. The idea of a weak coupling of different domains goes back to Nitsche [26] in 1971. Since the DOFs of both algorithms are the same, there is no difference in data formats and a FV sub-cell solution can be directly compared to the DG solution. This gives us also the ability to investigate the advantages and disadvantages of the Discontinuous Galerkin method by comparison with the finite volume method on the same mesh, where each DG element is a block of FV sub-cells.

In the following we will denote with ’FV sub-cells element’ the whole block of FV sub-cells that are located inside a DG element. This will be useful to describe the coupling of DG elements with elements, that are updated with the FV sub-cells method.

3.2 Indicator Based Switching to Finite Volume Sub-cells

In the presence of a shock inside a DG element the solution will start to oscillate, produce unphysical solutions and finally blow up the computation. Therefore, instead of using the DG method of Sect. 2 the finite volume sub-cell method should be applied to all elements containing a shock or a gradient that can not be resolved on the given grid and accuracy. One difficult part of this approach is the choice where to use the DG and where the finite volume sub-cell method. In our implementation an indicator function makes this decision. Among the various implemented indicators/sensors there are functions like the switching function proposed in the finite volume framework by Jameson et al. [21] (JST scheme), Ducros sensor [17], Persson indicator [27] or Jump indicator. All these functions are modified such that a low value denotes a smooth solution, while high values indicate shocks. At each stage of the explicit Runge Kutta time integration the indicator function is evaluated for each element. If this indicator value is greater than a user defined (upper) threshold the element is switched from DG to FV sub-cells. Numerical studies showed that a single threshold is often not the best solution. If the same singe threshold is used to switch from FV sub-cells back to DG, meaning that the implementation switches back to FV immediately when the indicator value falls below the single threshold, may lead to a switching back and forth between the to schemes if the indicator stays close to the threshold. Therefore we additionally introduce a lower threshold and only switch back a FV sub-cells element to DG if the indicator value falls below this threshold. This process is visualized in Fig. 5 and avoids ongoing switching between the two methods, if the indicator value is near a single threshold.

3.3 Second Order Reconstruction with Slope Limiting

It is well known, that a first order finite volume method as described above is very dissipative. To improve the dissipative behaviour of the FV sub-cell method we extend it by a second order reconstruction, coupled with a total variation diminishing (TVD) slope limiter.

Fig. 5

Indicator based switching between DG and FV sub-cell method

In a first step the slopes between the nodal values inside an element are computed direction by direction on the reference element by computing the difference quotient. These slopes can directly be limited with a TVD limiter, such as MinMod [32], Sweby [37] or van Leer [40], to obtain the slopes of the FV sub-cells in the reference element directions $\xi$ and $\eta$, compare Fig. 6a. Of course, the slopes of FV sub-cells laying next to the boundary of the reference element can not be computed element wise, since therefore the nodal values of the adjacent elements are needed. In a second step the slopes between nodal DOFs, separated by an element interface, are evaluated, see Fig. 6b. Again we use the limiter function to compute with these slopes and the inner slopes of the first step the slopes of the FV sub-cells at the element interfaces. The computation of the slopes over element interfaces gets complicated if this interface is also a MPI interface in a parallel context, where additional communications for the exchange of slope informations is needed.

Fig. 6

Computation of slopes for second order reconstruction (green: $\xi$-direction, red: $\eta$-direction, blue: interface slopes). a Inner slopes, b slopes over element interfaces

3.4 Flux Computation at MPI Interfaces

The computation of the numerical fluxes at MPI interfaces involving a FV sub-cell element at least at one side needs some extra communication and will be described here. Due to performance reasons in our implementation of the pure DGSEM, which is the basis of this paper, we strictly split all MPI interfaces in master and slave sides. The numerical fluxes are only evaluated at the master sides and then transferred to the slave on the other processor. This implicates additionally, that the state, needed for the numerical flux computation, has to be communicated the other way round from the slave to the master process only. All in all this approach minimizes the MPI communications and also the computational effort.

Fig. 7

Computation of the numerical flux over MPI interfaces, where the function R denotes a combination of slope limiter and prolongation to the face

We keep this basic structure for the evaluation of the numerical flux at MPI interfaces, if a FV sub-cells element gets involved. In total there are 4 different constellations. A DG element on both sides of the MPI interface, both sides FV or a FV/DG interface, where either the DG element is at the master or at the slave side. The following description of the flux computation will be written down in the point of view of the master element, which does all the work. A flow chart of this can be found in Fig. 7. If both elements are DG there is no difference to the pure DG code and the prolongated face states $\mathbf {u}^+$ from the adjacent and $\mathbf {u}^-$ from the local element can be directly fed into the Riemann solver. In case there is at least one FV sub-cells element involved, we first have to compute the slope over the MPI interface:

$$\begin{aligned} \nabla _{Face} \mathbf {u}= \frac{\mathbf {u}_0^+ - \mathbf {u}^-_0}{\varDelta x_{Face}}, \end{aligned}$$

where $\mathbf {u}^-_0$ denotes the nodal value next to the interface of the local element and $\mathbf {u}^+_0$ the corresponding nodal value of the adjacent element, which should have been received previously. Since the inner slopes of the FV sub-cells element are already computed, we now can limit the slope of the FV sub-cell next to the MPI interface $\nabla \mathbf {u}^-_0$, if the local element is a FV sub-cells element. Therewith we can compute the prolongated face value $\mathbf {u}^-$ at the MPI interface. In Fig. 7 the last to steps, limitation and prolongation, are combined in the operator R. If the adjacent slave element is a FV sub-cells element we have to do the same to compute $\mathbf {u}^+$, the prolongated face value from the other side. But before this we have to receive the first inner slope $\nabla \mathbf {u}^+_0$ of the slave element and then can apply the R operator to build $\mathbf {u}^+$. Therewith we have the face values $\mathbf {u}^-$ and $\mathbf {u}^+$ to compute the numerical flux with the Riemann solver. Notice that the face value $\mathbf {u}^+$ of the adjacent element must be received, if the element is a DG element. To reduce the transferred amount of data this communication can be combined with the communication of $\nabla \mathbf {u}^+_0$, which is only needed if the adjacent element is a FV sub-cells element. Like in the pure DG implementation the flux is now send back to the slave element. Additional the face slope $\nabla _{Face} \mathbf {u}$ has to be send to a FV sub-cells slave, since it is needed there to limit the slope of the first sub-cell at the MPI interface.

3.5 Time Step Restriction

One important issue of each technique to capture shocks in a high order method is the impact on the time step. For example it is well known that the artificial viscosity approach can tremendously decrease the overall time step [1] within an explicit time approximation. Therefore it is essential to investigate the time step restriction introduced by the FV sub-cells. The CFL condition by Courant, Friedrichs and Lewy [16] is given by

$$\begin{aligned} CFL = \frac{\varDelta t \cdot \lambda }{\varDelta x}. \end{aligned}$$

Rearranging this condition one gets the time step of the finite volume method

$$\begin{aligned} \varDelta t = CFL \cdot \alpha _{RK}(0) \frac{\varDelta x_{FV}}{\lambda }, \end{aligned}$$

(23)

where $\varDelta x_{FV}$ is the size of the cells and $\lambda$ the maximal propagation velocity. Additionally one has to take a factor $\alpha _{RK}(0)$ of the explicit Runge Kutta time integration into account.

The time step of the Discontinuous Galerkin Spectral Element Method has nearly the same structure

$$\begin{aligned} \varDelta t = CFL \cdot \frac{\alpha _{RK}(N)}{2N+1} \frac{\varDelta x_{DG}}{\lambda }, \end{aligned}$$

(24)

where N is the polynomial degree, $\varDelta x_{DG}$ the size of the DG element and the factor $\alpha _{RK}(N)$ now depends on the polynomial degree. The $\frac{1}{2N+1}$ in the time step restriction takes into account, that inside a DG element the number of DOFs in one space direction is $N+1$, which is apparently larger than 1 in the FV method and also takes into account that these DOFs inside an element are not distributed equidistantly [10, 14].

For the here presented FV sub-cells method we can combine the time step restriction for FV and DG to a time step restriction for FV sub-cells elements. It is clear that the time step of a FV sub-cells element is restricted by the size of the smallest sub-cell. Since we use the weights of the Gauss quadrature rule to define the sizes of the FV sub-cells the smallest Gauss weight is restricting the time step. The sum of the weights equals 2, which is also the size of the reference element and therefore we have to scale the DG element size with the factore $\frac{min(\omega )}{2}$ to take into account the smallest size of a FV sub-cell. Substituting this for $\varDelta x_{FV}$ in Eq. (23) we get

$$\begin{aligned} \varDelta t = CFL \cdot \alpha _{RK}(0)\frac{min(\omega )}{2} \frac{\varDelta x_{DG}}{\lambda }. \end{aligned}$$

(25)

where we have to divide the minimal weight by 2, since the weigts sum up to $\sum _{i=0}^N \omega _i = 2$. Looking at this time step and the time step of the DG method (24) one has to compare the factors

$$\begin{aligned} \frac{\alpha _{RK}(N)}{2N+1} \quad \text {and} \quad \alpha _{RK}(0)\frac{min(\omega )}{2}. \end{aligned}$$

(26)

In Fig. 8 these two factors are plotted over the polynomial degree for a third and a fourth order explicit Runge Kutta time integration. Since for both time integration the factor of the FV sub-cells method is always greater than the time step of the DG method, we don’t get a smaller time step compared to the DG time step, if we use the FV sub-cells method to resolve a shock inside a DG element.

Fig. 8

Factors in the time step restriction for FV sub-cells and the DG method

4 Numerical Examples

In this section we will show the application of our coupled method to several 1D, 2D and a 3D simulation. Besides this examples we will investigate the order of convergence and show the scaling properties of our implementation on high performance computing (HPC) systems.

4.1 Parallel Efficiency

Since our method will be applied to petascale simulations the scaling properties on high performance computing (HPC) systems is a major issue. The pure DG implementation in our CFD solver FLEXI already has proven its ability to efficiently scale on HPC systems of several 10.000 cores [3]. We even observe so-called super-linear scaling, i.e a scaling efficiency over 100 %, due to caching effects, depending on the polynomial degree and the elements per core. For rather moderate polynomial degrees (N = 3–5) this super scaling is achieved down to only eight DG elements per core. For higher polynomial degrees this effect is achieved even for the single element per core case.

This high parallel efficiency is transferred to our framework, which is an extension of the above mentioned pure DG code. To expose this, we performed strong scaling tests on the HLRS Cray XC40 cluster using up to 6144 physical cores. Of course this rather small number of processors is not the limit of our implementation and is only restricted to this amount to keep the computational costs low. Scaling results of our code for larger number of processors can for example found in [2]. The Figs. 9 and 10 contain the results for a setup with 49152 elements in a $32 \times 32 \times 48$ mesh. The polynomial degree is set to $N=5$ and we use four different types of ”indicators” to force the distribution of DG and FV elements:

• pure DG: all elements are marked as DG elements, but of course the algorithm has to check in each loop over elements/faces if it is a DG or FV element.

• pure FV: all elements are marked as FV elements. The same checks in all loops are needed.

• half/half: the left half in x-direction is set as DG, the right as FV.

• checkerboard: since the test-mesh is structured we mark the elements alternating DG and FV in a checkerboard pattern.

Fig. 9

Strong scaling results for polynomial degree $N=5$

Figure 9 shows the speedup of our implementation for a fixed number of DOFs, 10.6 million in total. The number of cores is doubled between each run, which leads to an elements per core load ranging from 2048 element on 24 cores down to 8 elements on 6144 cores. We achieve a perfect scaling until the second last run, where we have 16 element or 3456 DOFs per core. Beyond this point the latency hiding techniques of our implementation can no more hide the communication, which is of course a lot higher in our coupled method than in the pure DG framework, as already explained in Sect. 3.4.

Fig. 10

Performance index for polynomial degree $N=5$

In Fig. 10 we show the performance index (PID). The PID is a suitable measure to rate and compare the computational efficiency and is defined as the ratio of the total core-hour and the product of DOFs with number of time steps:

$$\begin{aligned} \text {PID} = \frac{\text {Wall-clock-time} \, \#\text {cores}}{\#\text {DOF} \, \#\text {time steps}}. \end{aligned}$$

(27)

It expresses the physical time needed to update one degree of freedom for one time step. For all loads the PID is nearly the same, except for the lowest load of only 8 elements or 1728 DOFs per core, which we already explained for the speedup plot. Differences can only be seen between the different “indicators”, which lead to different amounts of mixed element interfaces (DG/FV). The pure FV run shows a slightly better performance than the pure DG computation. Therefore the DG part of the half/half computation limites the performance in this case, which explains the almost matching curves for pure DG and half/half. In this case there are only a few mixed element interfaces compared to the total amount of interfaces, which do not affect the overall performance. This gets different in the checkerboard case, where all interfaces become mixed DG/FV interfaces. Here we see an increased PID for all loads, but it is nearly evenly distributed over all loads, which also leads to a perfect scaling.

4.2 Order of Convergence

In this subsection we investigate the order of convergence of our method. The first step is to verify the order of convergence of the pure Discontinuous Galerkin Spectral Element Method. Therefore we use a simple test case of a periodic sine wave, which is advected in x-direction. Since this is a totally smooth problem, there is no need to use FV sub-cells. In Table 1 the errors and convergence rates for the pure DG method are shown. The theoretical convergence rate is accurately matched for all tested polynomial degrees. Convergence rates for our DGSEM implementation on unstructured curved 3D meshes can be found in [19]. It is important to mention, that for polynomial degrees higher then the order of the time integration the overall error is of course limited by the order of the time integration. Nevertheless one can examine the spatial order of the scheme for higher polynomial degrees by reducing the CFL number. For example the $N=11$ convergence rates in Table 1 where computed using a CFL number of 0.005, even so the computation is also stable for $CFL=1$, but in in then the time integration error masks the spatial error and the convergence rate is limited by the temporal order. Of more interest for the here presented FV sub-cells shock capturing is the behaviour of the embedded FV sub-cells. Therefore we run the same test case but enforce the use of FV sub-cells in the whole computational domain. Since we use a second order reconstruction in the FV sub-cells the theoretical order of convergence is limited to two, nevertheless which polynomial degree for the DG elements is used. Furthermore this theoretical convergence rate is diminished by the use of TVD limiters as for example the MinMod limiter. The use of a central limiter, which takes the mean value of the right an left slopes in each FV sub-cell, should reach the full convergence rate of two, but is not stable in general. Nevertheless for this smooth test case it is possible to use the central limiter. To compare the different results for computations without reconstruction, with the use of the MinMod limiter and the central limiter we show in Table 2 only the $L^2$ errors and convergence rates. The $L^\infty$ values behave exactly the same. As expected the FV sub-cells method without any second order reconstruction only gives first order convergence and the central limiter reaches the full second order convergence. With the MinMod limiter we only get a convergence rate of about 1.6, which is well known and is due to the TVD property of this limiter [33, 34]. This lower convergence rate can be slightly increased by the use of more advanced limiter, like the van Leer or the Sweby limiter for example, but always stays clearly below the theoretical order of two. Nevertheless this is not a big issue since the FV sub-cells shock capturing should only be applied in the regions of the shock, where a high order of convergence is not expectable.

Table 1 Errors and convergence rates of the density for 1D advected sinus wave for pure DG method with a polynomial degree ranging from $N=2$ to $N=5$ and additionally for $N=11$

Table 2 $L^2$ errors and convergence rates of the density for 1D advected sinus wave for pure FV sub-cells method with a polynomial degree of the DG elements ranging from $N=2$ to $N=5$

4.3 Sod Shock Tube

The classical Sod shock tube problem is initialized by a discontinuity located in the middle of the computational domain $\varOmega = [0, 1]$. The initial conditions are $\rho = 1, u=0, p=1$ on the left side and $\rho = 0.125, u=0, p=0.1$ on the right. This classical 1D Riemann problem has an exact solution, which can be found in [39]. At both boundaries of the domain we use Dirichlet boundary conditions. To indicate the shock wave we apply a 3D modification of the switching function of the Jameson–Schmidt–Turkel scheme for DG elements on the density

$$\begin{aligned} I_{\text {JST}} = \sum _{i,j,k=0}^N \frac{\rho _{min,ijk} - 2 \rho _{ijk} + \rho _{max,ijk}}{\rho _{min,ijk} + 2 \rho _{ijk} + \rho _{max,ijk}} \frac{\omega _i \omega _j \omega _k}{Vol(Element)}, \end{aligned}$$

(28)

where $\rho _{min,ijk} = min(\rho _{i\pm \delta _{id}, j\pm \delta _{dj}, k \pm \delta _{dk}}, d=1,2,3)$ is the minimal value of the neighboring nodal values of the node $\xi _{ijk}$ with $i,j,k \in [0,N]$. While Vol(Element) is the volume of the DG element $\omega _i \omega _j \omega _k$ is the volume of the ijk-th FV sub-cell. Therewith we build the volume metric mean value of the all nodal values inside of a DG element. In Fig. 11 we present the density of our computation. For the very coarse grid of only 10 DG elements we observe a good agreement with the exact solution, where the shock wave is resolved by only one FV sub-cells element. Since the contact discontinuity lies near a element interface the DG element containing this discontinuity produces slight over- and undershoots, but resolves the contact discontinuity quite well. The same happens at the kinks at the begin and end of the rarefaction wave. Here the solution is smeared, since the DG polynomial can not resolve the sharp kinks on such a coarse grid. Nevertheless the shock position is matched perfectly.

Fig. 11

Density of Sod shock tube problem at $t=0.2$ with a DG polynomial degree of $N=11$. Only the DG element containing the shock wave is divided into FV sub-cells. Grid lines of the very coarse grid of 10 element are shown as gray dashed lines

4.4 Shu-Osher Density Fluctuations Shock Wave Interaction Problem

In [36] Shu and Osher proposed a test case where a Mach 3 shock front travels into a sinusoidal density wave. The shock is initially placed at $x=-4$ in the domain $[-5,5]$, where the conditions left and right of this shock are given by

$$\begin{aligned} (\rho , u, p) = {\left\{ \begin{array}{ll} (3.857143, 2.629369, 10.33333) &{} x < -4 \\ (1.0+0.2*\sin (5x), 0.0, 1.0) &{} x \ge 4 . \end{array}\right. } \end{aligned}$$

We use this test case to show the sensitivity of our scheme w.r.t. to the upper and lower thresholds, which is used to indicate the switching between DG elements and FV-sub-cells, compare Sect. 3.2. As in the shocktube example we use the JST like indicator and Dirichlet boundary conditions. The Riemann solver in this test case is the Roe Riemann solver. The polynomial degree for the DG elements is $N=3$ and the grid consist of 100 elements. The total variation diminishing property of our scheme introduces a noticable amount of dissipation to resolve the shock, which leads to the gaps in the region behind the shock, where the numerical solution does not reach the same amplitudes. Figure 12 shows the density of 10 computations with different upper threshold values of the indicator compared to a reference solution, which we obtained on a very fine grid with a pure second order finite volume method. Here the lower threshold value of the JST like indicator is fixed to 0.005 and the upper threshold varies between 0.007 and 0.12. A value above 0.12 leads to a unstable solution at the shock, which let the computation crash. As one can see, all curves lay on top of each other and the only noticable differences occur for the 3 sharp parts in the region from $x=-3$ to 0. Here a to high indicator value leads to small oscilliations but does not influence the stability of the computation. This oscillations only occur if no FV sub-cells are used there. Beginning with a upper threshold of 0.012 and above, in more and more timesteps these sharp parts are computed with DG and therefore introduce oscillations. In total the amount of elements over the whole computational time, where the FV sub-cells are used ranges between $\sim 2.5\,\%$ (for 0.007) and 1.6 % (for 0.12).

Fig. 12

Density of Shu-Osher fluctuations shock wave interaction problem at $t=1.8$ with a polynomial degree of $N=3$ on a grid with 100 elements. The results of 10 different computations with an upper threshold value of the indicator based switching between DG and FV sub-cells varying from 0.007 to 0.12. The lower threshold is 0.005

To examine the lower threshold we fix the upper threshold to 0.011 and vary the lower threshold between 0.001 and 0.008. Here the influence on the solution can be seen only in the amplitude as depicted in the close-up view in Fig. 13. The higher the lower threshold is the higher the amplitude becomes, which is quite clear, since a smaller value leads to a higher amount of FV sub-cells and therewith to more dissipation. For this computations the overall amount of elements where the FV sub-cells method is used ranges between ${\sim }3.1\,\%$ and ${\sim } 2.0\,\%$.

Fig. 13

Close-up view of the density of Shu-Osher fluctuations shock wave interaction problem at $t=1.8$ with a polynomial degree of $N=3$ on a grid with 100 elements. The results of 5 different computations with an lower threshold value of the indicator based switching between DG and FV sub-cells varying from 0.001 to 0.008. The upper threshold is 0.011

4.5 Double Mach Reflection

This test problem was originally described by Woodward and Colella [42]. The double mach reflection sends a shock wave of Mach 10 diagonally into a reflecting wall, which is equivalent to a horizontal travelling shock encountering a $30^\circ$ wedge. The initial conditions are given by the Rankine–Hugoniot conditions

$$\begin{aligned} (\rho , u, v, p) = {\left\{ \begin{array}{ll} (8.0, 8.25\cdot cos(30^\circ ), -8.25 \cdot sin(30^\circ )), 116.5 &{} x < x_0 + \sqrt{\frac{1}{3}} y \\ (1.4, 0.0, 0.0, 1.0) &{} x \ge x_0 + \sqrt{\frac{1}{3}} y \end{array}\right. }, \end{aligned}$$

(29)

where $x_0= \frac{1}{6}$ and the heat capacity ratio is $\gamma = 1.4$. The computational domain is given by $\varOmega = [0, 4] \times [0, 1]$ which is discretized equidistantly with a characteristic mesh size of $h = \frac{1}{120}$ resulting in $480 \times 120$ DG elements. At the boundaries in x-direction we impose inflow and outflow conditions. The bottom boundary is modelled by a reflecting wall, while at the upper boundary the exact solution of an oblique shock travelling with $M=10$ is imposed. As Riemann solver we use the HLLE and a polynomial degree of $N=5$ for the DG elements, which results in $6^3$ FV sub-cells in each DG element. Since this example is 2D, but our implementation 3D, only $6^2$ FV sub-cells are physically used. The indicator for the FV sub-cells shock capturing is the modified JST indicator (28), but with pressure instead of density. We compute this example until the final time $t = 0.2$. Figure 14 shows in red the elements which where updated with the FV sub-cells shock capturing approach, while the blue cells are computed by the DG method. A close-up of the interaction zone is plotted in Fig. 15. The view is coloured by the density and contains 20 density isolines ranging from $\rho = 1.5$ to 22.5. Additionally the grid is plotted in light gray, where the borders of the FV sub-cells are plotted as well to visualize the locations of the FV sub-cells. Remember, that there is no adaptive mesh refinement involved, just an implicit refinement due to our FV sub-cell shock capturing. Along the slip stream a lot of small vortices are generated, which interact with the second reflected shock wave. The JST indicator perfectly detects all the shock front, while ignoring all other small scale structures. Therewith the DG method can demonstrate its high order accuracy in these regions. All in all our results are in good accordance with other high order results from literature [18].

Fig. 14

Double Mach reflection at $t=0.2$. Red cells are detected by the JST indicator for the FV sub-cell shock capturing—blue cells are DG elements

Fig. 15

Close-up view of the interaction zone of the Double Mach reflection at $t=0.2$. The density is plotted along with 20 isoline ranging from $\rho =1.5$ to 22.5. In light gray the mesh is represented

4.6 Forward Facing Step

The forward facing step (FFS) is again a test problem of Woodward and Colella [42]. Air at Mach 3 is blown into a wind tunnel with a step. The wind tunnel has a length of 3, height of 1 and the step of height 0.2 starts at $x=0.6$, so the computatinal domain is given by $[0,3] \times [0,1] {\setminus } [0.6, 3] \times [0, 0.2]$. Inflow and outflow boundary conditions are applied in x direction, whereas the upper and lower boundaries are reflective walls. The domain is initialized with freestream with density $\rho = 1.4$, velocity $v = (3, 0)$, pressure $p=1$ and the heat capacity ratio of air $\gamma = 1.4$. We simulate this problem until the final time $t=4$ on a equidistant mesh with $h=1/100$, yielding in $300 \times 100 - 20 \times 240$ DG elements. The polynomial degree of the DG discretization is chosen to $N = 5$, leading to $6 \times 6$ inner FV sub-cells for the detection of shocks. For the numerical flux we use the HLLE Riemann solver and the indicator to detect the shocks is the Persson indicator. Figure 16 shows the density and density isolines at final time, while in Fig. 17 the shock detected elements are visualized. The FV sub-cells elements are only used at the shocks, which exhibits a perfect behaviour of the Persson indicator for this example. Besides the shock waves a Kelvin–Helmholtz instability developes along the top shear wave, which emits acoustic waves with small amplitudes. In contrast to more dissipative numerical schemes, these waves can be seen in the contour lines above the vortices in the upper panel.

Fig. 16

Density and isoline of the Forward Facing Step at $t=4.0$

Fig. 17

Forward facing step at $t=4.0$. Red cells are detected by the Persson indicator for the FV sub-cell shock capturing—blue cells are DG elements

Table 3 Initial conditions for 2D Riemann problems

4.7 2D Riemann Problem

In this subsection we show four configurations of two-dimensional Riemann problems which where classified by Schulz-Rinne in [35]. A detailed study, including numerical result, of all these problems can be found in [23]. The computational domain $\varOmega = [-0.5, 0.5] \times [-0.5, 0.5]$ is divided into four quadrants by $x=0$ and $y=0$. All 2D Riemann problems have in common, that a single wave is applied at each of the four interfaces of the quadrants. This can either be a shock, a contact discontinuity or a rarefaction wave. Of major interest for our shock capturing approach are configurations including shock waves. In Table 3 we summarize the initial conditions of the here presented computations. The numeration of the configurations is according to [23].

Fig. 18

Configurations 3, 4, 12 and 14 of the 2D Riemann problems. Left: density at final time. Right: cells marked for FV method (red)—blue cells are DG elements. Additional the density contour is plotted

4.7.1 CFG 3

This configuration is initialized by four shock waves at the quadrant interfaces travelling downwards and to the left, respectively. The mesh size is $200 \times 200$ DG elements with a polynomial degree of 5. The JST indicator is used to detect the shocks and the HLLE Riemann solver is used for numerical flux computations. Our results of this configuration are presented in Fig. 18 row 1. Compared to the results in [23] the computational results are in good agreement with respect to the main structures of this problem. Nevertheless we observe a lot more small scale features, which is in good agreement to the high order simulations of Dumbser et al. [18]. The main reason for capturing these small scale structures is the less dissipative behaviour of our high order DG method.

4.7.2 CFG 4

This example again is initialized with four shock waves the quadrant interfaces, but they are travelling in different directions compared to the configuration before. Since this example does not produce small structures, the mesh size is $67 \times 67$ elements. The other solver settings are the same as in configuration 3. Figure 18 row 2 shows our results at $t=0.3$. The shocks are resolved well within at maximum three DG elements and the results nicely match computations in [18] on an even coarser mesh.

4.7.3 CFG 12

This configuration consist of two shock waves at the right, upper quadrant interface and two non-moving contact discontinuities at the other interfaces. The mesh size is $100 \times 100$, the polynomial degree 5 and the simulation is run until $t=0.25$. In this case we use the Roe Riemann solver and the Persson indicator to detect the shock position. As can be seen in row 3 of Fig. 18 the indicator only marks the really necessary elements at the shock front, enabling the use of the high order DG method in most parts of the computational domain.

4.7.4 CFG 14

Here the horizontal quadrant interfaces are initialized by shock waves, travelling at different speeds downwards. The vertical interfaces consist of a non-moving contact discontinuity. Numerical results are plotted in row 4 of Fig. 18 at $t=0.1$. The solver settings are the same as in configuration 12, except to the indicator, which here is the JST indicator on the pressure. Since the JST acts on the pressure, only the shock is marked as FV elements, while the contact discontinuity is resolved with the high order DG method. Therewith it is possible to resolve the small structures, which occur in the center of the domain.

4.8 Strong Shock–Vortex Interaction

The interaction of travelling vortex with a steady shock was originally proposed by [30]. A steady shock wave with a shock Mach number $M_s$ is initialized at $x=0.5$ through the classical Rankine–Hugoniot condition [25] in a computational domain $\varOmega = [0, 2] \times [0, 1]$. Additional a vortex is placed in front of the shock wave at (0.25, 0.5). The Mach number of the vortex $M_v$ describes the maximum angular velocity of the vortex. For a detailed description of the initialization of this problem the reader is refered to [30]. This problem developes complex flow structures with smooth features and sharp discontinuities which are more complicated, the higher the Mach numbers of the shock and vortex are. We selected the Mach numbers to $M_v=1.7$ for the vortex and $M_s=7.0$ for the shock, which is the highest combination investigated in [30]. We used a polynomial degree of $N=5$ for the DG discretization and the JST indicator to detect the shock cells. Numerical results for a characteristic length of $h=1/100$ are presented in Fig. 19. The top panel shows the density at the final time $t=0.2$, while the bottom panel shows the distribution of DG and FV sub-cells. The computations demonstrate the good properties of our high order numerical scheme and are comparable to the results in [30]. Very strong shocks and fine smooth flow features can be captured at the same time.

Fig. 19

Strong shock–vortex interaction with a shock Mach number of $M_s=7$ and a vortex Mach number of $M_v=1$. Top: density at final time $t=0.2$. Bottom: Red elements detected by JST indicator for FV method—blue cells are DG elements

Fig. 20

Density of the 3D explosion problem at the final time $t=0.2$. The reference solution is plotted against the data of a computation on a fine and a coarse grid along the diagonal direction from the origin to (1, 1, 1)

4.9 3D Explosion Problem

The examples so far where all at most two dimensional problems. Nevertheless our implementation is 3D only and a validation of the code requires a three dimensional example. The 3D explosion problem is the natural extension of the one dimensional Sod shock tube problem from Sect. 4.3 to the three dimensional space. The computational domain is given by $\varOmega =[-1,1]^3$, which is divided into two regions. Inside the sphere located at the origin with radius $r=0.5$ and outside of this sphere. The initial conditions are the same as for the Sod shock tube problem where the inside of the sphere corresponds to the high density and high pressure initial state of the one dimensional example. Since this example is point-symmetric to the origin an equivalent reference solution can be computed in 1D on a very fine grid using spherical coordinates with a geometrical source term, see [38]. Even so the example is symmetric it is a good test case for the three dimensional implementation, as in this case the wave fronts are not parallel or perpendicular to the grid lines, but propagate in any direction. We use two different cartesian grids with $50^3$ and $100^3$ elements. The polynomial degree of the DG discretization of the coarse grid case is $N=4$ and for the fine case $N=5$, resulting in $250^3 \approx 15 \cdot 10^6$ and $600^3 =216 \cdot 10^6$ DOFs. The shock position is detected with the Persson indicator and the Riemann solver is the local Lax-Friedrichs. The computation was performed on the HLRS Cray XC40 cluster using 1536 physical cores until the end time $t=0.2$. In Fig. 20 the density along the diagonal line from the origin to the corner (1, 1, 1) is plotted. In this direction the waves travel diagonal through the cartesian grid cells, which is the most challenging direction, since in this direction the grid cells have their largest size. The diagonal is $sqrt(3) \approx 1.732$ times larger than the coordinate axis, which results in the fact, that the interval [0, 1] of the point-symmetric solution is resolved by only 15, respectively 29 elements in the diagonal direction. The reference solution is generated with a 1D finite volume code in spectral coordinates using 20.000 cells. Both calculations, on the coarse and the fine grid, show a good agreement with the reference solution. The positions of the shock wave and contact discontinuity are perfectly matched and the rarefaction wave is nicely resolved. Additionally we show in Fig. 21 the density contour of the fine solution in the $z=0$ plane at the final time. The grid lines are shown as black lines and in red we depicted the shock detected elements. All other (blue) elements are updated with the high order Discontinuous Galerkin method. The Persson indicator on the pressures detects really good the shock front within two elements and totally ignores the contact discontinuity, since there is no change in pressure. Only a few elements at the sharp kink of the beginning of the rarefaction wave are additionally switched to the FV sub-cells method. Over the whole computational time only 3.47 % of all elements are updated with the finite volume sub-cells method.

Fig. 21

3D explosion problem at $t=0.2$. Contour of Density from the $z=0$ plane. Red elements are detected by the Persson indicator and update with FV sub-cells method. Blue elements are DG elements and in black the grid lines are drawn

5 Conclusion

We have presented a shock-capturing strategy for Discontinuous Galerkin schemes, which uses a natural sub-cell decomposition and a total variation diminishing finite volume method on these sub-cells. This procedure preserves the whole data structure of the underlying DG scheme and can be used in an adaptive way in grid cells by a simple switch. Our Discontinuous Galerkin scheme is based on spectral elements and uses the same nodal DOFs for both numerical schemes. This approach may be considered as a combination of a DG scheme with a finite volume scheme on an h-refined grid. In smooth parts of the flow large grid cells are used and high order of accuracy, which is very efficient on massively parallel systems, while in troubled cells with strong gradients we switch to a total variation diminishing finite volume solver on sub-cells. In this sense the DG approach may be considered as a general framework of a heterogeneous domain decomposition.