1 Introduction

We consider the eikonal equation in an isotropic medium, given by

$$\begin{aligned} \begin{array}{ll} \left| \nabla u({\mathbf {x}})\right| =\frac{1}{F({\mathbf {x}})}, &{}\quad {\mathbf {x}}\in \varOmega \!\setminus \! P \\ u({\mathbf {x}}_s)=0, &{}\quad {\mathbf {x}}_s\in P \end{array} \end{aligned}$$
(1)

where \(\varOmega \subset {\mathbb {R}}^n\) is an open bounded domain, P is the set of sources, \(F({\mathbf {x}})\) is the wave velocity and \(u({\mathbf {x}})\) denotes the travel-time of the wave from the source \({\mathbf {x}}_s\) to a target point \({\mathbf {x}}\in \varOmega \). This first order Hamilton–Jacobi (HJ) equation is one of the fundamental building block for the level set method [24, 32] and such nonlinear partial differential equation can be found in a wide range of applications including geometrical optics, computer vision, geophysics, and etc. To numerically obtain the first arrival solution, tremendous number of efficient numerical methods have been proposed for approximating the viscosity solution [6, 7] to Eq. (1). These methods include the fast sweeping method [12, 13, 28, 29, 35, 40, 41] and the fast marching method [27, 33, 36].

In this paper, we consider a slightly more general equation where \(\varOmega \) is a general implicit surface \(\varSigma \), and the typical gradient is replaced by the surface gradient \(\nabla _{\varSigma }\), which is the gradient intrinsic to the surface. If the surface is embedded in the Euclidean space, the surface gradient is just the orthogonal projection of the usual gradient onto the tangent plane of the surface. Mathematically, if we consider a surface \(\varSigma \) in a scalar field u, the surface gradient is defined as

$$\begin{aligned} \nabla _{\varSigma } u = \nabla u - ( \mathbf {n} \cdot \nabla u ) \mathbf {n} , \end{aligned}$$

where \(\mathbf {n}\) is a unit normal vector defined on \(\varSigma \). We aim to develop an efficient and converging numerical algorithm for obtaining the viscosity solution of the surface eikonal equation given by

$$\begin{aligned} \begin{array}{ll} \left| \nabla _{\varSigma } u({\mathbf {x}})\right| =\frac{1}{F({\mathbf {x}})},&{}\quad {\mathbf {x}}\in \varSigma \!\setminus \! P \\ u({\mathbf {x}}_s)=0,&{}\quad {\mathbf {x}}_s\in P . \end{array} \end{aligned}$$
(2)

Similar to the typical eikonal equation (1), the viscosity solution can be interpreted as the first arrival time for high frequency surface wave propagation on \(\varSigma \), for example [10], and is useful in modeling constrained motions of curves/surfaces and image regularizations [18].

Numerically, on the other hand, there has not been much attention paid to the eikonal equation on surfaces (2). The first work in this direction was proposed in [14] to determine the geodesic paths on manifolds using the fast marching method. The method has extended the fast marching method on triangulated mesh by incorporating the local metric from the geometry. Similar idea can be found in [38, 39]. Some other methods have been proposed for surfaces represented by an explicit parametrization, see for example [4, 34, 37].

All approaches discussed above require some form of explicit representation of the interface. In this paper, we are interested in developing a numerical algorithm for implicit surfaces without any explicit interface triangulation. The resulting algorithm, coupled with the level set method [24, 32], will then be well-suited for applications which involve eikonal solution on dynamic surfaces, such as those biological modelings in [8, 26]. One approach for solving the surface eikonal equation on surfaces has been proposed in [21] based on the fast marching method. Since the solution of the surface eikonal equation on an implicit surface is the intrinsic weighted distance function, the paper has proposed to approximate such distance function by the Euclidean weighted distance function defined in a tubular neighbourhood of the implicit surface. In other words, one replaces the surface eikonal equation (2) by the typical eikonal equation (1) defined in a narrow computation tube \( \{ | \phi | \le h \} \) containing the original surface for some tube radius h. In the following context, this method will be called the embedding method for short.

Since the surface PDE is extended off the interface to a corresponding PDE in a small neighborhood of the surface on a fixed Eulerian mesh, we can first apply to the equation any well-developed numerical technique to determine the Euclidean weighted distance function and then use it to approximate the original intrinsic distance function on the surface. Fast marching method was used in [21]. In this work, we will explore the possibility of using fast sweeping methods instead. We will discuss two numerical Hamiltonians including the Godunov Hamiltonian, which has been widely used for the eikonal equation (1) because of its convergence behavior, and also the Lax–Friedrichs (LxF) Hamiltonian, which can be easily applied to even non-convex HJ equations.

In order to observe the numerical convergence to the exact solution in the expected order, some embedding methods require that the radius of the computational tube satisfies \(h=O(\varDelta x^{\gamma })\) for some \(\gamma <1\), such as [21]. This implies that the total number of mesh point in such a tube will be given by \(O(\varDelta x^{\gamma -d})\) for a codimension-one surface in \({\mathbb {R}}^d\). We will give a detailed study of this behavior in Sect. 3, at least in the context of the fast sweeping method. Yet a more important criteria in designing an embedding method for the problem is to take care of the causality in designing the numerical scheme. When incorporating with the embedding method with a computational tube radius \(h=O(\varDelta x)\), we have observed that a simple fast sweeping method based on the Godunov Hamiltonian fails to converges to the exact solution. The main reason, as will be analyzed, is that this approach has not been able to correctly take care of the characteristic directions. We therefore propose to introduce an extension equation in an extra layer of computational tube, which helps to fix the direction of the characteristics in the numerical scheme. Even with the extra layer of the computational cells, the proposed method only requires that the overall tube radius satisfies \(h=O(\varDelta x)\). This is, therefore, optimal in the sense that the total number of mesh points in the computational tube is \(O(\varDelta x^{1-d})\) for a co-dimensional one surface in \({\mathbb {R}}^d\).

It is worthwhile to compare our approach to some fast sweeping approaches and embedding ideas. Qian et al. [28, 29] has proposed a fast sweeping method for solving eikonal equations on surfaces explicitly represented by a triangulation. One main contribution in those work is a new ordering strategy for the fast sweeping method so that the alternating sweepings in each iteration can cover all directions of information propagation. That method has been shown to be computationally efficient and numerically convergent for a triangulated domain. Our proposed method in this paper, on the other hand, relies simply on the natural ordering provided by the underlying Cartesian mesh and the resulting sweeping strategy does not require to introduce any reference point on the surface.

In the level set framework, Bertalmio et al. [3] has proposed an embedding approach for solving time-dependent PDEs on surfaces. The main idea is to first express the surface gradient operator using the typical Euclidean gradient and a projection operator

$$\begin{aligned} \hbox {P}_{\mathbf {n}}=I-\mathbf {n} \otimes \mathbf {n} , \end{aligned}$$

where \(\mathbf {n}\) can be easily determined using the level set function. Related to this level set approach, Macdonald and Ruuth [19] has developed the Closest Point Method (CPM) to solve time-dependent PDEs on implicit surfaces. With the closest point function \(cp{:}\;{\mathbf {x}}\rightarrow \mathbf {y}\) which maps a grid point \({\mathbf {x}}\) to the closest point \(\mathbf {y}=\hbox {argmin}_{\mathbf {z}\in \varSigma } \Vert {\mathbf {x}}-\mathbf {z}\Vert _2\), one can show

$$\begin{aligned} \nabla _{\varSigma } u(\mathbf {y}) = \nabla u(\mathbf {y}) = \nabla u (cp({\mathbf {x}})) \end{aligned}$$

so that the surface gradient can be computed using the Euclidean gradient. Not only that those works have emphasized only on time-dependent equations while this paper concentrates on static Hamilton–Jacobi equations, the main difference between the current approach and these work is that the extrinsic surface gradient is now simply replaced by the Euclidean gradient. Since we are interested only in a robust convergent first order scheme, such approximation is significant for the current application and leads to a computationally efficient numerical algorithm.

The paper is organized as follows. In Sect. 2, we first summarize the fast sweeping method for HJ equations including the eikonal equation (1) and the hyperbolic conservation laws, which is the building block of our approach. In Sect. 3, we will then follow the approach in [21] but naively replace the fast marching method by the fast sweeping method. However, we are also going to show in the same section that the numerical approach will lead to a non-converging method. Based on the analysis in Sect. 3, we propose a simple yet converging numerical algorithm for Eq. (2) in Sect. 4. Some extensions will be discussed in Sect. 5. Section 6 shows various numerical examples to demonstrate the feasibility and robustness of the new formulation.

2 Fast Sweeping Methods for Eikonal Equations and the Advection Equations

In this section, we will briefly summarize the fast sweeping method for solving the HJ equations. For a complete description of the algorithm, we refer interested readers to [12, 13, 28, 29, 35, 40, 41] and thereafter for general HJ equations, and [5, 15–17] for extensions to advection equations and hyperbolic conservation laws.

The fast sweeping method was originated in [30] in the context of computer graphics for the shape-from-shading problem. For simplicity, we present the algorithm for the two-dimensional case only. Generalization to higher dimensions is rather straight-forward. We first discretize the computation domain into a uniform mesh \(\{{\mathbf {x}}_{i,j}\}\) with mesh size \(\varDelta x\) and represent the solution at the mesh points by \(u_{i,j}\). The fundamental idea is to design of an upwind, monotone and consistent discretization for the nonlinear term \(|\nabla u |\). Furthermore, if there is a simple local solver for the discretized system, one can then obtain an efficient numerical algorithm for solving the nonlinear partial differential equation. The term sweeping comes from the fact that all methods in this class can be easily incorporated with the symmetric Gauss–Seidel iterations, see Algorithm 1, which may lead to an O(N) algorithm with N the total number of mesh points in the computational domain.

figure a

The fast sweeping approach in Algorithm 1 can be easily adopted by the eikonal equations, advection equations or hyperbolic conservation laws. In particular, if we are solving the eikonal equation \( | \nabla u |=1\), we have a choice in picking a numerical Hamiltonian for the discretization. For example, for each \((x_i,y_j)\), we define \(u^x_{\min }=\min (u_{i-1,j},u_{i+1,j})\) and \(u^y_{\min }=\min (u_{i,j-1},u_{i,j+1})\). The Godunov Hamiltonian [41] has the following simple update formula, given by

$$\begin{aligned} u_{i,j} \leftarrow \left\{ \begin{array}{ll} \min \left( u^x_{\min },u^y_{\min }\right) {+\varDelta x} &{}\quad \hbox {if } \left| u^x_{\min }-u^y_{\min }\right| > \varDelta x \\ \frac{1}{2} \left[ u^x_{\min }+u^y_{\min }+\sqrt{2\varDelta x^2 -\left( u^x_{\min }-u^y_{\min }\right) ^2} \right] &{}\quad \hbox {otherwise.} \end{array}\right. \end{aligned}$$
(3)

The corresponding local solver for the LxF Hamiltonian [13] is given by

$$\begin{aligned} u_{i,j}\leftarrow & {} \frac{u_{i+1,j}+u_{i-1,j}+u_{i,j+1}+u_{i,j-1}}{4} \nonumber \\&+ \frac{\varDelta x}{2} \, \left[ 1- \sqrt{ \left( \frac{u_{i+1,j}-u_{i-1,j}}{2\varDelta x} \right) ^2 + \left( \frac{u_{i,j+1}-u_{i,j-1}}{2\varDelta x} \right) ^2} \right] . \end{aligned}$$
(4)

When solving the advection equations \(\mathbf {v}\cdot \nabla u=(p,q)\cdot (u_x,u_y) =0\), we can use the simple upwind differencing to discretize the equation and derive the update formula [5, 15–17]. At each point \((x_i,y_j)\), we define \(p^{\pm }=\frac{1}{2}(p_{i,j}\pm |p_{i,j}|)\) and, therefore, obtain the update formula given by

$$\begin{aligned} u_{i,j} \leftarrow \frac{p^+ u_{i-1,j}-p^- u_{i+1,j}+q^+ u_{i,j-1}-q^- u_{i,j+1}}{|p_{i,j}|+|q_{i,j}|} . \end{aligned}$$
(5)

3 The First Attempt

In this section, we first directly apply the embedding idea in [21] on a computational tube of radius \(O(\varDelta x)\) but replace the eikonal solver by the fast sweeping method. Because the Hamiltonian is convex and simple enough, the closed-form solution to the local problem from the Godunov discretization can be explicitly determined. This makes the Godunov fast sweeping particularly attractive.

Following the embedding idea in [21], we attempt to solve the surface eikonal equation \(| \nabla _{\varSigma } u | =1\) not only on the interface \(\varSigma \) but replace it by the typical eikonal equation \(|\nabla u|=1\) defined in a computational tube \(\varGamma _h\) of radius h enclosing the surface \(\varSigma \). In particular, we might simply update the numerical solution \(u_{i,j}\) only if the grid point \((x_i,y_j) \in \varGamma _h\) while keep it to be the numerical infinity otherwise. Therefore, the Godunov Hamiltonian will not pass any information from outside \(\varGamma _h\) to the interior. This numerical scheme is extremely easy to code, as demonstrated in Algorithm 2. Like other fast sweeping methods, the iterative scheme converges to an approximation to the eikonal equation for a given \(\varDelta x\). But in this section, we are going to demonstrate that this proposed scheme does not converge to the exact viscosity solution to the surface eikonal equation as \(\varDelta x\) tends to zero if we have the tube radius \(\varGamma _h=O(\varDelta x)\). Even so, the analysis of such a straight-forward scheme will still be important since it motivates us the proposed approach which will be discussed later in Sect. 4.

figure b

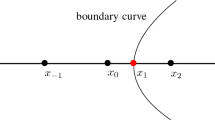
For simplicity, we analyze this scheme in the two-dimensional case and consider \(\varSigma =\{x=y\}\) with the point source located at the origin and we determine the solution in \([0,1]^2\). Therefore, the exact solution on \(\varSigma \) at (x, x) is simply the Euclidean distance from the origin and is given by \(\sqrt{2}x\). Since the geometry of this example is very simple, it turns out that we can calculate the explicit formula of the numerical solution from the Godunov Hamiltonian for some tube radius h with \(\frac{h}{\varDelta x}\in \left( \frac{1}{\sqrt{2}},\frac{3}{\sqrt{2}} \right) \). To do that, we first state some essential observations.

Observation 3.1

\(u_{i,j}\) depends only on \( u_{i-1,j} \) and \( u_{i,j-1}\).

Because of the special structure of our computational domain, information propagates only from the lower left part to the upper right part in the domain. The upwind Godunov Hamiltonian enforces a grid point \((x_i,y_j)\) to choose its lower and left neighbour grid values \( u_{i-1,j} \) and \( u_{i,j-1} \) in the update formula. This observation is crucial since it implies that the numerical solution will converge in only one sweeping direction (from lower left to upper right).

Observation 3.2

Assume \(\frac{h}{\varDelta x}\in \left[ \sqrt{2},\frac{3}{\sqrt{2}}\right) \) and consider a given level \(y=y_j\) where \( j \ge 3 \). There are only five grid points \( u_{j,j-2},\ldots ,u_{j,j+2} \) within the computation tube.

This is due to the construction of the computational tube and is clearly demonstrated in Fig. 1.

Fig. 1
figure 1

The red line is the interface \(\varSigma \) given by \( y-x=0 \). The green region indicates the computation tube \(\varGamma _h\). The blue dot denotes the source location at the origin \( (x_{1},y_{1}) = (0,0)\) (Color figure online)

Full size image

Observation 3.3

If \(\frac{h}{\varDelta x}\in \left[ \sqrt{2},\frac{3}{\sqrt{2}}\right) \), we have \(u_{i+2,i} = u_{i+1,i} + \varDelta x \) and \( u_{i,i+2} = u_{i,i+1} + \varDelta x \).

From Observation 3.2, \( u_{i+2,i} \) is a boundary point of the computational tube. Based on the Observation 3.1, the value depends only on \( u_{i+1,i} \) and \( u_{i+2,i-1} \). However, since \( u_{i+2,i-1} \) lies outside the computational tube, its default value is set to be the numerical infinity and will not be updated. When using the Godunov Hamiltonian, we therefore have \( u_{i+2,i} = u_{i+1,i} + \varDelta x \). The other formula can also be obtained in a similar argument.

We now state two propositions which lead to the closed form numerical solution from the Godunov Hamiltonian under some simple configurations. The first one is about a symmetry in the numerical solution, while the second one gives us the explicit formulae of the numerical solution.

Proposition 3.1

If \(\frac{h}{\varDelta x}\in \left( \frac{1}{\sqrt{2}},\frac{3}{\sqrt{2}}\right) \), we have \(u_{i,j} = u_{j,i} \).

Proof

By Observation 3.3, the proposition is equivalent to show that

$$\begin{aligned} u_{i,i+1} = u_{i+1,i} \, \hbox { and } \, u_{i,i+2} = u_{i+2,i} \end{aligned}$$

for \( i \ge 3 \). We prove it by induction. For case \( i \le 3 \), it can be shown by directly calculation. Now assume case \( i \le k \) is true, where \( k \ge 3 \). For the case where \(i = k+1\), we use Observation 3.1 and deduce that \( u_{k+1,k+2} \) depends on \( u_{k,k+2} \) and \( u_{k+1,k+1} \). And \( u_{k+2,k+1} \) depends on \( u_{k+1,k+1} \) and \( u_{k+2,k} \). By the induction hypothesis, \( u_{k,k+2} = u_{k+2,k} \). Therefore, \( u_{k+1,k+2} \) and \( u_{k+2,k+1} \) both use the same set of values in their updating formula based on the Godunov Hamiltonian, and therefore their values equal. Next, by Observation 3.3, we have \( u_{k+1,k+3} = u_{k+1,k+2} + \varDelta x \) and \( u_{k+3,k+1} = u_{k+2,k+1} + \varDelta x \). Since we have just shown \( u_{k+1,k+2} = u_{k+2,k+1} \). It follows that \( u_{k+1,k+3} = u_{k+3,k+1} \) and it leads to the proposition by induction. \(\square \)

Proposition 3.2

Denote \( \alpha _{\pm } = 1 \pm \frac{1}{\sqrt{2}} \). If \(\frac{h}{\varDelta x}\in \left[ \sqrt{2},\frac{3}{\sqrt{2}}\right) \), we have

  1. 1.

    \( u_{i,i} = u_{i-1,i} + \frac{\varDelta x}{\sqrt{2}} \);

  2. 2.

    \( | u_{i-1,i+1} - u_{i,i} | < \varDelta x \);

  3. 3.

    \( u_{i,i+1} = u_{i-1,i} + \frac{\varDelta x}{2} \left( \alpha _{+} + \sqrt{2 - \alpha _{-}^{2}} \right) \).

Proof

These expressions can be explicitly constructed.

  1. 1.

    \( u_{i,i} \) is updated based on \( u_{i-1,i} \) and \( u_{i,i-1} \). By the symmetry of the numerical solution, we have \( u_{i-1,i} = u_{i,i-1} \). Therefore,

    $$\begin{aligned} u_{i,i} = \frac{u_{i-1,i} + u_{i,i-1} + \sqrt{2 \varDelta x^{2} - (u_{i-1,i} - u_{i,i-1})^{2}}}{2} = u_{i-1,i} + \frac{\varDelta x}{\sqrt{2}} . \end{aligned}$$
  2. 2.

    We have

    $$\begin{aligned} | u_{i-1,i+1} - u_{i,i} |&= | u_{i+1,i-1} - u_{i,i} | = \left| ( u_{i,i-1} + \varDelta x ) - \left( u_{i,i-1} + \frac{\varDelta x}{\sqrt{2}} \right) \right| \nonumber \\&= \left( 1 - \frac{1}{\sqrt{2}} \right) \varDelta x < \varDelta x . \end{aligned}$$
  3. 3.

    \( u_{i,i+1} \) is updated using \( u_{i-1,i+1} \) and \( u_{i,i} \). Since \( | u_{i-1,i+1} - u_{i,i} | < \varDelta x \), we have

    $$\begin{aligned} u_{i,i+1}&= \frac{u_{i-1,i+1} + u_{i,i} + \sqrt{ 2 \varDelta x^{2} - (u_{i-1,i+1} - u_{i,i} )^{2}}}{2} \nonumber \\&= \frac{(u_{i-1,i} + \varDelta x) + \left( u_{i-1,i} + \frac{\varDelta x}{\sqrt{2}}\right) + \sqrt{2 \varDelta x^{2} - \left( 1 - \frac{1}{\sqrt{2}} \right) ^{2} \varDelta x^{2}}}{2} \nonumber \\&= u_{i-1,i} + \frac{\varDelta x}{2} \left( \alpha _{+} + \sqrt{2 - \alpha _{-}^{2}} \right) . \end{aligned}$$

\(\square \)

These observations and propositions provide us a recursive relation to explicitly construct the numerical solution from the Godunov Hamiltonian everywhere in the computation tube if the tube radius satisfies \(\sqrt{2} \le \frac{h}{\varDelta x}<\frac{3}{\sqrt{2}}\). In particular, we obtain

$$\begin{aligned} u_{i-1,i}&= u_{i-2,i-1} + \frac{\varDelta x}{2} \left( \alpha _{+} + \sqrt{2-\alpha _{-}^{2}} \right) = u_{i-3,i-2} + \frac{2 \varDelta x}{2} \left( \alpha _{+} + \sqrt{2-\alpha _{-}^{2}} \right) \nonumber \\&= \dots = u_{1,2} + \frac{(i-2) \varDelta x}{2} \left( \alpha _{+} + \sqrt{2-\alpha _{-}^{2}} \right) \end{aligned}$$

and

$$\begin{aligned} u_{i,i}&= u_{i-1,i} + \frac{\varDelta x}{\sqrt{2}} = u_{1,2} + \frac{(i-2) \varDelta x}{2} \left( \alpha _{+} + \sqrt{2-\alpha _{-}^2} \right) + \frac{\varDelta x}{\sqrt{2}} \nonumber \\&= \alpha _{+} \varDelta x + \frac{(i-2) \varDelta x}{2} \left( \alpha _{+} + \sqrt{2-\alpha _{-}^{2}} \right) . \end{aligned}$$

Now, we take \( \varDelta x = N^{-1}\) and consider the numerical solution at the location \((x,y)=(x_N,y_N)=(1,1)\). This implies

$$\begin{aligned} u_{N,N} = \frac{\alpha _{+}}{N} + \frac{N-2}{2 N} \left( \alpha _{+} + \sqrt{2 - \alpha _{-}^{2}} \right) . \end{aligned}$$

We have noticed, however, that this solution converges to \(\frac{1}{2} \left( \alpha _{+} + \sqrt{2 - \alpha _{-}^{2}} \right) \) but not to the exact solution \(\sqrt{2}\) as N goes to infinity. This simple example shows that a trivial embedding method coupled with the Godunov fast sweeping method might fail to converge to the exact solution as \(\varDelta x \rightarrow 0\) when choosing a tube radius \(h= O(\varDelta x)\).

In developing a fast method for solving the eikonal equation, it is extremely important to take care of the causality by considering the characteristic direction. The trivial embedding method developed above, however, does not provide correct information for the update formula near the boundary \(\partial \varGamma _h\), as shown in Fig. 2. Consider the numerical value of a grid point \( u_{i,j} \) which lies inside the computational domain \((x_i,y_j)\in \varGamma _h\) but adjacent to the boundary of the computational tube \(\partial \varGamma _h\), as shown in blue in Fig. 2. The corresponding update formula depends on the values at two adjacent grid points, marked in red. However, since \( u_{i-1,j} \) lies outside the computation tube, only \( u_{i,j-1} \) will be used. This implies that there is always a mismatch in the numerical upwind direction and the real characteristic direction at a grid point near the computational boundary, and this mismatch does not vanish as we decrease \(\varDelta x\). This is the main reason why the method does not converge to the correct solution.

Fig. 2
figure 2

The numerical upwind direction and the real characteristic direction near a boundary grid point

Full size image

In Fig. 3a, we have plotted several numerical solutions (in blue circles and blue solid lines) to the eikonal equation using various tube radius given by \(h=O(\varDelta x)\). The top blue data are obtained using the tube radius \(h=5\varDelta x/\sqrt{8}\), which has been analyzed above. We clearly see that the numerical solution converges to \(\frac{1}{2} \left( \alpha _++\sqrt{2-\alpha _-^2} \right) \), represented by the red dotted line on the top, as \(\varDelta x \rightarrow 0\). Using a larger ratio \(h/\varDelta x\) as we refine the mesh, the numerical solution does converge to a value closer to the exact solution \(\sqrt{2}\), as demonstrated by different blue solid curves in the figure. Nevertheless, for any finite fixed ratio \(h/\varDelta x\), the approach proposed earlier in this section does not converge to the exact solution.

Fig. 3
figure 3

Numerical solutions at \((x,y)=(1,1)\) on different \(\varDelta x\) and h. The exact solution \(\sqrt{2}\) and \(\frac{1}{2} \left( \alpha _++\sqrt{2-\alpha _-^2} \right) \) are plotted using the bottom and the top red dotted lines on both figures, respectively. a Blue solid lines with circles (from top to bottom) represent the numerical solutions from different \(\varDelta x\) using a fix ratio of \(h/\varDelta x\) changing from \(2.5/\sqrt{2}\) to \(7.5/\sqrt{2}\) in an increment of \(1/\sqrt{2}\). The black dashed line with squares represents the numerical solutions from different \(\varDelta x\) using \(h=1.5 (\varDelta x)^{\gamma }\) for \(\gamma =0.7\) and 0.8. b Numerical solution as \(\varDelta x \rightarrow 0\) while keeping \(h/\varDelta x\) fixed. c Error at the location \((x,y)=(1,1)\) versus the mesh size with \(h=O(\varDelta x^{\gamma })\) and \( \gamma =0.8 \) and \( \gamma =0.7\), respectively. A black dotted reference line has slope 0.5 . The case with \( \gamma =0.7 \) has a better behavior with the slope of the least squares fitting line 0.6546 (Color figure online)

Full size image

On the other hand, the numerical solution seems to converge to the exact solution if we have \(\varDelta x \rightarrow 0\) and \(h/\varDelta x \rightarrow \infty \) at the same time, as shown in Fig. 3b. Therefore, one possible attempt to fix this simple fast sweeping scheme is to follow a similar approach as in [21] by choosing the tube radius \(h = O( \varDelta x ^{\gamma } ) \) for some \( \gamma \in (0,1) \). In such a choice, the computation tube will shrink in a much smaller speed as we reduce the mesh size \( \varDelta x \). Their original intention is to increase the resolution of the numerical solution when approximating the Euclidean weighted distance function by having \( h \rightarrow 0 \) and \( \frac{h}{\varDelta x} \rightarrow \infty \) at the same time. We have preformed numerical experiments on the above example by choosing \(\gamma = 0.8 \) and \( \gamma =0.7 \), respectively, and we have checked the numerical error in the numerical solution at the point \((x,y)=(1,1)\). We have found that the solutions from these two cases seem to converge to the exact solution, but the smaller the value of \(\gamma \) the better the numerical convergence, as shown in Fig. 3a, c. In particular, for a relatively larger \(\gamma \) (\(=\)0.8), we found that the numerical solution converges slower than \(O(\sqrt{\varDelta x})\). For a smaller \(\gamma \) (=0.7), the convergence is faster than \(O(\sqrt{\varDelta x})\).

Such improvement in the numerical solution can be partially explained by the constructions in the explicit numerical solution using \(h=O(\varDelta x)\) as demonstrated above. The smaller value of \( \gamma \), the greater number of grid points lies inside the tube. As argued, the boundary grid points introduce problematic information in the characteristic direction. The further away (relative to \(\varDelta x\)) the boundary to the interface \(\varSigma \), the more the error gets diluted. But we again emphasize that it is not clear how small should \(\gamma \) be used in order to yield good numerical results. Also, since the number of mesh points across the computational tube is \(O(h/\varDelta x)=O(\varDelta x^{\gamma -1})\), the total number of mesh points within \(\varGamma _h\) is therefore

$$\begin{aligned} O(\varDelta x^{\gamma -1}) \cdot O(\varDelta x^{1-d})=O(\varDelta x^{\gamma -d}) . \end{aligned}$$

As a result, this approach has a heavy trade-off between the accuracy in the solution and the overall computational cost. In the next section, we are going to propose a simple numerical treatment by incorporating the true characteristic direction to the update formula, while keeping the radius of the computational tube \(h=O(\varDelta x)\).

4 Our Proposed Approach

Our proposed approach is motivated by the fact that the scheme has to take care of the correct characteristic direction even for those grid points adjacent to the boundary of the computational tube. This implies that instead of keeping \(u_{i,j}\) as the numerical infinity for all \((x_i,y_j) \notin \varGamma _h\), one has to also update the solution in the exterior of \(\varGamma _h\) if the grid location is adjacent to the computational tube.

To design a correct condition at those locations, we recall that the viscosity solution to the surface eikonal equation \( | \nabla _{\varSigma } u| =1 \) on an implicit surface can be seen as the intrinsic distance function of the surface itself. At each point on the surface, it is geometrically clear that the surface gradient \( \nabla _{\varSigma } u\) of the intrinsic distance function must lie on the tangent plane and it implies that the surface gradient should be orthogonal to the normal of the surface. If the level set function \(\phi \) is the signed distance representation of the surface given by \(\{\phi =0\}\) with \(|\nabla \phi |=1\), such condition can be expressed as

$$\begin{aligned} \mathbf {n}\cdot \nabla _{\varSigma } u = 0\, \hbox {on }\varSigma \end{aligned}$$
(6)

where \(\mathbf {n}=\nabla \phi \) is the unit normal defined on the interface \(\varSigma \). Our approach uses this expression to impose an extra boundary value condition for \(\varGamma _h\). Assuming that the solution to the surface eikonal equation is not only given on \(\varSigma \) but also all level sets given by \(\{|\phi |< h\}\), we have a natural extension of the solution to outside the tube using

$$\begin{aligned} \mathbf {n}\cdot \nabla u = 0 . \end{aligned}$$
(7)

Mathematically, this means that the function u has to be constant along the normal direction to the boundary and, therefore, such condition imposes simply a constant extrapolation of u away from \(\varGamma _h\).

In this work, we propose to extend the solution to eikonal equation within \(\varGamma _h\) by solving (7) outside the computational tube. One simple way to implement this extension idea is to introduce a time variable and solve the following linear advection equation in the computational domain except the tube, up to steady state

$$\begin{aligned} u_t + \hbox {sgn}(\phi ) \mathbf {n}\cdot \nabla u = 0 \, \hbox { on }\varOmega -\varSigma _h \end{aligned}$$

where \(\hbox {sgn}(x)\) is the signum function. Instead, we can also consider the time-independent version by solving

$$\begin{aligned} \left[ \hbox {sgn}(\phi ) \mathbf {n}\right] \cdot \nabla u = 0 \, \hbox { on } \varOmega -\varSigma _h \end{aligned}$$
(8)

where the extra signum function takes care of the upwind direction in the characteristics so that all information will flow outward from the interface to the rest of the computational domain.

Fig. 4
figure 4

The computational tube \(\varGamma \) consists of two separate layers, denoted by \(\varGamma ^{in}\) and \(\varGamma ^{out}\). The inner layer \(\varGamma ^{in}\) for the eikonal equation is represented by green, while the outer layer \(\varGamma ^{out}\) for the extension equation is highlighted by yellow (Color figure online)

Full size image

Recall that we require only a boundary condition at grid point adjacent to the computational tube, much computational efforts are wasted if this extension equation is solved on \(\varOmega - \varSigma _h\). The first step in our approach is to introduce a second layer of computational tube, as shown in Fig. 4. The inner computation layer (denoted by \(\varGamma ^{in}\) with radius \(h^{in}\)) is the same as our previous computation tube in Sect. 3 where we impose the eikonal equation, while the outer layer is an extension layer (denoted by \(\varGamma ^{out}\) with width \(h^{out}\)) in which we impose the constrained boundary condition (8). Numerically, the equation in each individual domain \(\varGamma ^{in}\) and \(\varGamma ^{out}\) can be efficiently solved by fast sweeping methods. The inner layer can be handled just like what we have discussed in Sect. 3. When we update \(u_{i,j}\) in the outer layer \(\varGamma ^{out}\) based on the advection equation (8), we apply the fast sweeping updating formula (5) by considering

$$\begin{aligned} p_{i,j}= & {} [\hbox {sgn}(\phi ) \phi _x]_{i,j}=\frac{\hbox {sgn}(\phi _{i,j})}{2\varDelta x} \left( \phi _{i+1,j}-\phi _{i-1,j} \right) \\ q_{i,j}= & {} [\hbox {sgn}(\phi ) \phi _y]_{i,j}=\frac{\hbox {sgn}(\phi _{i,j})}{2\varDelta x} \left( \phi _{i,j+1}-\phi _{i,j-1}\right) . \end{aligned}$$

Since we require that \(\varDelta x\) is small enough to resolve the interface, the level set function \(\phi \) is differentiable in the computational tube so that it is accurate to approximate the derivatives using the central difference. The algorithm can be easily implemented and we have summarized in Algorithm 3. If high order extrapolation is necessary, one can apply the PDE based extrapolation approach proposed in [1, 2].

figure c

Now, all grid points in the inner computational tube have correct characteristic information for updating its latest value. Returning to our previous simple example as demonstrated in Fig. 2, in particular, we find that \( u_{i,j} \) can now update its value using \( u_{i-1,j} \) which thus provides a better approximation to the characteristic direction. Furthermore, we also mention that constructing an extra extension layer is necessary anyway if we are using the LxF Hamiltonian instead of the Godunov Hamiltonian. In the original work [13], higher order extrapolation technique has been coupled with a maximization–minimization condition to determine a proper value for grid locations outside the computational boundary. On the other hand, we found that a constant extrapolation condition is already good enough to provide a convergent and robust algorithm for determining the values in the outer layer (Fig. 5).

Fig. 5
figure 5

a The numerical values in the outer layer are constantly extrapolated from those in the inner layer. The arrows in the figure show the unit outward normal directions, which are also the extrapolation direction. In the ideal situation, the same numerical value is found along the cross section in the outer layer. b The boundary point, represented by the blue dot, can now take the numerical value of its left neighbour point which lies in the extension layer. This extra point corrects the numerical upwind direction (Color figure online)

Full size image

In the current approach, we are able to use a tube radius \(h^{in}\) and \(h^{out}\) both of \(O(\varDelta x)\). Nevertheless, the tube radius has to be wide enough for resolving both the eikonal equation in inner layer and the extension equation in outer layer. Using the same lower bound proposed in [21], both layers should have at least \( h \sqrt{d} \) in their width which makes a lower bound of the whole tube \(h^{out}\) to be \( \sqrt{d} \varDelta x + \sqrt{d} \varDelta x = 2 \sqrt{d} \varDelta x \). In our numerical experiments, we choose \( 2 d \varDelta x \). Even though such choice is slightly larger than the theoretical lower bound, the total number of grid points increases only linearly as \(\varDelta x \rightarrow 0\).

In the following, we prove the numerical convergence of the LxF fast sweeping method on the two dimension eikonal equations \( | \nabla u | = R \), where \(R = R({\mathbf {x}})\) is some positive function.

Proposition 4.1

Suppose that the initial values of numerical solution are all set to be positive in both the inner and the outer layers (except the source points). Then the numerical solution always stays positive.

Proof

We split the discussion into two cases. First, we consider a location \((x_i,y_j)\) in the inner layer. Take \( \varDelta x = \varDelta y \), \( \sigma _{x} = \sigma _{y} = 1 \), the Hamiltonian for the eikonal equation is \( H(p,q) = \sqrt{p^{2}+q^{2}} \). The LxF fast sweeping has the following update formula,

$$\begin{aligned} u_{i,j}^{*}&=\frac{R_{i,j} \varDelta x}{2} + \frac{1}{4} \left[ u_{i+1,j} + u_{i-1,j} + u_{i,j+1} + u_{i,j-1} \right. \nonumber \\&\quad \left. - \,\sqrt{(u_{i+1,j}-u_{i-1,j})^{2}+(u_{i,j+1}-u_{i,j-1})^{2}} \right] \end{aligned}$$

It is clear that the sign of \(u_{i,j}^{*}\) solely depends on the second term of the above expression. Note that

$$\begin{aligned}&(u_{i+1,j}+u_{i-1,j}+u_{i,j+1}+u_{i,j-1})^{2} - \left[ \sqrt{(u_{i+1,j}-u_{i-1,j})^{2}+(u_{i,j+1}-u_{i,j-1})^{2}} \right] ^{2} \nonumber \\&\quad = 4 u_{i+1,j} u_{i-1,j} + 2 u_{i+1,j} u_{i,j+1} + 2u_{i+1,j}u_{i,j-1} + 2 u_{i-1,j} u_{i,j+1} \nonumber \\&\qquad + \,2 u_{i-1,j} u_{i,j-1} + 4 u_{i,j+1} u_{i,j-1} . \end{aligned}$$

The second term will always keep its positive sign if the values of \( u_{i \pm 1,j} \) and \( u_{i,j \pm 1}\) are all positive. So if the numerical solution starts with the positive initial values everywhere, the value of \( u_{i,j}^{*} \) always stays positive at the following iterations.

If \((x_i,y_j)\) is in the outer layer, we have

$$\begin{aligned} u_{i,j}^{*} = \frac{p^{+} u_{i-1,j} - p^{-} u_{i+1,j} + q^{+} u_{i,j-1} - q^{-} u_{i,j+1}}{|p| + |q|} , \end{aligned}$$

where (p, q) is the unit outward normal vector at \((x_{i},y_{j})\), and \( p^{\pm } := (p \pm |p|)/2 \). Since, \( u_{i,j}^{*} \) is just a convex combination of \( u_{i \pm 1,j} \) and \( u_{i,j \pm 1} \) with \(p^+,-p^-,q^+,-q^-\ge 0\), \( u_{i,j}^{*} \) stays positive as long as \( u_{i \pm 1,j} \) and \( u_{i,j \pm 1} \) do so. Its positiveness again inherits from the initial values of the numerical solution. \(\square \)

We recall a simple fact in analysis, a decreasing and bounded below sequence converges. We then have the following corollary.

Corollary 1

The LxF fast sweeping method on eikonal equations \( | \nabla \phi | = R(x) \) converges numerically.

Proof

Recall that we impose large values to the initial guess in the fast sweeping algorithm, the numerical solution based on the Godunov Hamiltonian is guaranteed to be decreasing. Even though there is no such property in the LxF Hamiltonian, on the other hand, we can explicitly impose this constraint in the iteration by updating the numerical solution only when the updated value is less than its old value. Now, since the numerical solution always approximates to the correct viscosity solution from above, the numerical solution at each grid point forms a decreasing sequence. And, because each of these sequences is bounded below by zero based on the above proposition, they converge as the iteration goes. \(\square \)

It does not seems to be trivial to rigorously prove that the numerical solution on \(\varSigma \) converges to the viscosity solution to the surface eikonal equation as \(\varDelta x\) goes to zero. Intuitively, as explained earlier, one has to provide the correct characteristic information in designing a local update formula. For the surface eikonal equation, such information might come from outside the inner computational domain. The extension step we proposed does give a way to bring the necessary information to the inner tube. To prove that the numerical solution indeed converges to the viscosity solution, however, one difficulty is that the computational domain depends explicitly on \(\varDelta x\). Also, one has to consider at the same time the coupling of the extension equation in the outer layer and the numerical solution to the eikonal equation in the inner tube. Nevertheless, the numerical examples in Sect. 6 have shown that the proposed numerical scheme does converge to the correct viscosity solution without any difficulty.

5 Extensions

The proposed approach can be easily extended to various equations and on general implicit surfaces. In this section, we discuss various straight-forward extensions and applications.

5.1 General Static HJ Equations on Surfaces

The proposed approach can be easily extended to other static HJ equations on surfaces. Suppose that we are given a HJ equation

$$\begin{aligned} H(\nabla _{\varSigma } u)=0 , \end{aligned}$$

defined only on the surface \(\varSigma \). Following the same idea in the previous section, we replace the intrinsic gradient \(\nabla _{\varSigma } u\) directly by the extrinsic gradient \(\nabla u\) and consider the equation

$$\begin{aligned} H(\nabla u)=H(u_x,u_y)=0 \end{aligned}$$

in a small neighborhood of the surface \(\varSigma \). Numerically, we first construct a two-layered computational tube that encloses the surface \(\varSigma \). In the inner layer \(\varGamma ^{in}\), we solve the HJ equation \(H(u_x,u_y)=0\) by replacing the Hamiltonian with the LxF Hamiltonian

$$\begin{aligned}&H\left( \frac{D_x^+ u_{i,j} + D_x^- u_{i,j}}{2} , \frac{D_y^+ u_{i,j} + D_y^- u_{i,j}}{2} \right) \nonumber \\&\quad - \,\sigma _x \, \left( \frac{D_x^+ u_{i,j} - D_x^- u_{i,j}}{2} \right) - \sigma _y \, \left( \frac{D_y^+ u_{i,j} - D_y^- u_{i,j}}{2} \right) , \end{aligned}$$

where

$$\begin{aligned} \sigma _x \ge \max \left| \frac{\partial H}{\partial u_x} \right| \, \hbox { and } \, \sigma _y \ge \max \left| \frac{\partial H}{\partial u_y} \right| \end{aligned}$$

and \(D_x^{\pm }\) and \(D_y^{\pm }\) are the forward and the backward difference operators along the x- and the y-direction, respectively. Numerically, we can follow the same approach as in Algorithm 3 but only need to replace the iterative update formula at each grid point \((x_i,y_j)\) within \(\varGamma ^{in}\) by

$$\begin{aligned} u_{i,j}\leftarrow & {} \left[ \frac{\sigma _x}{\varDelta x} + \frac{\sigma _y}{\varDelta y} \right] ^{-1} \left[ \sigma _x \, \frac{u_{i+1,j}+u_{i-1,j}}{2\varDelta x} \right. \nonumber \\&\left. +\, \sigma _y \, \frac{u_{i,j+1}+u_{i,j-1}}{2\varDelta y} - H\left( \frac{u_{i+1,j}-u_{i-1,j}}{2\varDelta x} , \frac{u_{i,j+1}-u_{i,j-1}}{2{\varDelta y}} \right) \right] . \end{aligned}$$

In the outer layer \(\varGamma ^{out}\), we keep the typical extension equation as before.

5.2 Implicit Surfaces in the Closest Point Representation

In above sections, all implicit surfaces are represented by the zero level set of some signed distance functions. Some implicit surfaces, however, cannot be defined using any signed distance function. Typical examples include open surfaces and non-orientable surfaces. Nevertheless, if an implicit surface is not pathological, it usually admits a closest point representation in an open set that contains the implicit surface. It is, therefore, not difficult to extend our proposed algorithm to surfaces with the closest point representation. For a point \(\mathbf{x }\) sufficiently close to a given surface \(\varSigma \), it is possible to find the unique projection of \(\mathbf{x }\) on \(\varSigma \) which gives the shortest Euclidean distance. Following the same notation as in the closest point method [19, 20, 31], we denote this unique projection \(cp(\mathbf{x })\), representing the closest point on \(\varSigma \) to \({\mathbf {x}}\). Then the surface \(\varSigma \) can be represented by the zero level set of the function \(F(\mathbf{x }) := |\mathbf{x }-cp(\mathbf{x }) |\). Using this function, we can similarly define the inner and outer layer by \(\varGamma ^{in} = \{F(\mathbf{x }) \le h^{in} \}\) and \(\varGamma ^{out} = \{ h^{in} < F(\mathbf{x }) \le h^{out} \}\), respectively.

Unlike the signed distance function as in the level set method, unit outward normal may not be well defined in surfaces with the closest point representation. For example, non-orientable surfaces like the Mobius band do not have any consistent outward normal at any point. It seems to cause trouble in our constant outward extrapolation in \(\varGamma ^{out}\). But we do not actually need the consistent outward normal on the surface everywhere. For a point \(\mathbf{x }\) in \(\varGamma ^{out}\), all we need is to extrapolate the numerical value at \(\mathbf{x }\) away the surface orthogonally. And this can be done by extrapolate along the unit vector

$$\begin{aligned} \hbox {sgn}(\phi ) \mathbf n (\mathbf{x }) = \dfrac{\mathbf{x }-cp(\mathbf{x })}{|\mathbf{x }-cp(\mathbf{x })|} . \end{aligned}$$

Since the closest point \(cp(\mathbf{x })\) has the shortest distance to \(\mathbf{x }\) on \(\varSigma \), this can only happen iff \(\mathbf{x }-cp(\mathbf{x })\) is orthogonal to the tangent plane at \(cp(\mathbf{x })\). So the unit vector \(\mathbf n (\mathbf{x })\) is orthogonal to \(\varSigma \) and pointing away from it.

Fig. 6
figure 6

(A six-folded star shaped curve) a The set up of the example. The point source is located at (0.5, 0) plotted using a red dot. b The slope of both linear fitting lines is clearly greater 1. The corresponding convergence order using the Godunov and the LxF Hamiltonians are 1.3413 and 1.0041, respectively (Color figure online)

Full size image

6 Numerical Examples

6.1 Eikonal Equations

In this section, we first investigate the convergence behavior of the proposed algorithm by solving the eikonal equation \( | \nabla u | =1 \) on some simple two-dimensional and three-dimensional implicit surfaces for which the exact solutions can be analytically found. Then we extend the approach to various complicated surfaces to demonstrate the effectiveness of the method.

In this first example, we consider solving the surface eikonal equation on the six-folded star-shape curve given by

$$\begin{aligned} r=r_0+\epsilon \sin ^2(3\pi \theta ) , \end{aligned}$$

with \(r_0=0.5\), \(\epsilon =0.2\) and the point source boundary condition \(u=0\) at \((x,y)=(0.5,0)\), as shown in Fig. 6a. The exact solution at a given point on the curve is simply the arclength from the source point. The infinity norm error on the solution using various meshes are plotted in Fig. 6b and are shown in Table 1. In Fig. 6b, we have plotted also two reference curves with slope equals 0.5 and 1, respectively. Even though the solutions from the LxF fast sweeping is in general more accurate than that using the Godunov fast sweeping, it is clear that our proposed approach using any of these numerical Hamiltonian converges to the exact solution with an order of approximately 1.

In Table 2, we summarize the number of sweepings required to reach the converged solutions using the Godunov hamiltonian and the LxF hamiltonian, respectively. The total number of iterations for any of two numerical Hamiltonians is approximately linear (0.7187 and 0.8213 for two Hamiltonians respectively) in the number of grid points in each physical direction. We have the following observations. Unlike the Godunov–FS scheme for the eikonal equation (1) which can be shown to converge in \(2^d\) iterations in \({\mathbb {R}}^d\), the proposed Godunov–FS method for the surface eikonal equation (2) takes more iterations to converge and the number of iterations now depends on N. This can be explained by the fact that in a part of the computational domain, we are solving an extension equation and the resulting solution is coupled with that from the eikonal equation. Therefore, the proof in, for example, Zhao [41] does not directly go through. Secondly, the LxF–FS requires a larger number of iterations than the Godunov–FS to converge. This is expected due to the excessive numerical dissipation and viscosity in the LxF hamiltonian. The same observation has been commonly reported in the fast sweeping community. Nevertheless, for a complicated Hamilton–Jacobi equation when the local solver for the Godunov hamiltonian cannot be easily constructed, the LxF hamiltonian still provides a simple strategy for designing a fast sweeping algorithm.

Table 1 (6-Folded star shaped curve) Errors (\(\times 10^{-2}\)) in the numerical solution on various meshes
Full size table
Table 2 (6-Folded star shaped curve) The number of sweepings required to obtain the numerical solution
Full size table

Next, we consider a sphere with radius of 0.5, where the radius of the inner computation tube and the extension tube are \(2 \varDelta x\) and \( 4 \varDelta x\), respectively. The point source is set at \((-0.5,0,0)\), and the infinity norm error is measured along a circle where the sphere intersects with the y–z plane. The numerical errors for various mesh size are given in Table 3. Like the low dimensional case, the convergence rate is again approximately 1, as shown in Fig. 7.

Table 3 (Sphere) Errors in the numerical solution to the eikonal equation by the LxF fast sweeping scheme on various meshes
Full size table
Fig. 7
figure 7

(Sphere) a The solution to eikonal equation on the sphere. The point source and the circle where we measure the error are represented by a red dot and a black dotted circle along the sphere respectively. b The error in the solution to the eikonal equation on a sphere. The convergence order using the LxF fast sweeping is approximately 1 (Color figure online)

Full size image

We also plot some eikonal solutions on other two dimensional manifolds represented implicitly using a level set function in Fig. 8. We use the same radius in the inner layer as the sphere, i.e. \(2 \varDelta x\). Except the Stanford bunny in which we choose a slightly larger outer tube (\(5\varDelta x\)), all other examples use the same radius \(4\varDelta x\).

6.2 Implicit Surfaces in the Closest Point Representation

In this section, we apply our algorithm to some implicit surfaces with closest point representations. We consider the upper hemisphere and also the Mobius band. We first obtain the viscosity solution in a small neighborhood of the implicit surface defined using a Cartesian mesh, then we interpolate the solution on the corresponding triangulate surface, as shown in Fig. 9.

Fig. 8
figure 8

Solutions to the eikonal equations on various implicit surfaces

Full size image
Fig. 9
figure 9

The eikonal solutions on a, b upper hemisphere and c, d the Mobius band

Full size image
Fig. 10
figure 10

The anisotropic eikonal equation in the three-vortex flow. The source point is set at (0.5, 0, 0), and the centers of vortex flow are set at (0, 0, 0.5), \((0,-0.5,0)\) and (0.5, 0, 0) respectively. Contour lines of our computed solution are plotted in black solid line on top of a, b the flow field and c, d the contour lines of the unperturbed first arrivaltime in magenta dotted lines (Color figure online)

Full size image

6.3 An Anisotropic Eikonal Equation

We extend our proposed approach to solve an anisotropic eikonal equation on a moving medium [25], given by

$$\begin{aligned} | \nabla u (\mathbf{x }) | = \frac{|1-\mathbf v (\mathbf{x }) \cdot \nabla u(\mathbf{x })|}{F(\mathbf{x })} . \end{aligned}$$

The equation has a wide range of applications in geophysics [11] and atmospherical sciences like noise propagation modeling [9] or underwater acoustics. If we interpret this eikonal equation in the context of wave propagation, u is the first arrival time that the wave propagates from the point source. \(\mathbf v (\mathbf{x })\) and \(F(\mathbf{x })\) are the ambient velocity field of the surrounding moving medium and the speed of the wave propagation, respectively. Various numerical methods might be used to solve the equation, but they are limited to a typical Euclidean space. In this part of the paper, we will solve this generalized eikonal equation on a sphere given by

$$\begin{aligned} | \nabla _{\varSigma } u (\mathbf{x }) | = \frac{|1-\mathbf v (\mathbf{x }) \cdot \nabla u(\mathbf{x })|}{F(\mathbf{x })} \end{aligned}$$

where the ambient velocity \(\mathbf {v}\in {\mathbb {R}}^3\) is orthogonal to the surface (\(\mathbf {v} \cdot \mathbf {n}=0\)) and has a small magnitude comparing to F (such that \(|\mathbf {v}| \ll F\)). One simple flow field is given by the following N-point vortex flow [22, 23]

$$\begin{aligned} \mathbf v (\mathbf{x })=\frac{1}{2\pi } \sum _{j=1}^{N} \frac{s_j (\mathbf{x }_{j} \times \mathbf{x })}{ | \mathbf{x }_{j}-\mathbf{x } |^{2} } , \end{aligned}$$

where \(\mathbf{x }_j\) is the center of a point vortex with the index j and \(s_i\) is the corresponding strength of the vortex. In the following examples, we take \(F=3\), the radius of the sphere as 0.5, \(s_j=4\) for all j and the point source is always located at \((-0.5,0,0)\). Figure 10 shows our solution to the three-point vortex flow (\(N=3\)) with the centers of the point vortex are located at (0, 0, 0.5), \((0,-0.5,0)\) and (0.5, 0, 0), which are highlighted by red stars in Fig. 10a, b. We plot the contours of our computed first arrival time on sphere in black solid lines. In Fig. 11, we repeat the same example but consider having four point vortices located at \((-1,\pm 1,\pm 1)/2\sqrt{3}\). To demonstrate the effect of the moving medium, we plot also the unperturbed traveltime corresponding to \(|\mathbf {v}|=0\) in magenta dotted lines in Figs. 10 and 11c, d. We can clearly see the perturbation in the arrival time due to the ambient flow on the surface.

Fig. 11
figure 11

The anisotropic eikonal equation in the four-vortex flow. The source point is kept at \((-0.5,0,0)\). Contour lines of our computed solution are plotted in black solid line on top of a, b the flow field and c, d the contour lines of the unperturbed first arrivaltime in magenta dotted lines (Color figure online)

Full size image

7 Conclusion and Future Work

In this paper, we have proposed a simple, computationally efficient and convergent numerical algorithm to solve surface eikonal equations on implicit surfaces. The approach is developed based on the embedding method so no surface triangulation is necessary. We have carefully studied a simple approach and have explained why we cannot simply solve the eikonal equation using the Godunov fast sweeping method in a small neighborhood of the implicit surface. Our proposed method only requires that the overall tube radius satisfies \(h=O(\varDelta x)\), which is optimal in the sense that the total number of mesh points in the computational tube is \(O(\varDelta x^{1-d})\) for a co-dimensional one surface in \({\mathbb {R}}^d\).

In the future, we plan to couple the level set method to extend the algorithm to simulate evolution of surfaces in which the motion law is modeled by the viscosity solution of a certain HJ equation. In addition, we also plan to develop higher order accurate schemes to HJ equations on implicit surfaces.