1 Introduction

Superconducting microwave resonators have been widely used for high sensitivity detection of excitations such as charge [1,2,3] and photons [4, 5] due to their simple fabrication process and frequency domain multiplexing capability. Among the various types of superconducting resonator-based detectors, Microwave Kinetic Inductance Detectors (MKIDs) [6, 7] have found broad application [8,9,10,11,12,13]. Over the past decade, arrays of MKIDs have evolved to thousands [14, 15] of detectors per wafer with improved noise equivalent power (NEP). However, scatter in resonator frequency placement, where the fabricated resonance frequencies are shifted from their designed values, has become a limiting issue for large array performance. Various parameters could contribute to this fluctuation such as nonuniformity in the critical temperature (\(T_c\)) and film thickness, nonuniformity in lithographic processing, and nonuniform etch profiles across the wafer.

One solution for mitigating frequency fluctuations is capacitor trimming [16], a method that improves the MKID frequency distribution at the cost of introducing additional fabrication steps. Another approach is to improve MKID materials and fabrication processes to improve resonator frequency placement, though this approach requires detailed studies to understand the fundamental parameters that result in scatter of the resonator frequency. This paper is an initial investigation along this direction, and studies how variations in resonator geometry arising from fabrication processes contribute to frequency scatter. Our work is motivated in part by results from previously fabricated MKIDs where we observed significant line width variation - up to 2 \(\upmu {\hbox {m}}\) for a 4 \(\upmu {\hbox {m}}\) wide feature - across a 6 inch wafer. Bearing in mind that the inductance of a microstrip inductor strongly depends on its line width, this variation will significantly change the inductance of our lumped element inductor and may well explain the resonant frequency shift of the resonators. To investigate the impact of the line width variation on resonator frequency placement we carried out a study using electron beam (e-beam) lithography to fabricate resonators with line widths varying in steps of 100 nm, and evaluated their resonance frequency placement as a function of their line widths.

2 Modeling the Microstrip Inductance

To develop some intuition about the relationship between line width and resonator frequency we look at S-shaped inductors fabricated on PCBs where the inductance per unit length and thickness is defined:

$$\begin{aligned} L_{m}= & {} \beta \cdot w^{\alpha } \end{aligned}$$
(1)

with w the width of the S-shaped strip and \(\beta\) and \(\alpha\) are determined by fitting to multiple resonators [17]. The inductance change, \(\varDelta L_{m}\), due to small line width change, \(\varDelta w\), can be approximated by Taylor expansion around w:

$$\begin{aligned} \varDelta L_{m}/L_{m}= & {} \alpha \varDelta w/w \end{aligned}$$
(2)

Similarly the kinetic inductance change, \(\varDelta L_{K}\), due to line width variation, \(\varDelta w\), is

$$\begin{aligned} \frac{\varDelta L_{K}}{L_{K}}= & {} -\frac{\varDelta w}{w} \end{aligned}$$
(3)

where we have used the kinetic inductance equation from reference [18]: \(L_{k}(T)=\mu _{o}\lambda ^{2}(T)\left( \frac{l}{wd}\right)\). l, w and d are the length, width and thickness of the superconducting strip. \(\lambda (T)\) is the Ginzburg–Landau (GL) magnetic penetration depth at temperature T and \(\mu _{o}\) is the permeability constant.

The corresponding shift in resonator frequency \(\varDelta f_{o}\) is then

$$\begin{aligned} f_{o} + \varDelta f_{o}= & {} \frac{1/2\pi }{\sqrt{(L+\varDelta L)C}} \end{aligned}$$
(4)
$$\begin{aligned}= & {} \frac{1/2\pi }{\sqrt{LC}}\left( 1-\frac{1}{2}\frac{\varDelta L}{L}\right) \end{aligned}$$
(5)
$$\begin{aligned}= & {} f_{o} -\frac{1}{2}f_{o}\frac{\varDelta L}{L} \end{aligned}$$
(6)

and the fractional frequency shift is given by

$$\begin{aligned} \frac{\varDelta f_{o}}{f_{o}}= & {} -\frac{1}{2}\frac{\varDelta L}{L} \end{aligned}$$
(7)
$$\begin{aligned}= & {} \frac{1}{2}\left( \alpha \frac{L_{m}}{L_{K}+L_{m}}+\frac{L_{K}}{L_{K}+L_{m}}\right) \frac{\varDelta w}{w} \end{aligned}$$
(8)

We also simulate the response of our lumped element resonators using Sonnet while varying the inductor width from 1.5 \(\upmu {\hbox {m}}\) to 2.5 \(\upmu {\hbox {m}}\) in steps of 0.25 \(\upmu {\hbox {m}}\). Figure 1 shows the result of our simulations for each of our two circuit capacitor designs (see Sect. 3).

Fig. 1
figure 1

Simulated fractional resonant frequency shift, \(\varDelta f_{o}/f_{o}\), versus fractional line width variation, \(\varDelta w/w\), for ‘X-pol’ and ‘Y-pol’ resonators as defined in Fig.  2. Inductor line widths were varied from 1.5 \(\upmu {\hbox {m}}\) to 2.5 \(\upmu {\hbox {m}}\) in steps of 0.25 \(\upmu {\hbox {m}}\). \(L_{K}\) is the kinetic inductance of the superconducting thin film in the simulation

Full size image

3 Test Resonator Design

To empirically study the impact of resonator geometry on frequency placement we designed a test device comprised of five nearly identical lumped element resonators with varying inductor line width. In our design (see Figure 2) we have five pixels with each pixel having a ‘X-pol’ resonator and a ‘Y-pol’ resonator. All of the ‘X-pol’ (‘Y-pol’) resonators have the same circuit capacitor design \(C_x\) (\(C_y\)), and the inductor line width for both resonators is varied from 1.8 \(\upmu {\hbox {m}}\) to 2.2 \(\upmu {\hbox {m}}\) in steps of 0.1  \(\upmu {\hbox {m}}\) across the five pixels. With this configuration we expect two groups of resonances corresponding to the two circuit capacitor designs \(C_{x}\) and \(C_{y}\). Within each group we expect five linearly distributed resonances corresponding to the five inductors with different line width.

Fig. 2
figure 2

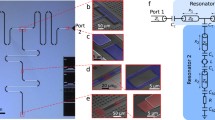
Images of the test chip and components. (a) Image of chip A which has five pixels and each pixel has two resonators named ‘X-pol’ and ‘Y-pol’ because of the orthogonal direction of the two inductors. (b) Zoom-in of the S-shaped inductors. (c) Zoom-in of one of the pixels. Left interdigital capacitor \(C_{x}\) is connected to the horizontal (X) S-shaped inductor and the right interdigital capacitor \(C_{y}\) is connected to the vertical (Y) S-shaped inductor. (d) Zoom in of a interdigital capacitor \(C_{y}\)

Full size image

4 Fabrication

The e-beam devices presented here were fabricated on a single silicon wafer, which minimizes the impact from comparing materials from different depositions. To achieve the required 100 nm line width resolution, the resonators were patterned using e-beam lithography with a resolution of 10 nm.

The fabrication process begins with vacuum baking the bare wafer at \({120}^\circ \,{\hbox {C}}\) for six minutes to remove moisture. E-beam resist (PMMA 950 A4) is spun on the wafer at a speed of 4000 rpm for 40 seconds and then baked at \({180}^\circ \,{\hbox {C}}\) for 4 minutes afterward. The resonators are patterned in a single lithography layer. The inductor, capacitor, and connection lines were written with a dose of 720  \({\upmu \,{\hbox {C}}/{\hbox {cm}}^{2}}\), while the feed-through lines as well as the contact pads were written with a dose of 800  \({\upmu \,{\hbox {C}}/{\hbox {cm}}^{2}}\); proximity effect correction effectively lowers the dose for large structures, and the dose was increased purposely to compensate for it. After the pattern is written the wafer was developed with MIBK and IPA with a ratio of 1:3 for 40 seconds and rinsed in IPA for 10 seconds. Following development a 20 second oxygen descum process was used to remove leftover e-beam resist. A 30 nm thick Al film is then deposited at rate of 0.17 nm/second via DC magnetron sputtering with 3 mTorr  Ar gas processs pressure and deposition system base pressure of \(1.7\times 10^{-8}\) mbar. The applied cathode voltage is 300  volts. The final processing step is an overnight soak in acetone for lift-off.

The two chips we chose to test were near the center of the wafer to minimize film thickness nonuniformity between the two chips. During fabrication, one of the capacitors on one of our devices (chip B) had a liftoff issue and was discarded from our measurements; this only impacted a single resonator.

5 Test Results

Fig. 3
figure 3

(a) Comparison of resonance frequencies from two chips with same resonator design. The blue trace is for chip A and the orange trace is for chip B. The inset is zoomed in to the two resonances from chips A and B around 1.3917 GHz; an offset of 15 kHz is observed. (b) Resonance frequency scatter for resonators patterned using e-beam lithography and lift-off and resonators patterned using optical lithography and wet etching. Significantly lower frequency scatter was observed in the resonator chips fabricated using e-beam lithography and liftoff

Full size image

We tested two chips (chip A and chip B) in a dilution refrigerator with base temperature of 10  mK. The input lines have \(\approx\) 70  dB attenuation and the output signal was amplified with a HEMT amplifier with gain of around 40 dB. Superconducting coaxial cables were used between the output of the sample box and the HEMT amplifier to minimize signal loss. The resonances were scanned with a standard \(S_{21}\) measurement using a VNA.

Figure 3(a) shows the measured resonances for both chip A and B. The trace for chip A shows ten resonances with the lower (higher) frequency resonances corresponding to resonators with ‘Y-pol’ (‘X-pol’) capacitor design. Within each group, the resonances differ due to the varying inductor line width. In Fig. 4, we plot the measured fractional frequency shift, \(\varDelta f_{o}/f_{o}\), versus the change in inductor line width, \(\varDelta w\). Our data exhibited a clear linear relationship as predicted by Eq. (8), with a slope that is consistent with predictions from our simulations.

We estimate the frequency scatter from our e-beam+Liftoff process by comparing the frequencies for identically designed resonators and found the largest scatter was \(\sim\) 1 MHz. This is consistent with the 10 nm e-beam resolution and our measured dependence of the inductance on line width. To give a sense of improvement in resonator frequency scatter with better inductor line width control, we compare our result with a similar measurement of frequency scatter for two other sets of resonators patterned with direct write optical lithography and wet etching. The lithography process uses SPR955 photoresist spin coated at 3000 rpm for 45 seconds and baked at \({90}^\circ \,{\hbox {C}}\) for 2 minutes. The wafer was patterned with a 405 nm laser with dose of 140 \({{\hbox {mJ}}/{\hbox {cm}}^{2}}\) followed by a post bake at \({110}^\circ \,{\hbox {C}}\) for 90 seconds. After exposure the wafer was developed with CD26 developer for 1 minute followed by a DI water rinse. The developed wafer was etched with Al etchant for 90 seconds followed by a DI water rinse. We expect a larger inductor line width variation from these resonators and as shown in figure 3(b) a much larger frequency scatter (\(\approx\) 30 MHz) is observed from these two sets of chips, which further validates our conclusion about the influence of inductor line width variation on resonator frequency scatter.

Fig. 4
figure 4

\(\varDelta f_{o}/f_{o}\) vs. \(\varDelta w\) for resonators from chip A and B. ‘X-pol’ stands for resonators that use \(C_{x}\) capacitor design and ‘Y-pol’ stands for resonators using \(C_{y}\) capacitor design

Full size image

6 Conclusion

We have demonstrated the impact of S-shaped inductor line width variation on the frequency scatter of lumped element resonators. Our results are in good agreement with our simulations and show that control of resonator geometry can be a significant contributor to frequency scatter in large arrays of MKIDs.