AC Conductivity and Dielectric Behavior of a New Double Perovskite PrNaMnMoO₆ System

Abstract

This work presents some electrical properties based on impedance measurements as well as the dielectric constants and electric modulus. In order to study the electrical conductivity and dielectric properties of PrNaMnMoO₆, complex impedance spectroscopy techniques were carried out in the frequency range 200 Hz–5 MHz at various temperatures (409–457 K). The complex impedance diagram at different temperatures showed a single semicircle, implying that the response originated from a single capacitive element corresponding to the grains. AC and dc conductivities were studied to explore the mechanisms of conduction. It can be seen from the experimental data that the AC conductivity of this compound is proportional to ω^s(s < 1), and the value of s is to be temperature-dependent, which has a tendency to decrease in temperature. Activation energy values deduced from both dc conductivity and hopping frequency are in the order of E_a = 0.32 eV and E_a = 0.29 eV, respectively. The two values E_a = 0.32 eV and E_a = 0.29 eV of activation energies obtained from the hopping frequency and equivalent circuit confirms that the transport is through an ion hopping mechanism dominated by the motion of the Na⁺ ion in the structure of the investigated material. In general, the size of the A ion influences the crystal symmetry significantly, while that of the B ion does not change the symmetry, but changes the lattice volume proportionally. The influence of the nature of the divalent A-site cations on the dielectric properties was evaluated by resistivity measurements in the frequency range. It is found that relative permittivity and dielectric loss regularly change with A cation size.

1 Introduction

Recently, perovskite multiferroic materials and their derivatives have been greatly studied thanks to their widely varying features and their numerous applications [1,2,3]. Specifically, A₂B′B″O₆ perovskite oxides have been reported with a wide range of properties: structural distortions, order–disorder phenomena of the B-site cations, and various electronic structures and magnetic orderings are of fundamental interest [4]. On the other hand, compounds with properties such as spin-polarized electron transport [5], high dielectric constant [6, 7], low thermal conductivity [8] or multiferroicity [9, 10] are also in a key position considering future technologies [11].

The A₂B′B″O₆ perovskite exhibits various electrical transport properties, ranging from insulators to metals and half metals. The electrical properties of most compounds have not been measured, but many are expected to be insulators. Such compounds could be good dielectrics, as many double perovskites have been found to have high dielectric constants. Semiconducting compounds with small band gaps are also prevalent in the double perovskite and could be useful as fuel-cell electrodes or thermoelectrics. Here the stoichiometric A₂B′B″O₆ composition may not be ideal, and partial substitutions may be required to improve the performance. The physical and chemical properties of the perovskite depend strongly on the A and B site substitution. The size of the A ion has a significant impact on crystal symmetry, whereas the size of the B ion has no effect on symmetry but does change the lattice volume proportionally [9, 10]. Resistivity measurements in the frequency range were used to assess the impact of the nature of the divalent A-site cations on the dielectric properties. It has been discovered that relative permittivity and dielectric loss vary with the size of the A cation.

A few multiferroic A₂B′B″O₆ compounds have been reported, and more could perhaps be made by a suitable combination of elements. Most A₂B′B″O₆ perovskites are insulators or semiconductors, with about 160 such compounds reported in the literature. Furthermore, there are several compounds for which electronic transport properties have not been determined, but which are reported to have a large band gap or a light color indicative of the insulating behavior. Different types of electrical conductivity have been found in the semiconducting A₂B′B″O₆ perovskite. Commonly the conduction happens by thermally excited small-polaron hopping, but occasionally Mott variable-range hopping (VRH) conduction is observed. The VRH behavior is rather reasonable in the case of disordered compounds like Sr₂MnRuO₆ [12] or Sr₂CoSbO₆ [13]. However, certain compounds have been found to show VRH at low temperatures, but small-polaron hopping-type conduction at high temperatures [14,15,16]. Some of the A₂B′B″O₆ compounds have been reported to show metal–insulator transitions (MITs) with changing temperature. Sr₂CoTiO₆ has an MIT at around 700 K [17]. The crystal structure can also affect the appearance of MIT, due to changes in orbital overlap, as for example Ca₂MnMoO₆ has an MIT at 209 K [15], whereas Sr₂MnMoO₆ is an insulator [18,19,20].

Let us remain in the same context of the electrical and dielectric properties of the oxides of the double perovskite type. It is found from the literature that there is no work done on this type of compound with general formula A'A''B'B''O₆ where A' and A″ represent, respectively, the rare earth trivalent and the alkaline monovalent cation. Thus, double perovskite materials have a wide application in modern electronics due to their high dielectric permittivity, high piezoelectric coefficient, ferroelectricity, semiconductivity, catalytic activity and thermoelectricity [4, 6, 11]. Therefore, we have proceeded with the preparation of a new compound homologous to (Sr, Ba, Ca)₂ MnMoO₆, named PrNaMnMoO₆ double perovskite oxide for the first time.

The present paper summarizes the results of an extensive study made on the electrical and dielectric properties by impedance spectroscopic technique which is a powerful tool in characterizing the electrical properties of grains in a novel double perovskite PrNaMnMoO₆ system. AC measurements are often used to probe the behavior of such low mobility. In order to analyze the dynamic response of the material as a function of the applied electric field, the study of the experimental data was performed on the conductivity, also called alternating current conductivity (σ_AC), this conductivity is associated with the conduction of electric charges whose direction is in phase with the applied electric field, and their frequency dependence also provides information on the nature of the charge carriers.

One can obtain information about the dielectric constant; the loss tangent, the mechanism of conduction and the activation energy from these measurements. The present work is purposed to investigate the temperature and frequency dependence of AC conductivity and dielectric properties of the material in order to understand the electrical conduction mechanism.

2 Experimental Details

2.1 Solid-State Synthesis

Sol–gel method was used to synthesize the PrNaMnMoO₆ double perovskite compound. In a typical process, the stoichiometric amounts of Pr₆O₁₁ (Merck, > 99.9%), Na₂CO₃ (Merck > 99.9%), MnO₂ (Merck, > 90%) and MoO₂ (Merck > 99%) were dissolved in a concentrated nitric acid solution resulting in a transparent solution with continuous stirring at 80 °C for about 6 h. After total dissolution, citric acid, a complexing agent, and ethylene glycol, a polymerization agent, were added and then evaporated at 130 °C to produce a gel. The latter was dried at 150 °C to obtain a dark brown powder and then preheated at 300 °C to remove the remaining organic and decompose the nitrates of the gel. In order to get the PrNaMnMoO₆ sample, the resulting powder was calcined at 600 °C and then at 800 °C during 12 h with intermediate grinding. The sample was then pressed into pellets (of about 1 mm thickness) and sintered at 1000 °C for 24 h.

The phase identification and structural analysis were performed using a ‘‘PANalytical X'pert Pro’’ diffractometer with Cu-K_α radiation (λ = 1.5406Ǻ). The structural refinement was carried out by the Rietveld analysis of the X-ray powder diffraction data with the help of Fullproof software [21].

Permanganate back titration was used to determine the oxygen nonstoichiometry of calcined powders as described in [22]. Finely ground samples were obtained, and a small amount of each sample was quantitatively transferred into an Erlenmeyer flask. The samples were dissolved in 0.5 M H₂SO₄, and 0.1 M H₃PO₄, and 0.05 M Mohr's salt solution (Fe(NH₄)₂(SO₄)₂). The samples were completely dissolved after 24 h of mixing on a magnetic stirrer at room temperature. The sample solution was then titrated with a 0.02 M KMnO₄ solution that had previously been calibrated with a standard 0.05 M Mohr's salt solution.

A pellet of about 0.503 cm² surface and about 0.14 cm thickness was used for the electrical measurements. The pellet disc was coated with Ag paste to ensure good electrical contact. All electrical measurements of real and imaginary components of the impedance parameters (Z′ and Z″) were made over a wide range of temperature (409–457 K) and frequency (200–10⁶ Hz) using a TEGAM 3550 impedance analyzer interfaced to a compatible computer.

3 Results and Discussion

3.1 Powder X-ray Analysis

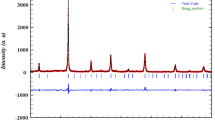
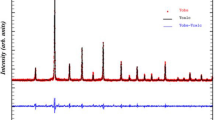
The X-ray diffraction study confirms that the compound PrNaMnMoO₆ is a single phase with no measurable impurity phases. The refinement of the XRD pattern with the Fullproof program (Fig. 1) shows that the sample is found to crystallize in the monoclinic structure with P2₁/n space group. The refined parameters of PrNaMnMoO₆ are listed in Table 1, whereas the important bond distances and bond angles associated with MnO₆, MoO₆ and PrO₁₂ and NaO₁₂ polyhedral are listed in Table 2.

Fig. 1

Powder X-ray diffraction pattern and Rietveld refinement for the sample PrNaMnMoO₆ (circle signs correspond to experimental data, and the calculated data are represented by the continuous line overlapping them: tick marks represent the positions of allowed reflection, and a difference curve on the same scale is plotted at the bottom of the pattern)

Table 1 Structural parameters obtained from the Rietveld refinement of the XRD pattern at room temperature of PrNaMnMoO₆ with P2₁/n space group

Table 2 Selected interatomic distances (Å) and selected bond angles (deg) of PrNaMnMoO₆

Further, the unit cell was drawn, and the interionic separations were determined using the visualization software ‘‘Vesta’’[23]. Figure 2 shows a representative crystal structure and the MnO₆/MoO₆ octahedron for the sample, which appears to be slightly distorted, in agreement with the previously reported results with his homologous powder Ca₂MnMoO₆ [24]. Due to the differences between the ionic radius of Pr³⁺ and Na⁺, MnO₆ and MoO₆ octahedra are forced to tilt in order to optimize the Pr–O and Na–O bond lengths. The tilting of the MnO₆ and NbO₆ octahedra leads to octahedral distortion as is evidenced from the tabulated bond lengths (Table 2).

Fig. 2

The crystal structure of PrNaMnMoO₆

3.2 IR Spectroscopy Investigation

The infrared (IR) spectra of PrNaMnMoO₆ are shown in Fig. 3. Usually, IR spectra of double perovskite oxides are characterized by the presence of two strong well-defined bands, because the spectroscopic behavior is dominated by the anti-symmetric stretching and deformational modes of the octahedral B′O₆ and B″O₆ blocks [21] of double perovskite oxide A₂B′B″O₆. From Fig. 3 it can be observed the two strongest bands characteristics for anti-symmetric (υ_as) octahedral MnO₆ (MoO₆) stretching vibration are in the range 900–776 cm⁻¹ and the octahedral MnO₆ (MoO₆) deformations vibration in the range 697–588 cm⁻¹, respectively. Similar spectral pattern with two strong and well-defined IR bands in the 588–900 cm⁻¹ region has been found in a number of Ba₂RESbO₆ perovskite-type materials [25,26,27].

Fig. 3

Infrared analysis spectrum of PrNaMnMoO₆

3.3 Electrical Properties

In order to characterize the microstructures and properties of electro-ceramics, different techniques are required that can probe or distinguish between the different regions of a ceramic. For instance, from a microscopic examination of ceramic texture, it is not usually possible to say whether the electrical properties of grain boundaries are likely to be similar to or significantly different from those of the individual grains. From an impedance/modulus spectroscopic plot in the former case, grains and grain boundaries can be distinguishable electrically. The value of presenting data as both M″ and Z″ spectroscopic plots is that they give different weightings to the data and, therefore, highlights different features of the sample. Figure 4 shows the temperature-dependent spectra (Nyquist plot) of material. By impedance spectrum we got the single semicircular arc in temperature range 409 K–457 K. The nature of variation of the arcs with temperature and frequency provides various clues of the materials. This single semicircular arc suggests the presence of grain interior (bulk) property of the material. As per the plots, the semicircles have their centers located slightly away from the real axis, which indicates departure from ideal Debye behaviour [28]. It is seen that the semicircular arcs are shifted toward the origin, indicating the increase in conductivity of all samples as the temperature increases. As temperature increases, the radius of the arc corresponding to bulk resistance of the material decreases, which indicates an activated conduction mechanism. An equivalent circuit is being used to provide a complete picture of the system and establish the structural property relationship of the materials. There is a comparison of complex impedance plots (symbols) with fitted data (lines) using Z View program. The results suggest that the non-Debye model is suitable for representing the samples and the impedance data are fitted by a parallel connection of an ohmic resistor R and a constant phase element (CPE) [29]. The experimental data show a depressed semicircle with the center below the real axis, which is the reason for using constant-phase elements CPE rather than ordinary capacitors in equivalent circuits. The CPE is used to describe (a) distribution of the value of some physical property of the system and (b) microscopic (non-Debye) process. The CPE is an empirical impedance function of the type:

$$Z_{CPE} = \left[ {Q(j\omega )^{\alpha } } \right]^{ - 1}$$

(1)

where Q indicates the value of the capacitance of the CPE element and α degree of deviation with respect to the pure capacitor.

Fig. 4

Complex impedance spectrum as a function of temperature with electrical equivalent circuit (inset), accompanied by theoretical data calculated with expressions (2) and (3)

The equivalent circuit modeling gives three parameters at each temperature: grain resistance, R_g, and two parameters (Q_g, α_g) for the CPE element. The extracted parameters for the circuit elements are summarized in Table 3. It is obvious all the capacitance values Q_g are in the range of pF. This implies that the single semicircle is from grain interiors [30].

Table 3 The extracted parameters for the circuit elements

The experimental data for the real and imaginary components of the whole impedance were calculated from the theoretical expression established with equivalent circuit:

$$Z^{\prime} = \frac{{R_{g}^{2} Q_{g} \omega \cos (\frac{{\alpha_{g} \pi }}{2}) + R_{g} }}{{\left( {R_{g} Q_{g} \omega^{{\alpha_{g} }} \cos (\frac{{\alpha_{g} \pi }}{2}} \right) + 1)^{2} + \left( {R_{g} Q_{g} \omega^{{\alpha_{g} }} \sin (\frac{{\alpha_{g} \pi }}{2}} \right))^{2} }}$$

(2)

$$- Z^{\prime\prime} = \frac{{R_{g}^{2} Q_{g} \omega \sin (\frac{{\alpha_{g} \pi }}{2}) + R_{g} }}{{\left( {R_{g} Q_{g} \omega^{{\alpha_{g} }} \cos (\frac{{\alpha_{g} \pi }}{2}} \right) + 1)^{2} + \left( {R_{g} Q_{g} \omega^{{\alpha_{g} }} \sin (\frac{{\alpha_{g} \pi }}{2}} \right))^{2} }}$$

(3)

The electrical impedance has been analyzed by plotting the real and imaginary part of impedance Z′ and Z″ versus frequency in a semi-log scale at different temperatures. This plot provides information on the dielectric processes taking place in the material.

Figure 5 shows the variation of Z′ as a function of frequency at different temperatures. The plots show a low-frequency dispersion followed by a plateau region, and finally all the curves merge/coalesce above 10⁵ Hz irrespective of temperature. Initial Z′ values decrease with frequency; this may be due to a slow dynamics relaxation process in the material probably due to space charges. At all temperatures, low frequency the appearance of plateau region may be related to frequency invariant (dc conductivity) electrical property of the material. The final merger of the pattern at higher frequency may be attributed to the release of space charge as a result of reduction in the barrier properties of material with the rise in temperature and may be a responsible factor for the enhancement of AC conductivity of material with temperature at higher frequencies [31].

Fig. 5

The real part of the impedance as a function of angular frequency at several temperatures

Figure 6 shows the frequency-temperature dependence of Z″. One peak at ω_max is observed in Z″ versus frequency which is shifted to higher frequency with increasing temperature, indicating the existence of relaxation processes in the system, while its broadening on increasing temperature suggests that those relaxation processes are temperature-dependent. This may be due to the immobile species/electrons at low temperatures and defect/vacancies at high temperatures. Further, the magnitude of Z″ decreases with the shift of peaks toward higher-frequency side. Finally, all the curves merge in the high-frequency region, which may be due to the accumulation of space charge of the material [32].

Fig. 6

The imaginary part of the impedance as a function of angular frequency at several temperatures

3.4 Conductivity Analysis

• DC Conductivity

As regards the bulk ohmic resistance values of the sample and electrode dimensions (S is the area of the sample and e is the sample thickness), they can be determined from the intercept Z₀ of the semicircle, at low frequency, with the real axe (Z′) [33]. The conductivity σ is obtained from Z₀ by means of the relation: σ_dc = e/RS, where e/S represents the geometrical ratio sample.

$$\sigma_{dc} = \frac{e}{S*R}$$

(4)

Electrical conductivity (σ_dc) is a thermally activated process and follows the Arrhenius law:

$$\sigma_{dc} T = A\exp (\frac{{ - E_{a} }}{{K_{B} T}})$$

(5)

where A is the pre-exponential factor, E_a the activation energy, T the absolute temperature and K_B the Boltzmann constant.

The activation energy for conduction (E_a) of grains could be calculated from the slope of the straight line obtained from log σ_dc versus 1/T plot. Figure 7 shows the Arrhenius plot of the dc conductivity evaluated from the impedance plots of PrNaMnMoO₆ sample. The activation energy was found to be 0.32(3) eV.

• AC Conductivity

Fig. 7

Dependence of Ln (σ_dc T) on temperature for PrNaMnMoO₆

The variation of alternating current (AC) conductivity as a function of frequency at different temperatures for the PrNaMnMoO₆ is shown in Fig. 8. The plot exhibits two different regions associated with different phenomena (i) an independent plateau region at low-frequency region corresponding to dc conductivity and (ii) a frequency dispersion region at higher frequencies. It is clearly seen that the frequency at which the dispersion becomes predominant shifts toward a higher-frequency region as the temperature increases [34]. To account for the high-frequency dispersion, the conductivity spectra can be modeled by the form predicted by Jonscher’s (1977) universal law:

$$\sigma_{ac} \left( \omega \right) = \sigma_{dc} + A\left( T \right)\omega^{s\left( T \right)}$$

(6)

Fig. 8

Frequency dependence of AC conductivity at various temperatures of PrNaMnMoO₆

According to Jonscher (1977), the origin of the frequency dependence of conductivity lies in the relaxation phenomena arising due to mobile charge carriers. When mobile charge carriers hop to a new site from its original position, it remains in a state of displacement between two potential energy minima, which includes contributions from other mobile defects. After a sufficiently long time, the defect could relax until the two minima in lattice potential energy coincide with the lattice site. Also, the conduction behavior of the materials obeys the power law σ (ω) α ω^s with a slope change governed by s in the low-temperature region. The solid lines are the fitted curves to the experimental AC conductivity data at different temperatures, and the goodness of the fitting is satisfactory. The frequency exponent s is found to decrease slightly with increasing temperature (Fig. 9). The study of the temperature dependence of s is very useful for determining the conduction mechanism in different materials. Various theoretical models for AC conductivity have been predicted to explain the temperature dependence of s. The ionic tunneling model suggests that s does not depend on temperature but depends on frequency. In the case of small polaron tunneling, s increases, whereas for the large polaron tunneling process, s decreases up to a certain temperature and then increases with a further increase of temperature [35,36,37,38,39]. As shown in Fig. 9, the appropriate theoretical model can be explained in terms of correlated barrier hopping model (CBH). In this model, the charge carriers hop between the sites over a potential barrier separating them. The binding energy has been calculated according to the following equation:

$$1 - s = \beta = \frac{{6K_{B} T}}{{W_{m} }}$$

(7)

W_m is the binding energy, which is defined as the energy required to remove an ion completely from one site to another site. The characteristic decrease in slope with the rise in temperature is due to the decrease in binding energy as illustrated in Fig. 9.

Fig. 9

Temperature dependence slope s and binding energy (W_m) for PrNaMnMoO₆

3.5 Modulus Analysis

The electrical response of PrNaMnMoO₆ has also been analyzed using the complex electrical modulus formalism. The modulus analysis has the advantage that it suppresses the information about electrode effects. This can also be used to study conductivity relaxation times. This method is useful for elucidating the relaxation mechanisms in a material having different magnitudes of resistance and/or capacitance. The complex modulus is defined as the inverse of the complex permittivity, and in the present work, the impedance data were converted into electrical modulus using the relations M′ (real part) = ωC₀Z'' and M″ (imaginary part) = ωC₀Z′, where C₀ = ε₀A/L, A is the area of the sample, L is the thickness of the sample and ε₀ = 8.854 × 10^–14 F/cm is the permittivity of the free space.

Figure 10a, b shows the variation of real and imaginary part of the electric modulus as a function of frequency at different temperatures, respectively. At lower frequencies, M' tends to be very small, confirming that the contribution from the electrode effect is negligible and hence can be ignored when the data are analyzed in the modulus formalism. The observed dispersion in M′ at higher frequencies may be due to conductivity relaxation. The M″ versus log ω plot shows broad and asymmetric peaks compared to the peak predicted for ideal Debye type. The asymmetric nature of M″ plot is suggestive of stretched exponential character of relaxation times of the material. The asymmetric broadening of the peak indicates the spread of relaxation with different time constant, and relaxation in the material is of non-Debye type.

Fig. 10

a Frequency dependence of the real part of electric modulus at different temperatures. b: Frequency dependence of the imaginary part of electric modulus at different temperatures, the solid lines are the theoretical fits

The imaginary part of the M″ (ω) has been approximated as [40, 41]:

$$M^{\prime \prime } \left( \omega \right) = \frac{{M_{\max }^{\prime \prime } }}{{\left( {1 - \beta } \right) + \left( {\beta /\left( {1 + \beta } \right)} \right)\left[ {\beta (\omega \beta \max_{\max } } \right]}}$$

(8)

where M″_max is the peak maximum of the imaginary part of the modulus and ω_max = 1/| is the peak frequency of the imaginary part of the modulus. The imaginary parts of electric modulus for different temperatures were fitted to Eq. (7), and the parameters M ^″_max , ω_max, and β were extracted from the analysis. Such fits at different temperatures are shown in Fig. 10b.

The frequency region below peak maximum M″ determines the range in which charge carriers are mobile on long distances. At frequency above peak maximum M″, the carriers are confined to potential wells, being mobile on short distances. The position of the peak M″_max shifts to higher frequencies as the temperature is increased.

Each peak attains a maximum value M″_max at frequency ω_max called conductivity relaxation frequency. The most probable relaxation time follows the Arrhenius law, given by:

$$\omega_{m} = \omega_{0} \exp \left(\frac{{ - E_{a} }}{{\kappa_{B} T}}\right)$$

(9)

where ω_o is the pre-exponential factor and E_⌉ is the activation energy. Figure 11 shows the plot of peak frequency (ω_max) versus 1000/T, and the activation energy is 0.29(1) eV.

Fig. 11

Dependence of Ln (ω_max) on temperature for PrNaMnMoO₆

3.6 Dielectric Study

In order to examine the effect of space charge polarization in low-frequency range and at high temperatures, we have plotted the imaginary part of dielectric constant ε′′ with frequency at different temperatures as shown in Fig. 12.

Fig. 12

Frequency dependence of the imaginary part ε″ of the permittivity for the PrNaMnMoO₆ compound at several temperatures

The measured impedance data are used to calculate the imaginary (ε″) parts of the complex dielectric permittivity as: ε^* = 1/ j⌉C₀Z^*⁄ where Z^* is the complex impedance, C₀ = ε₀S/e, S and e are the area and the thickness of the sample, respectively, and ε₀ is the permittivity of the vacuum. The expression of the imaginary part (ε″) of the dielectric permittivity is:

$$\varepsilon^{\prime\prime}\left( \omega \right) = \frac{{\left( {\varepsilon_{s} - \varepsilon_{\infty } } \right)(\frac{\omega }{{\omega_{1} }})^{1 - \alpha } \sin \left( {\frac{{\left( {1 - \alpha } \right)\pi }}{2}} \right)}}{{1 + 2(\frac{\omega }{{\omega_{1} }})^{1 - \alpha } \cos \left( {\frac{{\left( {1 - \alpha } \right)\pi }}{2}} \right) + (\frac{\omega }{{\omega_{1} }})^{{2\left( {1 - \alpha } \right)}} }} + \frac{{\sigma_{0} }}{{\varepsilon_{0} \omega }}$$

(10)

The first part in Eq. (10) is related to thermal polarization and the second one to electrical conductivity. Besides, the angular frequency dependence plots of the imaginary part of complex dielectric permittivity (ε″) at several temperatures are represented from fitting Eq. (10). There is a sharp decrease in the value of ε″ in the lower-frequency region and showing a frequency independent value of these parameters in the high-frequency region. The strong decrease of the imaginary part of dielectric constant toward low-frequency range may be due to space charge polarization and interface effect. The variation of ε″ with at different frequency is depicted in Fig. 13. Indeed, ε″ increases with the temperature. This phenomena may be due to the polarization [42]. Basically, with increasing temperature, the change in dielectric constant comes from the change in orientation polarization, as dipoles get more energy to orient with increasing temperature. Therefore, the dielectric constant increases with increasing temperature. Around the curie temperature, when the dielectric goes through a transition, the dipoles get their maximum energy to reorient and thus the maximum dielectric constant.

Fig. 13

Logarithm of ω versus tan ^TM at different temperatures for PrNaMnMoO₆

Figure 14 shows the plot between log ω and tanδ. It is clear that the loss decreases rapidly in the low-frequency region, while the rate of decrease is slow in the high-frequency region and it shows an almost frequency independent behavior in the high-frequency region. The behavior can be explained on the basis that in the low-frequency region, which corresponds to a high resistivity (due to the grain boundary), may be due to the presence of all the four polarizations, namely space charge, orientational, electronic, and ionic polarization. In the high-frequency region, which corresponds to a low resistivity (due to the grains), their low values might be due to the loss of importance of these polarizations [43].

Fig. 14

Plot between log ω and tanδ

3.7 Conclusion

The PrNaMnMoO₆ synthesized by sol–gel reaction technique is investigated using the impedance spectroscopy technique in the temperature range 409–457 K. The Cole–Cole plots exhibit depressed semicircles, which reflect the non-Debye behavior of the material. The relaxation mechanisms were fitted with a (R//CPE) equivalent circuit using a complex nonlinear least squares algorithm. The dc conductivity (σ_dc) follows the Arrhenius law with activation energy 0.32(3) eV. The electrical modulus spectra show the trend of ionic conductivity and are analyzed by Bergman’s equation, a modified KWW model. The AC conductivity is found to obey the universal power law. The CBH model was found to explain the mechanism of charge transport in PrNaMnMoO₆. The hopping frequency was determined and the activation energy of hopping is almost near to the activation energy of conduction. The variation of the dielectric constant with frequency is attributed to ion diffusion and polarization occurring in the sample. The tan (^TM) dependence on frequency is typically associated with losses by conduction in the sample.