Magneto-Oscillations and Anomalous Current States in a Photoexcited Electron Gas on Liquid Helium

Abstract

The paper reviews a novel class of phenomena observed recently in the two-dimensional (2D) electron system formed on the free surface of liquid helium in the presence of a magnetic field directed normally and exposed to microwave radiation. The distinctive feature of these nonequilibrium phenomena is magnetoconductivity oscillations induced by inter-subband (out-of-plane) and intra-subband (in-plane) microwave excitations. The conductivity magneto-oscillations induced by intra-subband excitation are similar to remarkable microwave-induced resistance oscillations (MIRO) reported for semiconductor heterostructures. Investigations of microwave-induced conductivity oscillations on liquid helium helped with understanding of the origin of MIRO. Much stronger microwave-induced conductivity oscillations were observed and well described theoretically for resonant inter-subband microwave excitation. At strong powers, such excitation leads to zero-resistance states, the in-plane redistribution of electrons, self-generated audio-frequency oscillations, and incompressible states. These phenomena are caused by unusual current states of the 2D electron system formed under resonant microwave excitation.

1 Introduction

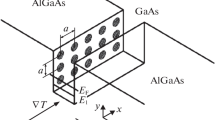
A two-dimensional (2D) electron gas on the free surface of liquid helium is formed by a one-dimensional (1D) potential well $V\left( z\right)$ created by a weak polarization attraction of an electron to the liquid medium and by a strong repulsion barrier $V_{0}\simeq 1\,\mathrm {eV}$ at the interface [1, 2]. In an experiment with surface electrons (SE), a pressing electric field $E_{\bot }$ is usually applied perpendicularly to the surface, which gives a correction $eE_{\bot }z$ to $V\left( z\right)$. If the source of electrons is not switched off, the equilibrium surface density of electrons $n_{e}$ is proportional to the pressing field: $n_{e}=E_{\bot }/2\pi e$. At this condition, the electric field of an electron layer $2\pi en_{e}$ compensates for the external field $E_{\bot }$ at large heights above the layer: $z\gg 1/\sqrt{n_{e}}$. For bulk liquid helium, the electron density is limited [3, 4] by a critical value $n_{c}\simeq 2\times 10^{9}\,\mathrm {cm}^{-2}$. Employing helium films allows obtaining substantially larger electron densities [5]. Still for nonequilibrium phenomena considered in this review, electron densities usually are much smaller than $n_{c}$.

In the limit of weak fields ($E_{\bot }\rightarrow 0$), the energy spectrum of an electron in the 1D potential well $\varDelta _{l}$ is similar to the spectrum of a hydrogen atom (the Rydberg states), $\varDelta _{l}=-\varDelta /l^{2}$, where $l=1,2,\ldots$ is the quantum number describing a surface electron level. The characteristic energy $\varDelta$ depends on the dielectric constant of liquid helium $\epsilon$ as

$$\begin{aligned} \varDelta =\frac{m_{e}\varLambda ^{2}}{2\hbar ^{2}}, \,\,\, \varLambda =\frac{ e^{2}\left( \epsilon -1\right) }{4\left( \epsilon +1\right) }, \end{aligned}$$

(1)

where $m_{e}$ and $-\,e$ are the free electron mass and charge, respectively. For liquid $^{4}\mathrm {He}$, $\varDelta \simeq 7.64\,\mathrm {K}$, and the average height $\left\langle 1\right| z\left| 1\right\rangle \simeq 114\,\mathrm {\mathring{A}}$. In the case of liquid $^{3}\mathrm {He}$, we have $\varDelta \simeq 4.3\,\mathrm {K}$ and $\left\langle 1\right| z\left| 1\right\rangle \simeq 152\,\mathrm {\mathring{A}}$. The pressing electric field $E_{\bot }$ increases the excitation energies $\varDelta _{l^{\prime },l}=\varDelta _{l^{\prime }}-\varDelta _{l}$ which allows to tune the electron system to the resonance with the microwave field. By analogy with semiconductor electron systems, electron states belonging to a certain surface level (l) are usually called “surface subband”.

Above the Wigner solid transition, the in-plane states of SE are well described by the 2D wave functions of free electrons and by the usual energy spectrum. In the presence of a magnetic field directed perpendicular to the interface, the in-plane electron states are squeezed into a set of Landau levels: $\varepsilon _{n}=\hbar \omega _{c}\left( n+1/2\right)$, where $n=0,1,2,\ldots$ , and $\omega _{c}=eB/cm_{e}$ is the cyclotron frequency. In this case, surface electrons on liquid helium represent a singular system of free particles with a purely discrete spectrum if interactions can be neglected. Electron scattering by helium vapor atoms and capillary waves (ripplons) leads to the collision broadening $\varGamma _{n}$ of the density of states function which is usually described by a set of Gaussian functions.

Generally, the 2D electron system formed on liquid helium is similar to 2D electron systems created in semiconductor devices [6] such as the metal-oxide-semiconductor field-effect transistor or GaAs/AlGaAs heterostructures. The broad study of the 2D electron gas in semiconductor devices revealed a number of fundamental discoveries, of which the most known example is the quantum Hall effect [7, 8]. There are definite differences between SE on helium and a 2D electron gas in semiconductors. The most important one is that the effective mass of SE, which is very close to the free electron mass $m_{e}$, is much larger than the effective mass of electrons in semiconductor devices ($m_{e}\gg m_{e}^{*}$). This means that, for actual electron densities, SE on liquid helium represent a nondegenerate 2D electron gas with a strong Coulomb interaction between electrons. Therefore, some well-known quantum effects, such as Shubnikov-de Haas oscillations, are impossible for SE on liquid helium. Moreover, strong electron–electron correlations and the Wigner solid transition [9] additionally suppress the quantum Hall effect (for a review, see [10]). On the other hand, SE levitate above a very clean surface of liquid helium with no impurities and defects. The only scatterers available are helium vapor atoms and capillary wave excitations (ripplons) whose densities decrease with temperature. At typical helium temperatures ($T<0.5\,\mathrm {K}$), electrons have very high mobility and well-defined Landau levels with an extremely small collision broadening: $\varGamma _{n}\ll T$. Therefore, SE on liquid helium represent a remarkable model system for studying quantum magnetotransport phenomena [11,12,13], and this system is complementary to the 2D electron systems in semiconductor devices.

At the beginning of this century, magnetotransport studies of a 2D electron gas in high-mobility GaAs/AlGaAs heterostructures subjected to a DC magnetic field and to strong microwave (MW) radiation led to an unexpected discovery: MW-induced resistance oscillations (MIRO) [14, 15]. The period of these oscillations is controlled only by the ratio of the microwave frequency $\omega$ to the cyclotron frequency $\omega _{c}$, and, therefore, they potentially can be expected in a nondegenerate 2D electron gas as well. At high radiation power, the minima of the oscillations evolve into zero-resistance states (ZRS) [16, 17]. Positions of the resistance minima reported [16] obey a universal law: $\omega /\omega _{c}=m+1/4$ (here $m=1,2,\ldots$). Special interest in ZRS observed is provoked by their plausible relationship with the concept of absolute negative conductivity [18] associated with photon-assisted scattering of electrons off impurities [19,20,21,22,23]. These discoveries have opened a new research area and triggered a large body of theoretical works (for a review, see [24]). The effect of MIRO was observed also in hole systems [25] and in MgZnO/ZnO heterostructures [26].

Similar MW-induced conductivity oscillations (MICO) and ZRS were discovered in the 2D electron gas on liquid helium [27, 28]. For SE on liquid helium, we use the abbreviation MICO instead of MIRO because in experiments the electron conductivity $\sigma _{xx}$ was actually measured using the Corbino setup. The important difference of these oscillations, as compared to the MIRO in semiconductor devices, is that they arise only when the excitation energy $\varDelta _{2,1}=\varDelta _{2}-\varDelta _{1}\equiv \hbar \omega _{2,1}$ is tuned to the resonance with the MW field ($\varDelta _{2,1}=\hbar \omega$) using the linear Stark effect for the 1D potential well $V\left( z\right)$ as illustrated in Fig. 1. Typical magnetoconductivity ($\sigma _{xx}$) oscillations of SE induced by the resonant MW excitation are shown in Fig. 2 for two values of excitation power. The absence of MICO for $\omega$ values slightly different from the condition $\hbar \omega =\varDelta _{2,1}$ means that the period of these oscillations is actually controlled by the ratio $\varDelta _{2,1}/\hbar \omega _{c}$ and the inter-subband (out-of-plane) excitation of SE is crucial for understanding the origin of these oscillations. Since the mechanisms proposed for explanation of the MIRO in semiconductors assume a pure intra-subband MW excitation, the MICO reported for SE on liquid helium [27, 28] must have a different origin. This conclusion is confirmed also by a noticeable increase in the amplitude of MICO with the ratio $\omega /\omega _{c}$ at $m\le 7$, which is opposite to the observation reported for semiconductor heterostructures. The explanation of remarkable features of MICO observed on liquid helium is given by the theory [29,30,31] based on a nonequilibrium population of the first excited surface subband which leads to sign-changing terms in the electron magnetoconductivity and even to absolute negative conductivity ($\sigma _{xx}<0$) at high radiation power.

Fig. 1

Schematic view of inter-subband resonant excitation of SE on liquid helium (Color figure online)

Fig. 2

Oscillations of $\sigma _{xx}$ induced by resonant MW excitation obtained [28] for $T=0.2\,\mathrm {K}$, $n_{e}=0.9\times 10^{6}\,\mathrm {cm}^{-2}$, and two MW powers (Color figure online)

Experimental investigations of MICO induced by inter-subband MW excitation revealed a number of new phenomena: the resonant photovoltaic effect and spatial redistribution of electrons [32], self-generated audio-frequency oscillations [33], and an incompressible state [34]. All these effects occur near the experimental condition $\sigma _{xx}\rightarrow 0$ which allows assuming that the instability of the spatially uniform distribution of SE is caused by absolute negative conductivity. Moreover, the self-generation of audio-frequency current oscillations at an electrode indicates that initially the damping of these oscillations is negative which also agrees with the concept of negative conductivity. A plausible explanation of these novel observations is based on the Coulombic effect on the stability range of the photoexcited electron gas which favors formation of domains of different densities [35]. Domains appear to eliminate or greatly reduce regions with negative conductivity.

The mechanisms of MIRO based on photon-assisted scattering of electrons [19, 20, 22] and reported for a degenerate 2D electron gas in semiconductors can also be applied to SE on liquid helium [36]. In this case, the probability of the intra-subband photon-assisted scattering is proportional to $E_{\mathrm {mw}}^{2}/m_{e}^{2}$, where $E_{ \mathrm {mw}}$ is the amplitude of the MW field. Therefore, in order to obtain the same amplitude of MIRO, the microwave field should be $m_{e}/m_{e}^{*}$ times larger than in semiconductor systems. Taking into account that $m_{e}^{*}\simeq 0.06\,m_{e}$, it was estimated that $E_{ \mathrm {mw}}$ should be about $10\,\mathrm {V/cm}$ to induce a substantial amplitude of oscillations. In a recent experiment [37], employing a semiconfocal Fabry–Perot resonator, the in-plane electric field $E_{\mathrm {mw}}$ of necessary amplitude was created in the layer of SE, and MW-induced DC magnetoconductivity oscillations governed by the ratio $\omega /\omega _{c}$ (analogous to MIRO in GaAs/AlGaAs heterostructures) were observed. This observation proved the universality of the effect of MIRO and gave rise to hopes that additional investigations of MICO in the system of SE on helium will help with identification of its origin. By present time, these hopes were justified at least partly by a discovery of a strong dependence of MICO on the MW circular polarization direction [38]. This discovery allowed reporting the first observation of the effect of radiation helicity, which provides crucial information for understanding the origin of intra-subband MICO in a 2D electron gas. In particular, these experiments unambiguously support theoretical mechanisms of MICO based on photon-assisted scattering off disorder.

The advances in experimental and theoretical investigations of nonequilibrium phenomena in the 2D electron gas on liquid helium induced by MW radiation have motivated us to write this review.

2 Mechanisms of MICO and Negative Conductivity

As noted above, for SE on liquid helium, MICO was initially observed for resonant inter-subband excitation as indicated in Fig. 1. Nevertheless, it is instructive to begin discussions of theoretical mechanisms of MICO with intra-subband models, assuming that all the SE occupy the ground surface subband.

2.1 Intra-subband Models

It is very surprising that by now there is a great body of different theoretical mechanisms explaining MIRO in semiconductor devices which use quantum and classical effects (see the review [24]), but the origin of these oscillations is still under debate. Among these theories, there is a large group of models whose description is based on the concept of the photon-assisted scattering off disorder which overcomes the selection rules existing for direct photon-induced transitions (direct transitions can be only between adjacent Landau levels).

2.1.1 Displacement Model

Magneto-oscillations and absolute negative conductivity induced by MW radiation in thin semiconductor films in transverse magnetic fields were predicted by Ryzhii [19] already in 1969. The physics of this effect is quite simple. In the presence of a driving DC electric field $\mathbf {E}_{\Vert }$ directed along the x-axis, the Landau spectrum acquires a correction depending on the center coordinate of the cyclotron motion (X):

$$\begin{aligned} \varepsilon _{n,X}=\hbar \omega _{c}\left( n+1/2\right) +eE_{\Vert }X . \end{aligned}$$

(2)

For an elastic scattering off disorder $n,X\rightarrow n^{\prime },X^{\prime }$ accompanied by absorption of a photon, the energy conservation yields

$$\begin{aligned} \hbar \omega _{c}\left( n^{\prime }-n\right) +eE_{\Vert }\left( X^{\prime }-X\right) -\hbar \omega =0. \end{aligned}$$

(3)

Using the notation $n^{\prime }-n=m>0$, one can represent this equation in the following form:

$$\begin{aligned} X^{\prime }-X=\frac{\hbar \omega _{c}}{eE_{\Vert }}\left( \frac{\omega }{ \omega _{c}}-m\right) . \end{aligned}$$

(4)

This simple relationship indicates that $X^{\prime }-X$ (the direction of scattering) changes its sign when the ratio $\omega /\omega _{c}$ passes an integer $m=1,2,\ldots$ . For example, at $\omega /\omega _{c}>m$, the difference $X^{\prime }-X>0$ which means that an electron is scattered in the direction opposite to the direction of the driving force $-e\mathbf {E}_{\Vert }$. Actually, this is a qualitative explanation of the origin of absolute negative conductivity.

The relationship of Eq. (4) is just a form of the energy conservation in a scattering event which is not convenient for the analysis of the limiting case $E_{\Vert }\rightarrow 0$. Nevertheless, the factor $(\omega /\omega _{c} -m)$ entering its right side remarkably appears in an accurate conductivity treatment. In the magnetoconductivity treatment discussed below, one has to take into account also the momentum conservation restricting $X'-X$ and the collision broadening of Landau levels restricting the factor $(\omega /\omega _{c} -m)$ and selecting the number m responsible for the major contribution to $\sigma _{xx}$ at a given magnetic field. More specifically, the left side of Eq. (3) represents the argument of the delta function describing the probability of scattering, and the latter is expanded in $eE_{\Vert }\left( X^{\prime }-X\right)$ to obtain the linear conductivity $\sigma _{xx}$.

Equation (4) explains why this mechanism of MIRO is called “displacement model”. For semiconductor heterostructures, it was developed in many works [20, 21, 39] (more references can be found in the review [24]). For SE on liquid helium, this model was extended [36, 40] to include strong Coulomb interaction between electrons. Considering the MW electric field as a classical field $\mathbf {E}_{\mathrm {mw}}\left( t\right)$, it is possible to show [40] that the contribution from photon emission processes contains an additional exponential factor $\exp \left( -\hbar \omega /T\right)$ which allows neglecting these processes at low temperatures.

Equations describing MICO can be found in a quite simple way by introducing the in-plane momentum exchange $\hbar \mathbf {q}$ at a collision. Indeed, $\sigma _{xx}$ can be calculated using clear relationships for the current

$$\begin{aligned} j_{x}=-en_{e}\sum _{\mathbf {q}}\left( X^{\prime }-X\right) _{\mathbf {q}}\bar{w }_{\mathbf {q}}\left( V_{\mathrm {H}}\right) =-en_{e}\ell _{B}^{2}\sum _{ \mathbf {q}}q_{y}\bar{w}_{\mathbf {q}}\left( V_{\mathrm {H}}\right) , \end{aligned}$$

(5)

where $\ell _{B}=\left( \hbar c/eB\right) ^{1/2}$ is the magnetic length, $\bar{w}_{\mathbf {q}}\left( V_{\mathrm {H}}\right)$ is the average probability of electron scattering with the momentum exchange $\hbar \mathbf { q}$ which is a function of the Hall velocity $V_{\mathrm {H}}=cE_{\Vert }/B$. In Eq. (5), we have used the usual momentum conservation equation $X^{\prime }-X=q_{y}\ell _{B}^{2}$ which follows from matrix elements of the operator $e^{-i\mathbf {q}\cdot \mathbf {r}}$ calculated for the Landau states (free electron states $\mathbf {k}^{\prime }$ and $\mathbf {k}$ obviously give $\mathbf {k}^{\prime }-\mathbf {k}=\mathbf {q}$). This equation defines also the dependence $\bar{w} _{\mathbf {q}}\left( V_{\mathrm {H}}\right)$, because the energy conservation delta function contains $eE_{\Vert }\left( X^{\prime }-X\right) =\hbar q_{y}V_{\mathrm {H}}$. It is instructive to note that the energy exchange $\hbar q_{y}V_{\mathrm {H}}$ appears also for quasi-elastic scattering in the moving reference frame [13] where $E^{\prime }_{\Vert } =0$. Equation (5) yields

$$\begin{aligned} \sigma _{xx}\simeq \frac{e^{2}n_{e}\nu _{\mathrm {eff}}}{m_{e}\omega _{c}^{2}} ,\,\,\,\,\,\, \nu _{\mathrm {eff}}=-\frac{1}{m_{e}V_{\mathrm {H}}}\sum _{\mathbf {q} }\hbar q_{y}\bar{w}_{\mathbf {q}}\left( V_{\mathrm {H}}\right) . \end{aligned}$$

(6)

Expanding $\bar{w}_{\mathbf {q}}\left( V_{\mathrm {H}}\right)$ in $V_{\mathrm { H}}$, one can obtain the linear DC magnetoconductivity. Usually, this procedure leads to the additional $q_{y}=\left( X^{\prime }-X\right) /\ell _{B}^{2}$ in the integrand of Eq. (6), and we have $q_{y}^{2}$ independent of the sign of $X^{\prime }-X$. Therefore, the appearance of sign-changing terms in the expressions for $\nu _{\mathrm {eff}}$ and $\sigma _{xx}$ is not that trivial as it might be concluded from Eq. (4). Actually, these terms appear because the probability of scattering $\bar{w}_{\mathbf {q}}$ as a function of the energy exchange has maxima at Landau excitation energies $m\hbar \omega _{c}$, and the derivative of $\bar{w}_{\mathbf {q}}$ near the maxima yields the necessary terms.

The most difficult part of the description of the displacement model is to obtain $\bar{w}_{\mathbf {q}}\left( V_{\mathrm {H}}\right)$ for the photon-assisted scattering. The Hamiltonian of the electron–ripplon interaction, which dominates at low temperatures, can be written in the form similar to that of the electron–phonon interaction

$$\begin{aligned} V_{\mathrm {e-r}}=\frac{1}{\sqrt{S_{A}}}\sum _{\mathbf {q}}U_{q}Q_{q}\left( b_{- \mathbf {q}}+b_{\mathbf {q}}^{\dag }\right) e^{-i\mathbf {q}\cdot \mathbf {r}}, \end{aligned}$$

(7)

where $S_{A}$ is the surface area (in the following, it will be set to unity), $\mathbf {r}$ is a 2D in-plane radius vector of an electron, $b_{\mathbf {q}}^{\dag }$ and $b_{\mathbf {q}}$ are creation and distraction operators of ripplons, $U_{q}$ is the electron–ripplon coupling [41], $Q_{q}^{2}=\hbar q/2\rho \omega _{r,q}$, $\omega _{r,q}\simeq \sqrt{\alpha /\rho }q^{3/2}$ is the ripplon spectrum and $\alpha$ and $\rho$ are the surface tension and mass density of liquid helium, respectively. The electron–ripplon coupling contains the contribution from polarization interaction with liquid helium and the pressing field term ($eE_{\bot }$).

There are two ways of finding scattering probabilities for the photon-assisted scattering. In the pure quantum approach, the electron–photon interaction $V_{\mathrm {e-p}}$ is proportional to the vector potential of the MW field $\mathbf {A}_{\mathrm {mw}}$ expressed in terms of creation and destruction operators of photons. Then, probabilities of the photon-assisted scattering are calculated [36] according to the Golden Rule with matrix elements $\left\langle f\right| \tilde{V}\left| i\right\rangle$ containing products of matrix elements of $V_{\mathrm {e-r}}$ and $V_{\mathrm {e-p}}$. Still, there is a more elegant and nonperturbative way using the Landau-Floquet states (for examples, see Refs. [40, 42]; the method is based on the early work of Husimi [43]). In this case, the interaction with the MW field is described using the classical correction to the Hamiltonian: $eE_{\mathrm {mw}}^{\left( x\right) }\left( t\right) x+eE_{ \mathrm {mw}}^{\left( y\right) }\left( t\right) y$. Then, using the Landau gauge for the vector potential of the magnetic field B, one can find the Landau-Floquet eigenfunctions $\psi _{n,X}^{\left( \mathrm {F}\right) }\propto \varphi _{n}\left( x-X-\xi ,t\right)$ containing some time-dependent parameters [like $\xi \left( t\right)$] and factors chosen to reduce $\varphi _{n}\left( x,t\right)$ to the usual oscillator eigenfunction. The important point is that n and X remain good quantum numbers so that we can use Eqs. (5) and (6) for obtaining $\sigma _{xx}$. Still, the additional time-dependent parameters and factors of $\psi _{n,X}^{\left( \mathrm {F}\right) }$ affect the matrix elements of $V_{\mathrm {e-r}}$ and the energy conservation delta function.

It is useful to specify the dependence $\mathbf {E}_{\mathrm {mw}}\left( t\right)$ as

$$\begin{aligned} E_{\mathrm {mw}}^{\left( x\right) }=aE_{0}\cos \omega t, \,\, E_{ \mathrm {mw}}^{\left( y\right) }=bE_{0}\sin \omega t, \end{aligned}$$

(8)

where $E_{0}$ is the amplitude parameter of the MW field and, generally, a and b are arbitrary parameters. For particular cases, we assume that a can be 0 or 1,  and b can be 0 or $\pm 1$. Thus, we can describe two linear polarizations [parallel ($a=1$, $b=0$) and perpendicular ($a=0$, $b=1$ ) to the DC electric field] and two circular polarizations ($a=1$, $b=\pm 1$ ). Respectively, we define the polarization index $p=\Vert ,\bot ,+,-$ , where the first two symbols ($\Vert$ and $\bot$) correspond to linear polarizations, and the last two symbols ($+$ and −) correspond to circular polarizations.

Scattering probabilities depend on the matrix elements $\left( e^{-i\mathbf {q }\cdot \mathbf {r}}\right) _{n^{\prime },X^{\prime },n,X}^{\left( \mathrm {F} \right) }$ calculated for the Landau-Floquet states which have an additional factor

$$\begin{aligned} \exp \left[ -i\beta _{p,\mathbf {q}}\sin \left( \omega t+\gamma \right) \right] \end{aligned}$$

(9)

as compared to the usual matrix elements $\delta _{X,X^{\prime }-\ell _{B}^{2}q_{y}}\left( e^{-iq_{x}x}\right) _{n^{\prime },X^{\prime };n,X}^{\left( \mathrm {L}\right) }$ obtained in the absence of the MW field. Here, the parameter $\beta _{p,\mathbf {q}}$ depends strongly on the MW polarization

$$\begin{aligned} \beta _{p,\mathbf {q}}=\frac{\lambda \omega _{c}\ell _{B}}{\left( \omega ^{2}-\omega _{c}^{2}\right) }\sqrt{q_{y}^{2}\left( a\omega _{c}+b\omega \right) ^{2}+q_{x}^{2}\left( a\omega +b\omega _{c}\right) ^{2}}, \end{aligned}$$

(10)

$\lambda =eE_{0}l_{B}/\hbar \omega$ describes the strength of the MW field, and the phase shift $\gamma$ is unimportant for the following. It should be emphasized that, in the presence of MW radiation, we still have the momentum conservation rule $X^{\prime }-X=q_{y}\ell _{B}^{2}$ used in Eq. (5). By means of the Jacobi–Anger expansion $e^{iz\sin \phi }=\sum _{k}J_{k}\left( z\right) e^{ik\phi }$ [here $J_{k}\left( z\right)$ is the Bessel function], one can find that scattering probabilities are proportional to the sum of delta functions [40]

$$\begin{aligned} w_{\mathbf {q};n,X\rightarrow n^{\prime },X^{\prime }}^{\left( \pm \right) }= & {} \frac{2\pi }{\hbar }\left| C_{\mathbf {q}}^{\left( \pm \right) }\right| ^{2}I_{n,n^{\prime }}^{2}\left( x_{q}\right) \delta _{X,X^{\prime }-l_{B}^{2}q_{y}} \nonumber \\&\quad \times \sum _{k=-\infty }^{\infty }J_{k}^{2}\left( \beta _{p,\mathbf {q} }\right) \delta \left( \varepsilon _{n^{\prime },X^{\prime }}-\varepsilon _{n,X}-k\hbar \omega \pm \hbar \omega _{r,q}\right) , \end{aligned}$$

(11)

representing the processes of absorption or emission of $\left| k\right|$ photons along with absorption or emission of a ripplon. Here, $x_{q}=q^{2}\ell _{B}^{2}/2$ is a dimensionless variable, $C_{\mathbf {q} }^{\left( \pm \right) }=\left( U_{q}\right) _{1,1}Q_{q}\left[ n_{\pm \mathbf { q}}^{(r)}+1/2\pm 1/2\right] ^{1/2}$, $n_{\mathbf {q}}^{(r)}$ is the number of ripplons with the wave vector $\mathbf {q}$,

$$\begin{aligned} I_{n,n^{\prime }}^{2}\left( x_{q}\right) =\frac{\min \left( n,n^{\prime }\right) !}{\max \left( n,n^{\prime }\right) !}x_{q}^{\left| n^{\prime }-n\right| }e^{-x_{q}}\left[ L_{\min \left( n,n^{\prime }\right) }^{\left| n^{\prime }-n\right| }\left( x_{q}\right) \right] ^{2}, \end{aligned}$$

(12)

and $L_{n}^{m}\left( x_{q}\right)$ are the associated Laguerre polynomials. Since the ripplon energy $\hbar \omega _{r,q}$ is usually much smaller than typical electron energies, it can be neglected in the argument of the delta functions. It is remarkable that considering the MW field in a pure classical way, we found that the energy exchange between the field and an electron is equal to an integer number of quanta of the electromagnetic field ($k\hbar \omega$).

According to the relationship $X^{\prime }-X=q_{y}\ell _{B}^{2}$, the quantity $\sum _{X^{\prime }}w_{\mathbf {q};n,X\rightarrow n^{\prime },X^{\prime }}^{\left( \pm \right) }$ to be used for obtaining $\bar{w}_{\mathbf {q}}\left( V_{\mathrm {H}}\right)$ of nondegenerate SE is independent of X, and, therefore, it can be averaged over discrete Landau numbers n only using the distribution function $e^{-\varepsilon _{n}/T_{e}}/Z_{\parallel }$, where $Z_{\parallel }$ is the partition function for the spectrum $\varepsilon _{n}=\hbar \omega _{c}\left( n+1/2\right)$. For a 2D electron gas under magnetic field, one has to take into account the collision broadening of Landau levels to obtain a finite result. In the self-consistent Born approximation (SCBA) [44], level densities have a semi-elliptic shape. The cumulant approach [45] yields a Gaussian shape with the same broadening parameter $\varGamma _{n}$. Generally, the level shape is a kind of average of elliptical and Gaussian forms [46], and the lowest level is shaped like a Gaussian. In the following, we shall use the Gaussian form because it simplifies evaluations and it is preferable for low levels. Introducing Landau level densities of states [45]

$$\begin{aligned} g_{n}\left( \varepsilon \right) =\frac{\sqrt{2\pi }\hbar }{\varGamma _{n}}\exp \left[ -\frac{2\left( \varepsilon -\varepsilon _{n}\right) ^{2}}{\varGamma _{n}^{2}}\right] , \end{aligned}$$

(13)

with a finite collision broadening $\varGamma _{n}$, the average probability of electron scattering $\bar{w}_{\mathbf {q}}\left( V_{\mathrm {H}}\right)$ with the momentum exchange $\mathbf {q}$ can be found in terms of the dynamic structure factor (DSF) $S\left( q,\varOmega \right)$ of a nondegenerate 2D electron gas [40]

$$\begin{aligned} \bar{w}_{\mathbf {q}}\left( V_{\mathrm {H}}\right) =2u_{1,1}^{2}\sum _{k=-\infty }^{\infty }J_{k}^{2}\left( \beta _{p,\mathbf {q}}\right) S\left( q,k\omega -q_{y}V_{\mathrm {H}}\right) . \end{aligned}$$

(14)

Here, we introduce $u_{l,l^{\prime }}^{2}=\left| \left( U_{q}\right) _{l,l^{\prime }}\right| ^{2}Q_{q}^{2}N_{r,q}/\hbar ^{2}$ defined by matrix elements of the electron–ripplon coupling $U_{q}\left( z\right)$, and the ripplon distribution function $N_{r,q}$. The DSF of the 2D Coulomb liquid under a magnetic field can be represented as a sum of Gaussians [13]

$$\begin{aligned} S\left( q,\varOmega \right) \simeq \frac{2\sqrt{\pi }}{Z_{\parallel }} \sum _{n,n^{\prime }}e^{-\varepsilon _{n}/T_{e}}\frac{I_{n,n^{\prime }}^{2}}{ \gamma _{n;n^{\prime }}} \exp \left[ -\frac{\left[ \varOmega -\left( n^{\prime }-n\right) \omega _{c}-\phi _{n}\right] ^{2}}{\gamma _{n;n^{\prime }}^{2}}\right] . \end{aligned}$$

(15)

It is quite usual that peaks of the DSF as a function of frequency occur at excitation energies of the system, while interactions affect the broadening of these peaks. If the Coulomb interaction can be neglected, the broadening of the Gaussians is determined by the average broadening of the respective Landau levels $\varGamma _{n;n^{\prime }}=\sqrt{ \varGamma _{n}^{2}/2+\varGamma _{n^{\prime }}^{2}/2}$. The Coulomb interaction affects the parameters $\gamma _{n;n^{\prime }}$ and $\phi _{n}$ in the following way [13]:

$$\begin{aligned} \hbar \gamma _{n;n^{\prime }}=\sqrt{\varGamma _{n;n^{\prime }}^{2}+x_{q}\varGamma _{C}^{2}},\,\,\, \phi _{n}=\frac{\varGamma _{n}^{2}+x_{q}\varGamma _{C}^{2}}{4T_{e}\hbar }, \end{aligned}$$

(16)

where $\varGamma _{C}=\sqrt{2}eE_{\mathrm {f}}^{(0)}\ell _{B}$ and $E_{\mathrm {f} }^{\left( 0\right) }\simeq 3\sqrt{T_{e}}n_{e}^{3/4}$ is the typical value of the internal electric field of the fluctuational origin [47].

Above given equations for the DSF of the Coulomb liquid were obtained [12, 13] considering an ensemble of noninteracting electrons whose orbit centers are moving fast in the uniform fluctuational electric field $\mathbf {E}_{\mathrm {f}}$. Therefore, plasmon excitations are not present in this DSF. It is remarkable that Eqs. (15) and (16) describing the DSF of SE are valid even for the Wigner solid state [13] if $\omega _{c}$ is much larger than the typical frequency of longitudinal phonons. At low electron densities $n_{e}$, the shift $\phi _{n}$ can be neglected because $\varGamma _{n}\ll T$ under usual experimental conditions. Thus, $S\left( q,\varOmega \right)$ has sharp maxima at Landau excitation frequencies $\varOmega \simeq m\omega _{c}$ which appeared to be a very useful property for the description of MICO.

The main features of the displacement model can be easily seen from the expression

$$\begin{aligned} \nu _{\mathrm {eff}}=\frac{2\hbar }{m_{e}}\sum _{\mathbf {q} }q_{y}^{2}u_{1,1}^{2}\sum _{k=-\infty }^{\infty }J_{k}^{2}\left( \beta _{p, \mathbf {q}}\right) S^{\prime }\left( q,k\omega \right) \end{aligned}$$

(17)

which is a direct consequence of Eqs. (6) and (14), if $\bar{w} _{\mathbf {q}}\left( V_{\mathrm {H}}\right)$ is expanded up to the linear term in $q_{y}V_{\mathrm {H}}$. The important point is that $\nu _{\mathrm {eff}}$ contains the derivative of the DSF: $S^{\prime }\left( q,k\omega \right)$. The presence of the derivative of the function $S\left( q,\varOmega \right)$ which has sharp maxima at Landau excitation frequencies ($m\omega _{c}$, $m=1,2,\ldots$) explains the appearance of sign-changing terms, in spite of the positive factor $q_{y}^{2}$. At the same time, for usual scattering processes (without any photon involved; $k=0$), the basic property of the equilibrium DSF $S\left( q,-\varOmega \right) =\exp \left( -\hbar \varOmega /T_{e}\right) S\left( q,\varOmega \right)$ gives $S^{\prime }\left( q,0\right) =\left( \hbar /2T_{e}\right) S\left( q,0\right) >0$ and, therefore, Eq. (17) reproduces the result of the SCBA theory [6, 13, 45] if $\varGamma _{C}\rightarrow 0$. The same property of the DSF allows transforming $\nu _{\mathrm {eff} }=\sum _{k=0}^{\infty }\nu _{k}$ where the terms with $k\ge 1$ have an additional factor $\left( 1-e^{-k\hbar \omega /T_{e}}\right)$ (here, some small corrections were neglected). The second term of this factor represents the contribution from photon emission processes; it can be neglected at low temperatures.

The term with $k=1$ describes one-photon-assisted scattering. According to Eq. (17), $\nu _{1}$ contains the sum of derivatives of the Gaussian functions entering $S\left( q,\omega \right)$:

$$\begin{aligned} \nu _{1}\propto -\sum _{m}\frac{2\left( \omega -m\omega _{c}-\phi _{n}\right) }{\gamma _{n;n^{\prime }}^{2}}\exp \left[ -\frac{\left( \omega -m\omega _{c}-\phi _{n}\right) ^{2}}{\gamma _{n;n^{\prime }}^{2}}\right] , \end{aligned}$$

(18)

where $m=n^{\prime }-n$. From this equation, one can see that $\nu _{1}<0$ when $\omega /\omega _{c}>m$ which is in accordance with Eq. (4). Thus, Eqs. (17) and (18) describe the shape of MIRO and MICO which agrees with expectations based on the qualitative analysis of Eqs. (3) and (4) and with experimental observations. For small broadening of the DSF maxima, the exponential factor of Eq. (18) selects the number $m\equiv n^{\prime }-n=1,2,\ldots$ which gives the major contribution into $\nu _{1}$ for a chosen $\omega$. This factor is close to unity only if $\omega -m\omega _{c}\simeq 0$, and it is exponentially small for other m or $\omega _{c}$ which do not meet this condition.

Fig. 3

Oscillatory contribution to the effective collision frequency $\nu _{1}$ versus B calculated for two different MW polarizations: parallel (to the DC electric field) $p=\Vert$ (blue dashed) and perpendicular $p=\bot$ (red solid) [40]. Black triangles indicate the values of B such that $\omega /\omega _c=m$. The conditions are the following: $E_{0}=10\,\mathrm {V/cm}$, $n_{e}=17\times 10^{6}\,\mathrm {cm}^{-2}$, $\omega /2\pi =88.34\,\mathrm {GHz}$, and $T=0.56\,\mathrm {K}$ (liquid $^{4}\mathrm {He}$) (Color figure online)

The effective collision frequency induced by one-photon-assisted scattering $\nu _{1}$ is shown in Fig. 3 for two linear MW polarizations. Firstly, we note that the minima occur at lower fields B than the respective maxima. Secondly, the amplitude of intra-subband MICO decreases steadily and strongly with m. It is interesting to note also that in the limit of large $\gamma _{n;n^{\prime }}$ (strong collision broadening $\varGamma _{n}$), the overlapping of the sign-changing terms in the sum over the all m limits the position of minima by a universal law $\omega / \omega _{c}\rightarrow m+1/4$, which coincides remarkably with that reported in Ref. [16].

2.1.2 Inelastic Model

When averaging $w_{\mathbf {q};n,X\rightarrow n^{\prime },X^{\prime }}^{\left( \pm \right) }$ given in Eq. (11), we naturally used the equilibrium electron distribution function $f\left( \varepsilon \right)$, which is indicated in Eq. (15) by the Boltzmann factor $e^{-\varepsilon _{n}/T_{e}}$. For the terms with $k>0$, in the regime $\beta _{p,\mathbf {q} }\ll 1$, this is a correct procedure. Still, as proven in Ref. [22] , the photon-assisted scattering leads to an oscillatory correction to the distribution function $f\left( \varepsilon \right)$. This correction cannot be neglected in Eq. (17) if we consider the term with $k=0$, because its contribution to $\nu _{ \mathrm {eff}}=\sum _{k=0}^{\infty }\nu _{k}$ can be comparable with (or even larger than) $\nu _{1}$ given by the displacement model.

In order to obtain the oscillating correction to $f\left( \varepsilon \right)$, we restrict ourselves to scattering events involving only one photon [$k=\pm 1$ in Eq. (11)] and assume $\beta _{p,\mathbf {q}}\ll 1$. Analyzing the average transition rate up ($n\rightarrow n^{\prime }$) and the all transition rates down ($n^{\prime }\rightarrow n$), we can represent them as integral forms ($\int d\varepsilon \int d\varepsilon ^{\prime }\ldots$) using the Landau level density of states $g_{n}\left( \varepsilon \right)$ in the way that was used for finding the DSF $S\left( q,\varOmega \right)$. Then, it is possible to obtain the rate-balance condition [40]

$$\begin{aligned} f_{n^{\prime }}\left( \varepsilon ^{\prime }\right) =\frac{ f_{n}\left( \varepsilon ^{\prime }-\hbar \omega \right) r_{n,n^{\prime }}\left( \varepsilon ^{\prime }\right) }{\nu _{n^{\prime }}^{\left( \mathrm { 2R}\right) }+r_{n,n^{\prime }}\left( \varepsilon ^{\prime }\right) }, \end{aligned}$$

(19)

where

$$\begin{aligned} r_{n,n^{\prime }}\left( \varepsilon ^{\prime }\right) =\frac{\lambda ^{2}T}{ 2\hbar }\bar{\chi }_{p}\nu _{R}P_{n,n^{\prime }}g_{n}\left( \varepsilon ^{\prime }-\hbar \omega \right) \end{aligned}$$

(20)

is the excitation rate, $\nu _{R}=\varLambda ^{2}/8\pi \hbar \alpha \ell _{B}^{4}$ is a characteristic collision frequency, the dimensionless parameter $P_{n,n^{\prime }}$ describes the strength of the electron–ripplon coupling in the presence of a magnetic field

$$\begin{aligned} P_{n,n^{\prime }}=\frac{\ell _{B}^{4}}{\varLambda ^{2}}\int \limits _{0}^{\infty }U_{q}^{2}I_{n,n^{\prime }}^{2}\left( x_{q}\right) \mathrm{d}x_{q}, \end{aligned}$$

(21)

$\bar{\chi }_{p}$ is the polarization factor

$$\begin{aligned} \bar{\chi }_{\bot }=\bar{\chi }_{\Vert }=\frac{2\omega _{c}^{2}\left( \omega _{c}^{2}+\omega ^{2}\right) }{\left( \omega ^{2}-\omega _{c}^{2}\right) ^{2}} ,\,\,\bar{\chi }_{\pm }=\frac{4\omega _{c}^{2}\left( \omega \pm \omega _{c}\right) ^{2}}{\left( \omega ^{2}-\omega _{c}^{2}\right) ^{2}}, \end{aligned}$$

(22)

$\nu _{n^{\prime }}^{\left( \mathrm {2R}\right) }$ is the inelastic transition rate from $n^{\prime }$ to the all $n<n^{\prime }$ caused by two-ripplon emission processes [48]. In the distribution function $f_{n^{\prime }}\left( \varepsilon ^{\prime }\right)$, the subscript $n^{\prime }$ indicates that its argument $\varepsilon ^{\prime }$ is close to $\varepsilon _{n^{\prime }}$.

Equation (19) reminds the solution of the rate equation of a two-level model usually obtained in quantum optics. The second term in the denominator of this equation is caused by backward electron transitions accompanied by emission of a photon. Here, the inelastic decay rate $\nu _{n^{\prime }}^{\left( \mathrm {2R}\right) }$ plays an important role in obtaining the oscillatory correction to the distribution function. Firstly, we note that in the absence of $\nu _{n^{\prime }}^{\left( \mathrm {2R}\right) }$, the solution of Eq. (19) satisfies the saturation condition $f_{n^{\prime }}\left( \varepsilon ^{\prime }\right) =f_{n}\left( \varepsilon ^{\prime }-\hbar \omega \right)$ which is quite obvious. Secondly, a sharp shape of $f_{n^{\prime }}\left( \varepsilon ^{\prime }\right)$ appears when the inelastic scattering rate is stronger then the excitation rate: $\nu _{n^{\prime }}^{\left( \mathrm {2R}\right) }\gg r_{n,n^{\prime }}$. In this limiting case, one can neglect $r_{n,n^{\prime }}$ in the denominator of the right side of Eq. (19) and set $f_{n}\left( \varepsilon \right)$ to the equilibrium function in the numerator. This treatment yields $f_{n^{\prime }}\left( \varepsilon ^{\prime }\right) \propto g_{n}\left( \varepsilon ^{\prime }-\hbar \omega \right)$, which means that at higher Landau levels we have a sort of population inversion eventually leading to MICO. This is the reason why this mechanism is called “the inelastic model”.

If electron–electron interactions are neglected, the inelastic model gives an additional correction to the effective collision frequency [40]

$$\begin{aligned} \nu _{\mathrm {in}}= & {} \pi \lambda ^{2}\bar{\chi }_{p}\nu _{R}^{2}T^{2}\hbar \omega _{c}\sum _{n^{\prime }=1}^{\infty }\frac{P_{n^{\prime },n^{\prime }}P_{0,n^{\prime }}}{\nu _{n^{\prime }}^{\left( 2R\right) }\varGamma _{n^{\prime }}G_{0;n^{\prime }}} \nonumber \\&\quad \times \frac{2\left( n^{\prime }\hbar \omega _{c}-\hbar \omega \right) }{ G_{0;n^{\prime }}^{2}}\exp \left[ -\frac{\left( n^{\prime }\hbar \omega _{c}-\hbar \omega \right) ^{2}}{G_{0;n^{\prime }}^{2}}\right] , \end{aligned}$$

(23)

where $G_{n;n^{\prime }}^{2}=\varGamma _{n;n^{\prime }}^{2}-\varGamma _{n^{\prime }}^{2}/4$. Equation (23) indicates that, in the inelastic model, the shape of MICO represents the derivative of a Gaussian similar to that of the displacement model [see Eq. (18)]. In contrast to the displacement model, additional large parameters $\nu _{R}/\nu _{n^{\prime }}^{\left( 2R\right) }$ and $T/G_{0;n}$ appear in the expression for $\nu _{\mathrm {in}}$ which can make MICO more pronounced.

Fig. 4

$\sigma _{xx}$ versus B for SE on liquid $^{4}\mathrm {He}$. Data (red) and theoretical results (blue dashed) were obtained for $n_{e}=1.7\times 10^{7}\,\mathrm {cm}^{-2}$, $T=0.56\,\mathrm {K}$ and $\omega /2\pi =88.34\,\mathrm {GHz}$ [37] (Color figure online)

Unfortunately, in the inelastic model, it is very difficult to describe the effect of Coulomb interaction on magnetoconductivity oscillations. Anyway, it is reasonable to expect that the fluctuational electric field $\mathbf {E} _{f}$ will increase the broadening of oscillations in the way similar to that of the displacement model. Typical conductivity variations caused by the inelastic model are shown in Fig. 4 by the blue dashed line. The experimental data [37] shown here by the red curve were obtained at a rather high MW frequency, where the contribution from the displacement model is small.

2.2 Inter-subband Model

For MICO induced by inter-subband MW excitation of SE on liquid helium [27, 28], contrary to MIRO in heterostructures, there is only one theoretical mechanism proposed by now [29,30,31]. Generally, it gives a quite well description of experimental observations. It is remarkable that this inter-subband model cannot be reduced to any intra-subband model of MIRO; moreover, it is not relevant to the photon-assisted scattering which plays the major role in the displacement and inelastic models. Nevertheless, it has something in common with both the displacement and inelastic models. This can be easily seen even from a qualitative analysis similar to that given above in Eqs. (3) and (4).

Consider an inter-subband scattering event $l,n,X\rightarrow l^{\prime },n^{\prime },X^{\prime }$. Now we have to include the Rydberg state energy $\varDelta _{l}$ into the electron spectrum in the presence of the magnetic and driving electric fields

$$\begin{aligned} \mathcal {E}_{l,n,X}=\varDelta _{l}+\hbar \omega _{c}\left( n+1/2\right) +eE_{\Vert }X . \end{aligned}$$

(24)

For usual elastic scattering off disorder (photons are not involved in this process), the energy conservation yields

$$\begin{aligned} \hbar \omega _{c}\left( n^{\prime }-n\right) +eE_{\Vert }\left( X^{\prime }-X\right) -\varDelta _{l,l^{\prime }}=0 , \end{aligned}$$

(25)

where we used the obvious relationship $\varDelta _{l^{\prime },l}=\varDelta _{l^{\prime }}-\varDelta _{l}=-\varDelta _{l,l^{\prime }}$. For electron decay processes from the first excited subband ($l=2$) to the ground subband ($l^{\prime }=1$), this scattering event is possible only if the magnetic field is close to the level matching condition $\hbar \omega _{c}\left( n^{\prime }-n\right) \approx \varDelta _{2,1}$, as shown in Fig. 5, because $X^{\prime }-X$ is limited by the magnetic length $\ell _{B}$ ($q\sim 1/\ell _{B}$). Under other conditions, quasi-elastic decay caused by a ripplon is impossible.

Assuming a decay process from the first excited subband down to the ground subband, and introducing the inter-subband excitation frequency $\omega _{2,1}=\varDelta _{2,1}/\hbar >0$, from Eq. (25) one can find the displacement of the electron orbit center

$$\begin{aligned} X^{\prime }-X=\frac{\hbar \omega _{c}}{eE_{\Vert }}\left( \frac{\omega _{2,1} }{\omega _{c}}-m\right) . \end{aligned}$$

(26)

Here, $n^{\prime }-n=m>0$ because in this process an electron scatters to a higher Landau level as illustrated in Fig. 5. Equation (26) is very similar to Eq. (4) used above for explaining MIRO and the effect of absolute negative conductivity in the displacement model. The only difference is that now we have the inter-subband excitation frequency $\omega _{2,1}$ instead of the MW frequency $\omega$.

Fig. 5

Dynamics of SE in perpendicular magnetic fields. MW photons of energy $\hbar \omega$ drive the transition $l=1\rightarrow 2$ (wavy arrow) without changing the quantum state n. Under the level matching condition, excited electrons can be scattered elastically (dashed blue arrow) and fill the state $n^{\prime } >n$ of the ground subband [28] (Color figure online)

At this stage, photons are not necessary to cause electron scattering against the driving force $-e\mathbf {E}_{\Vert }$. For example, quasi-elastic inter-subband scattering from $l=2$ to $l^{\prime }=1$ will be the scattering against the driving force ($X^{\prime }>X$), if $\omega _{2,1}/\omega _{c}>m$, or when B is a bit lower than the level matching point $\omega _{2,1}/\omega _{c}=m$. The important thing is that there are inverse scattering processes from $l=1$ to $l^{\prime }=2$. For these processes, the right side of the respective equation for $X^{\prime }-X$ [similar to Eq. (26)] has the opposite sign (minus) with $m=n-n^{\prime }>0$, because an electron scatters to a lower Landau level. Therefore, at the same conditions $\omega _{2,1}/\omega _{c}>m$, electron scattering up the surface subbands is obviously the scattering along the driving force ($X^{\prime }<X$). The average probability of scattering $\bar{\nu }_{l\rightarrow l^{\prime }}$ of SE usually satisfies the condition $\nu _{l^{\prime }\rightarrow l}=\nu _{l\rightarrow l^{\prime }}\exp \left( -\hbar \omega _{l,l^{\prime }}/T_{e}\right)$, where $\hbar \omega _{l,l^{\prime }}=\varDelta _{l}-\varDelta _{l^{\prime }}$. Thus, we can expect that the sign-changing correction to $\sigma _{xx}$ induced by inter-subband scattering will have the following form

$$\begin{aligned} \delta \sigma _{xx}^{\left( \mathrm {inter}\right) }\propto -\left( N_{2}-N_{1}e^{-\hbar \omega _{2,1}/T}\right) \sum _{m}\left( \frac{\omega _{2,1}}{\omega _{c}}-m\right) e^{-\left( \omega _{2,1} -m\omega _{c}\right) ^{2}/\gamma _{n;n^{\prime }}^{2}}, \end{aligned}$$

(27)

where $N_{l}$ is the number of electrons at the level l. In the right side of this equation, the exponential proportionality factor is introduced in order to select the number m giving the major contribution to $\delta \sigma _{xx}^{\left( \mathrm {inter}\right) }$ similar to Eq. (18). At equilibrium, we obviously have $N_{2}/N_{1}=e^{-\hbar \omega _{2,1}/T}$ and, therefore, $\delta \sigma _{xx}^{\left( \mathrm {inter}\right) }=0$. To obtain the sign-changing corrections to $\sigma _{xx}$ and even the absolute negative conductivity, we have to create an extra population of the first excited level

$$\begin{aligned} N_{2}>N_{1}e^{-\hbar \omega _{2,1}/T}, \end{aligned}$$

(28)

which can be naturally induced by the resonant MW excitation with $\omega =$$\omega _{2,1}$ shown in Fig. 5 by the wavy arrow.

In Eq.(27), the factor $\left( \omega _{2,1}/\omega _{c}-m\right)$, describing qualitatively the inter-subband mechanism of MICO, reminds the factor $\left( \omega /\omega _{c}-m\right)$ of the displacement model of MIRO. At the same time, the first factor $\left( N_{2}-N_{1}e^{-\hbar \omega _{2,1}/T}\right)$ requires a nonequilibrium electron distribution over surface subbands which has something in common with the inelastic model. Nevertheless, in contrast to the inelastic model, here the condition of Eq. (28) is created by direct resonant absorption of a MW quantum (without involving any kind of disorder), and the population inversion (important for the inelastic model) is not necessary. Moreover, both the displacement and inelastic models require photon-assisted scattering as the origin of MIRO, while the inter-subband mechanism remarkably has no relation to the photon-assisted scattering described in Sect. 2.1. In the inter-subband model, photons are used only for providing a nonequilibrium population of the excited subband; the sign-changing correction to $\sigma _{xx}$ and absolute negative conductivity are caused by usual scattering off disorder in a nonequilibrium multi-subband 2D electron system. In the qualitative analysis given above, we discussed only sign-changing corrections to $\sigma _{xx}^{\left( \mathrm {inter}\right) }$. The accurate treatment presented below indicates that there is also a normal (remaining positive) contribution to $\sigma _{xx}^{\left( \mathrm {inter}\right) }$ which exists even for $N_{2}/N_{1}=e^{-\hbar \omega _{2,1}/T}$, but it is less important if the MW power is strong enough.

The magnetoconductivity treatment given in Eqs. (5) and (6) can be extended to include inter-subband scattering

$$\begin{aligned} \nu _{\mathrm {eff}}=-\frac{1}{m_{e}V_{\mathrm {H}}}\sum _{l,l^{\prime }}\bar{n} _{l}\sum _{\mathbf {q}}\hbar q_{y}\bar{w}_{l,l^{\prime }}\left( \mathbf {q},V_{ \mathrm {H}}\right) , \end{aligned}$$

(29)

where $\bar{n}_{l}=N_{l}/N_{e}$ are the fractional occupancies of surface subbands, and $\bar{w}_{l,l^{\prime }}\left( \mathbf {q},V_{\mathrm {H} }\right)$ is the average probability of both intra- and inter-subband scattering ($l\rightarrow l^{\prime }$) which is accompanied by the momentum exchange $\hbar \mathbf {q}$. For usual scattering processes (MW photons are not involved in a scattering event), $\bar{w} _{l,l^{\prime }}\left( \mathbf {q},V_{\mathrm {H}}\right)$ is found as [49, 50]

$$\begin{aligned} \bar{w}_{l,l^{\prime }}\left( \mathbf {q}\right) =2u_{l,l^{\prime }}^{2}\left( x_{q}\right) S_{l,l^{\prime }}\left( q,\omega _{l,l^{\prime }}-q_{y}V_{\mathrm {H}}\right) , \end{aligned}$$

(30)

where the function $u_{l,l^{\prime }}^{2}\left( x_{q}\right)$ was introduced just under Eq. (14) and $S_{l,l^{\prime }}\left( q,\varOmega \right)$ is an extension of the DSF $S\left( q,\varOmega \right)$ given in Eq. (15) applicable for a multi-subband 2D electron system, because now we have to take into account that the broadening of a Landau level depends also on l ($\varGamma _{n}\rightarrow \varGamma _{l,n}$). For intra-subband scattering ($l=l^{\prime }$), the right side of Eq. (30) transforms naturally into the term with the photon number $k=0$ of Eq. (14). According to Eq. (30), the case $\omega _{l,l^{\prime }}>0$ ($\omega _{l,l^{\prime }}<0$) resembles electron scattering accompanied by absorbtion (emission) of a photon whose frequency $\omega =\left| \omega _{l,l^{\prime }}\right|$.

The accurate form of $S_{l,l^{\prime }}\left( q,\varOmega \right)$ can be formally obtained from the definitions of $S\left( q,\varOmega \right)$ given in Eqs. (15) and (16) using the following replacements: $\varGamma _{n}\rightarrow \varGamma _{l,n}$, $\varGamma _{n;n^{\prime }}\rightarrow \varGamma _{l,n;l^{\prime },n^{\prime }}$, $\gamma _{n;n^{\prime }}\rightarrow \gamma _{l,n;l^{\prime },n^{\prime }}$, and $\phi _{n}\rightarrow \phi _{l,n}$. We assume that the electron distribution over Landau levels can be still described by the Boltzmann function with an effective temperature $T_{e}$ due to the strong Coulomb interaction. In this case, $S_{l,l^{\prime }}\left( q,\varOmega \right)$ has an important property

$$\begin{aligned} S_{l,l^{\prime }}\left( q,-\varOmega \right) =e^{-\hbar \varOmega /T_{e}}S_{l^{\prime },l}\left( q,\varOmega \right) , \end{aligned}$$

(31)

which simplifies conductivity evaluations. The effective temperature approximation used here is based on the experimental fact [51] that the electron-velocity autocorrelation time $\tau _{c}$ is usually much shorter than all other relaxation times. For example, at a low electron density $n_{e}=1.5\times 10^{7}\,\mathrm {cm}^{-2}$, the reciprocal value $\tau _{c}^{-1}\simeq 10^{10}\,\mathrm {sec}^{-1}$ is close to the harmonic oscillator frequency in a 2D triangular lattice $\omega _{0}$, which means that the electron system resembles the Wigner solid. Even for the smallest density used in MICO experiments $n_{e}\simeq 10^{6}\,\mathrm {cm}^{-2}$, the average Coulomb interaction energy of SE is much larger than the average kinetic energy which means that the energy exchange between electrons is very strong. It should be emphasized additionally that the expression for the DSF of the Coulomb liquid given above remarkably coincides with the DSF of the Wigner solid [13] heated to $T_{e}$.

Fig. 6

Decay rate of the first excited subband $\nu _{2\rightarrow 1}$ versus the magnetic field B for $T=0.2\,\mathrm {K}$ and $n_{e}=10^{6}\,\mathrm {cm}^{-2}$: single-electron treatment (dotted); many-electron theory was calculated for different $T_{e}$ as indicated in the figure legend [31] (Color figure online)

The effective collision frequency of Eq. (29) depends on the fractional occupancies $\bar{n}_{l}$ which should be found from the rate equation (similar to that of the quantum optics) which contains the decay rate of the excited subband $\nu _{l\rightarrow l^{\prime }}$. Using Eq. (30), the later quantity can be found as

$$\begin{aligned} \nu _{l\rightarrow l^{\prime }}=2\sum _{\mathbf {q}}u_{l,l^{\prime }}^{2}\left( x_{q}\right) S_{l,l^{\prime }}\left( q,\omega _{l,l^{\prime }}\right) . \end{aligned}$$

(32)

In this equation, $q_{y}V_{\mathrm {H}}$ is set to zero because we consider the linear DC transport properties. Thus, the decay rate $\nu _{2\rightarrow 1}$ has sharp maxima near the level matching points: $\omega _{2,1}=m\omega _{c}$. The typical dependence of the decay rate $\nu _{2\rightarrow 1}$ on the magnetic field near the level matching point is shown in Fig. 6. The strong temperature dependence of $\nu _{2\rightarrow 1}$ maxima is caused by the Coulomb correction $\varGamma _{C}$ to $\gamma _{l,n;l^{\prime },n^{\prime }}$. The above noted Coulomb broadening of the decay rate $\nu _{2\rightarrow 1}$ affects strongly subband occupancies $\bar{n}_{l}=N_{l}/N$ in the presence of MW radiation. For the two-subband model, which is valid for $T_{e}\le 2\,\mathrm {K}$, the conventional rate equation yields [52]

$$\begin{aligned} \frac{\bar{n}_{2}}{\bar{n}_{1}}=\frac{1+\exp \left( -\hbar \omega _{2,1}/T_{e}\right) \nu _{2\rightarrow 1}/r_{\mathrm {mw}}}{1+\nu _{2\rightarrow 1}/r_{\mathrm {mw}}}, \end{aligned}$$

(33)

where $r_{\mathrm {mw}}$ is the MW excitation rate. Under the resonance condition, $r_{\mathrm {mw}}=\varOmega _{\mathrm {R}}^{2}/2\gamma _{\mathrm {mw}}$, where $\gamma _{\mathrm {mw}}$ is the half-width of the resonance and $\varOmega _{\mathrm {R}}$ is the Rabi frequency proportional to the amplitude of the MW field. According to Eq. (33) and Fig. 6, the ratio $\bar{n }_{2}/\bar{n}_{1}$ oscillates with B having minima near the level matching points and approaching the saturation condition $\bar{n}_{2}/\bar{n} _{1}\rightarrow 1$ between these points. Usually, even a small nonequilibrium filling of the excited subband $\bar{n}_{2}-\bar{n}_{1}e^{-\hbar \omega _{2,1}/T_{e}}>0$ can lead to giant oscillations in $\sigma _{xx}$ due to $\varGamma _{l,n}\ll T_{e}$.

Equations (29), (32) and (33) allow describing MICO induced by nonequilibrium population of the first excited subband. For example, consider scattering only between $l=2$ and $l=1$ (the two-subband model). Using the property of the DSF given in Eq. (31), the contribution of inter-subband scattering $\nu _{ \mathrm {inter}}$ to the effective collision frequency $\nu _{\mathrm {eff}}$ can be represented as a sum of two distinctive terms $\nu _{\mathrm {inter} }=\nu _{\mathrm {A}}+\nu _{\mathrm {N}}$, where

$$\begin{aligned} \nu _{\mathrm {A}}= & {} \frac{2\hbar }{m_{e}}\left( \bar{n}_{2}-\bar{n} _{1}e^{-\hbar \omega _{2,1}/T_{e}}\right) \sum _{\mathbf {q} }q_{y}^{2}u_{2,1}^{2}S_{2,1}^{\prime }\left( q,\omega _{2,1}\right) , \end{aligned}$$

(34)

$$\begin{aligned} \nu _{\mathrm {N}}= & {} \frac{2\hbar ^{2}}{m_{e}T_{e}}\bar{n}_{1}e^{-\hbar \omega _{2,1}/T_{e}}\sum _{\mathbf {q}}q_{y}^{2}u_{2,1}^{2}S_{2,1}\left( q,\omega _{2,1}\right) . \end{aligned}$$

(35)

The first term $\nu _{\mathrm {A}}$ represents an anomalous (sign-changing) contribution which is proportional to the derivative of the sum of Gaussians $S_{2,1}^{\prime }\left( q,\omega _{2,1}\right)$. Obviously, the shape of conductivity variations near the level matching points originated from this term is similar to that of MIRO and MICO caused by photon-assisted scattering. It is important that at equilibrium ($\bar{n}_{2}=\bar{n} _{1}e^{-\hbar \omega _{2,1}/T_{e}}$), this term vanishes. The second term $\nu _{\mathrm {N}}$ represents a normal contribution which oscillates with B remaining positive. One can use slightly different definitions [31] of $\nu _{\mathrm {A}}$ and $\nu _{\mathrm {N}}$ by subtracting

$$\begin{aligned} \frac{\hbar ^{2}}{m_{e}T_{e}}\left( \bar{n}_{2}-\bar{n}_{1}e^{-\hbar \omega _{2,1}/T_{e}}\right) \sum _{\mathbf {q}}q_{y}^{2}u^{2}_{2,1}S_{2,1}\left( q,\omega _{2,1}\right) \end{aligned}$$

(36)

from the right side of Eq. (34) and adding it into Eq. (35). Such redistribution does not change $\nu _{\mathrm {inter}}$ but leads to a more symmetrical form of $\nu _{\mathrm {N}}$ proportional to $\bar{n}_{2}+\bar{n}_{1}e^{-\hbar \omega _{2,1}/T_{e}}$. Anyway, for low electron densities, $\hbar \gamma _{l,n;l^{\prime },n^{\prime }}\ll T$ and, therefore, the corrections of Eqs. (35) and ( 36) are much smaller than $\nu _{\mathrm {A}}$ defined in Eq. (34 ).

Fig. 7

Magnetoconductivity versus B calculated for $T=0.2\,\mathrm {K}$ ($^{3}\mathrm {He}$) and $n_{e}=10^{7}\,\mathrm {cm}^{-2}$: the SCBA theory (dash-dotted), the Drude approximation (olive dotted), the dark many-electron theory (blue dashed), the theory based on the inter-subband mechanism of MICO (red solid) [31] (Color figure online)

Typical MICO calculated for MW radiation of medium power are shown in Fig. 7 by the solid red line. Here, the single-electron theory (dark) based on the SCBA is shown by the dash-dotted line. Without MW excitation, the many-electron theory (blue dashed) transforms from the SCBA result to the Drude approximation when B decreases. It should be noted that the amplitude of inter-subband MICO firstly increases with lowering B (increasing m), but then, at lower B, it decreases and vanishes due to the Coulombic effect. Eventually, $\sigma _{xx}$ is approaching the many-electron line (blue dashed) calculated for $\mathbf {E}_{\mathrm {mw}}=0.$ This behavior is in accordance with experimental observations [27, 28].

The multi-subband electron system on liquid helium can be tuned in resonance with the MW field for electron transitions to higher subbands ($l>2$). In this case, the DC magnetic (B) and electric ($E_{\bot }$) fields oriented normally to the multi-subband 2D electron system give a remarkable possibility to manipulate the inter-subband scattering probabilities and to realize the population inversion of electron subbands [50]. The theoretical analysis of the electron momentum relaxation rate under the resonant MW excitation of the third subband ($l=3$) indicates that such an excitation induces a variety of new magneto-oscillations of $\sigma _{xx}$. Among these, there are oscillations, accompanying by the population inversion ($\bar{n}_{2}> \bar{n}_{1}$), with a period which is incommensurate with the basic period determined by the resonant MW frequency, oscillations with a 1 / B periodic amplitude modulation, and oscillations located in the vicinity of some fractional values of the ratio $\omega /\omega _{c}$.

3 The Coulombic Effect on MICO

In order to test theoretical mechanisms and models by an experiment, it is always good to have variable parameters affecting the outcome. For SE on liquid helium, one of the important parameters is the electron density $n_{e}$ which defines the strength of the Coulomb interaction between electrons. In a nondegenerate electron system, the average Coulomb interaction energy per an electron $U_{\mathrm {C}}$ should be compared with the electron temperature $T_{e}$ which is the measure of the average kinetic energy. Therefore, it is conventional to describe the electron–electron coupling by the plasma parameter $\varGamma ^{\left( \mathrm {pl}\right) }=e^{2}\sqrt{\pi n_{s}}/T_{e}$. For example, the Wigner solid transition occurs [9] at $\varGamma ^{\left( \mathrm {pl}\right) }\simeq 131$. The MICO on liquid helium are usually studied under conditions $\varGamma ^{\left( \mathrm {pl} \right) }>10$ when $U_{\mathrm {C}}$ is much larger than the average kinetic energy. At first glance, it seems that the internal interaction of such a strength should ruin the quantum picture based on single-electron Landau levels. Nevertheless, the theoretical treatment using Landau levels works pretty well because the internal electric field $E_{\mathrm {f}}$ of fluctuational origin acting on an electron can be considered as a quasi-uniform electric field [53]. Such a field can be eliminated by a proper choice of the reference frame moving along with the electron orbit center [12, 13]. Thus, the 2D Coulomb liquid can be considered as an ensemble of electrons whose orbit centers are moving fast in the crossed fields $\mathbf {E}_{\mathrm {f}}$ and $\mathbf {B}$ . This leads to the Coulomb broadening of the DSF described by Eqs. (15) and (16). It should be noted that the quasi-uniform electric field $\mathbf {E}_{\mathrm {f}}$ does not introduce an additional broadening of Landau levels because they are defined in the moving frame, where $\mathbf {E}_{\mathrm {f}}^{\prime }=0$.

Fig. 8

$\sigma _{xx}$ versus $\omega _{2,1}/ \omega _{c} (B)$ calculated for $T_{e}=T=0.2\,\mathrm {K}$, and for three electron densities $n_{e}$ indicated in the figure legend in units $10^{6}\,\mathrm {cm}^{-2}$ [54] (Color figure online)

In the theory describing MICO of highly correlated electrons on liquid helium [31], the internal field of fluctuational origin $E_{\mathrm {f}}$ is much larger than the driving field $E_{\Vert }$. Therefore, at first, the probability of scattering is averaged over the fluctuational electric field $\mathbf {E}_{\mathrm {f}}$ entering the energy conservation delta function which leads to the DSF of the 2D Coulomb liquid [12, 13], and then the probability is expanded in $eE_{\Vert }\left( X^{\prime }-X\right)$ to obtain the linear conductivity $\sigma _{xx}$. The main influence of internal interactions on the shape of MICO can be described by means of the Coulomb broadening parameter $\varGamma _{\mathrm {C}}$ entering $\gamma _{l,n;l^{\prime },n^{\prime }}$ and $\phi _{l,n}$ given in Eq. (16). This parameter increases with electron density and electron temperature as $\varGamma _{\mathrm {C}}\propto n_{e}^{3/4}T_{e}^{1/2}$. Additionally, the many-electron effect becomes more pronounced at lower magnetic fields because $\varGamma _{\mathrm {C}}\propto 1/B^{1/2}$. Assuming $T_{e}=T=0.2\,\mathrm {K}$, the typical dependence of inter-subband MICO on electron density predicted by the theory is illustrated in Fig. 8. The blue solid line calculated for the lowest electron density has rather sharp variations of $\sigma _{xx}$ near the level matching points with $m\le 7$. The broadening of these oscillations steadily increases with m (the flat regions of $\sigma _{xx}$ are shrinking), and at $m\ge 9$, the shape of MICO is affected by overlapping of sign-changing terms which belong to different level matching points. The regions with negative conductivity ($\sigma _{xx}<0$) increase with m for chosen numbers $m<12$.

At higher electron densities presented in Fig. 8, the broadening of MICO strongly increases because of the Coulomb effect. The regions with $\sigma _{xx}<0$ start decreasing with $m\ge 10$ for the olive line ($n_{e}=5.3\times 10^{6}\,\mathrm {cm}^{-2}$), because $\varGamma _{\mathrm {C}}$ is larger at lower B; they completely disappear for the red line ($n_{e}=13\times 10^{6}\,\mathrm {cm}^{-2}$). There is also a remarkable prediction of the theory related to the positions of minima and maxima of the inter-subband MICO. Consider the shifts of conductivity minima $\delta _{+}=\omega _{2,1}/\omega _{c}\left( B_{+}\right) -m$ and maxima $\delta _{-}=\omega _{2,1}/\omega _{c}\left( B_{-}\right) -m$ with regard to the level matching point. Here, the sign ± in the subscript means that $\delta _{+}>0$ while $\delta _{-}<0$. Figure 8 indicates that the shift of minima $\delta _{+}$ increases monotonically with m, while the shift of maxima has a non-monotonic dependence clearly seen for olive dashed and red dashed–dotted curves: After an initial increase, $\left| \delta _{-}\right|$ attains a maximum value and then decreases strongly for larger m. This is the way the Coulombic corrections to $\gamma _{l,n;l^{\prime },n^{\prime }}$, and $\phi _{l,n}$ display themselves in the inter-subband MICO.

Fig. 9

$\sigma _{xx}$ versus $\omega _{2,1}/ \omega _{c} (B)$ obtained at $T=0.2\,\mathrm {K}$ ($^{3}\mathrm {He}$), input MW power $W=0\,\mathrm {dBm}$, and for two electron densities $n_{e}$ indicated in the figure legend in units $10^{6}\,\mathrm {cm}^{-2}$ [54] (Color figure online)

The evolution of the shape of $\sigma _{xx}$ oscillations with an increase in electron density found in the experiment [54] is shown in Fig. 9. The oscillations are the most pronounced for the lowest electron density. A noticeable influence of the Coulomb interaction on $\sigma _{xx}$ oscillations, which magnifies with m , is a strong suppression of the amplitude and an increase in the broadening of conductivity extrema in accordance with the inter-subband mechanism of MICO. It should be noted that theoretical lines shown in Fig. 8 were calculated under the assumption $T_{e}=T$. In an experiment with MW excitation of SE, the elastic decay of electrons to the ground subband is accompanied by electron heating [52]. Under a magnetic field, electron decay is possible only near the level matching points. Therefore, $T_{e}$ oscillates [29, 30] with $\omega _{2,1}/\omega _{c}$ attaining sharp maxima when $\omega _{2,1}/\omega _{c}\simeq m$. These oscillations of $T_{e}$ make the amplitude of conductivity minima larger than the amplitude of the respective maxima [29, 30] because the effective collision frequency caused by intra-subband scattering $\nu _{ \mathrm {intra}}\propto 1/T_{e}$. This also agrees with experimental observations [54] shown in Fig. 9. The electron temperature was estimated to be about $1\,\mathrm {K}$.

Fig. 10

Shifts of conductivity minima $\delta _{+}>0$ (circles) and maxima $\delta _{-}<0$ (triangles) versus the level matching number m for $n_{e}=2\times 10^{6}\,\mathrm {cm}^{-2}$: experimental data (filled symbols), and the many-electron theory (open symbols with line) [54] (Color figure online)

As expected, internal forces cause also nontrivial changes in the location of conductivity extrema. It is instructive to consider positions of conductivity extrema observed in the experiment versus m , as shown in Fig. 10. The uncertainty in the positions of oscillation extrema is mostly determined by the uncertainty in values of B. The latter was determined by in situ cyclotron resonance measurements [28]. Note that the uncertainty in $\omega _{2,1}/\omega _{c}\propto B^{-1}$ increases with decreasing B. For $m<6$, positions of minima cannot be determined accurately because of formation of ZRS. The shift of minima $\delta _{+}$ (red circles) increases monotonically with m , and at high m the $\delta _{+}\rightarrow 1/2$ which is substantially larger than the same quantity ($\delta _{+}\simeq 1/4$) reported for intra-subband MIRO in semiconductor devices [16]. In contrast, the shift of maxima $\delta _{-}$ (olive triangles) is non-monotonic. After an initial increase, $\left| \delta _{-}\right|$ reaches the maximum value of about $0.2<1/4$ at $m=13$ and decreases strongly for larger m. Calculations shown in Fig. 10 were performed for the MW field resulting in conductivity oscillations of approximately the same amplitude as in the experiment. Quantitative differences between data and the theory (open symbols) can be attributed to electron heating. Nevertheless, the delicate theoretical findings, which concern the difference in behavior of positions of conductivity extrema as functions of electron density and of the level matching number m, are clearly observed in the experiment. Thus, the behavior of positions of conductivity extrema observed is drastically different from the behavior of conductivity extrema in GaAs/AlGaAs heterostructures, in accordance with predictions of the inter-subband theory of MICO.

Regarding the MICO of SE caused by intra-subband photon-assisted scattering, the comparison between the experiment and theory shown in Fig. 4 indicates that Coulomb broadening $\varGamma _{\mathrm {C}}$ can correctly describe the width of oscillatory features of $\sigma _{xx}$. The experimental data [37] shown in Fig. 11 clear indicate that the shifts of conductivity minima $\delta _{+}=\omega /\omega _{c}\left( B_{+}\right) -m$ and maxima $\left| \delta _{-}\right| =\left| \omega /\omega _{c}\left( B_{-}\right) -m\right|$ steady increase with m, at least up to $m=5$ where they reach the number 1 / 4. Thus, for high magnetic fields, oscillatory variations are strongly confined near $\omega /\omega _{c}=2,3,$ and 4, and positions of minima are not fixed to “magic” numbers $m+1/4$ which is in contrast to data obtained for GaAs/AlGaAs in Ref. [16]. This difference can be attributed to a substantially smaller collision broadening of Landau levels of SE on liquid helium as compared to that of semiconductor devices. It should be noted also that deviations from a “1 / 4-cycle shift” are found in the ZRS regime ($m\le 4$) even for semiconductor electrons [55].

Fig. 11

$\sigma _{xx}$ versus $\omega / \omega _{c} (B)$ obtained at $T=0.56\,\mathrm {K}$, $\omega /2\pi =88.52\,\mathrm {GHz}$, $n_{e}=1.7\times 10^{7}\,\mathrm {cm}^{-2}$, and different values of the incident MW power P. For clarity, the curve for $65\,\mu \mathrm {W}$ (dark blue) is upshifted by $0.2\,\mathrm {nS}$ [37] (Color figure online)

4 Resonant Photovoltaic Effect

In the MICO experiments [27, 28] based on resonant inter-subband excitation, the magnetoconductivity data were obtained by measuring the average response of the electron system to a driving in-plane electric field. A remarkable result was found [32] by detecting the photoresponse of surface electrons in the absence of the driving electric field under the conditions where dissipative conductivity is vanishing $\sigma _{xx}$$\rightarrow 0$. The ultra-strong photovoltaic effect observed in this experiment is characterized by a nonequilibrium spatial distribution of electrons in the confining electrostatic potential. Moreover, the electrostatic energy acquired by an electron exceeds other relevant energies by several orders of magnitude.

Fig. 12

Schematic diagram of the experimental method. Detailed description is provided in the text [32] (Color figure online)

Redistribution of SE was detected by measuring photocurrents $I_{1}$ and $I_{2}$ induced in the inner (C$_{1}$) and outer (C$_{2}$) electrodes of a Corbino disk placed just above the electron pool, as shown in Fig. 12. In the absence of MW radiation, potentials applied to the guard electrodes G$_{1}$ and G$_{2}$ and to the bottom disk ($V_{\mathrm {B}}$) form a nearly uniform electron density along the liquid helium surface with a sharp edge. Electrons were tuned for the inter-subband resonance $\omega =\omega _{2,1}$ with the applied MW by adjusting $V_{\mathrm {B}}$. In order to study the transient photoresponse of SE, the incident MW power was pulse modulated using a low-frequency (0.5–6 Hz) square waveform. The results of the measurements are shown in Fig. 13 for currents $I_{1}$ and $I_{2}$ and the cumulative charge Q. The value of the magnetic field used for obtaining the current data shown in Fig. 13a corresponds to the $m=5$ conductance minimum. The modulation of the MW power by the square waveform is shown in Fig. 13a by a red dashed line. Sharp changes in $I_{1}$ and $I_{2}$ observed indicate that, upon switching the power on, the electrons are pulled by radiation toward the edge of the electron pool, causing the depletion of the charge in the central region of the pool. Correspondingly, the positive (negative) current is induced in electrode C$_{1}$ (C$_{2}$) by the flow of the image charge. The surface charge flows until a new spatial distribution of electrons in the unchanged confining electrostatic potential is established, after which the currents $I_{1}$ and $I_{2}$ become zero. Because of the displacement of SE with respect to the neutralizing background, a nonzero electric field is developed in the charged layer. Upon switching the power off, the displaced surface charge flows back to restore the equilibrium distribution of electrons. Correspondingly, a negative (positive) current of the image charge is induced in C$_{1}$ (C$_{2}$).

Fig. 13

a Transient signals of photocurrents $I_1$ (solid line, blue) and $I_2$ (dashed line, green) induced in electrodes $C_1$ and $C_2$, respectively, by the flow of the surface charge at $T=0.2\,\mathrm {K}$ and $B=0.62\,\mathrm {T}$. Short dashed line (red) is a square waveform, which switches the MW source on (off) at a high (low) signal level. b Cumulative charge Q obtained by integrating the current $I_1$ at three values of B corresponding to $m=4$ ($0.78\,\mathrm {T}$), $m=5$ ($0.62\,\mathrm {T}$), and $m=6$ ($0.52\,\mathrm {T}$) conductance minima [32] (Color figure online)

The cumulative charge Q flowing from, for example, the electrode C$_{2}$ is obtained by integrating the measured current $I_{1}$. The Q is shown in Fig. 13b in units of the elementary charge ($e>0$) for three values of B corresponding to the conductance minima $m=4$, 5, and 6. The estimation given in Ref. [32] indicates that a very large fraction (more than 50%) of the surface charge can be displaced upon irradiation. The numerical calculations show that the displacement of 50% of electrons leads to the potential difference between the central and peripheral parts $V_{e}\approx 0.3\,\mathrm {V}$. This result corresponds to the increase in electrical potential energy of a single electron exceeding other relevant energy scales such as the inter-subband energy difference or $T_{e}$, by several orders of magnitude.

A comparison between $\sigma _{xx}$ measured under MW irradiation and $\varDelta I=I_{1}-I_{2}$ recorded under 100% modulation of the incident MW power is shown in Fig. 14. Both sets of data were obtained [32] under the same experimental conditions and at the same level of MW power. Figure 14 proves a clear relationship between the conductance minima and the transient current: A nonzero signal $\varDelta I$ and a displacement of the surface change are observed only in the intervals of B near the conductance minima corresponding to $m=4$, 5 , 6, and 7. No signal is observed when electrons are tuned away from the inter-subband resonance by changing the electrical bias $V_{\mathrm {B}}$. Simultaneously, the detuning results in the complete disappearance of the MICO and ZRS.

Fig. 14

Current signal $\varDelta I$ (red solid) obtained under 100% modulation of the MW for $n_{e}=1.4\times 10^{6}\,\mathrm {cm}^{-2}$ and $T=0.2\,\mathrm {K}$ is compared with MICO (blue dashed) obtained under the same conditions. Black triangles indicate the values of B such that $\omega _{2,1}/\omega _c=m$ [32] (Color figure online)

A detailed relationship between $\sigma _{xx}$ and $\varDelta I$ in a narrow range of B near the $m=5$ conductance minimum is illustrated in Fig. 15. The signal $\varDelta I$ emerges sharply upon slowly increasing B when $\sigma _{xx}$ drops to zero. Thus, the abrupt change of $\varDelta I$ is an indication of instability of the electron system leading to formation of ZRS. Upon the downward sweep of B, $\sigma _{xx}$ (open circles) exhibits hysteresis. Such hysteresis is a feature of a metastable state coexisting with the global stable state of the electron system. We expect that such a hysteresis can be caused by decay heating of SE, which requires an additional theoretical investigation in the ripplon-dominated scattering regime.

Fig. 15

$\varDelta I$ (red) in the range of B close to $m=5$. For comparison, $2\sigma _{xx}$ is shown for upward (solid circles) and downward (open circles) sweeps of B. Experimental conditions are the same as in Fig. 14 [32] (Color figure online)

It is reasonable to attribute the resonant photovoltaic phenomena observed [32] to the effect of absolute negative dissipative conductivity ($\sigma _{xx}<0$) which appears in the inter-subband mechanism of MICO [29,30,31]. For example, in semiconductor systems, ZRS are explained [18] as a consequence of the negative linear conductivity condition $\sigma _{xx}<0$ which appears for high radiation power. Due to instability of the system under this condition, it enters a nonlinear regime and develops a steady current state $j_{0}$ with $\sigma _{xx}(j_{0})=0$. This predicts the existence of current domains, where electrons move in opposite directions [18]. Such a model of the ZRS is well applicable to semiconductor electrons. By the way, the current flow anomalies (similar to the photovoltaic effect discussed here) reported for the irradiated 2D electron gas in semiconductor structures [56] were ascribed to the theoretical pictures of instabilities due to local negative resistivities.

In the 2D Coulomb liquid on the surface of liquid helium, formation of current domains is unlikely because of strong electron correlations ($\varGamma ^{\left( \mathrm {pl}\right) }\gg 1$). The system of SE usually have no source and drain electrodes. Therefore, a steady current can be formed only by electrons circling the center of the electron pool. Since it is impossible to create a strong current density in the center, electrons will move to the edge of the electron liquid depleting the center. As a result, a nonuniform electron density distribution along the surface will be formed to provide radial electric field and a circling current, strong enough to make $\sigma _{xx}=0$. At a fixed magnetic field, a change in electron density additionally helps the system to leave the unstable regime, due to the Coulombic effect (see also related discussions in Chapter 7). It should be noted here that small transient photocurrents are also observed near the average conductivity minima corresponding to $m=6$ and 7 which do not reach zero. This can be explained by the assumption that under these conditions only a part of electrons has $\sigma _{xx}<0$ and moves uphill in the confining potential. Remarkably, for the $m=6$ minimum with $\sigma _{xx}>0$, a time delay of up to $0.1\,\mathrm {s}$ between the application of microwaves and the onset of the charge motion is observed, as indicated in Fig. 13b, which is in contrast to the results obtained for regions with $\sigma _{xx}=0$. The inter-subband mechanism of MICO and absolute negative conductivity do not require the in-plane component of the MW field. It should be noted that the in-plane component of $\mathbf {E}_{\mathrm {mw}}$ can also be a reason for an additional photocurrent [57], though its relation to the conductance minima is less evident.

5 Self-Generated Audio-Frequency Oscillations

In the regime of vanishing diagonal (dissipative) conductivity $\sigma _{xx}\rightarrow 0$, in addition to the static pattern (a strong depletion of charge at the center of the electron layer), the redistributed charge exhibits spontaneously generated oscillations in the audio-frequency range [33]. Oscillations reported were observed as an electrical current I induced in a circular metal electrode $\mathrm {C}_1$ ($7\,\mathrm {mm}$ radius), which was a part of the Corbino disk located $1.3\,\mathrm {mm}$ above the surface and used also for conductivity measurements (see Fig. 12).

The transient current triggered by switching on and off radiation pulses and shown above in Fig. 13a is actually an average over many traces. In a single trace, the current I shown in Fig. 16a has also oscillations which appear spontaneously. MW radiation was applied during $0\le t\le 1.0\,\mathrm {s}$, as indicated by the square red dashed line. The broad peak at $0< t < 0.25\,\mathrm {s}$ was due to the depletion of charge at the center of the pool as electrons were moving toward the edge. A peak of opposite sign at $1.0< t < 1.1 \,\mathrm {s}$ appeared as microwaves were switched off and the system restored the equilibrium charge distribution. According to Fig. 16a, there exists an additional oscillating signal at $0.25\le t\le 1.1 \,\mathrm {s}$, that persists as long as the system retains nonequilibrium distribution.

Fig. 16

Current at a metal electrode capacitively coupled to 2D electrons on the surface of liquid $^{3}\mathrm {He}$. The data were obtained at $T=0.2\,\mathrm {K}$ and $B=0.62\,\mathrm {T}$ using microwaves of frequency $\omega /2\pi =90.9\,\mathrm {GHz}$. The gain of current preamplifier sets its bandwidth, which was 100 and $2000\,\mathrm {Hz}$ for the data shown in panel (a) and (b), respectively. The high (low) level of the square waveform (dashed line) corresponds to microwave power on (off) [33] (Color figure online)

The trace of Fig. 16a was obtained similar to Ref. [32] using a current preamplifier with a bandwidth of $100 \,\mathrm {Hz}$, which attenuated significantly the high-frequency content of the current oscillations. This filtering was avoided by increasing the bandwidth to $2\,\mathrm {kHz}$. The respective time sequence of recorded oscillations is shown in Fig. 16b. In this case, the amplitude of the oscillating current was much larger than the current induced due to charge redistribution. The latter was too small to be seen in Fig. 16b because of the reduced sensitivity of the current preamplifier. The charge displaced during the half-period of the oscillations at their maximum amplitude was estimated to be about 5% of the total surface charge.

An important feature of the persisting oscillations shown in Fig. 16b is that they are not monochromatic. It is convenient to look at the wavelet transform, which provides information about the instantaneous frequency content of the recorded signal. The wavelet transform for the oscillations in Fig. 16b is shown in Fig. 17. The frequency varies periodically in time in the range of 100–500 Hz. These frequencies are in the audible range, which makes it possible to hear them by ear. In most experiments done with electrons on liquid $^{3}\mathrm {He}$, as well as superfluid $^{4}\mathrm {He}$, similar periodic variation in the frequency of oscillations with a period of about $0.2\,\mathrm {s}$ (independent of the substrate) was found. At the same time, the frequency of self-generated oscillations is about twice as large for electrons on superfluid $^{4} \mathrm {He}$ compared with electrons on liquid $^{3}\mathrm {He}$.

Fig. 17

Wavelet transform of oscillations shown in Fig. 16. Color represents intensity of the spectral component (Y-axis) of oscillations at a given time t [33] (Color figure online)

It is well known [58] that a 2D electron pool and the perpendicular electric field $E_{\bot }$ applied put pressure on the free surface of liquid helium causing a steady surface deformation proportional to the electron density and $E_{\bot }$. The depth of the surface depression h is substantial and can even be about $0.1\,\mathrm {mm}$ (at high $n_{e}$ and $E_{\bot }$). Obviously, the redistribution of the electron charge caused by the photovoltaic effect should induce a change in the surface depression reducing it in the center and increasing it in edge regions. For experimental conditions of Ref. [33], variations in the depth $\delta h$ induced by the redistribution of electrons can be about $10^{-6} \mathrm {cm}$. Therefore, the electron pool of displaced SE acquires a huge inertia. These changes of h in the central and edge regions cannot detune the electron system from the inter-subband resonance because respective corrections to $\varDelta _{2,1}$ are about four orders of magnitude smaller than the typical line width of the resonance caused by inhomogeneity of the electric field: $2\gamma _{\mathrm {mw}}\simeq 0.2\,\mathrm {GHz}$. Nevertheless, one can expect that the inhomogeneity is larger in the edge region than in the central part of the electron pool. In this case, even a small increase in $\gamma _{\mathrm {mw}}$ can detune slightly displaced SE from the inter-subband resonance in the edge region and eliminate the negative conductivity. The large deformation relief has a huge inertia leading to a delay before these electrons start moving back tuning themselves to the resonance again. This effect can cause radial oscillations of electron density coupled with gravity waves. The lowest frequency of the radially symmetrical mode of the gravity wave has an angular frequency [33] $\omega \approx 3.83\sqrt{gH}/R$ (here R is the radius of the electron pool, H is the height of the liquid surface, and g is the acceleration due to gravity) corresponding to about $3.6 \,\mathrm {Hz}$, which is close to the observed periodic variation in the self-generated frequency. Possible reasons for self-generated oscillations will be discussed in Sect. 7.

6 Incompressible States

A striking example of irradiation-induced self-organization was observed [34] in a coupled system of two electron gases of different densities. The 2D electron gases were formed on the surface of liquid $^{4} \mathrm {He}$: near the central Corbino electrode (with density $n_{\mathrm {e} }$) and near the guard-ring electrode (with density $n_{\mathrm {g}}$). The Corbino disk was similar to that shown in Fig. 12. The density of electrons coupled to the central electrode $n_{\mathrm {e}}\left( r\right)$ was approximately uniform. Regarding $n_{\mathrm {g}}\left( r\right)$, it was strongly nonuniform having a sharp maxima near the middle of the guard strip. Therefore, the notation $n_{\mathrm {g}}$ was attributed to the mean electron density in the guard region. At a fixed total number of electrons $N_{e}$, the ratio $n_{\mathrm {e} }/n_{\mathrm {g}}$ was varied by changing the potential $V_{\mathrm {g}}$ applied to the guard electrode. In the presence of resonant MW radiation, under the magnetic field fixed to the ZRS condition $\omega _{2,1}/\omega _{c}\left( B\right) =6.25$, the inner 2D electron gas enters an incompressible state with an electron density $n_{\mathrm {e}}=n_{\mathrm {c} }\simeq 3.4\times 10^{6}\,\mathrm {cm}^{-2}$ independent of $N_{e}$ and of the potential applied to the guard electrode for a wide range of parameters.

The compressibility of the 2D electron gas was defined as [34]

$$\begin{aligned} \chi =-\frac{\mathrm{d}n_{\mathrm {e}}}{\mathrm{d}V_{\mathrm {g}}}. \end{aligned}$$

(37)

In the absence of MW irradiation, over a large range of $V_{\mathrm {g}}$ and $N_{e}$, the compressibility was well approximated by the constant value $\chi _{0}\simeq 2.9\times 10^{6}\,\mathrm {cm}^{-2}\mathrm {V}^{-1}$ in good agreement with estimations obtained using the parameters of the experimental cell.

Outside the ZRS regions, the compressibility $\chi$ was not affected by MW irradiation because it is independent of $\sigma _{xx}$ for a stable regime ($\sigma _{xx}>0$). In a ZRS region, a remarkable change of $\chi$ was reported. The experimental dependence of $n_{\mathrm {e} }\left( V_{\mathrm {g}}\right)$ is shown in Fig. 18 for different $N_{e}$. In the dark case (dotted lines marked $n_{\mathrm {eD}}$ in the Legend), the electron compressibility defined by Eq. (37) is nearly constant. Under MW radiation in two distinct regions (I and II), the dependence $n_{\mathrm {e}}\left( V_{\mathrm {g}}\right)$ changes drastically, as shown by the solid lines marked $n_{\mathrm {eM}}$. For example, consider the blue solid line ($N_{e}=14.5\times 10^{6}$). Below $5.13 \,\mathrm {V}$, there is a sharp (nearly vertical) increase of $n_{\mathrm {eM}}$ up to a value $n_{\mathrm {c}}\simeq 3.4\times 10^{6}\,\mathrm {cm}^{-2}$. Then, there is a plateau with $\chi =0$. Remarkably, in the range $4.75\,\mathrm {V}<V_{\mathrm {g}}<4.9\,\mathrm {V}$ the system exhibits a negative (!) compressibility: $\chi <0$. At lower $V_{\mathrm {g}}$, the $n_{\mathrm {eM} }\left( V_{\mathrm {g}}\right)$ returns to the dependence observed for the dark case $n_{\mathrm {eD}}\left( V_{\mathrm {g}}\right)$. The value $n_{ \mathrm {c}}$ is not a universal constant because it depends on the conductivity minimum chosen: $n_{\mathrm {c}}$ decreases with the level matching number m. It was noted that for the magnetic field corresponding to $\omega _{2,1}/\omega _{c}=10+1/4$ the position of $n_{\mathrm {c}}$ is displaced toward significantly lower densities $n_{\mathrm {c}}\simeq 1.3\times 10^{6}\,\mathrm {cm}^{-2}$.

Fig. 18

Density of electrons coupled to the central electrode $n_{\mathrm {e}}$ versus the potential of the guard electrode $V_{\mathrm {g}}$ for $N_{e}=12.4, 14.5, 19\,[\times 10^{6}]$: in the dark $n_{\mathrm {eD}}$ (dotted) and under MW irradiation $n_{\mathrm {eM}}$ (solid) [34] (Color figure online)

The negative compressibility observed means that the electron pool squeezes when a potential gradient stretches it, and the pool expands when a potential gradient compresses it. This agrees with our understanding of negative conductivity effects: In an external electrostatic potential, electrons flow uphill. It should be noted that already from the existence of regions with $\sigma _{xx}<0$ ($\chi <0$) and $\sigma _{xx}>0$ ($\chi >0$), it follows that there should be at least one incompressible state ($\chi =0$) in between them. The most puzzling thing is that the incompressible state is observed in a quite broad region of $V_{\mathrm {g}}$. Upon a decrease in the total number of SE ($N_{e}$), the plateau of Fig. 18, as well as the regions with $\chi =\chi _{0}$, moves to a lower $V_{\mathrm {g}}$, while its vertical position remains unchanged: $n_{\mathrm {c}}\simeq 3.4\times 10^{6}\,\mathrm {cm}^{-2}$.

At $V_{\mathrm {g}}\approx 4\,\mathrm {V}$ (region II), there is another state with $\chi \rightarrow 0$; however, the plateau density value depends on $N_{e}$ in contrast to region I ($V_{\mathrm {g}}\approx 5\,\mathrm {V}$). It is reasonable to ascribe this plateau to an incompressible state of electrons situated above the guard ring, because the plot $n_{\mathrm {gM}}\left( V_{\mathrm {g} }\right)$ (not shown here) indicates that the vertical position of the corresponding plateau ($V_{\mathrm {g}}\approx 4\,\mathrm {V}$) is practically unchanged giving another critical density $n_{\mathrm {gM}}=n_{\mathrm {c}}^{\left( 2\right) }\simeq 1\times 10^{6}\,\mathrm {cm}^{-2}$. The relative “weakness” of this second incompressible state may be caused by the initial nonuniformity of the electron density near the guard-ring electrode $n_{\mathrm {g}}\left( r\right)$. Anyway, a mechanism selecting a particular density value was not explained in the original paper [34]. Possible relationship of the observed phenomenon with absolute negative conductivity and the Coulombic effect on MICO will be discussed in the next section.

7 Density Domains

A state of an electron system with $\sigma _{xx}<0$ is unstable, and usually a certain local current density $j_{0}$ is necessary to reach the stable state $\sigma _{xx}\left( j_{0}\right) =0$ owing to nonlinear effects [18]. According to this theory, the instability of a 2D electron system caused by negative conductivity leads to the pattern of the current distribution in a conducting strip: domain wall separating currents of the same amplitude $j_{0}$ but opposite directions. The position of the domain wall determines the net current. The current pattern in the Corbino geometry is obtained by connecting the edges of the current strip into a ring.

Surface electrons on liquid helium represent a highly correlated system, where the average Coulomb interaction potential energy per an electron is much larger than the average kinetic energy. In such an electron liquid, current domains are unlikely due to the strong mutual friction of currents in the domain wall (the electron system is close to the Wigner solid state). Therefore, the internal structure of the ZRS of SE on liquid helium requires an additional investigation. Considering only nonlinear effects of $\sigma _{xx}\left( j\right)$, as the origin of stability in a Corbino geometry (without current domains), we came to the conclusion [31] that the center of the electron pool should be depleted in accordance with experimental observation of the ultra-strong photovoltaic effect [32]. A strong displacement of electrons against the confining force of Corbino electrodes gives us an important insight into this problem because the Coulombic effect on magnetoconductivity minima discussed in Sect. 3 can also be the cause making $\sigma _{xx}\ge 0$.

At first, it is instructive to track the evolution of $\sigma _{xx}$ minima with increasing SE density $n_{e}$ qualitatively using simple analytical equations. According to Eq. (34), the integrand of the expression for $\sigma _{xx}$ contains derivatives of the sum of Gaussian functions entering the DSF of the Coulomb liquid. If we neglect overlapping of the sign-changing terms in the sum over the all m, then positions of minima of the integrand are given by

$$\begin{aligned} \frac{\omega _{2,1}}{\omega _{c}}=m+\frac{\gamma _{2,0;1,m}}{\sqrt{2}\omega _{c}}+x_{q}\frac{\varGamma _{\mathrm {C}}^{2}}{4T_{e}\hbar \omega _{c}}, \end{aligned}$$

(38)

where $\gamma _{l,n;l^{\prime },n^{\prime }}$ defines the broadening of $S_{l,l^{\prime }}\left( q,\varOmega \right)$ minima. The last term in the right side represents the Coulomb correction which depends on the wave vector $\mathbf {q}$. Therefore, integration over $\mathbf {q}$ affects the position of conductivity minima. Numerical calculations indicate that for estimation of positions of $\sigma _{xx}$ minima, we can use Eq. (38) with a simple replacement $x_{q}\sim m$. The results of accurate numerical calculations are shown below in Fig. 19. Thus, the shift of a conductivity minimum from an integer m increases monotonically with electron density due to the Coulomb broadening $\varGamma _{\mathrm {C}}$ entering also $\gamma _{2,0;1,m}$. At large m and $\varGamma _{\mathrm {C}}$ when the sign-changing terms become strongly overlapping, the positions of minima are asymptotically given by

$$\begin{aligned} \frac{\omega _{2,1}}{\omega _{c}}=m+\frac{1}{4}+x_{q}\frac{\varGamma _{\mathrm {C }}^{2}}{4T_{e}\hbar \omega _{c}}, \end{aligned}$$

(39)

where $x_{q}\sim m$. In this limiting case, the deviation of minima from the level matching point also increases monotonically with electron density.

Fig. 19

Magnetoconductivity in a DC electric field calculated for $T=0.3\,\mathrm {K}$ (liquid $^{4}\mathrm {He}$) and four values of $n_{e}$. Values of $n_{e}$ are shown in units of $10^{6} \,\mathrm {cm}^{-2}$. Circles indicate evolution of $\sigma _{xx}$ with varying $n_{e}$ for a fixed B (vertical line) [35] (Color figure online)

For a typical region of B, the evolution of the position of a conductivity minimum with varying $n_{e}$ is illustrated in Fig. 19. One can see that an increase in $n_{e}$ affects the chosen minimum in two ways: The position of the minimum moves to the region of larger $\omega _{2,1}/\omega _{c}$ and higher $\sigma _{xx}$. Therefore, at a fixed magnetic field shown by the vertical dotted line, and at the lowest density $n_{e}=5\times 10^{6}\,\mathrm { cm}^{-2}$, electron conductivity $\sigma _{xx}>0$, as indicated by the olive circle representing the cross point of the olive dash-dot-dotted line with the vertical line. The increase in $n_{e}$ up to $5.5\times 10^{6}\,\mathrm {cm} ^{-2}$ moves the cross point down making the ZRS ($\sigma _{xx}=0$), as indicated in Fig. 19 by the open blue circle. A further increase in $n_{e}$ makes absolute negative conductivity ($\sigma _{xx}<0$) shown by the red circle representing the cross point of the red dashed curve ($n_{e}=6\times 10^{6}\,\mathrm {cm}^{-2}$) and the vertical line. The vertical shift of the minimum caused by the Coulombic effect eventually makes $\sigma _{xx}\ge 0$, as shown by the solid curve calculated for $n_{e}=7.25\times 10^{6}\,\mathrm {cm}^{-2}$. Thus, for a fixed magnetic field, the instability ($\sigma _{xx}<0$) appears inside a certain region restricted by two critical densities (higher $n_{\mathrm {H}}$ and lower $n_{\mathrm {L}}$). At $n_{e}=n_{ \mathrm {L}}$, or at $n_{e}=n_{\mathrm {H}}$  the system is in the ZRS. The length of the unstable region $n_{\mathrm {H}}-n_{\mathrm {L}}$ depends strongly on the position of the vertical line (chosen B) with regard to the ZRS that appeared for the solid curve of Fig. 19. It should be noted that theoretical calculations shown in this figure were calculated assuming $T_{e}=T$. Heating of SE induced by decay of the excited electrons increases the fluctuational electric field and the Coulombic effect; therefore, it should decrease the estimated values of $n_{\mathrm {H}}$ and $n_{\mathrm {L}}$ .

A negative $\sigma _{xx}$ means that any density fluctuation $\delta n_{e}$ (positive or negative) diffusively grows, because it induces a potential gradient for electrons moving uphill. This is the natural reason for the instability. It is quite obvious that the density of growing regions is limited by the conditions: $n_{e}+\delta n_{e}=n_{\mathrm {H}}$ and $n_{e}+\delta n_{e}=n_{\mathrm {L}}$ (for $\delta n_{e}<0$). Indeed, a change of $n_{e}+\delta n_{e}$ above $n_{\mathrm {H}}$ (below $n_{\mathrm {L}}$) makes $\sigma _{xx}>0$ and the excess charge will move back in the field induced by the fluctuation. Therefore, the electron system with $n_{\mathrm {L }}<n_{e}<n_{\mathrm {H}}$ eventually will be separated into fractions (domains) with different densities $n_{\mathrm {L}}$ and $n_{\mathrm {H}}$.

Fig. 20

Pattern of the density distribution with a domain wall for the Corbino geometry [35] (Color figure online)

For a Corbino geometry, the simplest stable pattern of the density distribution with a domain wall is shown in Fig. 20. It is assumed that the direction of the charge displacement caused by negative conductivity should be opposite to the direction of the confining force of Corbino electrodes acting on SE. Two blue arrows indicate that in different domains near the domain wall (red dashed circle) local currents flow in the same direction in contrast to the case of current domains. The position of the domain wall (the areas $S_{\mathrm {H}}$ and $S_{\mathrm {L}}$) corresponding to the initial density $n_{e}$ is determined by the simple rule  [35]:

$$\begin{aligned} \frac{S_{\mathrm {H}}}{S_{\mathrm {L}}}=\frac{n_{e}-n_{\mathrm {L}}}{n_{\mathrm { H}}-n_{e}} \end{aligned}$$

(40)

representing the conservation of charge. One can imagine also an asymmetrical distribution of surface charges with a domain wall cutting the circle of the electron pool as a segment and rotating as a whole in the direction determined by $\mathbf {B}$. By now, the experiment on the resonant photovoltaic effect [32] favors the symmetrical distribution indicated in Fig. 20.

If the domain wall is sharp, the separation of charges shown in Fig. 20 is stable while the resonant MW excitation keeps $\sigma _{xx}=0$ in the domains. Assume some electrons by chance have moved from the area $S_{ \mathrm {L}}$ to the area $S_{\mathrm {H}}$. This will make $\sigma _{xx}>0$ in both areas, and the same amount of electrons will return back due to the inner electric field induced by charge separation. In the contrary case, when some electrons have moved from the area $S_{\mathrm {H}}$ to the area $S_{\mathrm {L}}$, in both domains $\sigma _{xx}$ becomes negative, and the same amount of electrons will return back moving uphill. Thus, under the condition of Eq. (40), the domain structure is in a dynamic equilibrium. The same arguments are valid also for an asymmetrical distribution of surface charges discussed above.

Formation of the domain structure caused by negative conductivity effects explains electron redistribution observed under resonant MW radiation [32]. According to theoretical estimations, the displaced fraction of electrons can be of the order of $N_{e}$ which agrees with observations. The domain structure of electron density can explain also self-generated oscillations observed in the experiment [33]. If the inter-edge profile of the density domain wall is sufficiently smooth, a negative dissipative conductivity $\sigma _{xx}$ can be ascribed to a narrow strip of the domain wall. It is quite obvious that this can lead to a negative damping and to self-generation of the inter-edge modes. The same argument is applicable to the edge excitations propagating along the edge of the electron pool if the net conductivity within the edge profile is negative.

There are two kinds of inter-edge modes: inter-edge magnetoplasmons (IEMP) [59] and boundary displacement waves (BDW) [60, 61]. Both of them have similar gapless spectra at strong magnetic fields, and usually they are strongly coupled. For example, the frequency of IEMP decreases with B as [59]

$$\begin{aligned} \omega _{\mathrm {IEMP}}=2q_{y}\left( \sigma _{yx}^{\mathrm {H}}-\sigma _{yx}^{ \mathrm {L}}\right) \left( \ln \frac{1}{\left| q_{y}\right| w} +C\right) , \end{aligned}$$

(41)

where $\sigma _{yx}^{\mathrm {H/L}}\propto n_{\mathrm {H/L}}/B$, the constant C depends on details of the density profile, w is the width of the transition layer, and $q_{y}$ is the wavevector component along the boundary. The frequency $\omega _{\mathrm {BDW}}$ of the BDW differs from Eq. ( 41) only by a numerical factor of the order of unity [60]. Experimental observations of the IEMP [62] and BDW [63,64,65] are in agreement with the theories. It should be noted that the BDW can propagate in an incompressible 2D electron liquid. For the typical length of the domain wall, both frequencies $\omega _{\mathrm {IEMP}}$ and $\omega _{\mathrm {BDW}}$ belong to the audio-frequency range which is approximately the same as that reported for self-generated oscillations observed [33]. Thus, experimental observation of self-generated audio-frequency oscillations can be considered as a convincing evidence for negative conductivity coexisting with the ZRS of surrounding domains.

Here, we would like to note an interesting analogy with current domains in a 2D electron gas formed in semiconductors. Nonuniformities in the electron density can lead, under certain circumstances, to time-dependent domain patterns in the microwave-induced ZRS [66]. This result was used for explanation of random telegraph signals observed in the zero-resistance regime [67]. As noted above, electrons on liquid helium form a highly correlated Coulomb liquid which in some respects resembles the Wigner solid. Therefore, electron velocities at the two sides of the domain wall are expected to be the same, and the results obtained for semiconductor electrons cannot be applied directly to the SE system.

The appearance of two critical electron densities $n_{\mathrm {H}}$ and $n_{ \mathrm {L}}$ restricting the instability range provides also an insight into the nature of the incompressible state observed for the system of two coupled 2D electron gases [34]. One can expect anomalies on the dependence $n_{\mathrm {eM}}\left( V_{\mathrm {g}}\right)$ near $n_{ \mathrm {H}}$ and $n_{\mathrm {L}}$. In Ref. [35], the plateau value $n_{\mathrm {c}}$ of Fig. 18 was naturally ascribed to $n_{\mathrm {H}}$ , while the density to which the solid line falls down at $V_{g}\simeq 5.13 \,\mathrm {V}$ was ascribed to $n_{\mathrm {L}}$. Note that the later density point is also practically independent of $N_{e}$ according to the data [34]. This assumption is in accordance with the conclusion that the system is unstable in the region $n_{\mathrm {L}}<n_{e}<n_{\mathrm {H}}$. Thus, we have $n_{\mathrm {H}}\simeq 3.4\times 10^{6}\,\mathrm {cm}^{-2}$ and $n_{ \mathrm {L}}\simeq 1.2\times 10^{6}\,\mathrm {cm}^{-2}$. It is remarkable that the small upper plateau of $n_{\mathrm {eM}}\left( V_{\mathrm {g}}\right)$ and the plateau of $n_{\mathrm {gM}}\left( V_{\mathrm {g}}\right)$ formed at $V_{G}\approx 4\,\mathrm {V}$ resulting in the second critical density $n_{ \mathrm {gM}}=n_{\mathrm {c}}^{\left( 2\right) }\simeq 1\times 10^{6}\,\mathrm {cm} ^{-2}$ are close to the condition $n_{\mathrm {c}}^{\left( 2\right) }=n_{ \mathrm {L}}$.

Of course, the experimental conditions of Ref. [34] were different from usual conditions of MICO experiments [32, 33] because in this work density domains were created artificially by applying different potentials to the guard ($V_{\mathrm {g}}$) and central ($V_{\mathrm {B}}$) electrodes of the Corbino geometry. In this case, the presence of a neighbor 2D electron gas located in the range of the guard electrodes affects properties of inner electrons, and compressibility $\chi$ defined in Eq. (37) using $n_{\mathrm {e}}\left( V_{\mathrm {g}}\right)$ cannot be ascribed solely to electrons of the central region. Nevertheless, $\chi$ measured gives important information about 2D electron gases under MW irradiation.

The regime of the experiment [34] can be related to the domain wall structure discussed here only if both densities $n_{\mathrm { e}}$ and $n_{\mathrm {g}}$ belong to the unstable region $n_{\mathrm {L}}<n_{ \mathrm {g}},n_{\mathrm {e}}<n_{\mathrm {H}}$. Luckily, such a regime occurs when $n_{\mathrm {e}}$ is a bit lower than $n_{\mathrm {c}}$ ascribed to $n_{ \mathrm {H}}$. As noted in Ref. [35], in this case, $n_{\mathrm {g}}$ is somewhat larger than $n_{\mathrm {L}}$, which allows explaining the stability of the state $n_{\mathrm {e}}=n_{\mathrm {c}}=n_{\mathrm {H}}$ for finite ranges of $V_{\mathrm {g}}$ and $N_{e}$. According to the theoretical analysis of the experimental situation, the whole electron system should be separated in two parts with fixed densities $n_{\mathrm {H}}$ and $n_{\mathrm {L}}$ with a domain wall positioned between the edge of the center electrode ($R_{I}=0.7 \,\mathrm {cm}$) and the edge of the guard electrode ($R_{\mathrm {G}}=1.3 \,\mathrm {cm}$). The high density domain with $n_{e}=n_{\mathrm {H}}$ is placed in the center of the electron pool because the potential applied to the guard electrode is opposite to the usual case (SE are attracted to the guard region). For such a distribution of SE, a change in the total number of electrons $N_{e}$ can only shift the position of the domain wall $R_{ \mathrm {D}}$ inside the region $R_{I}<R_{\mathrm {D}}<R_{\mathrm {G}}$ which cannot affect the number of electrons coupled to the central electrode and the current I. This explains the independence of the number of electrons coupled to the central electrode of the total number $N_{e}$ when $n_{\mathrm {e}}=n_{\mathrm {c}}=n_{\mathrm {H}}$.

One can imagine a distribution of SE with a domain wall placed inside the central electrode $R_{\mathrm {D}}<$$R_{I}$. In this case, the average density of electrons coupled to the central electrode will be dependent on $N_{e}$, while the average density of electrons coupled to the guard electrode will be approximately constant. This remarkably reminds the experimental situation related to the second plateau observed in the region II of Fig. 18 (at $V_{\mathrm {g}}\sim 4\,\mathrm {V}$).

8 Polarization Dependence

For the inter-subband mechanism of MICO and ZRS, the crucial point is that the MW field $\mathbf {E}_{\mathrm {mw}}$ should have a vertical component $E_{ \mathrm {mw}}^{\left( z\right) }\ne 0$. The in-plane component of this field is unimportant because at typical MW powers used in the experiments with inter-subband excitation [27, 28] the photon-assisted scattering of SE can be neglected due to $m_{e}\gg m_{e}^{*}$. At the same time, for the theory of photogalvanic current [57], the presence of the in-plane component of $\mathbf {E}_{\mathrm {mw}}$ is crucial, and its contribution to the photovoltaic effect can be verified by using the MW field of pure vertical polarization $E_{\mathrm {mw}}^{\left( z\right) }=E_{\mathrm {mw}}$.

Regarding the intra-subband mechanisms of MIRO and MICO, the polarization dependence of oscillations was considered as a major experimental test for theoretical models. Among these mechanisms, there is a large group of models whose description is based on the theory of photon-assisted scattering off disorder. The displacement and inelastic mechanisms discussed in Ref. [24] and in Sect. 2.1 (for SE on liquid helium) represent the most elaborated examples of such models. Both the displacement and inelastic models give satisfactory descriptions of MIRO in semiconductor heterostructures, if the dependence of MIRO on the direction of circular polarization is not considered. The results of theories based on the photon-assisted scattering are very sensitive to the direction of circular polarization. At the same time, the MIRO observed in semiconductor heterostructures are notably immune to the sense of circular polarization [68] or have a very weak dependence on the direction of circular polarizations in the terahertz range [69] which is at odds with existing theories of MIRO. Therefore, experiments on MICO caused by intra-subband excitation of SE on liquid helium were expected to help with understanding of the origin of these oscillations and ZRS.

It should be noted firstly that the displacement model gives a strong dependence of MICO on the direction of linear MW polarization shown in Fig. 3. In contrast, the MICO obtained in the inelastic model have the linear polarization immunity: $\bar{\chi }_{\bot }=\bar{\chi }_{\Vert }$ as indicated in Eq. (22). This immunity appears because the transition rate $r_{n,n^{\prime }}$ given in Eq. (20) is finite in the limit $E_{\Vert }\rightarrow 0$, and integration over the angle of the vector $\mathbf {q}$ results in equal averaging of $q_{x}^{2}$ and $q_{y}^{2}$ entering the polarization parameter $\beta _{p,\mathbf {q}}$ of Eq. (10 ). Obviously, the difference of the results given by these two models cannot be verified in the usual experimental setup employing the Corbino disks. On the other hand, the Corbino geometry of the experimental cell is very suitable for the test on the circular-polarization dependence of MICO.

Consider circular polarizations of the in-plane MW field ($p=+$ and $p=-$) determined by the following values of parameters a and b entering the definition of $\beta _{p,\mathbf {q}}$: $a_{\pm }=1$, $b_{\pm }=\pm 1$. The probability of one-photon-assisted scattering is proportional to $J_{1}^{2}\left( \beta _{p,\mathbf {q}}\right) \simeq \beta _{p,\mathbf {q} }^{2}/4$, if the parameter $\beta _{p,\mathbf {q}}$ is small. Therefore, the ratio of MW-induced corrections to the DC dissipative conductivity obtained for different directions of circular polarization is described as

$$\begin{aligned} \frac{\varDelta \sigma _{xx}^{\left( +\right) }}{\varDelta \sigma _{xx}^{\left( -\right) }}=\frac{\left( \omega /\omega _{c}+1\right) ^{2}}{\left( \omega /\omega _{c}-1\right) ^{2}} \end{aligned}$$

(42)

This equation is valid for both the displacement and inelastic mechanisms of MICO, because, for a circular polarization, $\beta _{p,\mathbf {q}}$ is independent of the direction of the wave vector $\mathbf {q}$. The ratio of Eq. (42) is large for $m=2$ (it equals 9) and $m=3$ (it equals 4), but it approaches unity if m increases.

Circular-polarization-dependent studies of MICO [38] were done in a 2D electron system formed on the free surface of liquid $^{3} \mathrm {He}$, which was contained in a closed cylindrical cell and cooled to $T=0.2\,\mathrm {K}$. The magnetic field B was applied perpendicular to the liquid surface, and the longitudinal conductivity of electrons $\sigma _{xx}$ was measured by the capacitive-coupling method using a pair of gold-plated concentric circular electrodes (Corbino disk) placed beneath and parallel to the liquid surface. Conductivity oscillations were excited by the electric field component of the fundamental $\mathrm {TEM}_{002}$ mode in a semiconfocal Fabry–Perot resonator [70]. The resonator is formed by the Corbino disk acting as a flat reflecting mirror and a copper concave mirror placed above and parallel to the Corbino disk (similar to the cell of the experiment [37] shown in Fig. 21). At liquid helium temperatures, the $\mathrm {TEM}_{002}$ mode had the frequency $\omega /2\pi \approx 35.21\,\mathrm {GHz}$, and the quality factor was about $10^{4}$.

Fig. 21

Sketch of the experimental cell. White lines show electric field contours calculated for $\mathrm {TEM}_{003}$ mode. The pool of 2D electrons (not shown) is formed on the surface of liquid helium above electrodes $C_1$ (central) and $C_2$ (middle) [37] (Color figure online)

The $\sigma _{xx}$ data [38] plotted as a function of the magnetic field B are shown in Fig. 22 for two opposite directions of circular polarization $p=\pm$. The strong dependence of the amplitude of oscillations on the direction of circular polarization indicated in this figure is at least in qualitative agreement with predictions of the theories based on photon-assisted scattering. In the region $B>0$, the MICO amplitude is larger for $p=+$ (red solid curve), while in the opposite region $B<0$, it is larger for $p=-$ (blue dashed curve).

Fig. 22

$\sigma _{xx}$ of SE at $T=0.2\,\mathrm {K}$ and $n_{e}=5.1\times 10^{6}\,\mathrm {cm}^{-2}$ versus B for two directions of circular polarization of the MW field ($\omega /2\pi =35.213\,\mathrm {GHz}$): $p=+$ (red solid) and $p=-$ (blue dashed). Black triangles indicate the values of B such that $\omega /\omega _c=m$ [38] (Color figure online)

Fig. 23

Ratio $\varDelta \sigma _{xx}^{\left( +\right) }/\varDelta \sigma _{xx}^{\left( -\right) }$ versus $\omega / \omega _{c}$: results obtained from experimental data for conductivity maxima (filled circles and squares) and minima (open circles and squares), the ratio of peak-to-peak amplitudes (triangles and crosses), the ratio of amplitudes obtained for positive and negative B using the red solid curve (SC) of Fig. 22, theory [Eq. (3)] calculated for the circular polarization (CP, red solid line), and theory using the elliptic polarization (EP) with $a_{\pm }=0.7$ and $b_{\pm }=\pm 1.3$ calculated for minima (open rhombuses) [38] (Color figure online)

The quantitative comparison of the theory and experiment is shown in Fig. 23. Here, the red solid line represents the ratio $\varDelta \sigma _{xx}^{\left( +\right) }/\varDelta \sigma _{xx}^{\left( -\right) }$ given in Eq. (42). Experimental results extracted from the data of Fig. 22 were plotted separately for maxima (solid circles and squares) and minima (open circles and squares), because the ratio $\varDelta \sigma _{xx}^{\left( +\right) }/\varDelta \sigma _{xx}^{\left( -\right) }$ depends strongly on B. The accuracy of this procedure was confirmed by the ratio of peak-to-peak amplitudes (triangles) which does not depend on the background. To ensure that a possible power difference did not affect the results, the ratio of respective amplitudes obtained at positive and negative B from the same curve (red solid) of Fig. 22 was plotted as squares and crosses. The experimental data show that $\varDelta \sigma _{xx}^{\left( +\right) }/\varDelta \sigma _{xx}^{\left( -\right) }$ increases with lowering $\omega /\omega _{c}$ in accordance with the theory. Still, at average, they are lower than theoretical values obtained for pure circular polarizations by about 1.4. This numerical discrepancy was explained [38] by deviation from circularity (ellipticity) of the MW field. Note that even a relatively small response at CR conditions for the MW field with $p=-$, which was observed in the experiment [38], suggests substantial deviations of parameters $a_{\pm }$ and $\left| b_{\pm }\right|$ from unity. In Fig. 23, the open-rhombus symbols show the result of calculations performed for polarization parameters $a_{\pm }$ and $b_{\pm }$ estimated from the photocurrent response at CR conditions. Thus, the dependence of MICO on the direction of circular polarization of the MW observed [38] is in a good (even numerical) agreement with the theory based on photon-assisted scattering.

Regarding the mysterious immunity of MIROs to the sense of circular polarization reported previously [68] for the 2D electron gas in GaAs/AlGaAs heterostructures, it could be a property of particular semiconductor samples. Recent numerical simulations [71] of electron dynamics in the vicinity of an impurity indicate that the MW irradiation generates a rotating charge density vortex whose field eventually leads to immunity of MIRO to the sense of circular polarization at high electron densities typical for semiconductor systems. The densities of SE on liquid helium usually are several orders of magnitude smaller than in semiconductor heterostructures.