1 Introduction

In restricted geometries, such as films and wires, the transition temperature \(T_c\) from the normal (N) state to an unconventional superconducting (SC) state is reduced compared to its value in bulk owing to pair-breaking at the surface. The pair-breaking effect extends over several coherence lengths from the surface, and thus the \(T_c\) reduction is substantial when the system size is of the order of the coherence length \(\xi _0\). A pioneering theoretical study of the size effect on the N–SC transition was reported by Nagato and Nagai [1] for a d-wave SC film with specular surfaces. They considered the situation in which one of the d-wave gap nodes points toward the surface. In this case, the gap function vanishes at the surface and, simultaneously, the Andreev bound states are formed at zero energy [2]. It was shown in Ref. [1] that the transition temperature \(T_c(D)\), as a function of film thickness D, exhibits reentrant behavior similar to that in the p-wave polar state confined in a slab [3].

Vorontsov [4] reconsidered the same film system and showed that a new SC state with broken time-reversal symmetry (\(\mathcal {T}\)) is stabilized at low temperatures, below the reentrant temperature. The \(\mathcal {T}\) breaking is due to a finite center-of-mass momentum \(\mathbf {q}\) of the Cooper pairs, inducing a spontaneous current along the film surface. In the d-wave SC film, the homogeneous (\(\mathbf {q} = 0\)) SC state becomes unstable at low temperatures because the Andreev bound states carry a large current in the direction opposite that of the condensate current and this backflow makes the total superfluid mass negative [5]. As a result, the \(\mathbf {q} \ne 0\) SC state is stabilized in the film at low temperatures [4, 6]. The negative mass can also be concluded from the fact that odd-frequency pairs, which are created at the surface, yield a negative superfluid density [7, 8].

Fig. 1
figure 1

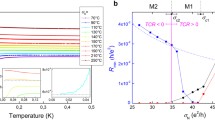
Phase diagram of the d-wave SC films with a \(\mu = -3.9t\), b \(\mu = -0.3t\), and c \(\mu = -0.01t\). The red solid line is the N–SC phase boundary. The numerical results of the phase boundary between the \(q \ne 0\) and \(q = 0\) SC states are shown by the symbol \( \bullet \) (the dotted line is a visual guide). The insets in a–c show the Fermi surfaces corresponding to the \(\mu \) values. A spontaneous current flows in the \(q \ne 0\) SC state, as depicted in the upper-right panel. The “backflow” near the surfaces is carried by the Andreev bound states. The lower-right panel shows the numerical results of the current distribution in the \(q \ne 0\) SC state with \(\pi \xi _0 / D = 0.3\). The total current \(J_\mathrm{tot}\) vanishes because of the backflow. (Color figure online.)

Full size image

An alternative viewpoint of the stabilization mechanism is provided by an analogy with the Fulde–Ferrell–Larkin–Ovchinnikov (FFLO) state [9, 10], which is a spatially nonuniform SC state stabilized in bulk spin-singlet superconductors in strong magnetic fields. When a strong magnetic field is applied, the spin-singlet pairing is suppressed. The corresponding suppression of the momentum-dependent pair amplitude can be diminished on some portions of the Fermi surface by inducing a spatial modulation of the gap function, so that the FFLO state is stabilized. In the case of a film, the surface pair-breaking triggers an additional spatial modulation along the film surface.

This viewpoint suggests that the transition to inhomogeneous SC states is sensitive to the Fermi surface shape. In fact, as has been shown in studies of FFLO states [11–13], the critical field is significantly enhanced when the Fermi surface has a good nesting property. In this work, we address the Fermi surface effect on the phase diagram of the d-wave SC film. In our previous work [14], we demonstrated that the critical thickness \(D_c\) between the normal and \(\mathcal {T}\)-breaking SC states is very sensitive to the Fermi surface shape. Here, we present numerical results of the temperature–thickness phase diagram, including the phase boundary between the \(\mathcal {T}\)-breaking and \(\mathbf {q} = 0\) SC states. We demonstrate the Fermi surface effect using a square-lattice tight-binding model and show that the stability region of the \(\mathcal {T}\)-breaking state is substantially enlarged as the Fermi surface approaches a square shape.

2 Model and Method

The d-wave SC film considered here is shown in Fig. 1. The film surfaces along the x axis are located at \(y = \pm D/2\). For simplicity, we assume that the film surfaces are specular (see Ref. [6] for the diffuse surface scattering effect in the d-wave SC film). The superconductivity in the film is characterized by the pairing interaction

$$\begin{aligned} V(\mathbf {p}_F^{}, \mathbf {p}_F') = -V\gamma (\phi )\gamma (\phi ') \end{aligned}$$
(1)

with \(\gamma (\phi ) \propto \sin (2 \phi ) \propto p_{x} p_{y}\). Here, \(\phi \) is the angle between the Fermi momentum \(\mathbf {p}_F\) and the x axis. The \(d_{xy}\) symmetry of \(\gamma (\phi )\) implies the existence of the Andreev bound states. We are interested in a SC state with the \(\mathcal {T}\)-breaking spin-singlet gap matrix [4, 6, 14]

$$\begin{aligned} \varDelta (\mathbf {r}, \mathbf {p}_F) = \gamma (\phi ) e^{iqx} \varDelta (y) i\sigma _2, \end{aligned}$$
(2)

where \(\sigma _2\) is a Pauli matrix. To demonstrate the Fermi surface effect, we employ the square-lattice tight-binding model, giving the dispersion

$$\begin{aligned} \xi _{\mathbf {p}} = -2t (\cos p_x + \cos p_y) - \mu . \end{aligned}$$
(3)

By controlling the chemical potential \(\mu \), we can change the Fermi surface shape from cylindrical (\(\mu \rightarrow -4t\)) to square (\(\mu \rightarrow 0\)).

Our theory for determining the phase diagram is based on the quasiclassical Green’s function method [15, 16]. The quasiclassical Green’s function \(\hat{g}\) is defined as a \(4 \times 4\) matrix in Nambu space and satisfies the Eilenberger equation

$$\begin{aligned} i\mathbf {v}(\mathbf {p}_F) \cdot \nabla _{\mathbf {r}}\, \hat{g} = \left[ \hat{g},\, \begin{pmatrix} i\epsilon _n \mathbf {1} &{} \varDelta (\mathbf {r}, \mathbf {p}_F) \\ -\varDelta (\mathbf {r}, \mathbf {p}_F)^\dag &{} -i\epsilon _n \mathbf {1} \end{pmatrix} \right] ,\ \hat{g}^2 = -1, \end{aligned}$$
(4)

where \(\mathbf {v}(\mathbf {p}_F)\) is the Fermi velocity, \(\epsilon _n\) is the Matsubara frequency, \(\mathbf {1}\) is the unit matrix in spin space, and \(\varDelta (\mathbf {r}, \mathbf {p}_F)\) is the spin-space gap matrix defined in Eq. (2). The boundary condition at the film surface is \(\hat{g}_\mathrm{out} = \hat{g}_\mathrm{in}\), where \(\hat{g}_\mathrm{in\, (out)}\) is the surface value of \(\hat{g}\) at the Fermi momentum along the incoming (outgoing) direction in a specular reflection process for a given parallel momentum \(p_x\). The quasiclassical Green’s function has the matrix structure

$$\begin{aligned} \hat{g} = \begin{pmatrix} g(y, \phi , \epsilon _n) \mathbf {1} &{} e^{iqx}f(y, \phi ,\epsilon _n)i\sigma _2 \\ e^{-iqx}f(y, \phi - \pi , \epsilon _n)^*i\sigma _2 &{} -g(y, \phi ,\epsilon _n) \mathbf {1} \\ \end{pmatrix}. \end{aligned}$$
(5)

The gap function \(\varDelta (y)\) is given in terms of the pair amplitude \(f(y,\phi ,\epsilon _n)\) as

$$\begin{aligned} \varDelta (y) = VN(0) \pi T \sum _{\epsilon _n}{}^{'} \left\langle \rho (\phi ) \gamma (\phi ) f(y, \phi , \epsilon _n) \right\rangle _{\phi }, \end{aligned}$$
(6)

where \(\left\langle \cdots \right\rangle _\phi = \int _{-\pi }^{\pi }(\cdots )d\phi /2\pi \) denotes the angle average. We denote the density of states in the normal state at the Fermi level by \(N(0)\rho (\phi )\) with \(\rho (\phi )\) normalized as \(\left\langle \rho (\phi ) \right\rangle _\phi = 1\). The prime on the sum means that a cutoff is necessary for the Matsubara sum. From \(g(y, \phi , \epsilon _n)\), we can obtain the current density as

$$\begin{aligned} \mathbf {J}(y) = -2N(0)\pi T \sum _{\epsilon _n}{}\left\langle \rho (\phi ) \mathbf {v}(\mathbf {p}_F) g(y,\phi ,\epsilon _n) \right\rangle _\phi . \end{aligned}$$
(7)

In the \(\mathcal {T}\)-breaking SC state, a finite current flows along the film (x direction). However, the total current

$$\begin{aligned} J_\mathrm{tot} = \int _{-D/2}^{D/2} \mathrm{d}y\, J_x(y) \end{aligned}$$

is zero, as it should be for the ground state. In the d-wave SC film, \(J_\mathrm{tot}\) can vanish because of the backflow carried by the Andreev bound states. Finally, the free energy (per unit volume) measured from the normal state is given as [17]

$$\begin{aligned} \Omega =&N(0)\int _{-D/2}^{D/2} \frac{\mathrm{d}y}{D}\, \Bigg [ \frac{|\varDelta (y)|^2}{VN(0)} \nonumber \\&- 2\pi T \sum _{\epsilon _n}{}^{'} \left\langle \rho (\phi )\gamma (\phi ) \int _0^1 d\lambda \, \mathrm{Re}\left[ \varDelta (y)^* f_\lambda (y, \phi , \epsilon _n)\right] \right\rangle _\phi \Bigg ], \end{aligned}$$
(8)

where \(f_\lambda (y,\phi ,\epsilon _n)\) is the pair amplitude obtained from the quasiclassical equations with \(\varDelta (y)\) replaced by \(\lambda \varDelta (y)\). The \(\mathcal {T}\)-breaking SC state corresponds to the free energy minimum at finite q, and at this q the total current \(J_\mathrm{tot}\) vanishes (cf., Fig. 2).

3 Results

In Fig. 1a–c, we show the temperature–thickness phase diagram of the d-wave SC films for three different Fermi surfaces. The horizontal axis is \(T/T_{cb}\) with \(T_{cb}\) being the transition temperature in the bulk d-wave superconductor. The vertical axis is \(\pi \xi _0 / D\), where the coherence length \(\xi _0\) is defined as

$$\begin{aligned} \xi _0 = \frac{\sqrt{\left\langle v^2(\mathbf {p}_F) \right\rangle _\phi }}{2\pi T_{cb}}. \end{aligned}$$
(9)

The result for \(\mu = -3.9t\) (Fig. 1a) reproduces well the phase diagram obtained by Vorontsov [4] for a cylindrical Fermi surface.

The N–SC phase boundary is determined from the gap equation, linearized with respect to \(\varDelta (y)\). In the film considered here, the linearized gap equation has the solution [4, 6, 14]

$$\begin{aligned} \varDelta (y) = \varDelta _0 \cos (Q_ly), Q_l = (2l+1)\pi /D (l = 0, 1,2, \ldots ). \end{aligned}$$
(10)

The gap function \(\varDelta (y)\) vanishes at the film surfaces because of the \(d_{xy}\) symmetry and the assumption of a specular surface. One can show that the instability of the normal state first occurs for the \(l = 0\) mode [6] and the linearized gap equation for that mode is [4, 6, 14]

$$\begin{aligned} \ln \frac{T}{T_{cb}} = 2\pi T \sum _{\epsilon _n > 0} \left\langle \frac{\rho (\phi )\gamma ^2(\phi )}{\left\langle \rho (\phi )\gamma ^2(\phi ) \right\rangle _\phi } \left[ \frac{\epsilon _n}{\epsilon _n^2 + \eta ^2(\phi )} -\frac{1}{\epsilon _n} \right] \right\rangle _\phi , \end{aligned}$$
(11)

where

$$\begin{aligned} \eta (\phi ) = \frac{1}{2}[v_x(\mathbf {p}_F) q + v_y(\mathbf {p}_F)Q_0]. \end{aligned}$$
(12)

Equation (11) determines the critical thickness \(D_c\) as a function of (T, q). For a given T, there is an optimum q value \(q^\mathrm{op}\) at which \(D_c\) is minimized. The N–SC phase boundary corresponds to \(D_c(T, q^\mathrm{op})\). Note that \(\eta (\phi )\) in Eq. (11) vanishes when the Fermi surface nesting condition \(\xi _{\mathbf {p} + \mathbf {Q}} - \xi _{\mathbf {p}} = 0\) is satisfied for the vector \(\mathbf {Q} \equiv (q, Q_0)\). As a result, a Fermi surface with a good nesting property helps stabilize the \(\mathcal {T}\)-breaking state, and the N–SC phase boundary is substantially enhanced for a square Fermi surface [14].

Fig. 2
figure 2

Numerical results for a the total current \(J_\mathrm{tot}(q)\) (normalized at \(q\xi _0=0.4\)), b the free energy \(\Omega (q)\), and (c) the self-consistent gap function \(\varDelta (y)\) at \(T = 0.2 T_{cb}\) for the same \(\mu \) value as in Fig. 1b. The red solid line and the blue dashed line are the results for the \(q \ne 0\) SC phase with \(\pi \xi _0/D = 0.3\) and for the \(q = 0\) SC phase with \(\pi \xi _0/D = 0.1\), respectively. (Color figure online.)

Full size image

We now turn to the SC phase in the film with \(D > D_c\). The SC phase is separated into two phases by a nearly straight line. The low-temperature phase is the \(\mathcal {T}\)-breaking state and the high-temperature phase is the homogeneous (\(q=0\)) state. The characteristic linear T-dependence of the phase boundary can be deduced as follows. The \(\mathcal {T}\)-breaking state is stabilized when the superfluid mass, proportional to the slope of \(J_\mathrm{tot}(q)\) at \(q = 0\), is negative (cf., Fig. 2a). Thus, the phase boundary is determined from the condition \([J_\mathrm{tot}(q)/q]_{q \rightarrow 0} = 0\). The total current \(J_\mathrm{tot}\) is approximately given as \(J_\mathrm{tot} = J_\mathrm{BS} + n_sv_sD\) (\(n_s\) is the superfluid density and \(v_s = q/2m\) is the superfluid velocity). The first term \(J_\mathrm{BS}\) comes from the zero-energy Andreev bound states and the second term \(n_sv_sD\) is the condensate current. Since the film considered here has one bound state for each parallel momentum \(p_x\), one can estimate the bound-state current from \(J_\mathrm{BS} = 2\sum _{p_x} v_x(\mathbf {p}_F) f(p_{Fx}v_s)\), where the factor 2 accounts for the contributions of bound states at the two surfaces of the film. Hence, in the limit \(q \rightarrow 0\),

$$\begin{aligned} J_\mathrm{tot} \rightarrow \left[ -\frac{1}{2T}\sum _{p_x} v_x(\mathbf {p}_F) p_{Fx} + n_sD\right] v_s. \end{aligned}$$
(13)

It follows that the T-D relation for the phase boundary is given as

$$\begin{aligned} n_sDT = \frac{1}{2}\sum _{p_x} v_x(\mathbf {p}_F) p_{Fx}. \end{aligned}$$
(14)

When the T-dependence of \(n_s\) is weak at low temperatures, Eq. (14) leads to a linear T-dependence of the phase boundary. In the limits of the cylindrical and square Fermi surfaces, Eq. (14) is reduced to

$$\begin{aligned} DT = {\left\{ \begin{array}{ll} (1/3)(n/n_s)v_F &{} \hbox {(the cylindrical Fermi surface)},\\ (1/2)(n/n_s)v_{F\Vert }^\mathrm{max} &{} \hbox {(the square Fermi surface)}, \end{array}\right. } \end{aligned}$$
(15)

where n is the total number density and \(v_{F\Vert }^\mathrm{max}\) is the maximum value of the Fermi velocity parallel to the surface.

In conclusion, we have discussed the effects of the Fermi surface shape on the temperature–thickness phase diagram of d-wave SC films with an SC phase in which the time-reversal symmetry \(\mathcal {T}\) is spontaneously broken. The phase boundary between the \(\mathcal {T}\)-breaking SC state and the trivial SC state is insensitive to the Fermi surface shape, though it slightly shifts to higher temperature when the Fermi surface changes from cylindrical to square. However, the critical thickness \(D_c\) is significantly reduced as the Fermi surface approaches the square shape, and as a result, the \(\mathcal {T}\)-breaking SC phase is substantially enlarged in the temperature–thickness phase diagram.