Spin Texture and Spin Dynamics in Superconducting Cuprates Near the Phase Transition Revealed by the Electron Paramagnetic Resonance

Abstract

A short review of experimental results and theoretical models of the spin texture and spin dynamics in superconducting cuprates near the phase transition developed on the basis of the EPR measurements is given. Distortions of the long-range antiferromagnetic order in the YBa$_2$Cu$_3$O$_{6+y}$ were investigated for $y=0.1-0.4$ using Yb$^{3+}$ ions as the EPR probe. In weakly doped samples with $y=0.1$, a strong anisotropy of the EPR linewidth is revealed which was related to the indirect spin–spin interaction between the ytterbium ions via antiferromagnetic spin-waves. In the case of the doping level $y=0.2-0.3$, the EPR signal consists of narrow and broad lines, which were attributed to formation of charged domain walls. A theoretical analysis is well consistent with experimental results for the case of coplanar elliptical domain walls. A discussion of possible reasons for the observed unusual planar oxygen isotope effect on a critical temperature T$_\mathrm {c}$ related to charge heterogeneity in underdoped cuprates is given.

1 Introduction

The phenomenon of a transformation of antiferromagnetic quasi-two-dimensional copper oxides into high-temperature superconductors still remains a subject of intensive investigations. Soon after the high-T$_\mathrm {c}$ superconductivity (HTSC) discovery in La$_{2-x}$Ba$_x$CuO$_4$ [1], the attention was attracted to the YBCO family. It was understood that their common features related to a strong dependence of their magnetic and kinetic properties due to doping of their CuO$_2$ planes with electronic holes. Detailed inelastic neutron scattering experiments in the bilayer compound YBa$_2$Cu$_3$O$_{6+y}$ reveal the long- range antiferromagnetic (AF) order at $y<0.15$ with the Neel temperature $T_N=415$ K [2–4] . The oxygen electronic p-holes appear in the CuO$_2$ planes at $y>0.15$ producing the local distortions of the AF order, and its full destruction happens at $y=0.4$. There were suggested many scenarios of this process, in particular due to creating of polarons, domain walls, vortices, skyrmions, and some others [5–8]. Although an enormous number of experiments using neutron scattering, angle-resolved photoemission, and other methods seem to reveal some of these scenarios, there is no common agreement which of them are the most actual. It was evident that additional experiments are desirable for the understanding of the next steps of an evolution of these oxides on the way to become metals and then superconductors. The nuclear magnetic resonance (NMR) and electron paramagnetic resonance (EPR) were found to be very powerful techniques for probing the local magnetic properties and studying the spin kinetics of HTSC (for a review on EPR in superconductors see [9]). The EPR method is usually based on the EPR signal from the magnetic probes using ions having local d- or f-electrons. In particular, the use of Mn$^{2+}$ as an EPR probe in the CuO$_2$ plane allowed revealing a very fast spin relaxation rate of the Cu-ions due to their spin–phonon interaction, which prevents the observation of the EPR signal directly from the Cu-ions [10]. A choice of the Yb$^{3+}$ ion as the EPR probe to study the temperature dependence of the spin relaxation in YBa$_2$Cu$_3$O$_{6+y}$ in a metal and superconducting state ($y=0.5,0.6,0.98$) was found also effective [11].

The present work gives a short review of experimental and theoretical investigations of the AF state evolution in YBa$_2$Cu$_3$O$_{6+y}$ with $y=0.1,0.2,0.3,0.4$ on the basis of the EPR measurements using the Yb$^{3+}$ ion as the EPR probe. The paper is organized as follows. The Sect. 2 gives a detailed description of spin relaxation of the Yb$^{3+}$ ions in YBa$_2$Cu$_3$O$_{6+y}$ having long-range AF order ($y<0.15$). This analysis is necessary in order to reveal new features of the EPR signal appearing due to additional doping. The Sect. 3 is dedicated to investigations of the destruction of the long-range AF order by the oxygen doping ($y=0.2,0.3,0.4$) and a phase separation revealed by the changing of the EPR signal. The last Sect. 4 contains a discussion of peculiar behavior of the isotope effect on critical temperature for a low doping level and its possible relation to the phase separation.

2 Spin Excitations and EPR in the AF System

2.1 Antiferromagnetic Spin-Waves in the Two-Layers Cuprate

As a first step of our consideration, we have to describe the main features of spin-waves in the antiferromagnetic state of the pure YBCO system [16]. In the YBa$_2$Cu$_3$O$_{6+y}$, the CuO$_2$ plains are grouped in bilayers with a small exchange interaction between different bilayers. In this study, we neglect this coupling. The exchange spin Hamiltonian can be written in the form:

$$\begin{aligned} \frac{\hat{H}_\mathrm{ex}}{J}= & {} \frac{1}{2}\sum _{nm}\left[ \mathbf {S}_{n1}^a \mathbf {S}_{m1}^b + \mathbf {S}_{n2}^b \mathbf {S}_{m2}^a - \xi \left( S_{n1}^{za} S_{m1}^{zb} + S_{n2}^{zb} S_{m2}^{za} \right) \right] + \nonumber \\+ & {} \delta \sum _{n} \mathbf {S}_{n1}^a \mathbf {S}_{n2}^b+\delta \sum _{m} \mathbf {S}_{m1}^b \mathbf {S}_{m2}^a \end{aligned}$$

(1)

Here a and b indicate two sub-lattices in every plane. In the layer 1 the sites n and m are related to the a and b sub-lattices correspondingly, while vice versa in the layer 2. Hereafter, we take into account the nearest neighbors only. J is the exchange constant within the plane, $\delta$ and $\xi$ correspond to the exchange coupling between the two planes and an anisotropic exchange term both measured in units J, respectively. According to Ref. [2–4], the experimental values of exchange parameters can be estimated as $J \approx 1700$ K, $\delta \approx 4 \times 10^{-2} - 7\times 10^{-2}$, $\xi \approx 2 \times 10^{-4} - 7 \times 10^{-4}$.

We choose the direction of the spontaneous magnetizations along the x-axis, since due to the axial symmetry it can be chosen arbitrarily. The external magnetic field is applied to the system within the plane and directed along the y axis:

$$\begin{aligned} \hat{H}_\mathrm{ZCu}= & {} -B_\mathrm{Cu}\sum _{n}\left( S_{n1}^{ya} + S_{n2}^{yb}\right) - B_\mathrm{Cu} \sum _{m}\left( S_{m1}^{yb} + S_{m2}^{ya}\right) ;\nonumber \\ B_\mathrm{Cu}= & {} g_\mathrm{Cu}\mu _\mathrm{B} H_0 \end{aligned}$$

(2)

Here $g_\mathrm{Cu}$ is the g-factor for the Cu ion, $\mu _\mathrm{B}$ is the Bohr magneton, and $H_0$ is the external magnetic field. Below the critical value of the external magnetic field, the magnetizations of both sub-lattices are slightly rotated toward the y direction by the angle $\varphi$ defined by the exchange couplings (found from the minima condition for the ground-state energy):

$$\begin{aligned} \sin \varphi =\frac{B_\mathrm{cu}}{4 J (1+\delta )} = b_\mathrm{cu} \end{aligned}$$

(3)

It is convenient to turn the axes so that the new x-axis will be directed along the corresponding magnetizations of the sub-lattices. Using the standard Holstein–Primakoff formalism we make the following transformation for the layer $j=1$:

$$\begin{aligned} S_{n1}^{xa}= & {} \frac{1}{2}-a_{n1}^\dag a_{n1},\nonumber \\ S_{n1}^{\dag }= & {} \left( 1-a_{n1}^\dag a_{n1}\right) ^\frac{1}{2} a_{n1},\nonumber \\ S_{n1}^{-}= & {} \left( 1-a_{n1}^\dag a_{n1}\right) ^\frac{1}{2} a_{n1},\\ S_{m1}^{xb}= & {} -\frac{1}{2}+b_{m1}^\dag b_{m1},\nonumber \\ S_{m1}^{\dag }= & {} b_{m1}^\dag \left( 1-b_{m1}^\dag b_{m1}\right) ^\frac{1}{2},\nonumber \\ S_{m1}^{-}= & {} \left( 1-b_{m1}^\dag b_{m1}\right) ^\frac{1}{2} b_{m1}\nonumber \end{aligned}$$

(4)

with $S^\pm = -S^z \pm i S^x$ . For the layer $j=2$ the transformation can be obtained by interchanging indices n and m. Here $a^\dag$, a, $b^\dag$, b are the boson creation and annihilation operators for the two sub-lattices. Then, we perform the Fourier transformation to the reciprocal lattice:

$$\begin{aligned} a_q = N^{-1/2} \sum _n e^{i\mathbf {qr_n}} a_\mathbf {n},\quad b_q = N^{-1/2} \sum _n e^{i\mathbf {qr_n}} b_\mathbf {n}. \end{aligned}$$

(5)

Here N is the number of unit cells in the bilayer.

To diagonalize the Hamiltonian $H=H_\mathrm{ex} + H_{ZCu}$, we perform the Bogoliubov transformation to new creation and annihilation boson operators $\alpha _q^\dag , \beta _q^\dag , \eta _q^\dag , \kappa _q^\dag , \alpha _q, \beta _q, \eta _q, \kappa _q$, which must satisfy the commutation relations of the following type:

$$\begin{aligned} \left[ \alpha _q, H\right] = E_{\alpha q}\alpha _q; \quad \alpha _q = u_q a- \nu _q b_{-q}^\dag . \end{aligned}$$

(6)

Using these equations we obtain the energy eigenvalues and explicit expressions for the eigenoperators for two acoustical and two optical modes of spin-waves.

For the acoustical modes we have

$$\begin{aligned} \left( \frac{E_{\alpha q}}{2 J}\right) ^2= & {} \left[ 1-\gamma _q + 2 b_\mathrm{cu}^2 \left( \gamma _q+\frac{\delta }{4}\right) \right] \left[ 1+\gamma _q+\frac{\delta }{2}-\xi \gamma _q\right] ,\nonumber \\ \left( \frac{E_{\beta q}}{2 J}\right) ^2= & {} \left[ 1+\gamma _q + \frac{\delta }{2} - 2 b_\mathrm{cu}^2 \left( \gamma _q+\frac{\delta }{4}\right) \right] \left[ 1 - \gamma _q + \xi \gamma _q\right] . \end{aligned}$$

(7)

Here,

$$\begin{aligned} \gamma _q = 1/2 \left[ \cos (q_x a) + cos(q_y a)\right] \end{aligned}$$

(8)

One can see that at the Brillouin zone center $q=(0,0)$ the mode $E_{\alpha q}$ has a gap at the value close to the Zeeman energy $E_{\alpha 0} \approx 4 b_\mathrm{cu} J \approx g_\mathrm{cu} \mu _\mathrm{B} H_0$, while the other mode $E_{\beta q}$ maintains almost the same gap due to anisotropy of the exchange interaction. The eigenoperators of these modes are

$$\begin{aligned} \alpha _q= & {} \frac{1}{2} \left\{ u_{\alpha q}\left( a_{1q}+a_{2q}+b_{1q}+b_{2q}\right) \right. \nonumber \\- & {} \left. \nu _{\alpha q}\left( a_{1-q}^\dag +a_{2-q}^\dag +b_{1-q}^\dag +b_{2-q}^\dag \right) \right\} ,\nonumber \\ \beta _q= & {} \frac{1}{2} \left\{ u_{\beta q}\left( a_{1q}+a_{2q} - b_{1q} - b_{2q}\right) \right. \nonumber \\- & {} \left. \nu _{\beta q}\left( a_{1-q}^\dag +a_{2-q}^\dag - b_{1-q}^\dag - b_{2-q}^\dag \right) \right\} , \end{aligned}$$

(9)

The coefficients of the transformation in (9) are given by

$$\begin{aligned} u_{\alpha ,\beta }^2= & {} \frac{J}{E_{\alpha ,\beta }}\left[ 1+\frac{\delta }{4} \mp \frac{\xi \gamma _q}{2} \pm b_\mathrm{cu}^2 \left( \gamma _q+\frac{\delta }{4}\right) + \frac{E_{\alpha ,\beta }}{2,J} \right] ,\nonumber \\ v_{\alpha ,\beta }^2= & {} \frac{J}{E_{\alpha ,\beta }}\left[ 1+\frac{\delta }{4} \mp \frac{\xi \gamma _q}{2} \pm b_\mathrm{cu}^2 \left( \gamma _q+\frac{\delta }{4}\right) - \frac{E_{\alpha ,\beta }}{2,J} \right] . \end{aligned}$$

(10)

For the optical modes, the eigenvalues of energy are

$$\begin{aligned} \left( \frac{E_{\eta q}}{2 J}\right) ^2= & {} \left[ 1 + \gamma _q - \alpha _{xy} \gamma _q\right] \left[ 1 - \gamma _q+\frac{\delta }{2} +2 b_\mathrm{cu}^2 \left( \gamma _q - \frac{\delta }{4}\right) \right] ,\nonumber \\ \left( \frac{E_{\kappa q}}{2 J}\right) ^2= & {} \left[ 1 + \gamma _q - 2 b_\mathrm{cu}^2 \left( \gamma _q - \frac{\delta }{4}\right) \right] \left[ 1 - \gamma _q + \frac{\delta }{2} + \alpha _{xy} \gamma _q\right] .\qquad \end{aligned}$$

(11)

At the zone center, the both modes have a gap defined by the exchange coupling between the two layers. The eigenoperators for the optical modes are the following:

$$\begin{aligned} \eta _q= & {} \frac{1}{2} \left\{ u_{q \eta }\left( a_{q1} - a_{ q2 }+b_{q1}-b_{q2}\right) \right. \nonumber \\- & {} \left. \nu _{q\eta }\left( a_{-q1}^\dag -a_{-q2}^\dag +b_{-q1}^\dag - b_{-q2}^\dag \right) \right\} ,\nonumber \\ \kappa _q= & {} \frac{1}{2} \left\{ u_{q \kappa }\left( a_{q1} - a_{ q2 }-b_{q1}+b_{q2}\right) \right. \nonumber \\- & {} \left. \nu _{q\kappa }\left( a_{-q1}^\dag -a_{-q2}^\dag - b_{-q1}^\dag + b_{-q2}^\dag \right) \right\} . \end{aligned}$$

(12)

The coefficients of the transformation in (12) are given by

$$\begin{aligned} u^2_{\eta ,\kappa }= & {} \frac{J}{E_{\eta ,\kappa }}\left[ 1+\frac{\delta }{4}m\frac{\alpha _{xy}\gamma _q}{2}\pm b^2_\mathrm{cu} \left( \gamma _q - \frac{\delta }{4}\right) +\frac{E_{\eta ,\kappa }}{2J}\right] ,\nonumber \\ \nu ^2_{\eta ,\kappa }= & {} \frac{J}{E_{\eta ,\kappa }}\left[ 1+\frac{\delta }{4}m\frac{\alpha _{xy}\gamma _q}{2}\pm b^2_\mathrm{cu} \left( \gamma _q - \frac{\delta }{4}\right) -\frac{E_{\eta ,\kappa }}{2J}\right] \end{aligned}$$

(13)

The obtained expressions are valid for an external magnetic field below the critical value, at which the two sub-lattices collapse into one with magnetic moments directed along the magnetic field.

The full Hamiltonian takes now the form:

$$\begin{aligned} \hat{H}_0= & {} \hat{H} _\mathrm{ex} + \hat{H}_{ZCu}\nonumber \\= & {} \sum _q \left( E_{q\alpha } \alpha ^+_q \alpha _q + E_{q\beta } \beta ^+_q\beta _q + E_{q\eta } \eta ^+_q\eta _q + E_{q\kappa }\kappa ^+_q\kappa _q \right) \end{aligned}$$

(14)

2.2 Interactions of the Yb3+-ions with the AF Spin-Waves and the Suhl–Nakamura interaction

An exchange interaction between the particular j-th Yb$^{3+}$-ion of the crystal lattice and the nearest eight Cu-ions lying in the two parallel CuO$_2$ planes can be written in the form

$$\begin{aligned} \hat{H}^j_\mathrm{YbCu}= A\mathbf Y _j \left[ \sum _\mathbf n \Big (\mathbf S ^a_\mathbf{n 1}+\mathbf S ^b_\mathbf{n 2}\Big )+\sum _\mathbf m \Big (\mathbf S ^b_\mathbf{m 1}+\mathbf S ^a_\mathbf{m 2}\Big )\right] \end{aligned}$$

(15)

Here A is the coupling constant, $Y_j$ is the spin of the j-th Yb$^{3+}$-ion. We perform again the axes-rotation for the Cu-spins, the Holstein–Primakoff transformation (5), and the Fourier transformation (both for the magnon and ytterbium operators). Taking into account the Zeeman interaction, we obtain after the Bogoliubov transformation the following result for the Hamiltonian $\hat{H}_\mathrm{YbCu} = \hat{H}_\mathrm{YbCu}^{(0)} + \hat{H}_\mathrm{YbCu}^{(1)} + \hat{H}_\mathrm{YbCu}^{(2)}$ for the magnetic field oriented along the y-axis:

$$\begin{aligned} \hat{H}^{(0)}_\mathrm{YbCu}= & {} 4Ab_\mathrm{cu}Y^y_0N^{1/2}-Ab_\mathrm{cu}Y^y_0N^{-1/2}\sum _q \left\{ \nu ^2_{q\alpha }+\nu ^2_{q\beta }+\nu ^2_{q\eta }+\nu ^2_{q\kappa } \right\} ,\nonumber \\ \hat{H}^{(1)}_\mathrm{YbCu}= & {} 2A\sum _q\left\{ F^{ac}_q \left[ Y^z_q(u_{q\alpha }+\nu _{q\alpha })(\alpha _q+\alpha ^+_{-q})+ib_\mathrm{cu}Y^x_q(u_{q\alpha }-\nu _{q\alpha })\right] \right. \\+ & {} F^{ap}_q \left[ Y^z_q(u_{q\kappa }+\nu _{q\kappa })(\kappa _q+\kappa ^+_{-q})+ib_\mathrm{cu}Y^x_q(u_{q\kappa }-\nu _{q\kappa })\right] \nonumber \\+ & {} \left. iY^y_q \Big (1-b^2_\mathrm{cu}\Big )^{1/2}\Big [F^{op}_q \Big (u_{q\beta }-\nu _{q\beta }\Big )\Big (\eta _q-\eta ^+_q\Big )+F^{ac}_q\Big (u_{q\eta }-\nu _{q\eta }\Big )\Big (\eta _q-\eta ^+_q\Big )\right\} \nonumber \end{aligned}$$

(16)

Here Y$^{x,y,z}_q$ is the Fourier-transform of the site operators similar to (5); F$^{a,c}_q$ and F$^{o,p}_q$ are form factors for the acoustical and the optical modes:

$$\begin{aligned} F^{ac}_q=\cos \frac{q_xa}{2} \cos \frac{q_ya}{2}, F^{op}_q=\sin \frac{q_xa}{2} \sin \frac{q_ya}{2} \end{aligned}$$

(17)

The quadratic in the boson operators term $H^{(2)}_\mathrm{YbCu}$ is responsible for two-magnon processes, which was described in detail in [16].

An exchange between the ytterbium ions by the AF magnons creates an indirect spin–spin coupling known as the Suhl–Nakamura(SN) interaction. An effective spin–spin Hamiltonian can be obtained by the unitary transformation with the following elimination of the magnon operators. Using the Hamiltonian (14,15) we make the following transformation:

$$\begin{aligned} \mathop {H}\limits ^{~}=e^LHe^{-L} = \hat{H}_0+\hat{H}_\mathrm{YbCu}+ \Big [L,\hat{H}_0+\hat{H}_\mathrm{YbCu}\Big ]+\frac{1}{2}\Big [L,\Big [L,\hat{H}_0+\hat{H}_\mathrm{YbCu}\Big ]\Big ]...\nonumber \\ \end{aligned}$$

(18)

Here L is some yet unknown operator linear in the YbCu coupling. To eliminate the linear terms we put

$$\begin{aligned} \hat{H}_\mathrm{YbCu} + [S,\hat{H}_0]=0; \; <m|S|n>=\frac{<m|\hat{H}_\mathrm{YbCu}|n>}{E^0_m-E^0_n} \end{aligned}$$

(19)

Here we have used the eigenstates of the unperturbed Hamiltonian. The SN interaction can be obtained from the (17, 18, 19) in the second-order coupling of YbCu:

$$\begin{aligned} \hat{H}_\mathrm{SN}= & {} -2A^2\sum _q\left\{ (F^{ac}_q)^2 \left[ \frac{(u_{q\alpha }+\nu _{q\alpha })^2}{E_{q\alpha }}Y^z_qY^z_{-q}+\frac{(u_{q\beta }-\nu _{q\beta })^2}{E_{q\beta }}Y^y_qY^y_{-q}\right] + \right. \nonumber \\+ & {} \left. (F^{op}_q)^2 \left[ \frac{(u_{q\eta }-\nu _{q\eta })^2}{E_{q\eta }}Y^y_qY^y_{-q}+\frac{(u_{q\kappa }+\nu _{q\kappa })^2}{E_{q\kappa }}Y^z_qY^z_{-q}\right] \right\} \end{aligned}$$

(20)

Taking into account the explicit expressions for the Bogoliubov coefficients (10, 13), we obtain the final result

$$\begin{aligned} \nonumber \hat{H}_\mathrm{SN}= & {} -\frac{2A^2}{J}\sum _qf_q\big (Y^y_qY^y_{-q}+Y^z_qY^z_{-q}\big );\\ f_q= & {} \frac{(F^{ac}_q)^2}{1+\gamma _q+\delta /2}+\frac{(F^{op}_q)^2}{1-\gamma _q+\delta /2} \end{aligned}$$

(21)

In the denominators the terms which are small compared to $\delta$ were omitted. In the coordinate representation, the dependence of the SN interaction on the distance between the ytterbium ions R can be roughly approximated as f(R)$\propto$ J$_1(R)/R$ where J$_1$(R) is the Bessel function. It means that this interaction is more long-range than the dipole–dipole one.

2.3 The Electron Paramagnetic Resonance of Yb$^{3+}$-ions in Antiferromagnetic YBCO Compound

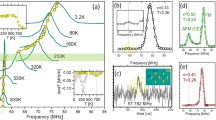
The EPR spectra were measured in the sample Y$_{0.98}$Yb$_{0.02}$Ba$_2$Cu$_3$O$_{6.1}$ with the external magnetic field along and perpendicular to the crystal c-axis and with an alternating field within the ab-plane [16]. We expect that at this level of oxygen doping ($y=0.1$), electronic holes are not yet present in the CuO$_2$ planes. It is well known that the ground-state multiplet $^2$F$_{7/2}$ of the Yb$^{3+}$ions $(4f^{13})$ is expected to be split by the crystal electric field of tetragonal symmetry into four Kramers doublets. Inelastic neutron scattering measurements showed that in YbBa$_2$Cu$_3$O$_7$, the first-excited doublet lies 1000 K above the ground-state doublet [13]. These measurements reveal a very strong anisotropy of the EPR linewidth in the antiferromagnetic sample Y$_{0.98}$Yb$_{0.02}$Ba$_2$Cu$_3$O$_{6.1}$. The g-factors g$_{\perp }=3.54$, g$_\mathrm{P}=3.23$ show an anisotropy similar to the one in the previous measurements for oxygen doping y=0.4 (where the AF state is suppressed, while the symmetry remains tetragonal, and g$^0_{\perp }$=3.49, g$^0_P$=3.13) with a shift of the resonance line to lower magnetic fields [11]. These features of the Yb$^{3+}$ EPR signal may be explained by the YbCu exchange interaction and the corresponding coupling of Yb$^{3+}$ ions with the AF spin-waves.

One can expect that at relatively low temperatures the broadening of the EPR signal is caused by the spin–spin interactions: the usual magnetic dipole–dipole interactions and the SN interactions between the Yb${^{3+}}$ ions. Their contribution can be calculated by the standard method of moments for the EPR line [14]. A contribution of the dipole–dipole interactions for the Yb$^{3+}$ ion concentration $x=0.02$ was estimated by calculations of the second and fourth moments using the experimental g-factors. For the external magnetic field perpendicular to the crystal c-axis the result is $\Delta B^{\perp }_\mathrm{dd} = 8$ mT, while for the parallel orientation it is slightly larger ($\Delta B^P_\mathrm{dd} = 8.2$ mT). The experimental values are significantly different: the calculated dipole–dipole contribution for the perpendicular orientation practically coincides with the experimental value $\Delta B^{\perp }_\mathrm{exp} = 7.8$ mT, while for the parallel orientation the experimental linewidth is five times larger ($\Delta B^P_\mathrm{exp} = 41.3$ mT). Such behavior can be related to the anisotropy of the SN interaction. For the external field below the critical value, the AF magnetization is almost perpendicular to external field. It means that if H $_{0}$ is directed along y-axis, the alternating field is directed along the x-axis and a contribution to the second moment is defined by a commutator of the total spin $Y^x_0$ with $\hat{H}_\mathrm{SN}$. However, one can see from Eq. 21 that the operator structure of $\hat{H}_\mathrm{SN}$ gives $[Y^x_0,\hat{H}_\mathrm{SN}]=0$, which means that for this orientation there is no contribution from the SN interaction to the EPR linewidth.

The situation is different for an external magnetic field oriented along the c-axis. In this case, the alternating field can be directed arbitrarily in the xy-plane. The standard calculations of second and fourth moments give the following results:

$$\begin{aligned} M_2=\frac{A^4}{J^2}\frac{a^2}{\pi ^2}\int _0^{\pi /a} \mathrm{d}q_x \int _0^{\pi /a} \mathrm{d}q_yf^2_q=0.14\frac{A^2}{J^2}\nonumber \\ M_4=\frac{8A^8}{J^4}\frac{a^2}{\pi ^2}\int _0^{\pi /a} \mathrm{d}q_x \int _0^{\pi /a} \mathrm{d}q_yf^4_q=0.051\frac{A^8}{J^4} \end{aligned}$$

(22)

For the diluted ytterbium spin-system, the peak-to-peak EPR linewidth can be calculated by the formula [14]:

$$\begin{aligned} \Delta B^P_\mathrm{SN}=\frac{\pi }{\sqrt{3}} x \left( \frac{M^3_2}{M_4}\right) ^{1/2}\approx 0.42 x \left( \frac{A^2}{J}\right) \end{aligned}$$

(23)

This result allows estimating the exchange coupling A between the ytterbium and copper ions, if we suppose that the main contribution for the parallel orientation comes from the SN interaction. Taking the experimental value $\Delta B^P_\mathrm{epx}=41.3$ mT and extracting the dipole–dipole contribution of 8.2 mT, we relate the rest to the SN interaction. Using [4] and the Yb concentration x=0.02, we find $|A|\approx$ = 120 K. The sign remains unknown.

An additional contribution to the EPR linewidth comes from the two-magnons processes due to quadratic in the boson operators term $H^{(2)}_\mathrm{YbCu}$ mentioned above. A detailed analysis of this contribution shows that it can be neglected at relatively low temperatures [16].

3 Evolution of the EPR Signal with Doping Antiferromagnetic Cuprates

The results of the EPR signal investigations in Y$_{0.98}$Yb$_{0.02}$Ba$_2$Cu$_3$O$_{6+y}$ with $y=0.2,0.3,0.4$ were published in the paper [16]. There it was found that the Yb$^{3+}$ EPR signal can be described by the sum of two Lorentzians with sufficiently different linewidths. The intensity of the broad line increases with doping and disappears at $y=0.4$. We assume that this EPR signal behavior can be explained by the electronic phase separation into the rich and poor in holes regions in the CuO$_2$ planes. The separation can be related naturally to a creation of charged domain walls (stripes). The local distortions of the antiferromagnetic order in the domain walls should give an additional inhomogeneous broadening to the Yb$^{3+}$ EPR signal due to exchange coupling between the ytterbium and copper ions. We will consider separately the collinear and coplanar antiphase domain walls, which are created by the p-holes localized in the CuO$_2$ planes on the oxygen ions around the Cu$_2^+$ ions.

3.1 Collinear Domain Walls

The detailed investigation of this type of charged domains was performed by Giamarchi and Lhuillier based on the standard two-dimensional Hubbard model with U as the on-site Hubbard repulsion, and t as the hopping parameter [17]. The numerical solutions were investigated by the Monte Carlo variational technique using the Hartree–Fock trial function. For a strong enough Hubbard repulsion $(U/t\ge 4)$, the stable collinear domain-wall solutions were found, where the doped p-holes are localized within a stripe around each Cu$_2^+$ site. This stripe separates two AF-ordered regions with opposite signs in the AF order parameter. For the case $U/t=10$, the calculated spin texture of the collinear domain wall along the y-axis could be well reproduced by the phenomenological model for the x-component of the order parameter for two sub-lattices:

$$\begin{aligned} <S^{xa}_n>=S_0\;\tan \textit{h}(x_n/d),\;\;<S^{xb}_n>=-S_0\;\tan \textit{h}(x_n/d). \end{aligned}$$

(24)

Here $x_n$ is the position of the site with respect to the stripe, d gives a width of the domain wall and $S_0$ is the order parameter on a long distance from the stripe. These results were confirmed later by Seibold, Sigmund, and Hizhnyakov by numerical calculations within the slave-boson mean-field approximation for the two-dimensional Hubbard model [20].

In a presence of the external magnetic field directed along the stripe, the order parameter component along the magnetic field appears according to Eq (3)

$$\begin{aligned} <S^{ya}_n>=<S^{yb}_n>=S_0\sin \varphi \tan \textit{h}(x_n/d); \;\;\sin \varphi =g_\mathrm{cu}\mu _\mathrm{B}H_0/4J. \end{aligned}$$

(25)

These magnetizations components of the AF sub-lattices give a contribution to the Yb$^{3+}$ ions Zeeman energy due to their exchange coupling with the neighboring Cu$^{2+}$ ions:

$$\begin{aligned} H^\mathrm{col}_\mathrm{YbCu}= 8A\sin \varphi S_0\sum _nY^y_n\tan \textit{h}(x_n/\xi ). \end{aligned}$$

(26)

This interaction is the source of the additional inhomogeneous EPR signal broadening due to the Yb$_3^+$ ions located in the domain walls. The corresponding contribution to the EPR linewidth can be estimated by the moments method. The calculated second moment gives

$$\begin{aligned} M_2=\sum _n(4A\sin \varphi )^2[\tan \textit{h}(x_n)]^2 \end{aligned}$$

(27)

We put here $S_0=1/2$. The forth moment can be calculated in a similar way. Transforming the sum over the sites inside the domain wall into the integral $(-2\xi \le x\le 2\xi )$, we can find the EPR linewidth:

$$\begin{aligned} M_2=0.5(4A\sin \varphi )^2,\;\;M_4=0.35(4A\sin \varphi )^4;\nonumber \\ \Delta H^\mathrm{col}_\mathrm{theor}\sim 2(M^3_2/M_4)^{1/2}\approx 4.8|A|\sin \varphi \approx 90\;\; G. \end{aligned}$$

(28)

The obtained value is much less than the experimental value of the broad EPR line $\Delta H^\mathrm{broad}_\mathrm{exp}\approx$1200 G.The smallness of the contribution calculated appears due to a very small value of sin$\varphi$ which is defined by the relation of Zeeman energy to the exchange coupling between the nearest Cu$^{2+}$ ions, which is sin$\varphi \approx$ 6$\times$10$^{-5}$ in our case. This argument stimulates the investigation of a possible role of the coplanar domain walls.

3.2 Elliptical Domain Walls

An existence of the coplanar domain walls in the AF order of the CuO$_2$ planes was predicted by Zachar, Kivelson, and Emery on the basis of the Landau theory of phase transitions [19]. Particular spin and charge textures for elliptical domain walls were calculated by Seibold within the two-dimensional Hubbard model [20]. It was shown that for the completely filled domain wall (i.e., one hole per site along the stripe) only the collinear solutions exist, whereas the coplanar structures become stable for half-filled walls for small hole concentrations. Fig. 2a shows the spin texture for the case when two holes occupy alternatively the neighboring sites along the charged stripe. In this case, the spin texture is similar to the coupled vortex–antivortex structure [20]. We suggest the following phenomenological model to reproduce the calculated spin texture.

a)The hole is present in the stripe:

$$\begin{aligned} S^{ya}_n=S_0\sin \alpha \frac{\tan \textit{h}(x_n/d)}{\cos \textit{h}(x_n/d)};\;\; S^{yb}_n=-S_0\sin \alpha \frac{\tan \textit{h}(x_n/d)}{\cos \textit{h}(x_n/d)}. \end{aligned}$$

(29)

b) The hole is absent in the stripe:

$$\begin{aligned} S^{ya}_n=S_0\sin \alpha \frac{\sin \alpha }{\cos \textit{h}(x_n/d)};\;\; S^{yb}_n=-S_0\sin \alpha \frac{\sin \alpha }{\cos \textit{h}(x_n/d)}. \end{aligned}$$

(30)

Here sin$\alpha$ defines the eccentricity of the elliptical domain wall; the case $\alpha$=$\pi$/4 describes an ideal spiral solution, whereas $\alpha$=0 reduces the spin structure to a collinear domain wall. Hereafter, we neglect an additional rotation of the magnetic moments caused by the external magnetic field. One can see (1b) that this model reproduces the calculated spin texture quite well. The secular part of the corresponding Hamiltonian for the exchange interaction between the ytterbium ion and the elliptical domain wall takes the following form

Fig. 1

Spin structures for the elliptical domain wall: a pattern on the left panel was calculated numerically by Seibold [20] ; b the pattern on the right panel shows our phenomenological model, calculated using formulas (29) and (30). From Ref. [16]

$$\begin{aligned} H^{ell}_\mathrm{YbCu}= & {} \frac{A}{2}\sin \alpha \sum _nY_n^yF(x_n/d),\nonumber \\ F \Big (\frac{x_n}{d}\Big )= & {} \left\{ \frac{\tan \textit{h}(x_n/d)-1}{\cos \textit{h}(x_n/d)}-\frac{\tan \textit{h}[(x_n+a)/d]-1}{\cos \textit{h}[(x_n+a)/d]}\right\} . \end{aligned}$$

(31)

Calculations similar to the case of the collinear domain wall give

$$\begin{aligned} M_2= & {} 0.064(A\sin \alpha )^2,\;\;M_4=8.9\times 10^{-3}(A\sin \alpha )^4;\nonumber \\ \Delta H^\mathrm{ell}_\mathrm{YbCu}= & {} 0.31|A|\sin \alpha . \end{aligned}$$

(32)

Taking again the value |A|=120K, we can achieve the experimental value for the broad EPR line $\Delta H^\mathrm{broad}_\mathrm{exp}\approx 1200\; G$ with a rather small eccentricity of the elliptical domain wall: sin$\alpha =5\times 10^{-3}$ .One could expect that at the level of oxygen doping approaching $y=0.4$, the AF order will be destroyed; the holes in the CuO$_2$ planes delocalized creating metal regions; and the inhomogeneous broadening of the Yb$^{3+}$ EPR line will vanish. Such a behavior was actually observed in the present case.

4 Planar Oxygen Isotope Effects Related to Charge Heterogeneity

It is remarkable that a subsequent transition of the metal cuprate into a superconducting state is accompanied by a strong isotope effect on the critical temperature T $_\mathrm{c}$ by substituting the naturally present $^{16}$O by the $^{18}$O isotope (T $_\mathrm{c}\propto$ M$^{-\alpha }$, M is the isotope mass).This effect is decreasing from underdoped region to almost negligible at optimal doping. It can indicate that the parameter $\alpha$ is carrier concentration n dependent: $\alpha$(n). Weyeneth and Müller [21] demonstrated that the isotope effect as a function of hole doping in various cuprate superconductors can be described very well by the formula:

$$\begin{aligned} \alpha (n,T_\mathrm{c})=\gamma (n)\frac{n}{T_\mathrm{c}(n)}\frac{\partial T_\mathrm{c}(n)}{\partial (n)}. \end{aligned}$$

(33)

As can be seen from the Fig. 2, this formula provides excellent description of the isotope effect from optimal doping down to very underdoped region with near-vanishing superconductivity.

Fig. 2

The oxygen isotope exponent $\alpha$ as a function of T $_\mathrm{c}$/T $_{\mathrm{c}, \mathrm{max}}$ for various high-T $_\mathrm{c}$ cuprate superconductors. The solid line represents fit using Eq. (33). From Ref. [21] (Color figure online)

Originally this formula in Eq. (33) was obtained by Kresin and Wolf [22] in the frame of a model describing the dynamic of apical oxygen along the c-axis in a double-well potential. As a result, the charge transfer between the charge reservoir and the CuO$_2$ planes which occurs through an apical oxygen depends on the tunneling of this oxygen to another minimum of the double-well potential. The tunneling is affected by the oxygen isotope mass M. In the case of a large asymmetry between the two different potential electronic terms (double-well structure), they found that the in-plane concentration of the charge carriers is proportional to the probability of charge transfer along the crystallographic c-axis from charge reservoir to the CuO$_2$ plane. However, the site-selective oxygen substitution $^{16}$O $\rightarrow$ $^{18}$O experiments showed the observed oxygen isotope effect is predominantly being due to oxygen atom vibrations in the CuO$_2$ planes [23].

Recently, there was proposed (Ref. [24]) that the local charge carrier concentration in CuO$_2$ planes can be influenced by isotope mass change of the in-plane oxygen ions due to the microscopic electronic phase separation into metallic and dielectric regions in the CuO$_2$ plane. The results of the EPR study of such a phase separation in lightly doped La$_{2-x}$Sr$_x$CuO$_4$ showed that the starting point for the creation of metallic regions is a formation of a bipolaron by two three-spin-polarons (3SP) via exchange by phonons [25, 26]. EPR experiments demonstrated that by cooling, bipolarons condense into metallic clusters or stripes similar to the process described in the previous Section. The percolation of these clusters/stripes leads to a superconducting transition [27].

5 Conclusions

We have described experimental and theoretical investigations of the AF order evolution in the two-layers cuprate YBa$_2$Cu$_3$O$_{6+y}$ for different doping levels on the basis of the EPR measurements. It was found using the Yb$^{3+}$ ion as the EPR probe that in the state with the long-range AF order, the EPR linewidth is very anisotropic, which is related to the Suhl–Nakamura interactions between the Yb$^{3+}$ ions. At the doping level $y>0.15$, the additional very broad EPR line appears which can be attributed to the charged antiphase elliptical domain walls (stripes) created by the doped oxygen electronic p-holes in the CuO$_2$ planes. The broad line disappears at $y=0.4$ which can be related to the delocalization of the electronic holes in the stripes. The CuO$_2$ planes experience the electronic phase separation into metal and dielectric regions which were detected earlier by the EPR study [25]. The phase transition of underdoped cuprates into the superconducting state is accompanied by a strong planar isotope effect on the critical temperature T $_\mathrm{c}$ what can indicate an important role of electron–phonon interactions in a formation of bipolarons and the metal regions in the CuO$_2$ planes.