A Phenomenological Theory of Metamagnetism in Ce-Based Heavy Fermion Compounds

Abstract

A phenomenological theory is developed for the metamagnetism observed in heavy Fermion compounds by extension of the Landau theory for phase transitions. From simple analysis, the crossover behavior in high magnetic fields is indicated for the extended Landau-type free energy density. According to the finite temperature behavior of the extended Landau free energy density, theoretical magnetic phase diagrams that resemble those observed in CeRu$_{2}$Si$_{2}$ and Ce(Ru$_{0.92}$Rh$_{0.08}$)$_{2}$Si$_{2}$ are obtained by using two sets of parameters, respectively.

1 Introduction

The fascinating behavior of heavy Fermion compounds (HFCs) has attracted much attention in the last forty years [1–3]. Among other phenomena, the unconventional superconductivity and/or non-Fermi liquid-like behaviors that emerge when HFCs are driven near to the quantum critical point are of much interest in current studies [4, 5]. In addition, the origin of the metamagnetism which is sometimes observed in HFCs is also the source of some controversy. On increasing the external magnetic field, some HFCs exhibit crossover or transition phenomena from the Pauli paramagnetic state to the highly polarized state (HPS) at low temperatures [6–8]. A transition from the antiferromagnetic state to the HPS is familiar for traditional metamagnetic materials, but the transition from the paramagnetic state to the HPS is specific to HFCs. While Fermi surface reconstruction and several other models are proposed as the microscopic mechanisms underpinning this phenomenon, it seems that theoretical consensus has not yet been achieved [9–19]. Whether the large Fermi surface changes its form under exposure to the metamagnetic field is a fundamental issue to be clarified. Although this question is beyond the scope of the present work, we comment on this point briefly in the final section.

Thus, in this report, we do not consider the microscopic origins of this phenomenon. Instead, a simple phenomenological theory is developed to describe the metamagnetism of HFCs, by extension of the Landau-type free energy density. We would like to emphasize that this theory does not rely on any microscopic model, and any appropriate microscopic model should obey the phenomenological behavior presented in this paper. We also note here that our focus is concentrated on the magnetic behavior of the systems under study, rather than the thermal or transport properties.

This paper is organized as follows: Firstly, the phenomenological theory regarding the Landau-type free energy density, including the higher order terms, is presented and analyzed in Sect. 2. Secondly, in Sect. 3, two examples, CeRu$_{2}$Si$_{2}$ and Ce(Ru$_{0.92}$Rh$_{0.08}$)$_{2}$Si$_{2}$, are discussed and analyzed using this theory. Finally, some discussions are given in Sect. 4.

2 The Extended Landau-Type Free Energy

The conventional Landau free energy density for ferromagnetism is given by

$$\begin{aligned} f_{\scriptscriptstyle {L}}(m,h)=a_{\scriptscriptstyle {f}}m^{2}+b_{\scriptscriptstyle {f}}m^{4}-hm, \end{aligned}$$

(1)

where m is the magnetization, $a_{\scriptscriptstyle {f}}$ and $b_{\scriptscriptstyle {f}}$ are parameters, and h is the effective external magnetic field. The last term of Eq.(1) is a Zeeman term. [20]

In this paper, we extend this free energy density to the antiferromagnetic ‘Ising’ systems with two sub-lattices, denoted A and B. So, m in Eq. (1) can be replaced by the net magnetization $m_{A}-m_{B}$, where $m_{A}$ and $m_{B}$ are the sub-lattice magnetizations of the sub-lattices A and B, respectively. However, by leading principles mentioned below, the extended Landau-type free energy density for an antiferromagnet is written as

$$\begin{aligned} f_{1}(m_{A},m_{B},h)=-a_{1}m_{A}m_{B}+a_{2}\big (m_{A}^{2}+m_{B}^{2}\big )+b\big (m_{A}^{4}+m_{B}^{4}\big )-h\big (m_{A}-m_{B}\big ), \end{aligned}$$

(2)

where $a_{1}, a_{2}$, and b are parameters to be determined. In such a system, metamagnetism is introduced via higher order terms of the form:

$$\begin{aligned} f_{2}(m_{A},m_{B},h)=c_{1}h\big (m_{A}^{3}-m_{B}^{3}\big )+c_{2}hm_{A}m_{B}(m_{A}-m_{B}), \end{aligned}$$

(3)

where $c_{1}$ and $c_{2}$ are also parameters to be found. In writing down the free energy densities of Eqs. (2) and (3), the following leading principles have been observed:

• 1. Terms up to the fourth-order terms with respect to $m_{A}$, $m_{B}$, and h are restored.

• 2. Symmetric restrictions are required. When h is reversed, the sub-lattices A and B interchange their roles. Furthermore, when the z-axis is reversed, the magnetizations $m_{A}$, $m_{B}$ are reversed simultaneously. Namely,

  

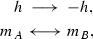  (4)

  and

  $$\begin{aligned} h\longrightarrow & {} -h, \nonumber \\ m_{A}\longrightarrow & {} -m_{A}, \nonumber \\ m_{B}\longrightarrow & {} -m_{B}. \end{aligned}$$

  (5)

  Under these transformations the free energy density should be invariant.

• 3. The terms $m_{A}^{2}m_{B}^{2}$ and $m_{A}m_{B}(m_{A}^{2}+m_{B}^{2})$ are dropped from Eq. (2), because it is not possible to deduce these terms using the Bragg–Williams entropy expression within mean-field theory.

• 4. Higher order terms, such as $h^{2}(m_{A}^{2}+m_{B}^{2})$ and $h^{2}m_{A}m_{B}$ terms are dropped from Eq. (3), because they cannot induce metamagnetism.

• 5. Since h is considered to be small (see below), higher order terms in h, such as $h^{3}m_{A}$, $h^{3}m_{B}$, and $h^4$ terms can be safely neglected.

Thus, the total free energy density is given by

$$\begin{aligned} f(m_{A},m_{B},h)=f_{1}(m_{A},m_{B},h)+f_{2}(m_{A},m_{B},h). \end{aligned}$$

(6)

The metamagnetism can be induced by the two terms in Eq. (3), because the Zeeman term $-hm$ and these two terms make two minima in the total free energy density Eq. (6).

Next, in order to determine the equilibrium values of $m_{A}$ and $m_{B}$, we include the stationary conditions for $f(m_{A},m_{B},h)$ with respect to $m_{A}$ and $m_{B}$. Hence, the following two equations should be satisfied simultaneously,

$$\begin{aligned} \frac{\partial f}{\partial m_{A}}= & {} 0, \end{aligned}$$

(7)

$$\begin{aligned} \frac{\partial f}{\partial m_{B}}= & {} 0. \end{aligned}$$

(8)

From these equations, we can determine the equilibrium values of $m_{A}$ and $m_{B}$, denoted $\bar{m}_{A}$ and $\bar{m}_{B}$, respectively, as a function of h. Furthermore, the sub-lattice susceptibilities can also be obtained from the derivatives of the equilibrium magnetizations $\bar{m}_{A}$ and $\bar{m}_{B}$ with respect to h:

$$\begin{aligned} \chi _{h}^{A}= & {} \frac{\partial \bar{m}_{A}}{\partial h}=\frac{DX-C_{B}Y}{C_{B}^{2}+DC_{A}}; \end{aligned}$$

(9a)

$$\begin{aligned} \chi _{h}^{B}= & {} \frac{\partial \bar{m}_{B}}{\partial h}=\frac{C_{B}X+C_{A}Y}{C_{B}^{2}+DC_{A}}, \end{aligned}$$

(9b)

where

$$\begin{aligned} C_{A}= & {} 2a_{2}+12b\bar{m}_{A}^{2}+6c_{1}h\bar{m}_{A}+2c_{2}h\bar{m}_{B}, \end{aligned}$$

(10a)

$$\begin{aligned} C_{B}= & {} -a_{1}+2c_{2}h(\bar{m}_{A}-\bar{m}_{B}), \end{aligned}$$

(10b)

$$\begin{aligned} D= & {} -2a_{2}-12b\bar{m}_{B}^{2}+6c_{1}h\bar{m}_{B}+2c_{2}h\bar{m}_{A}, \end{aligned}$$

(10c)

$$\begin{aligned} X= & {} 1-3c_{1}\bar{m}_{A}^{2}-c_{2}(2\bar{m}_{A}-\bar{m}_{B})\bar{m}_{B}, \end{aligned}$$

(10d)

$$\begin{aligned} Y= & {} 1-3c_{1}\bar{m}_{B}^{2}+c_{2}\bar{m}_{A}(\bar{m}_{A}-2\bar{m}_{B}). \end{aligned}$$

(10e)

In the following analysis, h is restricted to h $<$ 1, such that the expansions Eqs. (2) and (3) hold. Here, we note that the deviation of the $m_{A,B}$–h curves for each sub-lattice from those predicted by the mean-field theory would be small, except near the critical temperature. This is also found to be the case for the ferromagnetic Ising model. Thus, the above theory may be considered reliable in the region $\bar{m}_{A} <15/7$, $\mid \bar{m}_{B}\mid <15/7$, h $<$ 1. Here, the magnetic moment of Ce-ion is considered as $\mu =g_{J}J\mu _\mathrm{B} =15/7\mu _\mathrm{B}$ ($J=5/2$, $g_{J}=6/7$), where $\mu _\mathrm{B}$ is the Bohr magneton.

3 Analysis of Two Typical Examples

The group of HFCs that exhibit metamagnetism include CeRu$_{2}$Si$_{2}$ (metamagnetic behavior is observed experimentally at metamagnetic field $H_{m}$ = 7.7 T) [8] and the related compounds Ce(Ru$_{1-x}$Rh$_{x}$)$_{2}$Si$_{2}$ [21, 22] and Ce$_{1-x}$La$_{x}$Ru$_{2}$Si$_{2}$ [23]. Furthermore, CeNi$_{2}$Ge$_{2}$ ($H_{m}$ = 42 T) [24] and CeFe$_{2}$Ge$_{2}$ ($H_{m}$ = 30 T) [25] are also Ce-based HFCs that exhibit metamagnetic behavior. As illustrative examples, we pick the two conventional systems CeRu$_{2}$Si$_{2}$ and Ce(Ru$_{0.92}$Rh$_{0.08}$)$_{2}$Si$_{2}$. CeRu$_{2}$Si$_{2}$ is a proto-typical system which was discovered in the early stage of investigations into metamagnetic materials [2], while Ce(Ru$_{0.92}$Rh$_{0.08}$)$_{2}$Si$_{2}$ is of high interest, since the antiferromagnetically ordered and the metamagnetic states coexist separately [22].

Using the preceding theory of Sect. 2, magnetic phase diagrams can be drawn for these two example materials, so that the validity of this theory can be examined. To do so, the temperature effect must be taken into account. Although it is possible that all parameters, a’s, b, c’s, can depend on the temperature T, for simplicity we assume that only $a_{1}$ and $a_{2}$ are temperature dependent, by analogy with critical phenomena. Hence, in the following, we write $a_{1}(T)$ and $a_{2}(T)$ in place of $a_{1}$ and $a_{2}$.

For the effective external magnetic field h, we may take the Kondo temperature $T_{K}$ as the characteristic energy scale for the systems, i.e., h can be denoted as

$$\begin{aligned} h=\frac{\mu _\mathrm{B}H}{k_\mathrm{B}T_{K}}, \end{aligned}$$

(11)

where $k_{B}$ is the Boltzmann constant and H is the external magnetic field.

3.1 CeRu$_{2}$Si$_{2}$

CeRu$_{2}$Si$_{2}$ a is conventional system in the study of HFCs [2]. In order to determine the magnetic phase diagram from the extended Landau-type free energy density, all parameters $a_{1}(T)$, $a_{2}(T)$, b, $c_1$, and $c_2$ should be found. Firstly, the temperature dependence of $a_{1}(T)$ should be determined. When the temperature is increased, the strength of the effective antiferromagnetic interactions should be decreased. This temperature effect can be taken into account by $a_{1}(T)$ as

$$\begin{aligned} a_{1}(T)=-a_{10}\frac{T}{T_{K}}=-\frac{T}{T_{m}}, \end{aligned}$$

(12)

where $T_{m}$ is the susceptibility maximum temperature, which is a characteristic temperature for the Fermi liquid behavior of the system. In Eq. (12), a suitable temperature range may be $T<T_{m}$, so that $|a_{1}(T)|<1$ would hold by analogy with critical phenomena. In CeRu$_{2}$Si$_{2}$, $T_{K}\cong$ 24 K and $T_{m}\cong$ 10 K, so $a_{10}$ = 2.4 [6].

Secondly, the parameter $a_{2}(T)$ is determined by empirical fitting of the magnetic susceptibility at h = 0, given by

$$\begin{aligned} \chi _{0}(T)=\chi _{0}^{A}(T)=-\chi _{0}^{B}(T)=\frac{1}{a_{1}(T)+2a_{2}(T)}. \end{aligned}$$

(13)

From experimental data, the zero-temperature magnetic susceptibility is found to be $\chi _{0}^{\mathrm{\scriptscriptstyle {exp}}}(0)=\frac{M^{\mathrm{\scriptscriptstyle {exp}}}}{H}\cong 0.037$ emu mol$^{-1}$ G$^{-1}$ $= 0.065~\mu _\mathrm{B}$ T$^{-1}$. Theoretically the corresponding value of $\chi _{0}(0)$ should be 2.3 ($\chi _{0}(0)=\frac{m}{h}\cong \frac{0.065}{0.67/24}$;1 $\mathrm{T}\cong$ 0.67 K). In the same manner, $a_{2}(T)$ can be determined as a function of $a_{1}(T)$ using $\chi _{0}^{\mathrm{\scriptscriptstyle {exp}}}(T)$ [6]. When T is varied from 0 to 10 K, $(a_{1}(T),a_{2}(T))$ move on the trajectory as shown in Fig. 1.¹

Fig. 1

The trajectories of the parameters $a_{1}(T)$ and $a_{2}(T)$: the edges of the lines are ($a_{1}$,$a_{2}$) = (0, 0.22) at T = 0 and ($-$1, 0.7) at $T = T_{m}$ = 10 K for CeRu$_{2}$Si$_{2}$ (blue line); ($a_{1}$,$a_{2}$) = (0.84, 0.32) at T = 0 K, and (0.04, $-$0.11) at T = 4 K for Ce(Ru$_{0.92}$Rh$_{0.08}$)$_{2}$Si$_{2}$ (green line). The arrows show the directions from T = 0 K to T = 10 or 4 K. The first-order transition border is shown by the red line the parameters are b = 0.1, $c_{1}$ = 0.0, and $c_{2}$ = 1.0 (Color figure online)

Thirdly, to fix the parameters b, $c_{1}$, and $c_{2}$ we note that $H_{m}\cong$ 7.7 T, i.e., $h_{m}\cong$ 0.22 for this system at T = 0, where $h_{m}$ is the effective metamagnetic field [6]. Using Eqs. (9a), (9b), we find a parameter set to be b = 0.1, $c_{1}$ = 0.0, $c_{2}$ = 1.0. Here, we obtain the value b = 0.1 in order to fit $h_{m}\cong$ 0.22 when we suppose $c_{1}$ = 0.0 and $c_{2}$ = 1.0 for simplicity. It is noted that this set is not uniquely determined by the preceding theory.

Using the preceding theory, $\bar{m}_{A}$, $-\bar{m}_{B}$, and the sub-lattice susceptibilities $\chi _{h}^{A}$, $-\chi _{h}^{B}$ can be obtained from Eqs. (9a), (9b), and (10a)–(10e) as functions of h. Fig. 2(a) and (b) show the h-dependent behavior of the sub-lattice magnetizations and the sub-lattice susceptibilities for T = 0. In these graphs the kink and the peak in Fig. 2(a) and (b), respectively, correspond to the effective metamagnetic field.

At finite temperatures, these quantities can be found in a similar manner. Thus, we can obtain the magnetic phase diagram by tracing the susceptibility peak values as show in Fig. 2(c). When compared to the experimental observations, this theory seems to yield a satisfactory phase diagram [26]. Since this theory contains only two T-dependent parameters $a_{1}(T)$ and $a_{2}(T)$, this ability to reproduce the phase diagram ‘qualitatively’ is remarkable. However, the metamagnetic field slightly decreases with increasing temperature in contrast to the experimental observation. It is noted that the susceptibility is almost independent of temperature. This may correspond to the low-temperature behaviors of CeRu$_{2}$Si$_{2}$.

Fig. 2

a The m–h curve showing the sub-lattice magnetization $\bar{m}_{A}=-\bar{m}_{B}$ and b the sub-lattice magnetic susceptibility for CeRu$_{2}$Si$_{2}$ at T = 0 (parameters used are b = 0.1, $c_{1}$ = 0.0, $c_{2}$ = 1.0). c The magnetic phase diagram for CeRu$_{2}$Si$_{2}$. Line shows crossover line obtained using the Landau-type free energy density; experimental data are shown by ($+$) after Ref. [26]

3.2 Ce(Ru$_{0.92}$Rh$_{0.08}$)$_{2}$Si$_{2}$

Doping CeRu$_{2}$Si$_{2}$ with Rh leads to the appearance of an antiferromagnetic phase at field strengths less than the transition field, $H\le H_{c}$ = 2.8 T at T = 0, with $x\cong$ 0.1. The onset of metamagnetism occurs at a higher field of $H_{m}\cong$ 5.8 T [21].

In a similar manner as for CeRu$_{2}$Si$_{2}$, the temperature-dependent effects can be taken into account in the relationship

$$\begin{aligned} a_{1}(T)= & {} a_{10}\frac{T_{N}-T}{T_{K}}, \end{aligned}$$

(14)

$$\begin{aligned} a_{1}(T)= & {} \frac{T_{N}-T}{T_{m}}, \end{aligned}$$

(15)

in analogy with critical phenomena, where $T_{N}$ is the Néel temperature of this system. In Ce(Ru$_{0.92}$Rh$_{0.08}$)$_2$Si$_{2}$, $T_{K}\cong$ 20 K, $T_{N}\cong$ 4.2 K, and $T_{m} \cong$ 5 K [21].

Next, we can determine the other parameters using Eqs.(10a)–(10e); that is, they are fixed by fitting $h_{c}(0)$ = 0.087 and $h_{m}$ = 0.19, where $h_{c}(0)$ is the effective transition field at which the antiferromagnetic phase undergoes a transition to the paramagnetic phase at T = 0 [21, 22]. As a result, a set of parameters is found to be $a_{2}(0) =$ 0.32, $b=$ 1.5, $c_{1}=$ 0.5, $c_{2}=$ 9.0. Furthermore, $a_{2}(T)$ is determined by empirical fitting of $h_{c}(T)$, the phase boundary between the antiferromagnetic phase and the paramagnetic phase. The trajectory of $a_{1}(T)$ and $a_{2}(T)$ in this system is shown in Fig. 1.

Using the above parameters, the equilibrium sub-lattice magnetizations $\bar{m}_{A}$, $-\bar{m}_{B}$, their averaged values, and the sub-lattice susceptibilities can be found, as depicted in Fig. 3(a) and (b), respectively. In this way, the magnetic phase diagram of Fig. 3(c) is obtained. Although its metamagnetic field decreases rapidly with temperature when compared with the experimental observation, the smoothing of its sharpness of the magnetic susceptibility and disappearance of it are consistent with the experimental observation.

Fig. 3

a The sub-lattice magnetizations $\bar{m}_{A}$ (blue line), $-\bar{m}_{B}$ (green line), and the averaged magnetization $(\bar{m}_{A}-\bar{m}_{B})/2$ (red line); and b the sub-lattice susceptibility $\chi _{h}^{A}(T)=-\chi _{h}^{B}(T)$ for Ce(Ru$_{0.92}$Rh$_{0.08}$)$_{2}$Si$_{2}$ (parameters used are $b=$ 1.5, $c_{1}=$ 0.5, $c_{2}=$ 9.0). From the right, the temperatures are 0 K (blue line), 2 K (green line), and 4 K (red line). c The magnetic phase diagram for Ce(Ru$_{0.92}$Rh$_{0.08}$)$_{2}$Si$_{2}$. Lines show phase boundary and metamagnetic crossover line obtained using the Landau-type free energy density; experimental data are shown by (+), after Ref. [22] (Color figure online)

4 Discussions and Comment

We discuss about the improvement of the magnetic phase diagram which is shown in Fig. 3(c). If a lattice distortion is taken into account, we can add $-b^{\prime }m_{A}^{2}m_{B}^{2}$ ($h\ge h_{m}$) term to the extended Landau-type free energy density. Here, the coupling of the magnetic moments to phonons is assumed to be linear and the elastic energy is assumed to be harmonic. Furthermore, $b^{\prime }$ should be regarded as an even function of h by the symmetry requirements. Thus, this term repairs the metamagnetic crossover line to be flat with temperatures using the same method presented in Sect. 2. Although introduction of this term seems to be ad hoc, it may lead to whole understandings of the metamagnetism of HFCs.

In the above, we consider the phonon mechanism. However, another possibility which may induce $-b^{\prime }m_{A}^{2}m_{B}^{2}$ term exists: it is the Fermi surface instability (FSI) that sometimes comes from the Kondo destruction in HFCs. The Fermi liquid behaviors of the Kondo singlet which arise at low temperatures may break down by applying the magnetic fields, that is, the metamagnetism. According to the experimental facts, in HFCs which exhibit the metamagnetism, the density of states at Fermi energy $\rho (\epsilon _{F})$ is large for $h<h_{m}$, while $\rho (\epsilon _{F})$ may be small for $h_{m}<h$. If we suppose that $b^{\prime }$ is proportional to $1/\rho (\epsilon _{F})$, $-b^{\prime }m_{A}^{2}m_{B}^{2}$ term emerges at around $h_{m}$. Hence, we can again reproduce the magnetic phase diagram similar to observed one.

We comment on the relationship between our phenomenological theory presented here and microscopic theories. Every microscopic theory which explains metamagnetism must contain higher order terms, as in the theory put forward by Ohkawa. According to Ohkawa, the origin of higher order terms in the free energy density, such as the $c_1$ and $c_2$ terms, is the competition between the Kondo effect (the hybridization effect between localized magnetic moment and conduction electrons) and the Ruderman–Kittel–Kasuya–Yosida interaction (the indirect magnetic interaction between localized moments at each sites) with the lattice distortion [27]. In fact, by expanding Ohkawa’s result for the ground state energy, we can obtain explicit expressions for the parameters $a_{1}$(0), $a_{2}$(0), b, $c_1$, $c_2$, and even the parameter $b^{\prime }$, by putting $m_{A}=-m_{B}$. However, it is a hard task to derive parameters for higher order terms based on microscopic theories.

Finally, we describe the summary and the conclusion. The phenomenological theory is developed for the metamagnetism by the extension of the Landau-type free energy density incorporating the higher order terms. The theoretical magnetic phase diagram is consistent with the experimental observation qualitatively.

For the other heavy Fermion materials, we cannot apply this theory directly to Uranium compounds like URu$_{2}$Si$_{2}$ and/or UPt$_{3}$, since they have specific aspect for their own as like the quadrupole ordering.