1 Introduction and Scientific Background

The problem of modeling classical turbulence with a set of chaotic quantized vortices is undoubtedly in the mainstream of modern studies of vortex states in quantum fluids (see, e.g., [1–3]). One of the evidences of the quasi-classical behavior of QT is the k-dependence of the spectra of energyE(k), obtained in numerical simulations and experiments, and their comparison with the Kolmogorov law \( E(k)\propto \,k^{-5/3}\). The experimental observation of the Kolmogorov law is only obtained in presence of the normal component—see [4]. There is as yet no direct experimental evidence relating to the spectrum of the turbulent energy at very low temperatures [5]. Measuring the fluctuation of the vortex line density (VLD) [6, 7] gave results, which are, probably, inconsistent with the quasi-classical behavior of QT. As for numerical results, there are several works, which demonstrate the dependence \(E(k)\propto \,k^{-5/3}\). There are both the works, based on the vortex filament methods (VFM) [8–10] and works using the Gross–Pitaevsky Equation (GPE) [11–14].

The most common view of quasi-classical turbulence is the model of vortex bundles. The point is that the quantized vortices have a fixed core radius, so they do not possess the very important property of classical turbulence—stretching vortex tubes with a decrease in the core size. The latter is responsible for the turbulence energy cascade from large scales to the small scales. Collections of near-parallel quantized vortices (vortex bundles) do possess this property, so the idea that the quasi-classical turbulence in quantum fluids is realized via vortex bundles of different sizes and intensities (number of threads ) seems quite natural. However, the concept of the bundle structure does not explain the appearance of a Kolmogorov type spectrum \(E(k)\propto \,k^{-5/3}\), since the usual uniform vortex array just generates the coarse-grained solid body rotation.

In this work, we study nonuniform vortex arrays, whose structure is determined by the collapsing vortex dynamics.

2 Uniform Vortex Array

The energy of the vortex tangle, expressed via vortex filaments elements \(\mathbf { s}(\xi _{j})\) (\(\xi _{j}\) is the label variable of j-loop) is defined as (see [15–18])

$$\begin{aligned} E(k)=\frac{\rho _\mathrm{s}\kappa ^{2}}{(2\pi )^{2}}\sum _{i,j}\int \limits _{0}^{L_{i}}\int \limits _{0}^{L_{j}}\mathbf {s}_{j}^{\prime }(\xi _{i})\cdot \mathbf {s}_{j}^{\prime }(\xi _{j})d{\xi }_{i}d{\xi }_{j}\frac{ \sin (k\left| \mathbf {s}(\xi _{j})-\mathbf {s}(\xi _{j})\right| )}{ k\left| \mathbf {s}(\xi _{i})-\mathbf {s}(\xi _{j})\right| } \end{aligned}$$
(1)

For anisotropic situations, formula (1) is understood as an angular average, but one has to treat this formula with precaution (see [19]). Thus, for a calculation of the energy spectrum E(k) of the 3D velocity field, induced by the vortex filament, we need to know the exact configuration \(\{s(\xi )\}\) of vortex lines.

Let us study the question, what is the energy spectrum of 3D flow induced by the array of vortex filaments, imitating the bundle. First, we consider a set of straight vortex filaments forming the square lattice \(\bigcup s_{i}(\xi )=\bigcup (x_{i},y_{j},z)\). Points \(x_{i},y_{j}\) are coordinates for vortices on the xy-plane, indices i, j runs from 1 to N. The neighboring lines are separated by distance b, i.e., \(x_{i+1}-x_{i}=b\). In the case of different straight lines, we have to perform an integration between different lines and \(\left| \mathbf {s}_{1}(\xi _{1})-\mathbf {s}_{2}(\xi _{2})\right| =\sqrt{(x_{1i}-x_{2i})^{2}+(y_{1j}-y_{2j})^{2}+(z_{i}-z_{j})^{2}}=\sqrt{ d_{ij}^{2}+(z_{i}-z_{j})^{2}}\) where \(d_{ij}=\sqrt{ (x_{1i}-x_{2i})^{2}+(y_{1j}-y_{2j})^{2}}\) distances between vortices on the xy-plane. Then Eq. (1) is rewritten as

$$\begin{aligned} \frac{E(k)}{{\rho }_\mathrm{s}{\kappa }^{2}L}=\frac{1}{4\pi k} \sum _{i_{1},i_{2}=1}^{N}\sum _{j_{1},j_{2}=1}^{N}\int \limits _{0}^{L}\int \limits _{0}^{L}\frac{\sin (k\sqrt{d_{ij}^{2}+(z_{i}-z_{j})^{2}})}{(\sqrt{ d_{ij}^{2}+(z_{i}-z_{j})^{2}})}\;d(z_{1}-z_{2}) \end{aligned}$$
(2)

Integral over z is in the table by Gradshtein and Ryzhik (3.876) (see [20])

$$\begin{aligned} \frac{E(k)}{{\rho }_\mathrm{s}{\kappa }^{2}L}=\frac{1}{4\pi k} \sum _{i_{1},i_{2}=1}^{N}\sum _{j_{1},j_{2}=1}^{N}J_{0}(kd_{ij}). \end{aligned}$$
(3)

Thus, a determination of the spectrum on the basis (3) should be done with the use of the quadruple summation (over \( (x_{i},x_{j},y_{i},y_{j})\)), which requires large computing resources. Clear, however, that for very small k, which corresponds to very large distance, the whole array can be considered as large single vortex with the circulation \(N^{2}\kappa \). Accordingly, the spectrum (per unit height) should be (\(\rho _\mathrm{s}N^{4}\kappa ^{2}/4\pi )k^{-1}\). For large k, which corresponds to very small distance from each line, the spectrum (per unit height) should be \((\rho _\mathrm{s}\kappa ^{2}/4\pi )k^{-1}\) as for the single straight vortex filament. In the intermediate region \(kb<<1\), and \(Nkb>>1\) (this condition implies that inverse wave number \(k^{-1}\) is larger than the intervortex space between neighboring lines, but smaller than the size of the whole array Nb), we can replace the quadruple summation by the quadruple integration with infinite limits. This procedure corresponds that we exclude the fine-scale motion near each vortex, and are interested in the only large-scale, coarse-grained motion. After obvious change of variables \(x_{i}\rightarrow kx_{i},\ y_{i}\rightarrow ky_{i}\) etc. we get that the whole integral should scale as \(1/k^{4}\), and accordingly \(E(k)\propto 1/k^{5}\) (compare with [21]). As it is shown in [18], the velocity \(v(\mathbf {r})\) scales as \(\mathbf {r}^{1}\). Thus, the uniform vortex array creates the course-grained motion, which is rotation (velocity is proportional to the distance from center), as it should be. Moreover, the coefficient is proportional to \(\kappa /2b^{2}\), which corresponds to the Feynman rule. Concluding this subsection, we state that the uniform vortex bundles do not generate the Kolmogorov spectra.

3 Vortex Lines Breaking

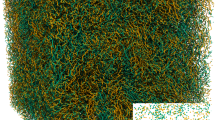
Currently, in classic hydrodynamics, the highly important topic—the role of hydrodynamic collapses in the formation of turbulent spectra—is being intensively discussed (See e.g., [22, 23]). Briefly, this phenomenon can be described as spontaneous infinite growth of the vorticity field \(\mathbf {\omega }=\nabla \times \mathbf {v}\) with formation of singularity in \(\omega (r)\). In particular, in the continuously distributed vortex field, the vortex lines (not quantized vortex filaments, just hydrodynamic vortex lines!) start to accumulate at some points \( a_{0}\) forming a singular distribution \( \omega (r)\sim r^{-2/3}\) as it is illustrated in Fig. 1. The latter results in the increment for velocity field \(\left\langle \mathbf {v}(\mathbf {r+\delta r)}\right\rangle \sim r^{1//3}\), which, in turn, results in the Kolmogorov spectrum \( E(k)\propto \,k^{-5/3}\). In classical hydrodynamics, this scenario is known as the vortex breaking. This phenomenon was analyzed in a series of papers by Kuznetsov with coauthors ( see/ e.g. [22, 24] and references therein) in the framework of the integrable incompressible hydrodynamic model with the Hamiltonian \(\int |\mathbf {\omega }|d\mathbf {r}\). Studying Euler equations in terms of vorticity (also known as Helmholtz’s vorticity equations)

$$\begin{aligned} \frac{\partial \mathbf {\omega }}{\partial t}=\nabla \times \,(\mathbf {v} \times \mathbf {\omega }), \end{aligned}$$
(4)

Kuznetsov concluded that in the vicinity of the touching point \(\mathbf {a} _{0}\) the maximum value of vorticity \(\omega _{\max }\) develops in the blow-up manner

$$\begin{aligned} \omega _{\max }\propto \frac{1}{t^{*}-t}, \end{aligned}$$
(5)

with approaching the infinity at some time \(t^{*}\). The domain of vorticity is not isotropic, it has a pancake structure. The main dependence of vorticity field is connected with the transverse to the bundle direction \( \rho _{\perp },\) and \( \omega (\rho _{\perp })\) scales as

$$\begin{aligned} \omega \propto \frac{1}{\rho _{\perp }^{2/3}}. \end{aligned}$$
(6)
Fig. 1
figure 1

Schematic picture illustrating the vortex bundle collapse [25]. The initially regular distribution of vorticity spontaneously concentrates, collapsing in some point \(\mathbf {a}_{0}\) and forming the singular structure (Color figure online)

Full size image

A similar consideration can be applied for quantum vortices. It, however, can be done only in the particular case of vortex bundles, when the quantum vortex filaments form a near-parallel structure. In this case the coarse-grained hydrodynamic equations for the superfluid vorticity are obtained from the Euler equation for the superfluid velocity \(\mathbf {v}_\mathrm{s}\,\mathbf {=}\left\langle \mathbf {v} _{\mathrm{s}}\right\rangle \) after averaging over the vortex lines . The coarse-grained hydrodynamic of the vortex bundles is studied by many authors (see e.g., [26–29]), but the basis of these studies was the hydrodynamics of rotating superfluids, or the Hall–Vinen–Bekarevich–Khalatnikov (HVBK) model (see e.g., book [30]). In the vortex bundles, the coarse-grained vorticity field of \(\omega _\mathrm{s}\), and the 2D vortex line density \(\mathcal {L}\) (which coincides with the areal density in the plane perpendicular to the bundle) are related to each other by means of Feynman’s rule, \(\omega _\mathrm{s}=\kappa \mathcal {L} \). In terms HVBK the dynamics of this vorticity obeys the following equation (see [30])

$$\begin{aligned} \frac{\partial \mathbf {\omega }_\mathrm{s}}{\partial t}=\nabla \times [\mathbf {v}_{L}\times \mathbf {\omega }_\mathrm{s}], \end{aligned}$$
(7)

where \(\mathbf {v}_{L}\) is the velocity of lines,

$$\begin{aligned} \mathbf {v}_{L}\mathbf {=} \mathbf {v}_\mathrm{s}\,\mathbf {+}\,\alpha \left[ {{\hat{\mathbf {\omega }}}_\mathrm{s}}\times \left( {{\mathbf {v}}_{n}-{\mathbf {v}_\mathrm{s}}}\right) \right] . \end{aligned}$$
(8)

It is easy to see that in case of zero temperature, when mutual friction vanishes \(\alpha =0\), and taking into account that vortex lines move with the averaged velocity \(\mathbf {v}_\mathrm{s}\mathbf {=}\left\langle \mathbf {v}_\mathrm{s}\right\rangle \), the dynamics of macroscopic (or the coarse-grained) vorticity is identical to the dynamics of classical field; therefore, all conclusions stated above concerning the collapse of vorticity are valid for quantum fluids.

4 Noninform Lattice

Let us now consider the nonuniform vortex bundle. To model this situation, we just can choose that the distance b between lattice points (see Sect. 2) is not constant, but depends on the numbers i, j of the cell nodes. We have to realize that the problem of the spontaneous formation of vortex bundles is only on the stage of discussion so far, and there are no ideas concerning an exact arrangement of these bundles. We will choose the power law dependence for the distance between the lattice points.

$$\begin{aligned} x_{i+1}-x_{i}=b_{0}i^{\lambda },\ y_{j+1}-y_{j}=b_{0}j^{\lambda }. \end{aligned}$$
(9)

We do not ascertain the quantity \(\lambda \), it is a free parameter of our approach. Under condition (9), the expression (3) turns into

$$\begin{aligned} \frac{E(k)}{{\rho }_\mathrm{s}{\kappa }^{2}L}=\frac{1}{4\pi k}\sum _{i=1}^{N} \sum _{j=1}^{N}J_{0}(kb_{0}i^{\lambda }) \end{aligned}$$
(10)

That means that while changing the summation by integration, we have to put \( x_{i}\rightarrow k^{1/\lambda }x_{i},\ y_{i}\rightarrow k^{1/\lambda }y_{i}\ \)(instead of the change of variables \(x_{i}\rightarrow kx_{i},\ y_{i}\rightarrow ky_{i}\)  made in Sec. 2). As a result we get that the whole integral should be scaled as \(1/k^{1+4/\lambda }\). It is easy to see that when \(\lambda \) \(=6\), the spectrum \(E(k)\propto k^{-5/3}\).

Let us find the 2D density of vortices on the xy plane under condition (), or, according to the Feynman rule, the distribution of vorticity \(\omega (r)\). In the “space” of indices \(\{i,j\}\) vortices are distributed uniformly (one vortex per lattice site \(\{i,j\}\)), but since the distances between the sites vary, the distribution of vortices in real xy space is nonuniform. Let us consider “the ring” of radius from I to \( I+\Delta I\) in \(\{i,j\}\). Then, the number of points \(\Delta N\) in the ring is just \(2\pi I\Delta I\), the radius of the ring in real xy space is \( r=b_{0}I^{\lambda }\), and the thickness of the ring is \(\Delta r=b_{0}\lambda I^{\lambda -1}\Delta I\). From these relations it follows that the real n(r) scales with r as

$$\begin{aligned} n(r)=\frac{\Delta N}{\Delta r}\propto \frac{1}{r^{1-2/\lambda }}. \end{aligned}$$
(11)

If \(\lambda \) \(=6\), then \(\kappa n(r)=\omega (r) \propto r^{-2/3}\), as it should be for the classical turbulence. This result is in agreement with works [22, 24].

5 Conclusions

Summarizing, it can be concluded that the 3D energy spectrum E(k) close to the Kolmogorov dependence \(\propto k^{-5/3}\)  which was observed in many numerical simulations on the superfluid turbulence [8–14, 31], can appear from the collapsing vortex bundle.