A Note on Empirical Studies of Life-Satisfaction: Unhappy with Semiparametrics?

Abstract

This article deals with the modeling of life-satisfaction, and estimating the impact of age on it. We investigate how findings and the interpretation of empirical studies hinge on the respectively assumed model. Assuming a specific model comprises various hypothesis made on the data generating process, like indicator selection, measurement, or functional form specifications. In this study we focus on the latter two issues. In particular, we show how different response behaviors (optimistic, pessimistic, extreme averse, etc.) lead to seemingly contradictory conclusions if the researcher does not address them adequately. In fact, we show that one can reproduce any shape found in the literature simply by modifying the way respondents rank life satisfaction on a bounded scale.

1 Introduction

Model misspecification has always been an important issue in empirical research. The debate on this issue has been stirred up again by the literature on impact evaluation and causal inference. Nonparametric techniques circumvent the problem of model misspecification by relaxing the assumption on any explicit functional form, and by considering the infinite parameter space [see the compendiums of Li and Racine (2006) or Henderson and Parmeter (2015) for details and examples]. However, various practical problems like the curse of dimensionality or the lack of explicit parameter estimates for the direct inference of marginal effects make these techniques less appealing.

In statistics, semiparametric techniques were introduced to circumvent the curse of dimensionality, and provide some sort of flexibility (see for example Härdle et al. 2004). In social sciences they became popular because of their ability to prefix parts of the model, for example to incorporate prior knowledge, or ‘to model where you want to model’. The elements for which available theory (of sociology, economics, medicine, psychology, etc.) is not specific, can be fit in good conscience nonparametrically (see e.g. Horowitz 2009 for more discussion and examples). Researchers parametrically modeled the parts they wanted to interpret, and all the rest was called ‘nuisance parameters’ (distribution, scedasticity function, impact of control variables, etc.) and fit nonparametrically. More recently, there has been a trend to let the part of the model unspecified which is in the focus of the study. For example, when studying life-satisfaction (LS), many researchers are particularly interested in estimating the impact of age. Consequently, its real shape is the center of controversy, especially because different researchers find contradicting shapes starting from similar theory and data. More specifically, misspecification becomes particularly relevant for correct interpretation, that is, when the researcher wants to deduce conclusions from some parts of the estimated model.¹ For a better understanding let us consider the tangible case of estimating the impact of age on LS.

In such a situation a seemingly attractive remedy is to estimate the marginal impact of age nonparametrically, while keeping the rest of the model parametric. To be more specific, suppose we are facing (bounded discrete) responses $LS_i$ for individuals $i=1,\ldots ,n$, observed together with $age_i$ and some (other) characteristics ${\mathbf {x}}_i\in {\mathbb {R}}^J$ for which we want to control when assessing the marginal impact of age. The classic literature typically considers a generalized linear model with a link function G and index function $\eta$, say

$$\begin{aligned} (GLM) \qquad \ E[ LS |X={\mathbf {x}} ,Age=age]=G( \eta ({\mathbf {x}},age) ) = G(\beta _0+ {\mathbf {x}}^{T}\mathbf {\beta }_1 + \sum _{k=1}^P age^k \gamma _k ) \ , \end{aligned}$$

(1)

where P is typically chosen along the researcher’s convenience. Moreover, G is often set to identity with different justifications for this choice. A necessary prerequisite for this particular link is that either LS is a cardinal variable or the index function $\eta$ is “sufficiently” flexible. It is clear that no link G is necessary if this index $\eta$ is entirely nonparametric.² However, the estimation can run into the curse of dimensionality, and more importantly, renders the interpretation of the impact of age very difficult. Therefore, Wunder et al. (2013) deemed the semiparametric partial linear model

$$\begin{aligned} (PLM) \qquad \ E[LS |X={\mathbf {x}} ,Age=age]= {\mathbf {x}}^{T}\mathbf {\beta } + m_a ( age ) , \end{aligned}$$

(2)

in which $m_a$ is a one-dimensional nonparametric function, an enticing compromise. As G is the identity with a quite flexible $\eta$, the impact of age is easy to estimate, illustrate, and interpret. Moreover, taking the responses as cardinal and using $G=identity$ is widely accepted in the literature of economics and other social sciences (see Ferrer-I-Carbonell and Frijters 2004) .

Applying the PLM to German and British household data, Wunder et al. (2013) obtained empirical evidence for the so-called midlife crisis at the age of around 50. But other researchers found either a U-shape, an inverse U-shape or simply a linear downslope impact of age. The difficulty of not obtaining the same results when analyzing LS was also observed and pointed out while studying the impact of determinants other than age (see for example the recent work of Ingenfeld et al. 2019). For the impact of age, we show that the estimate can actually take any of the shapes found in the literature, just because of different ways of self-reporting LS – even if the data generating process is identical in all other aspects. For example, a valley at age 50 can be caused by a natural link G, even when $m_a (\cdot )$ is indeed linear. By ‘natural’ we mean that people’s responses regress to the mean, that is, when they are reluctant to extreme responses for LS (individuals may not want to rank themselves as totally unsatisfied or perfectly satisfied). This shift toward the mean causes an unequal scaling which can be captured by a proper choice of G, whereas ignoring it results in a cubic shaped estimate of $m_a$. In other words, in the setting of a Generalized PLM

$$\begin{aligned} (GPLM) \qquad \ E[LS |X={\mathbf {x}} ,Age=age]=G\left\{ \eta ({\mathbf {x}},age) \right\} = G\left\{ {\mathbf {x}}^{T}\mathbf {\beta } + m_a(age) \right\} \ , \end{aligned}$$

(3)

a misspecified G, ignoring the non-linearity of the impact of x on $\eta$, or the suppressing of interactions with age, are sources of bias when estimating $m_a$. This leads to the peculiar situation where in a semiparametric model, the nonparametric estimate has to be interpreted with care. It is peculiar in the sense that one might think the nonparametric part is free from model misspecification. However, this part inherits the misspecification of the parametric part; and thanks to its flexibility, is even more susceptible to such misspecification than a parametric $m_a$ would be. While this is a general problem, it is especially serious in the analysis of data with bounded discrete responses (Studer and Winkelmann 2017). There is some controversy as to whether LS should be considered as ordinal or cardinal, but imposing assumptions on the nature of such responses pre-defines the functional form of G. Except for certain cases, such problems are not necessarily identifiable (Kahneman and Krueger 2006). Consequently, a proper empirical analysis would study a set of potential models, that is, conduct robustness checks.

The aim of this article is to provide awareness for empirical researchers on bias transfers between the components, even in semiparametric models. This is done along the example of a life-satisfaction study with a special focus on the link. This includes the problem with self-reported responses on a bounded scale. Note that we are not referring to the reliability of responses as recently discussed in Kapteyn et al. (2015), Dolan and Kavetsos (2016), and Teresi et al. (2017).

In Sect. 2 we formalize the aforementioned problem. Through a simulation study in Sect. 2.2 we illustrate the consequences of functional form misspecification for the transfer of bias between components of a semiparametric model. Section 3 provides an empirical study with a SOEP data set in which we explore to what extent different model specifications would lead to contradicting results for the impact of age on LS. Section 4 concludes.

2 Data Generating Process and Regression Model

When thinking about bias transfer toward the nonparametric part in semiparametric models, potential sources are obviously the link function, interactions, and the impact of further covariates as far as they are deferred to the parametric part. We start out by reflecting on the underlying data generating process (DGP) followed by simulations. The reason is that to fully understand what a method does to the data, it is necessary to know the true DGP. This makes it possible to reason back to the DGP of real data when applying the same model in practice. Note that the DGP of this section is a toy model; we do not claim completeness of this model, but we try to depict the general structure inherent in most studies we found in the literature.

2.1 A Model for Self-Reported Life-Satisfaction

Historically, methodological approaches to analyze LS evolved differently in each field. For example, Ferrer-I-Carbonell and Frijters (2004) point out in their paper, that in most economics papers the LS measure is taken as an ordinal variable, whereas in studies performed by psychologists it is assumed to be cardinal. The common ground is a direct link between the individual’s utility $U_{i}$ and the self-reported $LS_i$, such that one can write

$$\begin{aligned} \text {LS}_{i}={\tilde{G}} (U_i) \ \text { for utility } \ U_{i}= \sum _{j} m_{j}({x}_{ij}) \ , \end{aligned}$$

(4)

where $m_j$ are unknown functions. Therefore, it is assumed that the individual’s utility can be written as a sum of fundamental components such as wealth, health, etc. which in turn can be expressed as functions of personal characteristics and socio-economic indicators summarized in vector ${\mathbf {x}}_{i}$. Next, an error term $\varepsilon$ is typically added, as in practice only some of the $x_{ij}$, say for $j=1,\ldots ,J$, are observed (assuming $E[\varepsilon | X_1,\ldots ,X_J]=0$ for the random variables $X_j$). For a fully deterministic model many more covariates with some interactions would be needed. Clearly, the utility is a (not observable) latent variable, such that its realization is measured through indicators of which self-reported LS is a quite popular one, typically recorded on a bounded discrete support ${{\mathcal {K}}}=\{0,1,\ldots ,K\}$. ${\tilde{G}}$ links utility to LS. It can take different forms according to the assumptions that a researcher finds plausible to explain the behavior of an individual in choosing a number of ${{\mathcal {K}}}$ that corresponds to his/her feelings. The formulation of overall LS is then:

$$\begin{aligned} \text {LS}_{i}=C_{k} \qquad \text{ iff } \qquad a_{k} \le U_{i} < a_{k+1} \qquad \forall i \ , \end{aligned}$$

(5)

where $C_{k}$ is the level of LS chosen by the individual whose perceived utility lies between $a_{k}$ and $a_{k+1}$. We define set $\mathbb {a}=\{a_{1},a_2,\ldots ,a_{K}\}$ with $a_{0}=-\infty$ and $a_{K+1}=\infty$. With ${{\tilde{G}}}$ being an increasing step function we can think of it as a composition $(D \circ S)$ of a monotone link S that changes the scale of utility such that $S(a_{k+1})=S(a_k)+1$ for $0\le k\le K$ with $S(a_0)=0$. Further, D is the discretization $D: \sum \limits_{k=1}^{K} \mathbb {1} \{ S(U_i)\ge k \}$ that maps the responses to the bounded discrete scale with support ${{\mathcal {K}}}$. If all $m_{j}$ are linear, we end up in a GLM with link function G that combines ${{\tilde{G}}}$ with the distribution of $\varepsilon$ (the non-specified part of U). For example, with $\varepsilon$ being normal, one can think of an ordered probit model. If, however, the functions in U are flexible, then one will end up in identification problems unless restrictions are imposed on $\mathbb {a}$ like equidistance for $a_1$ to $a_{K}$. This is equivalent to specifying ${{\tilde{G}}}$, and thinking of

$$\begin{aligned} E[LS|x_1,\ldots ,x_J] = E[{{\tilde{G}}}(U) | x_1,\ldots ,x_J ] = \int {{\tilde{G}}}\left\{ \sum _{j=1}^J m_j(x_j) +\varepsilon \right\} dF_\varepsilon = G\left\{ \sum _{j=1}^J m_j(x_j) \right\} \end{aligned}$$

(6)

for $F_\varepsilon$ being the cumulative distribution of the random error. In sum, we have tried to be quite general but we have also followed some popular concepts. More specifically, we imposed additive separability of the utility function in Eq. (4). This is common, even though this admittedly does not mean that it must be correct, and has a long history (see e.g. Debreu 1960; Fishburn 1970). Equation (6) introduces a very general concept under high flexibility for modeling how people translate their utilities onto a bounded discrete scale. Therefore, once the additive separability of the utility function has been accepted, we may say that this presents a most general life satisfaction model. Clearly, in the simulation and application we additionally assume that the omitted variables cause no significant distortion.

From Eq. (6) we see that even if the sample is representative, and $m_1$ nonparametric, there are several potential sources for a bias when estimating the impact of $x_1$: misspecification of U, in particular of $m_2$ to $m_J$, or missing interactions, misspecification of ${{\tilde{G}}}$, and misspecification of $F_\varepsilon$. These problems are obviously not separable (like the interplay between ${{\tilde{G}}}$ and $F_\varepsilon$). Consequently, in order to understand the impact of a particular misspecification, it is helpful to rescind from any other source.

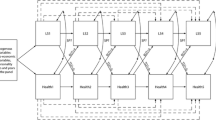
The topic of functional misspecification is as old as statistical (or econometric) modeling is, and has generated a huge amount of specification tests, especially since the rising popularity of nonparametric methods (see e.g. Gonzalez-Manteiga and Crujeiras 2013 for a recent review). However, if the interest is in the impact of $x_1$, the attention is usually focused on the specification of $m_1$. The concern about bias effects for $m_1$ in the case when other parts of the model are misspecified, has been discussed much less, although it is experiencing a revival in the literature on estimating impact evaluation (Frölich and Sperlich 2019). This is true also beyond biometrics and econometrics (see e.g. Achen 2005). Set $J=2$, and express $m_2$ in terms of a series $\alpha _1 x_2 + \sum _{l=2} \alpha _l \varphi _l (x_2)$ such that $\int v \varphi _l(v) dF_{x_2}(v) = 0$ for all $l>1$, and $F_{x_2}$ the distribution of $X_2$ (which is always possible under some mild smoothness conditions for $m_2$). If one pre-specifies the impact of $X_2$ to be linear, then even for $G=identity$, an estimate of $m_1$ will suffer from ‘omitted variable biases’ unless $X_1$ is (mean-) independent from all the $\varphi _l (X_2)$. The same certainly happens when we omit significant interactions. Imagine $G=identity$, $X_1=Age$, $X_2=Illness$, which exhibit a strong positive correlation, $m_1$ linear, and $m_2$ a third order polynomial, both decreasing (as the solid lines in Fig. 1). If $m_2$ is forced to be linear (dashed line in the left panel) but $m_1$ is estimated non-parametrically, an estimate similar to the dashed line in the right panel will consequently be obtained.

Fig. 1

Bias-transfer from the parametric (left) to the nonparametric part (right) when estimating the components of a PLM. The solid lines indicate the true functions, the dashed lines their estimates if the impact of illness is erroneously modeled linearly, and the impact of age non-parametrically. The signs ($-$,+) indicate the sign of the respective biases

What can be said about the link G? As previously mentioned, in practice ${{\tilde{G}}}$ is often set to identity, especially if the extreme values 0 and K are not frequently observed. Consider the simple setting where utility is a sum of two fundamental components $m_{1}$ and $m_{2}$ with correlated covariates as above. We are interested in the effect of $X_{1}$ on utility, $m_1$, or in

$$\begin{aligned} \left. \frac{\partial E[ LS | X_1,X_2 ]}{\partial X_{1}} \right| _{x_1}= m_{1}^{'}(x_{1}) \cdot (G^{-1})^{'} \left\{ m_{1}(x_{1})+m_{2}(X_{2}) \right\} \ . \end{aligned}$$

Clearly, if $m_2$ is misspecified, for example by using a linear function, then for correctly specified G its effect on the estimation of $m_1$ depends on the dependency between $\sum _{l=2} \alpha _l \varphi _l (x_2)$ and $X_1$, but also on G. If instead, we specify correctly $m_2$ but misspecify the link using ${\check{G}}$ in place of ${\widetilde{G}}$, then we obtain for $G_2 := {\check{G}}^{-1} \circ {\widetilde{G}}$

$$\begin{aligned} {\check{U}}= & {} {\check{G}}^{-1}(LS) = {\check{G}}^{-1}\left[ {\widetilde{G}} \left\{ m_{1}(X_{1})+m_{2}(X_{2}) \right\} \right] = G_{2}\left\{ m_{1}(X_{1})+m_{2}(X_{2}) \right\} \ , \\&\quad \text { giving } \quad \left. \frac{\partial {\check{U}}}{\partial X_{1}} \right| _{x_1,x_2} = \left( m_{1}^{'}(x_{1})\right) \cdot G^{'}_{2} \left\{ m_{1}(x_{1})+m_{2}(x_{2})\right\} \ . \end{aligned}$$

We see that in the case of a non-identity link, it is by no means obvious how misspecifications actually affect the final estimates. To gain some more intuition, one has to come up with practical examples and illustrations.

We start with discussing different ‘natural’ transformations ${{\tilde{G}}}$—or rather S, cf. definition above—that link the utility to self-reported LS. Consider Fig. 2 in which each S refers to a different population. In the first one (upper left) individuals are aware of the effective range of utility, neutral toward (bounded) scale, and convert their utility into discrete numbers by dividing the effective range of utility into intervals of equal length. In such a case one may conclude that ${{\tilde{G}}} = identity$ is an appropriate choice. But even this is only true if there are no effective boundaries, that is, if the boundaries describe the support of the utility distribution. Moreover, it is much more common for people to have an aversion to extremes, such that they tend to choose grades from the center (see Austin et al. 2006 and Wetzel et al. 2013), producing a link as shown in the upper right. In the lower left population, individuals tend to be optimistic, and exhibit an aversion to (quite) negative responses, thereby producing a right skewed link. A rather pessimistic population is averse to positive responses and chooses more from the lower scale, giving a right skewed distribution for the responses (lower right).

Fig. 2

Transformation function S for four typical populations

It is important to bear in mind that the differences between $S_1$, $S_2$, $S_3$, and $S_4$ are not due to different utility functions and thus not due to age. They just reflect differences in response behavior due to a bounded (discrete) scale. However, the choice of transformation has serious consequences for the empirical study, as will be illustrated next.

2.2 Potential Effects of Misspecifications

As previously mentioned, there is keen interest in the LS literature relative to studies in estimating the effect of age on LS (also referred to as ‘happiness’). The results have been controversially discussed and are contradictory even between quite similar case studies. For instance, Alesina et al. (2004) find that happiness increases with age till some point and then decreases, whereas Blanchflower and Oswald (2004) find a convex curvature for this relationship. Ferrer-I-Carbonell and Frijters (2004) claim that this ambiguity in the literature comes from a high correlation of age with all other observed and unobserved factors. That criticism points to a potential omitted variable bias, but not to the problematic choice of G [say S or/and F(u|x, age)], nor to a functional misspecification of index $\eta (x,age)$.

The first issue is that it is necessary to clearly say which impact of age on life-satisfaction is of interest: the total or some marginal effect? In practice almost all empirical studies include also covariates that are itself strongly impacted by age; they therefore do not study the total, but a particular marginal impact. Let us assume that our interest is to study the marginal effect of age on life-satisfaction after having controlled for health, and imagine that the true DGP for individual i is $U_{i} = W_{i} - I_{i}$ where $U_i$, $W_i$ , and $I_i$ present the individual’s utility, relative wealth (e.g. the own quantile in the distribution of household net income divided by household members),³ and illness. Both are strongly related to age. We assume relative wealth to slightly decrease with age (e.g. due to a cohort effect or household size, see Easterlin (2001) , but illness to increase. Now self-reported life-satisfaction is regressed on illness and years for people of age 20–80. Recall that in order to be flexible in age, Wunder et al. (2013) proposed a semiparametric partial linear model (PLM) of the form (2). Even if W and I are indeed linear in age, utility $U_i$ as above, then the links $S_2$, $S_3$ and $S_4$ from Fig. 2 cause non-linearity from LS to illness and age.

Fig. 3

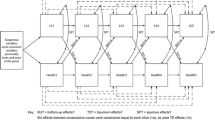
Bias-transfer from the parametric to the nonparametric part when estimating the components of a PLM. Solid lines indicate the true marginal impacts, dashed lines the expected PLM estimates. Left panel: bias when illness is forced to have a linear impact. Right panel: bias transfer from the left panel when age is positively correlated with illness and slightly negatively with relative wealth

Figure 3 illustrates the bias-transfer that occurs in a PLM fit if we face $S_2(\cdot )$ (extreme averse) and a utility function as above with $W_i$ and $I_i$ being linear in age. The solid lines in Fig. 3 are the marginal impacts of illness and age on LS. However, a PLM restricts illness to have a linear impact (dashed line) with positive bias for lower levels of illness, and negative bias for higher levels. Since illness is strongly correlated to age, the nonparametric estimator for age will account for the bias obtained in the left panel for the effect of illness. This results in the dashed line of the right panel. We see a valley at midlife (recall that the sample starts at 20) which is only due to the misspecification of S, that is, ignoring extreme aversion in responses. It is clear that we observe the same kind of bias-transfer if the link function is correctly specified but illness has a non-linear impact on LS. In both cases the forced linearity of the illness component causes a bias when estimating the (marginal) age effect.

While Fig. 3 gives an idea of what the PLM estimator does to the data, the actual numerical outcome is verified in a simulation study, because a nonlinear transformation S of U can also produce an interaction of the covariates on LS. In order to reproduce the effect of our different S in Fig. 2, we generate a random sample of size $n=1500$ with $Age \sim U \left[ 20,80 \right]$:

$$\begin{aligned} I_{i} = \epsilon _{I,i} +0.1\times Age_{i} ; \quad W_{i} = \epsilon _{W,i} - 0.03\times Age_{i} \, , \end{aligned}$$

where $\epsilon _{I} \sim N(-8,1)$ and $\epsilon _{W}\sim N(4.5,1)$. The $U_{i}$ are as above, wealth minus illness.⁴ The four links assign to the equidistant responses $\{ 0,1, 2, 3,\ldots , 9, 10 \}$ the following sets $\mathbb {a}$ :

• Neutral population: $\mathbb {a}= \{ 1,2,3,\ldots ,9,10 \},$

• Extreme averse population: $\mathbb {a}= \{ 1, 1.4, 1.9, 2.8, 4.2, 6.8, 8.2, 9.1, 9.6, 10 \},$

• Optimists population: $\mathbb {a}= \{ 1, 1.2, 1.6, 2.1, 2.7, 3.6, 4.9, 6.4, 8.2, 10 \},$

• Pessimistic population: $\mathbb {a}= \{ 1, 2.8, 4.6, 6.2, 7.3, 8.2, 8.8, 9.3, 9.7, 10 \}.$

Fig. 4

Results of the fitted PLM to data that emerged from the same DGP but are reported along different link functions ($S_1$ to $S_4$) to transform utility into responses on LS

We fit the PLM of (2) with $I_i$ being the only X included, and use cubic regression B-splines for $m_a(age)$. Typical outcomes of such a simulation run are shown in Fig. 4 (gray shades indicate 95% point-wise confidence bands). We repeated this many times always obtaining basically the same figures. The most interesting finding is that the different curvatures of the age effect on LS are exactly those found in the literature, namely the linearly decreasing, U-shape, inverse U-shape and that with a valley at midlife. These are all obtained from exactly the same estimator and DGP, with the only difference being the S, that is, looking at responses from a neutral, an extreme averse, an optimistic, and a pessimistic population, respectively. The data were therefore generated from a life cycle without ‘midlife crisis’, yet the second transformation (the extreme averse population in Fig. 4) indicates the presence of midlife crisis. However, this outcome is nothing but a numerical phenomenon; the transferred bias caused by ignoring the extreme aversion in responses on a bounded scale.

2.3 Recommendations for Robustness Checks

To stop and conclude here would result in a somehow destructive criticism. To respond to this negative finding, the next section demonstrates how such an empirical study could be completed. We do not say ‘we solve the problem’, because as long as the true link and functional form of U are unknown, it may be preferable to use purely nonparametric methods. But if the objective of selecting $G(\cdot )$ is to correct for the way people reported LS (e.g. to account for extreme aversion) which is not related to utility, then even the nonparametric methods cannot help. For instance, in case of extreme aversion we actually face a measurement error that is systematically positive for low utilities, and negative for large ones (see also Krueger and Schkade 2008 regarding the reliability of self-reported subjective well-being).

Without knowing function S, identification requires the imposition of (additional) model assumptions which should be based on studies that investigate the response behavior of people for the given scale. For instance, Bertrand and Mullainathan (2001) point out the necessity of studying attitudes toward subjective and categorical survey questions. Wooden and Li (2014) argue, in the context of subjective well-being, that individual fixed effects may help in the identification of some effects. Note that for estimating the impact of age, this does not make much sense as age equals birth date, which is time invariant, plus time t. This implies that the inclusion of individual fixed effects will change the meaning of $m_a$. For example, in a linear fixed effects panel model, age becomes equivalent to t [see also Baetschmann (2014) who discussed the fundamental problem of disentangling the effects of age, cohorts and time]. Chadi (2013) provides evidence of the effect of interviewer encounters on responses. Both suggest including interviewer fixed effects. Unfortunately, it is easy to see that panel fixed effects of this kind (the interviewed or the interviewer) do not correct for problems caused by given bounds on the response scale (such as extreme aversion). At the best, these propositions can only be regarded as robustness checks. They cannot guarantee an unbiased estimation for the functional form of life-satisfaction in age. A main reason is that the specification problems of link and index are not separable unless additional assumptions (restrictions) are imposed.

When applying non- or semiparametric methods, one should also mention the role of smoothing-, penalization- and regularization- parameters. They determine the degree of smoothness of the nonparametric part. These choices are made to minimize the average squared error of the data fit, but not to estimate the ‘true’ functionals in a potentially misspecified model. Therefore, they are not made for eliminating bias transfers and typically cannot eliminate them. To our knowledge there is no data driven technique for the choice of bandwidth that could prevent the bias transfer between the components of a semiparametric model. Note that for all semiparametric estimation in this paper we apply Generalized Cross Validation for cubic regression B-splines. Calculations are done in R with function ‘gam(.)’ from package ‘mgcv’.

3 Male Midlife Crisis in Germany: Empirical Evidence?

We study the impact function of age on LS, which is a topic of controversy in the literature. Data are taken from the German Socio-Economic panel (SOEP) of the years 1984 to 2013. Many studies directly concentrate on either men or women, other studies include gender dummies or separate their sample along gender. We concentrate only on men.⁵ This is certainly not a comprehensive analysis of life-satisfaction; we rather explore to what extent different model specifications lead to alternative conclusions. In particular, we seek to illustrate whether empirical evidence for a midlife crisis is maintained when varying the model specification. This is the robustness check discussed in the last (sub-)section to ensure that one is not just facing the bias transmission phenomenon.

Similar to Wunder et al. (2013) we include only observations for which all relevant questions were answered (see variable list below). For example, we exclude the years 1990 and 1993 for which the number of nights in hospital was not registered. This does not assume that all non-responses are missing-at-random, we rather concentrate on the population represented by the remaining sample. We have an unbalanced panel including 7205 individuals in total of which most reported the needed variables only for a few years. The total number of observations is therefore only 81, 845, that is, we have less than 12 waves per individual on average.

The response considered is ‘Overall Life-Satisfaction’ (LS), a discrete categorical response on a scale from 0 to 10, where ‘0’ corresponds to ‘completely dissatisfied’ and ‘10’ to ‘completely satisfied’. A histogram of the responses is shown in Fig. 5 exhibiting that the unconditional distribution is strongly skewed to the left with its mode at 8. Histograms of LS for different age groups are provided in Fig. 10 in the “Appendix”, showing similar features.

Fig. 5

Observed responses to ‘Overall Life-Satisfaction’ LS

We further restrict our sample to men between the ages of 18 and 100. The other covariates included are personal characteristics used in similar studies (see for example Wunder et al. 2013): illness (Nights in Hospital NinH), disabled (a dummy variable), relative wealth (household income and size, education, nationality, employment status), geographic location (states), marital status and year dummies (see Table 1 in the “Appendix”).

Like other existing studies, we cannot include individual fixed effects for several reasons. First, as said above, this would not allow us to identify the effect of age, because age is just the birth date plus a linear time trend. Including time effects (we included fixed effects for years) would render the entire model non-identifiable. Secondly, even if we concentrated on the impact of health, the inclusion of individual fixed effects for non-linear models would be quite complex or simply infeasible [see Profit and Sperlich (2004), Mammen et al. (2009) and Hoderlein et al. (2011)]. Stutzer and Frey (2004) insinuated that for some models the inclusion of individual random effects could account for response behavior if this difference is marked by individual location shifts. However, if the response behavior has a more complex distributional structure (like the extreme averse and optimistic individual’s example discussed in this paper), then it cannot be captured this way. As expected, when we reran the estimations including individual random effects, our findings did not change.

For the sake of illustration and in the spirit of our simulation study above, we run two sets of analyses: ‘A’ with only Age, NinH and Disabled, and ‘B’ including all the aforementioned covariates. In both cases we start from a PLM (2) with $G=identity$.

Figure 6 presents the marginal effect of age on LS for analyses ‘A’ and ‘B’. These seem to clearly indicate a midlife crisis around the age of 50. However, a simple diagnostic check for Analysis B, provided in Fig. 11 (left panel) in the “Appendix”, exhibits serious problems at the tails, indicating a potential problem with extreme aversion.

Fig. 6

The marginal effects of age on LS for German men, analyses A (left) and B (right)

For a robustness check against potential misspecification we tried different specifications like GPLM with a parametric link (Poisson, see below), partial linear additive models without (AM) and with a (GAM) link, some interactions added, etc. To be more specific, let us group the covariates into three sets: namely Age; one comprising the dummy variables,⁶D; and one comprising the others, X (the Nights in Hospital (NinH), years of education (YofEdu), log of net household income (LNHI), and log of household size (LHS)). Then we consider a general class of semiparametric models:

$$\begin{aligned} E[LS|Age, D, X] = G\left( m_a(Age) + m_{x}(X) + m_{I}(X,Age) + D^{T} \mathbf {\beta } \right) , \end{aligned}$$

(7)

with $m_{x}$ being either nonparametric or linear, and $m_{I}$ being a nonparametric interaction term or set to zero. We are aware of the fact that there exist many more model alternatives like for example generalized varying coefficient models [for a review see e.g. Roca-Pardiñas and Sperlich (2004)]. The aim, however, is to check whether intuitively plausible alternative model specifications make the valley, interpreted as ‘midlife crisis’, disappear.

3.1 Partial Linear Additive Model (AM)

Set $G=identity$ but give full flexibility to the impact of age and each covariate X, though under the restriction of additive separability. This gives a partial linear AM of the form

$$\begin{aligned} E[ LS \mid Age,\ldots , D]= m_a(Age)+ m_{1}(NinH)+m_{2}(YofEdu)+m_{3}(LNHI)+m_{4}(LHS)+D^{T}\mathbf {\beta } . \end{aligned}$$

Suppressing $m_2$ to $m_4$, and a reduced D gives Analysis A (in the following we will not repeat this statement but will always write only the full model for Analysis B). The estimates of $m_a(Age)$ are plotted in Fig. 8 at the top. We can see that the results are similar to those of the PLM, that is, the valley persists. The estimates of other nonparametric components are in compliance with the existing literature (cf. Ferrer-I-Carbonell 2005, Frey and Stutzer 2002 and Tella et al. 2003), like the clear downward slope for LHS.

3.2 Partial Linear Additive Model with Interactions

The nonparametric additive interaction model is as above with

$$\begin{aligned} m_{5}(Age, NinH)+ m_6(Age, YofEdu) + m_7(Age,LNHI) + m_8(Age, LHS) \end{aligned}$$

added, that is, the (2nd order) interactions of age with each element of X (see Sperlich et al. 2002). We use tensor product smoothers as these are expected to be appropriate when the main effects as well as the interactions are present. Thin-plate smoothers are only recommended when the one-dimensional functions are suppressed (Wood 2017). The estimates for $m_a$ are given in the center of Fig. 8. While there is a change in the curvature, a valley around 50 is still visible. It could be argued that for this model, the marginal impact of interest is $m_a(Age) + \int \sum _{j} m_{4+j} (Age\times X_j) dF_{X}(x)$ with $F_{X}(\cdot )$ being the cumulative joint distribution of X. Given the results for the purely additive model above, it is not surprising that this does not make the valley disappear at around age 50, as can be seen in Fig. 7 for Analysis B.

Fig. 7

Left: $m_a(Age) + \int \sum _{j} m_{4+j} (Age\times X_j) dF_{X}(x)$ for AM with interactions. Right: $E_{X,D}\left[ G\left( m(Age) + m_{x}(X) +D^{T}\mathbf {\beta } \right) \right]$ for GAM with Poisson link. Both for Analysis B

3.3 Generalized PLM and AM with Poisson Link Function for Dissatisfaction

The obvious alternative to relaxing index $\eta$ is to allow for more flexibility in the link G. But when considering a Generalized PLM or GAM, it is recommended to specify G. Although there exist estimators for GAM with an unknown monotone link (e.g. Horowitz 2001), they are numerically quite unstable unless all covariates are almost independent from each other, which is not the case for our data. For choosing a pre-specified link function G, consider Figs. 5 and 10: when looking at dissatisfaction DS$:=(10-LS)$ it follows almost a Poisson distribution. Therefore, we mirrored LS and applied a Poisson link to DS.

Fig. 8

Selected estimates of the marginal effect, plotted at the same scale, of age on LS for German men in Analyses A (left) and B (right) supposing different models: AM (top), AM with interactions (center), GPLM / GAM with Poisson link (bottom)

Some of the resulting estimates are plotted in Fig. 8 (bottom line),⁷ in which the midlife crisis is significantly moderated. Diagnostic graphs for GAM in Analysis B are shown in Fig. 11 (right panel) in the “Appendix”. We observe a much better behavior at the tails than for the original PLM. This indicates that a potential problem of extreme aversion or ‘optimistic response’ behavior is well captured by this link.

3.4 Ordered Logit with Cubic Age-Function

Finally we apply an ordered logit model. The problem in practice is that for unrestricted $a_j$, a flexible modeling of $\eta$ can easily lead to identification problems. We set $m_x$ to a linear, and $m_a(Age)$ to a cubic polynomial in order to allow for a valley. Although the estimation procedure converges with an estimate of $m_a$ and ${{\tilde{G}}}$ as shown in Fig. 9, its Fisher information is numerically not invertible. Additionally, the criticism that the function of interest might rather be $E_{X,D}\left[ G\left( m(Age) + m_x(X) +D^{T}\mathbf {\beta } \right) \right]$ applies here. But this time the problem is even more complex because G stands for all: the true ${{\tilde{G}}}$, the error distribution, and functional (mis-)specification of the index.

Fig. 9

Estimates of ordered logit model: impact of age on LS on the left, and a study of the link on the right (along the estimated cut points)

The estimated cut points do not correspond to the identity link function that is generally assumed in the related literature; they rather suggest a link function that presents a left skewed conditional distribution of the responses (see Fig. 9). Individuals in this dataset might therefore comply to the optimistic population group introduced in Fig. 2. This closely corresponds with our findings above.

4 Conclusions

In statistics the semiparametric techniques were introduced as a way to circumvent the curse of dimensionality of their nonparametric counterparts, while still providing some sort of functional form of flexibility. In social sciences they were quite welcome as they helped to avoid functional misspecification in the nuisance parts of the model, and because their outcomes were much easier to interpret than those of purely nonparametric models. In the more recent literature, semiparametric methods are also used to relax the functional form in the parts of interest, while applying stiff modeling to the ‘nuisance parameters’.

First we recall that the nonparametric part of the model is not free from the underlying model assumptions, especially those made for the parametric part. Along with the popular topic of analyzing life-satisfaction we show how biases caused by a misspecification in the parametric part can transfer to the nonparametric part. In fact, the flexibility of the nonparametric part even becomes a disadvantage in such a scenario, as it absorbs the bias coming from the parametric part. We have shown in a simulation study that ‘empirical evidence’ of all observed findings in the literature, namely monotone downward slope, U-shape, inverse U-shape, and midlife crisis could merely be a result of such a bias transfer caused by the way sampled individuals tend to self-report their LS. It is worth noting that an identity link function (as it is usually used in such studies) is inappropriate, especially when the boundaries of the response scale are effective.

In reference to the recently published study by Wunder et al. (2013) we illustrate our discussion along their application using SOEP data. Replicating their study we get the same results; we find a clear, deep valley between the ages of 45 and 50, typically interpreted as a midlife crisis. As we have shown that their PLM specification actually obliges the estimator to exhibit this functional form, we then illustrate robustness checks needed to distinguish a numerical artifact from empirical evidence. These control for (a) the functional form of the impact of other covariates, (b) possible interactions, (c) link specification, in particular to account for extreme aversion, optimisms, pessimisms, boundary effects, (d) a combination of all these problems. We verified that a valley at age 50 is visible in all the different models, though very much moderated for the (statistically) most trustworthy models, namely those where a Poisson link (for dissatisfaction) was used.

In this article we did not discuss the also frequently occurring problem of observing quite low variation in the responses. It is to be noted, however, that this problem would typically even boost the consequences of model misspecification, but not change them.

In the existing literature there are many justifications provided by psychologists, economists and sociologists for the existence of midlife crises. To cite one, Blanchflower and Oswald (2008) consider a U-Shape function of life-satisfaction in age, which is due to the underlying assumptions of the model. However, the first argument that they provide is that individuals learn how to adopt to their environment. At midlife they leave behind their unattainable dreams. This partially (and for some time) compensates the continuous negative effect of aging like health problems, and produces a valley that is regarded as a midlife crisis.

Appendix: Diagnostics on SOEP Data Analysis

See Tables 1, 2, 3 and Figs. 10, 11, 12.

Table 1 Descriptive statistics

Table 2 Correlation coefficient between continuous covariates

Table 3 PLM with Identity link: Fitted results for parametric components

Fig. 10

Distribution of LS by different age groups

Fig. 11

Diagnostic graphs of residuals for PLM (left) and GAM (right) with Poisson link for dissatisfaction

Fig. 12

AM with interaction: Marginal effect of age, where all interactions with the continuous variables are included in the model