1 Introduction

Consider the following optimization problem

$$\begin{aligned}&\min _{X,Y,Z} \; g(X, Y, Z) = f(Z) +r_1(X)+r_2(Y) \nonumber \\&~\mathrm{s.t.}\quad Z=XY, \end{aligned}$$
(1)

where \(X\in \mathbb {R}^{P\times K}\), \(Y\in \mathbb {R}^{K\times Q}\), \(Z\in \mathbb {R}^{P\times Q}\) are the optimization variables. The following assumption is made for problem (1).

Assumption A:

  1. 1.

    Function \(f: \mathbb {R}^{P\times Q}\rightarrow \mathbb {R}\) is a smooth function (possibly nonconvex), and gradient Lipchitz continuous with constant L; see (23) for precise definition.

  2. 2.

    Function g(X, Y, Z) is bounded from below, i.e. there exist \(\underline{g}\) such that \(g(X,Y,Z)\ge \underline{g}\) for all \(X,Y,Z \in \text {Dom}(g)\).

  3. 3.

    For each \(i=1,2\), the function \(r_i: \mathbb {R}^{P\times K}\rightarrow \mathbb {R}\) is either a convex or concave function (possibly nonsmooth) lower semi-continuous regularizer. Each \(r_i\) takes the following particular form: \(r_i(X) = h_i(l_i(X))\), where \(l_1:\mathbb {R}^{P\times K}\rightarrow \mathbb {R}\) and \(l_2:\mathbb {R}^{K\times Q}\rightarrow \mathbb {R}\) are convex, possibly nonsmooth functions, and \(h_i:\mathbb {R}\rightarrow \mathbb {R}\) is continuously differentiable and monotone non-decreasing function over an open set containing \(\text{ dom }\,(l_i)\).

Below we provide a list of popular regularizers that satisfy our model

  1. 1.

    The \(\ell _1\)-norm, i.e., \(r_i(X):=\Vert X\Vert _1\), \(X\in \mathbb {R}^{P\times K}\);

  2. 2.

    The indicator function of a convex set, i.e., for convex set S, \(r_i(X)=\iota _S(X)\), where \(\iota _{S}(X)=0\) if \(X\in S\), and \(\iota _{S}(X)=\infty \) otherwise;

  3. 3.

    The concave modified LSP (M-LSP), \(r_i(X)=\log (\epsilon +\Vert X\Vert _1)\), where \(\epsilon >0\) is a small constant.

The optimization problem in the form of (1) can be used to model a wide range of applications arising in signal processing [11, 42, 43] and machine learning [4, 18, 38], including matrix factorization type problems and sparse principal component type problems. These applications will be discussed in detail in Sect. 2.

1.1 Literature review

To deal with multi-block problems in the form of (1), the most popular method is the block coordinate descent (BCD) methods, or commonly known as alternating minimization (AM) when there are two blocks of variables. BCD is an iterative algorithm in which decision variable is partitioned into smaller blocks of variables, and in each iteration the minimization is carried out with respect to a single block variable while the rest of the blocks are held fixed [2]. The convergence of BCD is guaranteed under restrictive assumptions; see [33, 47] for detailed discussion. In order to overcome the BCD drawbacks, in [39] the authors designed a block successive upper-bound minimization (BSUM) algorithm, in which the objective function is approximated in each iteration using a particular upper bound. However, neither BCD nor BSUM is able to solve problem (1) due to the existence of nonconvex constraint set \(Z=XY\) which couples the variables. Another variant of AM-based method is called proximal alternating linearized minimization (PALM) which was proposed in [3]. PALM algorithm converges to the set of stationary solutions when function g satisfies in so-called Kurdyka–Lojasiewicz (KL) property.

A popular method for dealing with nonconvex coupling constraint in the form of \(Z=XY\) is the classical augmented Lagrangian (AL) method [17]. However, one potential drawback for this method is that the subproblems are not decomposable across the block variables; thus we cannot carry out distributed and parallel implementations over this algorithm; while this is an important property especially for big data applications in which the entire dataset may not fit readily into a single memory. A modified version of AL method named Prox-PDA has been proposed in [19] to solve distributed nonconvex, but smooth optimization problems over connected network.

Recently, the alternating direction method of multipliers (ADMM), a variant of the AL, has gained popularity for decomposing large-scale nonsmooth optimization problems [4, 8, 10, 13]. In particular, consider the following problem

$$\begin{aligned} \min _{x,y}&\quad f_1(x)+f_2(y) \nonumber \\ \mathrm{s.t.}&\quad Ax+By = c, \end{aligned}$$
(2)

where \(x\in \mathbb {R}^p\), \(y\in \mathbb {R}^k\), \(A\in \mathbb {R}^{m\times p}\), \(B\in \mathbb {R}^{m\times k}\), and \(c\in \mathbb {R}^m\). The augmented Lagrangian for this problem is given by

$$\begin{aligned} L_\rho (x,y,\lambda ) = f_1(x)+f_2(y) + \langle \lambda , Ax+By - c\rangle + \frac{\rho }{2}\Vert Ax+By-c\Vert ^2. \end{aligned}$$

The standard ADMM algorithm consists of the following iterations

$$\begin{aligned} x^{r+1}&=\mathop {\mathrm{argmin}}_x L_\rho (x,y^r,\lambda ^r), \end{aligned}$$
(3)
$$\begin{aligned} y^{r+1}&=\mathop {\mathrm{argmin}}_y L_\rho (x^{r+1},y,\lambda ^r), \end{aligned}$$
(4)
$$\begin{aligned} \lambda ^{r+1}&=\lambda ^r+\rho (Ax^{r+1}+By^{r+1} - c). \end{aligned}$$
(5)

It has been demonstrated through a large number of convex applications, that the ADMM possesses superior computational and theoretical properties [4, 9, 50]. Further, a few recent works have also applied the ADMM to nonconvex applications such as nonnegative matrix factorization [46, 55], phase retrieval [51], and nonconvex consensus problems [16, 54]. Unfortunately, unlike the AL, there has been no theoretical convergence guarantee for the ADMM when dealing with general multi-block nonconvex problems. To address this issue, there has been a flurry of recent works that focuses on analyzing the theoretical performance of ADMM for some special nonconvex problems. For example, in [31] it has been shown that ADMM converges to the set of stationary solutions when functions \(f_1\) and \(f_2\) are semi-algebraic, matrix A is full column rank, and matrix B is set to identity.

In [20] an ADMM algorithm have been proposed for solving certain nonconvex consensus and sharing problems. In [50] the convergence of ADMM has been studied for optimizing nonconvex and nonsmooth objectives subject to coupled linear equality constraints under a variety of assumptions (but weaker than [20, 31, 49]); see Table 1 in [50]. Unfortunately, none of these works are capable of dealing with problem (1), which carries nonconvex regularizer and nonconvex bilinear constraint \(Z=XY\) simultaneously.

In this work, we propose a new algorithm based on the ADMM for the nonconvex and nonsmooth optimization problems in the form of (1). We provide a rigorous convergence analysis for the proposed algorithm, and show that it converges to the set of stationary solutions as long as certain penalty parameters of the algorithm are chosen judiciously. We then test the proposed algorithm on two applications: nonnegative matrix factorization and sparse principal component analysis, and demonstrate that the proposed method also enjoys robust numerical performance compared with a number of state-of-the-art algorithms.

This paper is organized as follows. In Sect. 2 we discuss a few applications of the general formulation in (1). Sections 3 and 4 discuss the proposed algorithm and its convergence analysis. In Sects. 5 and 6 we specialize the proposed algorithms to a number of applications and test its numerical performance. The paper concludes in Sect. 7.

Notation We use \(\Vert \cdot \Vert _2\), \(\Vert \cdot \Vert _1\), and \(\Vert \cdot \Vert _F\) to denote the Euclidean norm, \(\ell _1\)-norm and the Frobenius norm respectively. For matrix A, \(A^\top \) represent its transpose. For two vectors a, b we use \(\langle a,b\rangle \) to denote their inner product.

2 Applications

In this section we present some popular applications of problem (1).

Application # 1: The NMF Problem. The nonnegative matrix factorization (NMF) problem aims to extract from a data matrix \(M\in \mathbb {R}^{P\times Q}\) two matrix factors \(X\in \mathbb {R}^{P\times K}\), and \(Y\in \mathbb {R}^{K\times Q}\), [\(K\ll \min (P,Q)\)] such that \(M\approx XY\), and \(X\ge 0\), \(Y\ge 0\). A common formulation is given below

$$\begin{aligned}&\min _{X,Y} \; f(X, Y) = \frac{1}{2}\Vert X Y - M\Vert ^2_F,\quad \mathrm{s.t.}~ X, Y\ge 0. \end{aligned}$$
(6)

NMF problem has been popular in a large number of applications, such as text mining [37], pattern discovery [5], bioinformatics [27], as well as clustering [48]; for a recent survey, see [12]. Several efficient numerical algorithms have been proposed for solving NMF. For example, Lee and Seung [30] developed a multiplicative update method, which alternates between solving certain surrogate functions for variables X and Y, respectively. Another framework of algorithms is based on the alternating nonnegative least square (ANLS). Some efficient methods in this class are the projected gradient descent method [32], the block principal pivoting method [28], as well as an algorithm proposed in [21].

Recently, several variants of ADMM have been developed to tackle the NMF problem, see [45, 46, 52, 53], including the one proposed in the survey by Boyd et al. [4, Chap. 9.2]. Despite the fact that these ADMM based algorithms all achieve relatively good numerical performance (compared with existing methods such as the ones in [30] and [32]), unfortunately there has been a gap between the algorithm’s good practical performance and its theoretical behavior. Up to this work there has been no rigorous convergence analysis for applying ADMM to such nonconvex problem.

To see the relationship between the NMF problem (6) and (1), we follow [4, Chapter 9.2] to reformulate (6) as

$$\begin{aligned}&\min _{X,Y,Z} \; g(X, Y, Z) = \frac{1}{2}\Vert Z - M\Vert ^2_F + \iota _{X\ge 0}(X) + \iota _{Y\ge 0}(Y)\nonumber \\&~\mathrm{s.t.}\quad Z= XY, \end{aligned}$$
(7)

which is clearly in the form of (1).

Application # 2: The NMF with missing values. Consider a nonnegative matrix factorization/completion (NMFC) problem, where the data matrix M contains some missing values. A popular formulation of the NMFC is given below [52]

$$\begin{aligned} \min _{X,Y}&\quad \hat{f}(X, Y) = \frac{1}{2}\Vert \mathcal {P}_{{\varOmega }}\left( X Y - M\right) \Vert ^2_F, \nonumber \\ \mathrm{s.t.}&\quad X\ge 0, \; Y\ge 0, \end{aligned}$$
(8)

where \({\varOmega }\) contains the indices of known entries, and \(\mathcal {P}_{{\varOmega }}\) denotes the projection on to the set \({\varOmega }\) i.e.

$$\begin{aligned} {[}\mathcal {P}_{\varOmega }(A)]_{i,j}= {\left\{ \begin{array}{ll} 0 &{} (i,j)\notin {\varOmega }\\ {[}A]_{i,j} &{} (i,j)\in {\varOmega }\end{array}\right. } \end{aligned}$$

Let us introduce new variables \(Z\in \mathbb {R}^{P\times Q}\) and \(W\in \mathbb {R}^{P\times Q}\). Then we have the following reformulation of problem (8)

$$\begin{aligned} \min _{X,Y,Z,W}&\quad \frac{1}{2}\Vert Z-W\Vert ^2_F, \nonumber \\ \mathrm{s.t.}&\quad X\ge 0, \; Y\ge 0,\nonumber \\&\quad Z=XY, \; \mathcal {P}_{{\varOmega }}\left( W-M\right) =0, \end{aligned}$$
(9)

which is again a special case of problem (1), by moving all the convex constraints to the objective function using indicator function. In [52] an ADMM based method has proposed to solve this problem. However, to prove convergence, it is assumed that the successive difference of the iterates goes to zero, an assumption which is impossible to verify in advance.

Application # 3: The Distributed sparse PCA problem. Principal component analysis (PCA) is another matrix factorization technique aiming to reduce the dimension of multi-variate data set while preserving the maximum variance among the data. Finding the first principal component (PC) is equivalent to solving the following problem [40]

$$\begin{aligned} \min _{z\in \mathbb {R}^P}\; -\frac{1}{2}\Vert Dz\Vert _2^2, \quad \mathrm{s.t.}\; \Vert z\Vert ^2_2\le 1, \end{aligned}$$
(10)

where \(D=[d_1,d_2,\ldots ,d_P]\in \mathbb {R}^{ N\times P}\) is data matrix with N data points and P attributes. Without loss of generality we assume that the mean of each column \(d_i\) is zero, thus the objective value \(\frac{1}{2}\Vert Dz\Vert _2^2\) represents the explained variance of the first PC [24]. In order to compute more PCs, one way is to solve problem (10) repeatedly with a sequence of deflated data matrices [34]. The nonconvexity of this optimization problem is due to maximizing a convex function.

One of the major drawbacks of the PCA is that most of the entries of PCs are non-zero, which makes the resulting solutions difficult to interpret. The sparse PCA (SPCA) is one popular variant of PCA to overcome this limitation, which is capable of finding PCs with only a few non-zero entires. The SPCA often involves adding a sparsity-promoting regularizer to the objective function of PCA problem (10). The resulting problem has the following generic form [6, 40, 59]

$$\begin{aligned}&\min _{z\in \mathbb {R}^P}\; -\frac{1}{2}\Vert Dz\Vert _2^2 +\gamma r(z),\quad \mathrm{s.t.}\; \Vert z\Vert ^2_2\le 1, \end{aligned}$$
(11)

where \(\gamma >0\) is a sparsity promoting parameter; r(z) is some regularizer, which can be nonconvex functions such as the \(\ell _0\) norm or the log sum penalty (LSP), or convex functions such as the \(\ell _1\) norm.

Recently, extensive research has been conducted on developing algorithms for solving special forms of SPCA. For instance, Jolliffe et al. [25] developed the SCoTLASS algorithm, which solves the \(\ell _1\) penalized formulation. Zou and Hastie [58, 59] solved the SPCA problem by imposing the LASSO as well as the elastic net constraints into the problem in order to generate modified PCs with sparse loading vectors. Shen and Huang [44] studied a series of algorithms named sPCA-rSVD. They utilized singular value decomposition to obtain low rank matrix factorization under a variety of sparsity-promoting regularizers. A block coordinate descent (BCD) based algorithm was developed by Zhao et al. [56] to produce PCs. D’Aspremont et al. [7] leveraged the classical representation of the maximum eigenvalue of a symmetric matrix while imposing cardinality constraint to derive a semi-definite relaxation problem. Journée et al. [26] developed a power method based algorithm called Gpower to solve four different formulations of the SPCA problem (with different sparsity inducing regularizers).

To the best of our knowledge, all the methods mentioned above are centralized methods, meaning that the entire data matrix D or the corresponding covariance matrix should be stored in a single computation node. However, in many practical scenarios data matrices are often stored in distributed nodes, either because they are collected in a distributed manner, or the sheer size of the data prevents any centralized storage/computation. In these cases, centralized methods like those developed in [7, 26] are no longer applicable. In the following, we present two different formulations of the SPCA problem (11) [both in the form of (1)], which split the entire data matrix in different ways to facilitate distributed computation/optimization.

Splitting the Rows of D Let D: \(\in \mathbb {R}^{N\times P}\) denote data matrix with N data points and P features such that \(N \gg P\). For example, social network data sets, or wireless sensor networks belong to this regime; see for example Household Electric Power Consumption, and PAMAP2 data sets in UCI Machine Learning Repository . In this situation, we can partition the data matrix D across the rows into a few matrices, each representing a subset of samples. For example, suppose there are Q distributed computing nodes in the system. For each \(i=1,2, \ldots Q\), let \(D_i\in \mathbb {R}^{N_i\times P}\) denote a submatrix of D that involves \(N_i\) non-overlapping rows of D (that is, \(D=[D_1;D_2;\cdots ;D_Q]\)), and each \(D_i\) is available at the ith node. According to such a data splitting structure, the SPCA problem (11) can be reformulated as follows

$$\begin{aligned}&\min _{z\in \mathbb {R}^P} \; -\sum _{i=1}^Q \frac{1}{2}\Vert D_iz\Vert _2^2 +\gamma r(z),\quad \mathrm{s.t.}\quad \Vert z\Vert _2^2\le 1. \end{aligned}$$
(12)

Since each \(D_i\) is only available at the ith agent, in order to facilitate distributed computation, let us define a new set of variable \(z_i \in \mathbb {R}^{P}\) for \(i=1,\ldots , Q\), and a new variable \(x\in \mathbb {R}^{P}\), and reformulate problem (12) into the following equivalent form

$$\begin{aligned} \min _{x,z}&\quad -\sum _{i=1}^Q \frac{1}{2}\Vert D_iz_i\Vert _2^2 +\gamma r(x) + \iota _{S_1}(x) \nonumber \\ \mathrm{s.t.}&\quad z_i=x \quad i=1,\ldots Q, \end{aligned}$$
(13)

where \(S_1:=\{x\in \mathbb {R}^P;~\Vert x\Vert _2^2\le 1\}\). Again, this optimization problem is a special case of the problem (1). Compare to the problem (1), in problem (13), decision variable Y becomes a constant, and we have the following correspondence: \(Z=[z_1,z_2,\ldots , z_Q]\in \mathbb {R}^{P \times Q}\), \(X=[x,x,\ldots ,x]\in \mathbb {R}^{P\times Q}\), and \(r_1(X) =\gamma r(x) + \iota _{S_1}(x)\).

Splitting the columns of D: In our second formulation we consider cases where the data matrix \(D\in \mathbb {R}^{N\times P}\) has a large number of columns, i.e., \(N\ll P\), and assume that a subset of columns is distributed to each agent. This scenario can happen for example, in human genome data sets where there are relatively few people in the experiment, but the feature space (represeneting the total number of genes) can be large; see examples of related data sets in Encyclopedia of DNA Elements.

Let us partition the columns of D by \(D:=[A_1, A_2, \ldots , A_M]\) where \(A_i\in \mathbb {R}^{N\times P_i}, \; i=1,\ldots , M\) denote submatrices consisting non-overlapping columns (or features) of D. Then the SPCA problem (11) is equivalent to

$$\begin{aligned}&\min _{y\in \mathbb {R}^P}\;-\bigg \Vert \sum _{i=1}^M A_i y_i\bigg \Vert _2^2 + \gamma r(y), \quad \mathrm{s.t.}\; \quad \Vert y\Vert _2^2\le 1, \end{aligned}$$
(14)

where \(y_i\in \mathbb {R}^{P_i}\) is a subvector of \(y\in \mathbb {R}^P\). Let us introduce a new set of variables \(z_i\in \mathbb {R}^N\), \( i=1,2, \ldots M\). Then the equivalent formulation for (14) is

$$\begin{aligned} \min _{z_i, y}&\quad -\left\| \sum _{i=1}^M z_i\right\| _2^2 + \gamma r(y) + \iota _{S}(y), \nonumber \\ \mathrm{s.t.}&\quad z_i=A_i y_i, \quad i=1,2,\ldots M, \end{aligned}$$
(15)

where \(S=\{y\in \mathbb {R}^P;~\Vert y\Vert _2^2\le 1\}\). Notice that here \(y_i\in \mathbb {R}^{P_i}\) is a subvector of \(y\in \mathbb {R}^P\) such that \(\sum _{i=1}^{M}P_i=P\). To cast this problem into the form of (1), let \(Z=[z_1; \cdots ; z_M]\in \mathbb {R}^{NM\times 1}\), \(Y=[y_1; \cdots ; y_M]\in \mathbb {R}^{P\times 1}\), \(X=blkdiag(A_1,\ldots ,A_M)\in \mathbb {R}^{NM\times P}\), (blkdiag denotes a block diagonal matrix) is a constant, \(r_1(X)=0\), and \(r_2(Y)=\gamma r(y) + \iota _{S}(y)\).

3 The proposed algorithm

To develop the proposed algorithm, we start with the original problem (1) and write down its augmented Lagrangian (AL)

$$\begin{aligned} L_\rho [Y, (X, Z), {\varLambda }] =&f(Z) +r_1(X)+r_2(Y) + \langle {\varLambda }, Z-XY \rangle \nonumber \\&+\frac{\rho }{2}\Vert Z-XY\Vert ^2_F, \end{aligned}$$
(16)

where \({\varLambda }\in \mathbb {R}^{P\times Q}\) is the dual variable and \(\rho >0\) is the penalty parameter. The ADMM algorithm performs the following steps

$$\begin{aligned} Y^{r+1}&= \arg \min _{Y} \; L_\rho [Y, (X, Z)^r, {\varLambda }^r]; \end{aligned}$$
(17a)
$$\begin{aligned} \left( X, Z\right) ^{r+1}&= \arg \min _{X, Z} \; L_\rho [Y^{r+1}, (X, Z), {\varLambda }^r]; \end{aligned}$$
(17b)
$$\begin{aligned} {\varLambda }^{r+1}&= {\varLambda }^r+\rho \left( Z^{r+1}-X^{r+1}Y^{r+1} \right) . \end{aligned}$$
(17c)

However, such iteration is difficult to perform for the considered nonconvex problem (1). This is because the existence of nonconvex regularizers makes the subproblems (17a) and (17b) also nonconvex, in which case they are difficult to be solved to global optimality.

To proceed, suppose that the regularizer \(r_1(X) = h_1(l_1(X))\) is concave. Then we will perform the following linear approximation

$$\begin{aligned} v_1(X,X^r)= r_1(X^r) + h'_1(l_i(X^r))\left[ l_1(X) - l_1(X^r)\right] . \end{aligned}$$
(18)

For simplicity of presentation let us define the following function:

$$\begin{aligned} u_1(X,X^r)= {\left\{ \begin{array}{ll} r_1(X) &{} \text {if}~ r_1\text { is convex};\\ v_1(X,X^r)&{} \text {if}~ r_1\text { is concave}. \end{array}\right. } \end{aligned}$$
(19)

Similarly we can define \(v_2(Y,Y^r)\) and \(u_2(Y,Y^r)\).

Using these definition, let us define the following functions

$$\begin{aligned}&G[Y; (X,Z)^r, Y^r,{\varLambda }^r] = f(Z^r) + r_1(X^r)+ u_2(Y; Y^r) \nonumber \\&\quad +\langle {\varLambda }^r, Z^r-X^rY \rangle +\frac{\rho }{2}\Vert Z^r-X^rY\Vert ^2_F + \frac{\beta }{2}\Vert Y-Y^r\Vert _F^2; \end{aligned}$$
(20)
$$\begin{aligned}&\quad H[(X,Z); X^r, Y^{r+1}, {\varLambda }^r] = f(Z) + r_2(Y^{r+1})+ u_1(X,X^r)\nonumber \\&\quad + \langle {\varLambda }^r, Z-XY^{r+1} \rangle +\frac{\rho }{2}\Vert Z-XY^{r+1}\Vert ^2_F+\frac{\beta }{2}\Vert X-X^r\Vert _F^2, \end{aligned}$$
(21)

where \(\beta \) is a positive constant. In particular, to get function \(G[Y; (X,Z)^r, Y^r,{\varLambda }^r]\) we replace \(r_2(Y)\) in AL function given in (16) with \(u_2(Y; Y^r)\) defined in (19), and then add a proximal term \(\frac{\beta }{2}\Vert Y-Y^r\Vert _F^2\). Similarly, in \(H[(X,Z); X^r, Y^r, {\varLambda }^r]\) we replace \(r_1(X)\) in AL with \(u_1(X,X^r)\) and add proximal term \(\frac{\beta }{2}\Vert X-X^r\Vert _F^2\). It is clear that by utilizing the approximation in (19), and by adding the proximal terms \(\frac{\beta }{2}\Vert Y-Y^r\Vert _F^2\) and \(\frac{\beta }{2}\Vert X-X^r\Vert _F^2\), functions (20) and (21) are strongly convex w.r.t. Y and (X, Z), respectively when \(\rho >L\).

The proposed algorithm replaces the ADMM steps (17a) and (17b) by steps that optimizes the functions \(G(\cdot )\) and \(H(\cdot )\), respectively. See the Algorithm 1.

figure a

We remark that it is easy to verify that the subproblem (22a) is strongly convex (with modulus \(\gamma _y\ge \beta \)) with respect to Y. Similarly, the subproblem (22b) is strongly convex with respect to X with modulus \(\gamma _x\ge \beta \). Further if f(Z) is gradient Lipchitz continuous, meaning there exists a positive constant \(L>0\) such that

$$\begin{aligned} \Vert \nabla f(Z_1)-\nabla f(Z_2)\Vert \le L \Vert Z_1-Z_2\Vert , \end{aligned}$$
(23)

and we pick \(\rho >L\), then from a well-known result of [57, Theorem 2.1], problem (22b) is also strongly convex with respect to variable Z with modulus \(\gamma _Z = \rho - L>0\).

4 Convergence analysis

In this section we present the convergence analysis of Algorithm 1. In order to see the detailed analysis for specific algorithms the readers are refereed to the conference versions of this work in [14, 15].

4.1 Preliminaries

Since problem (1) is not convex nor smooth, we need to introduce Clarke sub-differential [35, 41] to characterize its stationary solutions.

Definition 1

(Clark directional derivative) Clarke directional derivative of function p(x) at \(x = \widehat{x}\) along the direction \(\phi \), denoted by \(p^c(\widehat{x}, \phi )\), is defined as

$$\begin{aligned} p^c(\widehat{x}, \phi ) := \limsup _{x\rightarrow \widehat{x};\alpha \downarrow 0} \frac{p(x+\alpha \phi )-p(x)}{\alpha } . \end{aligned}$$
(24)

Now let us define Clarke sub-differential [35, 41].

Definition 2

(Clarke sub-differential) Suppose that \(p:\mathbb {R}^P\rightarrow \mathbb {R}\) is a locally Lipchitz continuous function. Then the Clarke sub-differential of p(x) at \(x=\widehat{x}\), denoted by \(\partial ^c p(\widehat{x})\), is defined as follows

$$\begin{aligned} \partial ^c p(\widehat{x}):= \{v\in \mathbb {R}^P :\quad p^c(\widehat{x}, \phi ) \ge \phi ^\top v,~ \forall ~ \phi \in \mathbb {R}^P\}, \end{aligned}$$
(25)

where \(p^c(\widehat{x}, \phi )\) is defined in (24).

Remark 1. If p(x) is a convex function, then the Clarke sub-differential reduces to the traditional sub-differential

$$\begin{aligned} \partial p(\widehat{x})=\{v\in \mathbb {R}^P :\langle v, x_1 - x_2\rangle \le p(x_1) - p(x_2)\}. \end{aligned}$$

Furthermore, the Clarke sub-differential reduces to classical gradient of p(x) when it is a differentiable function, which is denoted by \(\nabla p(x)\).

In this part we introduce the stationary solution for the problem (1). In a recent work by Jiang et al. [23] a systematic discussion has been provided on how to define stationary solutions for nonconvex and nonsmooth optimization problems. Let us denote the distance between matrix X and set S by \(\text {dist}(X,S)=\min _{Y\in S}\Vert X-Y\Vert _F\). Similar to [23, Defintion 3.8] we define stationary solution for problem (1).

Definition 3

(Stationary solution for problem (1)) Assume that \({\varLambda }\) is the dual variable associated with constraint set \(Z=XY\), regularizers \(r_1(X)\), and \(r_2(Y)\) are lower semi-continuous (Assumption A), then the point \(W^*= (Y^*, (X,Z)^*, {\varLambda }^*)\) is a stationary solution of the problem (1) if it satisfies in the following conditions

$$\begin{aligned}&\nabla f(Z^*)+{\varLambda }^* = 0; \end{aligned}$$
(26a)
$$\begin{aligned}&\quad \text {dist}\left( \partial ^c r_1(X^*), {\varLambda }^*Y^{*\top }\right) =0; \end{aligned}$$
(26b)
$$\begin{aligned}&\quad \text {dist}\left( \partial ^c r_2(Y^*), X^{*\top }{\varLambda }^*\right) =0; \end{aligned}$$
(26c)
$$\begin{aligned}&\quad Z^*= X^*Y^*. \end{aligned}$$
(26d)

In what follows we briefly summarize some noticeable characteristics of Clarke sub-differential which will be useful in the subsequent convergence analysis.

Proposition 1

Suppose that \(p_1:\mathbb {R}^P\rightarrow \mathbb {R}\) is a smooth function, \(p_2:\mathbb {R}^P\rightarrow \mathbb {R}\) is a convex possibly nonsmooth function, and \(p_3:\mathbb {R}^P\rightarrow \mathbb {R}\) is a nonconvex, and nonsmooth function. Then we have:

  1. (1)

    \(\partial ^c(p_1+p_2+p_3)(x)=\nabla p_1(x) + \partial p_2(x) +\partial ^c p_3(x)\).

  2. (2)

    Suppose \(p_4:\mathbb {R}\rightarrow \mathbb {R}\) is a smooth function, and \(L:\mathbb {R}^P\rightarrow \mathbb {R}\) is the composition of two function \(p_3\) and \(p_4\), i.e., \(L(x) =p_4 \circ p_3(x)\), then we have

    $$\begin{aligned} \partial ^c L(x) = p'_4(p_3(x))\partial ^cp_3(x). \end{aligned}$$
    (27)

The proof is provided in [36, Proposition 2.2, Theorem 3.7, and Corollary 3.8] in details, thus omitted here.

4.2 Proof of convergence for Algorithm 1

We start analyzing the convergence of the Algorithm 1. The analysis consists of the following steps

  1. 1.

    Bound the size of the successive difference of the dual variables by the successive difference of the primal ones.

  2. 2.

    Show that the augmented Lagrangian function \(L_\rho [Y^r, (X, Z)^r; {\varLambda }^r]\) is a decreasing function and also it is bounded from below.

  3. 3.

    Combine the previous two steps and show convergence to the stationary solution.

The following lemma provides the first step of the analysis. We relegate the proofs to the “Appendix”.

Lemma 1

Consider using the update rules (22) to solve problem (1). Then we have

$$\begin{aligned} \Vert {\varLambda }^{r+1}-{\varLambda }^r\Vert _F^2\le L^2\Vert Z^{r+1}-Z^r\Vert _F^2, \; \forall ~ r\ge 1. \end{aligned}$$
(28)

In the second step we show that when the penalty parameter \(\rho \) is chosen sufficiently large, the augmented Lagrangian is decreasing and lower bounded.

Lemma 2

Consider ADMM update equations (22). If \(\rho \ge \max \{\frac{2L^2}{\gamma _{z}}, L\}\) then the following two propositions hold true

  1. 1.

    The successive difference of augmented Lagrangian function is bounded above by

    $$\begin{aligned}&L_\rho \left[ Y^{r+1}, (X, Z)^{r+1}; {\varLambda }^{r+1}\right] -L_\rho \left[ Y^{r}, (X, Z)^{r}; {\varLambda }^{r}\right] \nonumber \\&\quad \le -C_z\Vert Z^{r+1}-Z^r\Vert ^2_F-C_y\Vert Y^{r+1}-Y^r\Vert _F^2-C_x\Vert X^{r+1}-X^r\Vert ^2_F. \end{aligned}$$
    (29)

    where \(C_z=\frac{\gamma _z}{2}-\frac{L^2}{\rho }\), \(C_y=\frac{\gamma _y+\beta }{2}\), and \(C_x=\frac{\gamma _x+\beta }{2}\) are positive constants.

  2. 2.

    There exists an \(\underline{L}\) such that

    $$\begin{aligned} L_\rho \left[ Y^{r+1}, (X, Z)^{r+1}; {\varLambda }^{r+1}\right] \ge \underline{L}. \end{aligned}$$
    (30)

    That is, the augmented Lagrangian is lower bounded.

The final step of convergence analysis utilizes the above results to verify that every limit point of the sequence generated by Algorithm 1 satisfies the stationary conditions given in (3).

Theorem 1

Consider Algorithm 1 for solving problem (1). If \(\rho \ge \max \{\frac{2L^2}{\gamma _{z}}, L\}\), then we have the following expressions

  1. 1.

    The duality gap goes to zero, i.e.

    $$\begin{aligned} \lim _{r\rightarrow \infty }\bigg \Vert X^{r+1}Y^{r+1}-Z^{r+1}\bigg \Vert _F\rightarrow 0. \end{aligned}$$
    (31)
  2. 2.

    Assume that \((Y^*, (X, Z)^*, {\varLambda }^*)\) denotes any limit point of the sequence generated by Algorithm 1, then it is a stationary solution for problem (1) which satisfies in (3).

5 Specialize algorithm 1 to applications

In this section we specify the proposed algorithm in the previous section for NMF/NMFC and SPCA problems.

Algorithm Steps for NMF problem. Consider the NMF problem

$$\begin{aligned}&\min _{X,Y,Z} \; g(X, Y, Z) = \frac{1}{2}\Vert Z - M\Vert ^2_F + \iota _{X\ge 0}(X) + \iota _{Y\ge 0}(Y) \nonumber \\&\quad \mathrm{s.t.}\quad Z= XY. \end{aligned}$$

The ADMM steps for this problem is shown in Algorithm 2.

figure b

It is worth mentioning that subproblems (32a) and (32b) are both convex optimization problems which can be solved very efficiently.

Following similar process as NMF problem we can derive the ADMM algorithm for NMFC problem (8). The details are presented in Algorithm 3.

figure c

Algorithm Steps for SPCA Problem. In what follows we consider distributed SPCA problem. First let us study problem (13) in which we will assume that the optimization is performed over a network with a central controller and a few distributed agents, each having a piece of the data set. Let us pick the concave regularization \(r(x) = c\log (1+\Vert x\Vert _1/\epsilon )\), where \(\epsilon >0\) is small constant, and c is picked such that \(r(1)=1\). According to definition in (19) we have the following form for surrogate function \(u_1(x,x^r)\)

$$\begin{aligned} u_1(x,x^r)=c\log (1+\Vert x^r\Vert _1/\epsilon )+\frac{c\epsilon }{\epsilon + \Vert x^r\Vert _1}\left( \Vert x\Vert _1-\Vert x^r\Vert _1\right) \end{aligned}$$
(34)

The algorithm steps are expressed in Algorithm 4.

figure d

A few remarks about Algorithm 4 are ready.

  1. 1.

    Node i only works with its local data \(D_i\), making the entire algorithm amendable to parallel implementation.

  2. 2.

    From the optimality condition of the x-update, we observe that at each iteration the central controller only collects the sum \(\sum _{i=1}^{N}\rho z^r_i+\lambda ^r_i\) from the users. This makes the users relatively anonymous, alleviating potential privacy issues.

Next let us consider problem (15) where we split the data matrix D across the columns. The distributed ADMM algorithm for this problem follows almost similar line of setup as the Algorithm 4. However there are some differences between these two cases which will be presented shortly. For notation simplicity let us set \(L_i:=\Vert A_iA^T_i\Vert _2\). The details is given in Algorithm 5.

figure e

Here is the step details of the Algorithm 5:

  • In step S3, when \(r_2(y)\) is concave function we approximate it using \(u_2(y, y^r)\) [details are given in (19)]. Here we need to assume two more assumptions: 1) \(u_2(y,y^r)\) is separable i.e. \(u_2(y, y^r)=\sum _{i=1}^{M} u_2^i(y_i,y_i^r)\), 2) \(u_2(y,y^r)\) should be \(\ell _1\) related. In particular for each i, \(u_2^i(y_i,y_i^r) = c_i\Vert y_i\Vert _1\) for some constants \(c_i\ge 0\). To see why these two assumptions are required the readers are refereed to [1]. Further, a linearization is done with respect to the variable \(y_i^r\) in order to solve the \(y_i\) subproblem.

  • Steps S4–S6 collectively address the constraint \(\Vert y\Vert ^2\le 1\). In particular, after updating \(\widetilde{y_i}\) in each node in S3, central controller gathers \(\Vert \widetilde{y_i}^{r+1}\Vert _2^2\) from all the nodes. Since \(\Vert \widetilde{y}\Vert _2^2=\sum _{i=1}^{M}\Vert \widetilde{y_i}\Vert _2^2\), central controller can simply measures \(\Vert \widetilde{y}\Vert _2^2\). Now if it is greater than 1, we need to normalize \(\Vert \widetilde{y_i}\Vert _2^2\) such that \(\Vert y\Vert _2^2\le 1\); that is what S6 does.

  • In step S7 the central node updates the z variable, and broadcasts it to the other nodes.

  • In step S8 each node i updates the dual variables \(\lambda _i\) in parallel.

6 Numerical results

In this section we evaluate the performance of proposed ADMM algorithms on synthetic sets as well as real data sets. In order to be fair in comparisons, all the serial (single node) computations are implemented in Matlab R2013b in a PC with Core (TM) i5 3.5 GHz and 8 GB of memory, and all parallel (multiple nodes) codes are written in C and implemented on a cluster with 168 nodes, each with 128 GB of memory. Our experimental results are divided into two parts. In the first part we evaluate the performance of serial and parallel codes on NMF and NMFC problems, while in the second part the algorithms for SPCA problem are tested. The bold values in the tables show better results compare to the other methods.

6.1 Experiments on NMF/NMFC problem

In this section we investigate the effectiveness of Algorithms 2 and 3 through comparing them with some existing methods for NMF and NMFC problems.

6.1.1 Procedures for solving the subproblems

The subproblems (32a) and (32b) in Algorithm 2 are convex problems. Inspired by [21], we apply standard ADMM method to solve these convex subproblems. Also, the subproblems (33a), (33b) in Algorithm 3 are convex optimization problems. Therefore, we can apply similar ADMM algorithm for solving them. In what follows we only present the procedure for (33a). The procedures for the rest of the subproblems are similar hence are omitted.

First, we introduce a new variable \(\hat{Y}\) to reformulate subproblem (33a) in the following way:

$$\begin{aligned} \min _{Y,W,\hat{Y}}&\quad \frac{1}{2}\Vert Z^r - W\Vert ^2_F+\frac{\rho }{2}\Vert Z^r-X^rY+{\varLambda }^r/\rho \Vert ^2_F \\ \mathrm{s.t.}&\quad Y=\hat{Y}, \quad \hat{Y}\ge 0; \\&\quad \mathcal {P}_{{\varOmega }}\left( W-M\right) =0. \end{aligned}$$

The augmented Lagrangian function for the above problem is given by

$$\begin{aligned} \tilde{L}_\alpha (Y, W, \hat{Y}; \hat{U})&=\frac{1}{2}\Vert Z^r - W\Vert ^2_F+\frac{\rho }{2}\Vert Z^r-X^rY+{\varLambda }^r/\rho \Vert ^2_F \\&\quad +\langle \hat{U}, Y-\hat{Y} \rangle +\frac{\alpha }{2}\Vert Y-\hat{Y}\Vert _F^2. \end{aligned}$$

Then, the ADMM steps are summarized in Algorithm 6.

figure f

Remark 2. Algorithm 6 involves performing the inversion of a \(K\times K\) matrix \({\rho }(X^r)^TX^r+\alpha I\). We note that:

  1. 1.

    Calculating this inversion is relatively easy because in most practical NMF/NMFC problems we have \(K\ll \min \{Q, N\}\).

  2. 2.

    We only need to perform this matrix inversion one time, and use it in all iterations.

6.1.2 The performance of Algorithm 2 on synthetic data set

In this subsection we compare the performance of Algorithm 2 with the following algorithms for solving optimization problem (6): (1) The multiplicative updating rule ( MULT)Footnote 1 proposed by Lee and Sueng [30]; (2) The AO-ADMMFootnote 2 proposed recently by Huang et al. [21]; (3) The AO-BPPFootnote 3 proposed by Kim et al. [28]; (4) The ADMFootnote 4 method proposed by Xu et al. [52].

The algorithm parameters are tuned by trying a range of values. We set \(\rho =1.1\), which satisfies the condition given in theorem (1). Furthermore, we choose \(\alpha =500\), \(\beta =0.01\) to solve the subproblems. The stopping criteria for Algorithm 2 is given by

$$\begin{aligned}&\frac{L_{\rho }(Y^{r+1}, (X,Z)^{r+1}, {\varLambda }^{r+1})- L_{\rho }(Y^{r}, (X,Z)^{r}, {\varLambda }^{r})}{L_{\rho }(Y^{r}, (X,Z)^{r}, {\varLambda }^{r})}\le 10^{-4}, \end{aligned}$$
(36)
$$\begin{aligned}&\quad \frac{\Vert M-XY\Vert _F}{\Vert M\Vert _F}\le 10^{-4}, \end{aligned}$$
(37)

or when the algorithms reaches 200 iterations.

The synthetic data set has been generated in the following way: First we randomly generate matrices \(W\in \mathbb {R}^{P\times R}\), and \(H\in \mathbb {R}^{R\times Q}\) with i.i.d entries from \({\texttt {Uniform}}(0,1)\). Then the noise matrix \(N\in \mathbb {R}^{P\times Q}\) is randomly generated from \(\mathcal {N}(0,0.01^2)\). Finally we set data matrix \(M=WH+N\). In this set of experiment we choose the problem dimension \(P=10000\), \(Q=5000\), \(R=500\), and \(K=50\). Different algorithms are compared according to criteria listed in Table 1. The results are averaged over 50 independent trials. As we can see, Algorithm 2 outperforms the rest of algorithms for this specific test problem in terms of absolute error of the final solution as well as the running time.

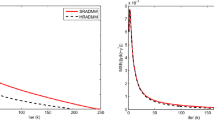
Table 1 The performance of Algorithm 2 on synthetic data sets
Full size table

We further demonstrate the convergence speed of different algorithms by testing on problems of different sizes. We set \(P=Q\in \{100,200,\ldots , 1000\}\), \(K=Q/2\), and \(R=Q/10\). The results are shown in Fig. 1. The x-axis displays the size of the problem (P, Q), and y-axis displays running time. The results are averaged over 50 independent trials. From Fig. 1 it can be seen that Algorithm 2 converges faster compared with other algorithms, especially for the large-size problems.

Fig. 1
figure 1

The convergence speed of different algorithms for different problem sizes

Full size image

6.1.3 The performance of Algorithm 2 on ORL face data set

Next we demonstrate the performance of various algorithms on the ORL face data set [29]. In this case the data matrix M is a 10,304 \(\times \) 400 matrix, each column of which is a picture with 112 \(\times \) 92 pixels. We apply different algorithms on this data set to achieve a nonnegative basis matrix \(X\in \mathbb {R}^{10{,}304\times 200}\) and a nonnegative coefficient matrix \(Y \in \mathbb {R}^{200\times 400}\) such that \(M\approx XY\). To see the effectiveness of the algorithms we recover some pictures and compare them with the original picture. The results are depicted in Table 2. From Table 2 we can observe that the quality of the recovered pictures are almost equal for Algorithm 2, AO-ADMM, and AO-BPP, and they are much better than MULT and ADM. Furthermore, we calculate the absolute error, and the running time for maximum 200 iterations. The results are given in Table 3. It can be seen that Algorithm 2 outperforms other methods in terms of absolute error as well as speed.

Table 2 The Recovered Pictures Using Different Methods
Full size table
Table 3 The performance of Algorithm 2 on ORL face data set
Full size table

6.2 The performance of Algorithm 3

In this subsection we compare the performance of Algorithm 3 with the ADM algorithm presnted in [52]. Both algorithms are capable of dealing with problems with missing values in the observation. The data matrices we use are two pictures: 1) The Owl which is a gray-scale picture with the size \(384\times 521\). 2) Te Squirrel with the size \(361\times 554\), which is a gray-scale picture too. The original pictures can be downloaded from www.imageemotion.org/. In this experiment we pick the missing ratio (MR) to be \(MR = 50\%\). The algorithm parameters are chosen the same as in the previous part. For ADM algorithm [52] we used the default settings. The original gray-scale, the picture with missing parts, and the recovered pictures are shown in Table 4. The absolute error of final solution \(\Vert \mathcal {P}_{{\varOmega }}\left( X Y - M\right) \Vert ^2_F\) is reported under each recovered picture. From this table we can observe that Algorithm 3 has slightly better performance than the ADM proposed in [52].

Table 4 Comparison of Algorithm 3 with ADM for data with missing values
Full size table

In order to do more comparisons in terms of MR, we randomly generate a data matrix similar to the previous section, except that the entries of M are sampled uniformly according to different missing ratio (MR\(\in \{25\%, 50\%, 75\% \}\)). In particular, we set \(P=Q=3000\), \(R=1000\), \(K=300\) and the comparison results are reported on Table 5. This results verify that Algorithm 3 achieves better performance than ADM in the case of data matrix with missing observations.

Table 5 The performance of Algorithm 3 on synthetic data sets
Full size table

6.3 Experiments on SPCA problem

In this part we evaluate the performance of ADMM algorithms on SPCA problem. The algorithm stops when \(|L_\rho (x^{r+1},z^{r+1},\lambda ^{r+1})-L_\rho (x^{r},z^{r},\lambda ^{r})| \le 10^{-2}\),and \(\max _i\Vert x_i-z\Vert \le 10^{-3}\), or when the iteration counter reach \(r=4000\).

6.3.1 Performance on centralized data

Jeffers [22] introduced a data set named Pitprops consisting of 180 observations and 13 variables. It has been shown that the results of classical PCA are difficult to interpret. Therefore, it is a popular to evaluate the effectiveness of algorithms on SPCA problem. We implement Algorithm 4 with \(Q=1\) (i.e. centralized version) with two different regularizations: (1) The nonsmooth and convex \(\ell _1\) penalization (referred to as \(\text {ADMM}_{\ell _1}\)); (2) the nonsmooth, and nonconvex M-LSP regularization with \(\epsilon =0.01\) (referred to as \(\text {ADMM}_\mathrm{MLSP}\)). We pick the sparsity parameter using trial and error in order to get solutions with similar sparsities as achived by other algorithms and compare the resulting explained variance (EV) of our algorithms with DSPCA [7], Gpower (with \(\ell _0\) and \(\ell _1\) penalization) [26], \(\text {sPCA-rSVD}\) (with \(\ell _0\) and \(\ell _1\) penalization) [44], and \(\text {BCD-SPCA}\) (with \(\ell _0\) and \(\ell _1\) penalization) [56]. The results are reported in Table 6.

Table 6 The Performance of Algorithms on Pitprops Data
Full size table

We observe that the proposed algorithms outperform other methods in terms of EV, under the same cardinality patterns. Furthermore, as expected \(\text {ADMM}_\mathrm{MLSP}\) achieves a higher EV than \(\text {ADMM}_{\ell _1}\).

6.3.2 Performance on distributed data

In this subsection we evaluate the performance of Algorithms 4 and 5 which are designed for distributed data sets. We consider two sets of synthetic data sets: (1) A dense data matrix with \(N=1{,}000{,}000\), and \(P=2000\), whose elements are uniformly picked form set \(\{0,1,2,3,4\}\) (the size of the data set is about 4GB); (2) A sparse data matrix, in which everything is similar to the dense case, but \(95\%\) of the elements are set to zero. We set the sparsity controlling parameter \(\gamma =5000\) for dense matrix and \(\gamma =1000\) for sparse case. We split the data matrix across the rows and store the submatrices into \(Q\in \{1,2,4,8,16,32,64\}\) distributed nodes in a cluster. By using the Massages Passing Interface (MPI) parallel interface we run the Algorithm 4, and compute the first sparse loading vector.

The results are shown in Table 7. This table contains two main columns denoted as Time, and Iteration. The first subcolumn of Time measures the total time used to solve the subproblems i.e., steps S3–S4 in the Algorithm 4 for the required number of iterations which is denoted in the Iteration column. The second subcolumn of Time represents the overall elapsed time of the algorithm i.e. S1–S4. Finally, the third subcolumn shows the time needed for running steps S3–S4 for 100 iterations (i.e., excluding the time needed for performing the initialization steps S1–S2). The results for dense data set are shown in Fig. 2.

Table 7 Performance of Algorithm 4
Full size table
Fig. 2
figure 2

Time needed versus number of nodes for Algorithm 4. Overall time counts the time needed for all steps (S1–S4) in Algorithm 4 to reach the stopping criteria. Loading Time counts the time to load data matrix into the nodes (S1). Cov Calculation Time measures the time for calculating covariance matrix (S2), and 100 Iterations Time is the time needed for solving subproblems (S3–S4) only during 100 iterations

Full size image

Comparing Table 7 and Fig. 2, we can observe that when the number of nodes increases in a network, the overall time to solve the problem decreases significantly. However, the amount of time the algorithm needs to solve the subproblems increases a little bit by increasing the number of nodes. The following are some remarks which justify such behavior.

  1. R1)

    Loading submatrices into the memory (step S1), and calculating the covariance matrix (step S2) are done completely in a distributed manner, meaning that the nodes do not need to share information in these cases. However, for solving the subproblems (step S3–S4), the nodes in the network are required to communicate with each other. Therefore, the time for solving the subproblems includes communication time as well as computation time.

  2. R2)

    When we have more nodes in the network, there will be more consensus constraints too, see problem (13). As a result, the algorithm needs to run more iterations to reach consensus.

  3. R3)

    When we split data matrix across the rows, in spite of having smaller data matrix, each node still operates on the full dimensional data with P variables. Therefore, the computation time for solving the subproblems does not change regardless of the number of nodes in the network.

It is worth mentioning that Algorithm 4 is faster on the sparse matrix than on the dense matrix in all cases.

In the next set of experiments we test the performance of Algorithm 5 where we split the data matrix across the columns. In this case we have a large number of variables and a moderate number of data samples. The data are generated similarly to the case with row splitting. Here, we set \(N=2{,}000\) and \(P=200{,}000\). In this model we split the matrix across the columns into M subset, we let \(M\in \{1,2, 4, 8, 16, 32, 64\}\). We choose the nonconvex M-LSP sparsity promoting function with \(\gamma =150\), and then compute the first sparse loading vector. The results are summarized in Table 8. The required time is plotted in Fig. 3.

Table 8 Performance of Algorithm 5
Full size table
Fig. 3
figure 3

Time needed versus number of nodes for Algorithm 5. Overall time counts the time needed for all steps (S1–S8) in Algorithm 5 to reach the stopping criteria. Loading Time counts the time to load data matrix into the nodes (S1). Cov Calculation Time measures the time for calculating covariance matrix (S2), and 100 Iterations Time is the time needed for solving subproblems (S3–S8) only during 100 iterations

Full size image

Here are some remarks about the behavior of Algorithm 5:

  1. X1)

    Similar to the Algorithm 4, step S1, and step S2 are performed completely in a distributed manner. Therefore, the time consumed by these two steps decrease significantly by increasing the number of nodes in MPI cluster.

  2. X2)

    Unlike the Algorithm 4, in Algorithm 5 the computational time in steps S3–S8 decreases as the number of nodes increases (except when \(M=64\), for which the reason will be explained in the next remark). The reason is that when splitting the columns, each node deals with a subvector of the original long loading vectors. Therefore, as the number of nodes increases, the computational burden will be shared among all nodes.

  3. X3)

    As we explained in remark (X1), the computational time required to perform steps S3–S8 includes communication time between the nodes. Therefore, when M is too large (\(M=64\) in Table 8) the disadvantages of the increased communication time outweighs the advantages of parallellization.

  4. X4)

    Similar to the Algorithms 4, 5 is also faster on the sparse matrix than on the dense matrix.

7 Conclusion

In this paper we propose an ADMM based algorithm which deals with popular nonconvex and nonsmooth optimization problems. We provided a rigorous convergence analysis for the proposed algorithm, which shows the algorithm converges to the set of stationary solutions under certain condition on the penalty parameter. Finally extensive numerical results are provided to showcase the theoretical achievements in this paper.