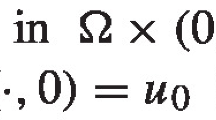Non-local Diffusion Equations Involving the Fractional $p(\cdot )$-Laplacian

Abstract

In this paper we study a class of nonlinear quasi-linear diffusion equations involving the fractional $p(\cdot )$-Laplacian with variable exponents, which is a fractional version of the nonhomogeneous $p(\cdot )$-Laplace operator. The paper is divided into two parts. In the first part, under suitable conditions on the nonlinearity f, we analyze the problem $({\mathscr {P}}_{1})$ in a bounded domain $\varOmega$ of ${\mathbb {R}}^N$ and we establish the well-posedness of solutions by using techniques of monotone operators. We also study the large-time behaviour and extinction of solutions and we prove that the fractional $p(\cdot )$-Laplacian operator generates a (nonlinear) submarkovian semigroup on $L^{2}(\varOmega ).$ In the second part of the paper we establish the existence of global attractors for problem $({\mathscr {P}}_{2})$ under certain conditions in the potential ${\mathbb {V}}.$ Our results are new in the literature, both for the case of variable exponents and for the fractional p-laplacian case with constant exponent.

1 Introduction

The main objective of this paper is to present new results concerning the existence of solutions and qualitative properties of the following parabolic problems involving variable exponent

where $\varOmega \subset {\mathbb {R}}^{N}$ is smooth bounded domain, $\partial _{t}u=\partial u/\partial t,$$s\in (0,1)$ and $p\in C({\overline{\varOmega }}\times {\overline{\varOmega }})$ with $s p(x,y)<N$ for any $(x,y)\in {\overline{\varOmega }}\times {\overline{\varOmega }}.$ We refer to [24] where this operator is introduced and the embedding theorems of fractional Sobolev spaces with variable exponents are established. The operator $(-\varDelta )_{p(\cdot )}^{s}$ is defined by

$$\begin{aligned} (-\varDelta )_{p(\cdot )}^{s}u(x)=\hbox {P.V.}\int _{\varOmega }\frac{|u(x)-u(y)|^{p(x,y)-2}(u(x)-u(y))}{|x-y|^{N+sp(x,y)}}\,dy,\quad x\in \varOmega , \end{aligned}$$

here P.V. is the principal value. We note that the operator $(-\varDelta )_{p(\cdot )}^{s}$ is a fractional version of the $p(\cdot )$-Laplacian operator, given by ${\text {div}}(|\nabla u|^{p(x)-2}\nabla u).$ The results in this paper improve, extend, complete and complement some results obtained in [1, 17, 19, 31, 34] in the sense that the authors have only considered the case when the problems (${\mathscr {P}}_{1}$) and (${\mathscr {P}}_{2}$) is replaced by the p-Laplacian operator and/or by p(x)-Laplacian operator. The main difficulties of this problem arise from the fact of working with this new nonlocal fractional $p(\cdot )$-Laplacian operator involving variable exponents, the respective Sobolev spaces with variable exponents, as well as dealing with the trace operator for these types of problems.

In more detail, we obtain qualitative properties of the solutions, large-time behaviour of solutions, decay and extinction properties, we prove that the operator $-(-\varDelta )_{p(\cdot )}^{s}$ generates a nonlinear submarkovian semigroup $\{S_{s,p(\cdot )}(t)\}_{t\geqslant 0}$ on $L^{2}(\varOmega ).$ We also prove that the semigroup $\{S_{s,p(\cdot )}\}_{t\geqslant 0}$ associated to problem (${\mathscr {P}}_{2}$) possesses a global attractor in $L^{2}(\varOmega ).$ Notice that when $s \nearrow 1^{-}$ and $p(\cdot )=p$ is constant, the equations (${\mathscr {P}}_{1}$) and (${\mathscr {P}}_{2}$) are reduced to

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _{t}u-\varDelta _{p}u= f(x,u) \quad \text { in }\varOmega \times {\mathbb {R}}^{+}, \\ u=0 \quad \text { on } \partial \varOmega \times {\mathbb {R}}^{+},\\ u(x,0)=u_{0} \quad \text { in }\varOmega . \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _{t}u-\varDelta _{p}u+{\mathbb {V}}(u)= 0 \quad \text { in }\varOmega , \\ u=0\quad \text { on } \partial \varOmega \times {\mathbb {R}}^{+},\\ u(0)=u_{0}\quad \text { on } \partial \varOmega . \end{array}\right. } \end{aligned}$$

which were studied in some recent works [1, 3, 4, 10, 11, 17, 19, 31, 34].

Recently, researchers have had a growing interest in the fractional Laplacian operator and related nonlocal operators of different types, this great interest is due to its numerous applications, such as, continuum mechanics, optimization, finance, phase transitions, population dynamics, image process, game theory, Levy processes, minimal surfaces, nonlinear stochastic dynamics, crystal dislocation, flame propagation, conservation laws, anomalous diffusion, the thin obstacle problem, stratified materials, nonlinear elastodynamics, for more details see for example [9, 14, 20, 26, 29] and references therein. In this article we focus on nonlocal operators acting on bounded domains, that is, regional fractional operators and the framework where the solutions belong to Sobolev–Slobodetskii space. Our main results are the following theorems.

Theorem 1

Assume that $p^{-}>1.$ For $u_{0}\in L^{2}(\varOmega )$ and $f\in L_{loc}^{2}({\mathbb {R}}_{0}^{+};L^{2}(\varOmega )),$ there exists a unique solution u of (${\mathscr {P}}_{1}$) such that the function $t\mapsto \varPhi (u(\cdot ,t))$ is absolutely continuous in ${\mathbb {R}}_{0}^{+}.$

In particular, if $u_{0}\in X,$ then

$$\begin{aligned} u\in W_{loc}^{1,2}({\mathbb {R}}_{0}^{+};L^{2}(\varOmega ))\cap C_{\omega }({\mathbb {R}}_{0}^{+};X) \end{aligned}$$

and $t\mapsto \varPhi (u(\cdot ,t))$ is absolutely continuous in ${\mathbb {R}}_{0}^{+}.$

Moreover, the unique solution u of problem (${\mathscr {P}}_{1}$) depends continuously on initial data $u_{0}$ and f in the following sense: Let $u_{i},\,i=1,2,$ denote the unique solutions of problem (${\mathscr {P}}_{1}$), with $u_{0}=u_{0,i}\in L^{2}(\varOmega )$ and $f=f_{i}\in L_{loc}^{2}({\mathbb {R}}_{0}^{+};L^{2}(\varOmega ))$ for $i=1,2.$ Then

$$\begin{aligned} \Vert u_{1}(\cdot ,t)-u_{2}(\cdot ,t)\Vert _{L^{2}(\varOmega )}\leqslant \Vert u_{0,1}-u_{0,2}\Vert _{L^{2}(\varOmega )}+\int _{0}^{t}\Vert f_{1}(\cdot ,\tau )-f_{2}(\cdot ,\tau )\Vert _{L^{2}(\varOmega )}\,d\tau \end{aligned}$$

for all $t\in {\mathbb {R}}_{0}^{+}.$

Theorem 2

(The Submarkovian Property) Let $p^{-}>1,$$s\in (0,1)$ and q(x),  p(x, y) be continuous variable exponents with $sp(x,y)<N$ for $(x,y)\in \varOmega \times \varOmega ,$ and $q(x)>p(x,x)$ for $x\in \varOmega .$ Then the operator $-(-\varDelta )_{p(\cdot )}^{s}$ generates a (nonlinear) submarkovian semigroup $S_{s,p(\cdot )}=\{S_{s,p(\cdot )}(t)\}_{t\geqslant 0}$ on ${\mathscr {H}}=L^{2}(\varOmega ).$ In particular, we have that the problem (${\mathscr {P}}_{1}$) with $f\equiv 0$ is well-posed on $L^{\varpi (\cdot )}(\varOmega ),$ with $1<\varpi ^{-}\leqslant \varpi (x)\leqslant \varpi ^{+}<+\infty$ for every $x\in {\overline{\varOmega }},$ that is, for every $u_{0}\in L^{\varpi (\cdot )},$ the problem (${\mathscr {P}}_{1}$) has a unique solution.

For $p^{-}>2,$ we have the following result.

Theorem 3

(Decay Property) Assume $p^{-}>2.$ Let $u_{0}\in {\mathcal {V}}{\setminus } \{0\}$ and let $u=u(x,t)$ be the unique solution of (${\mathscr {P}}_{1}$) with $f\equiv 0.$ Then there exists a constant $C>0$ such that

$$\begin{aligned} C^{-1}(1+t)^{\frac{-1}{p^{-}-2}}\leqslant \Vert u(t)\Vert _{L^{2}(\varOmega )}\leqslant C(1+t)^{\frac{-1}{p^{+}-2}}, \end{aligned}$$

for all $t\geqslant 0.$

For the case $p^{+}<2,$ we have the following result.

Theorem 4

(Extinction Property) Assume $2N/(N+2s)\leqslant p^{-}\leqslant p^{+}<2.$ Let $u_{0}\in {\mathcal {V}}{\setminus }\{0\}$ and let $u(\cdot ,t)$ be the unique solution of (${\mathscr {P}}_{1}$) with $f\equiv 0.$ Then, we have the following estimate

$$\begin{aligned} \Vert u(\cdot ,t)\Vert _{L^{2}(\varOmega )}\leqslant \Big (\Vert u_{0}\Vert _{L^{2}(\varOmega )}^{2-p^{-}}-(2-p^{-})p^{+}{\mathscr {R}}(0)t \Big )_{+}^{1/(2-p^{-})} \end{aligned}$$

for all $t\in {\mathbb {R}}_{0}^{+},$ where ${\mathscr {R}}(0)=\varPhi (u_{0})/\Vert u_{0}\Vert _{L^{2}}^{p^{-}}.$ Therefore the solution u is extinguished in a finite time $t^{*}.$

Theorem 5

(Existence of Global Attractor for Problem $({\mathscr {P}}_{2})$) For the problem (${\mathscr {P}}_{2}$) if either $p>2$, or $p=2$ and $L{\mathfrak {C}}_{s,p}^2<1$ (${\mathfrak {C}}_{s,p}$ being the constant for the embedding $W_{0}^{s,p}(\varOmega ) \hookrightarrow {\mathscr {H}}$ and L being the Lipschitz constant of ${\mathbb {V}}$), then the semigroup $\lbrace T(t) \rbrace _{t\geqslant 0}$ associated to (${\mathscr {P}}_{2}$) has a global attractor in $\overline{{\mathcal {D}}({\mathscr {A}}_{{\mathscr {H}}})}^{{\mathscr {H}}}={\mathscr {H}}$.

The main contributions of this research are the following:

• (1) We deal with evolution problems involving fractional $p(\cdot )$-Laplacian type operators in the context of semigroups generated by maximal monotone operators.

• (2) We obtain a version of the Stampacchia’s Lemma for fractional Sobolev–Slobodetskii spaces with variable exponents.

• (3) We prove that the fractional $p(\cdot )$-Laplacian operator is of the subdifferential type.

• (4) We obtain properties of submarkovian semigroup for the fractional $p(\cdot )$-Laplacian operator which up to our knowledge, is new in the sense that we are working in spaces with variable exponents.

• (5) As far as we know, we give the first answer about whether these type of problems involving the fractional p-Laplacian operator have a global attractor.

• (6) We prove a fundamental result on the qualitative study of the solutions for the anomalous diffusion model of evolution equations, specifically, we obtain a comparison principle.

Outline of the paper In Sect. 2 we introduce some notation and preliminary results about fractional Sobolev–Slobodetskii spaces. In Sect. 3 we study the fractional p-laplacian operator and its properties and we prove existence and uniqueness of solution to problem (${\mathscr {P}}_{1}$) for $\displaystyle {1<p^{-}=\min _{(x,y)\in {\overline{\varOmega }}\times {\overline{\varOmega }} }p(x,y)}$ via monotone operator theory. In Sect. 4 we prove that the associated operator generates a nonlinear submarkovian semigroup on $L^{2}(\varOmega ).$ In Sect. 5 we study the asymptotic behavior of solutions of problem (${\mathscr {P}}_{1}$). In Sect. 6 we obtain the existence of a solution and a global attractor for problem (${\mathscr {P}}_{1}$).

2 Preliminary Results

In this section, we review definitions for the Lebesgue and Sobolev spaces with variable exponent and some interesting properties that will be useful to discuss the problem (${\mathscr {P}}_{1}$). The basic properties of the variable exponent Lebesgue Sobolev spaces can be found in [13, 15, 16, 25] and the references therein.

Throughout the paper, without any mention, $\varOmega \subset {\mathbb {R}}^{N}$ denotes a smooth bounded domain. Denote

$$\begin{aligned} C^{+}({\overline{\varOmega }})=\{h\in C({\overline{\varOmega }}):h(x)>1 \quad \hbox {for all}\quad x\in {\overline{\varOmega }}\}. \end{aligned}$$

For any $h\in C^{+}({\overline{\varOmega }}),$ we define

$$\begin{aligned} h^{-}=\min _{x\in {\overline{\varOmega }}} h(x), \quad h^{+}=\max _{x\in {\overline{\varOmega }}}h(x). \end{aligned}$$

For every $h\in C^{+}({\overline{\varOmega }}),$ the variable exponent Lebesgue space $L^{h(\cdot )}(\varOmega )$ is defined by

$$\begin{aligned} L^{h(\cdot )}(\varOmega )=\Bigg \{u:\varOmega \rightarrow {\mathbb {R}} :\exists \lambda >0: \rho _{h(\cdot )}\Big (\frac{u}{\lambda } \Big )<+\infty \Bigg \}, \end{aligned}$$

where the mapping $\rho _{h(\cdot )}: L^{h(\cdot )}(\varOmega )\rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} \rho _{h(\cdot )}(u)=\int _{\varOmega }|u(x)|^{h(x)}\,dx, \end{aligned}$$

is called the $h(\cdot )$-modular of the Lebesgue space $L^{h(\cdot )}(\varOmega ).$

The function $\rho _{h(\cdot )}(\cdot )$ verifies the following properties:

• (1) $\rho _{h(\cdot )}(u)\geqslant 0$ for every $u\in L^{h(\cdot )}(\varOmega ).$

• (2) $\rho _{h(\cdot )}(u)= 0$ if and only if $u=0.$

• (3) $\rho _{h(\cdot )}(u)=\rho _{h(\cdot )}(-u)$ for every $u\in L^{h(\cdot )}(\varOmega ).$

• (4) $\rho _{h(\cdot )}(u)$ is convex.

Every functional that satisfies the properties $(1)-(4)$ is called convex modular.

The space $L^{h(\cdot )}(\varOmega )$ endowed with the Luxemburg norm,

$$\begin{aligned} \Vert u\Vert _{L^{h(\cdot )}(\varOmega )}:=\inf \Bigg \{\lambda >0: \rho _{h(\cdot )}\Big (\frac{u}{\lambda }\Big )\leqslant 1\Bigg \}, \end{aligned}$$

is separable and reflexive Banach space. Note that, when h is constant, the Luxemburg norm $\Vert \cdot \Vert _{L^{h(\cdot )}(\varOmega )}$ coincide with the standard norm $\Vert \cdot \Vert _{h}$ of the Lebesgue space $L^{h}.$

Denoting by $L^{h'(\cdot )}(\varOmega )$ the dual space of space $L^{h(\cdot )}(\varOmega )$, where $\frac{1}{h(x)}+\frac{1}{h'(x)}=1,$ for any $u\in L^{h(\cdot )}(\varOmega )$ and $v\in L^{h'(\cdot )}(\varOmega ),$ we have the Hölder inequality

$$\begin{aligned} \int _{\varOmega }|uv|\leqslant \Bigg ( \frac{1}{h^{-}} +\frac{1}{h'^{-}}\Bigg )\Vert u\Vert _{L^{h(\cdot )}(\varOmega )}\Vert v\Vert _{L^{h'(\cdot )}(\varOmega )}. \end{aligned}$$

If $h_{1}(x), h_{2}(x)\in C^{+}({\overline{\varOmega }})$ and $h_{1}(x)\leqslant h_{2}(x)$ for all $x\in {\overline{\varOmega }},$ then $L^{h_{2}(\cdot )}(\varOmega )\hookrightarrow L^{h_{1}(\cdot )}(\varOmega )$ and the embedding is continuous.

In the following proposition, we give some results regarding the relationship between the Luxemburg norm and the $h(\cdot )$-modular mapping.

Proposition 1

For $u\in L^{h(\cdot )}(\varOmega )$ and $\{u_{n}\}_{n\in {\mathbb {N}}}\subset L^{h(\cdot )}(\varOmega ),$ we have

• (1) $\Vert u\Vert _{L^{h(\cdot )}(\varOmega )}\leqslant 1\Rightarrow \Vert u\Vert _{L^{h(\cdot )}(\varOmega ) }^{h^{+}}\leqslant \rho _{h(\cdot )}(u)\leqslant \Vert u\Vert _{L^{h(\cdot )}(\varOmega ) }^{h^{-}};$

• (2) $\Vert u\Vert _{L^{h(\cdot )}(\varOmega )}\geqslant 1\Rightarrow \Vert u\Vert _{L^{h(\cdot )}(\varOmega ) }^{h^{-}}\leqslant \rho _{h(\cdot )}(u)\leqslant \Vert u\Vert _{L^{h(\cdot )}(\varOmega ) }^{h^{+}};$

• (3) $\lim \limits _{n\rightarrow +\infty } \Vert u_{n}\Vert _{L^{h(\cdot )}(\varOmega )}=0 \Leftrightarrow \lim \limits _{n\rightarrow +\infty } \rho _{h(\cdot )}(u_{n})=0;$

• (4) $\lim \limits _{n\rightarrow +\infty } \Vert u_{n}\Vert _{L^{h(\cdot )}(\varOmega )}=+\infty \Leftrightarrow \lim \limits _{n\rightarrow +\infty } \rho _{h(\cdot )}(u_{n})=+\infty .$

Proposition 2

It holds that

$$\begin{aligned} \sigma ^{-}(\Vert u\Vert _{L^{p(\cdot )}(\varOmega )})\leqslant \int _{\varOmega }|u|^{p(x)}\,dx\leqslant \sigma ^{+}(\Vert u\Vert _{L^{p(\cdot )}(\varOmega )}) \end{aligned}$$

for all $u\in L^{p(\cdot )}(\varOmega ),$ with $\sigma ^{-}(\tau ):=\min \{\tau ^{p^{-}},\tau ^{p^{-}}\}$ and $\sigma ^{+}(\tau ):=\max \{\tau ^{p^{-}},\tau ^{p^{-}}\}$ for $\tau \geqslant 0.$

We define the variable exponent Sobolev space $W^{1,h(\cdot )}(\varOmega )$ by

$$\begin{aligned} W^{1,h(\cdot )}(\varOmega )=\Bigg \{u\in L^{h(\cdot )}(\varOmega ): |\nabla u|\in L^{h(\cdot )}(\varOmega ) \Bigg \}, \end{aligned}$$

equipped with the norm

$$\begin{aligned} \Vert u\Vert _{W^{1,h(\cdot )}(\varOmega )}=\Vert u\Vert _{L^{h(\cdot )}(\varOmega )}+\Vert \nabla u\Vert _{L^{h(\cdot )}(\varOmega )}. \end{aligned}$$

We denoted by $W_{0}^{1,h(\cdot )}(\varOmega )$ the closure of $C_{0}^{\infty }(\varOmega )$ in $W^{1,h(\cdot )}(\varOmega )$ with respect to the above norm. The spaces $W^{1,h(\cdot )}(\varOmega )$ and $W_{0}^{1,h(\cdot )}(\varOmega )$ are separable and reflexive Banach spaces.

2.1 Fractional Sobolev–Slobodetskii Spaces

For $s\in (0,1)$ and $p\in (1,+\infty ),$ we denote by

$$\begin{aligned} W^{s,p}(\varOmega ):=\Bigg \{u\in L^{p}(\varOmega ):\int _{\varOmega }\int _{\varOmega }\frac{|u(x)-u(y)|^{p}}{|x-y|^{N+sp}}\,dx\,dy<+\infty \Bigg \}, \end{aligned}$$

the fractional Sobolev–Slobodetskii space endowed with the norm

$$\begin{aligned} \Vert u\Vert _{W^{s,p}(\varOmega )}:=\Bigg (\int _{\varOmega }|u|^{p}\,dx+ \int _{\varOmega }\int _{\varOmega }\frac{|u(x)-u(y)|^{p}}{|x-y|^{N+sp}}\,dx\,dy \Bigg )^{\frac{1}{p}}. \end{aligned}$$

Let

$$\begin{aligned} W_{0}^{s,p}(\varOmega )=\overline{C_{0}^{\infty }(\varOmega )}^{W^{s,p}(\varOmega )}. \end{aligned}$$

For $s\in (0,1),$$1<p<+\infty$ we have the following Sobolev–Slobodetskii embedding (see [14]):

$$\begin{aligned} {\left\{ \begin{array}{ll} W_{0}^{s,p}(\varOmega )\hookrightarrow L^{p^{*}}(\varOmega ),\quad p^{*}:=\frac{Np}{N-sp}>p \quad \text { if } N>sp, \\ W_{0}^{s,p}(\varOmega )\hookrightarrow L^{q}(\varOmega )\;\text { for all } q\in [1,+\infty ) \quad \text { if } N=sp,\\ W_{0}^{s,p}(\varOmega )\hookrightarrow C^{0,s-\frac{N}{p}}({\overline{\varOmega }})\quad \text { if } N<sp. \end{array}\right. } \end{aligned}$$

We have the following result contained in [8, Corollary 2.8 and Remark 2.3] for the case $p=2$ and in [21] for general case $p\in (1,+\infty )$.

Theorem 6

Let $\varOmega \subset {\mathbb {R}}^{N}$ be a bounded set with a Lipschitz continuous boundary and $p\in (1,+\infty ).$ Then for every $0<s\leqslant \frac{1}{p},$ the spaces $W^{s,p}(\varOmega )$ and $W_{0}^{s,p}(\varOmega )$ coincide with equivalent norms.

Due to Theorem 6, we have that if $s\in (0,\frac{1}{p}]$ and $\varOmega$ has a Lipschitz continuous boundary, then for all $u\in W^{s,p}(\varOmega )$ is zero $\sigma$ a.e. on $\partial \varOmega ,$ where $\sigma$ denotes the usual Lebesgue surface measure on $\partial \varOmega .$ Therefore, to talk about trace functions in $W^{s,p}(\varOmega )$ that are not necessarily null on $\partial \varOmega ,$ it is not a restriction to assume that $\frac{1}{p}<s<1.$ Next, for $p\in (1,+\infty )$ and $\tau \in (0,1),$ we denote by

$$\begin{aligned} W^{s,p}(\partial \varOmega ):=\Bigg \{u\in L^{p}(\partial \varOmega ):\int _{\partial \varOmega }\int _{\partial \varOmega }\frac{|u(x)-u(y)|^{p}}{|x-y|^{N-1+sp}}\,d\sigma _{x}\,d\sigma _{y}<+\infty \Bigg \}, \end{aligned}$$

the fractional Sobolev–Slobodetskii space endowed with the norm

$$\begin{aligned} \Vert u\Vert _{W^{s,p}(\partial \varOmega )}:=\Bigg (\int _{\partial \varOmega }|u|^{p}\,d\sigma + \int _{\partial \varOmega }\int _{\partial \varOmega }\frac{|u(x)-u(y)|^{p}}{|x-y|^{N-1+sp}}\,d\sigma _{x}\,d\sigma _{y} \Bigg )^{\frac{1}{p}}. \end{aligned}$$

Theorem 7

[21] Let $p\in (1,+\infty ),$$\frac{1}{p}<s<1$ and $\varOmega \subset {\mathbb {R}}^{N}$ be a bounded open set with a Lipschitz continuous boundary $\partial \varOmega .$ Then the following assertions hold:

• (1) If $N>sp,$ then $W^{s,p}(\varOmega )\hookrightarrow L^{q}(\varOmega )$ for every $q\in [1,p^{*}]$ where $p^{*}:=\frac{Np}{N-sp}>p.$

• (2) If $N=sp,$ then $W^{s,p}(\varOmega )\hookrightarrow L^{q}(\varOmega )$ for every $q\in [1,+\infty ).$

• (3) If $N<sp,$ then $W^{s,p}(\varOmega )\hookrightarrow C^{0,s-\frac{N}{p}}({\overline{\varOmega }}).$

• (4) The continuous injection $W^{s,p}(\varOmega )\hookrightarrow L^{p}(\varOmega )$ is compact.

• (5) There exists a linear continuous trace operator

  $$\begin{aligned} \mathrm {Tr}:W^{s,p}(\varOmega )\rightarrow L^{q}(\partial \varOmega ), \end{aligned}$$

  such that $\mathrm {Tr}(u)=u$ on $\partial \varOmega$ for all $u\in W^{s,p}(\varOmega )\cap C({\overline{\varOmega }})$ with $q=p^{*}=\frac{p(N-1)}{N-sp}$ if $N>sp,$q is any number in $[1,+\infty )$ if $N=sp$ and $q=+\infty$ if $N<sp.$ Furthermore, the continuous embedding $W^{s,p}(\varOmega )\hookrightarrow L^{p}(\partial \varOmega )$ is also compact.

• (6) There exists a linear continuous trace operator

  $$\begin{aligned} \mathrm {T}:W^{s,p}(\varOmega )\rightarrow W^{s-\frac{1}{p},p}(\partial \varOmega ). \end{aligned}$$

• (7) The trace operador $\mathrm {T}$ has a linear bounded right inverse

  $$\begin{aligned} {\mathbb {E}}:W^{s-\frac{1}{p},p}(\partial \varOmega )\rightarrow W^{s,p}(\varOmega ). \end{aligned}$$

• (8) Let $N\geqslant sp,$$r=p_{*}=\frac{p(N-1)}{N-sp}$ if $N>sp$ and $r\in [1,+\infty )$ any number if $N=sp.$ Then

  $$\begin{aligned} W^{s-\frac{1}{p},p}(\partial \varOmega )\hookrightarrow L^{r}(\partial \varOmega ). \end{aligned}$$

• (9) If $N<sp,$ then

  $$\begin{aligned} W^{s-\frac{1}{p},p}(\partial \varOmega )\hookrightarrow C^{0,s-\frac{N}{p}}(\partial \varOmega ). \end{aligned}$$

• (10) The continuous embedding $W^{s-\frac{1}{p},p}(\partial \varOmega )\hookrightarrow L^{p}(\partial \varOmega )$ is compact.

2.2 Fractional Sobolev–Slobodetskii Spaces with Variable Exponents

We consider two variable exponents $q:{\overline{\varOmega }}\rightarrow {\mathbb {R}}$ and $p:{\overline{\varOmega }}\times {\overline{\varOmega }}\rightarrow {\mathbb {R}},$ where both $q(\cdot )$ and $p(\cdot ,\cdot )$ are continuous functions. We assume that p is symmetric, that is, $p(x,y) = p(y,x)$, and that both p and q are bounded away from 1 and $\infty$, that is,

$$\begin{aligned} 1<p^{-}=\min _{(x,y)\in {\overline{\varOmega }}\times {\overline{\varOmega }} }p(x,y)\leqslant p(x,y)\leqslant p^{+}=\max _{(x,y)\in {\overline{\varOmega }}\times {\overline{\varOmega }}}p(x,y)<+\infty \end{aligned}$$

(1)

and

$$\begin{aligned} 1<q^{-}=\min _{x\in {\overline{\varOmega }}}q(x)\leqslant q(x)\leqslant q^{+}=\max _{x\in {\overline{\varOmega }}}q(x)<+\infty . \end{aligned}$$

(2)

We define the Banach space $L^{q(\cdot )}(\varOmega )$ as usual,

$$\begin{aligned} L^{q(\cdot )}(\varOmega ):= \left\{ u:\varOmega \rightarrow {\mathbb {R}}:\exists \lambda >0: \int _{\varOmega } \left| \frac{u(x)}{\lambda }\right| ^{q(x)}\,dx<+\infty \right\} , \end{aligned}$$

with its natural norm

$$\begin{aligned} \Vert u\Vert _{ L^{q(\cdot )}(\varOmega )} := \inf \left\{ \lambda >0: \int _{\varOmega } \left| \frac{u(x)}{\lambda }\right| ^{q(x)}dx< 1 \right\} . \end{aligned}$$

Now for $s\in (0,1)$ we introduce the fractional Sobolev–Slobodetskii space with variable exponents via the Gagliardo–Slobodetskii approach as follows:

$$\begin{aligned} \begin{aligned} {\mathcal {W}}&={\mathcal {W}}^{s,q(\cdot ),p(\cdot ,\cdot )}(\varOmega ) \\&:=\left\{ u:\varOmega \rightarrow {\mathbb {R}}:u\in L^{q(\cdot )}(\varOmega ), \int _{\varOmega }\int _{\varOmega } \frac{|u(x)-u(y)|^{p(x,y)}}{\lambda ^{p(x,y)}|x-y|^{n+sp(x,y)}}\,dx\,dy\right. \\&\quad \left. <+\infty , ~\hbox {for some}~ \lambda >0 \right\} \end{aligned} \end{aligned}$$

and we set

$$\begin{aligned}{}[u]_{\varOmega }^{s,p(\cdot ,\cdot )}:= \inf \left\{ \lambda >0:\int _{\varOmega }\int _{\varOmega } \frac{|u(x)-u(y)|^{p(x,y)}}{\lambda ^{p(x,y)}|x-y|^{n+sp(x,y)}}\,dx\,dy\leqslant 1 \right\} \end{aligned}$$

the variable exponent Gagliardo–Slobodetskii seminorm. It is already known (see [24]) that ${\mathcal {W}}$ is a Banach space with the norm

$$\begin{aligned} \Vert u\Vert _{{\mathcal {W}}}:=\Vert u\Vert _{L^{q(\cdot )}(\varOmega )}+[u]_{\varOmega }^{s,p(\cdot ,\cdot )}. \end{aligned}$$

Let ${\mathcal {W}}_{0}$ denote the closure of $C_{0}^{\infty }(\varOmega )$ in ${\mathcal {W}}.$ Then ${\mathcal {W}}_{0}$ is a Banach space with the norm

$$\begin{aligned} \Vert u\Vert =[u]^{s,p(\cdot ,\cdot )}_{\varOmega }. \end{aligned}$$

Theorem 8

[24, Theorem 1.1] Let $\varOmega \subset {\mathbb {R}}^{N}$ be a smooth bounded domain and $s \in (0, 1)$. Let q(x), p(x, y) be continuous variable exponents with $s\,p(x, y) < N$ for $(x, y)\in {\overline{\varOmega }}\times {\overline{\varOmega }}$ and $q(x) > p(x, x)$ for $x\in {\overline{\varOmega }}.$ Assume that $r :{\overline{\varOmega }}\rightarrow (1,\infty )$ is a continuous function such that

$$\begin{aligned} p^{*}(x):=\frac{Np(x,x)}{N-sp(x,x)}>r(x)\ge r^{-}>1, \end{aligned}$$

for $x\in {\overline{\varOmega }}$. Then, there exists a constant $C = C(N, s, p, q, r,\varOmega )$ such that for every $u \in {\mathcal {W}}$,

$$\begin{aligned} \Vert u\Vert _{L^{r(\cdot )}(\varOmega )} \le C\Vert u\Vert _{{\mathcal {W}}}. \end{aligned}$$

That is, the space ${\mathcal {W}}^{s,q(\cdot ),p(\cdot ,\cdot )}(\varOmega )$ is continuously embedded in $L^{r(\cdot )}(\varOmega )$ for any $r \in (1, p^{*})$. Moreover, this embedding is compact.

Lemma 1

[2, Lemma 3.1] Suppose that $\varOmega \subset {\mathbb {R}}^{N}$ is a bounded open domain. Furthermore, assume that (1) and (2) hold. Then ${\mathcal {W}}$ is a separable reflexive space.

Remark 1

An important role in manipulating the fractional Sobolev–Slobodetskii spaces with variable exponent is played by the $(s,p(\cdot ,\cdot ))$-convex modular function $\rho _{s,p(\cdot ,\cdot )}: {\mathcal {W}}\rightarrow {\mathbb {R}}$ define by

$$\begin{aligned} \displaystyle {\rho _{s,p(\cdot ,\cdot )}(u)=\int _{\varOmega }\int _{\varOmega }\Bigg (\frac{|u(x)-u(x)|}{|x-y|^{s}} \Bigg )^{p(x,y)}\frac{dx\,dy}{|x-y|^{N}}}. \end{aligned}$$

Note that the space ${\mathcal {W}}={\mathcal {W}}^{s,q(\cdot ), p(\cdot ,\cdot )}(\varOmega )$ can be rewritten as

$$\begin{aligned} {\mathcal {W}}=\Bigg \{u:\varOmega \rightarrow {\mathbb {R}}:u\in L^{q(\cdot )}(\varOmega ):\rho _{s,p(\cdot ,\cdot )}\Big (\frac{u}{\lambda } \Big )< +\infty , \hbox { for some } \lambda >0 \Bigg \} \end{aligned}$$

endowed with the Luxemburg norm

$$\begin{aligned} \Vert u\Vert _{{\mathcal {W}}}:=\Vert u\Vert _{L^{q(\cdot )(\varOmega )}}+[u]_{\varOmega }^{s,p(\cdot ,\cdot )}, \end{aligned}$$

where

$$\begin{aligned}{}[u]_{\varOmega }^{s,p(\cdot ,\cdot )}:=\inf \Big \{\lambda >0: \rho _{s,p(\cdot ,\cdot )}\Big (\frac{u}{\lambda }\Big )\leqslant 1\Big \}. \end{aligned}$$

For $0<s<1,$ the term $[\cdot ]_{\varOmega }^{s,p(\cdot ,\cdot )}$ is called the $(s,p(\cdot ,\cdot ))$-Gagliardo–Slobodetskii seminorm.

The following is a version of Stampacchia’s lemma for the space ${\mathcal {W}}^{s,q(\cdot ),p(\cdot ,\cdot )}(\varOmega )$.

Lemma 2

Let $\varOmega \subset {\mathbb {R}}^{N}$ be a smooth bounded domain and $s\in (0,1).$ Let q(x),  p(x, y) be continuous variable exponent with $s p(x,y)<N$ for $(x,y)\in {\overline{\varOmega }}\times {\overline{\varOmega }}.$ Then the following statements hold.

• (a) If $u\in {\mathcal {W}}^{s,q(\cdot ),p(\cdot ,\cdot )}(\varOmega ),$ then $|u|\in {\mathcal {W}}^{s,q(\cdot ),p(\cdot ,\cdot )}(\varOmega )$ and

  $$\begin{aligned} \Vert |u|\Vert _{ {\mathcal {W}}^{s,q(\cdot ),p(\cdot ,\cdot )}(\varOmega )}\leqslant \Vert u\Vert _{ {\mathcal {W}}^{s,q(\cdot ),p(\cdot ,\cdot )}(\varOmega )}. \end{aligned}$$

  (3)

• (b) If $u\in {\mathcal {W}}^{s,q(\cdot ),p(\cdot ,\cdot )}(\varOmega ),$ then $u^{+}\in {\mathcal {W}}^{s,q(\cdot ),p(\cdot ,\cdot )}(\varOmega )$ and

  $$\begin{aligned} \Vert u^{+}\Vert _{ {\mathcal {W}}^{s,q(\cdot ),p(\cdot ,\cdot )}(\varOmega )}\leqslant \Vert u\Vert _{ {\mathcal {W}}^{s,q(\cdot ),p(\cdot ,\cdot )}(\varOmega )}. \end{aligned}$$

  (4)

• (c) If $u\in {\mathcal {W}}^{s,q(\cdot ),p(\cdot ,\cdot )}(\varOmega ),$ then $u^{-}\in {\mathcal {W}}^{s,q(\cdot ),p(\cdot ,\cdot )}(\varOmega )$ and

  $$\begin{aligned} \Vert u^{-}\Vert _{ {\mathcal {W}}^{s,q(\cdot ),p(\cdot ,\cdot )}(\varOmega )}\leqslant \Vert u\Vert _{ {\mathcal {W}}^{s,q(\cdot ),p(\cdot ,\cdot )}(\varOmega )}. \end{aligned}$$

  (5)

Proof

Let $s\in (0,1),$q(x) and p(x, y) be continuous variable exponents and $u\in {\mathcal {W}}^{s,q(\cdot ),p(\cdot ,\cdot )}(\varOmega )$

• (a) Note that $|u|\in L^{q(\cdot )}(\varOmega )$ and that $\Vert |u|\Vert _{L^{q(\cdot )}(\varOmega )}=\Vert u\Vert _{L^{q(\cdot )}(\varOmega )}.$ By triangle inequality $||u(x)|-|u(y)||\leqslant |u(x)-u(y)|,$ we have

  $$\begin{aligned}{}[|u|]_{\varOmega }^{s,p(\cdot ,\cdot )}= & {} \inf \Bigg \{ \lambda>0:\rho _{s,p(\cdot ,\cdot )}\Bigg (\frac{|u|}{\lambda }\Bigg )\leqslant 1\Bigg \}\leqslant \inf \Bigg \{ \lambda >0:\rho _{s,p(\cdot ,\cdot )}\Bigg (\frac{u}{\lambda }\Bigg )\leqslant 1\Bigg \}\\= & {} [u]_{\varOmega }^{s,p(\cdot ,\cdot )}. \end{aligned}$$

  Hence, $|u|\in W^{s,q(\cdot ),p(\cdot ,\cdot )}(\varOmega )$ and we obtain the inequality (3).

• (b) Since $0\leqslant u^{+}\leqslant |u|,$ we have $u^{+}\in L^{q(\cdot )}(\varOmega )$ and $\Vert u^{+}\Vert _{L^{q(\cdot )}(\varOmega )}\leqslant \Vert u\Vert _{L^{q(\cdot )}(\varOmega )}.$ Let ${\mathfrak {A}}:=\{x\in \varOmega :u(x)\geqslant 0\}$ and ${\mathfrak {B}}:=\{x\in \varOmega :u(x)< 0\}.$ Then

  $$\begin{aligned} \begin{aligned} \int _{\varOmega }\int _{\varOmega }\frac{|u^{+}(x)-u^{+}(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy=&\int _{{\mathfrak {A}}}\int _{{\mathfrak {A}}}\frac{|u(x)-u(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\&+ \int _{{\mathfrak {A}}}\int _{{\mathfrak {B}}}\frac{|u(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\&+\int _{{\mathfrak {B}}}\int _{{\mathfrak {A}}}\frac{|u(x)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy. \end{aligned} \end{aligned}$$

  (6)

  Since $|u(y)|\leqslant |u(x)-u(y)|$ on ${\mathfrak {B}}\times {\mathfrak {A}}:=\{(x,y):\varOmega \times \varOmega :u(x)<0,\,u(y)\geqslant 0 \}$ and $|u(x)|\leqslant |u(x)-u(y)|$ on ${\mathfrak {A}}\times {\mathfrak {A}}:=\{(x,y):\varOmega \times \varOmega :u(x)\geqslant 0,\,u(y)<0 \},$ thus by (6), we have

  $$\begin{aligned} \begin{aligned} \int _{\varOmega }\int _{\varOmega }\frac{|u^{+}(x)-u^{+}(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy=&\int _{{\mathfrak {A}}}\int _{{\mathfrak {A}}}\frac{|u(x)-u(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\&+ \int _{{\mathfrak {A}}}\int _{{\mathfrak {B}}}\frac{|u(x)-u(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\&+\int _{{\mathfrak {B}}}\int _{{\mathfrak {A}}}\frac{|u(x)-u(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\ \leqslant&\int _{\varOmega }\int _{\varOmega }\frac{|u(x)-u(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy. \end{aligned} \end{aligned}$$

  (7)

  Hence,

  $$\begin{aligned}{}[u^{+}]_{\varOmega }^{s,p(\cdot ,\cdot )}= & {} \inf \Bigg \{\lambda>0:\rho _{s,p(\cdot ,\cdot )}\Bigg ( \frac{u^{ +}}{\lambda }\Bigg )\leqslant 1 \Bigg \}\leqslant \inf \Bigg \{\lambda >0:\rho _{s,p(\cdot ,\cdot )}\Bigg ( \frac{u}{\lambda }\Bigg )\leqslant 1 \Bigg \}\\= & {} [u^{+}]_{\varOmega }^{s,p(\cdot ,\cdot )}. \end{aligned}$$

  Thus $u^{+}\in {\mathcal {W}}^{s,q(\cdot ),p(\cdot ,\cdot )}(\varOmega )$ and we have the inequality (4).

• (c) Since $|u|=u^{+}+u^{-},$ we have $u^{-}\in W^{s,q(\cdot ),p(\cdot ,\cdot )}(\varOmega ).$ The inequality (5) is obtained as item (b).

$\square$

2.3 Maximal Monotone Operators and Semigroups

We present a brief review of some results of the theory of monotone operators, nonlinear semigroups and convex analysis with the purpose of obtaining our main results. Let H be a Hilbert space with scalar product $(\cdot ,\cdot )_{H}$ and let $\varphi :H\rightarrow (-\infty ,\infty ]$ be a proper, convex and lower semi-continuous functional with effective domain

$$\begin{aligned} {\mathcal {D}}(\varphi ):=\{u\in H:\varphi (u)<\infty \}. \end{aligned}$$

The subdifferential $\partial \varphi$ of the functional $\varphi$ is defined by

$$\begin{aligned} \begin{aligned}&\partial \varphi (u):=\{\omega \in H: \forall v\in H:\varphi (v)-\varphi (u)\geqslant (\omega ,v-u )_{H}\},\\&{\mathcal {D}}(\partial \varphi ):=\{u\in {\mathcal {D}}(\varphi ):\exists \omega \in H\,\forall v\in H:\varphi (v)-\varphi (u)\geqslant (\omega ,v-u )_{H}\}. \end{aligned} \end{aligned}$$

Theorem 9

(See [5]) The subdifferential $\partial \varphi$ is a maximal monotone operator. Furthermore, $\overline{{\mathcal {D}}(\varphi )}=\overline{{\mathcal {D}}(\partial \varphi )}.$ The operator $A:=-\partial \varphi$ generates a (nonlinear) strongly continuous semigroup $\{S(t)\}_{t\geqslant 0}$ on $\overline{{\mathcal {D}}(\varphi )}$ in the following sense: for every $u_{0}\in \overline{{\mathcal {D}}(\varphi )},$ the function $u(\cdot )=S(\cdot )u_{0}$ is the unique strong solution of the first order Cauchy problem

$$\begin{aligned} {\left\{ \begin{array}{ll} u\in C({\mathbb {R}}^{+};H)\cap W_{\text {loc}}^{1,\infty }(0,\infty ;H)\quad \text { and }u(t)\in {\mathcal {D}}(\partial \varphi )\text { a.e.,} \\ \partial _{t}u +\partial \varphi (u)\ni 0 \quad \text { a.e. on }{\mathbb {R}}^{+},\\ u(0,x)=u_{0}(x). \end{array}\right. } \end{aligned}$$

Let $S=\{S(t)\}_{t\geqslant 0}$ be a (nonlinear) semigroup on a real Hilbert lattice H.

Definition 1

We say that the semigroup S is order preserving, if

$$\begin{aligned} S(t)u\leqslant S(t)v\text { for all }t\geqslant 0\hbox { whenever }u,v\in H,\,u\leqslant v. \end{aligned}$$

The following result characterizes the property of order preserving in terms of the functional $\varphi .$

Proposition 3

(See [10, Theorem 3.6]) Let $\varphi :H\rightarrow (-\infty , \infty ]$ be a proper, convex, lower semi-continuous functional on a real Hilbert H with effective domain ${\mathcal {D}}(\varphi ).$ Let $S=\{S(t)\}_{t\geqslant 0}$ be the (nonlinear) semigroup on H generated by $-\partial \varphi .$ Then the following assertions are equivalent:

• (i) The semigroup S is order preserving.

• (ii) For all $u,v\in H$ one has

  $$\begin{aligned} \varphi \Bigg ( \frac{1}{2}(u+u\wedge v)\Bigg )+\varphi \Bigg ( \frac{1}{2}(v+u\vee v)\Bigg )\leqslant \varphi (u)+\varphi (v), \end{aligned}$$

  where $u\wedge v:=\inf \{u,v\}$ and $u\vee v:=\sup \{u,v\}.$

Remark 2

If ${\mathcal {D}}(\varphi )$ is a vector space, then (ii) of Proposition 3 is equivalent to the following: For all $u,v\in {\mathcal {D}}(\varphi )$ one has $u\wedge v,\,u\vee v\in {\mathcal {D}}(\varphi )$ and

$$\begin{aligned} \varphi (u\wedge v)+\varphi (u\vee v)\leqslant \varphi (u)+\varphi (v). \end{aligned}$$

We assume that $H:=L^{2}(X,m),$ where X is a locally compact metric space and m is a Radon measure on X. We introduce the notion of (nonlinear) submarkovian semigroups.

Definition 2

We say that the semigroup S is non-expansive on $L^{q}(X,m)(1\leqslant q\leqslant \infty )$ if

$$\begin{aligned} \Vert S(t)u-S(t)v\Vert _{q}\leqslant \Vert u-v\Vert _{q}\quad \forall t\geqslant 0,\quad \forall u,v\in L^{2}(X,m)\cap L^{q}(X,m). \end{aligned}$$

An order that preserves semigroup that is non-expansive $L^{\infty }(X,m)$ is called submarkovian.

The (nonlinear) submarkovian property is characterized by the following result.

Theorem 10

(See [32, Theorem 3.6]) Let $\varphi :L^{2}(X,m)\rightarrow (-\infty , +\infty ]$ be a proper, convex, lower semi-continuous functional. Let $S=\{S(t)\}_{t\geqslant 0}$ be the (nonlinear) semigroup on $L^{2}(X,m)$ generated by $-\partial \varphi .$ Suppose that S preserves order. Then, the following assertions are equivalent.

• (i) The semigroup S is submarkovian.

• (ii) For all $u,v\in L^{2}(X,m)$ and $\alpha >0,$

  $$\begin{aligned} \varphi (v+g_{\alpha }(u,v))+\varphi (u-g_{\alpha }(u,v))\leqslant \varphi (u)+\varphi (v), \end{aligned}$$

  where

  $$\begin{aligned} g_{\alpha }(u,v):=\frac{1}{2}\Big \{ (u-v+\alpha )_{+}-(u-v-\alpha )_{-}\Big \}, \end{aligned}$$

  with $u_{+}:=\sup \{0,u\},$ and $u_{-}:=\inf \{0,-u\}.$

The following lemma is a result of convex analysis [32, Lemma 3.3].

Lemma 3

Let ${\mathfrak {F}}:{\mathbb {R}}^{2}\rightarrow (-\infty , \infty ]$ be a convex and lower semi-continuous functional with effective domain ${\mathcal {D}}({\mathfrak {F}}):=\{(s,t)\in {\mathbb {R}}^{2}:{\mathfrak {F}}(s,t)<\infty \}.$ Assume that ${\mathbb {U}}:=\text {Int}({\mathcal {D}}({\mathfrak {F}}))\ne \emptyset .$ Then the following assertions are equivalent.

$({\mathbb {F}}_{1})$:

For all $(x_{0},x_{1}),\,(y_{0},y_{1})\in {\mathbb {R}}^{2}$ with $(x_{0}-y_{0})(x_{1}-y_{1})<0,$

$$\begin{aligned} {\mathfrak {F}}(x_{0},y_{1})+{\mathfrak {F}}(y_{0},x_{1})\leqslant {\mathfrak {F}}(x_{0},x_{1})+{\mathfrak {F}}(y_{0},y_{1}). \end{aligned}$$

$({\mathbb {F}}_{2})$:

$\frac{\partial ^{2}{\mathfrak {F}}}{\partial x_{0}\partial x_{1}}\leqslant 0$ on ${\mathscr {D}}'({\mathbb {U}})$ and

$$\begin{aligned} \forall (x_{0},x_{1}),\,(y_{0},y_{1})\in {\mathcal {D}}({\mathfrak {F}})\text { with } (x_{0}-y_{0})(x_{1}-y_{1})<0;\quad (x_{0},y_{1}),\,(y_{0},x_{1})\in {\mathcal {D}}({\mathfrak {F}}). \end{aligned}$$

3 Proof of Theorem 1 (Well-Posedness)

In this section, we prove the well-posedness of solutions of problem (${\mathscr {P}}_{1}$) by using a subdifferential approach. From now on in all our work, without causing confusion we consider indistinctly ${\mathscr {H}}:=L^{2}(\varOmega )$ and $X:={\mathcal {W}}_{0}.$

Definition 3

A function $u\in C({\mathbb {R}}_{0}^{+}; L^{2}(\varOmega ))$ is said to be a solution of (${\mathscr {P}}_{1}$), if the following conditions are all satisfied:

• (1) $u\in W_{loc}^{1,2}({\mathbb {R}}_{0}^{+};L^{2}(\varOmega ))\cap C_{w}({\mathbb {R}}_{0}^{+};X),$

• (2) $u(\cdot ,0)=u_{0}$ a.e. in $\varOmega ,$

• (3) For all $\varphi \in X,$ it holds that

  $$\begin{aligned} \begin{aligned}&\int _{\varOmega }\partial _{t}u(x,t)\varphi \,dx\\&\qquad +\int _{\varOmega \times \varOmega } \frac{|u(x,t)-u(y,t)|^{p(x,y)-2}(u(x,t)-u(y,t))\times (\varphi (x)-\varphi (y))}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\&\quad =\int _{\varOmega }f(x,t)\varphi \,dx \end{aligned} \end{aligned}$$

  for a.e. $t>0.$

We reduce problem (${\mathscr {P}}_{1}$) to the Cauchy problem of an abstract evolution equation. Define $\varPhi :{\mathscr {H}}\rightarrow [0,\infty ]$ by

$$\begin{aligned} \varPhi (u) = {\left\{ \begin{array}{ll} \displaystyle {\int _{\varOmega \times \varOmega }\frac{1}{p(x,y)}\frac{|u(x)-u(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy,}&{} \text {if }u\in X,\\ +\infty &{} \text {if }u\in {\mathscr {H}}{\setminus } X. \end{array}\right. } \end{aligned}$$

In order to prove the well-posedness for (${\mathscr {P}}_{1}$), we need check the lower semicontinuty of the functional $\varPhi$ in ${\mathscr {H}}=L^{2}(\varOmega ).$

3.1 The Fractional $p(\cdot )$-Laplacian Operator

Let $s\in (0,1)$ be a fractional parameter and consider the fractional $p(\cdot )$-Laplacian operator defined by

$$\begin{aligned} (-\varDelta )_{p(x)}^{s}u(x)={\mathscr {A}} u(x):=P.V.\int _{\varOmega }\frac{|u(x)-u(y)|^{p(x,y)-2}(u(x)-u(y))}{|x-y|^{N+sp(x,y)}}dy, \end{aligned}$$

(8)

where P.V. means the principal value.

This operator appears naturally associated with space ${\mathcal {W}}$. In the constant exponent case it is known as the fractional p-Laplacian, see [7, 14, 18, 22, 23, 27] and references therein. On the other hand, we emphasize that ${\mathscr {A}}$ is a version of the p-Laplacian operator in the case $p(x)=p.$

We will study some fundamental properties of the operator ${\mathscr {A}},$ which will be crucial for the development of this work. Namely, the operator ${\mathscr {A}}$ is monotone, coercive and hemicontinuous, therefore it is concluded that $(-\varDelta )_{p(\cdot )}^{s}$ is a maximal monotone operator in $L^{2}(\varOmega ).$ By Theorem 8 it follows that $X\hookrightarrow {\mathcal {W}}\hookrightarrow L^{q(\cdot )}(\varOmega ) \hookrightarrow L^{2}(\varOmega ).$ Therefore $X \hookrightarrow {\mathscr {H}}$ is a continuous and compact embedding. Identifying $L^{2}$ with its dual. Note also that we have $X\hookrightarrow {\mathscr {H}}\hookrightarrow X';$ these imbeddings are continuous and dense, we call $(X,{\mathscr {H}},X')$ a Gelfand–Hilbert Triple evolution. In order to define the fractional $p(\cdot )$-Laplacian operator for Dirichlet boundary conditions we consider the operator ${\mathscr {A}}: X\rightarrow X^*$ defined by

$$\begin{aligned} \langle {\mathscr {A}}(u),v\rangle _{X',X}=\int _{\varOmega }\int _{\varOmega }\frac{|u(x)-u(y)|^{p(x,y)-2}(u(x)-u(y))(v(x)-v(y))}{|x-y|^{N+sp(x,y)}}\,dx\,dy \end{aligned}$$

for all $u,v\in X.$

Remark 3

Notice that we can rewrite ${\mathscr {A}}$ in the following way:

$$\begin{aligned} \langle {\mathscr {A}}(u),v \rangle _{X,X'}=\int _{\varOmega }\int _{\varOmega }\Bigg (\frac{|u(x)-u(y)|}{|x-y|^{s}} \Bigg )^{p(x,y)-1}\frac{u(x)-u(y)}{|u(x)-u(y) |}\frac{v(x)-v(y)}{|x-y|^{s}}\frac{dx\,dy}{|x-y|^{N}}. \end{aligned}$$

3.2 Some Properties of Operator ${\mathscr {A}}$

Now we will prove the properties of the fractional $p(\cdot )$-Laplacian operator, that will be fundamental throughout the work.

Lemma 4

The operator ${\mathscr {A}}:X\rightarrow X'$ is monotone.

Proof

Remembering the Simon inequality [30], for any $a, b\in {\mathbb {R}}^{N},$ we have that

$$\begin{aligned} (|a|^{p-2}a-|b|^{p-2}b)(a-b)\geqslant {\left\{ \begin{array}{ll} (\frac{1}{2})^{p}|a-b|^{p}\quad \text { for }p\geqslant 2, \\ (p-1)\frac{|a-b|^{2}}{(|a|+|b|)^{2-p}} \quad \text { for } 1<p<2. \end{array}\right. } \end{aligned}$$

(9)

Let $u,v\in X.$ Assume $p(x,y)\geqslant p^{-}\geqslant 2,$ by (9) for each $(x,y)\in \varOmega \times \varOmega ,$ we have

$$\begin{aligned} \displaystyle&\langle {\mathscr {A}}u-{\mathscr {A}}v,u-v \rangle _{X',X}=\langle {\mathscr {A}}u,u-v \rangle _{X',X}-\langle {\mathscr {A}}v,u-v \rangle _{X',X}\\&\quad =\int _{\varOmega \times \varOmega } \frac{|u(x)-u(y)|^{p(x,y)-2}(u(x)-u(y))((u-v)(x)-(u-v)(y))}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\&\qquad -\int _{\varOmega \times \varOmega } \frac{|v(x)-v(y)|^{p(x,y)-2}(v(x)-v(y))((u-v)(x)-(u-v)(y))}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\&\quad \geqslant \int _{\varOmega \times \varOmega }\Big (\frac{1}{2}\Big )^{p(x,y)}\frac{|(u-v)(x)-(u-v)(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\&\quad \geqslant \Big (\frac{1}{2}\Big )^{p^{+}}\int _{\varOmega \times \varOmega }\frac{|(u-v)(x)-(u-v)(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\&\quad = \Big (\frac{1}{2}\Big )^{p^{+}} \rho _{s, p(\cdot ,\cdot )}(u-v)\geqslant 0. \end{aligned}$$

Now, let $u,v\in X$ and suppose that $1<p^{-}\leqslant p(x,y)\leqslant p^{+}<2,$ by (9) for each $(x,y)\in \varOmega \times \varOmega ,$ we have

$$\begin{aligned} \begin{aligned}&\langle {\mathscr {A}}u-{\mathscr {A}}v,u-v \rangle _{X',X}=\langle {\mathscr {A}}u,u-v \rangle _{X',X}-\langle {\mathscr {A}}v,u-v \rangle _{X',X}\\&\quad =\int _{\varOmega \times \varOmega } \frac{|u(x)-u(y)|^{p(x,y)-2}(u(x)-u(y))((u-v)(x)-(u-v)(y))}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\&\qquad -\int _{\varOmega \times \varOmega } \frac{|v(x)-v(y)|^{p(x,y)-2}(v(x)-v(y))((u-v)(x)-(u-v)(y))}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\&\quad \geqslant \int _{\varOmega \times \varOmega }\Big ((p(x,y)-1)\frac{|(u-v)(x)-(u-v)(y)|^{2}}{|x-y|^{N+sp(x,y)}(|(u-v)(x)|+|(u-v)(y)|)}\,dx\,dy\\&\quad \geqslant (p^{-}-1)\int _{\varOmega \times \varOmega }\frac{|(u-v)(x)-(u-v)(y)|^{2}}{|x-y|^{N+sp(x,y)}(|(u-v)(x)|+|(u-v)(y)|)^{2-p(x,y)}}\,dx\,dy\\&\quad \geqslant 0. \end{aligned} \end{aligned}$$

$\square$

Lemma 5

The operator ${\mathscr {A}}:X\rightarrow X'$ is coercive.

Proof

If $u\in X,$ by Proposition 1, we have

$$\begin{aligned} \begin{aligned} \langle {\mathscr {A}} u,u \rangle _{X',X}&=\int _{\varOmega \times \varOmega }\frac{|u(x)-u(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy \\&=\rho _{s,p(\cdot ,\cdot )}(u)\\&\geqslant {\left\{ \begin{array}{ll} \Vert u\Vert ^{p^{-}} &{} \quad \text {if }\Vert u\Vert >1,\\ \Vert u\Vert ^{p^{+}} &{}\quad \text {if }\Vert u\Vert <1,\\ \Vert u\Vert &{}\quad \text {if }\Vert u\Vert =1. \end{array}\right. } \end{aligned} \end{aligned}$$

Thus, since $p^{+}\geqslant p^{-}>1,$ we obtain

$$\begin{aligned} \lim _{\Vert u\Vert \rightarrow +\infty }\frac{\langle {\mathscr {A}}u,u \rangle _{X,X'}}{\Vert u\Vert }=+\infty . \end{aligned}$$

Therefore, ${\mathscr {A}}$ is coercive. $\square$

Lemma 6

The operator ${\mathscr {A}}:X\rightarrow X'$ is hemicontinuous.

Proof

We must prove that the map $t \mapsto \langle {\mathscr {A}}(u+tv),w \rangle _{X,X'}$ is continuous on [0, 1] for all $u,v,w\in X,$ i.e.,

$$\begin{aligned} \lim _{t\rightarrow 0}\langle {\mathscr {A}}(u+tv),w \rangle _{X,X'}=\langle {\mathscr {A}}(u),w \rangle _{X,X'} \end{aligned}$$

for all $w\in X.$

Fix $u,v,w\in X$ and $t\in (0,1).$ Remembering Remark 3, we have

$$\begin{aligned} \begin{aligned}&\langle {\mathscr {A}}(u+tv),w \rangle _{X,X'}\\&\quad =\int _{\varOmega \times \varOmega }\Bigg (\frac{|(u+tv)(x)-(u+tv)(y)|}{|x-y|^{s}} \Bigg )^{p(x,y)-1}\frac{((u+tv)(x)-(u+tv)(y))}{|(u+tv)(x)-(u+tv)(y) |}\\&\qquad \frac{w(x)-w(y)}{|x-y|^{s}}\frac{dy}{|x-y|^{N}}dx. \end{aligned} \end{aligned}$$

We define the function ${\mathfrak {G}}_{t}:\varOmega \times \varOmega \rightarrow {\mathbb {R}}$ by

$$\begin{aligned} {\mathfrak {G}}_{t}(x,y)= & {} \Bigg (\frac{|(u+tv)(x)-(u+tv)(y)|}{|x-y|^{s}} \Bigg )^{p(x,y)-1}\frac{((u+tv)(x)-(u+tv)(y))}{|(u+tv)(x)-(u+tv)(y) |}\\&\frac{w(x)-w(y)}{|x-y|^{s}}\frac{1}{|x-y|^{N}} \end{aligned}$$

and

$$\begin{aligned} {\mathfrak {G}}(x,y)=\Big (\frac{|u(x)-u(y)|}{|x-y|^{s}} \Big )^{p(x,y)-1}\frac{u(x)-u(y)}{|u(x)-u(y) |}\frac{w(x)-w(y)}{|x-y|^{s}}\frac{1}{|x-y|^{N}}. \end{aligned}$$

Then for a.e. $(x,y)\in \varOmega \times \varOmega ,$ we have

$$\begin{aligned} \lim _{t\rightarrow 0^+}{\mathfrak {G}}_{t}(x,y)={\mathfrak {G}}(x,y), \end{aligned}$$

besides, by Young’s inequality

$$\begin{aligned} \begin{aligned} |{\mathfrak {G}}_{t}(x,y)|&\leqslant \frac{p(x,y)-1}{p(x)}\frac{|u(x)-u(y)|^{p(x,y)}}{|x-y|^{sp(x,y)}}\frac{1}{|x-y|^{N}}\\&\quad +\frac{1}{p(x,y)}\frac{|w(x)-w(y)|^{p(x,y)}}{|x-y|^{sp(x,y)}}\frac{1}{|x-y|^{N}}\in L^{1}(\varOmega \times \varOmega ). \end{aligned} \end{aligned}$$

Thus by Lebesgue Dominated Convergence Theorem, we obtain that

$$\begin{aligned} \lim _{t\rightarrow 0^+}\langle {\mathscr {A}}(u+tv),w \rangle _{X,X'}=\langle {\mathscr {A}}(u),w \rangle _{X,X'}, \end{aligned}$$

which means that ${\mathscr {A}}:X\rightarrow X'$ is hemicontinuous. $\square$

Remark 4

Taking into consideration Lemmas 4, 5 and 6, the operator ${\mathscr {A}},$ with domain X,  is maximal monotone and $R({\mathscr {A}}):={\mathscr {A}}(X)=X'$(see [4, Theorem 1.3, p. 40]).

Remark 5

According to [5, Example 2.3.7, p. 26], the operator ${\mathscr {A}}_{{\mathscr {H}}},$ the realization of ${\mathscr {A}}$ at ${\mathscr {H}}=L^{2}(\varOmega )$ defined by

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {D}}({\mathscr {A}}_{{\mathscr {H}}}):=\{u\in X:{\mathscr {A}}\in {\mathscr {H}}\}, &{} \\ {\mathscr {A}}_{{\mathscr {H}}}(u)={\mathscr {A}}(u),\quad \text {if } u\in {\mathcal {D}}({\mathscr {A}}_{{\mathscr {H}}}), \end{array}\right. } \end{aligned}$$

is maximal monotone in ${\mathscr {H}}.$

Now we will write $(-\varDelta )_{p(\cdot )}^{s}(u)$ to mean ${\mathscr {A}}_{{\mathscr {H}}}(u)$ as we just defined above.

3.3 The Fractional $p(\cdot )$-Laplacian Operator is of Subdifferential Type

In this subsection we prove that ${\mathscr {A}}_{{\mathscr {H}}}$ is the subdifferential of a convex, proper and lower semi-continuous nonnegative functional.

Define the functional $\varPhi :{\mathscr {H}}\rightarrow {\mathbb {R}}\cup \{+\infty \}$ by

$$\begin{aligned} \varPhi (u) = {\left\{ \begin{array}{ll} \displaystyle {\int _{\varOmega \times \varOmega }\frac{1}{p(x,y)}\frac{|u(x)-u(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy,}&{} \text {if }u\in X,\\ +\infty &{} \text {if }u\in {\mathscr {H}}{\setminus } X. \end{array}\right. } \end{aligned}$$

and by ${\mathcal {D}}(\varPhi )=\{u\in {\mathscr {H}}:\varPhi (u)<+\infty \}$ the effective domain of $\varPhi .$

Now we will prove some lemmas that will be necessary to prove that the operator ${\mathscr {A}}_{{\mathscr {H}}}$ is of subdifferential type.

Lemma 7

The functional $\varPhi$ is convex and proper.

Proof

Remembering that $C_{0}^{\infty }(\varOmega )$ is dense in X,  we have that ${\mathscr {D}}(\varPhi )$ is nonempty.

Now we show that $\varPhi$ is convex in ${\mathscr {H}}.$ Let $u,v\in X$ and $\lambda \in [0,1].$ Since the function $\zeta ^{p}$ is convex, for $\lambda >0$ we have that

$$\begin{aligned} \varPhi (\lambda u +(1-\lambda )v)\leqslant \lambda \varPhi (u)+(1-\lambda )\varPhi (v). \end{aligned}$$

Indeed

$$\begin{aligned} \begin{aligned}&\varPhi (\lambda u+(1-\lambda )v)\\&\quad =\int _{\varOmega \times \varOmega }\frac{1}{p(x,y)}\frac{|(\lambda u+(1-\lambda )v)(x)-(\lambda u+(1-\lambda )v)(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy,\\&\quad \leqslant \int _{\varOmega \times \varOmega }\frac{1}{p(x,y)} \Bigg (\lambda \frac{|u(x)-u(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}+(1-\lambda )\frac{|v(x)-v(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\Bigg )\,dx\,dy\\&\quad \leqslant \lambda \int _{\varOmega \times \varOmega }\frac{1}{p(x,y)} \frac{|u(x)-u(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy{+}(1{-}\lambda )\int _{\varOmega \times \varOmega }\frac{|v(x)-v(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\&\quad \leqslant \lambda \varPhi (u)+(1-\lambda ) \varPhi (v). \end{aligned} \end{aligned}$$

and whenever either u or v in ${\mathscr {H}}{\setminus } X,$ the inequality holds, since $\varPhi (u)=+\infty$ or $\varPhi (u)=+\infty .$$\square$

Remark 6

To prove the following theorem we will use the following numerical inequality

$$\begin{aligned} p|r|^{p-2}r(s-r)\leqslant |s|^{p}-|r|^{p}\quad \forall s,r\in {\mathbb {R}}. \end{aligned}$$

Theorem 11

The operator $(-\varDelta _{p(x)})^{s}$ is the subdiferential $\partial \varPhi$ of $\varPhi$.

Proof

By Remark 5 and [4, Theorem 2.1, p. 54], we have that both operators, ${\mathscr {A}}_{{\mathscr {H}}}$ and $\partial \varPhi ,$ are maximal montone in ${\mathscr {H}}.$ This way it will be enough to prove $\partial \varPhi (u) \subset {\mathscr {A}}_{{\mathscr {H}}}(u).$

Let $u\in {\mathcal {D}}({\mathscr {A}}_{{\mathscr {H}}})=\{u\in X: {\mathscr {A}}(u)\in {\mathscr {H}}\}$ and $v={\mathscr {A}}_{{\mathscr {H}}}(u),$ then for all $w\in X,$

$$\begin{aligned} \begin{aligned}&\langle v,w-u \rangle _{X',X}=\langle {\mathscr {A}}_{{\mathscr {H}}}(u),w-u\rangle _{X',X}\\&\quad = \int _{\varOmega \times \varOmega }|u(x)-u(y)|^{p(x,y)-2}\frac{(u(x)-u(y))((w-u)(x)-(w-u)(y) )}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\&\quad \leqslant \int _{\varOmega \times \varOmega }\frac{1}{p(x,y)}\frac{|w(x)-w(y)|^{p(x,y)}-|u(x)-u(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\&\quad =\varPhi (w)-\varPhi (u). \end{aligned} \end{aligned}$$

(10)

If $w\in {\mathscr {H}}{\setminus } X$ we have $\varPhi (w)=+\infty$ and thus (10). Thus we have shown that ${\mathscr {A}}_{{\mathscr {H}}}(u)=v\in \partial \varPhi (u).$ We conclude that $\partial \varPhi (u)={\mathscr {A}}_{{\mathscr {H}}}(u).$$\square$

Remark 7

Note that $\overline{D(\partial \varPhi )}^{{\mathscr {H}}}=D(\varPhi )$ and $D(\varPhi )= X$ (see [4, Corollary 2.1, p. 55]), since the embedding $X\hookrightarrow {\mathscr {H}}$ is continuous and compact, we have $\overline{{\mathcal {D}}({\mathscr {A}}_{{\mathscr {H}}})}^{{\mathscr {H}}}={\mathscr {H}}.$

Lemma 8

The restriction ${\widehat{\varPhi }}$ of $\varPhi$ on X is of class $C^{1}(X,{\mathbb {R}}).$ Besides, the Fréchet derivative $d{\widehat{\varPhi }}$ of ${\widehat{\varPhi }}$ at $u\in X$ coincides with ${\mathscr {A}}u$ valuated at $u_{|_{\partial \varOmega }}=0$ in the sense of distribution, that is,

$$\begin{aligned} \langle \varPhi '(u),v\rangle _{X',X}=\langle {\mathscr {A}}(u),v\rangle _{X',X} \end{aligned}$$

for all $u,v \in X.$ Furthermore, ${\widehat{\varPhi }}$ is weakly lower semi-continuous in X.

Proof

Existence of the Gâteaux Derivative Let $u,v\in X.$ Fix $x\in \varOmega$ and $0<|r|<1.$ Then by the Mean Value Theorem, there exists $\vartheta \in [0,1]$ such that

$$\begin{aligned} \begin{aligned}&\Bigg | \frac{1}{p(x,y)}\frac{|(u+r v)(x)-(u+r v)(y)|^{p(x,y)}-|u(x){-}u(y)|^{p(x,y)}}{r|x-y|^{N+sp(x,y)}} \Bigg |\\&\quad =\frac{|(u{+}r\vartheta v)(x){-}(u{+}r\vartheta v)(y)|^{p(x,y)-2}((u{+}r\vartheta v)(x)-(u+r\vartheta v)(y))}{|x-y|^{N{+}sp(x,y)}}(v(x)-v(y)). \end{aligned} \end{aligned}$$

Note that

$$\begin{aligned} \begin{aligned} {\mathfrak {H}}(x):&=\frac{|(u{+}r\vartheta v)(x)-(u{+}r\vartheta v)(y)|^{p(x,y){-}2}((u{+}r\vartheta v)(x){-}(u{+}r\vartheta v)(y))}{|x{-}y|^{N+sp(x,y)}}(v(x)-v(y))\\&\quad \longrightarrow \frac{|u(x)-u(y)|^{p(x,y)-2}(u(x)-u(y))}{|x-y|^{N+sp(x,y)}}(v(x)-v(y)), \end{aligned} \end{aligned}$$

as $r\rightarrow 0.$ Note also that, by Young’s inequality, we have

$$\begin{aligned} \begin{aligned}&|{\mathfrak {H}}(x)|\leqslant \Bigg ( \frac{(u+r\vartheta v)(x)-(u+r\vartheta v)(y)|}{|x-y|^{s}}\Bigg )^{p(x,y)-1}\Bigg (\frac{v(x)-v(y)}{|x-y|^{s}} \Bigg )\frac{1}{|x-y|^{N}} \\&\quad \leqslant \frac{p(x,y)-1}{p(x,y)}\frac{(u+r\vartheta v)(x)-(u+r\vartheta v)(y)|^{p(x,y)}}{|x-y|^{sp(x,y)}}\frac{1}{|x-y|^{N}}\\&\qquad +\frac{1}{p(x,y)}\frac{|v(x)-v(y)|^{p(x,y)}}{|x-y|^{sp(x,y)}}\frac{1}{|x-y|^{N}}\in L^{1}(\varOmega \times \varOmega ). \end{aligned} \end{aligned}$$

It follows from the Lebesgue Dominated Convergence Theorem, that

$$\begin{aligned} \langle \varPhi '(u),v \rangle =\int _{\varOmega \times \varOmega } \frac{|u(x)-u(y)|^{p(x,y)-2}(u(x)-u(y))(v(x)-v(y))}{|x-y|^{N+sp(x,y)}}\,dx\,dy. \end{aligned}$$

Continuity of the Gâteaux Derivative Let $\{u_{n}\}_{n\in {\mathbb {N}}}\subset X,$$u\in X$ with $u_{n}\rightarrow u$ strongly in X as $n\rightarrow +\infty ,$ then by Theorem 8, without loss of generality, there exists a subsequence of $\{u_{n}\}_{n\in {\mathbb {N}}}$ still denoted by $\{u_{n}\}_{n\in {\mathbb {N}}}$ such that $u_{n}\rightarrow u$ a.e. in $\varOmega .$ Then the sequence

$$\begin{aligned} \Bigg \{\frac{|u_{n}(x)-u_{n}(y)|^{p(x,y)-2}(u_{n}(x))-u_{n}(y))}{|x-y|^{(N+sp(x,y))/p'(x,y)}} \Bigg \}_{n\in {\mathbb {N}}}, \end{aligned}$$

is bounded in $L^{p'(x,y)}(\varOmega \times \varOmega )$ and

$$\begin{aligned} {\mathscr {U}}_{n}(x,y):= & {} \frac{|u_{n}(x)-u_{n}(y)|^{p(x,y)-2}(u_{n}(x)-u_{n}(y))}{|x-y|^{(N+sp(x,y))/p'(x,y)}}\longrightarrow {\mathscr {U}}(x,y)\\:= & {} \frac{|u(x)-u(y)|^{p(x,y)-2}(u(x)-u(y))}{|x-y|^{(N+sp(x,y))/p'(x,y)}} \end{aligned}$$

a.e. in $\varOmega \times \varOmega .$ Thus, by the Brezis–Lieb Lemma (see [33]), we have

$$\begin{aligned} \begin{aligned}&\lim _{n\rightarrow +\infty }\int _{\varOmega \times \varOmega } |{\mathscr {U}}_{n}(x,y)-{\mathscr {U}}(x,y)|^{p'(x,y)}\,dx\,dy\\&\quad =\lim _{n\rightarrow +\infty }\int _{\varOmega \times \varOmega }\Bigg ( \Bigg | \frac{|u_{n}(x)-u_{n}(x)|^{p(x,y)-1}}{|x-y|^{(N+sp(x,y))/p'(x,y)}} \Bigg |^{p'(x,y)}\\&\qquad \qquad - \Bigg | \frac{|u(x)-u(x)|^{p(x,y)-1}}{|x-y|^{(N+sp(x,y))/p'(x,y)}} \Bigg |^{p'(x,y)} \Bigg )\,dx\,dy. \end{aligned} \end{aligned}$$

(11)

Now, since $u_{n} \rightarrow u$ strongly in X and by Proposition 1, we obtain

$$\begin{aligned}&\lim _{n\rightarrow +\infty }\int _{\varOmega \times \varOmega }\Bigg ( \Bigg | \frac{|u_{n}(x)-u_{n}(x)|^{p(x,y)-1}}{|x-y|^{(N+sp(x,y))/p'(x,y)}} \Bigg |^{p'(x,y)}- \Bigg | \frac{|u(x)-u(x)|^{p(x,y)-1}}{|x-y|^{(N+sp(x,y))/p'(x,y)}} \Bigg |^{p'(x,y)} \Bigg )\nonumber \\&\quad \,dx\,dy=0. \end{aligned}$$

(12)

From (11) and (12), we get

$$\begin{aligned} \lim _{n\rightarrow +\infty }\int _{\varOmega \times \varOmega } |{\mathscr {U}}_{n}(x,y)-{\mathscr {U}}(x,y)|^{p'(x,y)}\,dx\,dy=0. \end{aligned}$$

(13)

Combining (13) with the Hölder inequality, we have

$$\begin{aligned} \Vert \varPhi '(u_{n})-\varPhi '(u)\Vert _{X'}=\sup _{v\in X,\,\Vert v\Vert _{X}\leqslant 1}|\langle \varPhi '(u_{n})-\varPhi '(u),v \rangle |\longrightarrow 0 \end{aligned}$$

as $n\rightarrow +\infty .$ Hence, ${\widehat{\varPhi }}\in C^{1}(X,{\mathbb {R}}).$ By Lemma 7 we know that ${\widehat{\varPhi }}$ is a convex functional in X. Moreover, [36, Proposition 32.13] implies that ${\widehat{\varPhi }}$ is subdifferentiable and its subdifferential, denoted by $\partial {\widehat{\varPhi }},$ is given by $\partial {\widehat{\varPhi }}(v)=\{{\widehat{\varPhi }}'(v)\}$ for all $v\in X.$ Since ${\widehat{\varPhi }}$ is convex and of class $C^{1}(X,{\mathbb {R}}),$ then ${\widehat{\varPhi }}$ is weakly lower semi-continuous in X (see [6, Corollary 3.9]). $\square$

Lemma 9

Let $1<p^{-}<\infty .$ Then $\varPhi$ is lower semi-continuous in ${\mathscr {H}}.$

Proof

Let $\mu \in {\mathbb {R}}_{0}^{+}$ be fixed and set

$$\begin{aligned}{}[\varPhi \leqslant \mu ]=\{u\in {\mathscr {H}}: \varPhi (u)\leqslant \mu \}. \end{aligned}$$

Let $\{u_{n}\}_{n\in {\mathbb {N}}}$ be a sequence in $[\varPhi \leqslant \mu ]$ such that $u_{n}\rightarrow u$ strongly in ${\mathscr {H}}.$ Thus, $\varPhi (u_{n})\leqslant \mu$ for all $n\in {\mathbb {N}},$ it follows that

$$\begin{aligned} \frac{1}{p^{+}}\Vert u_{n}\Vert ^{p^{-}}\leqslant \frac{1}{p^{+}}\int _{\varOmega \times \varOmega }\frac{|u(x)-u(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy\leqslant \varPhi (u_{n})\leqslant \mu . \end{aligned}$$

Hence, $\Vert u_{n}\Vert \leqslant \zeta$ for some constant $\zeta$ independent of n. Since X is reflexive, by the $Eberlein-\check{S}mulian$ Theorem, up to a subsequence, still denoted by $\{u_{n}\}_{n\in {\mathbb {N}}}$ we have that $u_{n}\rightharpoonup u$ weakly in X. By Lemma 8, we have that ${\widehat{\varPhi }}$ is of class $C^{1}(X,{\mathbb {R}}),$ convex and weakly lower semi-continuous in X. Then, $\liminf \limits _{n\rightarrow +\infty }{\widehat{\varPhi }}(u_{n})\geqslant {\widehat{\varPhi }}(u)=\varPhi (u),$ combining this with the fact that ${\widehat{\varPhi }}(u_{n})=\varPhi (u_{n})\leqslant \mu ,$ it follows that $u\in [\varPhi \leqslant \mu ].$ Hence $[\varPhi \leqslant \mu ]$ is closed in ${\mathscr {H}},$ and so $\varPhi$ is lower semi-continuous in ${\mathscr {H}}.$$\square$

3.4 Proof of Theorem 1

Proof

The subdifferential operator $\partial \varPhi :{\mathscr {H}}\rightarrow {\mathscr {H}}$ of $\varPhi$ is given by

$$\begin{aligned} \partial \varPhi (u):=\{\varsigma \in {\mathscr {H}}:\varPhi (u)-\varPhi (v)\geqslant \langle \varsigma ,v-u \rangle \hbox { for all } v\in D(\varPhi ) \} \end{aligned}$$

for every $u\in D(\varPhi ),$ with $\langle \cdot ,\cdot \rangle _{{\mathscr {H}}}=\langle \cdot ,\cdot \rangle _ {L^{2}(\varOmega )}$ and the effective domain $D(\partial \varPhi )=\{u\in D(\varPhi ):\partial \varPhi (u)\ne \emptyset \}.$

Thus, the initial boundary value problem (${\mathscr {P}}_{1}$) is reduced in the following Cauchy abstract problem:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{d}{dt}u(t)+\partial \varPhi (u(t))= f(t) \quad \text { in }{\mathscr {H}} \hbox { for }t>0, \\ u(0)=u_{0}. \end{array}\right. } \end{aligned}$$

(14)

The well-posedness the abstract evolution Eq. (14) was well studied by Brezis [5, Chapter III]. Hence, by the results obtained in Sects. 3.2 and 3.3, Theorem 1 is proved. $\square$

Corollary 1

Let $p^{-}\geqslant 2.$ For all $u_{0}\in L^{2}(\varOmega )$(resp., $u\in X$) and all $f\in L_{loc}^{2}({\mathbb {R}}_{0}^{+};L^{2}(\varOmega ))$ the unique solution u of problem (${\mathscr {P}}_{1}$) is strongly continuous from ${\mathbb {R}}^{+}$ (resp., ${\mathbb {R}}^{+}$) into X.

Proof

Let $0<t_{0}<t<+\infty .$ Then $\varPhi (u(\cdot ,t))\rightarrow \varPhi (u(\cdot ,t_{0}))$ and $u(\cdot ,t)\rightharpoonup u(\cdot ,t_{0})$ weakly in $L^{2}(\varOmega )$ as $t\rightarrow t_{0}$ by Theorem 1. Since $p(x,y)\geqslant p^{-}\geqslant 2$ for $(x,y)\in \varOmega \times \varOmega ,$ remembering the numerical inequality:

$$\begin{aligned} \Bigg |\frac{z+w}{2} \Bigg |^{2}+\Bigg |\frac{z-w}{2} \Bigg |^{2} \leqslant \frac{1}{2}(|z|^{p}+|w|^{p}) \end{aligned}$$

for all $z,w\in {\mathbb {R}}.$

Then,

$$\begin{aligned} \begin{aligned}&\Bigg |\frac{u(x,t)-u(y,t)+u(x,t_{0})-u(y,t_{0})}{2} \Bigg |^{p(x,y)}\\&\qquad +\Bigg |\frac{u(x,t)-u(y,t)-u(x,t_{0})+u(y,t_{0})}{2} \Bigg |^{p(x,y)}\\&\quad \leqslant \frac{1}{2}\Big (|u(x,t)-u(y,t)|^{p(x,y)}+|u(x,t_{0})-u(y,t_{0})|^{p(x,y)}\Big ), \end{aligned} \end{aligned}$$

for a.e. $(x,y)\in \varOmega \times \varOmega .$

Thus,

$$\begin{aligned} \varPhi \Bigg (\frac{u(\cdot ,t)+u(\cdot ,t_{0})}{2}\Bigg )+\varPhi \Bigg (\frac{u(\cdot ,t)-u(\cdot ,t_{0})}{2}\Bigg )\leqslant \frac{1}{2}\Bigg (\varPhi (u(\cdot ,t))+\varPhi (u(\cdot ,t_{0}))\Bigg ). \end{aligned}$$

(15)

On the other hand, since $u(\cdot ,t)\rightharpoonup u(\cdot ,t)$ weakly in $L^{2}(\varOmega )$ and $\varPhi$ is weakly lower semi-continuous in ${\mathscr {H}},$ we get

$$\begin{aligned} \varPhi (u(\cdot ,t_{0}))\leqslant \liminf _{n\rightarrow +\infty } \varPhi \Bigg (\frac{u(\cdot ,t)+u(\cdot ,t_{0})}{2} \Bigg ). \end{aligned}$$

(16)

Combining (15), (16) and the assumption $\varPhi (u(\cdot ,t))\rightarrow \varPhi (u(\cdot ,t_{0}))$ as $t\rightarrow t_{0},$ we achieve

$$\begin{aligned} \limsup _{t\rightarrow t_{0}}\varPhi \Bigg (\frac{u(\cdot ,t)-u(\cdot ,t_{0})}{2}\Bigg )=0. \end{aligned}$$

Hence $u(\cdot ,t)\rightarrow u(\cdot ,t_{0})$ strongly in X as $t\rightarrow t_{0}.$ The other case is analogous. $\square$

In the following result, we have the existence of periodic solutions to the problem (${\mathscr {P}}_{1}$).

Remark 8

In the proof of the following corollary, we will use the Sobolev–Slobodetskii embedding $X\hookrightarrow L^{2}(\varOmega ),$ we require that $2< p^{*}(x),$ that is $p^{-}>\frac{2N}{N+2s},$ thus $p^{-}>\max \{1,\frac{2N}{N+2s}\}.$

Corollary 2

Let $p^{-}>\max \{1,\frac{2N}{N+2s}\}.$ Then for any $T>0$ and all $f\in L_{loc}^{2}({\mathbb {R}}_{0}^{+};L^{2}(\varOmega )),$ there exists a unique solution u of problem (${\mathscr {P}}_{1}$) such that $u(\cdot ,0)=u(\cdot ,T).$

Proof

Since $p^{-}>\frac{2N}{N+2s},$ by Proposition 8, we have

$$\begin{aligned} \begin{aligned} \varPhi (u)&\geqslant \frac{1}{p^{+}}\int _{\varOmega \times \varOmega } \frac{|u(x)-u(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\&\geqslant \frac{C}{p^{+}}\min \{\Vert u\Vert ^{p^{-}},\Vert u\Vert ^{p^{+}}\}, \end{aligned} \end{aligned}$$

for some $C>0.$ Since $p^{-}>1,$ we have

$$\begin{aligned} \lim _{\Vert u\Vert \rightarrow +\infty }\frac{\varPhi (u)}{\Vert u\Vert }=+\infty . \end{aligned}$$

Thus, $\varPhi$ is coercive. Then, by [5, Corollary 3.4], for any $T>0$ and $f\in L^{2}(0,T;{\mathscr {H}}),$ there exists a solution of (14) such that $u(0)=u(T).$ Furthermore, since $\varPhi$ is strictly convex, the periodic solution is unique. $\square$

4 Proof of Theorem 2 (The Submarkovian Property)

In this section we prove Theorem 2.

Proof

Let $s\in (0,1)$ and q(x),  p(x, y) be continuous variable exponents with $sp(x,y)<N$ for $(x,y)\in \varOmega \times \varOmega ,$ and $q(x)>p(x,x)$ for $x\in \varOmega .$ From Lemma 11 we have that $\partial \varPhi =(-\varDelta )_{p(\cdot )}^{s}.$ From Lemmas 7 and 8 the funcional $\varPhi$ is convex, proper and lower semi-continuous and ${\mathcal {D}}(\varPhi )={\mathscr {H}}.$ From [28] it follows that $-\partial \varPhi =-(-\varDelta )_{p(\cdot )}^{s}$ generates a (nonlinear) strongly continuous semigroup $S_{s,p(\cdot )}=\{S_{s,p(\cdot )}(t)\}_{t\geqslant 0}$ on ${\mathscr {H}}.$ Hence, for every $u_{0}\in {\mathscr {H}},$ the function $u(\cdot ,\cdot ):=S_{s,p(\cdot )}(\cdot )u_{0}(\cdot )$ satisfies:

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _{t}u+(-\varDelta )_{p(\cdot )}^{s}u= 0 \quad \text { for a.e. }t\in {\mathbb {R}}^{+}, \\ u(0,x)=u_{0} \quad x\in \varOmega ,\\ u(t,\cdot )\in {\mathcal {D}}((-\varDelta )_{p(\cdot )}^{s})\quad \text { for a.e. }t\in {\mathbb {R}}^{+},\\ u\in C([0,\infty );{\mathscr {H}})\cap W_{\text {loc}}^{1,\infty }((0,\infty );{\mathscr {H}}). \end{array}\right. } \end{aligned}$$

(17)

That is, u is the unique strong solution of (17).

Now, we prove that the order of the semigroup $S_{s,p(\cdot )}$ is preserved, that is,

$$\begin{aligned} S_{s,p(\cdot )}(t)u\leqslant S_{s,p(\cdot )}(t)v,\quad \hbox { for all }t\geqslant 0 \hbox { when }u,v\in {\mathscr {H}}, \quad u\leqslant v. \end{aligned}$$

(18)

From [10] [Theorem 3.6], to prove (18) is equivalent to prove $u\wedge v,\,u\vee v\in {\mathcal {D}}(\varPhi )$ for all $u,v\in {\mathcal {D}}(\varPhi )$ and

$$\begin{aligned} \varPhi (u\wedge v)+\varPhi (u\vee v)\leqslant \varPhi (u)+\varPhi (v). \end{aligned}$$

(19)

Let $A:=\{x\in \varOmega :u(x)\leqslant v(x)\}$ and $B:=\varOmega {\setminus } A=\{x\in \varOmega :u(x)>v(x)\}.$ Therefore

$$\begin{aligned} \begin{aligned}&\int _{\varOmega }\int _{\varOmega }\frac{|(u\wedge v)(x)-(u\wedge v)(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\&\quad =\int _{A}\int _{A}\frac{|u(x)-u(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy+\int _{A}\int _{B}\frac{|u(x)-u(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\&\qquad +\int _{B}\int _{A}\frac{|v(x)-u(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy+\int _{B}\int _{B}\frac{|v(x)-v(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy \end{aligned} \end{aligned}$$

(20)

and

$$\begin{aligned} \begin{aligned}&\int _{\varOmega }\int _{\varOmega }\frac{|(u\vee v)(x)-(u\vee v)(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\&\quad = \int _{A}\int _{A}\frac{|v(x)-v(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy+\int _{A}\int _{B}\frac{|v(x)-v(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\&\qquad +\int _{B}\int _{A}\frac{|u(x)-v(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy+\int _{B}\int _{B}\frac{|u(x)-u(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy. \end{aligned} \end{aligned}$$

(21)

Define the functional ${\mathfrak {F}}:{\mathbb {R}}^{2}\rightarrow [0,\infty )$ by ${\mathfrak {F}}(\xi ,\eta ):=|\xi -\eta |^{p(x,y)}.$ The functional ${\mathfrak {F}}$ satisfies the hypothesis of Lemma 3. Since $p^{-}>1,$ we have

$$\begin{aligned} \frac{\partial ^{2}{\mathfrak {F}}}{\partial \xi \partial \eta }=-p(x,y)(p(x,y)-1)|\xi -\eta |^{p(x,y)-2}(\text {sgn}(\xi -\eta ))^{2}\leqslant 0. \end{aligned}$$

Thus, Lemma 3$({\mathbb {F}}_{2})$ is satisfied, therefore on $A\times B$ and on $B\times A,$ we have that

$$\begin{aligned} |u(x)-v(y)|^{p(x,y)}+|v(x)-u(y)|^{p(x,y)}\leqslant |u(x)-u(y)|^{p(x,y)}+|v(x)-v(y)|^{p(x,y)}.\nonumber \\ \end{aligned}$$

(22)

By (20), (21) and (22) we get (19). Thus, the semigroup $S_{s,p(\cdot )}$ is order preserving.

Now, we show that the semigroup is non-expansive on $L^{\varpi (\cdot )}(\varOmega )$ for all $1\leqslant \varpi ^{-}\leqslant \varpi (x)<+\infty ,$ that is, $S_{s,p(\cdot )}$ maps $L^{\varpi (\cdot )}$ into $L^{\varpi (\cdot )}$ for all $t>0$ and

$$\begin{aligned} \Vert S_{s,p(\cdot )}(t)u-S_{s,p(\cdot )}(t)v\Vert \leqslant \Vert u-v\Vert _{L^{\varpi (\cdot )}(\varOmega )},\quad \text { for all }u,v\in L^{\varpi (\cdot )}(\varOmega ). \end{aligned}$$

(23)

From [10, Theorem 3.6], the inequality (23) is equivalent to

$$\begin{aligned} \varPhi (v+{\mathfrak {G}}_{\alpha }(u,v))+\varPhi (u-{\mathfrak {G}}_{\alpha }(u,v))\leqslant \varPhi (u)+\varPhi (v) \end{aligned}$$

(24)

for all $u,v\in L^{2}(\varOmega )$ and $\alpha >0$ where

$$\begin{aligned} {\mathfrak {G}}_{\alpha }(u,v):=\frac{1}{2}\Bigg \{ (u-v+\alpha )_{+}-(u-v-\alpha )_{-}\Bigg \}. \end{aligned}$$

If u or v do not belong to ${\mathscr {D}}(\varPhi ),$ then the inequality (24) is trivial. Then, we can assume that $u,v\in {\mathcal {D}}(\varPhi ).$ From [35, Lemma 2.6] it follows that ${\mathfrak {G}}_{\alpha }(u,v)\in {\mathcal {D}}(\varPhi )$ for every $\alpha >0.$ Therefore, $v+{\mathfrak {G}}_{\alpha }(u,v),\,u-{\mathfrak {G}}_{\alpha }(u,v).$ For $\alpha >0,$ we let $\lambda :=\chi _{\{u\ne v\}}\frac{{\mathfrak {G}}_{\alpha }(u,v)}{u-v}.$ Note that $\lambda \in [0,1].$ Furthermore, $u-{\mathfrak {G}}_{\alpha }(u,v)=\lambda v+(1-\lambda )u$ and $v+{\mathfrak {G}}_{\alpha }(u,v)=\lambda u+(1-\lambda )v.$ By the convexity of the functional $\varPhi ,$ we have

$$\begin{aligned} \begin{aligned}&\varPhi (v+{\mathfrak {G}}_{\alpha }(u,v))+\varPhi (u-{\mathfrak {G}}_{\alpha }(u,v))=\varPhi (\lambda u+(1-\lambda )v)+\varPhi (\lambda v+(1-\lambda )u)\\&\quad \leqslant \lambda \varPhi (u)+(1-\lambda )\varPhi (v)+\lambda \varPhi (v)+(1-\lambda )\varPhi (u)=\varPhi (u)+\varPhi (v), \end{aligned} \end{aligned}$$

and thus we have shown (24). Therefore, the semigroup $S_{s,p(\cdot )}$ is non-expansive on $L^{\varpi (\cdot )}(\varOmega )$ for every $1\leqslant \varpi ^{-}\leqslant \varpi (x)\leqslant +\infty .$

It has been shown that $S_{s,p(\cdot )}$ is a (nonlinear) submarkovian semigroup on $L^{2}(\varOmega ).$ Since $\varPhi$ is nonnegative, by [10, Theorem 2.4] it follows that $S_{s,p(\cdot )}$ can be extended to a strongly continuous, non-expansive semigroup on $L^{\varpi (x)}(\varOmega )$ for every $1\leqslant \varpi ^{-}\leqslant \varpi (x)<+\infty$ and to a non-expansive semigroup on $L^{\infty }(\varOmega ),$ and each of such semigroups is order preserving. Therefore, the Cauchy problem (${\mathscr {P}}_{1}$) with $f\equiv 0$ is well posed in $L^{\varpi (\cdot )}(\varOmega )$ for every $1\leqslant \varpi ^{-}\leqslant \varpi (x)<+\infty .$$\square$

5 Proof of Theorems 3 and 4 (Decay and Extinction Properties)

We study the decay and extinction properties of solutions to problem (${\mathscr {P}}_{1}$), with $f\equiv 0$ as $t\rightarrow +\infty .$ As far as we know this type of property is unknown both in the case of spaces with constant exponent and in the case of spaces with variable exponent.

Throughout this section we will assume that $p^{-}\geqslant \frac{2N}{N+2s}.$

Remark 9

If $q(x)=\overline{p}(x):=p(x,x),$ we denote ${\mathcal {W}}^{s,q(\cdot ),p(\cdot ,\cdot )}(\varOmega )$ and ${\mathcal {W}}_{0}^{s,q(\cdot ),p(\cdot ,\cdot )}(\varOmega )$ by ${\mathcal {W}}^{s,p(\cdot ,\cdot )}(\varOmega )$ and ${\mathcal {W}}_{0}^{s,p(\cdot ,\cdot )}(\varOmega )$ respectively (see [12]).

Analogously to the previous sections we obtain the same results in the space ${\mathcal {W}}_{0}^{s,p(\cdot ,\cdot )}(\varOmega )$ and we will use the notation ${\mathcal {V}}={\mathcal {W}}_{0}^{s,p(\cdot ,\cdot )}(\varOmega ).$

Proposition 4

(Comparision Principle) Suppose $p^{-}>1.$ Let $u_{1}$ be a solution for (${\mathscr {P}}_{1}$) in the ${\mathscr {H}}$-sense, that is, $u_{1}\in C([0,+\infty );{\mathscr {H}})\cap W_{loc}^{1,2}((0,+\infty );{\mathscr {H}}),$$u_{1}(t)\in {\mathcal {V}}$ for a.e. $t>0,$ and it holds that

$$\begin{aligned} \int _{\varOmega }\partial _{t}u_{1}(x,t)\varrho (x)\,dx+\langle \partial \varPhi (u),\varrho (x) \rangle \leqslant \int _{\varOmega }f(x,t)\varrho (x)\,dx \end{aligned}$$

for every non-negative function $\varrho \in {\mathcal {V}}$ and for a.e. $t>0.$ Let $u_{2}$ be a supersolution for (${\mathscr {P}}_{1}$) in the ${\mathscr {H}}$-sense, which is analogously defined to the above. If $u_{1}(x,0)\leqslant u_{2}(x,0)$ for a.e. $x\in \varOmega$ and $\gamma (u_{1}(\cdot ,t)-u_{2}(\cdot ,t))_{+}(x)=0$ for a.e. $x\in \partial \varOmega$ and $t>0,$ where $\gamma$ stands for the trace operator from $W^{s,p^{-}}(\varOmega )$ into $W^{s-\frac{1}{p^{-}},p^{-}}(\partial \varOmega ),$ then it follows that

$$\begin{aligned} u_{1}(x,t)\leqslant u_{2}(x,t)\quad \hbox { for a.e. }x\in \varOmega ,\quad t>0. \end{aligned}$$

Proof

Let $j:{\mathbb {R}} \longrightarrow {\mathbb {R}}$ be defined by

$$\begin{aligned} j(s)= {\left\{ \begin{array}{ll} \frac{s^{2}}{2}\quad \hbox { for }s\geqslant 0, \\ 0\quad \hbox { for } s<0. \end{array}\right. } \end{aligned}$$

Note that

$$\begin{aligned} \partial j(s)={\left\{ \begin{array}{ll} \{s\}\quad \hbox { for }s\geqslant 0, \\ \{0\}\quad \hbox { for } s<0. \end{array}\right. } \end{aligned}$$

Define a functional $\varphi :{\mathscr {H}}=L^{2}(\varOmega )\longrightarrow (-\infty ,+\infty ]$ by

$$\begin{aligned} \varphi (v):=\int _{\varOmega }j(v(x))\,dx\hbox { for }v\in {\mathscr {H}}. \end{aligned}$$

The functional $\varphi$ is proper and lower semi-continuous. Note also that,

$$\begin{aligned} \xi (x)\in {\mathscr {A}}(u)=\partial \varPhi (u)\Leftrightarrow \xi (x)\in \partial j(u(x))=(u(x))_{+}\hbox { for a.e. } x\in \varOmega , \end{aligned}$$

that is, $\partial \varphi (u)\in X$ is $u\in {\mathcal {V}}.$

Take $\omega :=u_{1}-u_{2}.$ Subtracting the inequality for the supersolution $u_{2}$ of the inequality for the subsolution $u_{1},$ we achieve

$$\begin{aligned} \begin{aligned}&\Bigg \langle \frac{d\omega }{dt}(t),\varrho (x)\Bigg \rangle +\int _{\varOmega \times \varOmega }\Bigg (\frac{|u_{1}(x)-u_{1}(y)|^{p(x,y)-2}(u_{1}(x)-u_{1}(y))}{|x-y|^{N+sp(x,y)}}\\&\qquad -\frac{|u_{2}(x)-u_{2}(y)|^{p(x,y)-2}(u_{2}(x)-u_{2}(y))}{|x-y|^{N+sp(x,y)}}\Bigg )(\varrho (x)-\varrho (y))\,dx\,dy\\&\quad \leqslant 0, \end{aligned} \end{aligned}$$

for every nonnegative $\varrho \in {\mathcal {V}}$ and for a.e. $t\geqslant 0.$

Now take $\varrho =\partial \varphi (\omega (t))=(\omega (\cdot ,t))_{+}.$ Indeed, since $\gamma (\omega (\cdot ,t))_{+}=0$ for a.e. $x\in \partial \varOmega$ and $t>0,$ we have that $\varrho \in {\mathcal {V}}.$ By chain rule for subdifferentials, we obtain

$$\begin{aligned} \begin{aligned}&\Bigg \langle \frac{d\omega }{dt}(t),\varrho (x)\Bigg \rangle \\&\quad \leqslant \int _{\varOmega \times \varOmega }\Bigg (\frac{|u_{1}(x)-u_{1}(y)|^{p(x,y)-2}(u_{1}(x)-u_{1}(y))}{|x-y|^{N+sp(x,y)}}\\&\qquad -\frac{|u_{2}(x)-u_{2}(y)|^{p(x,y)-2}(u_{2}(x)-u_{2}(y))}{|x-y|^{N+sp(x,y)}}\Bigg )(\omega (x,t)-\omega (y,t))_{+}\,dx\,dy\\&\quad =\int _{\varOmega \times \varOmega }\Bigg (\frac{|u_{1}(x)-u_{1}(y)|^{p(x,y)-2}(u_{1}(x)-u_{1}(y))}{|x-y|^{N+sp(x,y)}}\\&\qquad -\frac{|u_{2}(x)-u_{2}(y)|^{p(x,y)-2}(u_{2}(x)-u_{2}(y))}{|x-y|^{N+sp(x,y)}}\Bigg )\\&\qquad (\omega (x,t)-\omega (y,t))_{+}\times sgn(\omega (x,t)-\omega (y,t))\,dx\,dy\\&\quad \leqslant 0, \end{aligned} \end{aligned}$$

for a.e. $t>0,$ where $sgn(s)=0$ for $s\leqslant 0$ and $sgn(s)=1$ for $s>0.$ Integrating from 0 to t,  we have

$$\begin{aligned} \varphi (\omega (t))\leqslant \varphi (\omega (0))=0\quad \hbox { for all } t\geqslant 0, \end{aligned}$$

which implies $\omega (x,t)\leqslant 0$ for a.e. $x\in \varOmega$ and $t>0.$$\square$

In order to prove the Theorems 3 and 4 we will use two energy identities:

$$\begin{aligned}&\frac{1}{2}\frac{d}{dt}\Vert u(t)\Vert _{L^{2}(\varOmega )}^{2}+\int _{\varOmega \times \varOmega }\frac{|u(x)-u(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy=0, \end{aligned}$$

(25)

$$\begin{aligned}&\Bigg \Vert \frac{d}{dt}u(t)\Bigg \Vert _{L^{2}(\varOmega )}^{2}+\frac{d}{dt}\varPhi (u(t))=0 \end{aligned}$$

(26)

for a.e. $t\in (0,+\infty ).$ The first identity follows from the multiplication of (${\mathscr {P}}_{1}$) by u and integration over $\varOmega ,$ and the second one can be obtained multiplying (14) by du(t) / dt in $L^{2}(\varOmega )$ and using a chain rule for subdifferentials (see [5, Lemma 3.3]).

Lemma 10

(Upper Estimates) Assume $p^{-}\geqslant \frac{2N}{N+2s}.$ In case $p^{+}>2,$ there exists $C_{0}>0$ such that

$$\begin{aligned} \Vert u(t)\Vert _{L^{2}}\leqslant C_{0}(1+t)^{\frac{-1}{p^{+}-2}} \end{aligned}$$

for all $t\geqslant 0.$

In case $p^{+}<2,$ the solution vanishes at a finite time $t^{*}>0.$

Proof

From (25) and Proposition 2, we have

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}\Vert u(t)\Vert _{L^{2}(\varOmega )}+\sigma ^{-}(\Vert u(t)\Vert )\leqslant 0 \end{aligned}$$

(27)

for a.e. $t>0.$ By Sobolev embedding, there exits a constant $C_{p(\cdot ,\cdot ),2}>0,$ such that

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}\Vert u(t)\Vert _{L^{2}(\varOmega )}+\sigma ^{-}(C_{p(\cdot ,\cdot ),2}\Vert u(t)\Vert _{L^{2}(\varOmega )})\leqslant 0 \end{aligned}$$

(28)

for a.e. $t>0.$

Now, we will solve the Cauchy problem for the following ordinary differential equation:

$$\begin{aligned} \chi '(t)+2\sigma ^{-}\Big (C_{p(\cdot ,\cdot ),2}\chi (t)^{1/2} \Big )=0\hbox { for }t>0,\quad \chi (0)=\Vert u_{0}\Vert _{L^{2}}^{2}(\varOmega )>0. \end{aligned}$$

(29)

Then by Theorem 4,

$$\begin{aligned} \Vert u(t)\Vert \leqslant \chi (t) \hbox { for all } t\geqslant 0. \end{aligned}$$

(30)

Now we will analyze two cases:

(I) In case $\chi (0)=\Vert u_{0}\Vert _{L^{2}(\varOmega )}^{2}>C_{p(\cdot ,\cdot ),2},$ by 29, we have

$$\begin{aligned} \chi '(t)+\frac{2}{C_{p(\cdot ,\cdot ),2}^{p^{-}}}\chi ^{\frac{p^{-}}{2}}=0\,\hbox { for } t\in [0,t_{1}), \end{aligned}$$

(31)

with $t_{1}:=\sup \{\tau>0:\chi (t)>C_{p(\cdot ,\cdot ),2}^{2}\hbox { for all }t\in [0,\tau ]\}>0.$ Then it follows that $\sigma ^{-}\Big (C_{p(\cdot ,\cdot ),2}^{-1} \chi (t)^{1/2}\Big )=\frac{\chi (t)^{p^{-}/2}}{C_{p(\cdot ,\cdot ),2}^{p^{-}}}$ for $t\in [0,t_{1}),$ solving the Bernoulli equation, we have

$$\begin{aligned} \chi (t)= {\left\{ \begin{array}{ll} \Vert u_{0}\Vert _{L^{2}}^{2}\Bigg (1+\frac{p^{-}-2}{C_{p(\cdot ,\cdot ),2}^{p^{-}}}\Vert u_{0}\Vert _{L^{2}(\varOmega )}^{p^{-}-2}t \Bigg )^{\frac{-2}{p^{-}-2}} \quad \hbox { if }p^{-}\ne 2, \\ \Vert u_{0}\Vert _{L^{2}}^{2}\exp ^{\Big ( \frac{-2}{C_{p(\cdot ,\cdot ),2}^{2}}t\Big )}\quad \hbox { if }p^{-}=2 \end{array}\right. } \end{aligned}$$

(32)

for all $t\in [0,t_{1}).$ Therefore,

$$\begin{aligned} 0<t_{1}<+\infty \hbox { and } \chi (t_{1})=C_{p(\cdot ,\cdot ),2}^{2}. \end{aligned}$$

Then, we achieve that

$$\begin{aligned} \Vert u(t_{1})\Vert \leqslant C_{p(\cdot ,\cdot ),2}^{2}. \end{aligned}$$

(II) In case $\chi (0)=\Vert u_{0}\Vert _{2}^{2}\leqslant C_{p(\cdot ,\cdot ),2}^{2},$ since $\chi (t)$ is nonincreasing due to (31), we get

$$\begin{aligned} \chi '(t)+\frac{2}{C_{p(\cdot ,\cdot )}^{p^{+}}}\chi (t)^{\frac{p^{+}}{2}}=0\quad \hbox { for }t\geqslant 0. \end{aligned}$$

Then proceeding as in the previous case, for any $p^{+}\ne 2,$ we can obtain

$$\begin{aligned} \Vert u(t)\Vert _{L^{2}(\varOmega )}^{2}\leqslant \chi (t)=\left( \Vert u_{0}\Vert _{L^{2}(\varOmega )}^{2-p^{+}}+\frac{p^{+}-2}{C_{p(\cdot ,\cdot ),2}^{p^{+}}}t\right) _{+}^{\frac{-2}{2-p^{+}}} \end{aligned}$$

(33)

for all $t\geqslant 0.$

Combining the analysis done previously, we conclude that: in case $p^{+}<2,$ the solution u(t) converges to zero as $t\rightarrow +\infty$ such that

$$\begin{aligned} \Vert u(t)\Vert _{L^{2}(\varOmega )}\leqslant C_{0}(1+t)^{-\frac{1}{p^{+}-2}}\hbox { for all } t\geqslant 0, \end{aligned}$$

for some constant $C_{0}>0.$$\square$

The following result will be useful to obtain estimates of $\Vert u(t)\Vert _{L^{2}(\varOmega )}$, where we will introduce a modified Rayleigh quotient involving a Lyapunov energy.

Lemma 11

The function ${\mathscr {R}}:{\mathbb {R}}_{0}^{+}\rightarrow {\mathbb {R}}_{0}^{+}$ defined by

$$\begin{aligned} {\mathscr {R}}(t)=\frac{\varPhi (u(t))}{\Vert u(t)\Vert _{L^{2}(\varOmega )}^{p^{-}}} \end{aligned}$$

is nonincreasing on the interval $I:=\{t\geqslant 0:\Vert u(t)\Vert _{L^{2}(\varOmega )}>0\}.$

Proof

From (26), we have

$$\begin{aligned} \frac{d}{dt}{\mathscr {R}}(t)=\frac{-\Vert u'(t)\Vert _{L^{2}(\varOmega )}^{2}\Vert u'(t)\Vert _{L^{2}(\varOmega )}^{p^{-}}-\varPhi (u(t))\frac{d}{dt}\Vert u(t)\Vert _{L^{2}(\varOmega )}^{p^{-}}}{\Vert u'(t)\Vert _{L^{2}(\varOmega )}^{2p^{-}}} \end{aligned}$$

(34)

for all $t\in I.$ Note that

$$\begin{aligned} \frac{d}{dt}\Vert u(t)\Vert _{L^{2}(\varOmega )}^{p^{-}}=\frac{p^{-}}{2}\Vert u(t)\Vert _{L^{2}(\varOmega )}^{p^{-}-2}\frac{d}{dt}\Vert u(t)\Vert _{L^{2}(\varOmega )}^{2}. \end{aligned}$$

(35)

Substituting (35) in (34), we have

$$\begin{aligned} \frac{d}{dt}{\mathscr {R}}(t)=\frac{-\Vert u'(t)\Vert _{L^{2}(\varOmega )}^{2}\Vert u(t)\Vert _{L^{2}(\varOmega )}^{2}-\frac{p^{-}}{2}\varPhi (u(t))\frac{d}{dt}\Vert u(t)\Vert _{L^{2}(\varOmega )}^{2}}{\Vert u(t)\Vert _{L^{2}(\varOmega )}^{p^{-}+2}}. \end{aligned}$$

(36)

Note that from (25), we have

$$\begin{aligned} \begin{aligned} \varPhi (u(t))&=\int _{\varOmega \times \varOmega }\frac{1}{p(x,y)}\frac{|u(x)-u(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\&\leqslant \frac{1}{p^{-}}\int _{\varOmega \times \varOmega }\frac{|u(x)-u(y)|^{p(x,y)}}{|x-y|^{N+sp(x,y)}}\,dx\,dy\\&=-\frac{1}{2p^{-}}\frac{d}{dt}\Vert u(t)\Vert _{L^{2}(\varOmega )}^{2}. \end{aligned} \end{aligned}$$

Note also that by (25) $(d/dt)\Vert u(t)\Vert _{L^{2}(\varOmega )}^{2}\leqslant 0$ and by (36), we have

$$\begin{aligned} \begin{aligned} \frac{d}{dt}{\mathscr {R}}(t)&\leqslant \frac{-\Vert u'(t)\Vert _{L^{2}(\varOmega )}^{2}\Vert u(t)\Vert _{L^{2}(\varOmega )}^{2}+\Big (\frac{1}{2}\frac{d}{dt}\Vert u(t)\Vert _{L^{2}(\varOmega )}^{2}\Big )^{2}}{\Vert u(t)\Vert _{L^{2}(\varOmega )}^{p^{-}+2}}\\&=\frac{-\Vert u'(t)\Vert _{L^{2}(\varOmega )}^{2}\Vert u(t)\Vert _{L^{2}(\varOmega )}^{2}+\langle u'(t),u(t) \rangle _{L^{2}}^{2}}{\Vert u(t)\Vert _{L^{2}(\varOmega )}^{p^{-}+2}} \end{aligned} \end{aligned}$$

for all $t\in I.$

By Cauchy inequality, we get

$$\begin{aligned} \frac{d}{dt}{\mathscr {R}}(t)\leqslant 0 \end{aligned}$$

for all $t\in I.$

Therefore, the function ${\mathscr {R}}(\cdot )$ is nonincreasing on I. $\square$

5.1 Proof of Theorem 3

Proof

From Lemma 10 we have the upper estimate. Therefore, we will prove the lower estimate. Remembering (25) and since $p^{+}\geqslant p^{-}>2,$ we have

$$\begin{aligned} \frac{d}{dt}\Vert u(t)\Vert _{L^{2}(\varOmega )}^{2}+2p^{+}\varPhi (u(t))\geqslant 0, \end{aligned}$$

(37)

for all $t\geqslant 0.$ From Lemma 11, the function ${\mathscr {R}}$ is nonincreasing, thus, if $\Vert u(t)\Vert _{L^{2}(\varOmega )}>0,$ we have

$$\begin{aligned} \varPhi (u(t))={\mathscr {R}}(t)\Vert u(t)\Vert _{2}^{p^{-}}\leqslant {\mathscr {R}}(0)\Vert u(t)\Vert _{L^{2}(\varOmega )}^{p^{-}}. \end{aligned}$$

(38)

Hence by (37) and (38), we achieve

$$\begin{aligned} \frac{d}{dt}\Vert u(t)\Vert _{L^{2}(\varOmega )}^{2}+2p^{+}{\mathscr {R}}(0)\Vert u(t)\Vert _{L^{2}(\varOmega )}^{p^{-}}\geqslant 0\quad \hbox { for a.e. }t>0. \end{aligned}$$

Consider the following ODE:

$$\begin{aligned} \chi '(t)+2p^{+}{\mathscr {R}}(0) \chi (t)^{p^{-}/2}=0\hbox { for } t>0,\quad \chi (0)=\Vert u_{0}\Vert _{L^{2}(\varOmega )}^{2}>0, \end{aligned}$$

solving the ODE above and by Theorem 4, for $p^{-}>2,$ we get

$$\begin{aligned} \Vert u(t)\Vert _{L^{2}(\varOmega )}\geqslant \Bigg (\Vert u_{0}\Vert _{L^{2}(\varOmega )}^{2-p^{-}}+(p^{-}-2)p^{+}{\mathscr {R}}(0)t\Bigg )^{\frac{-1}{p^{-}-2}} \end{aligned}$$

for all $t\geqslant 0.$$\square$

Remark 10

In the Theorem 3 we can also estimate the ${\mathcal {V}}$-norm of u(t) from above and below since $\Vert u(t)\Vert \leqslant C_{p(\cdot ),2}\Vert u\Vert ,$ for all $u\in {\mathcal {V}}$ and the fact that

$$\begin{aligned} \sigma ^{-}(\Vert u\Vert )\leqslant p^{+}\varPhi (u(t))\leqslant p^{+}\frac{\varPhi (u_{0})}{\Vert u_{0}\Vert ^{p^{-}}_{L^{2}(\varOmega )}}\Vert u(t)\Vert _{L^{2}(\varOmega )}^{p^{-}}. \end{aligned}$$

For $p^{-}>2,$ we have that

$$\begin{aligned} {\mathfrak {C}}^{-1}(t+1)^{\frac{-1}{p^{-}-2}}\leqslant \Vert u(t)\Vert \hbox { and } \sigma ^{-}(\Vert u(t)\Vert )^{\frac{1}{p^{-}}}\leqslant {\mathfrak {C}}(t+1)^{\frac{-1}{p^{+}-2}} \end{aligned}$$

for some constant ${\mathfrak {C}}>0.$ Since $\sigma ^{-}(\tau )=\tau ^{p^{+}}$ for every $\tau \in [0,1],$ the decay rate will be equal to or faster than $(t+1)^{\frac{-p^{-}}{p^{+}(p^{+}-2)}}$ as $t\rightarrow +\infty$.

5.2 Proof of Theorem 4

Proof

First let us get the upper estimate for $\Vert u(t)\Vert _{L^{2}(\varOmega )}.$ Since $2>p^{+}\geqslant p(x)\geqslant p^{+}>1,$ by Lemma 11, we achieve

$$\begin{aligned} \frac{d}{dt}\Vert u(t)\Vert _{L^{2}(\varOmega )}^{2}+2p^{+}{\mathscr {R}}(0)\Vert u(t)\Vert _{L^{2}(\varOmega )}^{p^{-}}\geqslant 0, \end{aligned}$$

(39)

and note that

$$\begin{aligned} \frac{d}{dt}(\Vert u(t)\Vert _{L^{2}(\varOmega )}^{2-p^{-}})=\frac{2-p^{-}}{2}\Vert u(t)\Vert ^{p^{-}}\frac{d}{dt}\Vert u(t)\Vert _{L^{2}(\varOmega )}^{2}. \end{aligned}$$

(40)

From (39) and (40), we have

$$\begin{aligned} \frac{2}{2-p^{-}}\frac{d}{dt}\Vert u(t)\Vert _{L^{2}(\varOmega )}^{2-p^{-}}\geqslant -2p^{+}{\mathscr {R}}(0). \end{aligned}$$

(41)

Therefore, for $t>0$ arbitrary, we get

$$\begin{aligned} \Vert u(t)\Vert _{L^{2}(\varOmega )}\leqslant \Big (\Vert u_{0}\Vert _{L^{2}(\varOmega )}^{2-p^{-}}-2p^{+}(2-p^{-})t\Big )_{+}^{1/(2-p^{-})} \end{aligned}$$

(42)

for all $t\geqslant 0.$

Therefore the solution u vanishes at a finite time $t^{*}>0.$$\square$

6 Proof of Theorem 6 (Existence of Global Attractor for Problem (${\mathscr {P}}_{2}$))

We consider the existence of a global attractor for the following problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \partial _{t}u+(-\varDelta )_{p}^{s}u+{\mathbb {V}}(u)= 0 \quad \text { in }\varOmega , \\ u=0\quad \text { on } \partial \varOmega \times {\mathbb {R}}^{+},\\ u(0)=u_{0}\quad \text { on } \partial \varOmega . \end{array}\right. } \end{aligned}$$

where ${\mathbb {V}}:{\mathscr {H}} \rightarrow {\mathscr {H}}$ is a globally Lipschitz continuous operator. We denote as before ${\mathscr {H}}=L^{2}(\varOmega ).$

Remark 11

Here $(-\varDelta )_{p}^{s}$ is the fractional p-Laplacian defined by

$$\begin{aligned} (-\varDelta )_{p}^{s}u(x):=P.V.\int _{\varOmega }\frac{|u(x)-u(y)|^{p-2}(u(x)-u(y))}{|x-y|^{N+sp}}\,dy \end{aligned}$$

(43)

where P.V. means the principal value.

We define the operator ${\mathcal {A}}: W_{0}^{s,p}(\varOmega )\rightarrow (W_{0}^{s,p}(\varOmega ))'$ by

$$\begin{aligned} \langle {\mathcal {A}}(u),v \rangle =\int _{\varOmega \times \varOmega }\frac{ |u(x)-u(y)|^{p-2}(u(x)-u(y))(v(x)-v(y))}{|x-y|^{N+sp}}\,dx\,dy. \end{aligned}$$

This definition coincides with (43).

By virtue of the results obtained in the Sect. 3, we have that:

$({\mathcal {H}}_{1})$:

The fractional Sobolev–Slobodetskii space $W_{0}^{s,p}(\varOmega )$ is reflexive Banach space such that

$$\begin{aligned} W_{0}^{s,p}(\varOmega ) \hookrightarrow {\mathscr {H}} \hookrightarrow (W_{0}^{s,p}(\varOmega ) )', \end{aligned}$$

with continuous embeddings and with $(W_{0}^{s,p}(\varOmega ) )'$ denoting the topological dual of $W_{0}^{s,p}(\varOmega )$. Moreover note that $W_{0}^{s,p}(\varOmega )$ is dense in ${\mathscr {H}}$ and the continuous embedding $W_{0}^{s,p}(\varOmega ) \hookrightarrow {\mathscr {H}}$ is compact.

$({\mathcal {H}}_{2})$:

The operator ${\mathcal {A}}$ is a nonlinear, monotone, coercive and hemicontinuous operator such that ${\mathcal {A}}:W_{0}^{s,p}(\varOmega ) \rightarrow (W_{0}^{s,p}(\varOmega ))'$ (defined on all of $W_{0}^{s,p}(\varOmega )$). The operator ${\mathcal {A}}$ is odd, $(p-1)$-homogeneous, and

$$\begin{aligned} \langle {\mathcal {A}}(u),u\rangle =\Vert u\Vert ^{p},\,\Vert {\mathcal {A}}(u)\Vert _{(W_{0}^{s,p}(\varOmega ))'}\leqslant \Vert u\Vert ^{p-1}. \end{aligned}$$

for all $u\in W_{0}^{s,p}(\varOmega ).$

From [5, p. 26] and [4, theorem 1.3] it is known that the operator ${\mathcal {A}}_{H}:{\mathscr {H}} \rightarrow {\mathscr {H}}$ defined by

$$\begin{aligned} \displaystyle {{\mathcal {A}}_{{\mathscr {H}}}(u)={\mathcal {A}}(u) \hbox { for } u \in {\mathcal {D}}({\mathcal {A}}_{{\mathscr {H}}}):=\{ v \in W_{0}^{s,p}(\varOmega ); {\mathcal {A}}(v) \in {\mathscr {H}} \}} \end{aligned}$$

is a maximal monotone operator in ${\mathscr {H}}$.

Definition 4

A function $u \in C([0,\infty );{\mathscr {H}})$ is a strong solution to (${\mathscr {P}}_{2}$) if u is absolutely continuous in any compact subinterval of (0, T), $u(t) \in {\mathcal {D}}({\mathcal {A}}_{{\mathscr {H}}})$ for a.e. $t \in (0,T)$, and

$$\begin{aligned} \frac{du}{dt}(t)+{\mathcal {A}}(u(t))+{\mathbb {V}}(u(t))=0 \;\; \hbox {for a.e.} \;\; t \in (0,T). \end{aligned}$$

Definition 5

A function $u \in C([0,\infty );{\mathscr {H}})$ is called a weak solution to (${\mathscr {P}}_{2}$) if there is a sequence $\lbrace u_{n} \rbrace _{n\in {\mathbb {N}}}$ of strong solutions convergent to $u \in C([0,\infty );{\mathscr {H}})$.

From Lemmas 7, 11, 8, 9, Remark 11, [11, Proposition 8.6.1], and [5, Theorem 3.17, Remark 3.14] we have the following existence result.

Theorem 12

For all $u_{0}\in \overline{{\mathcal {D}}({\mathcal {A}}_{{\mathscr {H}}})}$ there exists a unique weak solution u of problem (${\mathscr {P}}_{2}$) such that $u(0)=u_{0}$. Furthermore, in the case $u_{0}\in {\mathcal {D}}({\mathcal {A}}_{{\mathscr {H}}}),$ the unique solution u is Lipschitz continuous, and therefore strong solution of (${\mathscr {P}}_{2}$).

Proposition 5

The $C^0$-semigroup $\lbrace T(t) \rbrace _{t\geqslant 0}$ of weak solutions of (${\mathscr {P}}_{2}$) is defined on $\overline{{\mathcal {D}}({\mathcal {A}}_{{\mathscr {H}}})}^{{\mathscr {H}}}$. Furthermore, whenever $u_0 \in {\mathcal {D}}({\mathcal {A}}_{{\mathscr {H}}})$, $T(\cdot )u_0=u(\cdot ,u_0)$ is a strong solution of (${\mathscr {P}}_{2}$) which is also Lispchitz continuous on $[0,\tau ]$ for each $\tau >0$.

Now we will prove the existence of a global attractor for $\lbrace T (t) \rbrace _{t\geqslant 0}$ associated with the problem (${\mathscr {P}}_{2}$).

6.1 Preliminary Results on the Existence of Global Attractor in ${\mathscr {H}}$

In this subsection we will show some results that will be necessary to prove our principal result.

By Remark 11 it follows that ${\mathcal {A}}$ holds $({\mathcal {H}}_{1}){-}({\mathcal {H}}_{2}).$ We denote by $\lbrace T(t) \rbrace _{t\geqslant 0}$ a $C^{0}$-semigroup of weak solutions $T(t)u_0=u(t,u_0)$ of (${\mathscr {P}}_{2}$) resulting from Proposition 5. Furthermore, the operator ${\mathcal {A}}$ satisfies the following two conditions:

$({\mathfrak {a}}_{1})$:

There are constants $w_1>0,$$c_1 \in {\mathbb {R}}$ and $p \geqslant 1,$ such that for all $u_0\in {\mathcal {D}}({\mathcal {A}}_{{\mathscr {H}}})$

$$\begin{aligned} \left\langle {\mathcal {A}}_{{\mathscr {H}}}(u(t,u_0)),u(t,u_0)\right\rangle _{(W_{0}^{s,p}(\varOmega ))',W_{0}^{s,p}(\varOmega )} \geqslant w_1\Vert u(t,u_0)\Vert ^{p}_{W_{0}^{s,p}(\varOmega )}+c_1 \end{aligned}$$

(44)

for a.e. $t>0.$

$({\mathfrak {a}}_{2})$:

There are constants $r>0,$$\theta >1$ and exists a function $C:[0,+\infty ) \times [0,+\infty ) \rightarrow {\mathbb {R}}$, locally bounded such that

$$\begin{aligned} \int _{0}^{\tau }\Vert {\mathcal {A}}(u(\tau ,u_0))\Vert ^{\theta }_{(W_{0}^{s,p}(\varOmega ))'}\,ds \leqslant C(\Vert u_0\Vert _{{\mathscr {H}}},\tau ). \end{aligned}$$

Proof

$({\mathfrak {a}}_{1})$ :

This follows from Remark 11.

$({\mathfrak {a}}_{2})$ :

From Proposition 5 the solution $u=u(\cdot ,u_{0})$ corresponding to $u_{0}\in {\mathcal {D}}({\mathcal {A}}_{{\mathscr {H}}})$ of problem (${\mathscr {P}}_{2}$) holds

$$\begin{aligned} \frac{du}{dt}(t)=-{\mathcal {A}}(u(t))-{\mathbb {V}}(u(t))\hbox { a.e. }(0,t_{0}). \end{aligned}$$

From Remark 11

$$\begin{aligned} \begin{aligned} \Bigg \Vert \frac{du}{dt}(t)\Bigg \Vert _{(W_{0}^{s,p}(\varOmega ))'}^{p'}&=\Vert -{\mathcal {A}}(u(t))-{\mathbb {V}}(u(t))\Vert _{(W_{0}^{s,p}(\varOmega ))'}^{p'}\\&\leqslant (\Vert A(u(t))\Vert _{(W_{0}^{s,p}(\varOmega ))'}+\Vert {\mathbb {V}}(u(t))\Vert _{(W_{0}^{s,p}(\varOmega ))'})^{p'} \\&\leqslant 2^{p'}(\Vert A(u(t))\Vert _{(W_{0}^{s,p}(\varOmega ))'} ^{p'}+\Vert {\mathbb {V}}(u(t))\Vert _{(W_{0}^{s,p}(\varOmega ))'}^{p'})\\&\leqslant \Vert u(t)\Vert ^{p}_{W_{0}^{s,p}(\varOmega )}+2^{p'}C^{p'}(L\Vert u(t)\Vert _{{\mathscr {H}}}+\Vert {\mathbb {V}}(0)\Vert _{{\mathscr {H}}})^{p'}\\&\leqslant 2^{p'}\Vert u(t)\Vert ^{p}_{W_{0}^{s,p}(\varOmega )}+2^{p'}C^{p'}(2^{p'}L^{p'}\Vert u(t)\Vert ^{p'}_{{\mathscr {H}}}+2^{p'}\Vert {\mathbb {V}}(0)\Vert ^{p'}_{{\mathcal {H}}})\\&\leqslant 2^{p'}\Vert u(t)\Vert ^{p}_{W_{0}^{s,p}(\varOmega )}+ 2^{2p'}C^{p'}L^{p'}\Vert u(t)\Vert ^{p'}_{{\mathscr {H}}}+2^{2p'}\Vert {\mathbb {V}}(0)\Vert ^{p'}_{{\mathscr {H}}}. \end{aligned} \end{aligned}$$

Taking ${\mathfrak {K}}:=\max \{2^{p'},2^{2p'}C^{p'}L^{p'},2^{p'}\Vert {\mathbb {V}}(0)\Vert ^{p'}_{{\mathscr {H}}}\},$ we get

$$\begin{aligned} \Bigg \Vert \frac{du}{dt}(t)\Bigg \Vert ^{p'}_{W_{0}^{s,p}(\varOmega )}\leqslant {\mathfrak {K}}(1+\Vert u(t)\Vert ^{p}_{W_{0}^{s,p}(\varOmega )}+\Vert u(t)\Vert _{{\mathscr {H}}}^{p'}). \end{aligned}$$

(45)

Note that

$$\begin{aligned} \Vert u\Vert _{L^{\infty }(0,T;{\mathscr {H}})}\leqslant {\mathfrak {C}}_{1}(\Vert u_{0}\Vert _{{\mathscr {H}}},T). \end{aligned}$$

Integrating (45) in $(0,t_{0}),$ we have

$$\begin{aligned} \begin{aligned}&\int _{0}^{t_{0}}\Big \Vert \frac{du}{dt}(t)\Big \Vert ^{p'}_{W_{0}^{s,p}(\varOmega )}\,dt\leqslant {\mathfrak {K}}t_{0}+{\mathfrak {K}}\int _{0}^{t_{0}}\Vert u(t)\Vert ^{p'}_{W_{0}^{s,p}(\varOmega )}\,dt+{\mathfrak {K}}\int _{0}^{t_{0}}\Vert u(t)\Vert ^{p'}_{{\mathscr {H}}}\,dt\\&\quad \leqslant {\mathfrak {K}}t_{0}+{\mathfrak {K}}{\mathfrak {C}}_{2}(\Vert u(t)\Vert _{{\mathscr {H}}},t_{0})+{\mathfrak {K}}(\mathfrak {C_{3}}(\Vert u_{0}\Vert _{{\mathscr {H}}},T))^{p'}:={\mathfrak {C}}_{4}\Vert u_{0}\Vert _{{\mathscr {H}}}. \end{aligned} \end{aligned}$$

$\square$

6.2 Proof of Theorem 5

Proof

Note that by Remark 11 and [4, Theorem 2.6] imply in particular that ${\mathcal {D}}({\mathcal {A}}_{{\mathscr {H}}})$ is dense in ${\mathscr {H}}.$ Finally due to the results obtained previously [see $({\mathfrak {a}}_{1})$ and $({\mathfrak {a}}_{2})$] and [11] [Theorem 8.6.1], we have proved the Theorem 5. $\square$

Remark 12

Let us consider in ${\mathscr {H}}=L^{2}(\varOmega )$ the following Cauchy Problem

The operator ${\mathscr {B}}:{\mathscr {H}}\rightarrow {\mathscr {H}}$ is a Lipschitz continuous operator with a Lipschitz constant C, i.e.,

$$\begin{aligned} \Vert {\mathscr {B}}(x)-{\mathscr {B}}(y)\Vert \leqslant C\Vert x-y\Vert \quad \forall x,y\in {\mathscr {H}}. \end{aligned}$$

Where the functional $\varPhi$ was defined in Sect. 3.

Finally, like consequence of the obtained results, we have the existence of solutions to nonhomogeneous problem (${\mathscr {EB}}$) (see, [3, Lemma 2.2]).

Theorem 13

Assume that $p^{-}>1$. For $u_{0}\in {\mathscr {H}}$ and $f\in L_{loc}^{2}({\mathbb {R}}_{0}^{+};{\mathscr {H}})$ with $u_{0}\in {\mathcal {D}}(\varPhi ),$ there exists a unique strong solution $u\in W_{loc}^{1,2}({\mathbb {R}}_{0}^{+};{\mathscr {H}})$ of problem (${\mathscr {EB}}$).