An improved approximation algorithm for the minimum 3-path partition problem

Abstract

Given a graph $G = (V, E)$, we seek for a collection of vertex disjoint paths each of order at most 3 that together cover all the vertices of V. The problem is called 3-path partition, and it has close relationships to the well-known path cover problem and the set cover problem. The general k-path partition problem for a constant $k \ge 3$ is NP-hard, and it admits a trivial k-approximation. When $k = 3$, the previous best approximation ratio is 1.5 due to Monnot and Toulouse (Oper Res Lett 35:677–684, 2007), based on two maximum matchings. In this paper we first show how to compute in polynomial time a 3-path partition with the least 1-paths, and then apply a greedy approach to merge three 2-paths into two 3-paths whenever possible. Through an amortized analysis, we prove that the proposed algorithm is a 13 / 9-approximation. We also show that the performance ratio 13 / 9 is tight for our algorithm.

1 Introduction

The order of a graph refers to the number of vertices in the graph. Given a simple graph $G = (V, E)$ (we only discuss simple graphs in this paper), we seek to find a minimum collection of vertex-disjoint paths of order at most k such that every vertex is on some path in the collection. The problem is called k-path partition (Yan et al. 1997; Monnot and Toulouse 2007), motivated by the data integrity of communication in wireless sensor networks and several other applications.

The k-path partition problem was first considered and shown to be NP-hard by Yan et al. (1997), for $k \ge 3$. (The 2-path partition problem is exactly the Maximum Matching problem, which is solvable in $O(m \sqrt{n} \log (n^2/m)/\log n)$-time (Goldberg and Karzanov 2004), where $n = |V|$ and $m = |E|$.) We point out the key phrase “at most k” in the definition of the k-path partition problem, that ensures the existence of a feasible solution for any given graph. On approximability, to the best of our knowledge, there is no existing approximation algorithm with proven performance for the general k-path partition problem, except the trivial k-approximation using all 1-paths and the 1.5-approximation for 3-path partition proposed by Monnot and Toulouse (2007), based on two maximum matchings.

In this paper, we pursue better approximation algorithms for the 3-path partition problem.

We first review some problems with the closest relationships to k-path partition, in particular the well-known Set Cover problem and the Path Cover problem.

Given a collection of subsets $\mathcal{C} = \{S_1, S_2, \ldots , S_m\}$ of a finite ground set $U = \{x_1, x_2, \ldots , x_n\}$, an element $x_i \in S_j$ is said to be covered by the subset $S_j$, and a set cover is a collection of subsets which together cover all the elements of the ground set U. In the Set Cover problem, the objective is to find a minimum cardinality set cover. Set Cover has numerous applications in various research areas, and it is one of the first proven NP-hard problems (Garey and Johnson 1979). Set Cover is also one of the most studied optimization problems for their approximability (Johnson 1974) and inapproximability (Raz and Safra 1997; Feige 1998; Vazirani 2001). The variant, in which the sizes of all given subsets in $\mathcal{C}$ are bounded from above by a constant $k \ge 3$, is referred to as k-Set Cover. It is APX-complete and can be approximated within 4 / 3 for $k = 3$ (Duh and Fürer 1997) and within $(H_k - {196}/{390})$ for $k \ge 4$ (Levin 2006), where $H_k = \sum _{i=1}^k 1/i$ is the k-th harmonic number.

We note that an approximation algorithm designed for k-Set Cover does not directly apply for k-path partition, by taking the vertex set V as the ground set and each path of order no more than k as a given subset. This is because in a feasible set cover, an element of the ground set U could be covered by multiple subsets, or equivalently the subsets of the set cover are allowed to overlap with each other; however, in k-path partition, every vertex is on exactly one path in a feasible solution, or equivalently the paths should be mutually disjoint.

One can actually enforce the mutually disjointness property in the Set Cover problem, by expanding the collection $\mathcal{C}$ to include all the proper subsets of each given subset $S_i$. Since in the instance graph of k-path partition not every subset of vertices on a path is traceable (i.e., has a hamiltonian path in the graph), such an expanding technique does not apply. In summary, k-path partition and k-Set Cover share some similarities, but none contains the other as a special case.

Given a simple graph $G = (V, E)$, if dropping the constraint on the order to find a minimum collection of vertex-disjoint paths to cover all the vertices, then we have the general path partition problem. path partition is also called the Path Cover (Franzblau and Raychaudhuri 2002) problem in the literature, which clearly contains the Hamiltonian Path problem (Garey and Johnson 1979) as a special case, and thus it is NP-hard, and it is outside APX unless P = NP. On the other hand, if one asks for a path partition in which every path has an order exactly k, then we have the so-called $P_k$-partitioning problem, which is also NP-complete for any fixed constant $k \ge 3$ (Garey and Johnson 1979; Lozin and Rautenbach 2003), even on planar bipartite graphs of maximum degree three (Monnot and Toulouse 2007), or on grid graphs with maximum degree three (van Bevern et al. 2014), or on chordal graphs (van Bevern et al. 2014).

Yan et al. proved that the k-path partition problem is NP-hard (Yan et al. 1997), for $k \ge 3$. On approximability, one easily sees a k-approximation by using all 1-paths and this is in fact the best approximation so far for k-path partition. For 3-path partition, Monnot and Toulouse (2007) proposed a 1.5-approximation. Their algorithm first computes a maximum matching $M^*$ in G, then computes another maximum matching between the edges of $M^*$ and the isolated vertices (that is, the vertices not incident with any edge of $M^*$), and outputs the achieved 3-path partition deduced from these two matchings and the remaining isolated vertices. Monnot and Toulouse (2007) showed that this is an O(nm)-time 1.5-approximation, where $n = |V|$ and $m = |E|$.

Our goal is to design an improved approximation algorithm with provable performance for 3-path partition, and we achieve an $O(n^3)$-time 13 / 9-approximation. Towards this goal, we first present an O(nm)-time algorithm to compute a 3-path partition with the least 1-paths inside, and then propose to merge three 2-paths into two 3-paths, whenever possible.

The rest of the paper is organized as follows. In the next section we present the algorithm to compute a 3-path partition with the least 1-paths. From the produced 3-path partition, we present the procedure to merge three 2-paths into two 3-paths, the entire approximation algorithm, and its performance analysis through an amortization scheme, in Sect. 3. We conclude the paper with some remarks in Sect. 4.

2 Computing a 3-path partition with the least 1-paths

In a 3-path partition, a 1-path contains only one vertex and in the sequel it is often referred to as a singleton of the 3-path partition.

In this section, we present an algorithm called Algorithm A for computing a 3-path partition with the least 1-paths, and show that Algorithm A runs in O(nm) time, where $n = |V|$ and $m = |E|$. We explain in the following the three steps in Algorithm A, the first two of which constitute exactly the 1.5-approximation by Monnot and Toulouse (2007). A high-level description of Algorithm A is depicted in Fig. 2.

2.1 Step 1: computing a maximum matching

Recall that a maximum matching of the graph $G = (V, E)$ can be computed in $O(m \sqrt{n} \log (n^2/m)/\log n)$-time (Goldberg and Karzanov 2004). In the first step, we apply an $O(m \sqrt{n} \log (n^2/m)/\log n)$-time algorithm to find a maximum matching in G, denoted as $M^*$; let $V_0$ denote the subset of vertices each is not incident with any edge of $M^*$. If $V_0 = \emptyset$, then we have achieved a 3-path partition without (and thus the least) 1-paths, in which a 2-path one-to-one corresponds to an edge of $M^*$. In the sequel we assume $V_0$ is non-empty. The following two lemmas are trivial due to the edge maximality of $M^*$.

Lemma 2.1

In the graph $G = (V, E)$, all the vertices of $V_0$ are pairwise non-adjacent to each other; for any edge $(u, v) \in M^*$, if u is adjacent to a vertex $x \in V_0$ and v is adjacent to a vertex $y \in V_0$, then $x = y$.

Lemma 2.2

In any 3-path partition for the graph $G = (V, E)$, the total number of 2-paths and 3-paths is at most $|M^*|$.

Proof

Clearly, if there were more than $|M^*|$ vertex disjoint 2-paths and 3-paths in the graph G, then selecting one edge per such path gives rise to a matching of size greater than $|M^*|$, contradicting the maximality of $M^*$. $\square$

2.2 Step 2: computing a second maximum matching

In the second step, we construct a bipartite graph $G' = (M^*, V_0, E')$ as follows:

• (1) each edge $e = (u, v) \in M^*$ is “shrunk” into a vertex denoted as e and the part containing all these vertices is denoted as $M^*$;

• (2) each vertex of $V_0$ remains as a vertex and the part containing these vertices is still denoted as $V_0$;

• (3) the vertices of $M^*$ ($V_0$, respectively) are non-adjacent to each other in $G'$;

• (4) a vertex $e = (u, v) \in M^*$ and a vertex $v_0 \in V_0$ are adjacent in $G'$ if and only if either $(u, v_0) \in E$ or $(v, v_0) \in E$ or both, and the set of edges in $G'$ is denoted as $E'$.

The graph $G'$ can be constructed in $O(n + m)$-time. Since $|M^*| + |V_0| \le n$, we then apply an $O(m \sqrt{n} \log (n^2/m)/\log n)$-time algorithm to find a maximum matching in $G'$, denoted as $M_1$. For each edge $((u, v), v_0) \in M_1$, we select the edge $(u, v_0)$ if $(u, v_0) \in E$ or otherwise the edge $(v, v_0)$ into the edge set $M_2$, which is a matching in the input graph $G = (V, E)$. The following lemma is trivial due to the construction of $M_1$ and $M_2$.

Lemma 2.3

In the graph $G = (V, E)$, the subgraph $\mathcal{Q} = (V, M^* \cup M_2)$ is a collection of vertex disjoint 1-paths, 2-paths, and 3-paths; moreover, the total number of 2-paths and 3-paths is $|M^*|$.

Let $E^* = M^* \cup M_2$ and $\mathcal{Q} = (V, E^*)$, which is the starting 3-path partition. Note that the above two steps constitute the 1.5-approximation by Monnot and Toulouse (2007), for which the ratio 1.5 is claimed tight. In other words, our Algorithm A builds on the 1.5-approximation and uses its output 3-path partition $\mathcal{Q}$ as the starting point. In the next subsection, we present the third step of Algorithm A to iteratively update both the edge set $E^*$ and the 3-path partition $\mathcal{Q}$, to maintain the total number of 2-paths and 3-paths in $\mathcal{Q}$ and to minimize the number of 1-paths. Therefore, the 3-path partition produced by Algorithm A is at least as good as the solution by the 1.5-approximation.

2.3 Step 3: reducing 1-paths to the minimum

Let $\mathcal{Q}_1$ ($\mathcal{Q}_2$, $\mathcal{Q}_3$, respectively) denote the collection of 1-paths (2-paths, 3-paths, respectively) in $\mathcal{Q}$. The third step is iterative, and in every iteration we try to eliminate one singleton while maintaining the total number of 2-paths and 3-paths to be $|M^*|$. That is, we have

$$\begin{aligned} {\textit{Invariant}} \hbox { The total number of }2\hbox {-paths and }3\hbox {-paths in the }3\hbox {-path partition }\mathcal{Q}\hbox { is }|M^*|. \end{aligned}$$

(1)

Clearly, if $\mathcal{Q}_1 = \emptyset$, then we are done with the third step. We thus assume $\mathcal{Q}_1$ is non-empty. For ease of presentation, a vertex that is an ending vertex of a 2-path or a 3-path in the current 3-path partition $\mathcal{Q}$ is called an endpoint; a vertex that is the middle vertex of a 3-path in $\mathcal{Q}$ is called a midpoint.

Consider a singleton $v_0$ (i.e., 1-path) in $\mathcal{Q}_1$. Due to Lemma 2.2, we conclude that $v_0$ cannot be adjacent to any endpoint of a 3-path, or any other singleton in the graph G. Therefore, if $v_0$ is adjacent to a vertex $w_1$ in G, then $w_1$ has to be either an endpoint of some 2-path (which is actually impossible due to the second maximum matching $M_1$ computed in the second step; nevertheless, it doesn’t matter as shown in the following) or the midpoint of some 3-path.

Case 1 In the case where $w_1$ is an endpoint of some 2-path, denoted as $P_1 \in \mathcal{Q}_2$, we add the edge $(v_0, w_1)$ to $E^*$ to merge the singleton $v_0$ and the 2-path $P_1$ into a 3-path. This process eliminates the singleton $v_0$ and maintains the total number of 2-paths and 3-paths to be $|M^*|$, and we say that the edge $v_0-w_1$saves the singleton $v_0$. We subsequently update the edge set $E^*$ and the 3-path partition $\mathcal{Q}$, and end the iteration.

Case 2 In the case where $w_1$ is the midpoint of some 3-path $u_1-w_1-v_1$, denoted as $P_1 \in \mathcal{Q}_3$. We claim that if the vertex $u_1$ is adjacent to a vertex $u_2$ in the graph G, then $u_2$ is not a singleton or an endpoint of a 3-path.

We prove this claim by contradiction. First, $u_2$ cannot be a singleton due to Lemma 2.2. Next, assume $u_2$ is an endpoint of a 3-path $u_2-w_2-v_2$. If $w_2 \ne w_1$, then we may remove the edges $(w_1, u_1)$ and $(w_2, u_2)$ while add the edge $(u_1, u_2)$ to $E^*$, resulting in $(|M^*| + 1)$ 2-paths and 3-paths in total and thus again contradicting Lemma 2.2. If $w_2 = w_1$, that is, $u_1 = v_2$ and $u_2 = v_1$, then we may remove the edges $(w_1, u_1)$ and $(w_1, v_1)$ while add the edges $(v_0, w_1)$ and $(u_1, v_1)$ to $E^*$, resulting in $(|M^*| + 1)$ 2-paths and 3-paths in total and thus again contradicting Lemma 2.2. This proves the claim.

It follows from the above claim that either $u_2$ is an endpoint of a 2-path or $u_2$ is the midpoint of another 3-path. (That is, $u_2$ now takes up the role of $w_1$.)

Subcase 2.1 In the case where $u_2$ is an endpoint of some 2-path $u_2-v_2$, denoted as $P_2 \in \mathcal{Q}_2$, we remove the edge $(w_1, u_1)$ while add the edges $(v_0, w_1)$ and $(u_1, u_2)$ to $E^*$, resulting in two new 3-paths $v_0-w_1-v_1$ and $u_1-u_2-v_2$ while destroying the two paths $P_1$ and $P_2$. This process eliminates the singleton $v_0$ and maintains the total number of 2-paths and 3-paths to be $|M^*|$, and we say that the alternating path¹$v_0-w_1-u_1-u_2$saves² the singleton $v_0$. We subsequently update the edge set $E^*$ and the 3-path partition $\mathcal{Q}$, and end the iteration.

Fig. 1

An alternating path $v_0-w_1-u_1-w_2-u_2-\cdots -w_i-u_i-u_{i+1}$ that saves the singleton $v_0$, where the first i paths are 3-paths and the last one is a 2-path. In the figure, solid edges are in the edge set $E^*$ and dashed edges are outside of $E^*$

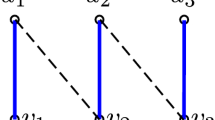
Subcase 2.2 In the general setting, in the graph G, $v_0$ is adjacent to the midpoint $w_1$ of a 3-path $P_1$, and for $j = 1, 2, \ldots , i-1$, one endpoint $u_j$ of $P_j$ is adjacent to the midpoint $w_{j+1}$ of another 3-path $P_{j+1}$, and lastly one endpoint $u_i$ of $P_i$ is adjacent to an endpoint $u_{i+1}$ of a 2-path $P_{i+1}$ (see Fig. 1 for an illustration). Then we may delete the edges $\{(w_j, u_j) \mid j = 1, 2, \ldots , i\}$ from $E^*$ while add the edges $(v_0, w_1)$, $\{(u_j, w_{j+1}) \mid j = 1, 2, \ldots , i-1\}$, and $(u_i, u_{i+1})$ to $E^*$ to obtain $(i+1)$ 3-paths from the collection of one singleton, i 3-paths, and one 2-path. This process eliminates the singleton $v_0$ and maintains in total $|M^*|$ 2-paths and 3-paths, and we say that the alternating path $v_0-w_1-u_1-w_2-u_2-\ldots -w_i-u_i-u_{i+1}$saves the singleton $v_0$. We remark that a length-$(2i + 1)$ alternating path connects a singleton to a 2-path, through a series of i 3-paths, where $i \ge 0$ (see Fig. 1). We subsequently update the edge set $E^*$ and the 3-path partition $\mathcal{Q}$, and end the iteration.

Lemma 2.4

In the graph $G = (V, E)$, given a 3-path partition $\mathcal{Q}$ containing $|M^*|$ 2-paths and 3-paths, finding a simple alternating path to save a singleton $v_0 \in \mathcal{Q}$, if exists, can be done in $O(n + m)$ time, where $n = |V|$ and $m = |E|$.

Proof

Let $E^*$ denote the edge set of the 3-path partition $\mathcal{Q}$. Firstly, if an alternating path is not simple, then a cycle that forms a subpath is also alternating and has an even length, and thus the cycle can be removed resulting in a shorter alternating path. Repeating this process if necessary, at the end we achieve a simple alternating path. Therefore, we can limit the search for a simple alternating path.

The edges on all possible alternating paths that save $v_0$ can be of the following four kinds:

• (1) all those edges incident at $v_0$, each oriented out of $v_0$;

• (2) all those edges of the 3-paths, each oriented from the midpoint to the endpoint;

• (3) all those edges each connecting an endpoint of a 3-path to the midpoint of another 3-path, oriented from the endpoint to the midpoint;

• (4) all those edges each connecting an endpoint of a 3-path to an endpoint of a 2-path, oriented out of the endpoint of the 3-path.

We thus construct a digraph on the vertex set V to contain all the above four kinds of oriented edges. It follows that by a BFS (breadth-first search) traversal starting from $v_0$ in the constructed digraph, if an endpoint of a 2-path can be reached then we achieve a simple alternating path saving $v_0$; otherwise, we conclude that no alternating path saving the singleton $v_0$ exists. Both construction of the digraph and the BFS traversal take $O(n + m)$ time. This proves the lemma. $\square$

Using Lemma 2.4, the third step of the algorithm is to iteratively find a simple alternating path to save a singleton of the current 3-path partition; it terminates when no alternating path is found. We still use $\mathcal{Q}$ to denote the 3-path partition at termination. A high-level description of our Algorithm A is provided in Fig. 2.

Fig. 2

A high-level description of Algorithm A for computing a 3-path partition $\mathcal{Q}$ in the graph $G = (V, E)$, where $\mathcal{Q}$ contains in total $|M^*|$ 2-paths and 3-paths and it contains the least singletons among all 3-path partitions

2.4 The main theorem

We prove in the next theorem that the 3-path partition $\mathcal{Q}$ produced by Algorithm A contains the least singletons among all 3-path partitions.

Theorem 1

Algorithm A is an O(nm)-time algorithm for computing a 3-path partition in the graph $G = (V, E)$ with the least 1-paths.

Proof

Recall that at the end of the second step, the achieved starting 3-path partition contains in total $|M^*|$ 2-paths and 3-paths. In the third step, in each iteration where an alternating path is found to save a singleton of the current 3-path partition, we swap the edges on the alternating path inside the edge set with the edges outside of the edge set to move from the current 3-path partition to another 3-path partition which contains still in total $|M^*|$ 2-paths and 3-paths (that is, an invariant) but one less singleton.

We prove the theorem by the minimal counterexample method. Assume that on the graph $G = (V, E)$ the 3-path partition $\mathcal{Q}$ produced by Algorithm A does not contain the least possible 1-paths, but on any subgraph of G induced by a proper subset of vertices Algorithm A is able to compute a 3-path partition with the least 1-paths.

Let $\mathcal{Q}_1$ ($\mathcal{Q}_2$, $\mathcal{Q}_3$, respectively) denote the collection of 1-paths (2-paths, 3-paths, respectively) in the 3-path partition $\mathcal{Q}$ produced by Algorithm A for $G = (V, E)$ (the associated edge set is $E^*$). Let $\mathcal{Q}^*$ be any 3-path partition in the graph $G = (V, E)$ with the least 1-paths, and let $\mathcal{Q}_1^*$ denote the collection of 1-paths in $\mathcal{Q}^*$. Our assumption is

$$\begin{aligned} |\mathcal{Q}_1| > |\mathcal{Q}_1^*| \ge 0. \end{aligned}$$

(2)

Since $G = (V, E)$ is the minimal (in terms of the number of vertices) graph for which Eq. (2) holds, $\mathcal{Q}_1$ and $\mathcal{Q}^*_1$ should not have any common element. Suppose to the contrary that a singleton $v_0 \in \mathcal{Q}_1 \cap \mathcal{Q}_1^*$. Then with respect to $\mathcal{Q}{ \setminus } \{v_0\}$, there is no alternating path to save any other singleton of $\mathcal{Q}$ in the induced subgraph $G[V { \setminus } \{v_0\}]$. That is, $\mathcal{Q} { \setminus } \{v_0\}$ would be the 3-path partition produced by Algorithm A for $G[V { \setminus } \{v_0\}]$, while $\mathcal{Q}^* { \setminus } \{v_0\}$ is a 3-path partition in $G[V { \setminus } \{v_0\}]$, contradicting the minimality of $G = (V, E)$. So we have

$$\begin{aligned} \mathcal{Q}_1 \cap \mathcal{Q}_1^* = \emptyset , \end{aligned}$$

(3)

i.e., a singleton $v_0 \in \mathcal{Q}_1$ is not a singleton in $\mathcal{Q}^*_1$, and consequently $v_0$ is on some path of $\mathcal{Q}^*_2 \cup \mathcal{Q}^*_3$.

Suppose the edge $(v_0, w_1)$ is on some path of $\mathcal{Q}^*_2 \cup \mathcal{Q}^*_3$. Let us examine where the vertex $w_1$ could be in the computed 3-path partition $\mathcal{Q}$. Recall that $\mathcal{Q}$ contains in total $|M^*|$ 2-paths and 3-paths. Due to Lemma 2.2, $w_1$ cannot be a singleton or an endpoint of a 3-path. From the non-existence of an alternating path at the end of the third step of Algorithm A, $w_1$ cannot be an endpoint a 2-path either. Therefore, $w_1$ has to be the midpoint of some 3-path $u_1-w_1-v_1$, denoted as $P_1 \in \mathcal{Q}$. (We refer the reader to Fig. 1 for an illustration, taking that the solid edges are in $\mathcal{Q}$ while the dashed edges are in $\mathcal{Q}^*$.)

Now we examine where the endpoints $u_1$ and $v_1$ of the path $P_1$ could be in $\mathcal{Q}^*$. Apparently not both of them are adjacent to $w_1$ in $\mathcal{Q}^*$, or otherwise the degree of $w_1$ in $\mathcal{Q}^*$ would be at least three. Assume without loss of generality $u_1$ is not adjacent to $w_1$ in $\mathcal{Q}^*$. If $u_1$ is a singleton in $\mathcal{Q}^*$, then we may add the edge $(u_1, w_1)$ to $\mathcal{Q}^*$ and remove the edge $(v_0, w_1)$ from $\mathcal{Q}^*$ to obtain another 3-path partition ${\mathcal{Q}^*}'$ in which $u_1$ is no longer a singleton but $v_0$ becomes a singleton. That is, ${\mathcal{Q}^*}'$ is also an optimal solution and shares a singleton $v_0$ with $\mathcal{Q}$, contradicting Eq. (3). This proves that $u_1$ is not a singleton in $\mathcal{Q}^*$ and consequently, exactly the same as $v_0$, it is on some path of $\mathcal{Q}^*_2 \cup \mathcal{Q}^*_3$. (Again, we refer the reader to Fig. 1 for an illustration.)

Suppose the edge $(u_1, w_2)$ is on some path of $\mathcal{Q}^*_2 \cup \mathcal{Q}^*_3$. We next examine where the vertex $w_2$ could be in the computed 3-path partition $\mathcal{Q}$. Due to Lemma 2.2, $w_2$ cannot be a singleton or an endpoint of a new 3-path (other than $P_1$). From the non-existence of an alternating path at the end of the third step, $w_2$ cannot be an endpoint a 2-path either. Therefore, $w_2$ either collides into $v_1$ or it has to be the midpoint of some new 3-path (other than $P_1$). If $w_2 = v_1$, then we may remove the edges $(u_1, w_1)$ and $(w_1, v_1)$ from $E^*$ and add the edges $(v_0, w_1)$ and $(u_1, v_1)$ to $E^*$ to obtain another 3-path partition that contains $(|M^*| + 1)$ 2-paths and 3-paths, contradicting Lemma 2.2. It follows that $w_2$ has to be the midpoint of some new 3-path $u_2-w_2-v_2$, denoted as $P_2 \in \mathcal{Q}$. (Again, we refer the reader to Fig. 1 for an illustration.)

Now we recursively examine where the endpoints $u_2$ and $v_2$ of the path $P_2$ could be in $\mathcal{Q}^*$. Apparently not both of them are adjacent to $w_2$ in $\mathcal{Q}^*$, or otherwise the degree of $w_2$ in $\mathcal{Q}^*$ would be at least three. Assume without loss of generality $u_2$ is not adjacent to $w_2$ in $\mathcal{Q}^*$. If $u_2$ is a singleton in $\mathcal{Q}^*$, then we may use the alternating path $v_0-w_1-u_1-w_2-u_2$ to obtain another optimal 3-path partition ${\mathcal{Q}^*}'$ that violates Eq. (3). This proves that $u_2$ is not a singleton in $\mathcal{Q}^*$ and consequently, exactly the same as $v_0$ and $u_1$, it is on some path of $\mathcal{Q}^*_2 \cup \mathcal{Q}^*_3$.

Suppose the edge $(u_2, w_3)$ is on some path of $\mathcal{Q}^*_2 \cup \mathcal{Q}^*_3$. We may repeat the above argument for $w_2$ to prove that $w_3$ has to be the midpoint of some new 3-path $u_3-w_3-v_3$, denoted as $P_3 \in \mathcal{Q}$, resulting in the same configuration as shown in Fig. 1. From the path $P_3$, repeating the same argument we will discover a new distinct path $P_4 \in \mathcal{Q}$. Repeatedly, we will discover an infinitely many distinct 3-paths in $\mathcal{Q}$, contradicting to the fact that $G = (V, E)$ is finite. Such a contradiction proves that the 3-path partition $\mathcal{Q}$ produced by Algorithm A has the same number of, and thus the least, singletons as $\mathcal{Q}^*$.

For the running time, since in each iteration of the third step we may “glue” all singletons as one for finding an alternating path. If no alternating path is found, then the algorithm terminates; otherwise one can easily check which singletons are the root of the alternating path and pick to save one of them, and the iteration ends. It follows that there could be O(n) iterations and each iteration needs $O(n + m)$ time, and thus the total running time for the third step is $O(n^2 + nm)$. Since the first two steps take $O(m \sqrt{n} \log (n^2/m)/\log n)$ time, the overall running time of Algorithm A is in O(nm). This finishes the proof of the theorem. $\square$

3 An $O(n^3)$-time 13 / 9-approximation algorithm

Our approximation algorithm for the 3-path partition problem consists of two phases. The first phase is Algorithm A, presented in the last section, that computes a 3-path partition $\mathcal{Q}$ with the least 1-paths for the input graph $G = (V, E)$. Algorithm A runs in O(nm) time, where $n = |V|$ and $m = |E|$.

In the second phase, the algorithm greedily merges three 2-paths in $\mathcal{Q}$ into two 3-paths, whenever possible (see the only configuration for such three 2-paths illustrated in Fig. 3). That is, the algorithm checks for a collection of three 2-paths, say for example $u_1-v_1$, $u_2-v_2$, and $u_3-v_3$. If there are two edges of E that connect them into a path, for example the edges $(u_1, v_2)$ and $(u_2, v_3)$, then this resulting 6-path is broken down into two 3-paths by removing the middle edge. In the above example, the middle edge is $(u_2, v_2)$ and the two resulting 3-paths are $v_1-u_1-v_2$ and $u_2-v_3-u_3$ (see Fig. 3).

Fig. 3

The only configuration for three 2-paths that can be merged into two 3-paths, where solid edges are in $\mathcal{Q}$ and dashed edges are in the graph G outside of $\mathcal{Q}$

Denote our entire approximation algorithm as Approx, of which a high-level description is depicted in Fig. 4. Since there are O(n) 2-paths and each collection of three 2-paths is examined at most once, the second phase takes $O(n^3)$ time and thus the total running time of Approx is in $O(n^3)$, which is slightly worse than the running time O(nm) of the previous 1.5-approximation by Monnot and Toulouse (2007). In the next theorem, we prove that Approx is a 13 / 9-approximation algorithm for the 3-path partition problem.

Fig. 4

A high-level description of Approx for computing a 3-path partition

Theorem 2

The algorithm Approx is an $O(n^3)$-time 13 / 9-approximation for the 3-path partition problem.

Proof

Given a graph $G = (V, E)$ with order n, we have shown that the total running time of Approx is in $O(n^3)$.

Let $\mathcal{Q}_1$ ($\mathcal{Q}_2$, $\mathcal{Q}_3$, respectively) denote the collection of 1-paths (2-paths, 3-paths, respectively) in the 3-path partition $\mathcal{Q}$ computed by the algorithm Approx. Let $\mathcal{Q}^*$ be an optimal 3-path partition, i.e., with the minimum total number of paths, and let $\mathcal{Q}_1^*$ ($\mathcal{Q}_2^*$, $\mathcal{Q}_3^*$, respectively) denote the collection of 1-paths (2-paths, 3-paths, respectively) in $\mathcal{Q}^*$. Since $\mathcal{Q}$ contains the least 1-paths (the second phase of Approx does not touch those 1-paths in $\mathcal{Q}_1$) among all 3-path partitions, we have

$$\begin{aligned} |\mathcal{Q}_1| \le |\mathcal{Q}_1^*|. \end{aligned}$$

(4)

Clearly, since both $\mathcal{Q}$ and $\mathcal{Q}^*$ are 3-path partitions, we have

$$\begin{aligned} |\mathcal{Q}_1| + 2 |\mathcal{Q}_2| + 3 |\mathcal{Q}_3| = n = |\mathcal{Q}_1^*| + 2 |\mathcal{Q}^*_2| + 3 |\mathcal{Q}^*_3|. \end{aligned}$$

(5)

We next estimate an upper bound on the cardinality of $\mathcal{Q}_2$ through an amortized analysis. To this purpose, each 2-path of $\mathcal{Q}_2$ (or equivalently, each edge on the 2-path of $\mathcal{Q}_2$) has 1 token to be distributed to the paths of $\mathcal{Q}^*$. We denote the set of the edges on the paths of $\mathcal{Q}_2$ as $E(\mathcal{Q}_2)$, and denote the set of the edges on the paths of $\mathcal{Q}^*_2 \cup \mathcal{Q}^*_3$ as $E(\mathcal{Q}^*)$. In the following we limit our discussion on the edge multi-set $E(\mathcal{Q}_2) \cup E(\mathcal{Q}^*)$. This way, only the midpoint of a 3-path of $\mathcal{Q}^*_3$ may have degree 3, that is, incident with three edges of $E(\mathcal{Q}_2) \cup E(\mathcal{Q}^*)$, while all the other vertices have degree at most 2 since each is incident with at most one edge of $E(\mathcal{Q}_2)$ and at most one edge of $E(\mathcal{Q}^*)$.

For each path $u-v \in \mathcal{Q}_2$, at most one of its two endpoints u and v can be a singleton in $\mathcal{Q}^*$, due to the minimality of $\mathcal{Q}^*$. If $u \in \mathcal{Q}^*_1$, then the whole 1 token of the path $u-v$ is distributed to u (see for an illustration in Fig. 5). On the other hand, any singleton of $\mathcal{Q}^*_1$ that is not an endpoint of a 2-path of $\mathcal{Q}_2$ receives no token. We conclude the following claim.

Claim 1

Every path of $\mathcal{Q}^*_1$ receives at most 1 token.

Fig. 5

A singleton $u \in \mathcal{Q}^*_1$ is an endpoint of the 2-path $u-v \in \mathcal{Q}_2$; u receives the whole 1 token from the 2-path $u-v$. In the figure, solid edges are in $E(\mathcal{Q}_2)$ and dashed edges are in $E(\mathcal{Q}^*)$, and the dotted arrow points where the token is distributed

We assume next that both u and v are incident with an edge of $E(\mathcal{Q}^*)$ (i.e., none of them is a singleton in $\mathcal{Q}^*_1$).

If one of them, say v, is on a 2-path $v-w \in \mathcal{Q}^*_2$, then the whole 1 token of the path $u-v$ is distributed to the 2-path $v-w \in \mathcal{Q}^*_2$ (see for an illustration in Fig. 6). We note that w could collide into u, that is, the 2-path $u-v \in \mathcal{Q}_2 \cap \mathcal{Q}^*_2$. But if w does not collide into u (that is, $w \ne u$) and u is another 2-path $u-x \in \mathcal{Q}^*_2$, then the 2-path $u-x$ receives no token from the path $u-v$. The choice of which one of the two vertices u and v comes first does not matter. Therefore, the 2-path $v-w \in \mathcal{Q}^*_2$ could receive another 1 token through w, from the 2-path of $\mathcal{Q}_2$ incident at w. We conclude the following claim.

Claim 2

Every path of $\mathcal{Q}^*_2$ receives at most 2 tokens.

Fig. 6

A 2-path $v-w \in \mathcal{Q}^*_2$ is adjacent to the 2-path $u-v \in \mathcal{Q}_2$; $v-w$ receives the whole 1 token from the 2-path $u-v$. In the figure, solid edges are in $E(\mathcal{Q}_2)$ and dashed edges are in $E(\mathcal{Q}^*)$, and the dotted arrow points where the token is distributed. The vertex u is incident to one or two edges of $E(\mathcal{Q}^*)$

In the other case, both vertices u and v are on some 3-paths of $\mathcal{Q}^*_3$, and we assume without loss of generality that u is on the 3-path $u_1-u_2-u_3$, denoted as $P_u$, and v is on the 3-path $v_1-v_2-v_3$, denoted as $P_v$, respectively. We remark that u can be either of $u_1, u_2, u_3$ and v can be either of $v_1, v_2, v_3$, and $P_u$ and $P_v$ could even collide into each other.

If $P_u$ and $P_v$ collide into each other, then the whole 1 token of the path $u-v$ is distributed to the 3-path $P_u \in \mathcal{Q}^*_3$.

Fig. 7

A 3-path $v_1-v_2-v_3 \in \mathcal{Q}^*_3$, denoted as $P_v$, is adjacent to the 2-path $u-v \in \mathcal{Q}_2$. The figure illustrates the scenario where $v_2 = v$, and both $v_1$ and $v_3$ are on some 2-path(s) of $\mathcal{Q}_2$ too. $P_v$ receives a fraction of 1 / 3 token from the 2-path $u-v$; the other 2 / 3 tokens from the 2-path $u-v$ are distributed to the 3-path $P_u \in \mathcal{Q}^*_3$. In the figure, solid edges are in $E(\mathcal{Q}_2)$ and dashed edges are in $E(\mathcal{Q}^*)$, and the dotted arrow points where the token is distributed. At most one of the vertices $u_2$ and $u_3$ can be on a 2-path of $\mathcal{Q}_2$

If $P_u$ and $P_v$ are distinct, then the six vertices $u_1, u_2, u_3$ and $v_1, v_2, v_3$ are distinct to each other. We claim that at least one of these six vertices is not on any 2-path of $\mathcal{Q}_2$. To prove this claim, we assume to the contrary that all these six vertices are on some 2-paths of $\mathcal{Q}_2$. Let x denote a vertex on $P_u$ which is adjacent to u, that is, (u, x) is an edge of $P_u$; similarly, let y denote a vertex on $P_v$ which is adjacent to v, that is, (v, y) is an edge of $P_v$. Assume that x is on a 2-path $x-z \in \mathcal{Q}_2$ and y is on a 2-path $y-w \in \mathcal{Q}_2$, where z and w may or may not be on $P_u$ or $P_v$. If $z \ne y$, then $z \ne w$ since any two 2-paths in $\mathcal{Q}_2$ do not have a common vertex. This gives rise to a configuration as shown in Fig. 3, where $P_1 = x-z$, $P_2 = u-v$, $P_3 = y-w$, a contradiction to the termination condition for the algorithm Approx, see Step 4 in Fig. 4. If $z = y$ (implying $x = w$), then let p denote the last vertex on $P_u$ other than u and x and assume that p is on a 2-path $p-q \in \mathcal{Q}_2$; this leads to a configuration as shown in Fig. 3, where $P_1 = p-q$, $P_2 = u-v$, $P_3 = x-y$, again a contradiction to the termination condition for the algorithm Approx, see Step 4 in Fig. 4.

Using the above claim, if each of the three vertices $u_1, u_2, u_3$ on $P_u$ is on a 2-path of $\mathcal{Q}_2$, then 1 / 3 token of the path $u-v$ is distributed to the 3-path $P_u \in \mathcal{Q}^*_3$ while the other 2 / 3 tokens are distributed to the 3-path $P_v \in \mathcal{Q}^*_3$; otherwise, 2 / 3 tokens of the path $u-v$ are distributed to the 3-path $P_u \in \mathcal{Q}^*_3$ while the other 1 / 3 token is distributed to the 3-path $P_v \in \mathcal{Q}^*_3$ (see for an illustration in Fig. 7). From the perspective of the 3-paths of $\mathcal{Q}^*_3$, each of them can receive at most 4 / 3 tokens, which is the maximum value in $\{1 + 1/3, 1/3 + 1/3 + 1/3, 2/3 + 2/3\}$ representing all the maximal token combinations. We conclude the following claim.

Claim 3

Every path of $\mathcal{Q}^*_3$ receives at most 4 / 3 tokens.

Fig. 8

The token distribution scheme from the paths of $\mathcal{Q}_2$ to the paths of $\mathcal{Q}^*$

The complete token distribution scheme from the paths of $\mathcal{Q}_2$ to the paths of $\mathcal{Q}^*$ is summarized in Fig. 8. At the end of the token distribution process, the 1 token of each 2-path of $\mathcal{Q}_2$ is distributed out to the paths of $\mathcal{Q}^*$. Every 1-path of $\mathcal{Q}^*_1$ receives at most 1 token (Claim 1), every 2-path of $\mathcal{Q}^*_2$ receives at most 2 tokens (Claim 2), and every 3-path of $\mathcal{Q}^*_3$ receives at most 4 / 3 tokens (Claim 3). It follows that

$$\begin{aligned} |\mathcal{Q}_2| \le |\mathcal{Q}^*_1| + 2 |\mathcal{Q}^*_2| + \frac{4}{3} |\mathcal{Q}^*_3|. \end{aligned}$$

(6)

Combining Eqs. (4, 5, 6), we have

$$\begin{aligned} 3 |\mathcal{Q}_1| + 3 |\mathcal{Q}_2| + 3 |\mathcal{Q}_3| \le 4 |\mathcal{Q}_1^*| + 4 |\mathcal{Q}^*_2| + \frac{13}{3} |\mathcal{Q}^*_3|, \end{aligned}$$

(7)

which results in $|\mathcal{Q}| \le \frac{13}{9} |\mathcal{Q}^*|$.

Figure 9 illustrates an instance with 27 vertices, which shows that the performance ratio 13 / 9 of Approx is tight. On this instance, the solution $\mathcal{Q}$ produced by the algorithm Approx contains 12 2-paths and 1 3-path (solid edges as shown) and an optimal 3-path partition $\mathcal{Q}^*$ contains 9 3-paths (dashed edges as shown). Using the token distribution scheme, each of the 9 3-paths of $\mathcal{Q}^*$ receives 4 / 3 tokens. The theorem is proved. $\square$

Fig. 9

A tight instance of 27 vertices, in which the 3-path partition $\mathcal{Q}$ produced by the algorithm Approx contains 12 2-paths and 1 3-path (solid edges) and an optimal 3-path partition $\mathcal{Q}^*$ contains 9 3-paths (dashed edges). The edges $(u_{3i+1}, v_{3i+1})$, $i = 0, 1, \ldots , 5$, are in $E(\mathcal{Q}_2) \cap E(\mathcal{Q}^*)$, shown in both solid and dashed (they are drawn as parallel edges), as $u_{3i+1}$ collides into $v_{3i+2}$, $i = 0, 1, \ldots , 5$

4 Concluding remarks

In this paper we studied the 3-path partition problem and designed a 13 / 9-approximation algorithm called Approx. Approx contains two phases, first to compute a 3-path partition with the least 1-paths and then to greedily merge a collection of three 2-paths into two 3-paths, whenever possible. We showed that the first phase can be done in O(nm) time, where n is the number of vertices and m is the number of edges in the input graph, and the overall running time of Approx is in $O(n^3)$. The performance analysis for Approx is done by an amortization scheme, using the structure properties of the 3-path partition obtained at the end of second phase. From the tight instance shown in Fig. 9, one sees that in the “bad” scenario there are too many 2-paths in the computed partition compared to the optimal partition, yet they cannot be merged by Approx. Designing a better merging scheme than the current simple scheme in the second phase of Approx can be a key to the next improvement. Ultimately, a 4 / 3-approximation, matching the best approximation ratio for the 3-Set Cover problem, is an exciting goal.