Trinque problem: covering complete graphs by plane degree-bounded hypergraphs

Abstract

Let $K_n$ be a complete graph drawn on the plane with every vertex incident to the infinite face. For any integers i and d, we define the (i, d)-Trinque Number of $K_n$, denoted by ${\mathcal {T}}^d_{i}(K_n)$, as the smallest integer k such that there is an edge-covering of $K_n$ by k “plane” hypergraphs of degree at most d and size of edge bounded by i. We compute this number for graphs (that is $i=2$) and gives some bounds for general hypergraphs.

In this paper, we consider a draw of complete graph $K_n$ on the plane such that every vertex is incident to the infinite face, i.e. every edge is drawn inside the cycle bounding the infinite face. This cycle is called the exterior cycle of $K_n$ and denoted $C(K_n)$. Let $V=\{0, \ldots , n-1\}$ be the vertex set of $K_n$ such that ij is an edge of $C(K_n)$ iff $\vert i-j\vert =1\hbox { mod }[n]$.

How to cover the edges of $K_n$ is a natural question which can be related to combinatorial optimization problems. One may add constraints on the element of the covering. Here we are interested on such a covering involving plane hypergraphs and a pair $i, j \in V$ is covered if it belongs to an edge of some “plane” hypergraph of the covering. Since several graphical representation for hypergraphs exist, there is also several definitions of a planar hypergraph. In this paper, we use the vertex-planarity as introduced by Johnson and Pollack. We discuss later (in Sect. 2) of this definition and of hypergraph planarity in general.

We define in this paper the (i, d)-Trinque Number of $K_n$, denoted by ${\mathcal {T}}^d_{i}(K_n)$, as the smallest integer k such that there is an edge covering of $K_n$ by k vertex-plane hypergraphs of degree at most d and size of edge bounded by i. One can observe that, in the case $i = 2$, we consider a graph covering.

The name of Trinque Number comes from the french verb “trinquer”, meaning “to clink glasses during a toast”. As in many countries, french toasts have their specific etiquette, in which every pair of glasses have to be clinked together while the two glass-holders maintain eye-contact. For some reason, it is very important that no two pairs of drinkers are crossing their arms while they trinque.

Finding an optimal ordering for our drinkers to obey french trinque etiquette corresponds to our Trinque Problem in the case $d = 1$ and $i = 2$. Larger values of d corresponds for the drinkers to use more than one arm at the same time, and larger values of i (i.e. hypergraph generalisation) corresponds to let the drinkers clink in groups of i glasses. As we will see, vertex-planarity definition corresponds to forbid arm crossing, except between two drinkers trying to reach groups of glasses they are both clinking in.

The following observation will be helpful for finding bounds on $\mathcal{T}^d_i$ :

FormalPara Observation 1

The value of ${\mathcal {T}}^d_{i}(K_n)$ is non-decreasing when n increases, and non-increasing when d or i increases.

In Sect. 1, we compute the Trinque Number in the graph-covering case ($i = 2$). Our main result corresponds to the following theorem:

FormalPara Theorem 2

For every $n \ge 3$, we have:

• ${\mathcal {T}}^1_{2}(K_n) = n$ and such a covering is unique,

• ${\mathcal {T}}^d_{2}(K_3)= {\mathcal {T}}^2_{2}(K_3)= 1$ for any $d\ge 2$,

• If $n\ge 4$ and $d\ge 2$ then ${\mathcal {T}}^d_{2}(K_n)= {\mathcal {T}}^2_{2}(K_n)= \lceil {n\over 2}\rceil$.

Section 2 is devoted to the case of hypergraphs for which we give bounds:

FormalPara Theorem 3

For every integers $n \ge 3$, $d \ge 1$ and $3 \le i \le n$,

• $\lceil {n-1\over i-1}\rceil \le {\mathcal {T}}^1_{i}(K_n) \le \left\lceil {n\over {\lfloor \frac{i}{2}\rfloor }}\right\rceil$.

• ${\mathcal {T}}^d_{3}(K_3)= {\mathcal {T}}^2_{2}(K_3)= 1$ for any $d\ge 2$,

• If $n\ge 4$ and $d\ge 2$, then ${\mathcal {T}}^d_{3}(K_n)= {\mathcal {T}}^2_{2}(K_n)= \lceil {n\over 2}\rceil$.

• For any $d \ge 2$ and $i \ge 4$, $\left\lceil {2 \times \lfloor \frac{n}{2} \rfloor \over 2 \times \lfloor \frac{i}{2} \rfloor }\right\rceil \le {\mathcal {T}}^d_{i}(K_n) \le \left\lceil {n\over {2 \times \lfloor \frac{i}{2}\rfloor }}\right\rceil$.

Finally, we conclude with related open problem.

1 Case of graphs

This section is dedicated to the proof of Theorem 2. We split this proof into two Lemmas corresponding to cases $d=1$ and $d\ge 2$.

Fig. 1

Decompositions into plane matchings. a $K_9$ and its sets $M_1$ and $M_2$. b $K_8$ and its sets $M_1$ (or $M_5$) and $N_{(01)}$ (or $N_{(45)}$)

Lemma 4

For every $n \ge 3$, ${\mathcal {T}}^1_{2}(K_n) = n$, and such a covering is unique.

Proof

Let $n \ge 3$ be an integer.

We first give a partition ${\mathcal M}$ of the edges of $K_n$ into n sets inducing plane matchings.

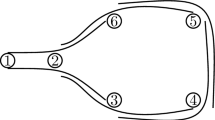
For any vertex u of $K_n$, let $M_u$ be the matching containing every edge between two vertices vw such that $|u - v| = |u - w|\hbox { mod }[n]$ (see Fig. 1). One can observe that this matching is planar.

We consider two cases.

• Integer n is odd. Let ${\mathcal M} = \{M_u | u \in V\}$. Since n is odd, for every edge xy in $K_n$, there is one and only one vertex u such that $|u - x| = |u - y|\hbox { mod }[n]$, i.e. such that $vw \in M_u$. Set ${\mathcal M}$ is an edge-covering of $K_n$. Still by the oddity of n, in the set $M_u$, vertex u is the only one having no neighbor. So, for two vertices $i \ne j$, we have $M_i \ne M_j$. This implies $|{\mathcal M}| = n$.

• Integer n is even. Since n is even, for every vertex u there is one and only one vertex $u'$ such that $|u - u'| = \frac{n}{2} \hbox { mod }[n]$. We can see that $M_u = M_{u'}$, and that u and $u'$ are the only vertices having no neighbor in this matching (see Fig. 1b). So ${\mathcal M}_1 = \{M_u | u \in V\}$ contains $\frac{n}{2}$ matchings.

  For any edge $e = uv$ of $C(K_n)$, say $v = u+1\hbox { mod }[n]$, we define $N_e$ as the matching containing every edge between two vertices xy such that $u - x = y - v \hbox { mod }[n]$. In other words, $xy \in N_e$ iff there is an integer k such that $x = u - k\hbox { mod }[n]$ and $y = v + k\hbox { mod }[n]$ (also see Fig. 1b). One could say xy is “parrallel” to uv. Let ${\mathcal M}_2 = \{N_e | e \in C(K_n)\}$. Observe this matching is plane, and that $e \in N_e$ and there is one an only one other edge of $C(K_n)$ being in $N_e$, namely $u'v'$ where $u - v' = u' - v\hbox { mod }[n] = \frac{n}{2} - 1$. This implies $|{\mathcal M}_2| = \frac{n}{2}$.

  Let xy be an edge of $K_n$ with $x \le y$.

  • If $y- x$ is even, then let $z = y - \frac{y - x}{2}$. We also have $z = x + \frac{y - x}{2}$, and so $xy \in M_z$, implying it is covered by ${\mathcal M}_1$.

  • If $y - x$ is odd, then let $e = uv$, where $u = x + \lfloor \frac{y - x}{2}\rfloor$ and $v = y - \lceil \frac{y - x}{2}\rceil$. For $k = \lfloor \frac{y - x}{2}\rfloor$, we have $x = u - k$ and $y = v + k$, so $xy \in N_e$ and so uy is covered by ${\mathcal M}_2$.

  So ${\mathcal M} = {\mathcal M}_1 \cup {\mathcal M}_2$ is a set, with cardinal $\frac{n}{2} + \frac{n}{2}$, of plane matchings that covers the edges of $K_n$.

We show there are no covering by a smaller set of matchings. Consider any covering ${\mathcal M}$ of $K_n$ by k plane matchings $S_1, \ldots , S_k$. Let u be a vertex of $K_n$, and v, w be its neighbors in $C(K_n)$. There are $n - 1$ edges incident to u, those edges and the edge vw have to be in different sets $S_i$, so $k \ge n$.

Finally, we show the coverings we give are unique. More precisely, we prove that, if there is a covering ${\mathcal M}$ of $K_n$ into n plane matchings, then this covering is unique. We denote the matchings of ${\mathcal M}$ by $S_0, \ldots , S_{n-1}$. In this covering, for any vertex v of V, any matching of ${\mathcal M}$ contains one edge incident to v except one. We assume the matchings of ${\mathcal M}$ are numbered such that, for any $i \in \{1, n -1\}$, the edge between vertex 0 and vertex i is in $S_i$. There is no edge of $S_0$ incident to vertex 0 (see Fig. 2).

By definition, edge (0, 1) is in $S_1$. Since (0, 2) is in $S_2$, there is no edge of $S_2$ incident to vertex 1. So there is an edge of $S_3$ incident to this vertex. Since (0, 3) is in $S_3$, edge (1, 2) has to be in $S_3$. By induction, we can prove (1, i) has to be in $S_{i+1}$ for any $i \in \{2, n - 2\}$, and that (1, 3) has to be in $S_0$

We just proved that the way we decompose the edges incident to a vertex into covering sets entirely depends on the way we decomposes the edges incident to one of its neighbor. This imply there is at most one way to partition the edges of $K_n$ into n plane covering matchings. $\square$

Fig. 2

The partition of the edges of 0 gives us the partition of the edges of 1

Lemma 5

${\mathcal {T}}^d_{2}(K_3)= {\mathcal {T}}^2_{2}(K_3)= 1$.

For every $n\ge 4$ and $d\ge 2$, we have ${\mathcal {T}}^d_{2}(K_n)= {\mathcal {T}}^2_{2}(K_n)= \lceil {n\over 2}\rceil$.

Proof

Let $d\ge 2$.

Since $K_3$ is a planar graph of degree two, we get ${\mathcal {T}}^d_{2}(K_3)= {\mathcal {T}}^2_{2}(K_3)= 1$.

So assume now that $n\ge 4$.

First, we prove that ${\mathcal {T}}_2^d(K_n)\ge \lceil {n\over 2}\rceil$. Let $G_1, \ldots , G_t$ be the planar graphs forming a covering of the edges of $K_n$. It is well known (simple application of Euler formulae, for instance) that the number of edges in $G_i\setminus C(K_n)$ is at most $n-3$. Since $n-3>0$ and since there are ${n.(n-1)\over 2}-n$ edges in $K_n\setminus C(K_n)$ then $t\ge {n\over 2}$.

Secondly, to establish Lemma 5, it is enough to prove that ${\mathcal {T}}_2^2 (K_n)\le \lceil {n\over 2}\rceil$.

Consider the path $P_0$ formed by the edges ab such that $a+b\equiv 0\hbox { or } 1\hbox { mod }{n}$ (see Fig. 3). Observe that 0 and $\lceil {n\over 2}\rceil$ are the extremities of $P_0$. Given an integer $i\in \{0,\ldots , \lfloor {n-1\over 2}\rfloor \}$, note $P_i$ the “$+i$” rotation of $P_0$ (see also Fig. 3). In other words, $P_i$ is the path defined by edges satisfying $a+b\equiv 2i\hbox { or } 2i+1\hbox { mod }{n}$. Now, we claim that the edges of $\cup P_i$ cover the ones of $K_n$.

Indeed, let ab be an edge of $K_n$. Let $c\equiv a+b\hbox { mod }{n}$. Then, by definition of $P_i$’s, the edge ab belongs to $P_{\lfloor {c\over 2}\rfloor }$.

Obviously, Theorem 2 holds from Lemmas 4 and 5. $\square$

Fig. 3

$K_8$ and its sets $P_0$ and $P_1$

2 Hypergraphs

In this section, we investigate Trinque problem in hypergraphs.

2.1 Planarity on hypergraphs

As there are several ways to draw hypergraphs, there are several ways to define its planarity. See the introductions of Kaufmann et al. (2009) or Verroust-Blondet and Viaud (2004) for surveys on those drawings. Among those definitions, we consider two: the vertex-planarity by Johnson and Pollak (1987) and the planarity defined by Zykov (or Zykov-planarity). Those can be seen as generalisation of planarity for graphs, since a graph is planar (in the ordinary sense) if and only if it is vertex-planar (resp. Zykov-planar) when viewed as a hypergraph (Johnson and Pollak 1987).

In a Zykov representation, the hyperedges are drawn as faces having their vertices as points in their boundaries (see Fig. 4c). A hypergraph is Zykov-planar if it has a Zykov representation on the plane. This definition is equivalent to the planarity in an edge-based representation, in which each hyperedge is drawn as a Steiner tree (Fig. 4b). A hypergraph ${\mathcal H}$ is vertex-planar if there is a subdivision of the plane in which each face corresponds to a vertex of ${\mathcal H}$ and each set of faces corresponding to a hyperedge is connected (Fig. 4d).

Every Zykov-planar graph is also vertex-planar. Intuitively, we could say that vertex-planarity permits more overlapping on the hyperedges than Zykov-planarity. For example, one can observe hypergraph ${\mathcal H}_3$ (Fig. 4e) is vertex-planar but not Zykov-planar. Note that we can represent a hypergraph ${\mathcal H}$ by a bipartite graph $({U}\cup {V},{E})$, where U is the vertex set of ${\mathcal H}$, V its hyperedge set, and every edge of E represent a vertex-hyperedge incidence in ${\mathcal H}$. The definition of planarity in this representation is equivalent to Zykov-planarity (Walsh 1975).

In this paper, we consider vertex-planarity for ${\mathcal {T}}^d_{~i}(K_n)$ as it is more permissive and consider vertices connections. We could define an equivalent trinque number for Zykov-planarity, denoted by ${\mathcal {T}}'^d_{~i}(K_n)$, since it is edge-crossing focused. One can observe that those two definitions are equivalent when $d = 1$.

Finally, to maintain the fact we are covering the edges of a plane graph, we need to add to the definition that the vertices have to be in the same place in our covering hyperedges than in our drawing of $K_n$, and that the hyperedges has to be drawn inside $K_n$, i.e. we consider a subdivision of the inside of $C(K_n)$ in the vertex-planarity, and we say the Steiner trees has to be drawn inside $C(K_n)$ in the edge-based definition.

Continuing on our trinque metaphor, vertex-planarity consider the more efficient way to clink glasses if we let drinkers trinque in groups of i glasses, without arm-crossing in the Zykov-planarity, and with arm-crossing between two drinkers, but only to reach groups of glasses they are both clinking in.

Fig. 4

An hypergraph and four representations (a–d) and a non-Zykov-planar vertex-planar hypergraph (e). a Eulerian. b Edge-based. c Zykov. d Vertex-based. e ${\mathcal H}_3$

2.2 Results on Trinque number

Here we demonstrate Theorem 3 through four Lemmas. The first one consider lower bounds, the second upper bounds, and the third one considers case $i = 3$.

Lemma 6

For every integers $n \ge 3$, $d \ge 1$ and $3 \le i \le n$,

$$\begin{aligned} {\mathcal {T}}^1_i(K_n)\ge \lceil {n-1\over i-1}\rceil \;{ and }\; {\mathcal {T}}^d_i(K_n)\ge \left\lceil {2 \times \lfloor \frac{n}{2} \rfloor \over 2 \times \lfloor \frac{i}{2} \rfloor }\right\rceil . \end{aligned}$$

Proof

Let $n \ge 3$, $d \ge 1$ and $3 \le i \le n$ be three integers. Any vertex of $K_n$ belongs to $n-1$ edges and an hyperedge of size i covers exactly $i-1$ such edges, so ${\mathcal {T}}^1_i(K_n)\ge \lceil {n-1\over i-1}\rceil$ is easy to observe. In the case $d \ge 2$, we consider two cases.

• If n is even, then a vertex u is diametral to v iff $u \equiv n-v\hbox { mod }[n]$. Clearly, any edge of size i contains at most $\lfloor \frac{i}{2} \rfloor$ pairs of diametral vertices. Moreover, two hyperedges $e_1$, $e_2$ are crossing if $e_1$ contains a diametral pair not contained in $e_2$ or conversely. Therefore, since all the ${n\over 2}$ pairs of diametral vertices must be covered, we get ${\mathcal {T}}^d_i(K_n)\ge \left\lceil {n\over 2 \times \lfloor \frac{i}{2} \rfloor }\right\rceil$.

• If n is odd, then ${\mathcal {T}}^d_i(K_{n-1})\ge \left\lceil {n - 1\over 2 \times \lfloor \frac{i}{2} \rfloor }\right\rceil$ by the previous item, which proves this case by Observation 1.

$\square$

Lemma 7

Let $n \ge 3$, $d \ge 1$ and $3 \le i\le n$ be integers.

We have ${\mathcal {T}}^d_{i}(K_n) \le {\mathcal {T}}^d_2(K_p)$, where $p = \left\lceil \frac{n}{\lfloor \frac{i}{2} \rfloor }\right\rceil$.

Proof

Let $n \ge 3$, $3 \le i \le n$ and $d \ge 1$ be three integers. We are looking for an edge-covering of $K_n$ with plane hypergraphs of maximum degree d and hyperedges of size at most i.

We partition the vertices of $K_n$ into a minimal number of sets of size at most $\lfloor \frac{i}{2}\rfloor$ (we need $\left\lceil \frac{n}{\lfloor \frac{i}{2} \rfloor }\right\rceil$ sets, we denote this number by p) such that all the vertices of a same set are consecutive in $C(K_n)$. Let this partition be denoted by ${\mathcal P}(K_n)$.

Observe that, from an a edge-partition ${\mathcal M}$ of $K_p$ into plane graphs of degree at most d, we obtain a solution to our problem by replacing each vertex x of $K_p$ by the set of ${\mathcal P}(K_n)$ containing vertex $x \times p \hbox { mod }[n]$, and by replacing every edge $e = uv$ of ${\mathcal M}$ by an hyperedge containing all the vertices of the sets of ${\mathcal P}(K_n)$ corresponding to u and v. $\square$

Thanks to Lemma 7 and Theorem 2, we get the following Corollary :

Corollary 8

Let $n \ge 3$ and $3 \le i\le n$ be integers,

• ${\mathcal {T}}^1_{i}(K_n) \le \left\lceil {n\over {\lfloor \frac{i}{2}\rfloor }}\right\rceil$.

• For any $d \ge 2$, ${\mathcal {T}}^d_{i}(K_n) \le \left\lceil {n\over {2 \times \lfloor \frac{i}{2}\rfloor }}\right\rceil$.

These results give the exact value of ${\mathcal {T}}^d_i(K_n)$ when $d \ge 2$ and (n is even) or (n is odd and $n\not \equiv 1\hbox { mod }{2\lfloor {i\over 2}\rfloor }$).

We finish this section, by considering the case of $i=3$. Our next result shows that, despite $n\equiv 1\hbox { mod }{2\lfloor {i\over 2}\rfloor }$ whenever n is odd, the bound given by Corollary 8 is tighted.

Theorem 9

Let $n\ge 3$ and $d\ge 2$ be integers then we have :

• ${\mathcal {T}}^d_{3}(K_3)= {\mathcal {T}}^2_{2}(K_3)= 1$ for any $d\ge 2$,

• If $n\ge 4$ and $d\ge 2$ then ${\mathcal {T}}^d_{3}(K_n)= {\mathcal {T}}^2_{2}(K_n)= \lceil {n\over 2}\rceil$.

Proof

Since an hyperedge of size 3 can be see as a triangle, a simple adaptation of the proof of Lemma 5 gives Theorem 9. $\square$

3 Concluding remarks

We give in this paper exacts results for the (i, d)-Trinque Number of $K_n$ when $i = 2$. Gaps still exist in the case $i \ge 3, d = 1$ where our upper bound is twice the lower bound, and in the case $i \ge 3$, $d \ge 2$ where there is still a gap of 1 for some values of n and i. We conjecture that, in this case, it is the upper bound that is tight.

Conjecture 1

For any $n \ge 3$, $d \ge 2$ and $3 \le i\le n$, ${\mathcal {T}}^d_{i}(K_n) = \left\lceil {n\over {2 \times \lfloor \frac{i}{2}\rfloor }}\right\rceil$.

A logical continuation of our work would be considering the variant where we cover $K_n$ with Zykov-planar hypergraphs. Since this definition is more restrictive, Lemma 6 also holds for this variant, as does our result of Corollary 8 when $d = 1$ (since the two planarity definitions are equivalent in this case).

Finally, we could consider a generalisation of the Trinque Number where, instead of covering $K_n$ with plane hypergraph such that all pairs of vertices belongs to a hyperedge, we need our covering such that for each j-sets S of vertices of $K_n$, there is an hyperedge of the covering containing S.