The Fåhræus-Lindqvist effect in small blood vessels: how does it help the heart?

Abstract

The Fåhræus-Lindqvist effect is usually explained from a physical point of view with the so-called Haynes’ marginal zone theory, i.e., migration of red blood cells (RBCs) to a core layer surrounded by an annular RBCs-free plasma layer. In this paper we show that the marginal layer, though causing a substantial reduction in flow resistance and increasing discharge, does not reduce the rate of energy dissipation. This fact is not surprising if one considers the electric analog of the flow in a vessel: a resistance reduction increases both the current intensity (i.e., the discharge) and the energy dissipation. This result is obtained by considering six rheological models that relate the blood viscosity to hematocrit (volume fraction occupied by erythrocytes). Some physiological implications are discussed.

1 Introduction

The Fåhræus-Lindqvist effect is a phenomenon that occurs in blood vessels less than 0.3 mm in diameter and is named after the two Swedish scientists Robin Fåhræus and Johan Torsten Lindqvist [1]. Actually, such a phenomenon was almost simultaneously reported by Martini, Pierach, and Scheryer in [2] and further investigated by Pries et al. [3], and by Secomb and Pries [4]. Fåhræus and Lindqvist showed in ex vivo experiments that the blood apparent viscosity varies according to the diameter of the tube in which it flows. Experimenting with blood flowing in glass capillaries, they found that the viscosity did not change when the capillary diameter was larger that 0.3 mm, but it kept decreasing for lower and lower diameters down to 4–5 μm. Therefore, they concluded that blood manifests a non-Newtonian behavior in vessels with a diameter less than 0.3 mm, while in vessels whose diameter is larger than 0.3 mm, the flow can be reasonably considered Newtonian (Fig. 1).

Fig. 1

Experimental results by Fåhræus and Lindqvist [1]. In the vertical axis the blood apparent viscosity relative to the plasma viscosity. The four series differ for the reference plasma viscosity (cP): 1.63, 1.65, 1.60, 1.72 (depleted plasma), respectively. Series 1, 2: blood from T. Lindqvist. Series 3, 4: blood from R. Fåhræus

The literature concerning the Fåhræus-Lindqvist effect is very large, since many scholars have analyzed this effect, proposing different interpretations. Here we refer to the recent comprehensive review by Secomb [5], and to the numerous references therein reported. The qualitative explanation on which there is a large agreement is the one proposed by Haynes [6]. According to his model the distribution of RBCs over the vessel cross section changes when the blood flows in vessels whose diameter is smaller than 0.3 mm. More precisely, RBCs migrate to the central part of the vessel (thus moving faster), while a layer of RBCs poor plasma forms close to the walls, thus favoring the flow. Haynes’ theory has been resumed and improved by many authors (Fournier [7], Chebbi [8], Sharan and Popel [9]). We refer the reader also to [10, 11] and to the recent book by Fasano and Sequeira [12], where more references can be found.

Another approach, [13] and [14], considers blood as a monomodal suspension of plasma and RBCs, whose diffusion is driven by the shear. According to such an approach [15,16,17], the net flux of particles consists of two contributions: a diffusive flux driven by the gradient of the shear rate and diffusion due to the gradient of the concentration (with a diffusivity proportional to the local shear rate). This model has been used to predict the formation of a region close to the wall relatively poor in particles, which acts as a lubricant layer accelerating the movement of the whole suspension. In the same spirit, using scaling arguments, Leighton and Acrivos [15] and Pranay et al. [18] showed that the net RBC flux is driven by a gradient in concentration whose diffusivity is proportional to the shear rate and the local hematocrit, and depends on the typical particle dimension. However, as pointed out in [17], such a model predicts that in a steady Poiseuille flow the particles, volume fraction attains a cusp at the centerline (never observed in experiments performed on suspensions) where it attains its maximum admissible value, a feature linked to the vanishing of the diffusion operator on the centerline. Such a drawback is absent in particle-migration models in which the solid-volume fraction advection-diffusion equation contains a driving term (for instance proportionale to the difference between the pressure and the integranular stress). Models of that kind have been recently developed by Monsorno et al. [19, 20], Lecampion, Garagashp [21] and Boyer et al. [22] and applied to confined pressure-driven laminar flow of neutrally buoyant non-Brownian suspensions [23]. Essentially they treat the suspension as a mixture [24] and are characterized by considerable mathematical difficulties due to the boundary conditions. Indeed, one of the thorny obstacles, when it comes to putting mixture theory in practice, is our inability to prescribe boundary conditions for stress boundary value problems, since we do not know how to distribute the traction (or compression) among the various mixture components.

In the framework of the non-colloidal suspensions (in the sense that the characteristic particle diameter is sufficiently large for Brownian effects to be negligible), the solid-fluid interaction term depends on Darcy’s number [24, 25], which can become quite large, being proportional to the square of the ratio between the macroscopic length scale and the particles size. Hence, for creeping flows (negligible Reynolds number), the two phases have practically the same velocity and the suspension can be considered as a non-homogeneous fluid [26,27,28], whose dynamics is essentially governed by the linear momentum equation and the continuity equation which, if the mixture components are incompressible, reduces to the density material derivative. Thus, the steady state (when attained) depends on the boundary conditions and on the initial conditions. Therefore, when no information on the initial conditions is available, the equilibrium distribution of the suspended particles is, in fact, arbitrary up to a certain extent (we shall resume this issue in Section 2). One therefore needs a criterion, based on reasonable physical assumptions, to select the concentration profile of the suspended particles.

Based on the hypothesis of spontaneous axial accumulation of RBCs, in his celebrated paper [6], Haynes assumed that the hematocrit profile in a tube, i.e., the function $H\left (r\right )$, is a step function equal to zero close to the vessel walls and taking a constant value in a central region. Actually, this is a well-known phenomenon in flows of suspensions (though the mechanism driving a redistribution of particles in vessels remains unknown) that was experimentally studied in the pioneering work by Segré and Sileberger [29] and the in subsequent works by Nott and Brady [16]. Actually, in a creeping flow with uniform shear rate (such as Couette flow), a neutrally buoyant rigid particle in dilute suspension does not generally migrate across the flow away from a solid boundary. For spherical particles, this result follows from the fact that the equations of fluid motion are linear and that a reversal of the flow direction would result in the opposite migration, which would be a contradiction. The same argument applies to particles having a symmetry with respect to a plane perpendicular to the flow [30]. On the contrary, this migration is shown to take place in three-dimensional simulations of motions of RBCs and of other deformable particles in shear flow near a solid boundary [31, 32]. A distinct mechanism for migration seems to arise when the flow has a curved velocity profile (such as Poiseuille flow), i.e., the shear rate is not uniform and its modulus increases from the centerline to the wall [31, 33].

For Stokes flow of suspensions in tubes, particle deformability seems to greatly affect migration away from the walls [34]. Moyers-Gonzalez and Owens [35] described the steady Poiseuille flow of blood in a small tube using a two-layer fluid consisting of an outer annulus filled with plasma and an inner core where the non-Newtonian fluid description is that of the hemorheological model of Moyers-Gonzalez et al. [36], which treats the blood as a suspension of simple rouleaux of various sizes represented by deformable dumbbells. Accordingly, the total stress is essentially viscoelastic, being composed of a small Newtonian-like contribution from the plasma and an elastic-like contribution from the RBCs. Such an approach has been used by Dimakopoulos et al. [37] for simulating the blood flow in a stenotic vessel. The results show that a cell-depleted layer develops along the vessel wall with an almost constant thickness for slow flow conditions and the viscoelastic effects significantly affect the blood flow. Actually, the viscoelastic properties of human blood plasma has been recently highlighted in [38] and [39]. This extra elastic contribution, caused by plasma, to the rheological response of whole blood can amplify RBC deformation, influencing the formation of the depletion layer close to the vessel walls. However, a general mechanistic understanding of RBC migration away from the vessel walls has proved elusive. Indeed, this phenomenon (i.e., particle migration away from the walls) has been observed and analyzed also in case of rigid spheres in Newtonian liquids [40,41,42].

Regarding the physical motivation of particle migration toward the vessel center, Haynes conjectured that the axial accumulation of RBCs would induce a substantial reduction in energy dissipation. In particular, since the dissipation is mainly effective in the arteriolar segments of the systemic vascular tree (where the majority of the total peripheral resistance resides), it has been suggested that the Fåhræus-Lindqvist effect is an evolutionary trait alleviating the impact of peripheral resistance. However, it remains to explain the reason why RBC migration occurs at the threshold of $\sim$0.3 mm and to verify if it actually reduces energy dissipation. To our knowledge the first problem is still open. The second question is addressed in this paper.

Starting from the Haynes assumption, i.e., the marginal layer theory, we compute the dissipation rate, namely the mechanical energy dissipated per unit time by the internal friction. We disregard the blood’s complex rheological behavior, proposing a Newtonian model for both the plasma and the core, but we take into account the local viscosity variations due to the discontinuous hematocrit. It is indeed well known that a hematocrit increase has the effect of increasing the apparent viscosity [3, 43, 44]. We neglect also the RBCs deformability, supposedly contributing to the Fåhraeus-Lindqvist effect [3, 5, 45]. Our study therefore applies to those flow regimes in which the non-Newtonian effects induced by the presence of RBCs and the cell’s deformability play a minor role. Adopting such an approach, we are able to obtain explicit expressions for the velocity and pressure fields which, in turn, allow simple estimates for the apparent viscosity and the rate of dissipation. Taking into account all other effects possibly affecting RBC migration, to which we may add their interaction with the cells of the vessel endothelium [46, 47], would lead to a model certainly more accurate, but no longer analytically tractable. Our aim is to see what can be concluded within the simple framework of Haynes’ model.

To keep our analysis as general as possible, we consider six empirical laws linking the blood viscosity to the hematocrit and, following the procedure illustrated in [7] and [8], we find, for each of them, the correlation between the inner core radius and its hematocrit. Then we compute the dissipation rate and the discharge in terms of the marginal layer amplitude, thus quantifying the Fåhraeus-Lindqvist effect from both the “energetic” and the perfusion points of view. The results obtained are discussed in the last Section. In summary, we can anticipate that the Fåhræus-Lindqvist effect increases the vessel discharge, but at the expense of a higher energy dissipation, contrary to the Haynes conjecture. Instead we shall see that the help the heart receives from the effect is a substantial decrease of the pressure it has to provide in order to maintain adequate oxygen supply to tissues.

2 Modelling the flow

We model the blood as an inhomogeneous mechanically incompressible linear viscous fluid, whose viscosity depends on the hematocrit H. Denoting by v the Eulerian velocity, the mathematical model is the following

$$ \frac{\partial H}{\partial t}+\boldsymbol{v}\cdot \nabla H=0, $$

(1)

$$ \nabla \cdot \boldsymbol{v}=0, $$

(2)

$$ \rho \left( \frac{\partial \boldsymbol{v}}{\partial t} +\left( \boldsymbol{v}\cdot \nabla \right) \boldsymbol{v}\right) =-\nabla p+\nabla \cdot \mathbb{T}, $$

(3)

where ρ is the blood density, p the pressure and $\mathbb {T}$ the is the non-spherical part of the Cauchy stress tensor whose constitutive equation is $\mathbb {T}=\mu \left (H\right ) \left (\nabla \boldsymbol {v} +\nabla \boldsymbol {v}^{T}\right )$, with $\mu \left (H\right )$ fluid viscosity (depending on the hematocrit). We note that the first equation is nothing but the hematocrit balance with no diffusion. The second equation expresses mass conservation, while in the third one (i.e., the momentum balance equation) we have neglected the body forces.

We recall that, strictly speaking, blood is a non-Newtonian fluid. The deviation from the classical Newtonian behavior is manifested in its shear-thinning and stress relaxation properties [12, 48]. For instance, many experiments show that for laminar flow in straight and uniform tubes, the velocity profile is blunted near the central axis [49, 50]. However, the importance of these non-Newtonian features depends both on the vessel size and on the flow regime. Here we consider regimes where non-Newtonian effects can be neglected to a certain extent in each of the two flow regions, with the aim of deriving explicit expressions describing the flow.

We now consider the steady flow in a cylindrical tube whose diameter is 2R and whose length is L. We denote by r the radial coordinate, and suppose that the flow attains a steady laminar state

$$ \boldsymbol{v}=v\left( r\right) \boldsymbol{e}_{x},H=H(r), $$

(4)

where e_x is the unit vector parallel to the cylinder axis. Equations (1) and (2) are automatically fulfilled, while (3) gives

$$ \left\{ \begin{array}{l} -{{\frac{\partial P}{\partial x}}}+{{\frac{1}{r}}}{ {\frac{\partial \left( \tau ~r\right) }{\partial r}}}=0, \\ \\ {{\frac{\partial P}{\partial r}}}=0, \end{array} \right. $$

(5)

where $\tau =\mathbb {T}\boldsymbol {e}_{r}\cdot \boldsymbol {e}_{x}$, i.e., the shear stress, is given by

$$ \tau =\mu \left( H\right) \frac{\partial v}{dr}~. $$

(6)

Assuming $\left . {P\left (x\right ) }\right \vert _{x=0}$= P₀, $\left . { P\left (x\right ) }\right \vert _{x=L}$= P₀ −ΔP and $\left . \tau \right \vert _{r=0}=0$, we have

$$ P\left( x\right) =-{{\frac{\Delta P}{L}}}x+P_{0}, $$

(7)

and

$$ \tau =-\frac{\Delta P}{2L}r. $$

(8)

The velocity profile, when no-slip is imposed on R, i.e., v(R) = 0, is given by

$$ v\left( r\right) =\frac{\Delta P}{2L}{{\int}_{r}^{R}}\frac{r^{\prime }}{\mu \left( H\left( r^{\prime }\right) \right) }dr^{\prime }~. $$

(9)

So, $v\left (r\right )$ depends on the profile $H\left (r\right )$, which, at this stage, is not specified. Computing the discharge

$$ \begin{array}{@{}rcl@{}} Q &=&2\pi {{\int}_{0}^{R}}v(r)rdr=\pi \frac{\Delta P}{L}{{\int}_{0}^{R}}r{{\int}_{r}^{R}} \frac{r^{\prime }}{\mu \left( H\left( r^{\prime }\right) \right) }dr^{\prime }dr\\ &=&\pi \frac{\Delta P}{2L}{{\int}_{0}^{R}}\frac{r^{3}}{\mu \left( H\left( r\right) \right) }dr, \end{array} $$

(10)

we define the apparent viscosity as

$$ \mu_{app}={{\frac{\pi {\Delta} P}{8L}}}{{\frac{R^{4}}{Q}=}}\frac{ R^{4}}{\mathop{ \int}_{0}^{R}{{\frac{4r^{3}}{\mu \left( H\left( r\right) \right) }}}dr}. $$

(11)

The convective RBCs flux along the x axis is

$$ \begin{array}{@{}rcl@{}} J &=&2\pi {{\int}_{0}^{R}}H\left( r\right) v(r)rdr=\pi \frac{\Delta P}{L} {{\int}_{0}^{R}}H\left( r\right) r{{\int}_{r}^{R}}\frac{r^{\prime }}{\mu \left( H\left( r^{\prime }\right) \right) }dr^{\prime }dr\\ &=&\frac{\Delta P}{2L}{{\int}_{0}^{R}}\frac{r^{\prime }}{\mu \left( H\left( r^{\prime }\right) \right) }\left[ 2\pi {\int}_{0}^{r^{\prime }}H\left( r\right) rdr\right] dr^{\prime }. \end{array} $$

(12)

Next, we remark that (1) calls for a boundary condition at the tube inlet. We therefore prescribe the inlet hematocrit as the one of blood in the main circulation. So, denoting by H_B the inlet hematocrit (typically 0.35 ≤ H_B ≤ 0.5), we have that H(r) has to verify the relationship

$$ H_{\mathrm{B}}~{{\int}_{0}^{R}}\frac{r^{3}}{\mu \left( H\left( r\right) \right) } dr={{\int}_{0}^{R}}\frac{2r^{\prime }}{\mu \left( H\left( r^{\prime }\right) \right) }\left( {\int}_{0}^{r^{\prime }}H\left( r\right) rdr\right) dr^{\prime }, $$

(13)

which we write also as

$$ H_{\mathrm{B}}Q=\frac{\Delta P}{2L}{{\int}_{0}^{R}}\frac{r^{\prime }}{\mu \left( H\left( r^{\prime }\right) \right) }\left[ 2\pi {\int}_{0}^{r^{\prime }}H\left( r\right) rdr\right] dr^{\prime}~. $$

(14)

Hence, for any H(r) fulfilling (13), the pair $\left (H(r) ,v(r) \right )$, with v(r) given by (9), is the steady solution to system (1)–(3) in a cylindrical domain, with the boundary conditions previously specified.

For the steady flow v(r) given by (9), the power dissipation rate ξ, due to viscous friction, is [51]

$$ \xi =2\pi {{\int}_{0}^{L}}{{\int}_{0}^{R}}\mu \left( H\left( r\right) \right) \left( \frac{\partial v}{\partial r}\right)^{2}rdrdx=\pi \frac{\left( {\Delta} P\right)^{2}}{2L}{{\int}_{0}^{R}}\frac{r^{3}}{\mu \left( H\left( r\right) \right) }dr~. $$

(15)

So, recalling (10) we have

$$ \xi ={\Delta} P~Q, $$

(16)

and, exploiting (13), also

$$ H_{\mathrm{B}}\xi =\frac{\left( {\Delta} P\right)^{2}}{2L}{{\int}_{0}^{R}}\frac{ r^{\prime }}{\mu \left( H\left( r^{\prime }\right) \right) }\left[ 2\pi {\int}_{0}^{r^{\prime }}H\left( r\right) rdr\right] dr^{\prime }~. $$

(17)

Let us now focus on the relationships between blood viscosity and hematocrit. In the literature there are numerous empirical formulas (see, for instance, [7, (Chapter 6); 52] and the recent review by Hund et al. [53]). Those models which do not account for shear-dependent viscosity have the general expression

$$ \mu \left( H\right) =\frac{\mu_{p}}{f\left( H\right) }, $$

(18)

where μ_p is the plasma viscosity

$$ \mu_{p}=\mu \left( 0\right) \ \ \ $$

(19)

and f(H) is such that f(0) = 1. More specifically, in this paper we shall consider:

• - $\mu \left (H\right ) ={{\frac {\mu _{p}}{1-\alpha (H,T)H}}}$, ⇒ $\ f\left (H\right ) =1-\alpha (H,T)H$, Charm and Kurland [54], with

  $$ \alpha \left( H\right) =c_{0}\exp \left\{ c_{1}H+{{\frac{c_{2}}{ T}}}\exp \left( -c_{3}H\right) \right\} , $$

  (20)

  where c₀ = 0.07, c₁ = 2.49, c₂ = 1107, $c_{3}=1.69\ {{}^{\circ }} \mathrm {K}^{-1}$, and T temperature in ^∘K.

• - $\mu \left (H\right ) ={{\frac {\mu _{p}}{1-H^{\frac {1}{ 3}}}}},\ \Rightarrow \ f\left (H\right ) =1-H^{\frac {1}{3}}$, Hatschek [55].

• - $\mu \left (H\right ) ={{\frac {\mu _{p}}{\left (1-H\right )^{2.5}}}},\ \Rightarrow \ f\left (H\right ) =\left (1-H\right )^{2.5}$, Cokelet [56].

• - $\mu \left (H\right ) ={{\frac {\mu _{p}}{1-H}}},\ \Rightarrow \ f\left (H\right ) =1-H$, Bingham and White [57].

• - $\mu \left (H\right ) ={{\frac {0.75\ \mu _{p}}{0.75-H}} },\ \Rightarrow \ f\left (H\right ) ={{\frac {0.75-H}{0.75}}}$, Nubar [58].

• - $\mu \left (H\right ) ={{\frac {\mu _{p}}{\left (1-{ {\frac {H}{H_{m}}}}\right )^{n}}}}$, HCode $\ \Rightarrow \ f\left (H\right ) =\left (1-{{\frac {H}{H_{m}}}}\right )^{n}$, Krieger and Dougherty [59], where n = 1.82, H_m = 0.67, with H < H_m.

The profiles for f(H) are displayed in Fig. 2.

Fig. 2

Behavior of f(H)

We remark that the last two models predict a diverging viscosity when H tends to a critical hematocrit H_m (H_m = 0.75, for the Nubar model). Not only that, but both models are formally defined for H larger than H_m, producing, in that range, a negative viscosity. To avoid this inconvenience it is necessary to insert a cutoff that prevents the hematocrit from exceeding that critical value. The latter represents the threshold for the so-called jamming, which describes a state of a suspension corresponding to the particles’ maximum packing [60].

3 Haynes’ model

As stated earlier, Haynes’ assumption [6] is that, below the critical diameter 0.3 mm, the RBCs migrate toward the center of the vessel (blood segregation) so that two distinct domains are identified:

• a central core in which RBCs are concentrated and uniformly distributed;

• an external annulus, also referred to as marginal layer or marginal zone, consisting almost exclusively of plasma.

Accordingly, if R is smaller than 0.3 mm, H(r) is a stepwise function (see Fig. 3)

$$ H(r)=\left\{ \begin{array}{ll} H_{\mathrm{C}}, & 0\leq r\leq s~, \\ & \\ 0, & s<r\leq R~, \end{array} \right. $$

(21)

with inner core radius s (which is not arbitrary since (13) has to be fulfilled).

Fig. 3

Schematic representation of the profile H(r) suggested by Haynes [6], when the cylinder radius is below the critical threshold

Of course, we could think of a different H(r) in which the hematocrit grows progressively from the outer edge to a maximum value (reached in the core). This kind of profile has been investigated in [14], where (1) has been modified, inserting on its r.h.s. a diffusive flux resulting from gradients in the hematocrit level, shear rate, and viscosity. Such an approach refers to the Phillips et al. model [17], which, in turns, extends the work of Leighton and Acrivos [15]. In the present paper, we use Haynes’ model, for which an explicit expression of the velocity field is available.

Let v_C(r) and v_A(r) be the axial fluid velocity in the core and in the annulus, respectively. The viscosity of the inner core is denoted by μ_C, namely

$$ \mu_{\mathrm{C}}=\mu \left( H_{\mathrm{C}}\right) , $$

(22)

Following the standard theory, well illustrated, e.g., in [7, 8], and [9], on r = s we require:

• 1. v_C(s) = v_A(s), continuity of velocity;

• 2. $\mu _{\mathrm {C}}{{\frac {\partial v_{C}}{\partial r}}} |_{r=s}=\mu _{p}{{\frac {\partial v_{\mathrm {A}}}{\partial r}}} |_{r=s}$, continuity of the shear stress.

Thus, recalling (8) the shear stress is related to the shear rate by

$$ \tau =\left\{ \begin{array}{lll} {{\mu_{\mathrm{C}}\cdot \frac{\partial v}{\partial r}}}, & & 0\leq r\leq s, \\ & & \\ {{\mu_{p}\cdot \frac{\partial v}{\partial r}}}, & & s\leq r\leq R, \end{array} \right. $$

(23)

from which, taking (6) into account, we obtain the velocity profile

$$ v(r)=\left\{ \begin{array}{lll} v_{\mathrm{A}}(r)={{\frac{\Delta P}{4L}}}\left( {{ \frac{s^{2}-r^{2}}{\mu_{\mathrm{C}}}}}+{{\frac{R^{2}-s^{2}}{ \mu_{p}}}}\right) , & & 0\leq r\leq s, \\ & & \\ v_{\mathrm{C}}(r)={{\frac{\Delta P}{4L}}}{{\frac{ R^{2}-r^{2}}{\mu_{p}}}}, & & s\leq r\leq R. \end{array} \right. $$

(24)

The discharges in the two regions are

$$ Q_{\mathrm{C}}=2\pi {{\int}_{0}^{s}}v\left( r\right) rdr={{\frac{ \pi {\Delta} P}{8L}}}s^{2}\left( {{\frac{s^{2}}{\mu_{\mathrm{C}}} }}+{{\frac{2\left( R^{2}-s^{2}\right) }{\mu_{p}}}}\right) \ \ \ \ \ \ \mathrm{(core)}, $$

(25)

$$ Q_{\mathrm{A}}=2\pi {{\int}_{s}^{R}}v\left( r\right) rdr={{\frac{ \pi {\Delta} P}{8L\mu_{p}}}}\left( R^{2}-s^{2}\right)^{2}\ \ \ \ \ \ \mathrm{ (outer\ \ layer)}, $$

(26)

and the total discharge is

$$ Q={{\frac{\pi {\Delta} P}{8L}}}\left( {{\frac{s^{4}}{ \mu_{\mathrm{C}}}}}+{{\frac{R^{4}-s^{4}}{\mu_{p}}}}\right) . $$

(27)

Recalling (11), the apparent viscosity is

$$ \mu_{app}={{\frac{\mu_{p}}{1+\sigma^{4}\left( {{\frac{\mu_{p}}{\mu_{\mathrm{C}}}}}-1\right) }}}, $$

(28)

where

$$ \sigma ={{\frac{s}{R}}},\ \ \ \ \ \ \ 0<\sigma \leq 1. $$

(29)

Applying (13), we have

$$ Q\cdot H_{\mathrm{B}}=Q_{\mathrm{C}}\cdot H_{\mathrm{C}}~, $$

(30)

which, exploiting (18), (25), and (27), gives the following implicit relation between H_C and σ (which, of course, involves also H_B)

$$ \frac{H_{\mathrm{C}}}{H_{\mathrm{B}}}=1+\frac{\left( 1-\sigma^{2}\right)^{2}}{\sigma^{2}\left[ 2-2\sigma^{2}+\sigma^{2}f\left( H_{\mathrm{C} }\right) \right] }, $$

(31)

which is exactly equation (4.39) of [7]. It is easy to check that the r.h.s. of (31) is a decreasing function for σ varying in (0,1). Thus, it is possible to derive from (31)

$$ H_{\mathrm{C}}=\widehat{H}_{\mathrm{C}}\left( \sigma \right) , $$

(32)

as shown in Fig. 4. Obviously, in all cases

$$ \widehat{H}_{\mathrm{C}}\left( 1\right) =H_{\mathrm{B}}, $$

(33)

while the maximum admissible value of H is taken for some finite sigma, depending on H_B.

Fig. 4

Implicit relation (31) for the six $f\left (H\right )$ considered. H_B = 0.35, H_B = 0.4, H_B = 0.45, and H_B = 0.5

It is remarkable that, despite the large differences exhibited in Fig. 3, the various models provide practically the same behavior of $\widehat {{H}}{_{\mathrm {C}}}\left (\sigma \right )$.

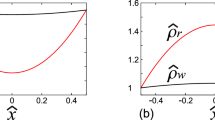
In Fig. 5 we report the relative apparent viscosity as a function of σ

$$ \frac{\mu_{app}\left( \sigma \right) }{\mu_{p}}=\frac{\mu \left( \widehat{H }_{\mathrm{C}}\left( \sigma \right) \right) }{\mu_{p}}=\frac{1}{1+\sigma^{4}\cdot \left[ f\left( \widehat{H}_{\mathrm{C}}\left( \sigma \right) \right) -1\right] }, $$

(34)

in terms of the six empirical models considered. We remark that when σ = 1, i.e., when there is no plasma layer, we have

$$ {{\frac{\mu_{app}\left( \sigma =1\right) }{\mu_{p}}=}}\frac{1 }{f\left( H_{\mathrm{B}}\right) }={{\frac{\mu_{\mathrm{B}}}{ \mu_{p}},}} $$

(35)

μ_B being the inlet blood viscosity which depends on the model considered. The ratios ${{\frac {\mu _{\mathrm {B}}}{\mu _{p}}}}$ are reported in Table 1.

Fig. 5

$\frac {\mu _{app}}{\protect \mu _{p}}$ for the six models. H_B = 0.35, H_B = 0.4, H_B = 0.45, and H_B = 0.5

Table 1 ${\frac {\protect \mu _{app}\left (\protect \sigma =1\right ) }{\protect \mu _{p}}}={{\frac {\protect \mu _{\mathrm {B} }}{\protect \mu _{p}}}}$ for different values of H_B and different rheological models

It can be noticed that, at least for the most significant cases (H_B = 0.40 and H_B = 0.45), μ_app is very close to μ_p for all σ < 0.7, independently of the viscosity model.

4 Dissipation and discharge

If we consider the hematocrit profile (21), and consequently the velocity profile (24), then the power dissipation rate is

$$ \xi =\frac{\pi }{8}\frac{\left( {\Delta} P\right)^{2}}{L}\frac{R^{4}}{\mu_{p} }\left[ \frac{\mu_{p}}{\mu_{\mathrm{C}}}\sigma^{4}+\left( 1-\sigma^{4}\right) \right] . $$

(36)

Recalling (18) and (32), we can write ξ as a function of σ

$$ \xi \left( \sigma \right) =\frac{\pi }{8}\frac{\left( {\Delta} P\right)^{2}}{L }\frac{R^{4}}{\mu_{\mathrm{B}}}{\Psi} \left( \sigma \right) , $$

(37)

and

$$ {\Psi} \left( \sigma \right) =\frac{1+\sigma^{4}\cdot \left[ f\left( \hat{H}_{C}\left( \sigma \right) \right) -1\right] }{f\left( H_{\mathrm{B}}\right) } , $$

(38)

which, thanks to (34), acquires the form

$$ {\Psi} \left( \sigma \right) ={{\frac{1}{f\left( H_{\mathrm{B} }\right) }}}\cdot {{\frac{\mu_{p}}{\mu_{app}\left( \sigma \right) }}}. $$

(39)

In particular, recalling that (33) entails ${\Psi } \left (1\right ) =1$, and setting

$$ \xi_{\mathrm{B}}=\frac{\pi }{8}\frac{\left( {\Delta} P\right)^{2}}{L}\frac{ R^{4}}{\mu_{\mathrm{B}}}, $$

(40)

which corresponds to the dissipation for the radially uniform hematocrit (i.e., σ = 1), we rewrite (37) as

$$ \xi \left( \sigma \right) =\xi_{\mathrm{B}}{\Psi} \left( \sigma \right) ~. $$

(41)

Proceeding similarly for the discharge (27), we obtain

$$ Q\left( \sigma \right) =Q_{\mathrm{B}}~{\Psi} \left( \sigma \right) , $$

(42)

where

$$ Q_{\mathrm{B}}={{\frac{\pi }{8}}}{{\frac{\Delta P}{ L}}}{{\frac{R^{4}}{\mu_{\mathrm{B}}}}} $$

(43)

is the discharge when there is no segregation. Hence, dissipation rate and discharge have exactly the same functional dependence on σ. Figure 6 displays the behavior of Ψ for the six rheological models considered. Hence, dissipation and discharge increase in the same way as σ decreases.

Fig. 6

Behavior of Ψ(σ) for the six viscosity laws considered. H_B = 0.35, H_B = 0.4, H_B = 0.45, and H_B = 0.5

Introducing next the hydraulic resistance of the vessel

$$ \mathfrak{R}=\frac{\Delta P}{Q}, $$

(44)

and defining

$$ \mathfrak{R}_{\mathrm{B}}=\frac{\Delta P}{Q_{\mathrm{B}}}, $$

(45)

the hydraulic resistance for the non-segregated flow, we have

$$ {{\frac{\mathfrak{R}}{\mathfrak{R}_{\mathrm{B}}}}}={ {\frac{1}{\Psi \left( \sigma \right) }}}. $$

(46)

Hence, ${\Psi } \left (\sigma \right )$ represents the ratio between the hydraulic resistances corresponding to non-segregated and to segregated flow. So, $\mathfrak {R}\left (\sigma \right )$ is maximum for σ = 1, that is when there is no segregation. Thus, recalling (39), Fig. 5 shows the behavior of $\mathfrak {R}\left (\sigma \right )$ except for a scale factor.

5 Conclusions

In this work we have studied the Fåhræus-Lindqvist effect, which consists in the decrease of the apparent viscosity of blood when it flows in vessels with a diameter smaller than 0.3 mm. Many models have been presented in the scientific literature to describe the Fåhræus-Lindqvist effect qualitatively, but, to our knowledge, no one gives an adequate explanation of the phenomenon on physiological grounds.

A model nowadays widely accepted, is the one introduced by Robert Haynes in his celebrated paper [6]. Haynes suggested two qualitative theories for explaining the effect. The first one, based on the so-called sigma effect theory [61], has not been further developed because it gave rise to physical inconsistencies [62]. The second theory has been accepted because supported by numerous experimental results. According to it, in specific conditions a RBC-free layer develops near the vessel wall and this leads to a reduction of marginal fluid viscosity. Starting from this theory, a model relating the core radius with its hematocrit can be developed [7, 8] . Following such an approach, we considered six different empirical laws providing the blood viscosity in terms of hematocrit. For each model we computed the viscous dissipation ξ and the discharge Q in terms of σ, i.e., the dimensionless radius of the inner RBC-rich core.

We found that RBC migration toward the vessel center increases the viscous dissipation with respect to the case in which there is no marginal layer and the RBCs are uniformly distributed over the cross section. Hence, the presence of a marginal “sleeve” of plasma, while decreasing locally the viscosity, increases the power dissipation rate, so imposing more strain to the heart. The result is not surprising if one considers the electric analog of power dissipation W on a resistance $\mathfrak {R}$: for a given potential difference V, $W=V^{2}/ \mathfrak {R}$. So a reduction of $\mathfrak {R}$ leads to an increase of W. On the other hand, the Fåhræus-Lindqvist effect increases the vessel discharge. Indeed, considering again the electric analog, the discharge parallels the current intensity which, for a given V, is inversely proportional to the resistance $\mathfrak {R}$.

We are therefore led to infer that the segregation takes place in order to increase the discharge, compensating the reduction of the pressure gradient in peripheral vessels, thus enhancing tissues perfusion. Such a conclusion agrees with an interesting experiment [63] in which the blood has been replaced with a Newtonian hemoglobin solution with a similar O₂ binding capacity. It was estimated that suppressing the Fåhræus-Lindqvist effect the pressure gradient had to be doubled to keep a comparable O₂ delivery rate to tissues. The latter observation reveals much about the Fåhræus-Lindqvist phenomenon. In the context of the present model it seems to suggest that σ is such that Ψ(σ) takes approximately the value 2. From the physiological point of view, it stresses its importance, since while heart can supply the energy required to double the RBC transportation rate via the Fåhræus-Lindqvist effect, it could not provide the pressure needed to sustain the same perfusion rate without it, leaving aside the fact that the entire blood vessels network is not designed to withstand such a pressure.