1 Introduction

Metal oxide materials have been the focus of much research based on the broad range of structures, properties, and exciting phenomena that are manifested in these materials [1, 2]. The perovskite structure, which has the chemical formula ABO3 (e.g., CaTiO3, SrRuO3, BiFeO3), is made up of corner-sharing octahedra with the A-cation coordinated with twelve oxygen ions and the B-cation with six. The structure can easily accommodate a wide range of valence states on both the A- and B-sites (i.e., A+1B+5O3, A+2B+4O3, A+3B+3O3) and can exhibit complex defect chemistry (including accommodation of a few percent of cation non-stoichiometry, large concentrations of oxygen vacancies, and exotic charge accommodation modes ranging from disproportionation to cation ordering) [3]. Selection of the appropriate A- and B-site cations can dramatically impact structural, electronic, magnetic, polar, and other properties. More comprehensively, the electronic structure and coordination chemistry of the cationic species control the wide range of physical phenomena manifested in these materials. Interestingly, most notable perovskites are not simple perovskites but rather complex oxides with two different kinds of B-site cations [4]. Correspondingly, they can be represented with the formula A(BxB1−x)O3. The discovery of lead–magnesium niobate PbMg1/3Nb2/3O3, as the first ferroelectric material belongs to the group 1:2 (x = 1/3) with a classical dielectric relaxation [5, 6], hence its name “ferroelectric relaxer”, opened the door to a research branch full of discussions and questions. Since then, a huge number of scientific papers has been raised to demystify this new material [7,8,9,10,11]. One of the things we understand today, that the complex ferroelectrics with disordered cationic arrangement have a diffuse phase transition, which is characterized by a high maximum for temperature dependence of permittivity, and are attracting more and more attention. In this context, another compound belonging to the 1:1 family (x = 1/2) with Fe and Nb transition metal cations in the B-site, Pb(Fe1/2Nb1/2)O3 (PFN) has also attracted considerable attention [11, 12]. However, in all these compounds, lead is an important “player” and it was not easy to dispense with him. We know that lead is an unfavorable material because of its toxicity which causes environmental pollution. Therefore, it is necessary to find lead-free compounds, which should have better dielectric properties [7, 13,14,15,16]. Ba(Fe1/2Nb1/2)O3 (BFN) presents itself as an alternative and effective substance. It is a relaxer-type material which has a disordered cationic arrangement.

BFN ceramics were first reported by Saha and Sinha [7, 13]. According to previous studies [13, 17,18,19], BFN had interesting dielectric and electrical properties over a wide temperature range.

Due to its interesting dielectric properties, much attention has been devoted to the study of barium iron niobate BFN. Indeed, it has been reported that this material is a ferroelectric relaxor possessing a high dielectric permittivity [7, 17, 19, 20] and frequency dependent maximum at a temperature around 170 °C [7]. The BFN ceramics is also an antiferromagnetic insulator at TN =  − 248 °C (25 K) with a weak ferromagnetic behavior at − 268 °C (5 K) [20]. This material has been synthesized with different methods: co-precipitation, solid-state reaction, sol–gel method, and molten salt route.

Barium iron niobate is a lead-free double pervoskite material having a mixture of two different cations (Fe3+ and Nb5+) at the B-site. The low temperature dielectric study, by Saha and Sinha, over a temperature range of 93 to 213 K, showed that BFN is a relaxor ferroelectric material [7, 13]. Another study over a higher range of temperatures (from 23 to 550 °C) further supported the relaxor behavior of BFN [21]. But, Wang et al. reported that BFN does not show relaxor ferroelectric behavior, rather it shows oxygen defect induced dielectric abnormity over an extensive temperature and frequency range [14]. All these reports raised doubts over the relaxor nature of BFN, leaving behind a debate. Moreover, irrespective of its relaxor nature, BFN show high dielectric constant at lower frequencies (≤ ~ 100 kHz), due to Maxwell–Wagner interfacial polarization effect related to the grain sizes and the density of the grain boundaries which must dominate in the case of small grain [19]. Impedance study by Intatha et al. confirmed the interfacial polarization induced high dielectric constant associated with BFN at lower frequencies [22]. Furthermore, it is also reported that the large value of dielectric constant observed sizes at higher frequencies is due to the rattling motion of uneven sized B-site cations, present within the oxygen octahedra of BFN [23]. There are also other methods of increasing dielectric constant of BFN, such as, through doping Ti, and adding another system in the parent BFN compound [24, 25].

Despite the attractive characteristics of the BFN ceramic, its high dielectric loss inevitably limits its practical application [21, 26]. Massive studies have been carried out on BFN thanks to these interesting properties but the electrical conductivity has not been studied sufficiently and such a deep discussion is still not taking place.

In this paper, we have studied the morphology, structure, and dielectric properties of BFN synthesized by solid-state reaction methods over a wide range of temperatures and frequencies. The dielectric properties were realized using complex impedance spectroscopy techniques, demonstrating the low dielectric loss obtained.

2 Experimental section

The BFN ceramic sample was prepared via the traditional solid-state reaction technique. Initially, the raw powders BaCO3 (barium carbonate), Fe2O3 (iron oxide), and Nb2O5 (niobium oxide) were mixed according to the stoichiometric formula. All chemicals are of high purity (over 99%). After drying at 100 °C, the starting materials were intimately mixed in an agate mortar and de-carbonated and pre-reacted by calcining in alumina crucibles at 900 °C for 24 h and then at 1000 °C for 4 h with intermediate grinding and mixing. After calcination, the formed powders were pressed into pellets. Finally, the pellets were sintered in air at 1300 °C for 2 h at a heating rate of 5 °C/min followed by furnace cooling. The phase structure, space group, and lattice parameters were identified by X-ray powder diffraction (XRD) using a Panalytical X’Pert PRO diffractometer using Cu Kα radiation of wavelength λ = 1.5406 Å. The morphology study of the BFN microstructures is carried out with a scanning electron microscope (Zeiss FE-SEM Ultra). Dielectric measurements were performed on ceramic disks after spraying silver electrodes on their circular faces. The dielectric measurements were recorded by impedance spectroscopy, under helium as a function of both temperature and frequency, using a PSM1735 of the N4L-NumetriQ type. The temperature was in the range of 160–600 K and frequency ranged between 100 Hz and 1 MHz.

3 Results and discussion

3.1 X-ray diffraction

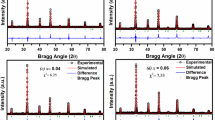
Figure 1 shows the final result of the structural refinement performed for the sintered BFN powder using Rietveld's “Full Proof” refinement program. From the XRD models, intense peaks are shown and no second phase was detected in the BFN ceramic. All the reflection peaks of the X-ray profiles were indexed using X’Pert HighScore Plus software. Rietveld refinement was made in order to clarify the constitution of the phase. In accordance with the recent work of Ganguly et al. [21], the optimal fit of the XRD data at room temperature was obtained using the Pm\(\overline{3 }\)m space group. The values of the Rwp reliability factors (the “wp” index stands for “weighted profile”) Rp (Bragg factor) and Rexp (expected error) in our compound were under 10% and goodness of fit (GOF) is 1.40, which indicates a high credibility of the refinement. The refined structural parameters and the refinement parameters of Rietveld Rwp, Rp, Rexp, and GOF are computed and listed in Table 1.

Fig. 1
figure 1

Rietveld refinement patterns of BFN ceramic. The black circles and the red lines represent the observed and refinement data, respectively. The blue lines are the difference between the observed and calculated diffraction patterns, the green bars are Bragg reflections for Pm-3m (Color figure online)

Full size image
Table 1 Calculated lattice and refinement parameters of BFN ceramic sample by refinement of room-temperature XRD data
Full size table

3.2 Scanning electron microscopy

Figure 2a illustrates the SEM images of BFN ceramic. It showed grains of different sizes homogeneously distributed. This may be due to the incorporation of Fe and Nb ions, of different radii, at site B. The smaller ion is more mobile and therefore has a faster movement. The difference in the diffusion velocity of the ions at the B-site leads to the formation of grains of different sizes. Figure 2b shows the EDX spectrum of BFN ceramic at room temperature. This spectrum demonstrates the existence of Ba, Nb, Fe, and O elements, proving that there is no integrated element loss during sintering in empirical errors and no impurity elemental peaks were observed.

Fig. 2
figure 2

a SEM images of BaFe1/2Nb1/2O3 ceramic sample, inset histograms of average grains size. b EDX analysis of the element distribution for the BFN ceramic

Full size image

3.3 Dielectric behavior

3.3.1 Conductivity analysis

Measuring conductivity as a function of frequency is an ideal tool for studying the nature of charge carriers and transport processes such as jumping or tunneling through an energy barrier. Figure 3a–c presents the conductivity data for BFN sample over a wide temperature range 160–600 K. It is clearly seen that the conductivity increases with the frequency; this behavior is attributed to the jump conduction mechanism. The existence of two regions can be seen in the experimental curves. First, in a low frequency range where the electric field cannot affect the jump conduction mechanism, corresponding to the DC conductivity. In the second region, the conductivity begins to gradually increase, corresponds to the alternating conductivity [27, 28]. This wide temperature range 160–600 K is divided into two sub-ranges, from 160 to 320 K and from 340 to 600 K. In the lower temperature range (160–320 K) and from the conductivity spectra (Fig. 3a, b), we can notice the presence of three distinct characteristics. According to the jump relaxation model introduced by Funke [29], there are two opposite relaxation processes, which are the successful jump and the unsuccessful jump. The latter occurs when ions jump to nearby sites and then return. The first, region I presented by a frequency independent plateau (over the low frequency range ~ 102–103 Hz), the conductivity is associated with successful jumps. In the mid-frequency region, region II extended over an intermediate frequency ~ 103–105 Hz, the conductivity curves show dispersion due to a greater number of unsuccessful hops. However, in the higher frequency region (~ 105–106 Hz), the failure/success ratio dominates. The AC conductivity at the given temperature is expressed by Jonscher’s power law [30]:

Fig. 3
figure 3

a and b frequency dependence of AC conductivity for low temperature BFN ceramics. c Frequency dependence of AC conductivity for high temperature BFN ceramics. d Temperature dependence of the exponents s1 and s2. e Temperature-dependent variation of conductivity at different indicated frequencies

Full size image
$$\sigma \left(\omega \right)={\sigma }_{\mathrm{dc}}+A{\omega }^{s},$$
(1)

where σdc is the DC conductivity, A is a temperature dependent parameter, ω is an angular frequency, and s is the power law exponent (dimensionless parameter) which represents the degree of interaction between mobile charge carriers and their environments 0 < s < 1. Nevertheless, the AC conductivity behavior in the low temperature region exhibits two regions of dispersion at each temperature (Fig. 3a, b). Therefore, the frequency dependence of the conductivity in this region follows Jonscher's double power law (DPL) with two values s1 and s2 at a temperature as indicated by the solid lines in Fig. 3a, b:

$$\sigma \left(\omega \right)={\sigma }_{\mathrm{dc}}+A{\omega }^{s1}+B{\omega }^{s2}.$$
(2)

Concerning the high temperature side (340–600 K), AC conductivity is held constant over a wide range of frequencies, so data above 320 K is adjusted by a simple power law. So, only s2 can be observed. The adjustment of the experimental data gives values of s1 and s2, which shows the variation of these parameters with respect to the increase in temperature.

In fact, the study of the behavior of the exponent s(T) is the useful solution in order to determine the mechanism of conduction. The variation of s(T) leads to different models. When the exponent “s” decreases with increasing temperature, we apply the correlated barrier hopping (CBH) model. In the case where the exponent “s” increases with the increase in temperature, we apply the NSPT (the non-overlapping small polaron tunneling) model. While when the exponent “s” decreases with the increase in temperature until reaching a minimum value, then increases when the temperature increases, we apply the model OLPT (overlapping-large polaron tunneling). If “s” is almost equal to 0.8 then it is independent of the temperature or increases slightly with the temperature we apply the model of quantum mechanical tunneling, QMT [27, 31]. Therefore this observed behavior corresponds to the change in the conduction mechanism. Figure 3d presents the temperature variations of power exponents s1 and s2 fitted by the DPL. The values of s1 vary between 0.9 and 1.1, which increases with increasing temperature. Therefore, conduction occurs in the intermediate frequency region and corresponds to the NSPT model [32]. In the case of s2, the figure shows that the value of s2 first decreases (from 0.2 to 0.13), after reaching a minimum value, an increase in the value s2 is observed. Therefore, the conduction mechanism in the higher frequency region corresponding to the OLPT model [28]. Figure 3d shows also the variation of the exponent s2 in the range 340–600 K which increases with the increase in temperature (in the region 340–420 K) then decreases; this behavior suggests that two conduction mechanisms exist in this temperature range. Thus, according to these variants, models NSPT and CBH are the appropriate models, respectively.

The thermal activation energy of the electrical conductivity was determined for BFN sample using the Arrhenius equation:

$$\sigma ={\sigma }_{0}\mathrm{exp}\left(\frac{-{E}_{\mathrm{a}}}{{k}_{\mathrm{B}}T}\right),$$
(3)

where σ0 is the pre-exponential factor, Ea is the activation energy of conduction, kB is the Boltzmann constant. Figure 3e shows the change in conductivity with the inverse of the absolute temperature at different frequencies. The values of the activation energy obtained are summarized in Table 2. As more than a single slope is obtained over a wide temperature range, it is easily understood that the activation process is multiple. It is clearly seen that the conductivities gradually increased with increasing temperature, indicating a thermally activated conduction process. The activation energy of conduction (the slope in Fig. 3e) showed different values in the low temperature range and in the high temperature range. In the same temperature range, Ea decreases with increasing frequency. At low frequency, conductivity is linked to the transport over long distances of mobile charge carriers, it therefore requires a high Ea, hence the origin of a high activation energy at low frequency. At high frequency, the charge carrier reorientation jump movement is limited to neighboring sites, thus corresponding to a small value Ea. At the same frequency, Ea in the higher temperature range was significantly greater than in the lower temperature range. At high temperature, the activation energy varied between 0.69 and 0.64 eV, which is close to the results reported in previous work [8].

Table 2 The activation energy of conduction
Full size table

3.3.2 Impedance analysis

The electrical transport property and the electrochemical reactions at interfaces of the prepared BFN were examined by measuring the impedance spectra (IS) of the pellets of the precursor powder in the frequency range from 100 Hz to 1 MHz. Shown in Fig. 4a–f are the Cole–Cole plots (a plot drawn between imaginary and real parts of the impedance) of BFN ceramics in a wide range of temperatures and frequencies. In the low temperature range (160–300 K), two semi-circles are clearly shown in Fig. 4a–c. The low frequency semicircles have an almost straight shape with a strong slope suggesting the very insulating character of ceramic. The high frequency semi-circle attributes to the contribution of the grain interior resistance, and the low frequency semi-circle represents the grain boundary resistance. However, as temperature increases, the intercept of the semicircular arcs on the real axis approaches the origin of the complex plane (resistance of the grain is gradually reduced from 109 kΩ to 655 Ω at 280 K), indicating a decrease in the sample’s resistivity properties. This behavior is apparently due to the presence of space charges in the material at higher measurement temperature [33]. Increasing the temperature further, the semicircular arc corresponds to the resistance of the grain disappears.

Fig. 4
figure 4

a–c Nyquist plot Z″ vs. Z′ at low temperatures range fitted with R-CPE equivalent circuit model. d–f Nyquist plot Z″ vs. Z′ at high temperatures range fitted with R-CPE equivalent circuit model. g Equivalent circuit model used for fitting non-ideal (Cole–Cole) behavior

Full size image

Figure 4d–f shows the Z″ vs. Z′ plots realized in the temperature range from 300 to 600 K. In this temperature range, the curves show a single semi-circular arc corresponding to the resistance of the grain boundaries. With increasing temperature, we notice that the radii of these arcs decrease, meaning reduced resistance values at higher temperatures, and that their centers shift from the axis of the real part (Z′), which indicates the presence of a non-Debye type of relaxation process occurs in the material. This again shows that conduction processes are thermally activated.

The IS was adjusted using the Zview software to extract the parameters that characterize the different contributions in BFN. The appearance of two arcs < 300 K suggested fitting the data by series combination of the two RC loops one branch is associated with the grain and other with the grain boundary present in the sample and above 300 K, where grain contribution is absent, one arc can be fitted with one RC loop. But, due to the deformed nature of the arc, parallel RC elements are not suited for fitting complex impedance plots of polycrystalline materials. However, we found that the complex plane plot of Z* is better described by replacing the ideal capacitor in the parallel RC element with a constant phase element (CPE, Fig. 4g). The CPE is used for the deviation of capacitance from ideal behaviors [34]. Where the CPE impedance expression is expressed as follows:

$${Z}_{\mathrm{CPE}}=\frac{1}{Q{(j\omega )}^{n}},$$
(4)

where Q is a proportional factor, ω is the angular frequency, n is the parameter which estimates the deviation from the ideal capacitive behavior, n is zero for the pure resistive behavior and is the unit for the capacitive [35].

3.3.3 Dielectric analysis

In order to determinate the dielectric properties we used the permittivity. Figure 5 illustrates the variations of permittivity as a function of temperature (from 160 to 600 K) at different frequencies (10 kHz, 50 kHz, 100 kHz, 500 kHz, and 1 MHz).

Fig. 5
figure 5

Dielectric constant as a function of temperature measured at different frequencies of BFN ceramic

Full size image

The dielectric study indicated the presence of two peaks in the studied temperature range. From Fig. 5, we note a decrease in the amplitude of the permittivity with the increase in frequency and a displacement of this peak toward a higher temperature, which was a clear signification of a relaxation process. The same behavior was also found by Wang et al. [14].

The high values of dielectric permittivity in a very wide temperature interval can be assigned to the disorder of B-site ions in the perovskite unit cell [36], which occur in complex perovskites type A(B′B″)O3. The Nb5+ and Fe3+ ions randomly occupy the octahedral B-sites surrounded by O2− anions. With the presence of larger Fe3+ (BI) cations, more space is available for the comparatively smaller Nb5+ (BII) cations. By applying an oscillating alternating signal to such systems, BII cations can move without distorting the oxygen structure due to the rattling space available for these cations. However, in an ordered perovskite, a smaller rattling space is available for the B-site cations. Consequently, a higher permittivity is expected in disordered perovskites than in ordered perovskites. Bochenek et al. and Ganguly et al. reported a similar explanation for the disorderness in the perovskite unit cell and reported also high permittivity values over a wide temperature range [8, 21].

The higher temperature relaxation in BFN ceramics is primarily contributed by the oxygen defect and this has been proven by Wang et al. when the dielectric peak at various frequencies is greatly suppressed by the annealing in oxygen [14]. Therefore we can associate the first peak, observed in Fig. 5, with an intrinsic relaxation and the second with an extrinsic relaxation.

The variations of dielectric loss as a function of temperature at various frequencies ranges are displayed in Fig. 6a. The temperature variation in tanδ (Fig. 6a) becomes strongly frequency dependent. High dielectric losses both at lower and higher temperatures are shown in Fig. 6a. Above 350 K there is a rapid increase in the dielectric losses connected with an increase in electric conduction what is confirmed by the direct current conductivity presented earlier (Fig. 3d). By increasing the probe frequency, the loss peaks move to higher temperatures, suggesting a thermally activated process.

Fig. 6
figure 6

a Dielectric loss as a function of temperature measured at different frequencies of BFN ceramic. b Comparison of the dielectric loss taken from literature with our results of the BFN at 10 kHz

Full size image

To promote our work, we must therefore compare our results with similar study. At RT and at 10 kHz, the dielectric loss reaches a value of 0.14, which is lower than that of Ganguly et al. (∼ 1.28) [21] and than that of Eitssayeam et al. (∼ 2.91) [26]. This comparison is illustrated in Fig. 6b and Table 3.

Table 3 Comparison
Full size table
3.3.3.1 Permittivity (deeper understanding)

Figure 7b shows the temperature dependence of the relaxation frequency for the sample, ln f vs. 1/T1/4 (red circles), where f is obtained from the position of the loss peak in the tanδ versus ln f plots (Fig. 7a). It is clear that there is a good linear relation between ln f and 1/T1/4 (R2 = 99.76%). However, the plot of ln f as a function of 1000/T (black circles) indicates an approximate Arrhenius relation. Based on this relation, the relaxation frequency at an infinite temperature (when 1000/T = 0) is 1.33 × 108 Hz and the activation energy for the dielectric relaxation is 133 meV, respectively. The values of the approach frequency and activation energy are in good agreement with those of other perovskite materials [37, 38] related to the process of localization of charge carriers. It should be noted that the relaxation frequency in Fig. 7b shows a deviation from Arrhenius behavior above 200 K (R2 = 97.94%). This deviation has been found in relaxations related to the polaron of some materials such as CCTO [38,39,40]. The source of the deviation from Arrhenius' law is possibly the transition from grain boundary conduction to volume limited conduction, according to the widely used “barrier layer model” [41, 42]. Thus, based on our results, Mott's VRH (variable range hopping) model [43]

$$ f = f_{1} \exp \left[ { - \left( {T_{1} /T} \right)^{1/4} } \right]. $$
(5)
Fig. 7
figure 7

a Variation of dielectric loss with frequency at different temperatures of BFN ceramics. b Temperature-dependent relaxation frequency (black circles, bottom and left axes) and VRH (red circles, top and left axes). The solid line is the fitting curve of the experimental data (red circles) according to Eq. (5) (Color figure online)

Full size image

may fit better the relaxation frequency, in which f1 and T1 are two constants. The values of f1 and T1 are determined to be 3.25 × 1019 Hz and 2.73 × 108 K, respectively. The values of T1 and f1 of BFN is similar to those of CCTO [38]. Due to its good description of the low temperature dielectric relaxation of BFN ceramics, the VRH mechanism supports the idea that disorder effects dominate the relaxation behavior of BFN’s semiconducting phase. Here, the kinetic energy (from thermal excitation) is insufficient to excite the charge carrier across the electronic band gap, so Eq. (5) is mainly due to the hopping of charge carriers within small regions. Figure 7b provides a good argument for the presence of (hopping) polarons in BFN.

Figure 8 illustrates the temperature dependence of the BFN permittivity measured at different frequencies. At the low temperature region, there is a rapid increase in permittivity which is closely related to the polaron jump. The curves in Fig. 8 show four phases: (1) a low permittivity region at the lowest temperatures (depends on the probing frequency; at 10 kHz, T < 150 K) in which the polarons are frozen. (2) With increased temperature, the dielectric permittivity increases sharply (at 10 kHz, 150 < T < 225 K), which is related to the thermal excitation of polarons inside the grains. Polaron hopping results in a semiconducting grain, where charge carriers can move inside (but not outside) the grain, causing the Maxwell–Wagner effect, which greatly improves the dielectric permittivity. (3) At even higher temperatures a plateau region is found (at 10 kHz, 225 < T < 325 K). (4) Due to the thermally activated conductivity over the bulk, there is another rapid increase in permittivity at higher temperatures. More importantly, Fig. 8 and the mentioned discussion show some similarity to the permittivity of relaxers [44] in which the contributions of various sources to the permittivity over the entire temperature range differ. As will be shown below, the statistical approach adopted by Liu et al. [44] can also be applied to the description of the response of polarons in BFN.

Fig. 8
figure 8

Temperature dependence of the real dielectric permittivity of the BFN measured at different frequencies. The solid lines are the fitting results according to Eq. (9)

Full size image

3.4 Fitting permittivity

In order to understand the properties of BFN, it is interesting to know the effective permittivity.

3.4.1 Effective permittivity

After simplification of the Maxwell–Wagner model we obtained the effective permittivity as [45, 46]

$${\varepsilon }^{*}={\varepsilon }_{\infty }+\frac{{\varepsilon }_{0}-{\varepsilon }_{\infty }}{1+i\omega \tau }-i\frac{\sigma \left(\upomega \right)}{{\varepsilon }_{0}\omega }.$$
(6)

The first term is a constant determined by the permittivity of both the grain and its boundary. The second contribution is of Debye type with the relaxation time determined by the conductivity and permittivity. The third term describes the contribution from the conductivity of grains and grain boundaries.

3.4.2 Broad temperature range

The Maxwell–Boltzmann distribution is used to estimate the number of active versus inactive polarons. [N1(Eb, T)] is the number of polarons with kinetic energy exceeding the potential well:

$${N}_{1}({E}_{\mathrm{b}},T)=N\sqrt{\frac{4}{\pi }}\sqrt{\frac{{E}_{\mathrm{b}}}{{k}_{\mathrm{B}}T}}\mathrm{exp}\left(-\frac{{\mathrm{E}}_{\mathrm{b}}}{{k}_{\mathrm{B}}T}\right)+N\mathrm{erfc}\sqrt{\frac{{E}_{\mathrm{b}}}{{k}_{\mathrm{B}}T}},$$
(7)

where Eb is the average depth of a potential well introduced to take into account the stress on the polarons, N is the total number of polarons in the system, kB is the Boltzmann constant, T is the temperature (in degrees Kelvin), and erfc is the complementary error function. The total dielectric permittivity is then given by

$$\varepsilon \left(T,\omega \right)={\varepsilon }_{1}\left(T,\omega \right){P}_{1}\left({E}_{\mathrm{b}},T\right)+{\varepsilon }_{2}\left(T,\omega \right){P}_{2}\left({E}_{\mathrm{b}},T\right),$$
(8)

where ε1(T, ω) and ε2(T, ω) represent the dielectric responses of the two polaron groups (active and inactive) ω is the probing frequency, and P1(Eb, T) = N1(Eb, T)/N, P2(Eb, T) = 1 − P1(Eb, T) account for the proportion of polarons in each group.

Based on the effective permittivity equation, we note that the permittivity results from the intrinsic polarization of polarons as well as the conductivity of the grains associated with the distribution of thermally activated polarons, which is often described by the Maxwell–Wagner effect. To account the contribution of grain conductivity associated with the distribution of thermally activated polarons in permittivity, Liu et al. [37] proposed to use the last term of the effective permittivity equation. Therefore, Liu L. et al. proposed the equation below to adjust the permittivity of CCTO over a wide temperature range

$$\varepsilon \left(T\right)=\frac{{\varepsilon }_{1}}{1+b\mathrm{exp}\left(-{\theta }/ {T}\right)} {P}_{1}\left({E}_{\mathrm{b}},T\right)+{\varepsilon }_{2}{P}_{2}\left({E}_{\mathrm{b}},T\right)+\frac{\sigma \mathrm{exp}\left(-{{E}_{\mathrm{con}}}/{{k}_{\mathrm{B}}T}\right)}{{\varepsilon }_{0}\omega },$$
(9)

where ε1, ε2, b, and θ are constants at a given frequency ω, ε0 is the vacuum permittivity, σ is the thermally activated conductivity including the contribution from the conductive charge carrier, and Econ is the activation energy for the conductive charge carrier’s migration and transport. Since CCTO ceramic has almost the same characteristics as BFN, we used this equation to simulate the permittivity over a wide temperature range.

We then use the last equation to adjust the permittivity as a function of temperature at different frequencies. The fit results are shown in Fig. 8 (solid line), we found that the fit curves are in good agreement with the experimental results (R2 > 99.98% in all frequencies). The results of the fit reveal a weak dependence of the value Eb on the probing frequency (Eb = 0.20 eV at 10 kHz). The activation energy Econ for the conductive charge carriers is generally more related to composition than to probing frequency. Econ = 0.25 eV is also calculated by simple average. For θ we notice a slight change with the probing frequency, θ = 2350 K.

To more understand the dielectric response of BFN, we also show P1(Eb, T), P2(Eb, T) and the function w1 in Fig. 9a, b

Fig. 9
figure 9

a P1 and P2 vs. temperature. b w1 vs. temperature

Full size image
$${w}_{1}\left(T\right)=\frac{1}{1+b\mathrm{exp}\left(\frac{-\theta }{T}\right)}.$$
(10)

Evidently, P1(Eb, T) and P2(Eb, T) show few changes with increasing temperature, which is in contrast to typical ferroelectric relaxers, such as Ba(Ti1−xZrx)O3 for x > 0.3, who has a smaller Eb [e.g., Ba(Ti0.6Zr0.4)O3] has Eb = 0.035 eV [47]. This characteristic implies a small number of “active” polarons which can overcome the potential confinement (P1 is small). Nevertheless, the large value of ε1 (2.24 × 108–1.25 × 1010 is significantly higher than that of typical relaxers) suggests a strong correlation of these polarons and may give a significant contribution to the permittivity once they overcome Eb. It is important to study P1 to have an idea about the active polarons but also it is necessary to know the ability of the polarons to align and this is what gives us the function w1.

The function w1(T) is a description of the ability of the polarons (which can surmount the potential well) to align with each other under thermal fluctuations. Figure 9b shows w1 vs. temperature. From this figure, we can see that at low temperature w1 is near one but near zero at high temperature (similar to the Fermi–Dirac function).

4 Conclusion

Dense BFN ceramic was made by solid-state reaction method at high temperature. The sample showed a single perovskite structure with no secondary impurities. X-ray diffraction refinement revealed a cubic phase at room temperature (space group Pm\(\overline{3 }\)m).

The electrical properties were found to be highly dependent on temperature and frequency. There are three regions of electrical conductivity in the lower temperature range, which are fitted by the DPL. As temperature increases, the DPL changes into a single power law. Multiple activation processes are detected. Cole–Cole plots provide that grain boundaries are more resistive than grains and reveal the presence of electrically inhomogeneous microstructure (grain surrounded by insulating grain boundary regions). The plot of dielectric constant as a function of temperature exhibits two broad peaks with high value of dielectric constant. The dielectric peaks observed were considered to be intrinsic and extrinsic type. Dielectric properties analysis exhibits a giant dielectric constant with low dielectric loss (0.14) at room temperature. We used the explicit formula proposed by Liu L. et al. to adjust the temperature dependence of the dielectric permittivity of BFN at different frequencies. This statistical model allows us to estimate the activation energy of the polarons and to show that the permittivity plateau comes from the equilibrium between the population and the polarizability of the active polarons. At high temperatures, conductive charge carriers play a key role in dielectric behavior.