1 Introduction

Magnetic refrigeration (MR) based on the magnetocaloric effect (MCE) is a promising technology that attracts growing attention because it consumes less energy and is more environment friendly than the current technology based on gas compression–expansion. Especially, the MCE taking place around room temperature was discovered recently [1] and this gives new opportunities for developing green cooling devices. The MCE is defined as the change in the adiabatic temperature of a magnetic material when it is magnetized or demagnetized. It is observed that the MCE greatly depends on temperature and is usually strongest around the phase transition temperature implying a close relationship between the MCE and magnetic-order changes [1]. Many magnetic materials with significant MCE near the Curie temperature (TC), such as Ni–Mn-based Heusler alloys, Gd-containing alloys, La–Fe-based alloys, rare-earth-based compounds, ferromagnetic perovskite manganite, and Fe–Zr-based amorphous alloys [1,2,3,4,5,6,7,8], were discovered. These materials have TC in the range of 200–400 K [1,2,3,4,5,6,7,8]. Therefore, they could be potential candidates for room-temperature MR.

Among advanced MR materials, Fe–Zr-based alloys recently have been studied extensively [9,10,11,12,13,14,15,16,17,18,19,20,21]. The main compositions of these alloys (Fe and Zr) are inexpensive. These alloys displayed a second-order magnetic phase transition. Magnetic entropy changes (ΔSm) of these materials are moderate but quite stable in a wide range of temperatures [9,10,11,12,13,14,15,16,17,18,19,20,21]. Therefore, the refrigerant capacity (RC) of these alloys is much broader than that of other typical magnetocaloric materials such as Gd, Gd–Si–Ge [22], Ni–Mn–Ga [23], and La–Fe–Si [24]. Besides, the TC of these alloys can be easily controlled by changing the Fe/Zr composition ratio or adding other elements. For example, the replacement of Fe or Zr in Fe–Zr–B–Co alloys by a small amount of Co gives an increase in the TC and ΔSm [13]. The TC of Fe88-xCoxZr8B4 alloys increases from 290 to 340 K when the Co content increases from x = 0 to x = 2 [13]. In Fe88-xZr11B1Cox and Fe88Zr11-xB1Cox ribbons, the largest value of the maximum magnetic entropy change (|ΔSm|max) of the Fe86Zr11B1Co2 alloy is 1.73 J kg−1 K−1 at 305 K, and the largest RC of the Fe88Zr9B1Co2 alloy is 149.7 J kg−1 for a magnetic field change (ΔH) of 15 kOe [13]. The effect of the B element was also found to be positive where a slight increase of the B content could improve the spontaneous magnetization (MS) as well as TC and in turn the room-temperature MCE of Fe–Zr–B alloys [15, 18]. The TC of Fe91-xZr9Bx amorphous alloys increases from 286 to 327 K corresponding to the B content changes from x = 3 to x = 5 [18]. The |ΔSm|max of the Fe87Zr9B5 amorphous alloy is 3.34 J kg−1 K−1 (ΔH = 50 kOe), which is about 1.5% and 5.4% higher than that of the Fe87Zr9B4 and Fe87Zr9B4 amorphous alloys [18]. On the other hand, some previous reports show that Mn or Cr substitution could reduce the TC of Fe–Zr-based alloys [11, 21, 25]. The TC of the Fe85-xZr10B5Mx (M = Mn, Cr) shifted down to room temperature via Mn or Cr substitution for Fe [25]. The glass-forming ability (GFA) of Fe–Zr-based alloys is improved significantly by a minor addition of Cr, so affecting both the |ΔSm|max and TC [11, 25, 26]. The TC of Fe84-xCrxB10Zr5Gd1 alloy linearly decreases from 410 to 300 K with the Cr content increasing from x = 2 to x = 8 [11], and a good RC = 110 J kg−1 was obtained with a magnetic field change of 15 kOe in an alloy with 4 at% of Cr [11].

Our previous work points out that the addition of the Nd element to Fe–Zr alloys can tune their TC in the range of room temperature [27]. However, some additional phases occurred with Nd doping as well, which could lead to a decrease of GFA and limit the MCE. Therefore, to get better GFA and for the goal of a higher MCE, in this study, we study the Fe–Zr alloy co-doping with Nd, Cr, and B. Namely, we investigated the crystalline structure, magnetic properties, and MCE of the Fe79Cr6B2Nd3Zr10 alloy ribbon prepared by the melt-spinning method. The results show that the |ΔSm|max value of the alloy is large in a wide range of operative temperature (i.e., a high RC) around room temperature. These characteristics and together with an easy fabrication make this alloy a good candidate for MR applications at room temperature.

2 Experimental

Alloy ribbons with nominal composition Fe79Cr6B2Nd3Zr10 were prepared from Fe, Cr, B, Nd, and Zr metals (purity of 99.9%) in an argon environment. Firstly, an alloy ingot was fabricated using the arc-melting method. The sample was turned over and re-melted five times to ensure its homogeneity. Then, amorphous alloy ribbons were prepared from the ingot by the rapid-quenching method using a single copper wheel. The highest velocity of the copper wheel, v = 40 m/s, was applied to prepare the alloy ribbons. The thickness of the obtained ribbons is about 30 μm. The crystalline phase structure of the alloy was investigated by powder X-ray diffraction (XRD) on an EQUINOX 5000 (Thermo Scientific, France) diffractometer with Cu-Kα radiation (λ = 1.5406 Å). All magnetic measurements were carried out using a vibrating-sample magnetometer with a maximum magnetic field of 12 kOe over a temperature range of 100–400 K.

3 Results and discussion

The room-temperature XRD pattern of the Fe79Cr6B2Nd3Zr10 alloy ribbon is shown in Fig. 1. One can see that there is only one low-intensity broad peak near 2θ = 43°, indicating the almost amorphous characteristics of this alloy. A similar result has been observed in many other Fe–Zr-based alloys such as Fe–Zr–Cu [10], Fe–Zr–B [15, 18], Fe–Zr–B–Co [13, 19], Fe–Sn–Zr [12], and Fe–Ni–Zr [28]. On the other hand, according to a previous research [27], the XRD pattern of the Fe87Nd3Zr10 alloy has diffraction peaks corresponding to Fe2Zr and α-Fe phase. Thus, it can be seen that the GFA of the Fe79Cr6B2Nd3Zr10 alloy ribbon was enhanced significantly by the replacement of a part of Fe by Cr and B. As shown in Refs. [14, 29], the TC of Fe–Zr-based alloys could be regulated around room temperature by making them amorphous. Therefore, the amorphous characteristics of the Fe79Cr6B2Nd3Zr10 alloy could be desirable for MR applications at room temperature.

Fig. 1
figure 1

XRD pattern (a) and EDS spectrum (b) of the Fe79Cr6B2Nd3Zr10 alloy ribbon

Full size image

The EDS spectrum (Fig. 1b) displays peaks corresponding to iron, chromium, neodymium, and zirconium. These are elements included in the nominal composition of the alloy, and no strange elements appeared. It should be noted here that boron is a light element with low photon energies, and therefore it is not detected by EDS. The obtained atomic percentages of the elements are quite close to those expected from the nominal composition. This means that the initial materials reacted completely to create the alloy.

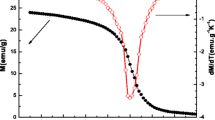
The temperature dependence of magnetization, M(T), of the Fe79Cr6B2Nd3Zr10 alloy measured in an applied magnetic field of 100 Oe is shown in Fig. 2a. It points out that the alloy has a ferromagnetic–paramagnetic (FM–PM) phase transition at its TC. The TC of the alloy, determined as the temperature at the minimum of the dM/dT versus T curve (see inset of Fig. 2a), is ~ 298 K. This reflects that the alloy is promising for MR at room temperature.

Fig. 2
figure 2

a Temperature dependence of magnetization (left) and magnetic susceptibility (right) at a field of 100 Oe, inset shows dM/dT versus T curve; b hysteresis loops at room temperature, the inset enlarges the hysteresis loops at the low magnetic field of the Fe79Cr6B2Nd3Zr10 alloy ribbon

Full size image

Figure 2a also shows the temperature dependence of the inverse magnetic susceptibility of the alloy, χ−1(T) = H/M, which was derived from the M(T) curve in the PM region. According to the Curie–Weiss law, the susceptibility χ in the PM region can be examined using the formula: χ(T) = C/(T − θ), where θ is the Curie–Weiss temperature and C is the Curie constant [30]. To determine the values of θ and C, the linear region of the χ−1(T) curve is fitted with the law [30]. One can see from Fig. 2a that the χ−1(T) curve of the Fe79Cr6B2Nd3Zr10 alloy becomes linear only in the temperature region above 310 K, which is resulted from the broad phase transition. The fitted value for θ is 303 K, which is almost equal to the TC. The FM–PM phase transition is re-confirmed by the positive value of θ. The value of θ is little different from the TC, which could be caused by the broad FM–PM phase transition [30] and related to FM clusters existing right above TC [28].

The effect of co-doping on magnetic properties of the alloy can be investigated through its effective magnetic moment µeff. From the Curie constant C (in the unit of emu K mol−1 Oe−1), we can calculate µeff (in the unit of Bohr magneton) via the expression/formula [31]: \(C = \frac{{N_{A} }}{{3k_{B} }}\mu _{{eff}}^{2}\) or \(\mu _{{eff}} = \sqrt {\frac{{3k_{B} C}}{{N_{A} }}} \approx \sqrt {8C}\), where NA = 6.022 × 1023 mol−1 is the Avogadro's number, µB = 9.274 × 10–21 emu is the Bohr magneton, and kB = 1.38016 × 10–16 erg/K is the Boltzmann constant. The obtained value of µeff for the alloy is 6.55 µB. This value is higher than the theoretical spin-only moment of Fe2+ (4.90 µB), Fe3+ (5.92 µB), Cr2+ (4.90 µB), Cr3+ (3.87 µB), and the moment with orbital contribution of Nd3+ (3.52 µB) [32]. This behavior possibly implies an enhancement of FM interaction in the alloy. Further, a value of µeff ≈ 5.0 µB was also evaluated for the Fe87Nd3Zr10 alloy from our reported data in Ref. [27], which is lower than the µeff of the Fe79Cr6B2Nd3Zr10 alloy. This result suggests that the FM exchange interaction in the Nd-doped-only alloy was enhanced more by B and Cr addition. Here, it should also remind that B dopant increases the direct Fe–Fe interaction and thus increases the µeff of Fe–Zr alloys [18]. According to Ding et al., a high value of µeff caused by strong interactions between magnetic moments broadens the phase transition region leading to an increase of RC [33, 34].

Figure 2b shows the hysteresis loop, M(H), of the Fe79Cr6B2Nd3Zr10 alloy ribbon measured at room temperature (300 K). The magnetization curve is unsaturated with the maximum magnetic field. This is a common characteristic of the M(H) curve of a ferromagnetic material when it is measured at temperatures near its magnetic transition temperature. The maximum magnetization at H = 12 kOe is M12kOe = 34.8 emu/g. The coercivity Hc is small, Hc < 20 Oe at room temperature (see inset in Fig. 2b). Therefore, the alloy is valuable for MR applications because the effect of magnetic hysteresis would be very small.

To quantify the MCE of the Fe79Cr6B2Nd3Zr10 alloy, the magnetic entropy change ΔSm and refrigerant capacity RC of the alloy were calculated. To examine ΔSm, the series of isothermal magnetization curves, M(H, T), around the magnetic phase transition temperature was determined at various temperatures with a magnetic field varying from 0 to 12 kOe (Fig. 3a). Then, ΔSm was calculated using Maxwell’s relation [35]:

$$\Delta S_{m} = \int\limits_{0}^{H} {\left( {\frac{{\partial M}}{{\partial T}}} \right)} _{H} dH$$
(1)
Fig. 3
figure 3

Magnetization versus magnetic field at various temperatures (a), and temperature and magnetic field change (up to 12 kOe) of the magnetic entropy change ΔSm of the Fe79Cr6B2Nd3Zr10 alloy ribbon (b)

Full size image

In practice, this equation can be approximately rewritten as follows [35]:

$$\Delta S_{m} = \sum\limits_{i} {\frac{{M_{{i + 1}} \left( {T_{{i + 1}} ,H} \right) - M_{i} \left( {T_{i} ,H} \right)}}{{T_{{i + 1}} - T_{i} }}} \Delta H.$$
(2)

Figure 3b represents the temperature dependence of − ΔSm of the Fe79Cr6B2Nd3Zr10 alloy ribbon in applied magnetic field changes which range from ΔH = 0–12 kOe. The results show that the magnitude of − ΔSm increases when ΔH increases. The − ΔSm increases with increasing temperature and reaches maximum values |ΔSm|max around the TC, corresponding to the FM–PM phase transition. Besides, one can also see that the temperature at the peak of the  − ΔSm(T) curves is almost unchanged, which is because of the nature of the second-order phase transition. The |ΔSm|max value of the Fe79Cr6B2Nd3Zr10 alloy was found to be 0.99 J kg−1 K−1 at T = 298 K with ΔH = 12 kOe. This value is similar or larger than that of other Fe–Zr-based amorphous alloys such as Fe89Zr8B3 [9], Fe91-xZr9Cux [10], Fe84-xCrxB10Zr5Gd1 [11], Fe91-xZr9Bx [15], Fe88-xZr8B4Cox, and Fe88-xZr8B4Mnx [21] (Table 1).

Table 1 The magnetocaloric effect of Fe79Cr6B2Nd3Zr10 alloy ribbon was studied in this work and the Fe–Zr-based amorphous alloys were reported previously
Full size table

After the  − ΔSm(T) curves were determined, one can derive the refrigerant capacity RC of the alloy. The RC of a magnetocaloric material is defined as the following equation [30]:

$${\text{RC}} = |\Delta S_{m} |_{{{\text{max}}}} \times \delta T_{{{\text{FWHM}}}},$$
(3)

where δTFWHM is the full width at half maximum of the  − ΔSm(T) curve. The δTFWHM is usually considered as the operating temperature range of a magnetic refrigerant [30].

The value of δTFWHM obtained from the  − ΔSm(T) curves in Fig. 3 is quite large, δTFWHM ≈ 85 K, leading to a high value of refrigerant capacity, RC ≈ 84.1 J kg−1 with ΔH = 12 kOe. One should be noted that this value of RC is comparable or greater than that of many other reported Fe–Zr-based amorphous alloys as shown in Table 1. On the other hand, comparing with the previous study of the Fe87Nd3Zr10 alloy [27], with the addition of Cr and B, though the |ΔSm|max of the Fe79Cr6B2Nd3Zr10 alloy is almost unchanged, the RC is significantly improved. Therefore, at a wide working temperature range and a high MCE around room temperature, Fe79Cr6B2Nd3Zr10 alloy ribbon becomes a good candidate for MR applications at room temperature.

To understand clearly the nature of the magnetic phase transition and magnetic ordering in the Fe79Cr6B2Nd3Zr10 alloy, Arrott plots (M2 versus H/M curves) were constructed based on M(H, T) data in the temperature range from 276 to 320 K (Fig. 4a). According to Banerjee’s criteria [36], the kind of magnetic phase transition can be easily specified from the slope of M2 versus H/M curves. Namely, a positive/negative sign of the slope of the Arrott plot corresponds to a second-/first-order phase transition, respectively [36]. Comparing these conditions, all the plots in Fig. 4a show positive slopes, revealing the FM–PM transition of the Fe79Cr6B2Nd3Zr10 alloy belonging to a second-order magnetic transition (SOMT).

Fig. 4
figure 4

Modified Arrott plots of M1/β versus (H/M)1/γ with the mean-field model (a), 3D Heisenberg model (b), 3D Ising model (c), and tricritical mean-field model (d) for the Fe79Cr6B2Nd3Zr10 alloy ribbon

Full size image

Besides, the characters of the FM interactions in the alloy can be examined from the critical parameters β, γ, and δ. These parameters of a magnetic material with a second-order magnetic transition can be derived from the following relations for the spontaneous magnetization MS below TC, the inverse initial susceptibility χ0–1 above TC, and the magnetization isotherm at TC [37]:

$$M_{S} (T) = M_{0} ( - \varepsilon )^{\beta } ,\,\,\,\varepsilon {\text{ < }}0,$$
(4)
$$\chi _{0}^{{ - 1}} {\text{ = (}}{{H_{0} } \mathord{\left/ {\vphantom {{H_{0} } {M_{0} }}} \right. \kern-\nulldelimiterspace} {M_{0} }}{\text{)}}\varepsilon ^{\gamma } ,\,\,\,\varepsilon {\text{ > }}0,$$
(5)
$$H = DM^{{{1 \mathord{\left/ {\vphantom {1 \delta }} \right. \kern-\nulldelimiterspace} \delta }}} ,\,\,\,\varepsilon = 0,$$
(6)

where Mo, Ho, and D are critical amplitudes, and ε (T − TC)/TC is the reduced temperature.

To evaluate the critical parameters in the Fe79Cr6B2Nd3Zr10 amorphous alloy, a standard procedure using the modified Arrott plots (MAPs) was applied. The procedure is based on the Arrott–Noakes equation of state as follows [37]:

$$\left( {H/M} \right)^{{{\text{1}}/\gamma }} = a \times \varepsilon + b \times M^{{{\text{1}}/\beta }},$$
(7)

where a and b are material-dependent parameters. According to this equation, the M1/β versus (H/M)1/γ curves at temperatures around TC in the high-field region should be parallel straight lines, and the line at TC should go through the coordinate origin. Figure 4a–d presents the MAPs for the Fe79Cr6B2Nd3Zr10 alloy constructed using four types of trial exponents: the mean-field model (β = 0.5, γ = 1.0) (Fig. 4a), the 3D Heisenberg model (β = 0.365, γ = 1.336) (Fig. 4b), the 3D Ising model (β = 0.325, γ = 1.24) (Fig. 4c), and the tricritical mean-field model (β = 0.25, γ = 1.0) (Fig. 4d) [35]. The obtained results show that in the high-magnetic-field region, all lines are nearly parallel to each other for the first three models but not for the latter one (Fig. 4d). The lines in Fig. 4d are not parallel, showing that the tricritical mean-field model is inappropriate to interpret the critical behavior of the alloy. For the three remaining models, relative slopes RS = S(T)/S(TC) of Arrott plots were calculated, where S(T) and S(TC) are the slopes of the quasi-straight lines in the high-field region at T and TC, respectively. The most suitable model is the one whose RS approaches to 1 independently of temperature [38]. The temperature dependence of the RS for the Fe79Cr6B2Nd3Zr10 alloy is presented in Fig. 5. It appears that the RS values of the mean-field model are much closer to unity. Therefore, the mean-field model is the most suitable one to determine the critical parameters of the Fe79Cr6B2Nd3Zr10 alloy, and the values of β = 0.5 and γ= 1.0 were applied for further calculations on critical behaviors. By linear fitting of M1/β versus (H/M)1/γ curves at high-field region, one can determine the values of the spontaneous magnetization MS(T) and inverse initial susceptibility χ−10(T) of the alloy, which are the intersections to M1/β and (H/M)1/γ axes, respectively. Next, by fitting these MS(T) and χo−1(T) data with Eqs. (4) and (5), a new set of β, γ, and TC was obtained. After that, these β and γ values are used to plot new MAPs. This procedure was repeated several times until β and γ reach stable values. The final values of critical parameters, MS(T), χo−1(T), and their fitting curves are presented in Fig. 6. The values of critical parameters found from the best fits are β = 0.486 ± 0.021 with TC = 297.9 K ± 0.115 (from Eq. 4) and γ = 1.068 ± 0.017, TC = 298.4 K ± 0.387 (from Eq. 5). Based on the statistical theory, the δ parameter can be determined from Widom’s scaling relation [39], δ = 1 + γ/β, yielding δ = 3.197 ± 0.038. So, the critical parameters β, γ, and δ determined by the MAPs method are β = 0.486 ± 0.021, γ = 1.068 ± 0.017, and δ = 3.197 ± 0.038. Among the examined models, the critical parameters of the Fe79Cr6B2Nd3Zr10 alloy are much closer to the mean-field theory, revealing the existence of long-range ferromagnetic orders [35]. Long-range FM interactions were also found in other Fe–Zr-based amorphous alloys such as Fe80Cr5B2Gd2Zr10 [26], Fe85Ni5Zr10 [28], (Fe0.74Cu0.26)85Zr15 [38], and Fe77Co5.5Ni5.5Zr7B4Cu [40] alloys. It should also be noticed that the β value of the alloy ribbon is smaller than 0.5, which indicates the existence of magnetic inhomogeneity in the alloy [26, 28]. However, on comparing with the β = 0.365 obtained previously in the Fe90Zr10 parent alloy [28], it can be seen that the β value of the Fe79Cr6B2Nd3Zr10 alloy is higher. This suggests that the Fe79Cr6B2Nd3Zr10 alloy becomes more magnetically homogeneous with Nd, Cr, and B co-doping. Besides, the values of TC of the alloy obtained from the fitting procedure and directly from the minimum of dM/dT versus T curve are almost equal, showing that the fitting procedure is correct.

Fig. 5
figure 5

Temperature dependence of the relative slope RS for the Fe79Cr6B2Nd3Zr10 alloy ribbon

Full size image
Fig. 6
figure 6

Temperature dependence of spontaneous magnetization Ms(T) (left) and inverse initial susceptibility χ−10(T) (right) along with Arrott plots of the Fe79Cr6B2Nd3Zr10 alloy ribbon

Full size image

Alternatively, the Kouvel–Fisher method (K–F plots) can be used to estimate the critical parameters of the alloy by reformulating Eqs. (1) and (2) as follows [41]:

$$M_{S} \left( T \right)\left[ {dM_{S} /dT} \right]^{{ - 1}} = \left( {T - T_{C} } \right)/\beta,$$
(8)
$$\chi _{0} ^{{ - 1}} (T){\text{[}}d\chi _{0} ^{{ - 1}} (T)/dT]^{{ - 1}} = (T - T_{C} )/\gamma.$$
(9)

The relations (8) and (9) show that Ms(T)/(dMS(T)/dT) and χ0−1(T)/(dχ0−1(T)/dT) are linearly dependent on temperature with slopes 1/β and 1/γ. Therefore, the critical parameters β and γ can be obtained by a linear fitting of the K–F plots with the experimental data, as shown in Fig. 7 for the Fe79Cr6B2Nd3Zr10 alloy. For temperature below TC, the fitted values of β and TC are β = 0.482 ± 0.008 and TC = 298.2 K ± 2.64. For temperatures above TC, the values of γ and TC are γ = 1.060 ± 0.024 and TC = 298.7 K ± 1.387. The value of δ, calculated using Widom’s scaling equation, is δ = 3.199 ± 0.032. One should be noted that these values of critical parameters are very compatible with those determined from the MAPs method, confirming that the calculated critical parameters are reliable.

Fig. 7
figure 7

Kouvel–Fisher plots for the Fe79Cr6B2Nd3Zr10 alloy ribbon

Full size image

We also use the static-scaling theory [35] to assess the reliability of the calculated critical parameters. The isothermal magnetization around the TC follows the magnetic equation of state [35]:

$$M(H,\varepsilon ) = \varepsilon ^{\beta } f_{ \pm } (H/\varepsilon ^{{\beta + \gamma }} ),$$
(10)

where \(f_{ + }\) and \(f_{ - }\) are regular functions for T > TC and T < TC, respectively. Equation (10) means that if β, γ, and TC have correct values, the M|ε|β versus H|ε|(β+γ) curve should fall into two branches corresponding to the functions \(f_{ + }\) and \(f_{ - }\) for T > TC and T < TC, respectively. Figure 8 presents the static-scaling plots of M|ε|β versus H|ε|(β+γ) with the critical parameters obtained from the MAPs method, and the inset of Fig. 8 shows the log–log scale plots of M|ε|β versus H|ε|(β+γ) with the ones obtained from the Kouvel–Fisher method. All the data points are separated into two universal branches, one for T > TC and the other one for T < TC. This behavior indicates the accuracy and reliability of the critical parameters obtained from the MPAs and Kouvel–Fisher methods.

Fig. 8
figure 8

Scaling plot of M|ε|β versus H|ε|(β+γ) for the Fe79Cr6B2Nd3Zr10 alloy ribbon at temperature T < TC and T > TC. The inset shows the same plots on a log–log scale

Full size image

There is an alternative method to assess the obtained critical parameters. The dependence of the maximum magnetic entropy change on the magnetic field is as follows [42,43,44,45,46]:

$$|\Delta S_{{\text{m}}} |_{{{\text{max}}}} = \alpha \times H^{n},$$
(11)

where α is a proportional constant and n is a scaling parameter. Therefore, by fitting |ΔSm|max data as a function of H to the Eq. (11), the value of n is found to be n = 0.671 ± 0.009 (shown in Fig. 9a). This value is close to that obtained by the mean-field theory approach, n = 2/3 [42, 46]. This result indicates an existence of long-range ferromagnetic orders in the alloy.

Fig. 9
figure 9

The maximum entropy change |ΔSm|max versus (ΔH)n and a universal ΔSm/(ΔSm)max versus θ curves

Full size image

At TC, the scaling parameter n can be associated with the critical parameters β, γ as follows [31, 43,44,45]:

$$n = 1 + ~\frac{{\beta - 1}}{{\beta + \gamma }}.$$
(12)

Using the β and γ values obtained by the MAPs and K–F methods, n values calculated from Eq. (12) are n = 0.669 ± 0.038 and 0.664 ± 0.032, respectively. These values of n are in good agreement with the value obtained from Eq. (11). Therefore, it re-confirms about accuracy of the above analysis methods for the critical parameters.

Once again, to understand the nature of phase transition, one can also follow a method proposed by Franco et al., which uses phenomenological universal curves  − ΔSm(T) [43]. These universal curves are constructed by rescaling the dependence of ΔSm on temperature. The ΔSm is normalized by (ΔSm)max, and the T is normalized by a new parameter θ. The parameter θ is determined as follows [43,44,45,46]:

$$\theta = \left\{ {\begin{array}{*{20}c} { - (T - T_{{\text{C}}} )/(T_{{{\text{r1}}}} - T_{{\text{C}}} ),{\text{ }}T \le T_{{\text{C}}} } \\ {(T - T_{{\text{C}}} )/(T_{{{\text{r2}}}} - T_{{\text{C}}} ),{\text{ }}T \ge T_{{\text{C}}} } \\ \end{array} } \right.,$$
(13)

where Tr1 and Tr2 are reference temperatures obtained from the relation ΔSm(Tr1) = ΔSm(Tr2) = k|ΔSm|max with the ratio k is an arbitrary number in the range of 0–1 [43,44,45,46]. In this study, k = 0.5 was chosen. Figure 9b shows universal curves of the Fe79Cr6B2Nd3Zr10 alloy. One can see that these ΔSm/(ΔSm)max curves determined for different ΔH values collapse into a universal curve in the whole temperature range. This behavior again proves that the alloy ribbon undergoes a second-order FM–PM phase transition.

4 Conclusion

In summary, we have studied the crystalline structure, magnetic properties, the magnetocaloric effect, and the critical behavior of the Fe79Cr6B2Nd3Zr10 alloy ribbon. The alloy is almost amorphous. This alloy undergoes a second-order FM–PM phase transition around its Curie temperature TC = 298 K. For a magnetic field change of 12 kOe, the alloy has a high magnetic entropy change (|∆Sm|max ≈1 J Kg−1 K−1) in a wide working temperature range (δTFWHM = 85 K) and at a large refrigerant capacity (RC = 84.1 J kg−1). Therefore, the alloy could be a potential magnetic refrigerant at room temperature. Using both MAPs and Kouvel–Fisher methods, and Widom’s equation, a set of the critical parameters was determined as β = 0.486 ± 0.021, γ = 1.068 ± 0.017, and δ = 3.197 ± 0.038. These values of critical parameters are close to those of the mean-field theory, revealing the existence of long-range ferromagnetic orders.