The main role of bismuth in controlling linear and nonlinear optical, electronic and electrical parameters of Se–Ge–Bi thin films

Abstract

A widespread analysis of the structural, optical, electronic and electrical properties of Se₈₀Ge_20-xBi_x with (x = 0, 5, 10, 15 and 20 at.%) glasses were carried out. The bulk materials of the studied films have been prepared utilizing the usual melt quench procedure. Thus, the thin film has been deposited under a vacuum of 10^–5 Torr on cleaned glass substrates by thermal evaporation. The supreme purpose of this research is to highlight the role of adding bismuth to the films studied as a regulator and controller for the linear and nonlinear parameters. The thickness of the studied thin films has been mathematically determined by the methods of Swanepoel. Using logarithmic functions, it has been proven that the electron transport mechanism between the valence and conduction bands is an allowed indirect transition. Linear optical parameters, dielectric constants and also dispersion parameters have been calculated. The energy-loss functions (VELF and SELF) were discussed. The effect of Bi concentration in the studied thin films on the linear and nonlinear optical properties is determined based on the optical measurements (transmittance and reflectance spectra). The optical bandgap decreases with increasing Bi concentration; while the tail energy portrays an opposite behavior. Linear optical and electrical parameters are found significantly affected by the change of Bi concentration. In contrast, the nonlinear optical parameters have been computed utilizing (H. Ticha and L. Tichy) and Boling formula. Energies of Plasmon, Penn and Fermi and the electronic polarizability have been determined. Furthermore, the DC electrical conductivity has been studied as a function of both temperature in the thermal range from 300 to 500 K and also Bi concentration. In the extended and hopping regions, the activation energy and pre-exponential factor were extracted from the slopes and intercepts of straight lines. It has been found that increasing Bi content is controlled the electrical parameters and reduces the activation energies in the regions of the extended and the hopping states.

1 Introduction

Chalcogenides are an essential group of supplies owing to their innovative and extensive variety of applications in various fields such as infrared optics, acousto-optical instruments, electronic and optoelectronic switching tools and optical phase-change recording PCOR systems [1]. This latter application has received a significant focus in recent years. In this, with the aid of a concentrated laser beam, the structure of the active material is often switched between amorphous and crystalline states. Due to their properties including such variable dimensionality of the network and a higher degree of contrapuntal independence, Chalcogenide materials are possible candidates for PCOR technologies [2].

Chalcogenide compounds of considerable importance due to their value in photographic memory maintenance [3] and their optical uses as a strong IR transmission medium [4, 5]. In addition, they are important as core materials for transmission fiber optics, especially when short length and flexibility are required [6, 7].

The optical properties of Se_0.62Ge_0.38 and Se_0.62Ge_0.35X₀.₀₃ where [X = In, Sb and Bi] thin films have been studied by Fayek and Ibrahim [8]. Thin films used in such analyses were generated on glass substrates through thermal evaporation. The spectral distribution and optical properties were studied using spectrophotometric transmittance and reflectance experiments from 400 to 2500 nm in the wavelength spectrum. Analysis of the optical absorption data shows the presence of allowed indirect transitions. The linear parameters for the optical dispersion were calculated using a single oscillator modeling from Wemple–DiDomenico. The Swanepoel model has been used to calculate the linear optical constants such as optical bandgap, complex dielectric constant and dissipation factor tan (δ).

Mitkova et al. [9] studied the thermal and photo-induced dispersion of Ag in thin amorphous Ge₂₀Se₈₀ films, with exacting consideration being paid to the kinetics of the reaction and the resulting local structure. Differences, such as the two diffusion methods, are presented and discussed around the volume of silver diffused in the films, and the variations in the host film’s backbone composition. The diffusion of Ag in this specific composition of chalcogenide glass results in the creation of a phase-separated structure composed of the Ge–Se backbone and Ag₂Se or Ag nanocrystals.

It was proposed that the integration of Bi into the Ge₂₀Se₈₀ system would contribute to improvements in the formation of evaporated ternary films. Possibly, there is a uniform network of tetrahedral GeSe_4/2 and pyramidal BiSe_3/2 structures linked by Se atoms in the glassy Ge–Se–Bi framework [10, 11].

Chalcogenide glasses typically tend to be p-type conductivity, which is endorsed to the pin of the Fermi stage [12, 13], the trapping of loads and carriers at high compactness localize gap states [14], and accordance by the Mott rule [15].

Tohge and his colleagues [16, 17] investigated the effects of Pb and Tl doping on chalcogenide materials. They found that Pb atoms reversed the form of the conductions. Thallium atoms simply enhance the electrons’ contribution to electrical conduction; therefore, there is no reversal of the conduction process. Such findings contribute to the inference that successful doping occurs horizontally in the periodic table, not in the vertical line (group V), and open the field for practical applications in the manufacture of p–n devices [18, 19].

The study focused on network modeling led Phillips [20] to infer that the inversion of this ternary structure happens in the vicinity of the percolation threshold and is the product of transport irregularities in the structure. Storiopoulos and Fuhs [21] demonstrate that a drastic decrease in the bandgap requires a rise in conductivity and a reversal of the type of conduction. Study into the compositional dependency of resistance, specific heat, etc. follows the Phillips model, where the predictions provided are that such glasses are inhomogeneous on a medium-range scale and at a critical concentration of the p-type conductivity, the transformation to the n-type happens.

The intrinsic defects in chalcogenide glasses derive primarily from the reconfiguration of the prevalent chain ends and are represented either as $D^{ + }$(donor) and $D^{ - }$(acceptor) charged dangling bonds or equivalently as $C^{ + }$ and $C^{ - }$ valence alternation pairs (VAP) [22, 23]. In comparison, VAPs that are very similar to each other are labeled romantic valence alternation pairs (IVAP).

The reduced disruption in the optical bandgap with annealing close crystallization temperature, $T_{c}$, may be explained based on amorphous–crystalline transformation, where the thermal mechanism is recognized to be essential for inducing crystallization in semi-conductive chalcogenide glasses [24, 25]. The crystallization of chalcogenide film is characterized by a reduction in the optical bandgap. Furthermore, there are great efforts and studies that indicate the importance of Ge–Se–Bi’s systems in the optical sides and among these efforts are the corresponding references [26,27,28].

The main goal of the present framework is extended to the previous studies by investigating the influence of the change of Bi content on the optical, electronic and electrical properties for the Se–Ge–Bi thin films. From this perspective, from the optical measurements, we will extract linear and nonlinear parameters. As well, to determine the structural nature and then correlate by the optical properties, XRD analysis is used. Thus, in this framework, these aspects and also the electronic properties are simply tackled.

2 Experimental procedures

Glassy alloys of Se₈₀Ge_20-xBi_xwith (x = 0, 5, 10, 15 and 20 at.%) were prepared by the usual melt quench technique. Highly pure materials (99.999%) were weighted according to their atomic percentages, using an electrical balance type (Sartorius) with accuracy (± 10⁻⁴ g) and sealed in an evacuated silica tube (10^–5 Torr) and it was heated at 1000 °C for 32 h. During the melting process, the tube was frequently rocked to intermix the constituents and to increase the homogenization of the liquid. The powdered samples were prepared by grinding of the resulting bulk alloy samples in a mortar whereas the thin films of Se₈₀Ge_20-xBi_xwere deposited onto well-cleaned glass substrate at room temperatures by thermal evaporation technique using a high vacuum coating unit (Edward E 306A, UK). The thickness of the investigated films was kept ~  750nm. The structure of the organized films was analyzed by XRD examination (Philips-X-ray diffractometry (1710) with Cu Kα radiation target (λ = 0.15418 nm)). The data of intensity were obtained using a small interval phase scanning mode (Δ2θ = 0.02°). Measurements of both reflection and transmission were performed via a double-beam spectrophotometer (Shimadzu UV-2101 in combination with PC), at the perpendicular light incidence and within a range of wavelength extended from 400 to 2500 nm. The measured transmittance spectra were used to calculate the refractive index and the film thickness of Se₈₀Ge_20-xBi_xthin films without a glass substrate in the reference beam. To obtain resistance–temperature measurements, the electric current at a constant voltage supply was measured against temperature and the phase transition temperature, T_c of the investigated film was computed. Post-deposited Al electrodes in a square geometry (5.0 mm) were used for resistance–temperature measurements, carried out in the running vacuum. The current was measured by a digital picoammeter (DPM-111 Scientific Instruments, Roorkee) and a four-point probe method was used for measuring electrical properties.

3 Results and discussion

3.1 XRD, TGA and DSC analyses

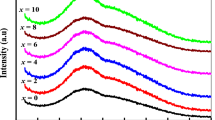
Figure 1a demonstrates the XRD patterns of the studied thin films. Such a figure reveals broad peaks without any sharp crystallization peaks, suggesting that such films have an amorphous nature. On the other hand, standard ChGs are produced for glass processing by co-fusion of sufficient raw elements, in appropriate quantities, under vacuum in silica reaction tubes. The melt is agitated at Tm to ensure the homogeneity of the melt and then quenched rapidly, usually in ice, to freeze the material into an amorphous block structure. For comparison with the different purification protocols described in the next section, we first prepared bulk Se–Ge–Bi glasses using standard melt-quenching technique. The high purity of Se, Ge and Bi (99.999%) were weighted according to their atomic percentages, using an electrical balance type (Sartorius) with accuracy (± 10–4 g), which assembled into a nitrogen-disinfected glove box and closed with a gas-oxygen torch under vacuum in silica ampoules. Before sealing and melting, the batch was preheated at 100 °C for 4 h under vacuum to remove surface moisture from the silica ampoule and the raw materials. The ampoule was then sealed and heated up for 24 h at 900 °C while kept under constant rocking to increase the homogeneity of the melt. To relax quench-induced stress in the glass ingot and to avoid its fracture during fabrication, the ampoule was subsequently returned to the furnace for annealing for 15 h at ~ 150 °C, that is to say 37 °C below the glass transition temperature of the glass. Figure 1b portrays both the glass transition temperature and the temperature of annealing in terms of DSC and TGA curves for Se₈₀Ge₁₅Bi₅ powder sample.

Fig. 1

XRD patterns of the films, TGA and DSC of the first powder sample

3.2 Optical measurements, T (λ) and R (λ)

While talking of the optical measurements in the thin films, two significant physical quantities automatically come to mind. The two quantities are the transmittance $T(\lambda )$ and the reflectance $R(\lambda )$. For the studied films, Fig. 2 depicts the behavior of these two quantities in terms of wavelength within a spectral range from 400 to 2500 nm. This spectral range was sufficient to show the behavior of the two quantities in the strong, weak, and medium absorption regions, not to mention the behavior in the transparency region. In exploring the depths of this figure, there is a strong convergence of the transmittance and reflectance of thin films from the transmittance and reflectance of the glass substrate in the region of transparency. This behavior makes the studied films highly eligible for use in modern electronics along with their uses in optical devices and all the related applications. Due to the appearance of the interference caused by the multiple reflections between the layers of the air—a thin film—a glass substrate, one must resort to the Swanepoel equations which are given for uniform thin films. These equations calculate the physical quantities of interference at the extreme points of two adjacent peaks or bottoms.

Fig. 2

Transmission and reflection spectra for the studied thin films

The following points summarize the interference steps and the equations that we ultimately will utilize to evaluate the precise thickness and indeed the precise refractive index of such films.

• According to the following relationship, the refractive index of the glass substrate $s(\lambda )$ has been computed as follows [29]:

$$s(\lambda ) = (T_{s} (\lambda ))^{ - 1} + \sqrt {((T_{s} (\lambda ))^{ - 2} - 1)}$$

(1)

Here, $T_{s} (\lambda )$ represents the transmission of the glass substrate theoretically computed by the subsequence equation:

$$T_{s} (\lambda ) = 0.89{ - 8}{\text{.024}} \times {10}^{{ - 5}} .\lambda + {6}{\text{.14}} \times {10}^{{ - 8}} .\lambda^{2} - {1}{\text{.39}} \times {10}^{{ - 11}} .\lambda^{3}$$

(2)

Mathematically, the reflectance of the glass substrate has been estimated from the following equation where its refractive index was defined:

$$R_{s} (\lambda ) = \left( {\frac{s(\lambda ) - 1}{{s(\lambda ) + 1}}} \right)^{2} .$$

(3)

The obtained values of $T_{s} (\lambda )$, and $R_{s} (\lambda )$ are deposited in Fig. 2 as straight lines.

• According to the idea of Manifacier et al. [29], the higher and lower extreme fingers of the envelope T_M (λ) and T_m (λ), respectively, have been determined utilizing envelope.exe program. The obtained values have been reported in Table 1 and also represented in Fig. 3 for the first sample as an example to the rest samples. In such a figure, $T_{\alpha } (\lambda )$ denotes the geometric mean of $T_{M} (\lambda )$ and $T_{m} (\lambda )$, namely, $T_{\alpha } (\lambda ) = \sqrt {T_{M} (\lambda ).T_{m} (\lambda )}$.

• The crude refractive index of the studied thin film have been easily calculated after knowing values of $s(\lambda )$, $T_{M} (\lambda )$ and $T_{m} (\lambda )$ depends on the following relation [30, 31] (see Table 1):

$$n_{j} (\lambda ) = 2.s.[\frac{{(T_{M} - T_{m} )}}{{(T_{M} .T_{m} )}}] + [\frac{{s^{2} + 1}}{2}] + \sqrt {\{ 2.s.[\frac{{(T_{M} - T_{m} )}}{{(T_{M} .T_{m} )}}] + [\frac{{s^{2} + 1}}{2}]\}^{2} - s^{2} } .$$

(4)

Table 1 Values of two envelopes, T_M, T_m and the rest interference parameters (according to text) for the first thin film with (750 nm)

Fig. 3

Variation of the typical spectral transmittances and reflectance vs. wavelength for the first thin film

The obtained values of $n_{j} (\lambda )$ show as $n_{1}$ in Table 1.

• The crude, and accuracy thickness ($d_{1}$ and $d_{2}$, respectively) and then the exact refractive index of the studied thin films, $n_{2}^{*}$ have been computed according to the following equations [31]:

$$d_{1} = \frac{1}{2}.(\lambda_{1} .\lambda_{2} ) \times [\lambda_{1} n_{2} - \lambda_{2} n_{1} ]\,^{ - 1} ,$$

(5)

$$m_{o} = \frac{{2 \times n_{1} \times \overline{{d_{1} }} }}{{\lambda_{1} }},$$

(6)

$$d_{2} = m.(\frac{{\lambda_{1} }}{{2n{}_{1}}}),$$

(7)

$$n_{2}^{*} = \frac{{m\lambda_{1} }}{{2 \times \overline{d}_{2} }}.$$

(8)

Here, $\lambda_{1}$ and $\lambda_{2}$ are wavelengths equivalent to the opposite extreme points of the spectrum (left and right, respectively). The values of $\lambda_{2}$ corresponding to the extrema points are $\lambda_{2M}$ (where M = 1, 2, 3….N) equivalent the $\lambda_{1(M + 2)}$. The same is for values of $n_{1}$ and $n_{2}$. $\overline{{d_{1} }}$ is the average of $d_{1}$ values, the same for $\overline{{d_{2} }}$. As well, $m_{o}$ is a set of order numbers while $m$ in the above equations represents an approximation of values $m_{o}$ to the nearest integer or half-integer values. $n_{2}^{*}$ is the accurate values of the refractive index for the studied thin films. All the mentioned values are offered in Table 1.

• The refractive index, $n(\lambda )$ of the analyzed samples across the entire spectrum (400–2500 nm) has been computed from the following equations [27]:

$$n(\lambda ) = [\overline{a} + \frac{{\overline{b}}}{{\lambda^{2} }}],$$

(9)

where $\overline{a}$ and $\overline{b}$ are given by

$$\overline{b} = \{ [n_{2M} - n_{1M} ].[\lambda_{1M} \times \lambda_{2M} ]^{2} .[\lambda_{1M}^{2} - \lambda_{2M}^{2} ]^{ - 1} \overline{\} },$$

(10)

$$\overline{a} = \{ n_{2M} - [\overline{b}.\lambda_{2M}^{ - 2} ]\overline{\} }.$$

(11)

Here, one must pay attention to that $n_{1M} \equiv n_{2M}^{*} \,\,\,and\,\,n_{2M} \equiv n_{1(M + 1)}$. Here, it should be noted that the values of the most accurate refractive index of thin films at the extrema points are calculated from the following relationship and are denoted in Table 1 with the symbol n₂:

$$n_{2} = \{ \overline{a} + [\overline{b}\lambda_{{_{1} }}^{ - 2} ]\} .$$

(12)

The two sets of values ($\overline{a}$,$\overline{b}$) of ${\mathrm{n}}_{2}$ $n$ for the analyzed samples are equaled to: (2.15, 1.10990 × 10⁵), (2.20, 1.12389 × 10⁵), (2.23, 1.24167 × 10⁵), (2.26, 1.28674 × 10⁵) and (2.28, 1.32715 × 10⁵), respectively.

3.3 The absorption coefficient diagram, Tauc and Urbach energy

The absorption coefficient for the studied samples has been calculated via the following equation [32, 33]:

$$\alpha (\lambda ) = \frac{1}{{\overline{d}_{2} }} \times \ln [\frac{{(1 - R)^{2} + \sqrt {\{ (1 - R)^{4} + 4(R.T)^{2} \} } }}{2.T}],$$

(13)

where $d$ (cm) is the film thickness. Here, $\overline{d}_{2}$ (cm) is the average value of the accurate thickness of thin films, (see Table 1). Figure 4 reveals the reliance of the absorption coefficient $\alpha (\lambda )$ on the photon energy ($h\nu$). One can realize that the increase of Bi content in the studied samples enabled us to control the absorption coefficient. This quantity increases with increasing Bi concentration especially in the visible region (400–700 nm) but it shifts toward the lower photon energy as the Bi content increases. It is due to an improvement in the concentration of the localized states created by the impurities between the valence and the conduction bands, in which these values act as a supplementary rate for the transport of electrons obtaining photons with far less energy than the optical energy gap and afterward the incidence of absorption.

Fig. 4

The dependence of the absorption coefficient, $\alpha$ on the incident photon energy ($h\nu$) for the studied films

The optical energy gap is one of the most significant optical factors through which many electronic devices, such as solar cells, polymers, optical electrodes, have been developed in the field of semiconductor technology especially in systems where the optical bandgap between the valence and conduction states decreases. For this reason, the main objective of this research was to introduce a bismuth element to regulate the energy of the bandgap in such a way that these studied films own great opportunities in the field of optical and electrical development. According to Tauc relationship in the strong absorption region (α > 10⁴ cm⁻¹), the energy bandgap for the studied system is determined [34,35,36]:

$$(\alpha .h\nu ) = B.(h\nu - E_{g} )^{r} .$$

(14)

Here $B$ is a constant factor that relies on the probability of transformation, $E_{g}$ is the energy bandgap of the sample, and r is a number that represents the transformation phase, and has a value of 1/2 for the direct transition and a value of 2 for the indirect transition. Making the substitution that _{Y =} αhν, Eq. (14) can be written in the form [37]:

$$\frac{Y}{{Y^{\prime}}} = \frac{1}{r}(h\nu - E_{g} ),$$

(15)

where Y' is the derivative of Y concerning the photon energy ($h\nu$). Equation (15) is used to analyze the experimental data since it gives the ratio of Y/Y' as a linear function of ($h\nu$) and offers a direct method for determining the exponent r. Figure 5 displays the dependence of the ratio of Y/Y' on the photon energy for the studied thin films. The best straight line is drawn through plotted points using the linear regression so the values of r are 2 ± 0.05. The value of r is closed to 2 indicating the electronic transition responsible for the photon absorption is a non-direct process.

Fig. 5

The dependence of the ratio of Y/Y' on the photon energy for the studied thin films

Figure 6 displays the dependence of $\sqrt {(\alpha .h\nu )}$ on the photon energy, ($h\nu$) for the studied samples the x-axis intercept indicates the value of the indirect optical bandgap, $E_{g}$. The energy bandgap values of the studied thin films are determined by extrapolation of the linear regions on the energy axis ($h\nu$) as given in Fig. 6. These values of the optical bandgap of the investigated films are summarized in Table 2. It was found that the optical bandgap decreases with increasing Bi content. The results are interpreted in terms of the change in concentration of localized states due to the shift in the Fermi level as a result of varying Bi content. These optical results confirm that increasing the Bi content increases the effect of scattering on free carriers from ionized impurities. Thin films with a small bandgap have a good potential to absorb ultraviolet rays from electromagnetic radiation by blocking and allowing visible and infrared energy to be transmitted. These values make films perfect and appropriate for solar processing and thermal insulation protective coatings.

Fig. 6

The plot of ($\alpha$.$h\nu$)^0.5 versus photon energy, ($h\nu$) for the studied films

Table 2 Values of the optical, dispersion and dielectric parameters for Se–Ge–Bi thin films with (750 nm)

For the absorption coefficient (α) of less than 10⁴ cm⁻¹, namely, (10^–1 < α < 10⁴) cm⁻¹, the exponential edge region, there is usually Urbach tail, where (α) increases exponentially with the photon energy ($h\nu$) according to Urbach’s empirical relation, we utilized Pankove’s expression [38]:

$$\alpha (h\nu ) = \alpha_{0} \exp [\frac{h\nu }{{E{}_{e}}}] = ME_{e}^{3/2} \exp [\frac{h\nu }{{E{}_{e}}}],$$

(16)

where $\nu$ is the frequency of the radiation, $M$ is a constant, $E_{e}$ is interpreted as the width of the tails of localized states in the gap region and, in general, represents the degree of disorder in an amorphous semiconductor and $\alpha_{0}$ represents a constant and it equals to $ME_{e}^{3/2}$. Therefore, plotting the reliance of $\ln (\alpha )$ on $h\nu$ gives a straight line as offered in Fig. 7. The inverse of the yield slope gives the band tail width, $E_{e}$ of the localized states. The effects of an increase of Bi content on E_g and $E_{e}$ are summarized in Table 2. It is observed from this table that the band tail width $E_{e}$ increased with increasing Bi content and the optical energy gap E_g changes in an exactly opposite manner. The increase in value of $E_{e}$ with the increasing Bi content may also be attributed to the increase in the film structural disorders. Here, it should be noted that E_g and $E_{e}$ are called the linear optical parameters. In addition, by increasing the bismuth content, one can control both of these optical parameters.

Fig. 7

The plot of $\ln (\alpha )$ versus photon energy, ($h\nu$) for the studied films

3.4 Components of the linear optical constants

Linear optical constants are the expressions used only to define the refractive index, n, and the absorption index (the extinction coefficient), $k_{ex}$ of the studied samples.

According to Eq. (12), Fig. 8 highlights the reliability of the refractive index of the analyzed thin films on the wavelength of the photon. The decrease of the refractive index by increasing the wavelength is called the normal dissipation (as in our current work), and this dissipation is anomalous if the refractive index increases with increasing wavelength. On the other hand, it is evident from Fig. 8 that the evidence for the refraction of thin films is increased by increasing the content of bismuth (this behavior was observed in other works [39, 40]), due to several reasons we have listed as follows:

• The behavior of the refractive index as a function of wavelength is linked to the behavior of the transmission of thin film as a function of wavelength, as well as to the well-known physical relationship: (the lower the transmittance of the medium, the higher the refractive index).

• The atomic radius of the Bi element (156 pm) is higher than that of the Ge element (122 pm), where the addition of the bismuth element to the studied system reduces the addition of new energy levels, which in turn increases the refractive index and the dissipation of light in the medium.

• The change in the refractive index is linked to the polarity of the atoms of the medium as their behavior is associated with the energy of the gap and, as the energy of the gap drops significantly, the polarity is also decreasing (as we will see later in this research) and thus increasing the refractive index in the end.

Fig. 8

The spectral dependence of the refractive index, $n$ on the wavelength for the studied films

The incremental reduction of the reflective indexes with the wavelength and the increase it with increasing Bi concentration of the studied thin films implies the effective transmitting of UV, IR and visible light; thus, it is proposed that these films be used as a control in the thermal systems and also utilized it in the coating of the optical glasses.

The spectral variation of the calculated absorption index (the extinction coefficient, $k_{ex}$) against the wavelength of the investigated samples is illustrated in Fig. 9 according to the following formula [41]:

$$k_{ex} = \frac{1}{4\pi }(\alpha .\lambda ).$$

(17)

Fig. 9

Variation of extinction coefficient, ($k_{ex.}$) vs. wavelength, ($\lambda$) for the studied films.

The scattering of light and the decrease of absorption are significant factors for the reduction of absorption coefficients in a relatively high absorption area, with their total absence in the rest of the absorption regions and transparency. It serves to ensure that the light rays do not dissipate and lose in these areas, as opposed to the strong absorption region. In general, the optical constants, $n$ and $k_{ex}$ increase with increasing Bi concentration.

3.5 Dispersion parameter analysis

According to the Wemple–DiDomenico method, the dissipation of the refractive index was studied based on the single oscillator principle [42, 43] as follows:

$$n^{2} = 1 + \frac{{E_{o} E_{d} }}{{E_{o}^{2} - (h\nu )^{2} }},$$

(18)

where $E_{o}$ is the oscillator energy, and $E_{d}$ is the dispersion energy that determines the average strength of inter-band optical transitions. For chalcogenide materials which have diamagnetic properties, like our present scenario, Eq. (18) should be rewritten as follows [42]:

$$n^{2} = 1 + \frac{{\hat{E}_{o} \hat{E}_{d} }}{{\hat{E}_{o}^{2} - (h\nu )^{2} }} + \frac{{E_{o} E_{d} }}{{E_{o}^{2} - (h\nu )^{2} }}.$$

(19)

Here, $\hat{E}_{o}$ and $\hat{E}_{d}$ express the transformations from f to d level but $E_{o}$ and $E_{d}$ express the transitions from s, p → d. The association $(n^{2} - 1)^{ - 1}$ and ($h\nu$)² provides Fig. 10. The fitting of the straight lines of the curve in the high energy area allows it possible to obtain the values of $E_{o}$ and $E_{d}$ from the slopes and the intercepts for these lines and also in the low energy region, one can obtain the values of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{o}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{E}_{d}$. The derived values for such quantities are presented in Table 2. The noticed values of $E_{o}$ and $\hat{E}_{o}$ decrease while the values of $E_{d}$ and $\hat{E}_{d}$ increase with increasing Bi concentration. This behavior—in the high and low energy regions—may be due to several factors, as follows:

• Rise in the number of dispersion centers due to disruption of Bi particles in the sequence of the glass network [44].

• The reduction in oscillator energy is associated with the decrease in energy bandgap (Tauc energy), i.e., the greater the lattice oscillator energy, the greater the optical bandgap, namely, $E_{o} \approx 2E_{g}^{ind}$ [45]. This is not surprising, as the energy of the oscillators is usually believed to be the overall energy of the material.

• In the meanwhile, an improvement in dispersion energy with a higher concentration of Bi-enrichment can be due to a rise in interlayer bonding increasing efficient communication over the nearest-neighbor value [46].

• A similar trend was obtained for the addition of Bi to the Se–Te system [47].

Fig. 10

The plot of the relation between $(n^{2} - 1)^{ - 1}$ and ($h\nu$)² for the studied films

Extra analysis of $(n^{2} - 1)^{ - 1}$ vs. ($h\nu$)² enables the measurement of the linear static refractive index in the low and high energy regions utilizing the general formula:

$$\left. \begin{gathered} \hat{n}_{0} = (\frac{{\hat{E}_{d} }}{{\hat{E}_{o} }} + 1)^{0.5} \hfill \\ n_{0} = (\frac{{E_{d} }}{{E_{o} }} + 1)^{0.5} \hfill \\ \end{gathered} \right\}.$$

(20)

The obtained values of $\hat{n}_{0}$ and $n_{0}$ are reported in Table 2. It is noted from this table that $n_{0} > \hat{n}_{0}$ and the values of $n_{0} \,\,and\,\,\,\hat{n}_{0}$ increased with rising Bi concentration.

Another optical parameters can be computed in terms of refractive index such as the high-frequency dielectric constants, ($\varepsilon_{\infty }$) and the charge carrier concentration (N/m^*). Such parameters are used for a finer interpretation of the optical properties of the evaluated films, which is why the relationship between the actual dielectric constant ($\varepsilon_{r}$), and wavelength (λ²) needs to be assessed as shown in Fig. 11 based on the following equation [44, 48]:

$$n^{2} \approx \varepsilon_{r} = \varepsilon_{\infty } - \left( {\frac{{e^{2} N}}{{4\pi c^{2} \varepsilon_{o} m^{*} }}} \right)\lambda^{2} ,$$

(21)

Fig. 11

The plot of the relation between $n^{2}$ and $\lambda^{2}$ for the investigated films

where $\varepsilon_{\infty }$ is the high-frequency dielectric), c is the speed of the light, e is the electronic charge which equals to (1.6 × 10^–19 C) and $\varepsilon_{0}$ is the vacuum permittivity ( 8.854 × 10^–12 F/m.

). The determined values of such quantities are reported in Table 2. It is obtained that such quantities increase with increasing Bi concentration and this manner was noticed in several chalcogenide materials [44, 45, 48,49,50]. The plasma resonance frequency $\omega_{p}$ can also be computed depending on the following relationship [44, 48]:

$$\omega_{p} = \sqrt {\frac{{e^{2} }}{{\varepsilon_{o} \varepsilon_{\infty } }}\frac{N}{{m^{*} }}} .$$

(22)

The computed values of $\omega_{p}$ are listed in Table 3. It is observed that the computed values for these parameters increase and this is due to the increasing in refractive index.

Table 3 Values of electronic parameters for Se–Ge–Bi thin films with (750 nm)

3.6 Dielectric constant parts and dissipation loss

As a component of the two optical constants, n and k, the real and imaginary parts of the dielectric constant [51] of the films under investigation have also been calculated utilizing the following relationship (see Fig. 12a, b):

$$\begin{aligned} \varepsilon_{r} = n^{2} - k^{2} , \hfill \\ \varepsilon_{i} = 2nk. \hfill \\ \end{aligned}$$

(23)

Fig. 12

The plot of the dielectric constant parts vs. wavelength (a, b) and dissipation loss vs. photon energy (c) for the investigated films

The values of ε_r and n for the tested thin films show a similar trend in the same spectrum of photon energy while the values of and k reveal similar behavior in the same range of photon energy. To be technically accurate, we pay careful attention to the material refraction index, more than the dielectric constants. There are a few reasons for that. First, the most famous, in accordance with empiric Miller’s rule, the weaker the linear response cannot be expounded, the more undetermined the refraction. Second, IR and its anisotropy deduce the material of phase matching under nonlinear interaction of the main wave and its harmonics [51].

Now, the dissipation factor,—a measure of the loss of power in a mechanical phase, such as oscillation in the dissipative method—which may be computed as a function of and utilizing the following relation and plots as a function of photon energy [52] (see Fig. 12c):

$$\tan (\delta ) = (\frac{{\varepsilon_{i} }}{{\varepsilon {}_{r}}}).$$

(24)

It is obtained that the dissipation loss increases with increasing the photon energy and Bi concentration of the studied samples.

3.7 The energy-loss functions

The energy-loss functions are related by the real and imaginary parts of the complex dielectric constants (${\varepsilon }_{\mathrm{i}}$ and ${\varepsilon }_{\mathrm{r}}$) via the following equations [53]:

$$\begin{aligned} &&VELE = \left[ {\frac{{\varepsilon _{i}^{2} }}{{\varepsilon _{i}^{2} + \varepsilon _{r}^{2} }}} \right], \hfill \\ &&SELE = \left[ {\frac{{\varepsilon _{i}^{2} }}{{\varepsilon _{i}^{2} + (\varepsilon _{r} + 1)^{2} }}} \right]. \hfill \\ \end{aligned}$$

(25)

The dependency of these functions on the photon energy in the basic absorption area for the tested thin films is seen in Fig. 13. Two functions increase with increasing the photon energy and Bi concentration of the studied samples.

Fig. 13

The dependency of VELF and SELF functions on the photon energy for the investigated films

3.8 Non-linear refractive index, n₂

In keeping with the law of Ticha and Tichy [54], which is the dependency of the nonlinear refractive index on the bandgap of materials, one can express the nonlinear refractive index as follows:

$$n_{2} = \frac{{1.3 \times 10^{ - 9} }}{{E_{g}^{4} }}(esu.eV^{4} ).$$

(26)

Figure 14a plots the relationship between $n_{2}$ and photon energy. On the other side, the dependence of the second-order refractive index, $n_{2}$, for the linear refractive index, $n$, in chalcogenide materials is given Boling et al. formula [55, 56]:

Fig. 14

The dependency of $n_{2}$ on photon energy a and $n_{2}$ on the wavelength, $\lambda$ for the investigated films

$$n_{2} ( \times 10^{ - 13} esu) = 391\frac{(n - 1)}{{\nu_{d}^{5/4} }}.$$

(27)

Here,

$$\nu_{d} = \frac{{\left( {n_{{(\lambda_{a} )}} - 1} \right)}}{{\left( {n_{{(\lambda_{b} )}} - n_{{(\lambda_{c} )}} } \right)}},$$

(28)

where $\lambda_{a} = 589\,\,{\text{nm}}$, $\lambda_{b} = 486\,\,{\text{nm}}$ and $\lambda_{c} = 656\,\,{\text{nm}}$.

Figure 14b shows the relationship between $n_{2}$ and the wavelength, $\lambda$ based on Eqs. (27–28). From Fig. 14a, b, one can observe that the second-order refractive index, $n_{2}$ increases with increasing Bi content and decreases with increasing the wavelength $\lambda$. The nonlinear refractive index $n_{2}$ is increasing as the linear refractive index n and for the same reasons mentioned.

3.9 Electronic analysis

3.9.1 Evolution of Plasmon, Penn and Fermi energies

The empirical equations tend to reflect optical evidence such as the high-frequency dielectric constant, ε_∞—which is extracted from the intercepts of the straight lines of the plot n² against λ²—is efficient in the determination of electronic properties such as valence electron plasma energy ($\Psi = \hbar \omega _{p}$), the typical energy gap or gap of the Penn, (E_P), Fermi energy (E_F) and also the electronic polarization variable (parameter of electronic polarization), α_p of the investigated films. As a consequence, the values of $\Psi = \hbar \omega _{p}$ can be determined from the following relationship [57]:

$$\Psi = \hbar \omega_{p} , \quad \hbar=h/2 \pi$$

(29)

Here, h represents Planck’s constant, $h = 4.135 \times 10^{ - 15} \,(eV/s)$ and ω_p represents the plasma resonance frequency as already mentioned. On the other side, one can be computed the total effective count of the valence electrons as follows [57]:

$$n_{eff} \simeq ({0}{\text{.121}} \times \Psi^{{2}} ).V_{m} ,$$

(30)

where $V_{m}$ is the molar volume provided by $\frac{M}{\rho }$, here, ρ represents the density (g/cm³) and M represents the molecular weight (g/mol.).

Depending on the pattern of Penn [58], the Penn energy E_p is computed in terms of plasma energy ($\Psi = \hbar \omega _{p}$) as follows:

$$E_{p} = \Psi \times \sqrt {(\varepsilon_{\infty } - 1)} .$$

(31)

Relatively, focusing on Phillip’s principles [58], one can easily determine the Fermi energy E_F via the general formula:

$$E_{F} = 0.3 \times \Psi^{{(\frac{4}{3})}} .$$

(32)

It is observed that these quantities are increased with increasing Bi concentration (see Table 3).

3.9.2 Computation of the electronic polarizability

Polarization is believed to be the predominant cause of the generation of waves in glass materials during the electronic processes. Inner charge transfer enables the cloud of electron gas to travel farther away from the nucleus, resulting in an overall dipole moment. Continuous focus has been given to developing the computing of polarization in solids owing to their wide variety of applications [59, 60]. Now, one can compute the electronic polarization, α_p as a function of ε_∞ (Clausius–Mossotti (CM) equation) [61] and also as a function of the optical bandgap, $E_{g}$(according to Reddy et al. equation) [62], receptivity:

$$\alpha_{p} = \frac{{10^{ - 24} }}{2.53} \times \left( {\frac{{(\varepsilon_{\infty } - 1)}}{{(\varepsilon_{\infty } + 2)}}} \right) \times V_{m} ,$$

(33)

$$\alpha_{p} = (3.9 \times 10^{ - 25} ) \times \left( {\frac{{4.06 - \sqrt {E_{g} } }}{4.06}} \right) \times V_{m} \,\,\,(cm^{3} ).$$

(34)

The obtained values of α_p are summarized in Table 3. It is noticed that the values of α_p increase with increasing Bi concentration for the investigated samples.

3.10 Electrical conductivity analysis

First, a detailed mathematical characterization that explains the temperature of the thin films studied must be given. The temperature of the thin film was determined in agreement with the equation below [63]:

$$T_{\text{Film}}={\frac{U_s\, (\text{mV})}{0.033}}+298\,{\rm K}$$

(35)

Here, U_s (mV) represents the Seebeck voltage. Now, the relationship of electrical resistivity by surface resistance and thickness of thin studied films can be mathematically expressed as:

$$\rho (T)=R_s (T) \times d$$

(36)

Therefore, from the inverse of electrical resistivity, electrical conductivity may be represented mathematically as follows [64]:

$$\sigma_{dc}\, (T)=[1/\rho_{dc}\, (T)]=[1/(R_s \times d)]$$

(37)

It is assumed that the electrical conductivity measured corresponds to the sum of the two key components as follows:

$$\sigma_{dc}\, (T)=\sigma_{0[ext]}\times \exp\left[-\frac{\Delta E_{ext.}}{K_B T}\right] +\sigma_{0[hop]}\times \exp\left[-\frac{\Delta E_{hop.}}{K_B T}\right]$$

(38)

where $\Delta E$ is the activation energy, is the pre-exponential factor, is the contribution of conduction as a result of the hopping between the nearest localized states and is the contribution of conduction between the extended states. Depending on Eq. (37), the influence of variation in temperatures on the electrical conductivity for fresh studied thin films deposited onto the glass layer (substrate) grasped at 25 ºC (298 K) has been investigated in the ranging from 300 to 500 K. The logarithm of dark electrical conductivity as a function of the reciprocal temperature is shown in Fig. 15. From this figure, one can observe that the electrical results display two types of conduction channels and this means there are two main types of connection mechanisms. In the range of temperature from 300 to the onset of crystallization temperature, for each thin film, the electrical conductivity appears a slight increase with increasing of temperature and this behavior corresponds to the conduction is attributed to band conduction through extended states, while the increasing is rapidly in the range of temperature after for each film until the end of the thermal temperature range where the energy states are the hopping energy. From the slope of the resulting lines and their intercepts, the values of activation energy (ΔE) and pre-exponential factor in every range have been computed and summarized in Table 4. In the extended states, the values of activation energy, ΔE getting close to 0.5 Eg as confirmed by several authors. Both parameters have the same behavior in the same thermal range that characterizes the extended and hopping regions, and these results are fully consistent with the results of other studies [65, 66]. This proves that the behavior of is linked to a corresponding behavior of ΔE. The noted decrease in the activation energy with increasing the Bi concentration may be explicated on the grounds of the doping hypothesis of Fritsche and Kastner [67]. It is hypothesized that the existence of charged bismuth atoms promotes the accumulation of positively charged chalcogen defect centers at the detriment of negatively charged defects and thus raises the electron accumulation. On the other side, the sharp decrease in activation energy with the increase in bismuth content can be explained based on the fast transformation between Fermi levels in the existence of the charged centers produced by impurity atoms that do not follow the criteria of the bonding and contribute to the deviation from standard structural bonding [67]. The existence of other forms of charged defects and disorders, including the Valence Alternating Pairs (VAPs) and Intimate Valence Alternating Pairs (IVAPs) may aim to explain the transport process in chalcogenide materials [48]. In the case of chalcogenide materials, the creation of charged defects is as follows (see Fig. 16 according to D. J. Adler’s scheme [68]):

$$2C_{2}^{0} \to C_{3}^{ + } + C_{1}^{ - }.$$

(39)

Fig. 15

The logarithm dark electrical conductivity, as a function of reciprocal temperature, (1000/T) of fresh thin films

Table 4 The values of activation energy, (ΔE) and pre-exponential factor in both extended and hopping regions of fresh Se–Ge–Bi thin films

Fig. 16

Schematic illustration displaying the stages E_F and levels of the charged centers for the case of positive correlation energy for: a Ge–Se glasses b Ge–Se glasses with bismuth as a modification [68]

Here, the subscript signifies the coordination and the superscript signifies the charge state. As well, $C_{2}^{0}$ refers to the neutral centers (singly occupied), $C_{3}^{ + }$ refers to unoccupied centers, and $C_{1}^{ - }$ represents the doubly occupied centers. Besides, the typical energy required to produce a VAP, $E_{VAP} \simeq 0.08\,\,\,\,eV$[69], while, the required energy to generate the VAPs may be diminished when the charged defects form near to each other due to the Coulomb energy of attraction, in the end, it creates the so-called IVAPs [70]. It should be noted that the VAPs are pinning the Fermi level, the IVAPs are not [68]. The level of the Fermi is seen to be in the undoped Se–Ge material located somewhere between the highest occupied and the lowest unoccupied level as shown in Fig. 16a, while in the existence of Bi content, $C_{1}^{ - }$ centers raise and this matter contributes to a change of the Fermi level towards the conduction band, as illustrated in Fig. 16b. Briefly, the value of the pre-exponential factor is useful to determine the electrical conduction mechanism. For the conduction in extended states, the value of the pre-exponential factor reported for a-Se and other Se alloyed films is of the order of 10⁴ (Ω.cm)⁻¹. A lower value for pre-exponential factor, 2–3 orders of magnitude, indicates the conduction in the localized states in the band tails [36, 71]. Even smaller values for σ₀ indicate conduction in the localized states near the Fermi level [72]. At lower temperatures, we argue that hopping conduction in the localized states near the Fermi level is dominant.

4 Conclusions

The amorphous materials of Se₈₀Ge_20-xBi_x with (x = 0, 5, 10, 15 and 20 at.%) were prepared by the usual melt quench technique. Thin films of these compositions were deposited onto the glass substrates by the thermal evaporation technique. The influence of the change in Bi concentration on the structural, optical and electrical properties of the as-prepared thin film of such alloys has been documented. The most important finding is outlined as follows:

• The X-ray diffraction indicates the amorphous structure of the as-deposited thin films.

• Optical measurements mean both the transmittance and reflectance spectra of thin films, linear optical parameters mean both gap and tail energies ($E_{g}$ and $E_{e}$), linear optical constants mean both the refractive index n and the absorption index k (extinction coefficient) of the thin films, linear dispersion parameters denote both of the single oscillator energy $E_{o}$ and the dispersion energy $E_{d}$ while the nonlinear optical parameter refers to the second refractive index $n_{2}$.

• Linear electronic parameters denote Plasmon energy $\Psi$, Penn energy, E_p, Fermi energy, $E_{F}$ and electronic polarization parameter that is associated with linear optical parameters.

• The gradual addition of bismuth content to the analyzed thin films acted as a regulator and controller of linear and nonlinear constants and parameters. Namely, it served to reduce both the energy of the optical gap and the energy of the single oscillator and, in turn, to improve the rest of the other optical and electronic parameters.

• The electrical results of as-deposited thin films show two types of conduction channels contribute two conduction mechanisms, namely, contributions in the extended and hopping states. It was found that in both regions the activation energy decreased with increasing bismuth content.