Interplay between the ferrimagnetic and ferroelectric phases on the large magnetoelectric coupling of xLi_0.1Ni_0.2Mn_0.6Fe_2.1O₄–(1 − x)Bi_0.8Dy_0.2FeO₃ composites

Abstract

The multiferroic composites of ferromagnetic Li_0.1Ni_0.2Mn_0.6Fe_2.1O₄ (LNMFO) and ferroelectric Bi_0.8Dy_0.2FeO₃ (BDFO) with the general formula xLi_0.1Ni_0.2Mn_0.6Fe_2.1O₄–(1 − x) Bi_0.8Dy_0.2FeO₃ have been prepared by the solid-state reaction route. The XRD analysis has ensured that the composites are composed of a mixture of cubic spinel LNMFO and orthorhombic perovskite BDFO phases. Field Emission Scanning Electron Microscope is used to investigate the surface morphology of the studied compositions. The average grain size of the composites has reduced slightly with the enhancement of ferrite part up to 20% and after that it has increased again. The real part of the initial permeability $(\mu^{\prime}_{i} )$ was found to be increasing with ferrite content. The real part of dielectric constant $(\varepsilon^{\prime})$ exhibits dispersion at low-frequency region because of Maxwell–Wagner type interfacial polarization. The complex impedance spectroscopy has been used to separate the grain and grain boundary contribution to the total resistance. Existence of the hopping conduction mechanism has been confirmed through the study of electric modulus. The hysteresis loops of the compositions are studied to confirm the response of ferrite part to the applied magnetic field. The magnetoelectric voltage coefficients of the composites have reduced with the ferrite part. The maximum magnetoelectric voltage coefficient is nearly 158 × 10³ Vm⁻¹ T⁻¹ for the 0.1LNMFO–0.9BDFO composite, which is about three times of the reported value compared to other composites.

1 Introduction

Multiferroics are regarded as an attractive category of multifunctional compounds which show different ferroic orders like ferromagnetism and ferroelectricity simultaneously [1]. These types of materials have many other supplementary characteristics in the same phase for making emergent phenomena which are not always present in the individual components [2]. Multiferroics have the potentiality to make possible the conversion between electrical energy and magnetic energy, that can be applied in waveguides, magnetoelectric (ME) memories, actuators, sensors, and transducers [3, 4]. In 1894, Curie predicted the perception for the first time [5] followed by the theoretical confirmation by Dzyaloshinsky in 1959–1960 [6], and experimental confirmation in the Cr₂O₃ by Astrov [7], Folen [8], and Rado [9]. After that, multiferroic materials grabbed the attention from both fundamental research and application in practical devices [10,11,12,13]. At the beginning, multiferroic properties were investigated only in the single-phase materials. However, later it was expanded to any material that demonstrates various types of spontaneous (ferromagnetic, ferroelectric, and ferroelastic) orderings [14]. Various single-phase multiferroics, e.g., RMnO₃, RMn₂O₅ (R: rare-earth ions), and BiFeO₃ (BFO) show that the order parameters usually coexist either at low temperatures or at the room temperature and have weak ME responses. It is also possible to obtain multiferroics by producing composites that consist of piezoelectric and magnetostrictive phases. Because of the magnetic–mechanical–electric interplay between the two phases, multiferroic materials may represent a high ME coupling [4]. The sum or product properties may be represented by composite materials [4, 15, 16]. The sum properties arise from the weighted sum of the component phases that is proportional to the fraction of the volume of these phases. The density, magnetization, and dielectric properties fall under the class of sum properties. The product property is remained in the composites but absent in individual phases.

In order to get an enhanced ME effect, choice of suitable ferroelectric and ferrite material is very crucial. It is known in advance that piezoelectric coefficient of ferroelectric part and magnetostriction coefficient of ferrite part must be high for enhanced ME effect [4]. High magnetostriction coefficient can be found in Ni–Mn ferrite due to the presence of Ni [17]. Moreover, Mazen et al. [18] observed improvement in the permeability, saturation magnetization, and Néel temperature (T_N) in Li–Mn ferrites. On the other hand, the perovskite BFO is composed of both antiferromagnetic (T_N = 643 K) and ferroelectric (T_C = 1103 K) phases. The BFO and other materials of this family are not suitable for practical applications as hindered by some problems, e.g., large leakage current density and existence of secondary phases [19]. An enhancement in electric properties (ferroelectric, leakage current density, dielectric properties etc.) with rare-earth ion (Dy³⁺) substitution in BFO was observed [20]. Multiferroic properties of various composites such as MnFe₂O₄–BiFeO₃ [21], BiFe_0.5Cr_0.5FeO₃–NiFe₂O₄ [22], Ni_0.75Zn_0.25Fe₂O₄–BiFeO₃ [23], yNi_0.50Cu_0.05Zn_0.45Fe₂O₄–(1 − y)BiFeO₃ [24], yNi_0.5Zn_0.5Fe₂O₄–(1 − y)Bi_0.8Dy_0.2FeO₃ [25], CoFe₂O₄–PbTiO₃ [26] (1 − x)Ba_0.6(Ca_1/2Sr_1/2)_0.4Ti_0.5Fe_0.5O₃ + xNi_0.4Zn_0.45Cu_0.15Fe_1.9Eu_0.1O₄ [27] xBi_0.95Mn_0.05FeO₃–(1 − x)Ni_0.5Zn_0.5Fe₂O₄ [28] (1 − x)Bi_0.85La_0.15FeO₃–xNiFe₂O₄ [29], and (1 − x)Pb(Zr_0.52Ti_0.48)O₃–xCoFe₂O₄ [30] have been reported previously. However, there is a scope of investigation in various xLi_0.1Ni_0.2Mn_0.6Fe_2.1O₄–(1 − x)Bi_0.8Dy_0.2FeO₃ (LNMFO–BDFO) composites as per the literature survey. It is therefore necessary to explore the possible variations in the different physical properties of xBDFO–(1 − x)LNMFO composites. This study presents a systematic investigation of structural, magnetic, dielectric, and magnetoelectric properties of various xLi_0.1Ni_0.2Mn_0.6Fe_2.1O₄–(1 − x)Bi_0.8Dy_0.2FeO₃ composite materials.

2 Experimental

2.1 Sample preparation

Composites of xLNMFO–(1 − x)BDFO with LNMFO as ferrimagnetic phase and BDFO as ferroelectric phase were prepared by the standard solid-state reaction technique. To prepare BDFO, high-purity raw materials of Bi₂O₃ (99.5%, CAS No. 1304-76-3), Dy₂O₃ (99.9%, CAS No. 1308-87-8), and Fe₂O₃ (99.5%, CAS No. 1309-37-1) were weighed and mixed thoroughly in accordance with the stoichiometric formula in an agate mortar with pestle for 5 h using acetone as mixing medium. The BDFO powder was calcinated at 1073 K for 4 h. Then the powder was pre-sintered at 1123 K for 4 h. Appropriate amount of high-purity raw materials of Li₂CO₃ (99.0%, CAS No. 554-13-2), NiO (99.9%, CAS No. 1313-99-1), MnCO₃ (99.2%, CAS No. 598-62-9), and Fe₂O₃ (99.5%, CAS No. 1309-37-1) were mixed to prepare LNMFO in the same way as BDFO. The mixed powder was then pre-sintered at 1473 K for 4 h. To obtain a homogeneous mixture of the desired compound, the pre-sintered powders were again ground thoroughly. The powders of BDFO and LNMFO were mixed in weight proportions to prepare xLNMFO–(1 − x)BDFO composites. The composite powders were mixed with polyvinyl alcohol (PVA) as a binder for granulation. A uniaxial pressure of 60 MPa was applied for making pellet and toroid-shaped samples. Every sample was sintered at various sintering temperature, T_s, and finally find out the optimum sintering temperatures, 1198 K for x = 0.0; 1223 K for x = 0.1, 0.2, and 0.3; 1248 K for x = 0.4 and 0.5; and 1573 K for x = 1.0 for 4 h. We measured bulk density and also taken Field Emission Scanning Electron Microscopy (FESEM) image. Optimum T_s is that temperature for which sample shows the maximum density and better FESEM micrographs (i.e., less- porous and absence of liquid phase). It was observed that optimum T_s is different for different chemical compositions. With the increasing value of x, the amount of ferrite part in the composites increase. The optimum T_s of BDFO is smaller than that of LNMFO due to low melting temperature of Bi, and hence, with the increase of ferrite part, optimum T_s was increased.

2.2 Characterizations

The phase formation and the structure of crystal of the sintered composites were characterized by an X-ray diffractometer with CuK_α radiation (λ = 1.5418 × 10⁻¹⁰ m). From X-ray diffraction (XRD) data, the lattice parameters were evaluated. The grain distribution on the samples surface of the composites was studied by FESEM (model JEOL JSM 7600F). The bulk density ($\rho_{\text{B}}$) of each composite was calculated using the relation: $\rho_{\text{B}} = \frac{m}{{\pi r^{2} t}}$, where r is the radius, m is the mass, and t is the sample thickness. The density of X-ray ($\rho_{x}$) was determined by the formula, $\rho_{x} = \frac{nM}{{N_{{{\text{A}} }} V}}$, where the number of atoms is $n$, the sample’s molar mass is $M$, Avogadro’s number is N_A, and the unit cell volume is V. The X-ray density of the composites was measured by the method, $\rho_{x} \left( {\text{composite}} \right) = \frac{{M_{1} + M_{2} }}{{V_{1} + V_{2} }},$ where (1 − x) times molecular weight of BDFO is $M_{1}$ and ‘xʼ times molecular weight of LNMFO is $M_{2}$, $V_{1} = \frac{{M_{1} }}{{\rho_{x} }}$ (ferroelectric) and $V_{2} = \frac{{M_{2} }}{{\rho_{x} }}$ (ferrite), x is the weight fraction of LNMFO in the samples [31]. The porosity of the compositions was determined using the formula, $P\left( \% \right) = \frac{{\rho_{x} - \rho_{\text{B}} }}{{\rho_{x} }} \times 100\%$. The dielectric properties were studied as a function of frequency by using an Impedance Analyzer (WAYNE KERR 6500B). In order to determine dielectric properties, the samples were painted with silver paste on both sides to confirm good electrical contacts. The dielectric constant $(\varepsilon^{\prime})$ was measured by using the relation: $\varepsilon^{\prime} = \frac{Ct}{{\varepsilon_{\text{o}} A}}$, where $C$ is the pellet’s capacitance, the electrode’s cross-sectional area is $A$ , and the permittivity in vacuum is $\varepsilon_{0}$. The ac conductivity ($\sigma_{\text{ac}}$) was calculated using the formula: $\sigma_{\text{ac}} = \omega \varepsilon^{\prime}\varepsilon_{\text{o}} { \tan }\delta_{\text{E}}$, where the angular frequency is $\omega$ and the dielectric loss is ${ \tan }\delta_{\text{E}}$. The real component $(\mu^{\prime}_{i} )$ and imaginary component $(\mu^{\prime\prime}_{i} )$ of the complex initial permeability were measured by the formula: $\mu^{\prime}_{i} \; = \frac{{L_{\text{s}} }}{{L_{0} }}$ and $\mu^{\prime\prime}_{i} = \mu^{\prime}_{i} \;{ \tan }\delta_{\text{M}}$, where L_s$L_{\text{s}}$ and $L_{0}$ are the self-inductance with and without the sample, and the magnetic loss is ${ \tan }\delta_{\text{M}}$. $L_{\text{o}}$ is measured from the formula, $L_{\text{o}} = \frac{{\mu_{\text{o}} N^{2} S}}{{\pi \bar{d}}}$, where the permeability in free space is $\mu_{\text{o}}$, the number of turns of the coil is N (N = 4), the cross-sectional area is S, $\bar{d}\left[ { = \frac{{d_{1} + d_{2} }}{2}} \right]$ is the mean diameter, where d₁ and d₂ are the inner and outer diameter of the toroidal sample, respectively [32]. The magnetic hysteresis (M–H) loops were determined using a vibrating sample magnetometer (VSM, model Micro Sense, EV9). The number of Bohr magneton, $n(\mu_{\text{B}} )$, was calculated using the formula: $n = \frac{{M \times M_{\text{s}} }}{{N_{\text{A}} \times \mu_{\text{B}} }}$, where $M_{\text{s}}$ is the saturation magnetization and $\mu_{\text{B}}$ is 9.27 × 10⁻²¹ emu. The ME effect was achieved through the introducing an ac magnetic field superimposed on the sample’s dc magnetic field and then determine the output signal. A magnetic field of dc (up to 0.77 T) was provided using an electromagnet. A signal generator was used to drive the Helmholtz coil to generate an ac magnetic field (h₀) of 0.0008T. The output voltage ($V_{\text{o}}$) generated from the composite was determined using a Keithley multimeter (Model 2000) as function of dc magnetic field. The ME voltage coefficient (α_ME) was determined by the formula [33] $\alpha_{\text{ME}} = \left( {\frac{{{\text{d}}E}}{{{\text{d}}H}}} \right)_{{H_{\text{ac}} }} = \frac{{V_{\text{o}} }}{{h_{\text{o}} t}}$.

3 Results and discussion

3.1 Crystal structure, lattice parameters, density, and porosity

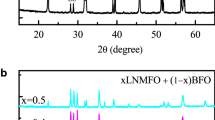
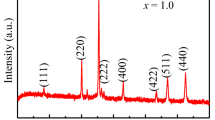
The XRD patterns of LNMFO, BDFO, and xLNMFO–(1 − x)BDFO composites are illustrated in Fig. 1. As indicated in Fig. 1a, BDFO forms orthorhombic perovskite structure which is in good agreement with other reports on bulk BDFO [34, 35] and on the other hand, Fig. 1b indicates that LNMFO have spinel structure. From Fig. 1c, it is observed that the composites exhibit both ferroelectric and ferrite phases in their elementary phases without any structural modification. Perovskite peak intensity decreases while that of spinel peaks intensity increases in the composites with increase of ferrite content. The lattice parameters obtained for each reflected plane are plotted against the Nelson–Riley function [36]: $F\left( \theta \right) = \frac{1}{2}\left( {\frac{{{ \cos }^{2} \theta }}{{{ \sin }\theta }} + \frac{{{ \cos }^{2} \theta }}{\theta }} \right)$, where θ is Bragg’s angle. Obtained lattice parameters are plotted against F(θ). A straight line fit is achieved and from the extrapolation of these lines to $F\left( \theta \right) = 0$, accurate values of the lattice parameters are noted and tabulated in Table 1. In case of composites, it is observed that there is a small change in the lattice parameters of ferrite and ferroelectric phases which may be due to the stress exerted on each other by the two phases [37], and also because of the inter-diffusion of a small number of unreacted elements into the two phases.

Fig. 1

XRD patterns of a BDFO, b LNMFO, and c various xLNMFO–(1 − x)BDFO composites

Table 1 The lattice parameters, X-ray density, bulk density, porosity, average grain size, and real part of initial permeability of various xLNMFO–(1 − x)BDFO composites

Figure 2 indicates the variation of $\rho_{\text{B}} , \rho_{x}$ and $P$ as a function of ferrite content. Both $\rho_{\text{B}}$ and $\rho_{x}$ decrease with the increasing LNMFO content because the density of LNMFO is less than that of BDFO. Density reduces linearly obeying the sum rule. In the composite, porosity decreases with increasing ferrite content because porosity of the ferrite phase is higher than the perovskite phase.

Fig. 2

X-ray density, bulk density, and porosity as a function of ferrite content of xLNMFO–(1 − x)BDFO composites

3.2 Microstructure and EDX analysis

The FESEM images of various xLNMFO–(1 − x)BDFO composites are displayed in Fig. 3. From these micrographs, it can be noticed that the multiferroic composites have fine crystallite structure. The microstructure of multiferroic materials contributes not only in the magnetic and electric properties, but also in the ME coupling [38]. It is observed that the microstructures of all composites are made of non-uniform randomly oriented grains with varying size and shape, and a certain amount of intergranular pores. Such behavior of grain growth reflects the competition between the retarding force exerted by pores and the driving force for grain boundary movement. Due to the existence of inhomogeneous driving force, non-uniform grain growth occurs [39]. Uniform grain growth may be obtained when the driving force of the grain boundary in the grains is homogeneous. The average grain diameter $(\bar{D})$ has been measured using the formula: $\bar{D}$ = 1.56 $\bar{L}$ [40], where $\bar{L}$ is the average intercept length of a line in the microstructure. Initially, $\bar{D}$ of the composite decreases with ferrite concentration up to x = 0.2, beyond this value of x the $\bar{D}$ increases with LNMFO. This initial decline in $\bar{D}$ may be due to the stress exerted on each other by the two phases. It is also because of the inadequate sintering temperature for ferrite phase. The increase in $\bar{D}$ with ferrite content may be due to reduced stress resulting from the increased porosity of the composites [25]. The FESEM images also expressed that the microstructure of the sample is found in uniformly dispersed fine grains without any pores trapped in the grains. This is expected that the employed sintering temperature in the present study is relatively kept low, keeping in mind to maintain the stoichiometric balance and to minimize Bi volatilization.

Fig. 3

FESEM images of xLNMFO–(1 − x)BDFO composites ax = 0.0, bx = 0.1, cx = 0.2, dx = 0.3, ex = 0.4, fx = 0.5, and gx = 1.0

EDX spectra for ferroelectric and ferrites phases are shown in Fig. 4a, b, respectively. FESEM image with the corresponding EDX spectra for x = 0.5 composite is shown in Fig. 4c–e. Among them, Fig. 4c, d represents EDX spectra for ferroelectric grain and Fig. 4e represents EDX spectra for ferrite grain. Figure 4f shows the FESEM image used for EDX study of 0.5LNMFO–0.5BDFO composite. The EDX spectra for ferroelectric phase (Fig. 4a) and ferroelectric grains of composite (Fig. 4c, d) describe the presence of Bi, Dy, Fe, and O elements according to stoichiometry. The EDX spectra for ferrite phase (Fig. 4b) and ferrite grain of composite (Fig. 4e) display the presence of constitute elements except Li according to stoichiometry. Therefore, EDX spectra confirmed the mass percentage of the elements of the component phases is well consistent with the nominal composition except oxygen.

Fig. 4

EDX spectrum of a BDFO, b LNMFO, c point 001, d point 003, and e point 002 of 0.5LNMFO–0.5BDFO composite, f image used for EDX study of 0.5LNMFO–0.5BDFO composite

3.3 Dielectric properties

Figure 5a displays the change of $\varepsilon^{\prime}$ with frequency at room temperature. The high value of $\varepsilon^{\prime}$ at low frequency and the low value at higher frequencies indicate usual dielectric dispersion due to Maxwell–Wagner [41, 42] type interfacial polarization, which is in agreement with the phenomenological theory of Koops [43]. The large values of $\varepsilon^{\prime}$ at low frequency can be described by space charge polarization because of the inhomogeneities present in dielectric structure, viz. porosity and grain boundary for the present ferrite and ferroelectric system. This can be ascribed to the dipoles resulting from changes in valence states of cations and space charge polarization. The space charge polarization is correlated with the number of space charge carriers and the resistivity of the grain boundary. The charge carriers that involve in the exchange can be generated during the sintering process [41, 42]. As the frequency increases, the orientational and ionic sources of polarizability decline and eventually disappear due to ionic and molecular inertia. At higher frequency region, the values of $\varepsilon^{\prime}$ for all composites become frequency independent because of the failure of electrical dipoles to align with the applied electrical field [44], and therefore, the friction between the dipole will decline. The dipoles dissipate heat energy because of the friction, affecting the internal viscosity of the system; thus, these frequency-independent values are known as the static value of $\varepsilon^{\prime}$. In composites, the higher values of $\varepsilon^{\prime}$ at low frequencies are because of the heterogeneity [45] but sometimes polar hopping mechanism results in electronic polarization that contributes at low-frequency dispersion. The $\varepsilon^{\prime}$ of the compositions reduces with the ferrite concentration (Table 2) and does not follow the sum rule. The low value of $\varepsilon^{\prime}$ of the ferrite-rich composites is because of high porosity (inadequate sintering temperature)

Fig. 5

Variation of a dielectric constant and b dielectric loss with frequency of various xLNMFO–(1 − x)BDFO composites

Table 2 Dielectric constant, grain, and grain boundary resistances of various xLNMFO–(1 − x)BDFO composites

The ${ \tan }\delta_{\text{E}}$ arises mainly because of imperfections and impurities in the crystal, causing polarization to lag behind with the alternating field. The frequency variation of ${ \tan }\delta_{\text{E}}$ is shown in Fig. 5b. Composites show a of dielectric loss peak according to Debye relaxation theory. The peak in the ${ \tan }\delta_{\text{E}}$ arises when the hopping frequency of exchange electron among Ni²⁺ and Ni³⁺ and Fe²⁺ and Fe³⁺ is almost equal to the frequency of applied field and satisfies the condition $\omega \tau = 1$ [46]. The maximum value of ${ \tan }\delta_{\text{E}}$ can be ascribed due to the fact that the period of relaxation process is equal as the period of the applied field. Similar behavior is also observed in other reports, [25, 47]. The maximum value of the ${ \tan }\delta_{\text{E}}$ peak reduces with ferrite content in the composites. The ${ \tan }\delta_{\text{E}}$ peak of the present composites depends on the ferrite phase. It was observed that peak frequency shifted towards higher frequency up to x = 0.4. Beyond x = 0.4, peak frequency shifted to lower frequency. This is perhaps due to mutual interaction between ferrite and ferroelectric phases. Because of decreased charge carrier mobility, the composite shows low loss compared to BDFO which means composite can be used in practical applications.

3.4 The ac conductivity

The ac conductivity is a significant parameter to understand the conduction phenomena in different materials. Frequency dependence $\sigma_{\text{ac}}$ is displayed in Fig. 6. In general, the change of $\sigma_{\text{ac}}$ with frequency in ferroelectrics, ferrites, and their composites can be described with the mechanism of polaron hopping based on the available free charge carriers. The electron mobility in oxide materials tends to distort (polarize) the surrounding lattice to produce polarons. The small polarons are produced if the extension of such distortion along the lattice is just about the order of lattice constant, while the large polarons occur when the distortion extends beyond the lattice constant. The model of large polaron describes the behavior when the $\sigma_{\text{ac}}$ decreases with frequency, while the model of small polaron can be used to describe the variation for increasing $\sigma_{\text{ac}}$ with frequency [48, 49]. The change of $\sigma_{\text{ac}}$ as a function of frequency can be explained according to the Jonscher’s power law [50]: $\sigma_{\text{ac}} \left( \omega \right) = \sigma_{0} + A\omega^{n}$, where $\sigma_{0}$ is the frequency-independent conductivity; while the coefficient A and $n$ (0 < $n$ < 1) depend on temperature and intrinsic property of materials [51]. From Fig. 6, it is found that $\sigma_{\text{ac}}$ increases almost linearly with frequency which indicates that the mechanism of conduction is because of small polaron hopping. Other researchers also reported similar results [52, 53]. According to Jonscher’s power law, the change of log $\sigma_{\text{ac}}$ with log(ω) should be linear. However, a small plateau region in $\sigma_{\text{ac}} \left( \omega \right)$ is attributed to mixed polarons (small/large) conduction. Hopping phenomenon is privileged in ionic lattices where two different states of oxidation have the same type of cation. Hopping of 3d electrons in between Fe²⁺ and Fe³⁺ and in between Mn²⁺ and Mn³⁺ would play a crucial role in the process of conduction. The polaron hopping phenomenon is very helpful for investigating the conduction process in materials to determine the activation energy and the phonon coupling [54, 55].

Fig. 6

Variation of ac conductivity with frequency of various xLNMFO–(1 − x)BDFO composites

3.5 Complex impedance spectra analysis

Complex impedance spectroscopy is used to study the electrical properties of compositions and its correlation with microstructures. It is used for exploring the dynamics of mobile or bound charge in bulk or interfacial regions. Debye model [56] describes the impedance behavior and express as, $Z^{*} = Z^{\prime} - jZ^{\prime\prime},$ where $Z^{\prime}$ and $Z^{\prime\prime}$ are the real and imaginary part of impedance. Figure 7a shows the change of $Z^{\prime}$ as a function of frequency. It is seen that $Z^{\prime}$ quickly reduces with frequency up to a certain frequency (~ 1 MHz). Reducing of $Z^{\prime}$ with frequency specifies that the conduction is rising with frequency and it becomes nearly constant at higher frequency (≥ 1 MHz). The high values of $Z^{\prime}$ at low-frequency region reveal that the polarization is larger because all types of polarization are present there. The small values of $Z^{\prime}$ at higher frequency region indicate possible release of space charge polarization/accumulation at the boundaries with the applied field [57, 58] because they are unable to follow the rapid change of frequency of external field. As the ferrite content increases, $Z^{\prime}$ increases in the low-frequency region (up to a particular frequency) and then appears to merge. The frequency at which space charge is released depends on ferrite concentration. The value of $Z^{\prime}$ enhances with ferrite concentration indicating the improvement of resistive property of the compositions. This type of behavior is common due to the existence of space charge polarization within the samples [59, 60]. The change of $Z^{\prime\prime}$ as a function of frequency (Fig. 7b) displays similar behavior as $Z^{\prime}$ , in addition, some relaxation peaks start to appear because of the existence of immobile charges [61].

Fig. 7

Variation of a$Z^{\prime}$ and b$Z^{\prime\prime}$ with frequency of xLNMFO–(1 − x)BDFO composites

In order to measure the total resistance of grain and grain boundary, Cole–Cole or Nyquist plot for all samples with frequency is displayed in Fig. 8 and two semicircular arcs are obtained; one in high frequency (as shown in the insert of each plot) and the other at low frequency. According to brick-layer model [62], polycrystalline ceramics can be described with an equivalent circuit consisting of three parallel RC circuits and these circuits are connected in series to each other. Every RC element of these equivalent circuits in Cole–Cole plot makes a semicircle. The first semicircle is found for grain effects, the second semicircle for the effect of grain boundary, and third semicircle observed for the effects of the electrode. The behavior of present composites can be explained by the equivalent circuit consists of two series connected sub-circuits as displayed in Fig. 8a. The low- and high-frequency semicircular arcs correspond to the R_gbC_gb and R_gC_g responses, respectively. According to equivalent circuit, impedance can be described as

Fig. 8

Nyquist plots of various xLNMFO–(1 − x)BDFO composites: bx = 0.0, cx = 0.1, dx = 0.2, ex = 0.3, fx = 0.4, gx = 0.5, and hx = 1.0

$Z^{*} = R_{\text{g}} - \frac{1}{{j\omega C_{\text{g}} }} + R_{\text{gb}} - \frac{1}{{j\omega C_{\text{gb}} }}$, where the resistance of grain and grain boundary are $R_{\text{g}}$ and $R_{\text{gb}}$; the capacitance of grain and grain boundary are $C_{\text{g}}$ and $C_{\text{gb}}$. Non-Debye-type relaxation is presented in the study composites because each sample exhibits semicircle of distorted/depressed. A perfect semicircle with its center at X-axis is observed for an ideal Debye-type relaxation [63]. In the high-frequency region, a single semicircle is found for all composites because of overlapping of the individual semicircle of the two different phases. This can be due to the small deviation of relaxation time constants because of the grains of the two phases. If the difference of relaxation time constants is sufficiently large, two semicircles would be found. The diameters of semicircles are very small in the higher frequency region compared to the lower frequency region. This indicates the dominant grain boundary contribution to the overall resistance. Both the grain and the grain boundary resistance are measured from the intercepts on the real part of X-axis. The resistance of the grain boundary increases with ferrite content. This is because the less conductive ferrite grains separate the conductive ferroelectric grains. The resistance of the grain is very small (Table 2) than the grain boundary exhibiting the grain’s conducting behavior. In the present study, it is found that the Cole–Cole plot for ferrite shows a single semicircular initiating from the origin. A single semicircle suggests that the electrical conduction is responsible for only one primary phenomenon. In other words, the absence of another semicircle in the Cole–Cole plot suggests the dominance of grain boundary effect within the sample.

3.6 Electric modulus spectra analysis

Complex modules study is an alternative approach to investigate electrical properties and modify any other effects present in the sample as a result of different relaxation time constants. It is an essential method to determine the electrical transport phenomena such as carrier/ion hopping rate, conductivity relaxation time, etc. The complex electrical module ($M^{*}$) is given by the reciprocal of the complex dielectric constant $\left( {\varepsilon^{*} } \right)$, as formulated by Macedo et al. [64],

$$\begin{aligned} M^{*} \left( \omega \right) = & \frac{1}{{\varepsilon^{*} }} \\ = \frac{1}{{\varepsilon^{\prime} - j\varepsilon^{\prime\prime}}} \\ = \frac{{\varepsilon^{\prime}}}{{\varepsilon^{{\prime^{2} }} + \varepsilon^{{\prime \prime^{2} }} }} + j\frac{{\varepsilon^{\prime\prime}}}{{\varepsilon^{{\prime^{2} }} + \varepsilon^{{\prime \prime^{2} }} }} \\ = M^{\prime}\left( \omega \right) + M^{\prime\prime}\left( \omega \right) \\ \end{aligned}$$

Simplifying and substituting $\varepsilon^{\prime\prime}$ by $\varepsilon^{\prime}\;{ \tan }\delta_{\text{E}}$, we get

$$M^{*} \left( {\omega } \right) = M^{\prime}\left( \omega \right) + M^{\prime\prime}\left( \omega \right)$$

$$= \frac{1}{{\varepsilon^{\prime}\left( {1 + { \tan }^{2} \delta_{\text{E}} } \right)}} + j\frac{{{ \tan }\delta_{\text{E}} }}{{\varepsilon^{\prime}\left( {1 + { \tan }\delta_{\text{E}} } \right)}},$$

where $M^{\prime}$ and $M^{\prime\prime}$ are the real and imaginary parts of $M^{*}$. The $M^{\prime}$ and $M^{\prime\prime}$ are associated to the energy giving to system and that dissipation from it during the process of conduction. Figure 9a displays the change of $M^{\prime}$ with frequency. It is observed that $M^{\prime}$ is almost zero at low frequencies and then enhances dispersion with frequency. This dispersion moves to the higher frequency region with increasing LNMFO content for all samples and here $M^{\prime}$ tends to saturate to the maximum value due to the relaxation process. In the low-frequency regions, $M^{\prime}$ values approach to zero, confirming the large value of capacitance and electronic polarization is negligible, while $M^{\prime}$ enhances very fast at higher frequencies representing the conduction process because of short-range mobility of the charge carriers. This may be due to the lack of restored force for flowing of charge carriers under the influence of an induced steady electric field. Figure 9b shows the change of $M^{\prime\prime}$ with frequency for various composites. The modulus curves indicate not only the significant shift in the $M^{\prime\prime}_{\text{max }}$ to the lower frequency side but also broadening of peaks with LNMFO content. It is found that $M^{\prime\prime}$ enhances and displays a relaxation peak in the dispersion region of $M^{\prime}$. In the low frequencies, $M^{\prime\prime}$ is low because of the absence of electrode polarization phenomena. In higher frequencies, $M^{\prime\prime}$ reduces and becomes almost constant which can be accredited because of the limited number of charge carriers in potential wells. Below the peak frequency in $M^{\prime\prime}$ pattern measures the mobility range of charge carriers over long distances (between grains) and above the peak frequency, the carriers are confined to their potential wells, being mobile over short range (within the grains) related with relaxation polarization process. The module peaks observed shift towards lower frequency side with LNMFO content indicating that ferrite concentration activated the behavior of relaxation time [65]. The asymmetricity in peak broadening indicates the spread of relaxation times in composites with different time constants that support the non-Debye type of relaxation. The peak value region is a directory of transition from long-range to short-range mobility with the increase in frequency. Thus, this type of behavior of the modulus spectrum indicates the presence of hopping phenomenon of electrical conduction (charge transport) in the composites.

Fig. 9

Electric modulus spectra of xLNMFO–(1 − x)BDFO composites a real part ($M^{\prime}$) and b imaginary part ($M^{\prime\prime}$)

3.7 Complex initial permeability

Permeability is one of the most significant features of ferromagnetic materials in investigating magnetic properties. The complex initial permeability can be expressed as, $\mu_{i}^{*} = \mu^{\prime}_{i} - j\mu^{\prime\prime}_{i}$, where the real and imaginary parts of $\mu_{i}^{*}$ are $\mu^{\prime}_{i}$ and $\mu^{\prime\prime}_{i}$, respectively. The $\mu^{\prime}_{i}$ describes the energy that stores within the system declaring the magnetic induction part (B) in phase with the alternating magnetic field (H). The $\mu^{\prime\prime}_{i}$ expresses energy dissipation that explains the component of B out of phase with H. Figure 10a displays the change of $\mu^{\prime}_{i}$ with frequency for xLNMFO–(1 − x)BDFO composites. For all samples except LNMFO, the $\mu^{\prime}_{i}$ remains nearly constant over the whole range of frequency because the cut-off frequency (resonance frequency, $f_{\text{r}}$) lies beyond the measurement frequency range. According to the Snoek’s relation [66], for all ferromagnetic materials, the product of $\mu^{\prime}_{i}$ and $f_{\text{r}}$ is constant, i.e.,$\left( {\mu^{\prime}_{i} - 1} \right)f_{\text{r}} = \gamma /2\pi M_{\text{s}}$, where $M_{\text{s}}$ is the saturation magnetization and $\gamma$ is the gyromagnetic ratio. With the increase of LNMFO, concentration in the composite magnetization becomes stronger. Therefore, the cut-off frequency is decreased. The $\mu^{\prime}_{i}$ enhances with LNMFO content in the composite (Table 1), which is expected according to the sum rule.

Fig. 10

Variation of a$\mu^{\prime}_{i}$, b$\mu^{\prime\prime}_{i}$ and c RQF with frequency of various xLNMFO–(1 − x)BDFO composites at room temperature

The change of $\mu^{\prime\prime}_{i}$ as a function of frequency is displayed in Fig. 10(b). It is shown that at low-frequency region $\mu^{\prime\prime}_{i}$ has a high value after that decreases exponentially with rising frequency. The $\mu^{\prime\prime}_{i}$ remains almost frequency independent after 1 MHz except x = 1.0. Magnetic loss $\left( {{ \tan }\delta_{\text{M}} } \right)$ arises due to lag of domain wall motion with the external field as well as defect in the lattice. The $\mu^{\prime\prime}_{i}$ reduces with ferrite content due to reduction of defects domain and mobility of charge carriers. At high-frequency region, $\mu^{\prime\prime}_{i}$ increases which may be because of enhanced eddy current loss.

The plot of relative quality factor, RQF, $\left( {{\text{RQF}} = \frac{{\mu^{\prime}_{i} }}{{{ \tan }\delta_{\text{M}} }}} \right)$ with frequency is displayed in Fig. 10c. For practical purposes, relative quality factor is used as a performance measurement. It is found that RQF rises with increasing frequency and then reduces with further increase in frequency showing a peak. The RQF peak becomes broader with ferrite content in the composite thus increasing the utility range of frequency. The peak corresponding to maxima in RQF shifts to lower frequencies with the LNMFO content. The LNMFO possesses the highest value of RQF.

3.8 M–H hysteresis loop

The magnetic properties of composites with variation of ferrite content were characterized by its magnetization versus magnetic field (M–H) hysteresis loop which is displayed in Fig. 11a. The LNMFO and composites show usual ferrimagnetic behavior at room temperature, whereas BDFO exhibits weak ferro-/antiferromagnetic behavior. The value of $M_{\text{s}}$ for BDFO sample estimated approximately 2.9 Am²/kg. Since the ferrite concentration increases in the compositions, the value of $M_{\text{s}}$ is enhanced up to 20 Am²/kg for x = 0.5. The $M_{\text{s}}$ of composites increases with ferrite quantity which ensures the ordered magnetic behavior of the composite because of LNMFO as ferrite phase in all sample. The large value of LNMFO is due to the possible migration of Fe³⁺ into B-site and non-magnetic Li¹⁺ prefers to A-site. This Fe³⁺ migration to B-site enhances the magnetic moment of B-site causes the increase in A–B interaction. The enhanced A–B interaction consequences an increase in the net magnetization $\left( {M_{\text{s}} = M_{\text{B}} - M_{\text{A}} } \right)$. The theoretical values of magnetic parameters (MP) were predictable using the sum rule [67], ${\text{MP}}\left( {\text{composite}} \right) = \left( {1 - x} \right){\text{MP}}\left( {\text{ferroelectric}} \right) + x{\text{MP}}\left( {\text{ferrite}} \right)$.

Fig. 11

a Magnetic hysteresis loops of xLNMFO–(1 − x)BDFO composites, b an enlarged view of the low-field M–H hysteresis loop

The measured values of MP from hysteresis loops and calculated values from equation are shown in Table 3. The $M_{\text{s}}$ of the samples closely follows the sum rule. However, the magnetic parameters (i.e., remnant magnetization $\left( {M_{\text{r}} } \right)$ and coercivity $\left( {H_{\text{C}} } \right)$) do not follow the sum rule. The values of $M_{\text{r}}$ of the compositions are higher than predicted values (Table 3). This is the result of intergrain coupling between the two different phases in the composites [68]. The BDFO shows an antiferromagnetic behavior with a low value of $M_{\text{r}}$ (0.22 Am²/kg) and incorporation of LNMFO and BDFO into composite leads to improvement of magnetization as the interfacial strain present leads to change in orientation of the spins [22]. The multiferroic composites have higher value of reduced magnetization ($M_{\text{r}} /M_{\text{s}}$) as compared with pure LNMFO. This reduced magnetization is also called squareness of hysteresis loop. It has values lying in range 0–1. It is a measure of application in memory devices [69], hence, these composites can be used in memory devices.

Table 3 Measured and predicted magnetic parameters of xLNMFO–(1 − x)BDFO composites observed at room temperature

3.9 Magnetoelectric effect

The $\alpha_{\text{ME}}$ depends on the ac resistivity, mechanical coupling as well as the sample ingredient. The ME effect in samples is achieved due to the interaction of the ferroelectric and magnetic phases. Applied magnetic field induces a strain in magnetic domains because of coupling of the magnetic and ferroelectric domains, the strain produces a stress (strain—mediated stress) in ferroelectric domains, and eventually improves the polarization of ferroelectric domains; therefore, a voltage develops in the grains. Figure 12 shows the change of $\alpha_{\text{ME}}$ with applied DC magnetic field for all composites. It is observed that the $\alpha_{\text{ME}}$ of the materials can be influenced by the ferrite content (LNMFO). We observe that $\alpha_{\text{ME}}$ increases with increasing magnetic field, reaches a highest value and then decreases for the higher magnetic field. This initial increase in ME output is attributed to the increase in magnetostriction induces strain in LNMFO phase which was confirmed by hysteresis. The reduction of $\alpha_{\text{ME}}$ with the DC magnetic field is due to the fact that at certain value of magnetic field the magnetostriction coefficient of LNMFO phase reaches its saturation value [70]. In these samples, above 0.2 T, the magnetostriction would generate constant electrical field in the ferrite part as a result decreases the value of $\alpha_{\text{ME}}$ with increasing magnetic field.

Fig. 12

Variation of $\alpha_{\text{ME}}$ with DC magnetic field with ferrite content for various xLNMFO–(1 − x)BDFO composites

The ME effect of the samples depends on the magnetostriction of the ferrite part and the piezoelectricity of the ferroelectric part. A small amount of the ferrite or ferroelectric part results in the reduction of magnetostriction or piezoelectricity, respectively, leading to a reduce in the static $\alpha_{\text{ME}}$ as theoretically predicted [71]. Furthermore, in order to obtain enhanced ME response in composites, two individual parts should be in equilibrium and mismatching between grains should not be presented [17]. The maximum value of $\alpha_{\text{ME}}$, 158 × 10³ Vm⁻¹ T⁻¹, is observed for the composite with 0.1LNMFO–0.9BDFO. The remarkable point to be noted here that the present samples exhibits better results than the other previously reported composites. The maximum values of $\alpha_{\text{ME}}$ of the reported composites are presented in Table 4. This is because a balance between the concentration of the two phases and matching between the grains of the two phases has been established for these compositions. The decrease of $\alpha_{\text{ME}}$ for the composite with high concentration of ferrite part is ascribed to the increased porosity in the sample. The existence of the pores breaks the magnetic contacts among the grains. Therefore, increase in porosity may reduce the net magnetization in the bulk and effects on ME response in these compositions [72].

Table 4 Comparison of the maximum ME coefficient ($\alpha_{\text{ME}}$) with the present investigation

4 Conclusions

The mixed spinel-perovskite multiferroic composites of xLNMFO–(1 − x)BDFO have been fabricated by mixing LNMFO and BDFO which are prepared separately by standard solid-state reaction method. The XRD study ensures the coexistence of both the ferroelectric and ferrite phases in the composition. The $\bar{D}$ is found to be reduced slightly with the increase of ferrite part up to x = 0.2 and for higher value of x after that it has increased. The change of dielectric properties with frequency indicates the typical dielectric dispersion behavior at low-frequency region for all the composites because of interfacial polarization. Because of reduced mobility of charge carriers, the composites show low dielectric loss. The $\sigma_{\text{ac}}$ rises with increasing frequency confirm the small polaron hopping-type conduction mechanism. Both the modulus study and $\sigma_{\text{ac}}$ reveal polaron hopping type conduction in the composites. The composites have both the grain and grain boundary effects to the electric properties. In the Cole–Cole plots, asymmetric semicircular arcs are observed which indicate non-Debye-type relaxation exists in the present compositions. The $\mu^{\prime}_{i}$ enhances and the $\mu^{\prime\prime}_{i}$ reduces with ferrite concentration for all composites. The highest value of RQF is found for x = 0.5. The $M_{s}$ of all samples increases with ferrite part. The highest value of $\alpha_{\text{ME}}$ (158 × 10³ Vm⁻¹ T⁻¹), is observed for the composite with 0.1LNMFO–0.9BDFO. At last, the prepared composites in the present investigation can be used for various technological applications in device.