Microstructural and electrical transport properties of uniaxially pressed $\text {Bi}_{1.65}\text {Pb}_{0.35}\text {Sr}_2\text {Ca}_{2.5}\text {Cu}_{3.5}\text {O}_{10+\delta }$ ceramic superconductors

Abstract

We have studied the effect of the pelletization pressure on microstructural and electrical transport properties of superconducting ceramics with starting composition given by the formula $\text {Bi}_{1.65}\text {Pb}_{0.35}\text {Sr}_2\text {Ca}_{2.5}\text {Cu}_{3.5}\text {O}_{10+\delta }$. The experimental data of electrical measurements was processed in order to obtain the weak-link resistivity, the orientation probability of the grains’ a-axes along a certain preferential direction, the slope of the linear part in the temperature dependence of the ab-planes resistivity, and the intrinsic effective anisotropy of the grains, of each sample. In contrast with the behaviour of $\text {Bi}_{1.65}\text {Pb}_{0.35}\text {Sr}_2\text {Ca}_{2}\text {Cu}_{3}\text {O}_{10+\delta }$ ceramics, the Ca, Cu enriched samples exhibit a reduction of their effective anisotropy at sample level and weak links resistivity with increasing compacting pressures. In addition, a compacting pressure of around 488 MPa may affect considerably the electrical and structural parameters of the material. The results suggest that a combined effect of the pelletization pressure and the doping with Ca and Cu can be used to improve the electrical transport properties of these materials for technological applications.

1 Introduction

The search of new superconducting compounds continue to be active areas of the superconductivity with fundamental and applied goals [1,2,3,4,5]. A prominent feature of several superconductors for large scale applications is their polycrystalline structure [1, 5,6,7,8,9]. Within this context, two essential issues should be taken into consideration when the performance of high critical temperature superconductors (HTS) is evaluated. One is the intergrain weak links related with the low texture [5], porosity and the presence of spurious phases [5]. The other is the intragranular flux pinning [1], which is rather low in several HTS, because of their layered structure and high anisotropy [1].

A large body of research of the properties of $\text {Bi}_{1.65}\text {Pb}_{0.35} \text {Sr}_2\text {Ca}_{2}\text {Cu}_{3}\text {O}_{10+\delta }$ (Bi,Pb)2223 ceramic and the materials based on it shows that some impurity phases, which are almost inevitable found in such multicomponent system can favourably influence the superconducting properties of these materials [10].

Previous investigations show that an excess of Ca and Cu in the initial nominal composition affects the (Bi,Pb)2223 phase growth and the intergranular coupling in (Bi,Pb)2223 ceramics [11]. Using this modification technique, the excess of Ca and Cu separates out as the $\text {Ca}_2\text {CuO}_3$ compound is located between the (Bi,Pb)2223 crystallites providing the connection, which in turn is beneficial to the electrophysical properties both in normal and superconducting states [11, 12]. The best electrophysical properties are observed in the ceramic of nominal composition $\text {Bi}_{1.8}\text {Pb}_{0.3}\text {Sr}_{1.9}\text {Ca}_{2+2x}\text {Cu}_{3+x}\text {O}_{n}$ (x = 0.4) [11]. Introducing excess quantities of Ca and Cu by doping pure (Bi,Pb)2223 with calcium cuprate leads to a gradual deterioration of the electrophysical properties in the normal state [11]. In the superconducting state the properties are almost independent of the quantity of introduced $\text {Ca}_2\text {CuO}_3$. This indicates that the formation of connections occurs in the phase growth stage [11]. On the whole, all Ca, Cu enriched (Bi,Pb)2223 samples have higher critical temperature and current density than those of pure (Bi,Pb)2223 for all values of x from 0.2 to 1.0 [11].

By using an Effective Medium Approximation model [13] applied to electric transport measurements of (Bi,Pb)2223 polycrystals, the effective anisotropy of the grains, $t=\rho _c/\rho _{ab},$ their orientation probability, $\gamma _{xa},$ the weak links resistivity, $\rho _{wl},$ and the slope of the temperature dependence of the grains’ resistivity, $A_{ab}=\varDelta \rho _{ab}/\varDelta T$ can be determined, where $\rho _c, \rho _{ab}$ and T are the out-of-plane resistivity, the in-plane resistivity and the temperature of the samples, respectively [14]. These recent results for superconducting polycrystals, show that high compacting pressures affect not only the intergranular, but also the intragranular transport properties by increasing the density of defects and reducing the effective anisotropy of the grains [15,16,17]. A similar procedure with Effective Medium Approach may be applied to study the behaviour of the conductance in disordered or not disordered graphene [18].

In this paper we have studied the effect of the pelletization pressure on the crystallite size and electrical transport properties of superconducting ceramics with starting composition given by the formula $\text {Bi}_{1.65}\text {Pb}_{0.35}\text {Sr}_2\text {Ca}_{2.5}\text {Cu}_{3.5}\text {O}_{10+\delta }$. The experimental data of electrical measurements were processed in order to obtain the weak-link resistivity, $\rho _{wl},$ the orientation probability of the grains’ a-axes along a certain preferential direction, $\gamma _{xa},$ the slope of the linear part in the temperature dependence of the ab-planes resistivity, $A_{ab}=\varDelta \rho _{ab}/\varDelta T,$ and the intrinsic effective anisotropies, $t=\rho _c/\rho _{ab}$ of each sample following the method described in reference [15] (see Appendix). Here, $\rho _{ab},\rho _{c}$ and T are the main values of the grain’s resistivitity tensor and the measurement temperature, respectively. In contrast with the behaviour of (Bi,Pb)2223 ceramics, the Ca, Cu enriched samples exhibit a reduction of their anisotropy, $\mu =\rho _{z}/\rho _{x},$ and weak links resistivity, $\rho _{wl},$ with increasing compacting pressures. We found that a compacting pressure of around 488 MPa may affect considerably the electrical and structural parameters of the material, which is observed in the obtained results for $t,\gamma _{ab},$ unit cell volume and the residual strain percentage, $\varepsilon,$ respectively.

2 Experimental details

$\text {Bi}_{1.65}\text {Pb}_{0.35}\text {Sr}_2\text {Ca}_{2.5}\text {Cu}_{3.5}\text {O}_{10+\delta }$ polycrystalline samples were prepared from powders of $\text {Bi}_2\text {O}_3,$ PbO, $\text {SrCO}_3, \text {CaCO}_3,$ and CuO which were mixed in the atomic ratios of Pb:Bi:Sr:Ca:Cu (0.35:1.65:2:2.5:3.5). The mixture was first calcined in air at 750 $^\circ$C for 40 h. After that, the powder was reground and pressed into pellets of 8 mm in diameter and 2 mm in thickness at a pressure of 196 MPa. These pellets were heat treated at 800 $^\circ$C in air for 40 h. Subsequently, the samples were reground, pressed again, and treated in air for 40 h at 826 $^\circ$C. This step was repeated two more times, as described elsewhere [19]. Finally, the pellets were reground and pressed at three different uniaxial compacting pressures to obtain cylindrical samples with dimensions of 8 mm in diameter and 5 mm in height. The compacting pressures were 230, 488 and 780 MPa for the GD2P1, GD2P2 and GD2P3 samples, respectively. The last heat treatment of the pellets was performed in air for 40 h at 826 $^\circ$C, followed by slow cooling.

The densities of the three samples compacted at different pressures were determined by mass to volume ratios. The volumes were determined considering the pellets as cylinders and determining their dimensions with a resolution of 0.05 mm. The masses were measured with a digital balance with resolution of 0.1 mg. With the resulting density and the structural one, which in the cases of (Bi,Pb)2223, $\text {Bi}_{1.65}\text {Pb}_{0.35}\text {Sr}_2\text {CaCu}_{2}\text {O}_{8+\delta }$ ((Bi,Pb)2212) and $\text {Bi}_{1.65}\text {Pb}_{0.35} \text {Sr}_2\text {Cu}_{1}\text {O}_{8+\delta }$ ((Bi,Pb)2201) are $\sim$6.3 g/$\text {cm}^3$ [20,21,22], $\sim$6.7 g/$\text {cm}^3$ [22] and $\sim$7.2 g/$\text {cm}^3$ [22], respectively, the volume fraction of pores and insulating phases, p was estimated.

The microstructure of the samples was studied by means of Scanning Electron Microscopy (SEM) of fractured surfaces. The study was performed with a microscope model Hitachi S-530, which has nominal resolution of $\sim$ 30–40 nm operating within an interval of 15–20 kV. The platelet shape of grains typical in Bi-2223 phase is observed in all samples.

We have evaluated the phase identification in powder samples and the degree of texture in bulk samples by means of X-ray diffraction patterns. The powders were obtained from the three samples after the last heat treatment, grinding a piece taken from each pellet. The X-ray diffraction patterns were obtained in a Bruker-AXS D8 Advance diffractometer. These measurements were performed at room temperature using Cu K$\alpha$ radiation in the $3^\circ \le$ 2$\theta$ $\le$ 60$^\circ$ range with a $0.02^\circ (2\theta )$ step size and 100 s per step. The Standard Reference Material 640c (SRM) consists of SiO powder. The measurement of the SRM was accomplished at the same previous conditions, but within an angle range of $27^\circ \le 2\theta \le 90^\circ$. From the X-ray diffraction patterns taken on pellet samples, the texture of three specimens was evaluated by means of the Lotgering factors [23]. In addition, estimates of the crystallites size, residual strains, lattice parameters and unit-cell volumes were performed throught profile fitting of the X-ray patterns of the three powder samples.

In order to measure the temperature dependence of the electrical resistivity tensor and its components in the paracoherent state, the samples were cut from the pellets in slab form, as showed in Fig. 1. The dimensions of the three cut samples are displayed in Table 1.

Fig. 1

Slab extracted from a pellet to be measured using the Levin-Gonzalez method

Table 1 Dimensions of the samples

Electrical contacts were prepared using silver paint with a heat treatment at 730 $^\circ \text {C}$ for 20 min, these were as small as possible in order to minimize their effects on the voltage measurements. The contact size was about $10\%$ of the block dimensions. Before each measurement, the samples were cooled from room temperature down to $\approx$ 80 K. The excitation current was injected according to the Levin-Gonzalez method (LGM) as shown in Appendix 2 6 [15, 24, 25]. Both the voltage across the sample and its temperature were collected while the temperature was raised slowly to 300 K for the case of the temperature dependence of the electrical resistivity tensor.

Regarding the measurements of the resistivity tensor components in the paracoherent state, in which the dissipation is mainly intergranular [26], the samples were cooled down to 103 K and the $I-V$ curve was taken. It was transformed into a resistivity versus current density curve starting from which the paracoherent resistivity tensor component was determined by taking the resistivity value at the point where the slope of the $\rho -J$ curve starts to decrease. With this selection of the level of paracoherent resistivity we are avoiding the “contamination” of the measurements due to the presence of intragranular dissipation sources [14, 15].

In both types of measurements described before, six electrical contacts were placed on the samples according to the LGM [15]. The two components of the electrical resistivity tensor $\rho _x$ and $\rho _z$ were calculated from these measurements and the dimensions of the sample through the equations 24 and 25 see Appendix 1 2 6 [15].

3 Results and discussion

The diagram displayed in Fig. 2 sketches the procedure we will follow to get information from our samples. In subsection 3.4, we describe the measurements resulting in the different input parameters indicated at the top of the diagram (see results in Table 6). And we describe too, how the model works to obtain the parameters shown at the bottom of Fig. 2 (see results in Table 7), and then we compare them back with the experiment.

Fig. 2

Diagram of the method to separate the intra and intergranular parameters starting from microstructural and electrical transport characterizations (taken from Ref. [15])

3.1 X-ray diffraction patterns analysis

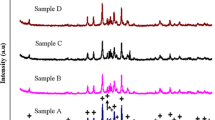
Fig. 3 displays the X-ray diffraction patterns taken on powder and pellet samples extracted from GD2P1, GD2P2 and GD2P3 samples.

Fig. 3

X-ray diffraction patterns of powder and pellet samples. The reflections belonging to the (Bi,Pb)2223, (Bi,Pb)2212, (Bi,Pb)2201, $\text {Ca}_2\text {PbO}_4$ and $\text {Ca}_2\text {CuO}_3$ phases are marked by “H”, “L”, “(Bi,Pb)2201”, “$\text {Ca}_2\text {PbO}_4$” and “$\text {Ca}_2\text {CuO}_3$”, respectively. The main peaks display their Miller’s indexes

As an example, we show the calculations for the relative volume fractions of the high-$\text {T}_c$ (Bi,Pb)2223 phase, $f_H,$ which is calculated based on the following equation [7, 27, 28]:

$$\begin{aligned} f_{H}=\frac{\varSigma I_{H(hkl)}}{\varSigma I_{H(hkl)}+\varSigma I_{L1(hkl)}+\varSigma I_{L2(hkl)}+\varSigma I_{E_1(hkl)}+\varSigma I_{E_2(hkl)}} \end{aligned}$$

(1)

Here, $I_{H(hkl)},I_{L1(hkl)},I_{L2(hkl)},I_{E_1(hkl)}$ and $I_{E_2(hkl)}$ are the intensities of the (hkl) diffraction lines for high-$\text {T}_c,$ low-$\text {T}_c$ ((Bi,Pb)2212), low-$\text {T}_c$ ((Bi,Pb)2201), $\text {Ca}_2\text {PbO}_4$ and $\text {Ca}_2\text {CuO}_3$ phases, respectively. The volume fractions of the phases are showed in Table 2 for the three samples.

Table 2 Volume fractions of the phases and lotgering factors $F_L$

Also, we have used the X-ray diffraction patterns shown in Fig. 3a–f, to evaluate the sample texture by means of the Lotgering factors calculated for the (00l) peaks. They were calculated by means of the formula [23, 29]:

$$\begin{aligned} F=(N-N_{0})/(1-N_{0}), \end{aligned}$$

(2)

where,

$$\begin{aligned} N=\sum \limits _lI(00l)/\sum \limits _{hkl}I(hkl). \end{aligned}$$

(3)

Here, I refers to the X-ray peak intensity; N is the sum of the integrated intensities for all (00l) reflections divided by the sum of all intensities of (hkl) in the textured specimen. $P_{0}$ is an equivalent parameter for a random specimen taken from the powder sample. A seemingly contradictory result was obtained. The Lotgering factor of the samples is almost the same for the samples obtained at different uniaxially compacting pressures as shown in Table  2. A possible explanation of this behaviour is given in reference [15].

Finally, an important feature of the X-ray diffraction patterns to be mentioned here, is the presence of the (008) peak corresponding to the low $T_{c}$ (Bi,Pb)2212 phase in the three pellet samples, but it is almost absent in the powder ones. So, everything indicates that a thin layer of this phase is covering the compaction surface of the sample on which the X-rays were reflected. Similar results were obtained in samples with starting composition $\text {Bi}_{1.65}\text {Pb}_{0.35}\text {Sr}_2\text {Ca}_{2}\text {Cu}_{3}\text {O}_{10+\delta }$ [15].

As we will see in the subsection 3.4 these main microstructural features of the pellets samples have a fingerprint in the electrical transport measurements.

3.2 Profile fitting of the X-ray powder diffraction

The XRD peak profiles of (Bi,Pb)2223, (Bi,Pb)2212, (Bi,Pb)2201, $\text {Ca}_2\text {PbO}_4$ and $\text {Ca}_2\text {CuO}_3$ (see Table 3) were analysed by the free Rietveld refinement software FullProf-2000 version June-2015. With this software, the lattice strain can be evaluated from refined profile parameters when a pseudo-Voigt function of Thompson-Cox-Hastings (TCH) is chosen to express peak profiles [30]. In this function, the Full Width at Half Maximum (FWHM) of the Gaussian and Lorentzian parts, $H_{G}$ and $H_{L},$ respectively, are expressed as follows [31]:

$$\begin{aligned} H_{G}= & {} [8\ln 2(U\tan ^2\theta +V\tan \theta +W+P\sec ^2\theta )]^{1/2} \end{aligned}$$

(4)

$$\begin{aligned} H_{L}= & {} (Y-Y_a\cos \phi )\sec \theta +(X-X_a\cos \phi )\tan \theta \end{aligned}$$

(5)

where $H_G$ is the Gaussian full width at half maximum, modified by an additional broadening parameter, P; $\theta$ is the Bragg angle; V and W in the Gaussian part are parameters depending on the instrument; $H_L$ is the Lorentzian full width at half maximum, which accounts for the anisotropic FWHM behavior by introducing two anisotropic broadening parameters, $Y_a$ (crystallite size) and $X_a$ (strain), and $\phi$ is the angle between a common anisotropy axis and the corresponding reciprocal lattice vector; in the Lorentzian part, Y is a parameter for isotropic crystallite-size effect; U and X are isotropic strain parameters [32]. On the other hand, the profile fitting results indicated only isotropic parameters, for that reason anisotropic broadening parameters are equal to zero ($X_a=0$ and $Y_a=0$). In this case, the crystallite size from Gaussian and Lorentzian parts, $\tau _G$ and $\tau _L$, respectively, can be obtained as follows [32]:

$$\begin{aligned} \tau _G(\AA )=\frac{180K\lambda }{\pi \sqrt{P}} \end{aligned}$$

(6)

$$\begin{aligned} \tau _L(\AA )=\frac{180K\lambda }{\pi Y} \end{aligned}$$

(7)

and the lattice strain from Gaussian and Lorentzian parts, $\epsilon _G$ and $\epsilon _L,$ respectively, were evaluated by the following equations [32]:

$$\begin{aligned} \epsilon _G(\%)=\frac{\pi }{1.8}[8\ln 2(U-U_{ins})]^{1/2} \end{aligned}$$

(8)

$$\begin{aligned} \epsilon _L(\%)=\frac{\pi }{1.8}(X-X_{ins}) \end{aligned}$$

(9)

where K is the Sherrer constant, with typical value of 0.9; $\lambda$ is the X-ray wavelength; and $U_{ins}$ and $X_{ins}$ are instrument contributions, which are evaluated from peak profiles of a reference sample (in this case, SiO).

Table 3 Crystallographic data [22] of the phases used in profile fitting

The reliability of the refinement is shown by the values of the fit parameters, $S=R_{wp}/R_e,$ where $R_{wp}$ is the weighed sum of residuals of the least squares fit; and $R_e$ is the value statistically expected (see values in Fig. 4). If $S=1$ the refinement is perfect [33]. However, for values between $0.62\le \text {S}\le 1.3$ the refinement is considered satisfactory [32].

Fig. 4

Profiles fitting of all X-ray diffraction patterns of powder samples. The reflections belonging to the (Bi,Pb)2223, (Bi,Pb)2212, (Bi,Pb)2201, $\text {Ca}_2\text {PbO}_4$ and $\text {Ca}_2\text {CuO}_3$ phases are marked by “H”, “L”, “(Bi,Pb)2201”, “$\text {Ca}_2\text {PbO}_4$” and “$\text {Ca}_2\text {CuO}_3$”, respectively. Panels a–c show the profiles of the samples GD2P1, GD2P2 and GD2P3

FullProf-2000, version June-2015 has included the previous equations in the calculation methods and accepts several phases to be refined. We refined five phases (see Table 3) and 21 parameters simultaneously in a maximum. We referred to [11, 22, 33,34,35,36] for the crystallographic data of the phases, such as space group and lattice parameters at room temperature. V, W and peak-shift parameters related to instrument and sample displacement were previously refined using a SiO reference sample. In the analysis, we refined the scale factor s; zero-shift $Z_0$; lattice parameters a, b and c; preferred-orientation parameter r; and profile parameters U, Y and P. We fixed the parameters of crystallite structure, atomic positions and site occupancies at room temperature.

For the (Bi,Pb)2223 phase, the unit-cell parameters were calculated assuming an orthorhombic unit cell and the obtained values shown in Table 4 are in excellent agreement with those reported for the same compound elsewhere [7, 37]. However, an appreciable decrease in the a parameter of the sample GD2P2 is observed. This change provokes a decrease in the volume of the cell as compared with the other two samples. Also an appreciable change in $\varepsilon$ is observed. We will analyse the influence of this structural change on the electrical transport properties in section 3.4.

Table 4 The profile fitting parameters obtained for the (Bi,Pb)2223 phase. Unit-cell parameters, unit-cell volume, $V_{uc},$ crystallite size, $\tau,$ and residual strain percentage, $\epsilon$

3.3 Micro-structural analysis

Table 5 displays a summary of the microstructural properties of the three samples studied in this paper. The densities of the samples substantially increase with increasing pressures and as a result an appreciable reduction of the volume fraction of pores and insulating phases is observed. Here, $p=(V_{p}+V_{np})/V_T,$ where $V_T,V_{p}$ and $V_{np}$ are the volumes of samples, pores and non-conductivity phases, respectively. Finally, p parameters were obtained by means of $p=1-[d_{r}(f_{H}/d_{H}+f_{L1}/d_{L1}+f_{L2}/d_{L2})],$ here $d_{r}$ is the experimental density, $f_{H},f_{L1},f_{L2}$ are the relative volume fraction of the high-$\text {T}_c$ (Bi,Pb)2223, low-$\text {T}_c$ (Bi,Pb)2212 and low-$\text {T}_c$ (Bi,Pb)2201 phases, respectively, $d_{H}\approx 6.3~{\text{g/cm}}^{3},d_{L1}\approx 6.7~{\text{g/cm}}^{3}$ and $d_{{L2}} \approx 7.2~{\text{g/cm}}^{3}$ are the structural densities of (Bi,Pb)2223 [20,21,22], (Bi,Pb)2212 [22] and (Bi,Pb) 2201 [22], respectively.

The effect of the compacting pressure has its counterpart in the microstructure of these samples. This can be inferred from the fracture micrographs of samples GD2P1, GD2P2 and GD2P3 which are shown in Fig. 5a–c, respectively. In all micrographs it is observed that the granular morphology of the samples is similar, exhibiting grains with nearly platelet-like shape. A careful inspection also reveals changes in both the grain size and the grain orientation.

Table 5 Mass density, $d_r,$ volume fraction of pores and insulating phases, p, and shape anisotropy of the grains, $L_{a}/L_{c}$

Fig. 5

Fracture micrographies of the samples obtained by SEM. a GD2P1, b GD2P2 and c GD2P3 samples

The average grain size in the sample GD2P1 was found to be $L_a$ = (6.6 ± 0.4) $\mu m$ long and as thick as $L_c$ = (0.57 ± 0.03) $\mu m$; for the sample GD2P2, the grains were found to have dimensions $L_a$ = (5.8 ± 0.3) $\mu m$ long and $L_c$ = (0.38 ± 0.01) $\mu m$ thick; in sample GD2P3 the grains have dimensions $L_a$ = (12.6 ± 0.7) $\mu m$ long and $L_c$ = (0.44 ± 0.03) $\mu m$ thick. The ratio $L_a/L_c,$ which is referred to as the mean aspect ratio of the grains [26], has been found to be very sensitive to the applied pressure and was 11.6, 15.3 and 28.6 for the samples GD2P1, GD2P2 and GD2P3, respectively (see Table 5). These values are higher than those of 2.5 and 4.5 in ceramic samples of $\text {YBa}_2\text {Cu}_3\text {O}_{7-\delta }$ [26], but similar to those estimated for both (Bi,Pb)2223 superconducting bulk samples and tapes [16, 17, 38].

3.4 Electrical transport measurements

Let us analyze the results of electrical transport measurements. The experimental values are shown in Table 6. The parameters $\rho _{x}(0),\rho _{z}(0),A_x$ and $A_z$, are obtained by linear fitting of the curves of electrical resistivity dependence with the temperature in the linear region at high temperatures (see Fig. 6). Here $A_x,A_z$ are the slopes of the electrical resistivity and the $\rho _{x}(0),\rho _{z}(0)$ the residual electrical resistivity in the two principal directions of the sample, respectively.

Table 6 Slopes of electrical resistivity at the sample level, $A_x$ and $A_z,$ residual electrical resistivities, $\rho _{x}(0)$ and $\rho _{z}(0),$ electrical resistivities at 300 K, $\rho _x$ and $\rho _z$ for samples GD2P1, GD2P2 and GD2P3

Fig. 6

Temperature dependencies of the resistivity tensor component, $\rho _x(T),$ of the samples GD2P1, GD2P2 and GD0P3. The inset shows the temperature dependencies of the resistivity tensor component, $\rho _z(T),$ of the same samples. Some physical parameters extracted from $\rho _i(T)$ $i=x,z$ curves are displayed in Table 6 and discussed in the text

In Fig. 7 the way of determining the paracoherent resistivity, $\rho _{px}$ of each sample is displayed. The $\rho _{px}$ value is selected in the point where the straight line separates from $\rho _{x}-J$ curve (see the Fig. 7). The explanation of this method of selection was discussed in detail in [15].

Fig. 7

The mean current density dependencies of the x-axis resistivity component, $\rho _x(J)$ for the samples GD2P1, GD2P2 and GD2P3 measured at constant temperature $T=103 K$. The method to determine $\rho _{px}$ is sketched

An issue to be highlighted in Table 6 is that the external electric anisotropy, $\mu$, has a minimum for the sample GD2P2 while the values of the orientation factor of the grain decreases when the compacting pressure increases from 230 till 780 MPa. We will return to this aspect later.

Let us apply the model described in reference [15] to our sample set (see Appendix 1 5 and diagram in Fig. 2). The main results are reported in Table 7. First, we have calculated the $A_{ab}$ values by using two different expressions $A_{x}\alpha _{nx}$ and $A_{z}\alpha _{nz}$. However, the difference between the obtained values does not exceed 0.5$\%$ for each sample. This result is supported by the behaviour of $\mu$ as a function of the temperature displayed in Fig. 8. It exhibits a very small variation, 2$\%$ approximately, when T decreases from 300 K to the superconducting transition temperature for both samples. Such a behaviour of $\mu$ is also reflected in the $\rho _{wl}$ values which are very similar in the two main directions of the samples. Thus, one obtains $\mu =\alpha _{nx}/\alpha _{nz}$

Table 7 Outputs parameters of the model described in Appendix 1 and showed in Fig. 2

.

Fig. 8

Anisotropy parameter as a function of the temperature, $\mu (T)$, for a GD2P1, b GD2P2 and c GD2P3 samples

However, the obtained $A_{ab}$ values are twice smaller than those reported elsewhere for single crystals without Pb doping [39, 40]. It seems to be that the doping with Pb has a great influence in the properties of the crystallites.

Another important issue, to be considered, is that the calculated $\gamma _{ab}$ value is greater for the sample compacted at higher pressure GD2P3. This sample shows a greater orientation of its grains with the c axes parallel to the z axis as compared to the GD2P1 sample (see Fig. 5). A third relevant issue is found when $A_{ab}$ and $\rho _{wl}$ of the samples are compared. There is a systematic decrease in $A_{ab}$ with increasing compacting pressures and an abrupt fall in $\rho _{wl}$ when the compacting pressure increases from 488 to 780 MPa. It very important to note that the sample GD2P2, which exhibits an anomalous behaviour in its electrical transport properties obtained experimentally and by means of the model (see Appendix 5 and Fig. 2), also has clear differences in its unit cell volume and residual strain percentage $\epsilon,$ as compared to the two other samples. The experimental results show that the compacting pressure of 488 MPa in Ca, Cu enriched samples favors an appreciable reduction of the a parameter that is reflected in the unit cell volume. A subsequent increase of the compacting pressure to 780 MPa restores similar unit cell parameters than a compacting pressure of 230 MPa and provokes a decrease in $\epsilon$. The structural changes in the sample GD2P2 seems to be the cause of the abrupt decrease in the external anisotropy, $\mu,$ and the effective anisotropy of the grains t, respectively. Moreover, these structural changes could be the cause of the small reduction in the orientation probability of the grains. Nevertheless, more experiments are needed to understand the main causes of these changes in the structural and electrical transport properties with the compacting pressure. Here, we would like to point out that these results as compared with those obtained in samples with starting composition $\text {Bi}_{1.65}\text {Pb}_{0.35}\text {Sr}_2\text {Ca}_{2}\text {Cu}_{3}\text {O}_{10+\delta }$ [15] show changes not only in the effective anisotropy of the grains, t, but in $A_{ab}$ and $\rho _{wl}$ as well. The Ca, Cu enriched samples show an improvement in the junctions with a reduction of the weak links resistivity of 50 $\%$ approximately, which agrees with the results obtained in reference [11].

Another way to verify the model is to compare the experimental results of $f_{z}$ direction with those predicted by the model. However, the $\rho _{z}(T)$ dependencies do not go completely to zero for temperatures at which the x component of the resistivity is already zero as shown in Fig. 9. Such effect provokes that the anisotropy factor $\mu$ of the samples increases during the superconducting transition of the samples instead of decreasing, as expected. The cause of this behaviour is related to the thin layer of (Bi,Pb)2212 observed in the X-ray diffraction patterns of the pellets samples as discussed previously. This film is in parallel for the measurements in the x-direction, but in series for the z direction, preventing the achievement of the zero resistivity in the $\rho _{z}(T)$ curve. Similar results were obtained in reference [15] for sample without Ca, Cu excess.

Fig. 9

$\rho _{i}(T)$ (with $i=x, z$) dependencies in the two main directions for the three samples studied in this article

4 Conclusions

We have applied successfully the model described in reference [15] to estimate inter and intragranular magnitudes in samples with starting composition given by the formula $Bi_{1.65}\text {Pb}_{0.35}\text {Sr}_2\text {Ca}_{2.5}\text {Cu}_{3.5}\text {O}_{10+\delta }$.

The results show that the samples sintered in a Ca, Cu enriched environment exhibit a more pronounced modification of their intragranular properties with increasing compacting pressures than that observed in samples without excess of Ca and Cu [15]. In addition, a decrease of the external anisotropy and weak links resistivity is obtained with increasing pressures, which could benefit the electrical transport performance of this material.

An appreciable change in the unit cell parameter, a, is revealed for a compacting pressure of 488 MPa. For this sample the external anisotropy, the effective one of the grains and the unit cell volume are minimal. Modifications of the crystalline structure with the compacting pressure have also been reported elsewhere [21], but assuming a tetragonal symmetry. In that case an increase of the unit cell parameter, c, was observed in samples without excess of Ca and Cu.

We have verified the presence of a thin layer of (Bi,Pb)2212 at the surface of the samples. This layer prevents that the resistivity along the z direction of the sample, $\rho _{z},$ goes to zero at the same temperature in which $\rho _{x}$ vanishes. A similar result was obtained for samples without Ca, Cu excess [15]. The X-ray diffraction patterns in pellet and powder samples support this statement.

Even when the Lotgering factors, $F_{L}$ and the orientation probability of the grains represent, on the whole, different magnitudes in our sample set, both obtained values are similar and greater than 0.4.

Finally, we would like to remark that the obtaining of the (Bi-Pb)2223 phase in a Ca, Cu enriched environment may improve the properties of this compound for some applications and simplify its fabrication process. However, it is an issue not enough treated in the literature.

Appendices

Appendix 1: A model to anisotropic granular superconductors

In this Appendix 1 we summarize the main features of the model previously published in references [14, 15]. The model is based on two main ideas. The goal here is to make the article more self-consistent. First, the resistivity of the polycrystalline sample can be written as

$$\begin{aligned} \rho =\frac{1}{\alpha _{n}}(\rho _{ab}+\rho _{wl}). \end{aligned}$$

(10)

Eq. (10) expresses that the resistivity of the sample depends on the in-plane resistivity of the crystallites plus the resistivity of the Josephson junctions or weak links. This sum is amplified by a factor $1/\alpha _{n}$ that represents the combined effects of the grains’ misalignment and the defects in the polycystalline sample. Here, $\rho _{ab}=A_{ab}T$ and $\alpha _{n}=f\alpha _{str}$ where $\alpha _{str}$ represents the effects of the defects on the resistivity of the sample [26]. When we compare (10) with the linear part of experimental dependence $\rho (T),$

$$\begin{aligned} \rho =AT+\rho (0), \end{aligned}$$

(11)

$A_{ab}/\alpha _{n}=A$ and $\rho _{wl}/\alpha _{n}=\rho (0)$ are obtained easily [26, 41, 42].

In the case of a sample with two main directions, Eqs. (10) and (11) should be written for each of them [14]. If $\mu$ does not depend on the temperature or has a weak dependence with it, then one may take $\mu =\alpha _{nx}/\alpha _{nz}$ where x and z are the two main directions of the samples. Here, z is taken along the compacting direction and x is perpendicular to it. For high $T_{c}$ superconductors, like YBCO and Bi-based samples, have a very high intragranular anisotropy parameter in the range $10^{2}-10^{4}$ [39, 43, 44]

The orientation factor of the grains, $f_{x},$ has been expressed as a function of the orientation probability along the x-axis, $\gamma _{xa},$ the shape anisotropy of the grains, $L_{a}/L_{c},$ and the intrinsic effective anisotropy of the grains, t, as already was reported elsewhere [14]. The calculations are based on EMA [13], which constitutes the second pillar of the model: here it is assumed the pollicrystalline sample made up of two different phases represented by the grains oriented with their a or b axes parallel to the x-axis of the sample and those with their c axes oriented along the x-axis of the sample, respectively. Thus, the orientation probability, $\gamma _{xa},$ can be also interpreted as the probability of finding the first phase in the polycrystalline sample.

In this paper we will use a similar description to that presented before [14], but modified in some aspects. Here, we are including a new phase in the calculations of the effective conductivity, which accounts for the pores. These will be assumed spherical with conductivity zero, probability of appearance, p, and randomly distributed inside the polycrystalline sample. Moreover, all the contributions of the defects to the resistivity of the polycrystalline sample will be included in this new phase. Finally, in the present approach, the effects of the grains’ disorientation and defects are not separated into two factors, but contained in the same fraction $\alpha _{n}$.

In Appendix 1 of the reference [15] the calculations to obtain the functions $\mu =F(\mu ,\gamma _{xa},L_a/L_c,p,t)$ and $\alpha _{nx}=\alpha _{nx}(\mu ,\gamma _{xa},L_a/L_c,p,t)$ of the polycrystalline sample based on EMA [13, 14] are presented in detail. Notice that once having $\mu$ and $\alpha _{nx}$ it is easy to find $\alpha _{nz}$ since $\alpha _{nz}=\alpha _{nx}/\mu.$

Now it is described how the experimental data is processed by means of the model.

From the Eq. (10), the tensor resistivity component of the paracoherent resistivity along the x-axis is given by the equation

$$\begin{aligned} \rho _{px}=\frac{1}{\alpha _{nx}(\mu ,\gamma _{xa},L_{a}/L_{c},p,1)}(\rho _{wl_{x}}). \end{aligned}$$

(12)

Here, $t=1,$ because the grains are in the superconducting state. On the other hand, the extrapolation of the normal-state resistivity to zero temperature is given by a similar expression, but in this case $t\ne 1$ if the grains are anisotropic:

$$\begin{aligned} \rho _{x}(0)=\frac{1}{\alpha _{nx}(\mu ,\gamma _{xa},L_{a}/L_{c},p,t)}(\rho _{wl_{x}}). \end{aligned}$$

(13)

The ratio of Eqs. (12) and (13) gives

$$\begin{aligned} f_{x}=\frac{\rho _{px}}{\rho _{x}(0)}= \frac{\alpha _{nx}(\mu ,\gamma _{xa},L_{a}/L_{c},p,t)}{\alpha _{nx}(\mu ,\gamma _{xa},L_{a}/L_{c},p,1)}, \end{aligned}$$

(14)

which was experimentally determined. If we add to the Eq. (14) the equation of the anisotropy parameter $\mu,$ which was also experimentally determined

$$\begin{aligned} \mu =\frac{\alpha _{nx}(\mu ,\gamma _{xa},L_{a}/L_{c},p,t)}{\alpha _{nz}(\mu ,\gamma _{xa},L_{a}/L_{c},p,t)}, \end{aligned}$$

(15)

a system of equations with $\gamma _{xa}$ and t as unknown quantities is obtained. After finding $\gamma _{xa}$ and t it is easy to obtain $A_{ab}=A_{x}\alpha _{nx}$ where $\alpha _{nx}$ is calculated and $A_{x}$ is experimentally determined [15].

As an example of how the model works the dependence of $\alpha _{nx}$ and $\alpha _{nz}$ as functions of $\gamma _{xa}$ are shown in reference [15]. The variation provoked by a 15 $\%$ or 28 $\%$ of pores is quite small when 0.4 $<\gamma _{xa}<$ 0.48. The significant differences appear in the region of very low and very high values of $\gamma _{xa}$. The values of the intrinsic anisotropy parameter and shape anisotropy of the pollycrystalline sample were taken similar to those that will be used in this work.

Appendix 2: Analytical procedure for Levin-Gonzalez’ method

We have applied the measurement model proposed by González et. al. [25] for measuring the different components of the resistivity tensor in $\text {Bi}_{1.65}\text {Pb}_{0.35}\text {Sr}_2\text {Ca}_{2.5}\text {Cu}_{3.5}\text {O}_{10+\delta }$ polycrystalline superconductors. For the $\rho _z$ experimental determination, the current is injected onto the top surface of the sample and extracted at the bottom. Two aligned contacts recording the voltage are located according to Fig. 10b.

Fig. 10

Measurement configurations. a Experimental configuration used for the determination of the x-axis effective resistivity, $\rho _x$. b Experimental configuration used in the determination of the z-axis effective resistivity, $\rho _z$

In the quasistatic limit, the expression which satisfies the Laplace’s differential equation with the first boundary condition is [25]:

$$\begin{aligned} V(x,z)= & {} \displaystyle V_0z+\sum _{n=1}^\infty \!\!V_n\cos \left( \frac{n\pi x}{L}\right) \times \nonumber \\&\displaystyle \times \sinh \left[ \frac{n\pi \sqrt{\rho _z}}{\sqrt{\rho _x}L}(D/2-z)\right] \end{aligned}$$

(16)

Hence, the $V_0$ and $V_n$ coefficients can be found through the Fourier methods using the last boundary condition on the transport current applied. Here, we just give the explicit coefficients, leaving the detailed development for Appendix 1 in reference [25]: $V_0=I\rho _z/bL$ and $V_n=-2I/n\pi b \cosh (n\pi \sqrt{\rho _z}D/2\sqrt{\rho _x}L)$. Establishing that the voltage signal in a measurement is $\varDelta V=V(x_0,D)-V(x_0,0)$ and taking in account Eq. (16) where it has been substituted the $V_0$ and $V_n$ dependence, it can be deduced an expression for the measured resistance as a function of the parameters of the sample $\sqrt{\rho _x},\sqrt{\rho _z},D, b$ and L:

$$\begin{aligned} \displaystyle R_z=\frac{\rho _zD}{bL}\left[ 1+\sum _{n=1}^\infty \!\!\frac{4L\cos \left( \frac{n\pi x_0}{L}\right) \tanh \left( \frac{n\pi \sqrt{\mu } D}{2L}\right) }{n\pi \sqrt{\mu }D} \right] \end{aligned}$$

(17)

where $\mu _=\rho _z/\rho _x$. An important point here is that the series for $R_z$ is a slowly (conditionally) converging one, which cannot be truncated for any value of anisotropy $\sqrt{\mu, }$ large or small. This is a common feature of the potential distributions due to arrays of charges [45]. A way to solve this problem is to separate the slowly converging series of $R_z$ into slowly and rapidly converging parts in such a way that would allow to carry out the summation of the slowly converging part exactly (analytically or numerically). For example, Eq. (17) can be rewritten as follows:

$$\begin{aligned} \displaystyle R_z=\frac{4\sqrt{\rho _z\rho _x}}{b\pi }\left[ \frac{\pi \sqrt{\mu }D}{4L}+Y_z(x_0)+S_z(\sqrt{\mu }) \right] \end{aligned}$$

(18)

where

$$\begin{aligned} \displaystyle Y_z(x_0)=\sum _{n=1}^\infty \frac{\cos (n\pi x_0/L)}{n}=\ln \left[ 2\sin \left( \frac{\pi x_0}{2L} \right) \right] \end{aligned}$$

(19)

and

$$\begin{aligned} \displaystyle S_z(\sqrt{\mu })=\sum _{n=1}^\infty \frac{\cos (\frac{n\pi x_0}{L})}{n}\left[ \tanh \left( \frac{n\pi \sqrt{\mu }D}{2L} \right) -1 \right] \end{aligned}$$

(20)

The term $Y_z(x_0)$ is reported in reference [25] and characterizes the sample’s geometry, but does not depend on the resistivity. On the other hand, $S_z(\sqrt{\mu })$ is a rapidly (exponentially) converging series, which can be truncated and therefore lends itself easily to numerical evaluation even for relatively small values of anisotropy such that $\frac{\pi \sqrt{\mu }D}{2L}\sim 1$.

The other configuration in which the contacts are located on the face perpendicular to the z-axis, as in Fig. 10a, was analyzed by reference [24] in the single harmonic approximation and for a multi-terminal contact configuration. By using analogous boundary conditions on the current like in the paragraphs above, it is easy to show that the final expression for the resistance in this configuration is [24]:

$$\begin{aligned} \displaystyle R_x=\frac{8\sqrt{\rho _z\rho _x}}{b\pi }\left[ Y_x(l)+S_x(\sqrt{\mu }) \right] \end{aligned}$$

(21)

where

$$\begin{aligned} Y_x(l)= & {} \displaystyle \sum _{n=1}^\infty \!\!(-1)^{n-1}\frac{\cos [\pi l(2n-1)/2L]}{2n-1}\nonumber \\= & {} \frac{1}{2}\ln \left[ \tan \left( \frac{\pi }{4}+\frac{\pi l}{4L} \right) \right] \end{aligned}$$

(22)

and

$$\begin{aligned} \displaystyle S_x(\sqrt{\mu })= & {} \displaystyle \sum _{n=1}^\infty \!\!(-1)^{n-1}\frac{\sin \left[ \frac{(2n-1)\pi l}{2L}\right] }{2n-1}\times \nonumber \\&\displaystyle \times \left[ \coth \left[ \frac{(2n-1)\pi \sqrt{\mu }D}{L}\right] -1 \right] \end{aligned}$$

(23)

In reference [24] was reported than even for the samples with the lowest anisotropy ($\frac{\pi \sqrt{\mu }D}{2L}\sim 1$) it was sufficient to retain only the first three terms, $n=1, 2, 3,$ to obtain convergence of the results better than 0.1% [24]. For that reason in the series given to Eqs. (18) and (21) only the first three terms will be taken into consideration. From the ratio $R_z/R_x,$ they can be obtained all values of anisotropy $\sqrt{\mu }$ after solving a transcendental equation. The result may be substituted into Eqs. (18) and (21) and both resolved later to give the true resistivities $\rho _x$ and $\rho _z,$ through the following expressions:

$$\begin{aligned} \rho _x=\frac{\displaystyle R_xb\pi /8\sqrt{\mu }}{\displaystyle \left\{ \frac{1}{2}\ln \left[ \tan \left( \frac{\pi }{4}+\frac{\pi l}{4L}\right) \right] +S_x(\sqrt{\mu })\right\} ^{-1}} \end{aligned}$$

(24)

and

$$\begin{aligned} \rho _z=\frac{\displaystyle R_z\sqrt{\mu }b\pi /4}{\displaystyle \left\{ \frac{\sqrt{\mu }\pi D}{4L}+\ln \left[ 2\sin \left( \frac{\pi x_0}{2L}\right) \right] +S_z\left( \sqrt{\mu }\right) \right\} ^{-1}} \end{aligned}$$

(25)