Toward the correlation of indentation hardness in micro- and nano-scale: understanding of indentation edge behaviors in Fe–Cr alloys

Abstract

Nanoindentation hardness tests are used to measure indentation hardness at the micro- and nanoscales and further to predict Vickers hardness on larger scales. Hence, the relationship between Vickers and nanoindentation hardness has gained considerable research interest. Here we introduce the concept of Meyer hardness as a mean contact pressure correctly into the two hardness in order to explain their linear correlation. The Vickers hardness is converted to the Vickers Meyer hardness (HVM) as defined by a load divided by the projected contact area; the Nix–Gao model is used to calculate the bulk-equivalent nanoindentation hardness (H₀) from depth-dependent nanoindentation hardness. A linear relationship HVM = 0.86 × H₀ is observed in the Fe–Cr alloys with a wide range of elastic modulus to hardness ratios and is suggested to be a universal relationship for various metallic materials. A tangent method can distinguish the indentation edge behaviors such as pile-up, sink-in, and the pseudo-pile-up phenomenon. A novel pile-up correction estimates the real contact area in nanoindentation tests, and actual residual contact area is measured to correct the pile-up around Vickers imprints. The corrected HVM and corrected H₀ show almost same values after both pile-up corrections.

Introduction

Instrumented indentation test, also known as nanoindentation test, has been widely used to evaluate the local indentation hardness of materials at the nano- and micro-scales for academic and industrial purposes; it has been frequently compared with the Vickers hardness (HV) test used on larger scales [1]. A considerable number of studies have investigated the relationship between nanoindentation hardness and HV. For example, Rice et al. [2] and Taylor et al. [3] reported a linear correlation between the HV and nanoindentation hardness at various loads on ferritic alloys and DP980 steels. Such linear correlation was reported in various materials such as Cu and carbon steel in Sawa's work [4]. During the comparison between nanoindentation hardness and micro-hardness, Qian et al. [5] noticed that the Vickers hardness is always stable against different loads, while nanoindentation hardness decreases with the increase in indentation depth, which is known as indentation size effect (ISE). Further, one author [6] showed that the ratio of HV evaluated with a projected area of contact divided by the bulk-equivalent nanoindentation hardness (${H}_{0}$) is 0.85 for F82H ferritic martensitic steels considering the ISE based on the Nix–Gao model [7]. Recently, Zhu et al. [8] obtained the linear relationship between HV and ${H}_{0}$ on pure Fe and Fe-(3–25 wt.%) Cr alloys and then clarified the effect of ISE, strain-rate sensitivity, surface condition and pile-up height on the hardness correlation. Including this great effort, many studies have been conducted to obtain the correlation between the HV and nanoindentation hardness; however, limited attention has been focused on the definitions of hardness and their related theories that can significantly affect the value of hardness. Thus, current correlations between different hardness values are empirical, and their applicability is limited.

The difference in hardness definitions should be considered to obtain a theoretical correlation of hardness. In particular, the different definition of areas used in various indentation hardness tests make it difficult to correlate with each other [9]. HV was calculated using the indenter load and surface area of the impression. According to its definition, HV is lower than the mean contact pressure (HVM) by 7%. In contrast, the most commonly used nanoindentation hardness is the Meyer hardness, which corresponds to the mean contact pressure [10]. The contact area used in the nanoindentation hardness was the projected area of contact instead of that used in the HV test. Therefore, the HV should be converted to a value based on the concept of the mean contact pressure for obtaining a hardness correlation.

Besides the hardness definitions, the effect of the pile-up and sink-in behaviors (known as indentation edge behaviors) is also one of the most difficult points in obtaining an actual area of contact in elastic–plastic materials. The pile-up behavior has been a concern in estimating the indentation hardness as a mean contact pressure in nanoindentation tests as well as Vickers hardness tests [11][11][11][11]. In literatures [8, 15], the values of Vickers hardness and nanoindentation hardness became consistent after pile-up correction. In nanoindentation tests, the Oliver–Pharr method is used to evaluate the contact depth and projected contact area based on Sneddon’s elastic contact theory [15]. However, Saha [16] found that the Oliver–Pharr method underestimates the actual contact depth because of the pile-up behavior. While the pure sink-in behavior with a complicated shape is believed to be corrected by the Oliver–Pharr method, Qian [5] reported that the residual contact area is always larger than the area given by the contact depth even for sink-in. Li [17] and Kucharski [18] found a pseudo-pile-up phenomenon that differs from the ideal pile-up behavior. Currently, the relationship between the elastic–plastic properties of materials and their indentation edge behavior, such as pile-up, sink-in, and pseudo-pile-up, is still unclear, which essentially affects the correlation between the nano- and micro-hardness.

This study provides new insights from the view of mean contact pressure (i.e., Meyer hardness) in the correlation between indentation hardness obtained by nanoindentation and HV in order to clarify the origin of hardness correlation. Various Fe–Cr alloys in a wide compositional range after heat treatment were examined to determine the relationship between the HV and nanoindentation hardness because these alloys can be model metallic materials through their wide range of elastic modulus and hardness. A novel pile-up correction was proposed to obtain the modified nanoindentation hardness in the form of the mean contact pressure.

In Sect. 2, the definitions of HV, HVM, and nanoindentation hardness are explained in order to understand the effects of indentation edge behavior. A novel pile-up correction method is introduced here. Then, Sect. 3 provides the details on samples, hardness tests, and evaluation methods used in the present study. Also, the tangent method is introduced to distinguish the indentation edge behaviors. In Sect. 4, the results of hardness tests and residual imprint measurement are given, and the linear relationship between the HVM and ${H}_{0}$ is stated. Section 5 discusses the hardness correlation based on the correction of the indentation edge behaviors.

Theory

It is beneficial to review the theories on indentation hardness and related issues to understand the differences and similarities between the HV and nanoindentation hardness. The Vickers Meyer hardness is defined for a comparison with the nanoindentation hardness; the theoretical background of nanoindentation is explained; the indentation edge behavior and pile-up corrections are modeled; and finally, the ISE is introduced.

Vickers Hardness and Vickers Meyer Hardness

In the HV test, the diagonal of the residual indentation imprint after unloading was measured to calculate the surface area of the contact. HV is defined by

$${\text{HV}}\left[ {\frac{{kgf}}{{mm^{2} }}} \right] = \frac{{{\text{Load}}}}{{{\text{residual~surface~area}}}} = \frac{{2P{\text{sin}}\left( {\frac{{136^{ \circ } }}{2}} \right)}}{{d^{2} }}$$

(1)

where $P$ and $d$ represent the load applied to the indenter and the diagonal length of the residual indent impression, respectively. The value of the HV deviates from the Meyer hardness (or mean contact pressure) using the surface area of the contact calculated by the diagonals of the imprint after unloading. Although some recent studies described the HV as a value with the SI unit system [19][19], it is necessary to focus on the definition of the contact area used. The present study defines a Vickers Meyer hardness ($HVM$) in the SI unit [GPa] with the projected area of the contact calculated from the diagonals of the imprint after unloading to maintain a clear physical meaning. Therefore, $HVM$ [GPa] is converted from the conventional $\mathrm{HV}$ [kgf/mm²] with the contact surface area using

$$HVM{ }\left[ {{\text{GPa}}} \right] = \frac{{g_{0} }}{1000}\frac{{{\text{HV}} \left[ {\frac{{{\text{kgf}}}}{{{\text{mm}}^{2} }}} \right]}}{{\sin 68^{^\circ } }} = 0.01058 {\text{HV}} \left[ {\frac{{{\text{kgf}}}}{{{\text{mm}}^{2} }}} \right]$$

(2)

where ${g}_{0}$ represents the standard gravitational acceleration and the face angle of the Vickers indenter is 68°.

Nanoindentation

The Oliver–Pharr method is applied to obtain the contact depth ${h}_{c}$ without imaging the imprint because of the small size of the imprint for evaluating the indentation modulus and hardness by nanoindentation tests, as shown in the ISO 14577 standard of the nanoindentation test (so-called instrumented indentation test). The Berkovich tip (“modified” Berkovich tip) used for the nanoindentation hardness tests was designed from the Vickers tip to have an equivalent cone angle of 70.3° with a single point apex.

First, the indentation modulus E_IT is derived using the following procedure. For a conical indenter [21], the indentation profile is related to load ${P}_{max}$ as

$$P_{max} = \frac{2}{\pi }E_{IT}^{*} h_{max}^{2} {\text{tan}}\alpha$$

(3)

where ${E}_{IT}^{*}$ and $\alpha$ represent the reduced elastic modulus and semi-angle of the indenter, respectively. The quantity of $dP/dh$ during unloading is used and often referred to as the contact stiffness $S$. Based on Eq. (3), $S$ is given as

$$S = \frac{dP}{{dh}} = \frac{4}{\pi }hE_{IT}^{*} {\text{tan}}\alpha$$

(4)

In the CSM method with a sinusoidal harmonic load during the loading portion, the displacement response of the indenter at the excitation frequency and phase angle between the two are measured continuously as a function of depth, finally resulting $S$ [22].

$S$ is measured during the loading portion of an indentation test using the CSM technique.

Based on the conical indenter, the radius of the impression $a$ is

$$a = \frac{2}{\pi }h_{max} {\text{tan}}\alpha$$

(5)

From Eqs. (4) and (5), ${E}_{IT}^{*}$ is [15]

$$E_{IT}^{*} = \frac{1}{2\beta }S\frac{\sqrt \pi }{{\sqrt A }}$$

(6)

where $A$ and $\beta$ denotes the projected contact area and geometry correction factor which is 1 for conical indenter. In the case of the Berkovich indenter [10], Eq. (6) changes to

$$E_{IT}^{*} = \frac{1}{2 \times 1.034}S\frac{\sqrt \pi }{{\sqrt A }}$$

(7)

The reduced elastic modulus $E_{IT}^{*}$ is a complex of the indenter and tested material; it is expressed as

$$\frac{1}{{E_{IT}^{*} }} = \frac{{\left( {1 - \nu_{{\text{s}}}^{2} } \right)}}{{E_{{\text{s}}} }} + \frac{{\left( {1 - \nu_{{\text{i}}}^{2} } \right)}}{{E_{{\text{i}}} }}$$

(8)

where $E_{{\text{i}}}$ = 1140 GPa and $v_{i}$ = 0.07 are the elastic modulus and Poisson’s ratio of the diamond indenter, respectively; $E_{{\text{s}}}$ and $\nu_{{\text{s}}}$ represent the elastic modulus and Poisson’s ratio of the indented sample, respectively.

Indentation hardness $H_{IT}$ is defined as a mean contact pressure under loading as

$$H_{IT} = \frac{{P_{max} }}{A}$$

(9)

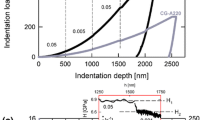
where $P_{max}$ and $A$ represent the maximum load and projected area of the contact between the indentation tip and tested material derived by the Oliver–Pharr method, respectively. The contact depth necessary to calculate the projected area of the contact using an area function is obtained as shown below. As shown in Fig. 1, the Oliver–Pharr method derives the contact depth $h_{c}$ from the unloading curve as

$$h_{c} = h_{max} - h_{s}$$

(10)

Figure 1

Schematic of nanoindentation and geometrical parameters used in the Oliver–Pharr method

where $h_{max}$ and $h_{s}$ represent the maximum depth from the initial surface and displacement of the surface at the contact periphery, respectively. Sneddon provided a force–displacement relationship for the conical indenter as

$$h - h_{f} = h_{e} = 2\frac{P}{S}$$

(11)

where $h_{f}$ denotes the depth of the residual impression after unloading, and $h_{e}$ denotes the elastic deflection of the impression vertex. Sneddon’s analysis [23] provides the relationship of $h_{e}$ and deformed shape of the free surface $u_{z}$ for a conical punch as

$$u_{z} \left( r \right)_{z = 0} = \frac{2D}{{\pi a}}\left( {asin^{ - 1} \frac{a}{r} - r + \sqrt {r^{2} - a^{2} } } \right) r > a$$

(12)

where $D$, $a$, and $r$ denotes the depth at which the tip of the punch penetrates the elastic half space, the radius of the contact area, and the distance from the punch, respectively. When $r = a$, Eq. (11) yields

$$u_{z} = h_{s} = \frac{{2h_{e} }}{\pi a}\left( {a\frac{\pi }{2} - a} \right) = \frac{\pi - 2}{\pi }h_{e}$$

(13)

Using Eqs. (11) and (13),

$$h_{s} = \varepsilon \frac{{P_{\max } }}{S}$$

(14)

where the geometric constant $\varepsilon$ is given as 0.72 and 0.75 for the conical and spherical indenters, respectively. Finally, the contact depth $h_{c}$ can be calculated by combining Eqs. (10) and (14) based on

$$h_{c} = h_{\max } - h_{s} = h_{\max } - \varepsilon \frac{{P_{\max } }}{S}$$

(15)

The projected area of contact with the Berkovich tip, which corresponds to the modified Berkovich tip and is widely used for nanoindentation hardness tests with small loading, can be calculated geometrically using the obtained h_c. The modified Berkovich tip, which is a three-sided pyramidal tip, was designed to provide the same ideal area function (projected area-to-depth ratio) as the four-sided pyramidal Vickers tip using

$$A\left( {h_{c} } \right) = 24.50 \times h_{c}^{2}$$

(16)

where $A\left( {h_{c} } \right)$ denotes the ideal projected area of contact at the contact depth h_c. However, the actual Berkovich tip deviates from the ideal sharp tip geometry because of the tip rounding, and it affects the results at a shallow depth. The area function of the Berkovich tip used in nanoindentation should be corrected by considering the tip roundness. Oliver and Pharr [24] established a correction method for the area function using a polynomial area function

$$A\left( h \right) = 24.5h^{2} + C_{1} h + C_{2} h^{\frac{1}{2}} + C_{3} h^{\frac{1}{4}} + C_{4} h^{\frac{1}{8}} + C_{5} h^{\frac{1}{16}} + C_{6} h^{\frac{1}{32}} + C_{7} h^{\frac{1}{64}} + C_{8} h^{\frac{1}{128}}$$

(17)

where $C_{i}$ represents the fitting parameter calculated from the reference material. A curve-fitting procedure gives these parameters based on the depth-dependent indentation results of reference materials such as fused silica with a specific elastic modulus. Tip rounding, typically several tens or hundreds of nanometers for diamond tips, severely affects the hardness and modulus values at a shallow depth. Therefore, the indentation hardness is given by the projected area of the contact calculated from the contact depth using the area function. The area for hardness calculation in nanoindentation is the essential difference from the HV obtained from the surface area of the contact predicted from the optically measured imprint diagonals after unloading.

Further, frame compliance is an important factor in the case of deep (high load) indentation. Frame compliance at shallow-depth indentation may be affected by setting and fixing a specimen tested using a nanoindentation device. Ethyl cyanoacrylate glue (Aron Alpha® or Krazy Glue®) is used to create a skinny and uniform fixing layer between the specimen and the stage. The depth profile of the modulus of the specimen showed no evident influence of the glue.

Pile-up Corrections of Contact Depth and Area

The Oliver–Pharr method, which is a standardized procedure of nanoindentation tests, assumes that the shape outside the area of contact in the indented material is deflected downward elastically, which results in a sink-in behavior. However, in the case of the pile-up, the Oliver–Pharr method is not suitable for obtaining the true contact depth [25].

The direct measurement of the pile-up height after unloading was performed to obtain a pile-up-corrected indentation hardness. Here, the true contact depth under loading is given by

$$h_{c} = h_{max} + h_{pile}^{loading}$$

(18)

where $h_{max}$ denotes the maximum penetration depth from the free surface, and $h_{pile}^{loading}$ denotes the height of the pile-up under loading. After unloading, the height of the pile-up may contain elastic deflection $h_{d}$ as

$$h_{pile}^{unloading} = h_{pile}^{loading} + h_{d}$$

(19)

In most previous studies, the elastic deflection $h_{d}$ was implicitly assumed to be obtained by the Oliver–Pharr method even for the case of pile-up, which means $h_{s} = h_{d}$. From Eqs. (10), (18), and (19), the true contact depth $h_{c}$ is estimated from the direct measurement of the pile-up height after unloading as

$$\begin{gathered} h_{c} = h_{\max } + h_{pile}^{loading} \hfill \\ = \left( {h_{c}^{O - P} + h_{s} } \right) + \left( {h_{pile}^{unloading} - h_{d} } \right) \hfill \\ = h_{c}^{O - P} + h_{pile}^{unloading} \hfill \\ \end{gathered}$$

(20)

where $h_{c}^{O - P}$ represents the contact depth given by the Oliver–Pharr method. Consequently, the pile-up corrected indentation hardness reflects the mean contact pressure with the measured pile-up height after unloading. Although Choi et al. described a pile-up correction to obtain a true contact depth by measuring the pile-up height after unloading [26], the present view of elastic deflection in the case of pile-up under loading and after unloading was not mentioned clearly.

In the above description, the pile-up height was modeled as a representative value whereas the actual imprint of the Berkovich tip has three edges and three corners. Various studies on pile-up correction were found in the literature, such as the triangle and the semi-ellipse method [13][13]; these only consider the projected contact pile-up area surrounded by indentation corners and the highest pile-up point at a vertex of a triangle or a minor vertex of a semi-ellipse, respectively. In these studies, the pile-up around the indentation corners was not considered in addition to the pile-up area around the edge above, which results in the underestimation of the contact area. We suggest a pile-up correction based on the pile-up around both the edges and corners of the nanoindentation, as follows:

As shown in Fig. 2a, we consider the gray-colored contact area caused by the pile-up $h_{{p\left( {corner} \right)}}$ at the corners of the imprint; the red-colored contact area caused by the pile-up $h_{{p\left( {edge} \right)}}$ at the edges of the imprint even though the value of $h_{{p\left( {corner} \right)}}$ is considerably smaller than $h_{{p\left( {edge} \right)}}$ because of the lower plastic flow at corners [28]. The polygon of the imprint containing pile-up was modeled as a triangle with yellow line to use the area function in nanoindentation tests, as shown in Fig. 2b. After the calculation given in Supplement A, the actual projected area with the pile-up $A_{actual} \left( h \right)$ is given as

$$A_{actual} \left( h \right) = A_{actual} \left( {h_{c}^{O - P} + h_{p}^{*} } \right) = A_{actual} \left[ {h_{c}^{O - P} + \frac{1}{2}\left( {h_{{p\left( {corner} \right)}} + h_{{p\left( {edge} \right)}} } \right)} \right]$$

(21)

Figure 2

(a) Illustration of the projected area of the residual imprint in the nanoindentation test and (b) schematic of area calculation for the pile-up corrected nanoindentation hardness. Blue, gray, and red triangles are defined by the contact depth in the Oliver–Pharr method, the pile-up around the corner, and the pile-up around the edge, respectively. Yellow line triangle is the integration of solid triangles, which has the same area with them

Here, $A\left( h \right)$ denotes the area function of the Berkovich indenter, and $h_{p}^{*}$ represents the equivalent pile-up height of the entire imprint.

Indentation Size Effect

The ISE as “the smaller the stronger” on indentation hardness appears at the indentation depths of micrometers or less, wherein the nanoindentation test is applied [29]. Although the higher hardness value at smaller depths was attributed to extrinsic factors in the past [10], the ISE is recognized as an intrinsic phenomenon in metallic materials based on the study of Nix and Gao [30]. The Nix–Gao model has been widely recognized as a standard model to explain the ISE based on geometrically necessary dislocations (GNDs) and strain-gradient theory. Further, the Nix–Gao model can evaluate the bulk-equivalent indentation hardness $H_{0}$ from the depth-dependent indentation hardness values as an ISE-free indentation hardness extrapolated at infinite depth using

$$H = H_{0} \sqrt {1 + \frac{{h^{*} }}{h}}$$

(22)

where $H_{0}$ and $h^{*}$ represent the bulk-equivalent hardness corresponding to the infinite depth and the length that characterizes the depth dependence of the hardness, respectively. Recently, researchers found that the data extremely closed to sample surface deviates from the Nix–Gao model because of the evoluted GND zone [31]. As a result, the nanoindentation hardness used for the Nix–Gao model will not be chosen from such a region.

Experimental

Materials

Fe–Cr alloys with the nominal Cr concentrations of 0, 9, 15, 30, 45, 50, 70, and 100 at. % were fabricated by arc-melting. For homogenization, alloys with Cr concentrations of 0, 9, 15, 30, 45, and 50 at. % were annealed with a vacuum of $4 \times 10^{ - 4}$ Pa at 1000 °C for 24 h, whereas the alloys with the Cr concentrations of 70 and 100 at. % were annealed with a vacuum of $2 \times 10^{ - 3}$ Pa at 1300 °C for 48 h. After the heat treatment, $\varphi 5 mm \times 0.25 mm$ discs were machined by the electro-deposition wire from the center of the initial samples. The discs were sealed in quartz cubes under a vacuum of $4 \times 10^{ - 4}$ Pa. Furthermore, disc specimens with 0, 9, and 15 at. % Cr were annealed at 800 °C for 1 h to avoid the α/γ phase transformation, whereas the others were annealed at 1000 °C for 1 h and followed by water quenching. Finally, specimens with different Cr concentrations were divided into three groups and aged at 475 °C for 0, 300, and 1000 h under a vacuum of $3 \times 10^{ - 5}$ Pa. Totally, there are twenty-four specimens (8 with various Cr at. % $\times$ 3 with distinct aging times) used in the present study.

The specimens were mechanically polished using #400, #800, #1200, #1500, #2000, and #4000 SiC paper for both sides and then finely polished with 3 μm, 1 μm, and 0.25 μm diamond spray. Finally, 0.04 μm colloidal silica was used on a Vibromet 2 vibratory polisher (Buehler) which combines chemical and mechanical polishing to remove the remaining surface defects and the residual work-hardening layer introduced during mechanical polishing [32].

Indentation Hardness Tests

Ten HV measurements were performed on each prepared specimen with a load of 0.1 kgf for a holding time of 15 s using an HMV-G micro HV tester. The HV number with a load of 0.1 kgf (${\text{HV}}_{0.1}$) was converted to the Vickers Meyer hardness value ($HVM_{0.1}$) in the form of the mean contact pressure using Eq. (2).

A total of 12 nanoindentation tests were performed on the same specimens with HV measurements using a Nano Indenter G200 (Agilent Technologies) with a modified Berkovich tip to obtain the indentation hardness $H_{IT}$ and indentation elastic modulus $E_{IT}$. The continuous stiffness measurement (CSM) method [22] with the frequency of 45 Hz, harmonic amplitude of 2 nm, and strain rate of 0.05 s⁻¹ yields the values of $H_{IT}$ and $E_{IT}$ as the functions of the penetration depth $h$ via a single indent up to the depth limitation of 2000 nm. Here, the effective zero-point propose by the authors is used to reduce the effects of the environment and sample surface [33].

For both hardness tests, the sufficient spacing (at least five times the length of imprints) was ensured to prevent the influence of the other indents according to ASTM standard E384 [34].

Measurement of Residual Imprints

The pile-up correction of HV was performed by the ratio of the square area calculated by diagonals and the actual area obtained by the following imaging analysis. First, some HV imprints that show the pile-up behavior were captured using a Primotech optical microscope (Zeiss); then, the actual area covering the Vickers imprint was measured with ImageJ [35] software in terms of the number of pixels. (Appendix 1).

The pile-up correction of indentation hardness obtained by nanoindentation tests was performed on half of the total specimens (twelve) to evaluate indentation edge behaviors by referring to the range of $E_{IT} /HVM_{0.1}$ which is defined by the elastic modulus in nanoindentation tests ($E_{IT}$) and Vickers Meyer hardness ($HVM$) in the unit of [GPa]. $HVM$ in [GPa] is used here considering the Taylor relation between HV and yield stress [1]. Two nanoindentation imprints on these twelve specimens were measured using a confocal laser microscope (CLM) VK-X1100 (KEYENCE). Ten parallel line analyses were set perpendicular to each edge of one imprint; the highest point of each line was connected to determine the maximum pile-up height of an edge ($h_{{p\left( {edge} \right)}}$). Further, three line-analyses were set along the traces left by the edges of the triangle imprint to obtain the pile-up height of the corners ($h_{{p\left( {corner} \right)}}$). The details of the CLM measurements are presented in Appendix 2.

In previous studies, only the height of the pile-up was measured to correct the contact depth; however, the actual geometry of the pile-up has two or three dimensions. Here, we combine the contour maps of nanoindentation imprints generated by CLM and introduce the tangent method to accurately distinguish the edge behaviors, as shown in Fig. 3. The top point is the highest point at the residual indented surface, and the cross point is the intersection of the initial sample surface and residual indentation surface; θ represents the angle between the initial sample surface and the line between the cross and top points. If the imprint was obtained by an ideal indentation with pile-up and without any elastic recovery, $\tan \theta$ is 0.46, which obeys the shape of the Berkovich indenter. The top point should coincide with the cross point located on the initial sample surface if ideal sink-in behavior occurs, which result in in $\tan \theta$ being zero. However, $\tan \theta$ can be different from the above ideal values because of the elastic recovery and/or plastic deformation in the actual elastic–plastic metallic materials. The intermediate state of pile-up behavior, where the value of $\tan \theta$ is varied from 0 to 0.46, is called pseudo-pile-up.

Figure 3

Schematic of the tangent method

Results

Indentation Hardness Tests

Figure 4a shows the Cr dependence of ${\text{HV}}_{0.1}$ in the Fe–Cr alloys before and after thermal aging. The Fe-30, 45, 50, and 70 at.% Cr alloys show age hardening because of the phase separation of Fe and Cr [36]. As expected for homogeneous metallic materials, the indentation elastic modulus is almost constant against the indentation depth, as shown in Appendix 3. Further, the nanoindentation hardness of the Fe–Cr alloys showed a typical ISE. Therefore, the $H_{0}$ calculated from 200 to 2000 nm of Fe–Cr alloys shown in Fig. 4b considered to be reliable; the Nix–Gao model is shown in Appendix 4. The Cr dependence of $H_{0}$ was similar to that of ${\text{HV}}_{0.1}$.

Figure 4

Results of indentation tests. (a) Vickers hardness and (b) bulk-equivalent nanoindentation hardness on Fe–Cr alloys. (c) Average indentation elastic modulus in the nanoindentation test and (d) ratio of E_IT/HVM_0.1

The average elastic modulus obtained from the indentation depth range of 1500–2000 nm is shown in Fig. 4c. According to the ${\text{HV}}_{0.1}$ and average indentation elastic modulus from the nanoindentation test, the $E_{IT} /HVM_{0.1}$ ratio is considered an indicator of plasticity. Present Fe–Cr alloys can be considered a reasonable basis for investigating the indentation hardness of metallic materials because an extensive range of $E_{IT} /HVM_{0.1}$ is covered as shown in Fig. 4d. The samples used in Fig. 4d are shown in Appendix 5.

Measurements of Residual Imprints

Data from the CLM measurement are shown in Appendix 6.; the pile-up heights around the corner are summarized in Table 1. Figure 5a shows the $\tan \theta$ values obtained by the tangent method using the contour maps of nanoindentation imprints against the ratio of $E_{IT} /HVM_{0.1}$. The pile-up behavior occurred in specimens with lower $E_{IT} /HVM_{0.1}$ values, which exhibited red pile-up hills where the hilltops were located near the indentation edges. In contrast, sink-in behavior occurs in specimens with higher values of $E_{IT} /HVM_{0.1}$; this displays the deformation plateaus and blue depressed region. Furthermore, the samples within the transition region between the pile-up and sink-in show red pile-up hills with the hilltops moving out from the blue depressed area, which indicates the characteristics of both the pile-up and sink-in behaviors. As the $\tan \theta$ value increased, the pile-up behavior became dominant around the indentation edges.

Table 1 Pile-up around the corner (nm)

Figure 5

Analysis of residual imprints. (a) Analysis of pile-up and sink-in behaviors using the Tangent method. (b) Pile-up occurred in the 1000-h aged Fe-70Cr alloy (red) and the pseudo-pile-up occurred in the 1000-h aged Fe-0Cr alloy (blue)

The pseudo-pile-up phenomenon only refers to the edge behavior of the samples located within the transition region; this is different from the ideal sink-in and pile-up mechanism. Specimens showing pile-up behavior in the nanoindentation test also exhibited a pile-up in the impressions of the HV tests, as indicated in Appendix 7. Based on the number of pixels counted by ImageJ, the average ratio of the actual projected area to the diagonal-based Vickers projected area was estimated to be 105.6%, and this is attributed to the occurrence of pile-up behavior. Detailed results are shown in Table 2.

Table 2 Vickers measured and actual areas for the pile-up behavior in the Vickers hardness test

The Fe–Cr alloys within the transition region in Fig. 5a exhibited significant pile-up and partly sink-in characteristics as gradient edges and depressed regions, respectively. Such indentation edge behavior is known as the pseudo-pile-up rather than an ideal pile-up or sink-in [17]. For the imprints exhibiting pseudo-pile-up behavior as shown on the right of Fig. 5b, the slope of the upper part of the indentation edge significantly deviates from that of the lower part (blue dotted line) even though the deformation induced by indentation is beyond the initial sample surface and no longer fits the geometry of the indenter. Therefore, the projection of the pile-up deformation sometimes cannot be used as the actual contact area. In contrast, on the left side of Fig. 5b, the indentation edge is straight until the top point, which results in a typical pile-up behavior.

Hardness Correlation between HVM _0.1 and H ₀

Figure 6a shows the relationship between $HVM_{0.1}$ and $H_{0}$ in Fe–Cr alloys before and after thermal aging. In the present Fe–Cr alloys, $H_{0}$ is higher than their $HVM_{0.1}$. The least-squares fitting resulted in a good linear relationship between $HVM_{0.1}$ and H₀ by

$$HVM_{0.1} = 0.86 \times H_{0}$$

(23)

Figure 6

Correlation between HVM_0.1 and H_0 (a) without any correction and (b) after the pile-up correction

with a coefficient of determination $R^{2} = 0.999$. Equation (23) comprises both pile-up and sink-in behaviors, which means the edge behaviors do not affect the correlation between the Vickers (Meyer) hardness and nanoindentation hardness of the Fe–Cr alloys.

The contact areas used for Vickers Meyer hardness and nanoindentation hardness are not the actual residual projected area, and therefore, their difference in the definition of the contact area is inevitably considered to influence the linear coefficient of Eq. (23). Thus, the indentation hardness values would be identical if the actual contact area is used for both indentation hardness tests. We correlated the $HVM_{0.1}$ and $H_{0}$ after pile-up correction to clarify the influence of pile-up. For the Fe–Cr alloys with pile-up behavior, the novel pile-up correction method was applied for H₀, and the ImageJ pile-up correction was performed for $HVM_{0.1}$. As a result, the pile-up corrected $H_{{0\left( {{\text{pile}}} \right)}}$ and $HVM_{{0.1\left( {{\text{pile}}} \right)}}$ have the relationship

$$Corrected HVM_{{0.1\left( {pile} \right)}} = 0.99 \times Corrected H_{{0\left( {pile} \right)}}$$

(24)

where $Corrected H_{{0\left( {pile} \right)}}$ represents the $H_{0}$ after the novel pile-up correction and $Corrected HVM_{{0.1\left( {pile} \right)}}$ represents the $HVM_{0.1}$ after the ImageJ pile-up correction. Relationships given by Eqs. (23) and (24) are shown in Fig. 6b. $Corrected HVM_{{0.1\left( {pile} \right)}}$ almost equals $Corrected H_{{0\left( {{\text{pile}}} \right)}}$ because of pile-up correction. The detailed hardness values are listed in Table 3. Fe–Cr alloys with significant sink-in behavior were not used for pile-up correction.

Table 3 Bulk-equivalent nanoindentation hardness before and after pile-up correction

Discussion

Tangent Method to Distinguish the Transition of Pile-up and Sink-in

According to the tangent method shown in Fig. 5a, $\tan \theta$ yielded a clear transition of pile-up and sink-in behaviors against $E_{IT} /HVM_{0.1}$, wherein the typical pile-up and sink-in behaviors occurred at smaller $E_{IT} /HVM_{0.1}$ and higher $E_{IT} /HVM_{0.1}$, respectively. The ratio of elastic modulus to indentation hardness or flow stress has been used for the dimensional analysis of indentation in elastic–plastic solids with work hardening [37]. Therefore, the $\tan \theta$ reflects the mode change in the plastic flow around the indentation edges. The obtained transition behavior indicates that the Fe–Cr alloys have upper and lower shelves in the values of $\tan \theta$. The $\tan \theta$ at the lower shelf is 0.0612, which is attributed to the elastic recovery and plastic flow in the case of sink-in behaviors. The $\tan \theta$ of the upper shelf is smaller than the theoretical indenter angle because of the non-negligible elastic recovery in the material with the low $E_{IT} /HVM_{0.1}$. Further research is required to determine the actual upper shelf value of the lower $E_{IT} /HVM_{0.1}$ materials.

This transition implies that the plastic flow and elastic recovery around the imprint determine the type of phenomenon that occurs in the alloys together: pile-up, sink-in, or pseudo-pile-up. The plastic flow leads to deformation beyond the initial sample surface for all three phenomena; the location and direction of the plastic flow are essential for this phenomenon. It is vital of importance for strain hardening in this process. The lower hardness (i.e., strength) increases the difference in the deformation ability between the deformed indentation region and undeformed basal material after indentation. This difference causes the plastic flow to be distributed within the basal materials further away from the indentation surface leading to a pile-up deformation over the sample surface, but the pile-up deformation does not contact the indenter, which forms a sink-in plateau. For hard materials, the slight difference in hardness (the resistance to plastic deformation) between the deformed indentation region and basal materials after indentation leaves plastic flow near the indentation, which results in pile-up hills on the indentation edges. The location of the deformation induced by indentation tests has a certain correlation; the effect of elastic recovery on the edge geometry remains unclear. The elastic deflection $h_{s}$ is fully recovered in the consideration of Oliver and Pharr, which shows the essential impact of the elastic property on the residual indentation after unloading. The elastic modulus of Fe–Cr alloys is considerably lower than that of materials such as ceramics with substantial elastic recovery. The scenario of the elastic recovery after unloading is not fully understood in previous studies, and it requires further investigation.

The result of the tangent method showed an apparent transition of pile-up and sink-in behaviors in the Fe–Cr alloys. Although the ratio of $E_{IT} /HVM_{0.1}$ is not sufficient for the dimensional analysis of edge behaviors [38], the tangent method can be an excellent approach to clearly distinguish the edge behaviors in various materials.

Universal relation between ${\varvec{HVM}}_{0.1}$ and ${\varvec{H}}_{0}$

A linear relationship between $HVM_{0.1}$ and $H_{0}$ was obtained for Fe–Cr alloys, as shown in Eq. (22). The physical basis of the linear correlation between $HVM_{0.1}$ and $H_{0}$ is yet to be identified. Two significant factors can be considered responsible for the correlation based on the area calculations in these indentation hardness tests: compatibility and discrepancy in the contact area measurement/calculation.

For the HV test, the conventional contact area measurement uses the diagonals of the imprint after unloading, as measured by optical microscopy. The diagonal length hardly suffered from the indentation edge behaviors because of the limited plastic flow around the corner. Thus, the pile-up and sink-in behaviors rarely affect the Vickers (Meyer) hardness measured from the diagonals. The contact area in the nanoindentation tests is calculated using the Oliver–Pharr method shown in Fig. 7 which assumes an ideal sink-in behavior. The O-P point in Fig. 7 determines the contact area in the Oliver–Pharr (O–P) method [16]. The sink-in behavior determined by the O-P point always exists in either the pile-up or the sink-in case. Thus, the nanoindentation hardness using the Oliver–Pharr method does not contain any characteristic of pile-up, and this is the core of the Meyer hardness. Therefore, the Vickers (Meyer) hardness and nanoindentation hardness obtained by the Oliver–Pharr method are almost independent of the edge behaviors and are consistent in the form of mean contact pressure, resulting in a good linear relationship in the present study and possibly in other studies.

Figure 7

Schematic of nanoindentation using the Oliver–Pharr method based on [15]. Black lines and red lines represent the original O-P method and new content added in this study, respectively

The slope of 0.86 obtained from various Fe–Cr alloys is an interesting point in this relationship. This slope is attributed to the discrepancy between the actual projected area and the area used for hardness calculation in these two hardness tests. The nanoindentation Berkovich imprint was also used to explain the Vickers imprint. In Fig. 2a, the central blue area represents the Oliver–Pharr area; the gray area, the pile-up around the corner; and the red area, the pile-up around the edge.

The square used in the HV test is equal to the blue and gray triangles, and it includes the O-P area and the pile-up around the corner. The conventional nanoindentation test using the O-P method considers only the ideal sink-in behavior, which is the blue O-P area. For the two area measurements in the Vickers and nanoindentation tests, the pile-up around the corner is considered differently, leading to a slope of 0.86 in the correlation.

Based on this discussion, $HVM_{0.1} = 0.86 \times H_{0}$ is not considered an empirical relation but a universal one for the $HVM_{0.1}$ and $H_{0}$ supported by the contact theory. This offers a simple relationship to bridge the Vickers (Meyer) hardness and bulk-equivalent nanoindentation hardness. A further examination of this relationship is expected for various metallic materials.

Pile-up Correction for ${\varvec{HVM}}_{0.1}$ and ${\varvec{H}}_{0}$

The actual projected contact area in the nanoindentation test was obtained using the correction method presented in Sect. 2.2. The necessary data can be obtained at any depth using the CSM method. A proportional relation was used to calculate the $h_{p}^{*}$ at different contact depths according to the positive correlation between the $h_{c}$ and pile-up height [8, 39, 40]. After applying the Nix–Gao model, the corrected $H_{0}$ shows Meyer hardness without the ISE.

Based on the pile-up profile in Fig. 5b, it is easy to distinguish the pile-up boundary because of the sharp change in the indentation edge. Based on the conventional Vickers area measurements, the actual projected area was measured using ImageJ. The missing pile-up around the edge was obtained using ImageJ analysis. Subsequently, the corrected Vickers Meyer hardness using the actual projected area reached the actual Meyer hardness.

After the above pile-up corrections, the relationship between the Meyer hardness obtained by the HV and nanoindentation hardness tests is

$$Corrected HVM_{{0.1\left( {pile} \right)}} = 0.99 \times Corrected H_{{0\left( {pile} \right)}}$$

(25)

Here, the actual Meyer hardness values obtained from the HV and nanoindentation tests were found to be similar. Therefore, the ImageJ analysis for the HV test and the tangent method for the nanoindentation test are good choices for obtaining the Meyer hardness that corresponds to the mean contact pressure.

It is notable that the previous 0.86 correlation is free from the under-loading or after-unloading condition because of the corner-based hardness calculation [24]. In contrast, the pile-up corrected Vickers and nanoindentation hardness demonstrate the hardness after unloading owing to the measurement of the pile-up around the edge after unloading. Based on Sect. 2.3, the pile-up corrected nanoindentation hardness also reflects the under-loading hardness. Interestingly, the after-loading Vickers hardness is consistent with under-loading bulk-equivalent nanoindentation hardness after pile-up correction, which may be attributed to the low elasticity–plasticity ratio in Fe–Cr alloys and needs further investigation.

Pseudo-pile-up and Sink-in in the Present Study

The conventional O-P method overestimates the nanoindentation hardness for the pseudo-pile-up phenomenon and sink-in behaviors. As shown in Fig. 8, there is considerable plastic deformation near the indentation and a transition point separating the straight and curved parts. Although both the pseudo-pile-up phenomenon and the sink-in behavior show a curved edge, their mechanisms are different. The plastic flow near the indentation surface caused by the pile-up behavior and basic sink-in behavior works simultaneously for the pseudo-pile-up phenomenon. A large amount of deformation within the basal materials moves away from the indentation surface and expands the contact area owing to the hardening near the indentation surface for the sink-in behavior. Eventually, this sink-in behavior exhibits a pile-up-like pattern with the mechanism of the sink-in behavior that leads to a larger projected area than that calculated by the O-P method with the O-P point. In addition, this can be found in Fig. 5a, where tan ${ }\theta$ shows the lowest value for pure sink-in behavior, while it shows a changed value for the pseudo-pile-up phenomenon.

Figure 8

Schematic of the pseudo-pile-up

The transition point must be determined in the pseudo-pile-up phenomenon to obtain the actual hardness. However, it is difficult to find the transition point precisely because the geometry is rugged in these cases instead of the mountain shape in the pile-up case. In practice, the novel pile-up correction is acceptable when the pile-up behavior is dominant, as indicated in Fig. 6b; this includes the pseudo-pile-up samples.

Confusion about Edge Behaviors

The occurrence of edge behaviors highly depends on strain hardening, and this affects whether plastic flow occurs near the indentation surface (contact area). Here, the word “behavior” focuses on the response of indented materials; however, the observed phenomenon of edge behaviors can be evaluated only from the surface using experimental instruments. Thus, the observed phenomena and actual behaviors may not correspond to each other.

The current evaluation of edge behaviors can mislead researchers on their essence. In theory, the difference between the pile-up and sink-in behaviors is the reaction of materials to indentation tests. Such reactions can lead to plastic deformation with distinct modes, which can result in different indentation geometries. In practice, researchers often evaluate and distinguish pile-up and sink-in behaviors based on the height of the pile-up deformation. This is possible for the pile-up behavior because pile-up deformation always occurs over the post-test surface, and this means the height of the pile-up deformation is necessary but insufficient for evaluating pile-up behavior.

The sink-in behavior and pseudo-pile-up phenomenon are rarely mentioned in the case of metallic materials because the height of pile-up deformation exists as shown in the present study; it has been neglected by many researchers. The pile-up deformation is not the pile-up behavior; instead, it is the plastic deformation caused by the indentation tests. In other words, pile-up behavior is always accompanied by pile-up deformation, which is not a unique symbol of pile-up behavior. It is unwise to distinguish the pile-up and sink-in behaviors by utilizing only the height of the pile-up deformation. The geometry of the indentation edge provided more powerful evidence. The geometry of the indentation edges is supposed to be a better criterion than the height of the pile-up deformation.

Figure 5a shows that the pseudo-pile-up may be a phenomenon rather than a new mechanism because it simultaneously contains pile-up and sink-in behaviors. The geometry of the pseudo-pile-up gradually changes between the pile-up and sink-in patterns, which is similar to their superposition.

Conclusions

The indentation hardness obtained by the HV test and nanoindentation hardness test was investigated for various Fe–Cr alloys. The indentation hardness is unified as the Meyer hardness, which corresponds to the mean contact pressure despite the different hardness measurements. The following results were obtained.

• 1) The tangent method describing the indentation edge geometry successfully distinguished pile-up, sink-in, and pseudo-pile-up. The apparent transition from pile-up to sink-in exhibits that the tangent method can be an accurate method for the edge behaviors rather than the conventional pile-up height measurement.

• 2) A linear relationship $HVM_{0.1} = 0.86 \times H_{0}$ was obtained between Vickers Meyer hardness and bulk-equivalent nanoindentation hardness, which are calculated by diagonal length and Oliver–Pharr method, respectively; the same form of mean contact pressure and area measurements used in the two hardness tests contributed to the linear correlation. By this relationship, the Vickers Meyer hardness can be well predicted from the bulk-equivalent nanoindentation hardness.

• 3) The proposed pile-up correction method for nanoindentation hardness considering the pile-up deformation at indentation edges and corners accurately corrected the nanoindentation hardness in the case of pile-up behavior even pseudo-pile-up phenomenon. The correction of the actual residual contact area also corrected the pile-up around Vickers hardness imprints. Finally, the two pile-up corrected hardness values are almost the same with each other.

Appendices

Appendix

Appendix 1: Pile-up Area Calculation

In Fig. 2, $l$ and $h$ are the horizontal length and height, respectively.The details for the pile-up area calculation are

$$A_{c} + A_{p} = \frac{\sqrt 3 }{4} \times W^{2} + 3 \times \frac{1}{2} \times W \times a, A_{c + P} = \frac{\sqrt 3 }{4} \times \left( {W + 2\sqrt 3 l} \right)^{2}$$

Let $A_{c} + A_{p}$ be equal to $A_{c + P}$; then,

$$3Wl + 3\sqrt 3 l^{2} = 3 \times \frac{1}{2} \times W \times a$$

Here, $A_{c} + A_{p}$ and $A_{c + P}$ represent the residual projected areas calculated step-by-step and one-time, respectively. In Fig. 2, $A_{c}$ represents the central triangle (blue plus gray), which includes the conventional contact area and the pile-up around the corners; $A_{p}$ represents the total of three red triangles outside.

The high-order minimum can be neglected because $l$ is considerably smaller than the length of the edges $W$. Thus, we have

$$l = \frac{1}{2} \times a = \frac{1}{2} \times \left( {l_{{p\left( {edge} \right)}} - l_{{p\left( {corner} \right)}} } \right)$$

$$l_{p} = \frac{1}{2} \times \left( {l_{{p\left( {edge} \right)}} + l_{{p\left( {corner} \right)}} } \right)$$

Similarly,

$$h_{p} = \frac{1}{2} \times \left( {h_{{p\left( {edge} \right)}} + h_{{p\left( {corner} \right)}} } \right)$$

where $h_{p}$ represents the equivalent pile-up height.

The following $h_{total}$ will be used for the actual projected area.

$$h_{total} = h_{c} + h_{p} = h_{c} + \frac{1}{2} \times \left( {h_{{p\left( {edge} \right)}} + h_{{p\left( {corner} \right)}} } \right)$$

APPENDIX 2: Residual Nanoindentation Measurement

The twelve selected specimens were used to measure the pile-up height; two nanoindentation imprints were used for confocal laser microscope measurements. (Fig. 9) For each triangle nanoindentation, ten parallel line analyses were set perpendicular to each edge of one imprint, and the highest point of each line was used to determine the maximum pile-up height of an edge ($h_{{p\left( {edge} \right)}}$) as shown in Fig. 10. The maximum pile-up height was used as the pile-up height for the tangent method.

In addition, three-line analyses were set along the traces left by the edges of the triangle imprint to obtain the pile-up height of the corners ($h_{{p\left( {corner} \right)}}$) as shown in Table 1.

Figure 9

CLM measurements on the nanoindentation imprint for the pile-up around the edge (a) and the pile-up around the corner (b). Red lines represent the line analysis in the CLM measurements

Figure 10

An example of pile-up height analysis of 1000 h Fe-30Cr alloy obtained by confocal laser microscope

See Figs 9 and 10 Table 1

Appendix 3: Indentation Elastic Modulus in Nanoindentation Tests

The elastic modulus is obtained using the nanoindentation test. Figure 11 shows an example on 1000h Fe-50Cr.

Figure 11

Elastic modulus obtained via nanoindentation test on 1000 h Fe-50Cr

See Fig. 11

Appendix 4: Hardness in Nanoindentation Tests

The raw data of the nanoindentation tests are used for the bulk-equivalent nanoindentation hardness using the Nix–Gao model, as shown in Fig. 12.

See Fig. 12.

Figure 12

(a-c) Nix–Gao model for Fe–Cr alloys aged for different hours. (d) Indentation depth of Vickers imprints

Appendix 5: Ratio of ${\varvec{E}}_{{{\varvec{IT}}}} /{\varvec{HVM}}_{0.1}$ in Aged Fe-Cr Alloys

Based on the HV (H) and average elastic modulus (E) in the nanoindentation test, the $E_{IT} /HVM_{0.1}$ ratio is shown in Fig. 13. The specimens marked by dashed lines were selected to analyze the pile-up height using a confocal laser microscope. Modulus.

See Fig. 13.

Figure 13

Ratio of E_IT/HVM_0.1 in Fe–Cr alloys

Appendix 6: ImageJ Analysis

See Fig. 

Figure 14

Image area analysis from the residual surface area measured by the diagonals (left) to the residual projected area (right)

14 and Table 2.

Appendix 7: Corrected Nanoindentation Hardness

After the pile-up analysis, the corrected bulk-equivalent nanoindentation hardness H₀ was calculated using the novel correction method. The average bulk equivalent nanoindentation hardness values of the two nanoindentations used for the pile-up analysis before and after the correction are shown in Table 3. Here, only specimens showing pile-up behavior are included.

See Table 3.