Mechanical insights into the stability of heterogeneous solid electrolyte interphase on an electrode particle

Abstract

Solid electrolyte interphase (SEI) is known to be heterogeneous which comprises inorganic and organic decomposition products. To assess the effects of heterogeneity on the stability of the SEI, we establish a mathematical model in simulating the stress of heterogeneous SEI. Comparing with the analytical solution of stress in the homogeneous film, the heterogeneity of SEI is identified to be essential in the stress calculation of the inorganic layer, which is proven decisive for the stability of SEI. Further, the peak tensile stress within the inorganic layer is found in the bilayer SEI. It generates at the interface between the active material and the inorganic layer when the battery is fully charged. In addition, the impacts of the interface parameter, modulus, Poisson’s ratio, thickness of SEI and lithiation properties of active material on SEI stress are systematically investigated. Based on the simulation results, this work provides insights into the stress analysis of the heterogeneous SEI, as well as suggestions in pursuing a well-designed SEI, i.e., a functional gradient heterogeneous SEI in which the inner layer close to the active material provides sufficient mechanical performance while the outer layer near the electrolyte performs good chemical and electrochemical behaviors, to enhance the battery performance.

Introduction

Presently, intense worldwide efforts are being dedicated to improve the performance of the lithium ion battery to meet the demand for the applications such as consumer electronics, all-electric vehicles, transport and large-scale renewable energy storage systems [1]. Amongst the many factors which cause decay in cells, the solid electrolyte interphase (SEI) which is essentially formed on the surface of active particle has drawn more attention since the fractured SEI would expose the bare active material to the electrolyte, leads to further reduction of the electrolyte and consumption of transferable lithium ions, and significantly causes battery capacity to fade. Therefore, how to properly evaluate the stress and thereby seeking feasible methods to sustain a robust SEI have become the key issues in the battery systems [2].

In the literature, numerous theoretical researches have been devoted to the continuum model of the stress in the electrode. Among these works, the majority focused on the stress in active materials [3–16]. Relatively much fewer studies pay close attention to the stress in SEI. Sheldon and co-workers delivered their findings of a disrupted structure on the carbon surface during the first cycle. They showed that this amorphous interlayer helps to soften the impact of carbon swelling on SEI and hence decreases the SEI stress [17, 18]. Laresgoiti et al. simulated the stress of a homogeneous SEI which was formed on graphite particle and found that fatigue failure of the SEI is the main cause of battery capacity fade [19]. Zhao et al. [20] investigated the stresses of homogeneous SEI layers which were coated on spherical and cylindrical nanostructures and identified surface cracking and debonding as the failure modes of these structures. For the higher scale of layered structure, we also developed an analytical expression of the SEI stress within a uniform cylindrical graphite anode with results indicating that the SEI stress depends strongly on its modulus and the constraint from the electrode structure [21].

With the help of in situ atomic force microscopy (AFM) technology, the morphology changes of the SEI formed on graphite [22–24], LiMn₂O₄ [25], and MnO [26] have been thoroughly investigated. It is demonstrated that naturally formed SEI renders a non-uniform feature and comprises inorganic and organic decomposition products. Typically, it is observed that the organic products are more near the electrolyte side, while the inorganic products are closer to the SEI/electrode interface [23, 25–28]. Although the component diversity and heterogeneity of SEI have gradually been recognized, the stress of the heterogeneous SEI is unexplored nowadays.

In this paper, a mathematical model for simulating the stress in heterogeneous SEI on the electrode particle will be established. The analytical solution of stress in homogeneous SEI is given to identify the influence factors on mechanical stability of SEI. Furthermore, with the purpose of demonstrating the role of SEI heterogeneity, the evolutions of SEI stresses for the heterogeneous and homogeneous cases are compared in detail. Moreover, the influences of the dimensionless parameters on the peak stress of the SEI are investigated, and sensitivity analysis is further carried out for providing advice to sustain a stable SEI, and therefore prolong the cycle life of lithium batteries.

Model description

The heterogeneous SEI

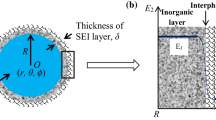
Figure 1 illustrates the heterogeneous structure of SEI which comprises the inorganic and organic compounds and forms on the bare surface of the active particle with a radius of R. As revealed by the experiments [22, 25, 26, 28–30], the inorganic materials are close to the SEI/electrode interface and have higher elastic moduli compared to the organic materials which are on the electrolyte side. Based on these features, we set the modulus of SEI to be composition dependent in the following continuum modeling which takes the formula:

$$ E_{s} \left( r \right) = E_{O} + \frac{{E_{I} - E_{O} }}{{1 + \exp [\alpha \left( {r - R - h_{I} } \right)/R]}}. $$

(1)

Figure 1

Schematic of a spherical active particle and the coated heterogeneous SEI

Here, E _O and E _I correspond to the modulus of the organic layer and inorganic layer, respectively. h _I is the thickness of the inorganic layer. α is a positive constant accounting for the interface between the inner and outer layers. Equation (1) allows flexible control of the SEI heterogeneity. When E _I equals to E _O , the second term in the above equation vanishes, and thus, the equation describes exactly the modulus of a single layered homogeneous SEI. When α tends to infinity, it reproduces exactly the bilayer SEI. For other types of heterogeneous SEI, Eq. (1) is applied by adjusting αand h _I to adapt the different inorganic/organic interfaces.

Continuum modeling of the SEI stress

In commercial lithium ion batteries, radius of the active particle shown in Fig. 1 is commonly at the micron scale. Thus, in the following continuum model of stress, we would neglect the impact of surface stress on the diffusion-induced stress which may be significant as the particle size is in nanoscales [31, 32]. Lithium migration in the active particle is much slower than the elastic deformation, so that mechanical equilibrium of the electrode is considered as a static equilibrium problem [5]. In the absence of any body force, the static mechanical equilibrium demands that stress components along radial and tangential directions in both active material and SEI should satisfy

$$ d\sigma_{r} /dr + 2\left( {\sigma_{r} - \sigma_{\theta } } \right)/r = 0 . $$

(2)

The corresponding strain components can be expressed as functions of radial displacement u in the infinitesimal formulation of deformation as

$$ \varepsilon_{r} = du/dr,\;\;\;\varepsilon_{\theta } = u/r . $$

(3)

Using the analogy between thermal stress and atomic diffusion-induced stress and assuming that both active material and SEI deform isotropically during insertion or extraction of Li/lithium ion, we can write the stress–strain relationship as [5]

$$ \sigma_{r} = \frac{E}{1 + v}\left( {\frac{v}{1 - 2v}\theta + \varepsilon_{r} } \right) - \frac{1}{3}\frac{E\Omega c}{1 - 2v},\;\;\;\sigma_{\theta } = \frac{E}{1 + v}\left( {\frac{v}{1 - 2v}\theta + \varepsilon_{\theta } } \right) - \frac{1}{3}\frac{E\Omega c}{1 - 2v}, $$

(4)

where v is the Poisson’s ratio, Ω is the partial molar volume, and c is the lithium concentration. θ = ɛ _r  + 2ɛ _θ is the volumetric strain. The first term on the right side of Eq. (4) is the mechanical elastic stress. The second concentration-related term represents the stress induced by atomic diffusion. It should only be retained for active material.

Here, we assume that the deformation of the SEI and the active particle is small and thus apply the mechanics of infinitesimal straining. This assumption is valid for most of the commercial active material such as graphite, LiCoO₂, LiFePO₄, and LiMn₂O₄ because their volume strain at maximum lithium concentration is less than 9% [33]. For the material that undergoes large deformation in lithiation, for example silicon which has a maximum volumetric swelling of ~400%, the strict derivation should be based on the theory of finite deformation [34]. The governing equations and corresponding initial and boundary conditions for this case can be found in the Appendix.

Numerical methods

Focusing on the stress of SEI, it is shown in Eqs. (3) and (4) that the radial displacement has to be solved beforehand. Substituting Eq. (4) into Eq. (2) and replacing the strain components by the radial displacement given in Eq. (3), the radial displacement for the heterogeneous SEI satisfies

$$ \frac{d}{dr}\left( {r^{2} E_{s} \frac{{du_{s} }}{ dr}} \right) + 2\left( {r\frac{{v_{s} }}{{1 - v_{s} }}\frac{{dE_{s} }}{dr} - E_{s} } \right)u_{s} = 0 . $$

(5)

In order to solve this second-order partial differential equation, the following two boundary conditions should be introduced: (i) the displacement at the interfaces of active material and SEI should be continuous to keep a geometry continuity, i.e., u _s | _r=R  = u _a | _r=R ; (ii) for a free standing electrode particle, the radial stress in the particle surface should be zero, i.e., $\left. {\sigma_{rs} } \right|_{{r = R + h_{s} }} = 0$, which requires

$$ \left. {\frac{{du_{s} }}{dr}} \right|_{{r = R + h_{s} }} + \frac{{2v_{s} }}{{1 - v_{s} }}\frac{1}{{R + h_{s} }}\left. {u_{s} } \right|_{{r = R + h_{s} }} = 0 . $$

(6)

Noting that the radial displacement of active material at the interfaces of active material and SEI.u _a | _r=R is unknown, the displacement of the active material has also to be solved beforehand. Using the same method as shown above, the radial displacement for the active particle is given by

$$ \frac{d}{dr}\left( {r^{2} \frac{{du_{a} }}{dr}} \right) - 2u_{a} = \frac{\Omega }{3}\frac{{1 + v_{a} }}{{1 - v_{a} }}r^{2} \frac{dc}{dr} . $$

(7)

The analytic solution for Eq. (7) can be given as

$$ u_{a} = \frac{\Omega }{3}\frac{{1 + v_{a} }}{{1 - v_{a} }}\frac{1}{{r^{2} }}\int_{0}^{r} {r^{2} cdr} + C_{1} r + \frac{{C_{2} }}{{r^{2} }} , $$

(8)

where C ₁ and C ₂ are integration constants. u _a at the center of the particle should be zero due to the spherical symmetry, which requires C ₂ = 0. Considering that the radial stress at the interfaces of active material and SEI should also be continuous to sustain a mechanical contact, i.e., σ _ra | _r=R  = σ _rs | _r=R , C ₁ is given by

$$ C_{1} = \frac{{\left( {1 - 2v_{a} } \right)}}{{E_{a} }}\left( {\left. {\sigma_{rs} } \right|_{r = R} + \frac{{2E_{a} \Omega }}{{3\left( {1 - v_{a} } \right)}}\frac{1}{{R^{3} }}\int_{0}^{R} {r^{2} cdr} } \right) . $$

(9)

Substituting into Eq. (8) and replacing the stress components by the radial displacement, we have

$$ E_{s} \left. {\frac{{du_{s} }}{dr}} \right|_{r = R} + \left( {E_{s} \frac{{2v_{s} }}{{1 - v_{s} }} - E_{a} \frac{1}{{v^{\prime}_{s} \left( {1 - 2v_{a} } \right)}}} \right)\frac{1}{R}\left. {u_{s} } \right|_{r = R} { = } - \frac{{E_{a} \Omega c_{\hbox{max} } }}{{3v^{\prime}_{s} \left( {1 - 2v_{a} } \right)}}SOC . $$

(10)

Here, v ^′ _s  = (1 − v _s )/[(1 + v _s )(1 − 2v _s )]. The state of charge SOC is defined as the average lithium concentration within the particle of radius R,

$$SOC = {\raise0.7ex\hbox{${\int_0^R {c{r^2}dr} }$} \!\mathord{\left/ {\vphantom {{\int_0^R {c{r^2}dr} } {\int_0^R {{c_{\max }}{r^2}dr} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\int_0^R {{c_{\max }}{r^2}dr} }$}}$$

(11)

where c _max is maximum concentration of lithium at the saturation state in the active material.

Previously, Shi et al. [35] investigated the mechanism of Li⁺ transport within the SEI and found that the diffusion of Li⁺ in SEI follows a two mechanism model, i.e., pore diffusion in the organic layer and knock-off diffusion in the inorganic layer. Although diffusion kinetics of Li⁺ in the SEI may regulate the distributions of lithium ion and lithium and even impact the stress in the active material and lead to lithium plating on the interface between the active layer and the SEI at higher rate of charging [21], it shows in Eq. (10) that the radial displacement of SEI depends only on the average amount of lithium in the active particle. This is can be attributed to the neglect of the SEI swelling in Eq. (4) as the deformation caused by the lithiation of the active particles is predominant.

With the help of the boundary conditions Eqs. (6) and (10), the radial displacement of SEI as shown in Eq. (5) can then be obtained. The stresses in SEI are thereby expressed as

$$ \sigma_{r} = \frac{{E_{s} }}{{\left( {1 + v_{s} } \right)\left( {1 - 2v_{s} } \right)}}\left( {\left( {1 - v_{s} } \right)\frac{{du_{s} }}{dr} + 2v_{s} \frac{{u_{s} }}{r}} \right),\;\;\;\sigma_{\theta } = \frac{{E_{s} }}{{\left( {1 + v_{s} } \right)\left( {1 - 2v_{s} } \right)}}\left( {v_{s} \frac{{du_{s} }}{dr} + \frac{{u_{s} }}{r}} \right) . $$

(12)

To ensure that the analytical results are applicable to a wide range of geometries and material properties of SEI and active particle, a set of dimensionless work as $\bar{r} = r/R$, $\bar{u}_{s} = u_{s} /R$, $\bar{E}_{s} = E_{s} /E_{a}$, and $\bar{\sigma } = \sigma /E_{a} \Omega c_{\hbox{max} }$ are employed. The displacement governing equation of SEI as shown in Eq. (5) is normalized as

$$ \frac{d}{{d\bar{r}}}\left( {\bar{r}^{2} \bar{E}_{s} \frac{{d\bar{u}_{s} }}{{d\bar{r}}}} \right) + 2\left( {\frac{{v_{s} }}{{1 - v_{s} }}\bar{r}\frac{{d\bar{E}_{s} }}{{d\bar{r}}} - \bar{E}_{s} } \right)\bar{u}_{s} = 0 . $$

(13)

The dimensionless forms of boundary conditions are

$$ \bar{E}_{s} \left. {\frac{{d\bar{u}_{s} }}{{d\bar{r}}}} \right|_{{\bar{r} = 1}} + \left( {\bar{E}_{s} \frac{{2v_{s} }}{{1 - v_{s} }} - \frac{1}{{\left( {1 - 2v_{a} } \right)v^{\prime}_{s} }}} \right)\left. {\bar{u}_{s} } \right|_{{\bar{r} = 1}} { = } - \frac{{\Omega c_{\hbox{max} } }}{{3\left( {1 - 2v_{a} } \right)v^{\prime}_{s} }}SOC , $$

(14a)

$$ \left. {\bar{E}_{s} \frac{{d\bar{u}_{s} }}{{d\bar{r}}}} \right|_{{\bar{r} = 1 + h_{s} /R}} + \left( {\bar{E}_{s} \frac{{2v_{s} }}{{1 - v_{s} }}\frac{1}{{1 + h_{s} /R}}} \right)\left. {\bar{u}_{s} } \right|_{{\bar{r} = 1 + h_{s} /R}} = 0 . $$

(14b)

The dimensionless stresses in SEI are then given by

$$ \bar{\sigma }_{{r{\text{s}}}} = \frac{{\bar{E}_{s} }}{{\Omega C_{s} }}v^{\prime}_{s} \left( {\frac{{d\bar{u}_{s} }}{{d\bar{r}}} + \frac{{2v_{s} }}{{1 - v_{s} }}\frac{{\bar{u}_{s} }}{{\bar{r}}}} \right),\;\;\;\bar{\sigma }_{\theta s} = \frac{{\bar{E}_{s} }}{{\Omega C_{s} }}\frac{{v^{\prime}_{s} }}{{1 - v_{s} }}\left( {v_{s} \frac{{d\bar{u}_{s} }}{{d\bar{r}}} + \frac{{\bar{u}_{s} }}{{\bar{r}}}} \right) . $$

(15)

Results and discussion

Comparison with the homogeneous results

In this section, based on the above heterogeneous model, the Li/Li⁺ concentration and stress profiles across the SEI thickness are calculated using the difference methods and compared with that obtained by the homogeneous model.

Figure 2 shows the comparison of Li/Li⁺ concentrations from the models with heterogeneous and homogeneous SEI. The governing equations and corresponding initial and boundary conditions are shown in the Appendix. In the calculation, the active material is regarded as graphite and thus the calculation is performed under the assumption of infinitesimal deformation. The diffusion coefficient of lithium in the graphite is set as 3.9 × 10⁻¹⁰ cm²/s [36]. The particle radius is 7μm according to the published work [37]. The diffusion coefficients for the Li ion in the inorganic and organic layers are considered as 1.1 × 10⁻⁷ cm²/s and 8.4 × 10⁻¹² cm²/s, respectively, according to the work by Shi et al. [35]. SEI is assumed as 50 nm thick and with a thickness ratio of the inorganic layer to the organic part of 1 according to Lee et al. [38]. α is set as 15,000 to adapt a typical bilayer SEI. The equivalent diffusion coefficient of Li⁺ in the homogeneous condition is calculated by

$${D_{s\_average}} = {\raise0.7ex\hbox{${\int_R^{R + {h_s}} {{D_s}{r^2}dr} }$} \!\mathord{\left/ {\vphantom {{\int_R^{R + {h_s}} {{D_s}{r^2}dr} } {\int_R^{R + {h_s}} {{r^2}dr} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\int_R^{R + {h_s}} {{r^2}dr} }$}}$$

(16)

Figure 2

Li/Li⁺ concentration profile across the radial direction; simulations with heterogeneous SEI (solid lines) versus predictions with homogeneous SEI (dash lines)

In Fig. 2, we find that in the absence of SEI heterogeneity the concentration profiles of Li⁺ in the organic layer are clearly underestimated. The concentration of Li/Li⁺ in the active material and inorganic layer is not affected by the SEI heterogeneity. This may be ascribed to the efficiently knock-off diffusion mechanism of lithium ions in the inorganic layer [35].

To examine further the effect of SEI heterogeneity on its stress, we consider the special case $d\bar{E}_{s} /d\bar{r} = 0$ in Eq. (13) and write the displacement governing equation for the homogeneous SEI as

$$ \frac{d}{{d\bar{r}}}\left( {\bar{r}^{2} \frac{{d\bar{u}_{s} }}{{d\bar{r}}}} \right) - 2\bar{u}_{s} = 0 . $$

(17)

Similar govern equation can also be seen in the work of Cheng et al. [39] The analytical solution that satisfies the boundary condition (Eq. (14)) is given by

$$ \bar{u}_{s} = \left[ {2\left( {1 - 2v_{s} } \right)\bar{r} + \frac{{1 + v_{s} }}{{\bar{r}^{2} }}\left( {1 + \frac{{h_{s} }}{R}} \right)^{3} } \right]\frac{{\Omega c_{\hbox{max} } }}{3\zeta }SOC , $$

(18)

where $\zeta = 2\left( {1 - 2v_{s} } \right) + \left( {1 + v_{s} } \right)\left( {1 + \frac{{h_{s} }}{R}} \right)^{3} + 2\bar{E}_{s} \left( {1 - 2v_{a} } \right)\left[ {\left( {1 + \frac{{h_{s} }}{R}} \right)^{3} - 1} \right]$.

Substituting into Eq. (12), the analytical solutions of stress for the homogeneous SEI along radial and tangential directions can be given by

$$ \bar{\sigma }_{rs} = - \frac{{2\bar{E}_{s} }}{3\zeta }\left[ {\frac{1}{{\bar{r}^{3} }}\left( {1 + \frac{{h_{s} }}{R}} \right)^{3} - 1} \right]SOC,\;\;\;\bar{\sigma }_{\theta s} = \frac{{\bar{E}_{s} }}{3\zeta }\left[ {2 + \frac{1}{{\bar{r}^{3} }}\left( {1 + \frac{{h_{s} }}{R}} \right)^{3} } \right]SOC . $$

(19)

It shows that stress in a homogeneous SEI rises proportionally with increasing state of charge and reaches its peak when the battery is fully charged. Furthermore, as dimensionless parameter ζ is positive, we see that the radial stress of SEI is compressive and increases monotonically from its maximum at the active material and SEI interface ($\bar{r} = 1$) to zero at the SEI surface ($\bar{r} = 1 + h_{s} /R$) due to the traction-free boundary condition, indicating that delamination of the SEI from the active material is hard to occur during the battery operation. By contrast, the tangential stress is always tensile and increases as $\bar{r}$ decreases from 1 + h _s /R to 1, suggesting that the tangential tension may cause SEI surface cracking.

Figure 3 depicts further the comparison of stress between the two models. The elastic modulus of the graphite is considered as 10 GPa [37, 40]. The modulus of the organic and inorganic parts of SEI is considered to be 1GPa and 40 GPa, respectively, according to the atomic force microscopy measurement [22, 23, 38]. Effects of variations of modulus, thickness and the interface parameter will be discussed later. Similar to the homogenization of the diffusion coefficient as shown in Eq. (16), the equivalent modulus in the homogeneous condition is calculated by $E_{s\_average} = \int_{R}^{{R + h_{s} }} {E_{s} r^{2} dr} /\int_{R}^{{R + h_{s} }} {r^{2} dr}$.

Figure 3

Stress profile across the SEI thickness: a radial stress; b tangential stress

As expected, Fig. 3 shows that the predicted stresses in the heterogeneous SEI increase with increasing state of charge and attain their peak when SOC reaches to 1, similar to the stress variation in homogeneous case. This is because stresses of the SEI stem from the swelling deformation of the active material and thus increase upon lithiation [21]. Since the modulus of the inorganic layer is much larger than that of the organic layer, the heterogeneous modulus drops remarkably at the interface between the inorganic and organic part, as shown in Fig. 3a. Accordingly, we see that the spatial distribution of stress in the heterogeneous SEI differs significantly from the homogeneous one, especially at the interface. As stress along tangential direction is tensile and much higher than the radial one both in heterogeneous and homogeneous simulations, tangential stress is therefore the main cause of cracking in both models. However, neglecting the heterogeneity of SEI, Fig. 3b tells that tangential stress in the inorganic layer of SEI is significantly underestimated, while stress in the organic part is overestimated. As far as the peak tensile stress in inorganic layer, the discrepancy between heterogeneous model and the analytical solutions for homogeneous SEI increases with SOC and is up to 96% when SOC = 1. Since surface cracking in the inorganic layer caused by tangential stress would expose the active material to electrolyte and results in continuous SEI growth as well as lithium consumption [2, 41], underestimation of the stress in the inorganic part is fatal for the SEI and battery stability. Therefore, heterogeneity should be taken into account during modeling and designing for the heterogeneous SEI.

It should be pointed out that in order to demonstrate the impact of heterogeneity and simplify the model, we neglect the possible inelastic deformation. For example, the organic material can have plastic or viscoplastic deformation and the inorganic material may also yield at a much higher stress than the organic material. Therefore, the above results are strictly valid for elastic conditions. However, as the tangential stress, which is the main cause SEI failure, in the inorganic part is much higher than that in the organic layer, it may be believed that the outcomes are also applicable for the cases that the organic materials deform inelastically. As far as the yield behavior that may occur in the inorganic layer, here we would like to take the related yield stress instead of the ultimate tensile strength of material as the stress of failure. Hence, the result still remains. The reason for this is that the yield of the inorganic layer in lithiation may cause delamination between SEI and active material in delithiation within the subsequent cycles due to the irreversible deformation.

Stress analyses and design insights

To demonstrate the role of the various physical parameters of a heterogeneous SEI and identify the key factors that impede its mechanical stability, we focus on analyzing the tangential stress of the inorganic layer in the following discussion.

Impacts of the SEI heterogeneity

Figure 4a plots the dimensionless stress profile across the SEI thickness for different α to ascertain the effects of the SEI heterogeneity on the SEI stress. It shows that the tangential stress of SEI all decline with the dimensionless $\bar{r}$, indicating that peak tensile stress in the inorganic layer is at the interface between the inorganic layer and the active material. For a homogeneous SEI, the elastic modulus is uniform in composition and requires α = 0 according to Eq. (1). When α increases, the heterogeneity arises. Therefore, it also tells that peak tensile stress in the inorganic layer will increase as SEI heterogeneity enhances, which is displayed further in Fig. 4b. For a small α, such as α ≤ 10, the SEI heterogeneity as well as the peak tensile stress in the inorganic layer $\bar{\sigma }_{\theta s\_peak}$ are facile. Afterwards, the SEI heterogeneity advances quickly as α increases, especially in the interval between 10 and 1000. Accordingly, $\bar{\sigma }_{\theta s\_peak}$ increases significantly and levels off thereafter as α ≥ 1000. This is ascribed to the exponential expression of modulus as shown in Eq. (1). When α is large enough (e.g., α ≥ 1000), the heterogeneous SEI exhibits a bilayer structure; thus, the peak stress of the inorganic layer approaches to a stable value. As peak stress in the bilayer structure is the largest among all the others, Fig. 4 suggests that in pursuing a robust heterogeneous SEI we should concentrate further on the peak stress of the bilayer structure in the following discussions.

Figure 4

Effects of the SEI heterogeneity on a the dimensionless stress profile and b the corresponding peak tensile stress of the inorganic layer within SEI

Impacts of the SEI thickness and modulus

For bilayer SEI, Fig. 5 displays how dimensionless peak stress of the focused inorganic layer $\bar{\sigma }_{\theta s\_peak}$ varies with SEI modulus and thickness. It shows that $\bar{\sigma }_{\theta s\_peak}$ decreases with increasing thickness ratio of $\bar{h}_{I} /\bar{h}_{O}$ and rises as the modulus ratio of $\bar{E}_{I} /\bar{E}_{O}$ enhances. This is because an increase in the relative thickness of the inorganic layer would constrain its tangential deformation and hence eliminates the related stress, while an increase in the relative modulus would lead to higher SEI rigidity and gives rise to a large stress. Thus, the inorganic layer in a SEI with relatively higher parameter of $\bar{h}_{I} /\bar{h}_{O}$ or lower value of $\bar{E}_{I} /\bar{E}_{O}$ is expected to experience lower stress in lithiation. Therefore, from the viewpoint of reducing the peak stress, it seems that employing a thinner and stiffer organic layer or a thicker and softer inorganic layer is preferred in SEI designing. This may be true for the organic layer, but may not be feasible for the inorganic layer because increasing the thickness of inorganic layer can introduce additional SEI resistance and decreasing the modulus of inorganic layer can reduce the energy barrier for its crack nucleation and propagation, which makes it easier to failure. Noting that the purpose of stress analysis is to ensure the mechanical stability of the SEI, which depends further on whether the inorganic layer is robust or not, the trade-off between SEI resistance and modulus modulation of the inorganic layer should be therefore based on the relative change of stress in lithiation and material failure.

Figure 5

Effects of the relative thickness (a) and modulus (b) of the inorganic part (I) to the organic part (O) on the peak stress of the inorganic layer in various thicknesses of bilayer SEIs

Figure 5 also shows that the peak stress of the inorganic layer would go up in the thin SEI as tangential deformation is relatively larger in the film. If the ratio of SEI thickness to the particle radius h _s /R approaches to zero, the heterogeneous model acts like an ultrathin homogeneous SEI and results in a consistent maximum tensile stress. According to Eq. (19), it can be given by

$$ \bar{\sigma }_{\theta s\_\hbox{max} } = \bar{E}_{I} /\left[ {3\left( {1 - v_{s} } \right)} \right] . $$

(20)

This result is consistent with the work of Verbrugge et al. on homogeneous SEI [42]. It suggests that if the SEI is ultrathin or the active particle is considerably large compared with each other, for example h _s /R ≤ 0.001 as shown in Fig. 5, the value of the peak stress in a heterogeneous SEI will be the same as the homogeneous one. For these films, we may write the failure criteria as

$$ \bar{\sigma }_{\theta s\_\hbox{max} } < \bar{\sigma }_{I\_y} , $$

(21)

where $\bar{\sigma }_{I\_y}$ represents the dimensionless yield stress of the inorganic layer. It tells the design constraint for a large electrode particle surrounded by an ultrathin SEI.

Equation (20) is depicted further in Fig. 6 for representative values of Poisson’s ratio (−1 ≤ v _s  ≤ 0.5) and dimensionless modulus of inorganic layer from 0.1 to 10. It shows that the increase in $\bar{E}_{I}$ would cause higher tensile stress. As expected, this result consists with that shown in Fig. 5. Moreover, Fig. 6 also shows that the stress in the inorganic layer with higher Poisson’s ratio would be larger since more radial displacement is generated. In a uniaxial tensile test, the Poisson’s ratio is the negative ratio of transverse to axial strain. It exhibits a value of about 0.3 for most steels and rigid polymers before yield and increases to 0.5 for post-yield deformation. Due to the lack of experimental data of Poisson’s ratio for SEI as well as for the inorganic layer, it is difficult to affirm that v _s evolves upon lithiation. However, it is coherent to admit from Fig. 6 that relatively large Poisson’s ratio of the inorganic layer would enlarge the maximum tensile stress and therefore be harmful for SEI.

Figure 6

Effects of dimensionless modulus and Poisson’s ratio (v _s ) of the inorganic layer on its maximum tensile stress

Impacts of the active material

As shown in Eqs. (13–15), properties of the active material, such as the maximum swelling deformation of the active material upon lithiation Ωc_max and Poisson’s ratio (v _a ), also affect the stress of the inorganic layer. As for Ωc _max, it is explicitly shown in Eq. (4) as well as Eq. (14) that higher Ωc _max would bring about larger radial displacement and higher SEI stress both in the inorganic and organic layers. Especially, from the expression of the maximum tensile stress in the ultrathin heterogeneous SEI, i.e., σ _{θs_max} = E _I Ωc _max/[3(1 − v _s )] as shown in Eq. (20), linear dependency on Ωc _max for SEI stress can be proposed.

As for the Poisson’s ratio of the active material, i.e., v _a , Fig. 7 is prepared to depict the variation of the peak tensile stress of the inorganic layer, i.e., $\bar{\sigma }_{\theta s\_peak}$, with changing v _a and SEI thickness h _s /R. We observe that the variation of v _a nearly does not affect $\bar{\sigma }_{\theta s\_peak}$ within the ultrathin heterogeneous SEI. This is consistent with the result shown in Eq. (20). For a relatively thick SEI, Fig. 7 tells that higher v _a leads to larger $\bar{\sigma }_{\theta s\_peak}$ and would be significant as the thickness of SEI increasing. Therefore, active materials with larger maximum swelling deformation upon lithiation and higher Poisson’s ratio may give rise to severe tensile stress in the inorganic layer and thereby being impeditive for SEI stability.

Figure 7

Effect of Poisson’s ratio (v _a ) of active material on the peak stress of the inorganic layer in various thicknesses of SEIs

Sensitivity analysis of the model parameters

To compare the influence extent of the dimensionless parameters on the peak stress of the SEI, we carry out a sensitivity analysis. This quantitative method has been utilized by Vogler et al. [43] in clarifying the roles of different parameters. In the calculation, each parameter P has been increased by 10% from its baseline value P ₀ and the normalized sensitivity index S evaluates the relative changes of the stress in comparing with the parameter P. To identify influence factors of the peak stress in SEI (σ _{θs_peak} ), S is defined as

$${S_i} = {{\frac{{{\sigma _{\theta s,peak}} - {\sigma _{\theta s,peak\_0}}}}{{{\sigma _{\theta s,peak\_0}}}}} \mathord{\left/ {\vphantom {{\frac{{{\sigma _{\theta s,peak}} - {\sigma _{\theta s,peak\_0}}}}{{{\sigma _{\theta s,peak\_0}}}}} {\frac{{P - {P_0}}}{{{P_0}}}}}} \right. \kern-\nulldelimiterspace} {\frac{{P - {P_0}}}{{{P_0}}}}}$$

(22)

Here, we use σ _{θs_peak} instead of the dimensionless one $\bar{\sigma }_{\theta s\_peak}$ to take account of the impact of the Ωc _max on SEI stress.

Figure 8 depicts the obtained sensitivity index for each parameter. Since the higher sensitivity index indicates changes of the parameter that would obviously affect the peak stress of the inorganic layer, we observe that the main contributors to the peak stress in the inorganic layer are the lithiation property of the active material (Ωc _max), the relative modulus $\bar{E}_{I}$, and Poisson’s ratio v _s of the inorganic layer. Actually, this result can be explicitly found in the expression of the maximum tensile stress in the homogenous or ultrathin heterogeneous SEI, i.e., σ _{θs_max} = E _I Ωc _max/[3(1 - v _s )]. Besides that, the Poisson’s ratio of the active material, the relative thickness and modulus of the inorganic layer, the relative SEI thickness and especially the heterogeneity parameter α also plays the important roles in affecting the peak stress of the inorganic layer. Moreover, the positive index represents an increase of the parameter would intensify the peak stress of the inorganic layer, while a negative index implies the stress would be reduced, and vice versa. Therefore, Fig. 8 discloses further that the peak stress of the inorganic layer can be reasonably reduced according to the sign of the sensitivity index shown in the figure.

Figure 8

Sensitivity analysis of different dimensionless parameters affecting the peak stress in the inorganic layer. Baseline values of each parameter are shown in “ Comparison with the homogeneous results ” section except the parameterα. Based on the results shown in Fig. 4b, we set P _α0 as 100 in calculating S _α

The above conclusions are drawn under a mechanical point of view. Ideally, a well-designed SEI for the lithium ion battery should be robust enough to achieve mechanical stability, chemically and electrochemically stable to withstand the reactive electrolyte environments, as well as ionic conductive well to provide paths for the ionic charge carriers during the passage of current in an electrochemical cell. Although the mechanical reliability is the prerequisite, other properties should not be overlooked. Unfortunately, it is sometimes hard to find a compromise between them. For example, thick SEI helps to prevent mechanical failure, while it increases the impedance of the cell due to the insulating nature of SEI [44]. Stiffer SEI that contains higher modulus LiF may improve coulomb efficiency of the cell [45], while it may compromise the corresponding mechanical stability as shown in Fig. 8. A careful balance of the mechanical reliability and well chemical and electrochemical performance needs to be optimized. Based on the mechanical analysis of the heterogeneous SEI shown in the above sections, it is fortunately to find that the mechanical stability of SEI depends only on the inorganic layer, especially the portion adjacent to the electrode. Therefore, it is logical to suggest that the heterogeneous SEI should be prepared as a functional gradient layer in which the specified inorganic layer provides sufficient mechanical performance for the SEI, the elaborate designed organic layer performs good chemical and electrochemical behaviors. This may be feasible because properties of SEI are now being adjustable. For example, Zhang et al. [46] found that additions of additives would affect the SEI thickness and stiffness. The SEI formed from vinylene carbonate (VC) additive is thick and soft, formed from lithium bis(oxalate)borate (LiBOB) additive is thin and stiff, and adding VC and LiBOB mixtures to liquid electrolyte would form the good performance SEI with moderate thickness and stiffness. Tokranov et al. [47] observed that the stiffness of SEI on silicon can be altered by potential treatment, i.e., longer time at higher potentials produces softer SEI. Agubra et al. [48] also reported that battery potential and charge rate can adjust the SEI thickness. As for the estimation of SEI failure, Kumar et al. [49] proposed a feasible approach which combines controlled SEI strains and direct observations of atomic force microscopy.

In addition, to compare with the existing AFM observation, we consider that the modulus of SEI is composition dependent in which the inner inorganic layer has relatively higher elastic moduli compared to the outer organic layer on the electrolyte side. Since this division of inorganic or organic layer is only based on the material modulus, the results are thus believed to be applicable for any heterogeneous SEI that has higher moduli inside and softer modulus outside. Therefore, as expected, the present opinion, i.e., fabricating the SEI to be a functional gradient layer in which the inner layer that near the active material provides sufficient mechanical performance and the adjacent outer layer performs good chemical and electrochemical behaviors is in line with the latest experimental results [50], where a gradient SEI of the hard inside and soft outside was found to be more mechanical stable to protect the electrode surface and also improve cell current efficiency.

Conclusion

In this paper, we develop a continuum model to study the stress of a heterogeneous solid electrolyte on a spherical electrode particle. Comparing the stress of heterogeneous SEI with the homogeneous one, we show that taking into account the heterogeneity of SEI is essential for predicting the SEI stress since it significantly increases the tensile stress in the inorganic part of SEI, which is proven decisive for preventing the instability of a heterogeneous SEI. The peak tensile stress within the SEI generates at the interface between the active material and the inorganic layer when the battery is fully charged. Moreover, the influences of each possible dimensionless parameter on the peak stress of the inorganic layer are elucidated and summarized. Finally, a functional gradient heterogeneous SEI is therefore suggested to improve the performance of lithium batteries.

Appendix

The governing equations for the spherical particle and SEI that undergo large deformation can be specified as follows:

Consider that an isotropic element with radial coordinate $\tilde{R}$ in the undeformed reference configuration moves to the radial coordinate $\tilde{r}$ in the current state at time t. The radial stretches along radial and hoop directions are

$$ \lambda_{R} = \partial \tilde{r}/\partial \tilde{R},\;\;\;\;\;\;\;\lambda_{\theta } = \tilde{r}/\tilde{R} . $$

(23)

According to the works of Zhao and Li et al. [15, 16], the relationship between stress and strain for a heterogeneous material can be written as

$$ \begin{aligned} S_{R} = \frac{J}{{\lambda_{R} }}\frac{{E\left( {\tilde{R}} \right)}}{1 + v} \left[\frac{v}{1 - 2v}\ln J + ln\lambda_{R} \right] - \frac{1}{3}\lambda_{\theta }^{2} \frac{{E\left( {\tilde{R}} \right)}}{1 - 2v}ln\left( {1 + \Omega C} \right) \hfill \\ S_{\theta } = \frac{J}{{\lambda_{\theta } }}\frac{{E\left( {\tilde{R}} \right)}}{1 + v} \left[\frac{v}{1 - 2v}\ln J + ln\lambda_{\theta } \right] - \frac{1}{3}\lambda_{R} \lambda_{\theta } \frac{{E\left( {\tilde{R}} \right)}}{1 - 2v}ln\left( {1 + \Omega C} \right). \hfill \\ \end{aligned} $$

(24)

Here, S _R and S _θ are the radial and hoop nominal stress components. J = λ _R λ ² _θ denotes the ratio of the volume change during deformation. E is the composition dependent modulus, v is the Poisson’s ratio, and Ω and C represent the partial molar volume and molar concentration of the solute, respectively. Noting the relationship between engineering strain ɛ and λ, i.e., λ = ɛ + 1, the above Eq. (24) recovers exactly to the relations for infinitesimal of deformation as shown in Eq. (4). It should be pointed out that the last term on the right of Eq. (24) which represents the stress caused by swelling deformation should be removed for SEI because the stress of the SEI is believed mainly induced by the deformation of the active material.

In the absence of external body force, the static mechanical equilibrium requires

$$ \partial S_{R} /\partial \tilde{R} + 2\left( {S_{R} - S_{\theta } } \right)/\tilde{R} = 0 . $$

(25)

Therefore, for any given concentration of solute C, substituting Eqs. (23) and (24) into Eq. (25) and introducing the related boundary conditions, the relationship between the current configuration $\tilde{r}$ and the reference configuration $\tilde{R}$ can be numerically obtained. Then the radial and hoop stretches as well as the nominal stress components are therefore determined. The boundary conditions are as follows: the center of the active sphere remains stationary, i.e., r ^a(0, t) = 0; the displacement and radial stress are continuous at the active particle/SEI interface, i.e., r ^a(R, t) = r ^s(R, t) and S ^a _R (R, t) = S ^s _R (R, t), where the superscripts a and s denote the active material and SEI, respectively, and R is the radius of the undeformed active particle; the radial stress at the SEI free surface is zero, i.e., S ^s _R (R + h _s , t) = 0 where h _s represents the thickness of the undeformed SEI.

To determine the concentrations of lithium in active particle and lithium ion in SEI, corresponding diffusion equations and conditions of solution should also be specified. Assuming that the diffusion is driven only by concentration gradient, the governing equation of solute in a composition dependent material can be given by

$$ \tilde{R}^{2} \frac{\partial C}{\partial t} = \frac{\partial }{{\partial \tilde{R}}}\left( {D\tilde{R}^{2} \frac{\partial C}{{\partial \tilde{R}}}} \right), $$

(26)

where D is the diffusion coefficient and is a function of $\tilde{R}$. For SEI, it can be analogous to the variation of elastic modulus as shown in Eq. (1) and given by

$$ D_{s} \left( \tilde{R}\right) = D_{O} + \frac{{D_{I} - D_{O} }}{{1 + \exp [\alpha \left( {\tilde{r} - R - h_{I} } \right)/R]}}, $$

(27)

where D _O and D _I represent the diffusion coefficients of lithium ion in organic and inorganic layers, respectively.

The initial Li/Li⁺ concentrations are considered as zero, i.e.,

$${C^a}\left( {\tilde R,0} \right) = 0,\;\;\;\;\;\;\;\;{C^s}\left( {\tilde R,0} \right) = 0$$

(28)

The boundary conditions for the inlet SEI surface associated with the charging conditions are

$$ \left. {D^{s} \frac{{\partial C^{s} }}{{\partial \tilde{R}}}} \right|_{{\tilde{R} = R}} = - \frac{{i_{n}^{ + } }}{F}, $$

(29)

for the galvanostatic charging, where i ⁺ _n is the surface current density, F is Faraday’s constant, and

$$ C^{s} \left( {R + h_{s} ,0} \right) = C_{b} , $$

(30)

for potentiostatic charging, where C _b is the constant surface concentration. The flux of lithium and lithium ion is continuous and the particle/SEI interface and lithium flux at the center of the particle is zero due to symmetry. These require

$$ \left. {D^{a} \frac{{\partial C^{a} }}{{\partial \tilde{R}}}} \right|_{{\tilde{R} = R}} = \left. {D^{s} \frac{{\partial C^{s} }}{{\partial \tilde{R}}}} \right|_{{\tilde{R} = R}} \;\;\;\;\;{\text{and}}\;\;\;\;\;\left. {D^{a} \frac{{\partial C^{a} }}{{\partial \tilde{R}}}} \right|_{{\tilde{R} = 0}} { = }0. $$

(31)