Residual stress evaluation in friction stir-welded aluminum plates using finite element method and acoustic emission

Abstract

Acoustic Emission (AE) method proposed in this paper as a novel approach was used to evaluate residual stress in friction stir welding (FSW) of 5086 aluminum plates. A finite element method was used to evaluate residual stresses in aluminum plates caused by FSW, which was validated by the hole-drilling process. Moreover, fundamental antisymmetric Lamb wave mode (A ₀) was implemented to measure the residual stresses produced by FSW process. The novelty of this investigation is the combination of a robust signal-processing analysis and theory of acoustoelastic Lamb wave. In this analysis, an envelope of A ₀ mode is used instead of signal time of flight, which obliterates the need to utilize a synchronizing clock of receiving sensors. It was shown that the duration of the signal changes linearly with residual stress variation, and a new equation was then established. Finally, it is confirmed that AE as a nondestructive approach can be an efficient tool for residual stress measurement in welded plate.

Introduction

The aluminum components used in many industrial applications should have decent mechanical properties in combination with lower residual stress levels. The residual stresses can affect some engineering properties of these structural components, such as fatigue life, deformation, dimensional stability, corrosion resistance, and brittle fracture. Residual stresses can be defined as “locked-in” stresses that exist in the structural components in the absence of any external loads [1]. These stresses can seriously shorten the component’s life and cause a brittle fracture. Considerable effort is currently allocated to the improvement of an efficient method for evaluation of residual stresses in industrial applications. Therefore, it is imperative to assess residual stresses effectively.

One of the main sources of residual stress in the industry is a welding process, which occurs due to nonuniform thermal expansions and solidifications during this process. One of the most prevalent welding processes is friction stir welding (FSW), which is a solid-state welding process, and due to compressional residual stress formation, this process does not involve the melting of the joined materials [2, 3]. Bussu and Irving [4] found that the residual stress can improve the fatigue life of aluminum joints. Their results showed that crack growth characteristics in the FSW joints were largely dominated by the weld residual stress rather than the changes in the microstructure and hardness. Peel et al. [5] used the X-ray methodology to examine the tool transverse speed effect on the distribution of the residual stresses caused by FSW of the 5083 aluminum plates. Sadeghi et al. [6] measured the through-thickness residual stress in the aluminum plate using longitudinal critically refracted (L_CR) ultrasonic method and finite element approaches. Javadi et al. [7] employed the Taguchi method to optimize the FSW parameter using the ultrasonic method. They concluded that the most integral effect on the longitudinal residual stress peak is related to the transverse speed.

Over the recent years, various methods have been applied to evaluate residual stress in order to achieve reliable assessment. Many of these approaches are described in [8]. Among these approaches, nondestructive measurement techniques are the key tools due to their applicability to real structure elements. Lamb wave or guided waves in plates are of great importance for nondestructive evaluation (NDE) due to their ability to keep their sensitivity to damage during long distance propagation [9, 10]. Lamb waves are especially sensitive to environment propagation changes such as stress, temperature, and surface conditions [11–13]. Hughes and Kelly [14] explained the dependence of wave speed on stress in an initially isotropic solid. Toupin and Bernstein [15] applied this method to materials of arbitrary symmetry under a specified stress. Husson [16] used the theoretical acoustoelastic Lamb wave to investigate the frequency dependence of the acoustoelastic constants. Qu and Liu [17] obtained the waves dispersion curve in a stressed aluminum plate. Rizzo and Lanza di Scalea [18] studied the wave speed variations of Lamb waves under tensile loading. Lematre et al. [19] presented a theory for propagation of guided wave in stressed piezoelectric plates. They only showed numerical results for propagation along the direction of the applied stress. Although acoustoelasticity is now a well-established technique used in the NDE of residual stresses, ample research has not been conducted on improving measurement accuracy using the acoustoelastic concept.

This paper presents a new method to more accurately measure residual stresses in welded aluminum plates using acoustic emission. Lamb waves were utilized to evaluate the residual stresses caused by the FSW of the aluminum plate. Toward this aim, AE method was used to extract the acoustoelastic constant related to another mode of the propagating wave, which is called fundamental anti-symmetric mode of Lamb wave. Although there are several studies on measuring residual stresses using Lamb waves, to the authors’ best knowledge, however, there has been almost no report of acoustic emission associated with the analysis of residual stress using Lamb waves. The Finite Element Method (FEM) was also employed to obtain the residual stresses in welded zone, validated by hole-drilling technique. The comparison between the applied methods showed that the new AE-based approach has a good potential to evaluate the residual stresses.

Theoretical background

Finite element method

In recent years, finite element (FE) simulation has become a valuable tool in the design of the FSW processes. Residual stress determination using FE, which leads to the estimation of welded joint fatigue life, has a strategic significance for many industrial applications. In this work, the FEM model was based on a thermomechanically coupled analysis with the assumption of rigid-viscoplastic material behavior. The plate seam was considered to be continuum to decrease the numerical instabilities due to discontinuities at the plate edges. The variational approach was implemented for rigid-viscoplastic FE model. The stationary value for the variation of governing functional $\pi$ was used for determining the actual velocity field. The formula is expressed as follows [20] :

$$ \delta \pi = \int\limits_{V} {\bar{\sigma }\delta \dot{\bar{\varepsilon }}{\text{d}}V} + k\int\limits_{V} {\dot{\varepsilon }_{V} \delta \dot{\varepsilon }_{V} {\text{d}}V} - \int\limits_{{S_{F} }} {F_{i} \delta u_{i} {\text{d}}S} = 0. $$

(1)

In the above equation, ${\dot \varepsilon _V} = {\dot \varepsilon _u}$ is the volumetric strain-rate, and $\bar{\sigma } = \bar{\sigma }\left( {\bar{\varepsilon },\dot{\bar{\varepsilon }},T} \right)$. In order to have incompressibility, the constant $k$ should assume a very large positive value. The generated temperature has an integral effect on the mechanical response of the FSW process. The final thermal equilibrium equation is expressed as

$$ [{\text{C}}]\{ {\text{T}}^{\bullet}\} + \, [k_{\text{C}} ]\{ {\text{T}}\} = \{ {\text{Q}}\} $$

(2)

The tool is considered as a rigid body because of its higher strength in comparison with the plates. In order to acquire the residual stresses at the end of the process, the additional elastoplastic material model was used. For the boundary condition of the FE model, the workpiece was clamped at its sides. The FE analysis comprised two stages. In the first stage, the pin entered into the plate which moved down vertically while it was rotating. The tool then moved along the welding line to join the plates in the second step. At the end of the first stage, a dwelling time was applied to obtain appropriate heating of the workpiece for the subsequent welding stage.

The thermal conductivity and thermal capacity of the aluminum plate were $k = 120 N/s$ °C and $c = 2.4 N/mm^{2}$ °C, respectively, for the FE model. The thermal analysis was considered linear as a result of temperature independencies of $k$ and $c$, which led to better convergence. Meshing of the FE model was chosen based on the accuracy of the FE results and computational time, which is presented in Fig. 1. As obviously seen from this figure, in order to decrease the time of FE analysis and acquire accurate results, the mesh sensitivity was obtained in the FSW-welded part using finer and coarser mesh models, and a finer mesh was finally selected for the FSW-welded section (see Fig. 1).

Figure 1

Basic finite element model of the FSW process

Hilbert–Huang transform

Traditional data analysis approaches were mostly based on Fourier analysis of the physical processes. These methods have some basic problems discussed in details by Huang et al. [21]. Hilbert–Huang transform (HHT) is a capable tool for signal analysis in order to solve some aspects of these issues. The most beneficial point of this approach is the ability to analyze nonstationary and nonlinear data. The adaptive approach of HHT makes this approach a more robust tool for data analysis, and applicable to a wide variety of applications. Hilbert transform (HT) of the real-valued signal $x(t)$ is defined as [22]

$$ y\left( t \right) = H\left( {x\left( t \right)} \right) = \frac{1}{\pi }p\mathop \smallint \limits_{ - \infty }^{\infty } \frac{x\left( \eta \right)}{t - \eta }{\text{d}}\eta $$

(3)

$$ x\left( t \right) = H^{ - 1} \left( {y\left( t \right)} \right) = - \frac{1}{\pi }p\mathop \smallint \limits_{ - \infty }^{\infty } \frac{y\left( \eta \right)}{t - \eta }{\text{d}}\eta $$

(4)

where p is the Cauchy principal value. Therefore, an analytic signal like $z\left( t \right)$ can be expressed as per the following equation:

$$ z\left( t \right) = x\left( t \right) + iy\left( t \right) = a\left( t \right){ \exp }^{i\theta \left( t \right)} $$

(5)

where

$$ a\left( t \right) = \left( {x^{2} \left( t \right) + y^{2} \left( t \right)} \right)^{{\frac{1}{2}}} $$

(6)

$$ \theta \left( t \right) = arctan\frac{y\left( t \right)}{x\left( t \right)} .$$

(7)

The above-mentioned $a\left( t \right)$ and $\theta \left( t \right)$ are instantaneous amplitude and phase angle of $z\left( t \right)$, respectively. The weakness of HT is the presence of spurious amplitudes at negative frequencies as a result of the nonlinear and nonstationary processes. To compensate the HT fault in this case, Huang [21] projected the original signal onto a set of basis functions by means of empirical mode decomposition and the projections termed intrinsic mode functions (IMFs). Toward this aim, the sifting algorithm decomposes the signal $x(t)$ into nIMFs $c_{i} (t)$ and the residue $r_{n} \left( t \right)$, and the original signal $x(t)$ is as follows:

$$ x\left( t \right) = \mathop \sum \limits_{i = 1}^{n} c_{i} \left( t \right) + r_{n} (t) $$

(8)

Then the instantaneous amplitude $a_{j} (t)$ and instantaneous frequency $\omega_{j} (t)$ are determined for each of the IMFs $c_{j} (t)$ using Eqs. (6) and (7), respectively, and hence the signal $x(t)$ can be expressed as

$$ x\left( t \right) = {\text{Re}}\left[ {\mathop \sum \limits_{j = 1}^{n} a_{j} \left( t \right){ \exp }^{{i\mathop \smallint \nolimits \omega_{i} \left( t \right){\text{d}}t}} } \right]. $$

(9)

In this case, Re[] denotes the real part of terms within brackets. Finally, the amplitudes of both $a_{j} (t)$ and $\omega_{j} \left( t \right)$ in terms of time–frequency space are called Hilbert–Huang spectrum $H(\omega , t)$.

Lamb wave acoustoelasticity

The presence of the stress field in an elastic continuum results in variation of acoustic velocities which is defined as acoustoelasticity [23]. As a consequence, acoustic wave flight time varies linearly with stress which is formulated as follows:

$$ {\text{d}}\sigma = \frac{{E({\text{d}}V/V)}}{L} = - \frac{E}{L}{\text{d}}t/t_{0} $$

(10)

where ${\text{d}}\sigma$ is the stress variation, E is the modulus of elasticity, $L$ is the dimensionless acoustoelastic constant, and $t_{0}$ is time of flight (TOF) corresponding to the wave propagating in a stress-free medium. Considering a specific distance of $\Delta x$ for wave propagation in case of L_CR method, the sensitivity of TOF variation respect to applied stress is governed by the following equation:

$$ \Delta TOF|_{\Delta \sigma } = - L.\frac{\Delta \sigma }{E}. \frac{\Delta x}{{C_{\text{p}} }} .$$

(11)

where $C_{\text{p}}$ is the pressure wave velocity, and the other parameters are as the same before. Considering the order of these parameters induces a necessity to measure TOF with the accuracy of better than 1 ns which demands for an instrument with sampling frequency of 1 GHz. Therefore, based on the Eq. (11), to refine the stress measurement resolution, $\Delta x$ should be selected larger, while the attenuation of low-amplitude L_CR wave is a crucial barrier to this elementary solution.

To overcome this issue, low-frequency A ₀ mode was implemented in which the fraction $\frac{L}{{C_{{A_{0} }} }}$ [Eq. (11)] is significantly higher and the attenuation effect generally decreases due to low excitation frequency. Consequently, a higher sensitivity to stress variation can be achieved using this mode. Similar to acoustoelastic bulk waves, the phase velocity of Lamb wave modes changes linearly with stress and can be formulated as

$$ \frac{{c_{\sigma }^{\varGamma } - c_{0}^{\varGamma } }}{{c_{0}^{\varGamma } }} = K^{\varGamma } (f)\sigma $$

(12)

where $c_{\sigma }^{\varGamma }$ is the phase velocity corresponding to $\varGamma$ mode shape under stress of $\sigma$. The term $K^{\varGamma } (f)$ is acoustoelastic constant corresponding to exciting frequency $f$. In this investigation, in order to evaluate acoustoelastic constant, a novel method is presented which eliminates the demand for accuracy of TOF measurement.

As is well known, the velocity of A ₀ mode depends on excitation frequency, which is called dispersion. High-dispersive inherency of the A ₀ mode results in frequency explosion during propagation. Therefore, the duration of incident A ₀ mode increases as the wave propagates longer distances.

Considering the difference between the arrival time of the slowest and the fastest frequency components of Lamb waves to the sensors which are placed apart in distance of $\Delta x$ and neglecting the attenuation effect, the increase in duration time throughout the propagation between two sensors can be formulated as

$$ \delta d^{\varGamma } = \Delta x\left( {\frac{1}{{c^{\varGamma } (f_{ \hbox{min} } )}} - \frac{1}{{c^{\varGamma } (f_{ \hbox{max} } ) }}} \right) $$

(13)

where d is the duration, and $c^{\varGamma } \left( {f_{ \hbox{min} } } \right)$ and $c^{\varGamma } \left( {f_{ \hbox{max} } } \right)$ are the phase velocities of Γ mode corresponding to the minimum and the maximum frequencies, respectively. By combining Eqs. (12) and (13), the increase in duration under homogeneous stressed condition is as follows:

$$ \delta d_{\sigma }^{{A_{0} }} \cong \Delta x\left( {\frac{1}{{c_{0}^{{A_{0} }} \left( {f_{ \hbox{min} } } \right)}} - \frac{1}{{c_{0}^{{A_{0} }} \left( {f_{ \hbox{max} } } \right)}}} \right)\left( {1 - K^{{ A_{0} }} (\bar{f})\sigma } \right) $$

(14)

where $K\left( {\bar{f}} \right)$ is the acoustoelastic constant of centered frequency $\bar{f}$, $\sigma$ is the applied stress, and $c_{0} \left( {f_{ \hbox{min} } } \right)$ and $c_{0} \left( {f_{ \hbox{max} } } \right)$ are the phase velocities of $A_{0}$ mode in stress-free state corresponding to the minimum and the maximum frequencies. With adoption of Eq. (12), the relative variation of the increases in duration can be obtained as follows:

$$ \frac{{\delta d_{\sigma }^{\varGamma } - \delta d_{0}^{\varGamma } }}{{\delta d_{0}^{\varGamma } }} = - K^{\varGamma } \sigma. $$

(15)

Experimental procedure

Description of the samples

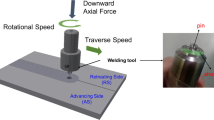
The experimental work was carried out on six rectangular plates of 5086 aluminum with 100 × 500 mm dimensions and 8-mm thickness. The plates were friction stir welded in butt joint geometry using H13 steel tool. The tool was of 55-mm shoulder height, 8-mm pin diameter, and 7.6 mm pin length, as shown in Fig. 2.

Figure 2

Specifications of friction stir welding tool

A vertical milling machine was used to weld the specimens in the butt configuration. The welding procedure was based on the TWI method presented in the patent by Thomas et al. [24]. Figure 3 shows the experimental setup of FSW process. During the welding process, the workpiece was clamped at its sides as shown in this figure, and its bottom was supported by a back plate.

Figure 3

Experimental setup of the FSW process

The process parameters as mentioned in Table 1 were used in the butt configuration for three different specimens (two samples of each specimen were welded). The operating ranges of transverse speed and rotational speed were chosen in order to experimentally obtain three distinct levels of the residual stresses in the aluminum plates.

Table 1 Constant process parameters for FSW of the aluminum plates

AE sensors

Two AE sensors were used to record the generated AE signals. The resonance frequency of single-crystal piezoelectric AE sensor was 513.28 kHz with an optimum operating range of 100–750 kHz. The 2/4/6-AST preamplifier was used to enhance the AE signals with a gain selector of 40 dB. The sampling rate of AE data acquisition board was adjusted to 40 × 10⁶ samples per second. The threshold of receiving AE signals was adjusted to 30 dB. The Pencil Lead Break (PLB) method was used several times to calibrate the AE sensors according to ASTM E976-10 [25] standard. The contact surface of the sensor was covered with grease to create good acoustical coupling.

Acoustoelastic measurement

To evaluate the acoustoelastic constant, tensile test specimens were extracted from the welded zone (WZ) and the parent material (PM) zone separately. Evenly distributed stress field was applied using a calibrated universal tensile test machine in displacement control mode. The load cell capacity was 50 kN with ±5 N resolution. Prior to each tensile test, specimens were stress relieved after annealing at temperature 350 °C for 1 h. During the tensile test, stress (σ) was increased step by step, while PLB tests were accomplished in each step. The experimental setup for the extracting acoustoelastic constants is shown in Fig. 4.

Figure 4

Experimental setups for obtaining acoustoelastic constants

In order to measure longitudinal residual stresses on the welded plates, the following steps were precisely accomplished:

• 1. Fundamental Lamb wave modes were activated in the pitch-catch mode. The increase in duration ($\delta d$) related to $A_{0}$ mode was calculated during propagation between two sensors by applying HHT on the received signals.

• 2. The value $\delta d_{0}$ was measured directly on the stress-free samples which were the tensile test specimens extracted from the WZ and the PM zones.

• 3. Acoustoelastic constants were measured on samples extracted from the Wi specimen by means of a uniaxial tensile test, and using Eq. (15) in the WZ and PM zones, separately.

• 4. Assuming the same acoustoelastic constants for the two Plates (samples 1 and 2), and substituting the results of previous steps in Eq. (15), longitudinal residual stresses were recalculated for the plate Wi sample. The experimental setup for the stress evaluation is shown in Fig. 5.

  Figure 5

  

  Experimental setups for residual stress evaluation using the A_LW approach

Completing steps 1–4, which are summarized in Fig. 6, will lead to nondestructive evaluation of longitudinal residual stresses in the friction stir-welded aluminum plates using the acoustoelastic Lamb wave (A_LW) method.

Figure 6

Flowchart of the nondestructive stress evaluation using the acoustoelastic Lamb wave

Results and discussion

Evaluation of acoustoelastic constant

A crucial stage in the acoustoelastic-based assessment of residual stresses is to precisely evaluate acoustoelastic constant. To achieve this goal, there exist two opposing factors including the attenuation and accurate TOF measurement. Due to the attenuation, there is a possibility of vanishing low-amplitude modes, which leads to inaccurate measurement of TOF, especially in multimode cases. Since higher frequencies experience more attenuation, appropriate selection of frequency level is the key factor to minimize and control the attenuation effect. In this investigation, in contrast to the conventional ultrasonic technique (L_CR method), a novel approach was developed based on waveform features of lower order frequencies which eliminates demand for accuracy of TOF measurement. The basic concept utilized is a dispersion of the acoustoelastic waves which has been discussed in “Lamb wave acoustoelasticity” section.

The characteristic equation of lamb waves is solved numerically in the stress-free situation. In Fig. 7, dispersion results are presented in terms of the phase velocity as a function of frequency for the investigated aluminum plates. Besides, to verify the numerical results of dispersion curve, phase velocities of fundamental modes of Lamb waves were experimentally determined in some frequency regimes, and a good agreement was observed. As obviously observed from Fig. 7, for the low-frequency regime, in spite of S ₀, A ₀ behaves in a nonstable dispersive manner.

Figure 7

Dispersion curve of Lamb wave propagating in an aluminum plate

Figure 8a, b shows two normalized AE signals which were acquired by both sensors (sensor 1 placed closer to the AE source) during the PLB test using the standard test at the stress level of 30 MPa. Given that in all frequencies the S ₀ mode propagates faster than A ₀ mode, in the both signals (a) and (b), the first package corresponds to the S ₀ mode, and the second highlighted package corresponds to the A ₀ mode. Also, the wave package that reaches the sensors with a delay after A ₀ mode is the reflection from the boundaries. It should be noted that in order to remove the frequency-dependent factor of the acoustoelastic constant, the frequency was tuned at 100 kHz during the test procedure. For insurance, the frequency magnitude of the acquired signals was analyzed using fast Fourier transform (FFT) analysis. Figure 8c, d show the resultant frequency magnitudes of sample signals (a) and (b), respectively, which are centered at about 100 kHz.

Figure 8

Samples of acquired signals by a sensor 1, b sensor 2 and FFT of signals for c sensor 1, d sensor 2

According to the Eq. (15), an increase in duration for dispersive modes changes linearly with stress. To precisely extract partial duration ($d^{{A_{0} }}$) corresponding to $A_{0}$ mode, Hilbert–Huang transform was applied on the AE signals which were acquired during the test procedure. Figure 9a illustrates $A_{0}$ mode which is extracted from signals (a) and (b) in Fig. 8. Using the HHT, the resultant envelope was calculated to evaluate the duration of $A_{0}$ mode, which is defined as the time interval of the threshold crossing. As a result of dispersion phenomenon, envelope of $A_{0}$ mode expands and its duration increases, which is shown in Fig. 9b. The relative variation in the increase of duration with respect to natural state is proportional to the stress applied on plate. The results of tensile test for the processed AE duration data ($\frac{{\delta d_{\sigma } - \delta d_{0} }}{{\delta d_{0} }})$ against applied stress are presented in Fig. 10, where the slopes of the lines represent the acoustoelastic constant corresponding to A₀. The resultant acoustoelastic coefficients related to each zone are reported in Table 2. According to achieved results, it was found that the acoustoelastic constants for different metallurgical zones, e.g., WZ and PM zones are not the same. In addition, with the increasing transverse speed, the acoustoelastic constant of WZ slightly increases.

Figure 9

Hilbert–Huang transform for extracting partial duration of the signals, a signal with their envelopes, b shifted envelopes of the signals

Figure 10

Results of tensile test for the processed AE duration data to obtain acoustoelastic constants

Residual stress evaluation of FSW using FEM and acoustoelastic Lamb wave (A_LW)

Steps 1–4 in “Acoustoelastic measurement” section were accomplished to nondestructively evaluate the longitudinal residual stresses in the friction stir-welded aluminum plates using A_LW method. The 3D finite element analysis was then employed to assess the capability of acoustoelastic Lamb wave method. Moreover, the hole-drilling method was applied to four different points on each aluminum plate according to the configuration in Fig. 11 in order to verify the results of the finite element method.

Figure 11

Hole-drilling procedure of FSW in the aluminum plate

The average results of finite element residual stresses in 2-mm depth from the surface are obtained using the hole-drilling approach (see Fig. 12). The results confirm that there is a good consistency between the residual stress values along the 2-mm depth using the hole-drilling method and those obtained from the finite element method.

Figure 12

Results of finite element and hole-drilling residual stresses for the three different welded specimens

Figure 13 shows the M-shaped (double-peak feature) longitudinal residual stress distributions of the FSW aluminum plates. As is clear from this figure, the residual stress is higher in the advancing side (AS) of FSW in comparison with the retreating side. The maximum welding temperature takes place at the AS zone of the joints as a result of the nonsymmetric temperature distribution of FSW [26]. Moreover, higher residual stress in AS zone is because of stretching the stirred zone into the AS zone due to the higher material flow [27]. Comparing the results of the validated FE reveals that higher longitudinal residual stress is created as the transverse speed increases. Transverse speed is closely correlated to the thermal cycles induced in FSW process. The increasing transverse speed leads to a reduction of the diffusion time of the heat dissipated in the material away from the FSW-welded line. As a result, higher stresses due to higher temperature gradients are seen during the cooling process which is in harmony with other research results [28].

Figure 13

Results of finite element and A_LW residual stresses for different welded specimens

Using the A_LW method, the stress distribution patterns corresponding to the three different transverse speed levels are shown in Fig. 13. The displacement fields of particles due to the existence of the Lamb wave modes are distributed in through-thickness of the plates. Therefore, the average values of the FE residual stresses (validated by hole-drilling), located in through-thickness of the plates for all of the nodes, were measured to compare with the A_LW results. As can be seen in Fig. 13, an acceptable agreement was achieved which shows that the A_LW method can be a powerful approach for the residual stress assessment.

Table 2 Resultant acoustoelastic coefficients related to each zone

The A_LW package instrument equipped with the three-axis scan machine (see Fig. 5) was used to examine some defined parts of the W2 plate in order to acquire the residual stress distribution in the whole plate. The AE data were captured in five appropriate sections and were then analyzed in these zones. Figure 14 shows the ultrasonic 3D distribution patterns of the longitudinal residual stresses of the main weld. Comparing these results to those obtained from FE method, a good harmony was observed.

Figure 14

A_LW 3D distribution patterns of longitudinal residual stress in W2 specimen

Conclusion

In this study, AE methodology was used to nondestructively evaluate residual stresses of friction stir-welded 5086 aluminum plates. A novel residual stress measurement method, called A_LW, was used to evaluate residual stresses in the FSW process. The variations of duration of Lamb waves captured by AE sensors were implemented as a novel feature to evaluate the residual stresses. The 3D finite element analysis validated by hole-drilling procedure was employed to assess the capability of acoustoelastic Lamb wave method. According to the obtained results, the following conclusions can be drawn:

• (1) The results of the FE based on a thermomechanically coupled analysis and the hole-drilling method show a good agreement at a distance of 2 mm from the weld surface.

• (2) The presented A_LW method is a capable tool to measure efficiently the average through-thickness stresses in the FSW aluminum plates.

• (3) The A_LW approach has a good capability to measure the FSW residual stress trends which were validated by FE results. The A_LW exhibits a double peak feature (a maximum on the AS and a minimum in the weld zone of the FSW plates) for the longitudinal residual stresses.

• (4) In conventional methods of residual stress evaluation, attenuation has a considerable effect on TOF and duration of the measurement, which can be controlled efficiently using A_LW approach by selecting a reasonable and appropriate frequency range. The best frequency range centering at about 100 kHz was selected by means of a trial and error procedure.

• (5) In addition to the attenuation effect, in conventional methods, the selection of higher frequency level causes the excitation of the higher lamb wave modes, which makes it difficult for further analysis of residual stresses in these approaches.

In conclusion, based on the obtained results from the A_LW procedure, this presented method can evaluate the longitudinal residual stresses in the aluminum FSW plates in a very efficient manner. The A_LW is a novel cost-effective method which can be considered as an effective tool for the measurements of residual stresses in welded plates.