Fast and accurate prediction of temperature evolutions in additive manufacturing process using deep learning

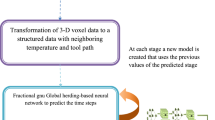
Abstract

Typical computer-based parameter optimization and uncertainty quantification of the additive manufacturing process usually requires significant computational cost for performing high-fidelity heat transfer finite element (FE) models with different process settings. This work develops a simple surrogate model using a feedforward neural network (FFNN) for a fast and accurate prediction of the temperature evolutions and the melting pool sizes in a metal bulk sample (3D horizontal layers) manufactured by the DED process. Our surrogate model is trained using high-fidelity data obtained from the FE model, which was validated by experiments. The temperature evolutions and the melting pool sizes predicted by the FFNN model exhibit accuracy of $99\%$ and $98\%$, respectively, compared with the FE model for unseen process settings in the studied range. Moreover, to evaluate the importance of the input features and explain the achieved accuracy of the FFNN model, a sensitivity analysis (SA) is carried out using the SHapley Additive exPlanation (SHAP) method. The SA shows that the most critical enriched features impacting the predictive capability of the FFNN model are the vertical distance from the laser head position to the material point and the laser head position.

Introduction

Additive Manufacturing (AM) is nowadays a versatile technology and has been successfully applied in many applications such as aerospace (Ngo et al. 2018; Lyons 2014; Kumar and Nair 2017), robotics (Shen et al. 2019; Bhatt et al. 2019), and biomedical applications (Hann et al. 2020; Culmone et al. 2019; O’Malley et al. 2016; Javaid and Haleem 2018). Directed Energy Deposition (DED) is an AM technique in which metallic powders are deposed and melted simultaneously via a focused heat source for creating complex metallic parts (Jardin et al. 2019, 2020). During the DED process, many complex physical phenomena occur in a short period and at a high-temperature level, generating fast heating and cooling rates and strong thermal gradients (Jardin et al. 2019).

Experimental campaigns to understand these phenomena are often expensive and time-consuming. Another issue is that the experiments provide incomplete and limited information on the microstructure evolutions during the manufacturing process. To overcome these shortcomings, the physical-based computational models, such as the finite element (FE) method, have been widely used to gain more insights into the manufacturing processes (Jardin et al. 2019; Yang et al. 2016; Baykasoğlu et al. 2020; Kolossov et al. 2004). The fabricated product quality and manufacturing conditions involve multiple uncertainty sources, such as material properties, operator skills, process parameters, and boundary conditions. The computer-based optimization of the manufacturing process accounting for these uncertainties requires a large number of high-fidelity FE simulations (Lin et al. 2020; Manjunath et al. 2020; Hoang et al. 2017), which are usually computationally expensive.

A common strategy for improving the computational efficiency is to develop a surrogate model for the FE model (Hoang and Matthies 2021; Cheng et al. 2021; Guo et al. 2021; Park et al. 2021). In many AM process applications, the surrogate model must have the capability to predict the temperature evolutions under different process settings (Kolossov et al. 2004; Yang et al. 2016; Baykasoğlu et al. 2020), which are encoded with many input parameters. Deep Learning (DL) is a promising tool to build such the surrogate model (Haghighi and Li 2020; Lee et al. 2020; Garland et al. 2020; Hofmann et al. 2014; Kamath 2016; Kamath and Fan 2018; Levine et al. 2018; Mozaffar et al. 2018), owing to their advantages in approximating complex functions over high-dimensional spaces, along with its reusability and the advanced hardware technologies designed for DL. Several studies develop the DL-based surrogate models to predict the temperature evolutions for the AM process (Mozaffar et al. 2018; Ren et al. 2020; Zhu et al. 2020; Li et al. 2018; Roy and Wodo 2020). For instance, the recurrent neural network (RNN) was used to predict the temperature field for an arbitrary geometry with different scanning strategies in Mozaffar et al. (2018), Ren et al. (2020). The obtained results indicated that the RNN-based models could predict the temperature histories of any given point with high accuracy, however, only for two printing layers. In Li et al. (2018), Roy and Wodo (2020), Bayesian analysis was used to predict the temperature field with high accuracy for three printing layers. In addition, Zhu et al. (2020) used physics-informed neural networks (PINN) to approximate the Navier-Stokes equation to predict the temperature field of a one dimensional solidification process, which can be cumbersome for scaling up to predict a whole multi-layers printing process.

Although the above mentioned studies (Mozaffar et al. 2018; Ren et al. 2020; Zhu et al. 2020; Li et al. 2018; Roy and Wodo 2020) have achieved good accuracy, they require either a significant training time, e.g., a 40-hour training process in Mozaffar et al. (2018), or complex analytical capabilities (Ren et al. 2020; Zhu et al. 2020; Li et al. 2018; Roy and Wodo 2020). Moreover, the demonstrated numerical results of RNN and Bayesian analysis in Mozaffar et al. (2018) and Roy and Wodo (2020) are limited to three and nine printing layers, respectively, while a higher number of layers printing process generates more complex thermal histories (Jardin et al. 2019). To the best of the authors knowledge, there is no work considering a simple architecture and fast training DL-based surrogate model such as feedforward neural network (FFNN) to predict the temperature evolutions of a metal bulk sample with high number of layers (e.g., $\ge 30$) manufactured by the AM process. This work aims to develop a simple, fast, and effective DL-based model to accurately predict the temperature evolutions for AM process. In particular, we apply the method for the DED process with bulk samples of many printing layers (up to 36) reported in Jardin et al. (2019). To achieve this goal, the DL-based model must be able to capture the temperature cycles and their peak values, which are crucial for determining the microstructure (Jardin et al. 2019; Gockel and Beuth 2013; Fetni et al. 2020). Moreover, we employ the DL-based model to examine the melting pool sizes, which strongly impact the evolutions of microstructures, residual stresses, voids, and crack events during the process (Jardin et al. 2019).

Fig. 1

The flowchart to predict and analyze the temperature field of the AM process using FE and DL-based models

The contribution of this work is threefold. First, instead of using a complex DL architecture such as RNN and PINN, we use a simple FFNN for predicting the temperature evolutions and melting pool sizes in the DED process. The FFNN hyperparameters are optimized using the data obtained from the high-fidelity FE model. Second, to improve the predicting accuracy, in particular the local behavior such as the temperature cycles and their peak values, we propose a systematical feature enrichment and selection procedure. The proposed procedure incorporates the physical knowledge about the heat transfer problem into the input features of the FFNN model and is implemented in combination with the sensitivity analysis (SA). In this study, we use the SHapley Additive exPlanation (SHAP) method (Lundberg and Lee 2017) for the SA. The SHAP method provides a measure for the contribution of each input feature to the prediction of temperature and explains the accuracy of the DL-based model in more detail. Based on SHAP results, we carry out the DL model interpretation, which reflects the thermal properties of the DED process. Finally, we assess the predictive capability of the developed DL-based surrogate model with process settings randomly distributed on the studied range. Moreover, we quantify the distribution of the melting pool sizes inherited from the laser power to illustrate the difficulty in maintaining a stable melting pool geometry when printing several layers.

The paper is organized as follows. In “Methodology” section, we introduce the FE model and its experimental validation, the DL-based surrogate models, and the SA using the SHAP method. In “Data collection and feature selection” section, the data description and feature selection are discussed. In “Results and discussion” section, the numerical results of the feature selection procedure, the SA, the DL-based model predictions, uncertainty quantification, and the computational efficiency are presented and discussed. Finally, in “Conclusion” section, conclusions and future research directions are discussed.

Methodology

A common numerical method for analyzing the AM process is to perform the high-fidelity FE model for different settings (geometry of printed parts, process parameters, and material properties). However, the AM FE simulations are usually computationally expensive. This work develops a DL-based framework for accelerating these numerical analyses (see Fig. 1). First, we develop a DL-based surrogate model trained using data obtained from the high-fidelity FE model. The developed surrogate model can then be used to perform SA, uncertainty quantification, and process optimization. Owing to its fast execution time, the proposed framework is significantly efficient compared to that solely based on the FE model.

The methodology section is organized as follows. In “Finite element simulation of DED process” section, the FE simulation of the DED process is described. In “DL-based surrogate model for DED process” and “Training procedure of DL-based surrogate model” sections, the architecture and the optimization procedure of the DL-based model are introduced. Finally, in “Sensitivity analysis using SHAP method” section, the SA using SHAP method (Lundberg and Lee 2017) is summarized.

Finite element simulation of DED process

In this study, we consider a DED experiment of a bulk sample of M4 High-Speed Steel (HSS) (Jardin et al. 2019) for demonstration of the proposed framework. A validated two-dimensional (2D) FE model for the process has been developed by the authors in previous works (Jardin et al. 2019; Fetni et al. 2020), which is used herein. The HSS material has the advantage of withstanding severe mechanical and physicochemical stresses in service. The composition of the HSS M4 powder consists of (in wt %) 1.35 C, 4.30 Cr, 4.64 Mo, 4.10 V, 5.60 W, 0.34 Mn, 0.9 Ni, 0.33 Si, and balance Fe (Hashemi et al. 2017). In the considered DED experiment, the laser power, nozzle scanning speed and powder feed rate are equal to $1100\, \text {W}$, $6.87\, \text {mm/s}$, and $76\, \text {mg/s}$, respectively. The preheating temperature of the 42CrMo4 substrate is $573\, \text {K}$. This preheating technique is important to avoid the early crack as it helps to reduce the temperature difference between the first printing layer and the substrate, resulting in lower internal stresses (Kempen et al. 2014).

Fig. 2

The 2D FE mesh and the printed part (36 layers) of the considered DED experiment of the M4 High Speed Steel (HSS) clad sample ($40\times 40\times 27.54\; \text {mm}$, 36 layers, and 27 tracks per layer). The temperature values of 293 K and 573 K correspond to the ambient and the substrate preheating temperatures, respectively. The total process time is 246.46 s

The governing equations of the DED process are given as

$$\begin{aligned}&\dfrac{\partial }{\partial x} \left( k\dfrac{\partial T}{\partial x}\right) + \dfrac{\partial }{\partial y} \left( k\dfrac{\partial T}{\partial y}\right) +\dfrac{\partial }{\partial z} \left( k\dfrac{\partial T}{\partial z}\right) + Q_{\text {int}} \nonumber \\&\qquad \quad = \rho C_{p}\frac{\partial T}{\partial t}, \end{aligned}$$

(1)

over the printing body and

$$\begin{aligned} k\left( \varvec{\nabla } T\cdot \ {\mathbf {n}} \right) = h\left( T-T_0\right) + \varepsilon \sigma \left( T^4 - T^4_0 \right) + Q_{{\text {laser}}}, \end{aligned}$$

(2)

on the body boundary. In Eqs. (1,2): T is the temperature of the material point located at spatial coordinates (x, y, z), k is the thermal conductivity, $Q_{{\text {int}}}$ is the power generated per volume in the work-piece, $C_{p}$ is the apparent heat capacity, t is the time, $\rho$ is the material density, $\varvec{\nabla }$ is the gradient operator, ${\mathbf {n}}$ is the outward unit normal of the boundary, h is the convective heat transfer coefficient, $\sigma$ is the Stefan-Boltzmann constant, $\varepsilon$ is the emissivity coefficient, $T_0$ is the ambient temperature, and $Q_{{\text {laser}}}$ is the laser input energy. Because the thermal conductivity and the heat capacity values depend on temperature, the considered heat transfer problem is non-linear.

Because a 3D FE model for this sample requires a huge computational cost, we use the 2D FE model (Jardin et al. 2019; Fetni et al. 2020), which simulates the temperature evolutions of the middle vertical cross-section that aligns with the printing direction of the bulk sample. In 3D FE model, the laser input energy ($Q_{{\text {laser}}}$) is computed using the laser power (P) as

$$\begin{aligned} Q_{{\text {laser}}} = \beta \frac{2P}{\pi r_L^2}, \end{aligned}$$

(3)

where $\beta$ is the absorption factor and $r_L$ is the laser beam radius. To be representative of the 3D phenomenon, the 2D FE model uses an effective laser input energy ($Q_{{\text {laser}}} = Q_0$), where $Q_0$ is obtained by fitting the experimental and numerical temperature evolutions.

Figure 2 shows the 2D FE mesh and the printed part (36 layers) of the considered DED experiment (Jardin et al. 2019). More technical details of the FE model, including the experimental set-up, numerical solver, and meshing strategy, can be found in “Appendix A”.

Fig. 3

Locations of thermocouples within the substrate (a) and experimental measurement of the temperature evolutions at thermocouple North and its corresponding FE prediction (b)

Figure 3a shows the locations of four thermocouples within the substrate used in the experiment. Figure 3b illustrates the temperature evolutions at thermocouple North (see also Fig. 2), obtained from the experiment and the FE model, showing a good agreement. As shown in Fig. 3b and discussed in Jardin et al. (2019), the FE model to compute temperature history evolution can be considered to be validated against the available experimental results. This validated FE model is used in this study to generate the database for the DL-based models.

DL-based surrogate model for DED process

In this section, we present a DL-based surrogate model to predict the temperature history of the DED process. The temporospatial temperature field, as a solution of Eqs. (1,2), can be expressed in a general form as

$$\begin{aligned} T = T(\varvec{q}), \end{aligned}$$

(4)

where

$$\begin{aligned} \varvec{q} = [x,\;y,\;z,\;t, \;m_1,\;\dots , m_{\mu },\;p_1,\;\dots , p_{\nu }] \end{aligned}$$

(5)

is a multi-dimensional vector of spatial coordinates ($x,\;y,\;z$), time (t), material properties $m_1,\;\dots , m_{\mu }$ of the printed pieces, and process parameters $p_1,\;\dots , p_{\nu }$ of the DED process.

For the sake of simplicity, in this study, we consider the following simplified input parameter $\varvec{q}$ as

$$\begin{aligned} \varvec{q} = [x,\;y,\;t, \;Q_{{\text {laser}}}], \end{aligned}$$

(6)

where $Q_{{\text {laser}}} \in [0.8,\;1.2]Q_0$. In other words, we aim to predict the temporospatial temperature field as in the 2D FE model with varying values of effective laser input energy in the studied range $[0.8,\;1.2]Q_0$. It is expected that the developed approach is still applicable for more complex scenarios, i.e., the one with many input parameters (scanning speed, material properties, etc.) and the one with different printing geometries by the similar data pre-processing and training procedures of the proposed DL model. We will consider these scenarios in our future study to further demonstrate the above conclusion.

We develop a DL-based surrogate model for predicting the temporospatial temperature field $T(\varvec{q})$ with the following steps:

• (i) choosing an appropriate deep neural network (DNN) architecture,

• (ii) collecting and preprocessing data from the high-fidelity FE model,

• (iii) training the DL-based model, and

• (iv) evaluating the predictive capability of the model.

For step (i), the FFNN is selected because it has the advantage of approximating highly non-linear and high-dimensional functions (Winkler and Le 2017), such as the temperature fields generated by the FE model. Compared with other DNN architectures such as the RNN, the FFNN is significantly simpler for implementation, which is also a crucial criterion of this study. For step (ii), the training data are collected from the numerical simulations of the FE model discussed in “Finite element simulation of DED process” section. For step (iii), the optimization of the hyperparameters is carried out using the backpropagation method (Amari 1993) and the gradient descent algorithm (Amari 1993). For step (iv), the results obtained from the DL-based models are verified with the temporospatial temperature fields obtained from the FE model using the process parameters randomly distributed on the studied range.

Fig. 4

Schemes of an artificial neural (a) and a feedforward neural network used in this study (b)

DNN is a computational tool inspired by the biological nervous system, which has several layers. The basic component of a DNN is the artificial neural as shown in Fig. 4a. Each neuron performs a dot product of the input and its corresponding weights, adds the bias, and applies a non-linearity activation function to produce the output.

A common architecture of the DNN-based model is the feedforward neural networks (FFNN). Given a set of input-output pairs, the FFNN model refers to training the weight parameters $\varvec{w}^{\kappa }$ and bias $\varvec{w}_0^{\kappa }$, with $\kappa = 1,\dots ,a$, where ($a-1$) is the number of hidden layers.

In this study, the FFNN is used to approximate the relationship between the input physical parameters $\varvec{q}$ (see Eq. (6)) and the temperature T of the DED process (see Fig. 4b) as

$$\begin{aligned} f\left( \varvec{q}^+|\varvec{W}\right) \approx T\left( \varvec{q}\right) , \end{aligned}$$

(7)

where $\varvec{W}$ denotes weights and biases of the FFNN model and $\varvec{q}^+ = [\varvec{q}, \varvec{q}^a]$ is a vector of the essential input parameters $\varvec{q}$ (see Eq. (6)) and enriched features $\varvec{q}^a$. The use of the enriched features is justified by an improved predicting accuracy of the temperature, explained in “Feature selection” section.

Training procedure of DL-based surrogate model

From the FE simulations, the collected data can be represented as

$$\begin{aligned} \varvec{D}_T = \left\{ (\varvec{q}^{(j)}, T^{(j)}); j = 1, \dots ,N\right\} , \end{aligned}$$

(8)

where $\varvec{q}^{(j)}$ is given by Eq. (5), $T^{(j)}$ is the temperature values corresponding to each data point at each input $\varvec{q}^{(j)}$, and N is the size of the training dataset $\varvec{D}_T$. N can be computed as

$$\begin{aligned} N = n_s \times n_p, \end{aligned}$$

(9)

where $n_s$ is the number of simulations and $n_p$ is the number of data points per simulation. To enhance the stability of the training process, the data are normalized to the range of 0 and 1 as

$$\begin{aligned} {\widetilde{q}}_i^{(j)}&= \frac{q_i^{(j)} - \min _{q_i} }{\max _{q_i} - \min _{q_i}}, \quad i=1,\dots ,n,\; j = 1,\dots ,N, \end{aligned}$$

(10a)

$$\begin{aligned} {\widetilde{T}}^{(j)}&= \frac{T^{(j)} - \min _T }{\max _T - \min _T}, \quad j = 1,\dots ,N, \end{aligned}$$

(10b)

where $\min _{q_i}$ and $\max _{q_i}$ are the minimum and maximum values of the feature $q_i$, respectively; $\min _T$ and $\max _T$ are the minimum and maximum values of the temperature in the training dataset $\varvec{D}_T$, respectively. After normalizing, the training dataset is partitioned into two disjoint sets: set $\varvec{D}_T^\text {g}$ for computing gradients during the optimization procedure and set $\varvec{D}_T^{\text {nb}}$ for evaluating non-biased cross-validation loss, such that $\varvec{D}_T = \varvec{D}_T^\text {g} \cup \varvec{D}_T^{\text {nb}}$. We choose the sizes of $\varvec{D}_T^\text {g}$ and $\varvec{D}_T^{\text {nb}}$ as 0.7N and 0.3N, respectively—a typical splitting ratio. The optimal parameters $\varvec{W}$ from Eq. (7) are identified by minimizing the mean squared error (MSE) as

$$\begin{aligned} \varvec{W} = \arg \; \min _{\varvec{W}^*} \pounds \left( \varvec{W}^*|\varvec{D}_T^\text {g}\right) , \end{aligned}$$

(11)

where $\pounds \left( \varvec{W}|\varvec{D}_T^\text {g}\right)$ is the MSE loss function estimated using the training dataset $\varvec{D}_T^\text {g}$ as

$$\begin{aligned} \pounds \left( \varvec{W}|\varvec{D}_T^\text {g}\right) = \frac{1}{N_T}\sum _{j=1}^{N_T}\left( f\left( {{{\varvec{q}}}}^{(j)}|\varvec{W}\right) - T^{(j)}\right) ^2, \end{aligned}$$

(12)

where $N_T$ is the size of the training dataset $\varvec{D}_T^\text {g}$. The training process is performed using the Adaptive Moment Estimation (Adam) method and backpropagation with a learning rate of 0.001—a conventional setting for training the FFNN model (Amari 1993; Kingma and Ba 2014; Wilson and Martinez 2003). In this study, we use the Tensorflow software (Gulli and Pal 2017; Abadi et al. 2016) for implementing the FFNN model.

After being trained, the FFNN model is validated on a testing dataset $\varvec{D}_V$, which is independent of the training dataset. To assess the performance of the DL-based model, we use the metric of the coefficient of determination, known as $R^2$, which is widely used in DL-based applications (Nagelkerke 1991; Mozaffar et al. 2018; Roy and Wodo 2020). The value of $R^2$, between prediction temperatures and their corresponding FE simulation data, is defined as

$$\begin{aligned} R^2 {=} 1 - \dfrac{\sum _{j=1}^{N_V} \left( f\left( \varvec{q}^{(j)}\right) -T^{(j)}\right) ^2}{\sum _{j=1}^{N_V} \left( {\overline{T}} - T^{(j)}\right) ^2},\quad (\varvec{q}^{(j)}, T^{(j)}) \in \varvec{D}_V,\nonumber \\ \end{aligned}$$

(13)

where $N_V$ is the size of the testing dataset and ${\overline{T}}$ is the mean temperature. We also use $R^2$ metrics for subsets of prediction temperatures, e.g., the temperature history at a certain point of interest. The closer to one the value of $R^2$ is, the better the model prediction achieves.

Table 1 The selected training and testing data simulations to develop the FFNN model

Sensitivity analysis using SHAP method

To provide a deeper understanding of the predictive capability of the FFNN model f ( Eq. (7)), we perform a SA of the FFNN model. In this work, the SA is performed using the SHAP method (Ribeiro et al. 2016; Shapley 1953; Lundberg and Lee 2017), which belongs to the class of additive features attribution method. The SA results serve as an explanation for the accuracy of the FFNN and provide a measure for the contribution of each input feature described in “Feature selection” section to the model prediction.

Let G be the set of all input features (i.e., components of vector $\varvec{q}$ see Fig. 4b) of the FFNN f. The SHAP value that measures the importance of the i-th input feature is defined locally as

$$\begin{aligned} \phi _{i}(\varvec{q}) = \sum _{\textit{S} \subseteq \textit{G}\backslash \{q_i\}} \frac{|S|!(n - |S| - 1)!}{n!}[f_{\varvec{q}}(S\cup \{q_i\}) - f_{\varvec{q}}(S)],\nonumber \\ \end{aligned}$$

(14)

where

$$\begin{aligned} f_{\varvec{q}}(S) = {\mathbb {E}}[f(Z)| \varvec{z}_S = \varvec{q}_S)], \end{aligned}$$

(15)

where ! is the factorial operator, S be a subset of G, and |S| is the number of features in the set S. In Eq. (14), $\varvec{q}_S$ and $\varvec{z}_{S}$ are |S|-dimensional vectors that collect values of the features in S from vectors $\varvec{q}$ and $\varvec{z}$ respectively, i.e. $\varvec{q}_{S} = [q_{S_1},\ldots , q_{S_{|S|}}]^T$ with $S = \{S_1,\ldots , S_{|S|}\}$. In words, $f_{\varvec{q}}(S)$ is the conditional expectation of the model prediction when values of the features that belong to S is fixed as $\varvec{q}_S$, and other features follow certain distributions, such as those characterized from dataset. The term $[f_{\varvec{q}}(S\cup \{q_i\}) - f_{\varvec{q}}(S)]$ represents the expected difference of the model predictions when activating additionally feature $q_i$ to the set S while the others are deactivated. Finally, $\phi _{i}$ is obtained by averaging the expected difference $[f_{\varvec{q}}(S\cup \{q_i\}) - f_{\varvec{q}}(S)]$ for all possible feature subsets. The SHAP value $\phi _i(q)$ satisfies the local accuracy properties:

$$\begin{aligned} f(\varvec{q}) = \phi _{0} +\sum _{i=1}^n \phi _i(\varvec{q}), \end{aligned}$$

(16)

where $\phi _{0} = {\overline{T}}$, which is the mean temperature over the dataset.

Intuitively, a large value of $|\phi _{i}(\varvec{q})|$ indicates a significant contribution of feature $q_i$ to the model f and vice-versa. In this study, we use the SHAP software (Lundberg and Lee 2017) to perform the Eqs. (14, 15). Owing to the local evaluation of the SHAP values, we carry out the interpretation of the FFNN model, which reflects the thermal histories present during DED process (reported in ““Sensitivity analysis and model interpretation using SHAP method” section).

Data collection and feature selection

This section discusses the training data obtained from the validated FE model and selects the appropriate input features for the FFNN model.

Data collection

The training data of the FFNN model are obtained by launching the FE model described in “Finite element simulation of DED process” section using different values of the DED process parameters. As explained in “Finite element simulation of DED process” section, for the sake of simplicity, we vary only one process parameter, i.e., $Q_{\text {laser}}$, and fix other parameters, i.e., material properties and boundary conditions. The FE model setup for the data generation is described in detail in “Finite element simulation of DED process” section and “Appendix A.” The training dataset consists of five different simulations, as listed in Table 1. Each FE simulation provides a temporospatial temperature field for a value of the effective laser input energy $Q_{\text {laser}}$ (Jardin et al. 2019).

Fig. 5

The nine input features of the FFNN model

The number of data points ($n_p$) of each FE simulation corresponding to a value of an effective input laser energy $Q_{{\text {laser}}}$ is 4.98 million ($2519 \; \text {nodes} \times 1978\; \text {time steps} = 4.98\; \text {million}$). As listed in Table 1, four FE simulations with $Q_{\text {laser}} = 0.8Q_0, 0.9Q_0, 1.1Q_0, 1.2Q_0$ are used for training the FFNN model, resulting in approximately 19.92 million data points. To evaluate the predicting accuracy, we first validate the FFNN model with the FE simulation for $Q_{\text {laser}} = 1.0Q_0$ in “Temporospatial temperature field and melting pool sizes prediction for $Q_{\mathrm{laser}} = 1.0Q_{0}$” section. Then, the FE simulations for different values of $Q_{{\text {laser}}}$ uniformly distributed on $[0.8Q_0,\;1.2Q_0]$ are used to assess the predictive capability of the model with unseen inputs in “Temporospatial temperature field prediction for $Q_{\mathrm{laser}}$ randomly distributed on [0.8, 1.2]$Q_{0}$” section. In addition, the range of x and y are $[0, 0.195] \text {m}$ and $[0, 0.15454]\text {m}$, respectively. The mean and standard deviation of the temperature are 904.422 K and 370.227 K, respectively, showing a strong variation in the training data.

Feature selection

For the DED under investigation, four basic features include the x-coordinate, the y-coordinate, the time (t) and the effective laser input energy ($Q_{\text {laser}}$) (see Eq. (6)). To enhance the predicting accuracy, in particular for the local behaviors such as temperature cycles and their peak values, while keeping the FFNN complexity remaining feasible, we add certain physical characteristics as the input features. Two important aspects that should be explicitly accounted for are the current printing layer number and the laser location. The former is required because the temperature of points located above and below the printed layer is significantly different. Moreover, the temperatures of the clad and the substrate strongly depend on the location of the current printed layer numbers (see Fig. 2). For the latter, the laser head location plays an important role in predicting the temperature field, as it is associated with a very high gradient temperature. In contrast, at locations far from the laser head, the heating or cooling rates are relatively low. In this work, rather than solely using the spatial coordinates for a given laser position, we use its relative distances to the considered point, which is more explicitly representative. The following nine features are considered as the input of the FFNN model, as shown in Fig. 5:

• (i) x-coordinate (x),

• (ii) y-coordinate (y),

• (iii) time (t),

• (iv) effective laser input energy ($Q_{{\text {laser}}}$),

• (v) x-coordinate of the laser head position ($l_x$),

• (vi) y-coordinate of the laser head position ($l_y$),

• (vii) distance from the laser head in x-direction to (x, y) point ($d_x = l_x - x$),

• (viii) distance from the laser head in y-direction to (x, y) point ($d_y = l_y - y$), and

• (ix) number of the current printed layer (L).

The first four features are essential, while the others, $l_x$, $l_y$, $d_x$, $d_y$, and L, are the enriched ones. The enriched features are set to zero for all the substrate points to account for the fact that the substrate point stays far from the laser head and that its temperature value is not significantly affected by these features.

Finally, the input vector $\varvec{q}^+$ of the FFNN model in Eq. (7) used to predict the output temperature T can be expressed as:

$$\begin{aligned} \varvec{q}^+ = [\varvec{q}, \varvec{q}^a] = [x,\;y,\;t,\;Q_{\text {laser}},\;l_x,\;l_y,\;d_x,\;d_y,\;L], \end{aligned}$$

(17)

where $\varvec{q}^a = [l_x,\;l_y,\;d_x,\;d_y,\;L]$ is the vector of enriched features.

Results and discussion

This section reports the numerical results of the temperature evolutions predicted by the FFNN model. In addition to the global analysis of the temporospatial temperature field, we report the numerical results at five clad points ($\text {P}_1,\;\text {P}_2,\dots ,\text {P}_5$) and one substrate point ($\text {N}$) (see Fig. 6) to study the local behavior. Point $\text {P}_1$ is the first printed point and points $\text {P}_2$, $\text {P}_3$, $\text {P}_4$, and $\text {P}_5$ are located on the symmetry axis of the bulk sample.

Fig. 6

Positions of the points ($\text {P}_1,\dots ,\text {P}_5,\; \text {and}\; \text {N}$) at which the temperature evolutions are examined. The origin of the coordinate system is located at bottom left of the aluminum plate in Fig. 2

The structure of this section is organized as follows. In “Feature selection procedure” section, we discuss the feature selection procedure. In “Sensitivity analysis and model interpretation using SHAP method” section, we present the SA analysis using the SHAP method to explain the FFNN model. In “Assessment of predictive capability of the FFNN model” section, the assessment of the FFNN model prediction is discussed. In “Distribution of the melting pool sizes inherited from laser power uncertainty” section, the distribution of the melting pool sizes inherited from the laser power uncertainty is performed. Lastly, in “Computational efficiency assessment” section, the computational efficiency of the FFNN model is reported.

Table 2 The description and $R^2$ values of three FFNN models

Feature selection procedure

This section discusses the feature selection procedure of the FFNN model to assess the contribution of the enriched features to the predicting accuracy, not only in terms of the global thermal behavior but also the local one, such as temperature cycles and their peak values. Particularly, the local thermal history of each material point plays an essential role in determining the microstructure (Jardin et al. 2019).

We implement three different FFNN models, which are reported in Table 2. The first one is the base model (BM), which uses only the essential features $x,\;y,\;t,\;\text {and}\;Q_{{\text {laser}}}$. The BM is then enriched with two more features and named as an intermediate model (IM). Compared to the BM, the IM includes the features $l_x$ and $l_y$, which are the coordinates of the laser source. The last one, the full model (FM), uses all the enriched features described in Eq. (17).

The architecture of the FFNN models, such as the number of nodes and neurons, is chosen based on a trial and error procedure (Stathakis 2009), which is discussed in detail in the “Appendix B”. The selected architecture has four hidden layers, whose numbers of neurons are 400, 200, 200, and 100, respectively. The training process of the FFNN models is also reported in the “Appendix B”.

The obtained value $R^2$ metrics (see Eq. (13)), computed on the testing dataset $\varvec{D}_V$ ($Q_{{\text {laser}}}=1.0Q_0)$, see Table 1), of the three FFNN models are reported in Table 2. Using only the essential features, the BM shows a poor prediction of the temperature evolutions with a low $R^2$ value of 0.798. Owing to the enriched features related to the laser source, the predicting accuracy is significantly improved (See Table 2); in particular, the $R^2$ value of the FM is almost close to the unit.

Fig. 7

The comparison of the temperature evolutions at point $P_4$ obtained from the FE model and the corresponding results obtained with BM (a), IM (b), and FM (c) with zoom on the cyclic zones

Figure 7 shows the comparison of the temperature evolutions at point $P_4$ (see Fig. 6) obtained from the FE and the corresponding results obtained with three FFNN models. We choose point $P_4$ to report the temperature results because this point is representative of a material zone characterized by its homogeneity and some well-identified carbides generated by the applied thermal history during DED process (Jardin et al. 2019). The results obtained from BM, IM, and FM are illustrated in Fig. 7a–c, respectively. The BM can not capture the temperature cycles and their peak values at $\text {P}_4$. The IM is able to mimic the cyclic behaviors of the temperature evolutions at $\text {P}_4$; however, it can not capture the temperature peak, which plays a significant role in determining the material microstructures. Owing all the enriched features described in Eq. (17), the temperature cycles and their peak values are well captured by the FM.

The comparison among the three models shows that selecting appropriate physical characteristics of the DED process as input features of the FFNN model significantly improves the predicting accuracy not only in terms of the global behavior but also the local one, such as temperature cycles and their peak values.. As shown in Fig. 8, the temperature strongly depends on the feature $d_y$, which explains the accuracy improvement achieved by the FM compared with the IM.

Sensitivity analysis and model interpretation using SHAP method

In this section, a SA is performed to evaluate the importance of each enriched feature on the prediction of the target output and to interpret the FM, which is the best surrogate model reported in “Feature selection procedure” section.

Fig. 8

The temperature evolutions predicted by the FM at clad point $\text {P}_4$ with respect $d_y$

Sensitivity analysis

The SHAP values corresponding to each feature are illustrated in Fig. 9a, and the maxima of their absolute values are shown in Fig. 9b. An absolute SHAP value is a measure of the feature contribution to the difference between the predicted temperature and its average value ${\overline{T}}$, see Eq. (16). Because the local properties such as temperature cycles and their peak values are crucial for determining the microstructure in the DED process (Jardin et al. 2019), the absolute maximum-based ranking (see Fig. 9b) is more important than the average-based ranking. As shown in Fig. 9b, four features y, $d_y$, $l_x$, and $l_y$ appear to be the most influential features on the temperature prediction. This result reaffirms the importance of the enriched feature $d_y$ in the predicting accuracy as reported in “Feature selection procedure” section (see Fig. 8). In addition, L, $d_x$, t, x, and $Q_{{\text {laser}}}$ have lesser impacts on the temperature prediction (see Fig. 9b). While the $Q_{{\text {laser}}}$ feature is the only one belonging to the process parameters class, the others are not, as discussed in “Finite element simulation of DED process” section. Therefore, the least SHAP values of the $Q_{{\text {laser}}}$ feature should not be translated as a negligible parameter. Note that the relative variation range of $Q_{{\text {laser}}}$ to its nominal value $Q_0$ is much smaller than those of the other features. Consequently, the least SHAP values of the $Q_{{\text {laser}}}$ feature are expected.

Fig. 9

The SHAP values corresponding to each feature (a) and their maximum absolute values (b) for the FM. a Ranks features by their average absolute SHAP value. The SHAP values are computed on the testing dataset $\varvec{D}_V$ ($Q_{{\text {laser}}}=1.0Q_0$, see Table 1)

Fig. 10

The SHAP values for y (a), $d_y$ (b), $l_x$ (c), and $l_y$ (d)

Model interpretation

Figure 10 shows the SHAP values for the four most important features y, $d_y$, $l_x$, and $l_y$. For the feature y (Fig. 10a), at a clad point ($y \ge 0.127764$), its SHAP value increases more rapidly compared to a substrate point ($y \in [0, 0.127764]$).

Fig. 11

The temperature field prediction and relative differences using FE model and FM at 71.72 s (a), 174.5 s (b), and 243.1 s (c) for $Q_{{\text {laser}}} = 1.0Q_0$ (testing dataset $\varvec{D}_V$). Note that the color map of the three sub-figures shares the same tendency as the one in Fig. 10c. The light-blue area above the laser head (red color) is the unprinted zone (Color figure online)

Figure 10b illustrates the SHAP values of the $d_y$ feature. The SHAP values decrease with the increase of $d_y$ value. The near-zero values of $d_y$ indicate that the points are closed to the laser head. Consequently, the temperature of these points is increasing rapidly, which leads to an increase in the SHAP value. Conversely, the farther the distance of a point to the laser head becomes, the greater its $d_y$ value is, and therefore the SHAP value decreases.

Finally, Fig. 10c, d show the SHAP values of the $l_x$ and $l_y$ features. Note that these features are set to zero for all the substrate points, as discussed in “Feature selection” section. Consequently, the SHAP values of $l_x$ and $l_y$ only show the effect from 0.078 and 0.127764, respectively,—the first printed location. As observed in Fig. 10c, d, the SHAP values of $l_x$ and $l_y$ do not follow a specific rule since they do not represent the location of the material point.

In brief, the evolution of SHAP values agrees with the physical properties of the DED process. Such explainability confirms the reliability of the FM in predicting the DED temperature evolutions.

Assessment of predictive capability of the FFNN model

This section assesses the predictive capability of the FM, discussed in “Feature selection procedure” section. We test the FM model prediction for $Q_{{\text {laser}}}=1.0Q_0$ in “Temporospatial temperature field and melting pool sizes prediction for $Q_{\mathrm{laser}} = 1.0Q_{0}$” section, and for $Q_{{\text {laser}}}$ randomly distributed on $[0.8Q_0, 1.2Q_0]$ in “Temporospatial temperature field prediction for $Q_{\mathrm{laser}}$ randomly distributed on [0.8, 1.2]$Q_{0}$” section (see Table 1).

Temporospatial temperature field and melting pool sizes prediction for $Q_{{\text {laser}}}=1.0Q_0$

Temperature fields Figure 11 shows the comparison of the FE model and FM in terms of the temperature field at three specific times of 71.72 s, 174.5 s, and 243.1 s. For reference, the total process time is 246.46 s. In all three cases, the results show excellent agreement between the FE model and FM. The mean values of relative error are smaller than $0.75 \%$ for all three considered time-steps.

Local prediction error of the FM To assess the error at each printing data point, we compute the relative errors $\alpha$ as

$$\begin{aligned} \alpha ^{(j)} = \frac{f\left( \varvec{q}^{(j)}\right) -T^{(j)}}{T^{(j)}} \times 100\%, \end{aligned}$$

(18)

where $(\varvec{q}^{(j)}, T^{(j)}) \in \varvec{D}_V$ excluding points that are not yet printed. Figure 12 shows the histogram of the relative error of the temperature history predicted by the FM compared with the FE model for $Q_{{\text {laser}}}=1.0Q_0$. The empirical mean and standard deviation values of the relative errors are $0.013\%$ and $0.501\%$, respectively. The empirical minimum and maximum errors are $-1.08 \%$ and $1.02 \%$, respectively. The reported results show that the FM accurately predicts the temporospatial temperature field at both global and local levels.

Temperature cycles and their peak values Figure 13 shows the temperature evolutions at six selected points of interest for $Q_{{\text {laser}}}=1.0Q_0$. At each point, the temperature profiles show cyclic heating-cooling waves (also called temperature oscillations). The predicted results show good agreement between the FE model and FM. The $R^2$ metrics computed for the temperature evolutions at point $\text {P}_1,\dots ,\text {P}_5,\;\text {and}\;\text {N}$ are 0.995, 0.998, 0.990, 0.999, 0.999, and 0.999, respectively. The temperature cycles and their peak values are well captured by the FM as observed in Fig. 13. Because the temperature peaks play a significant role in determining the material microstructures, the ability of the FM to capture these peaks is crucial. These results confirm the importance of enriched features to the local predicting accuracy.

Fig. 12

The histogram of the relative errors of the temperature history predicted by the FM compared with the FE simulation for $Q_{{\text {laser}}}=1.0Q_0$

Melting pool sizes The melting pool plays an important role in determining the microstructures of the printed sample and its subsequent mechanical properties. It is defined as the liquid zone generated by the laser and is built by the melted powder flow induced by the laser energy and the fusion of the previously printed layers. The sizes of the melting pool are numerically identified as the area where the temperature T is greater than the melting temperature, which is estimated as $1676.15\; \text {K}$ for the M4 HSS material (Jardin et al. 2019). Figure 14 shows the melting pool (red color) predicted by the FE and FM at $t=243.1$ s (last printing layer).

Figure 15 illustrates the comparison in terms of the evolutions of the melting pool sizes (width and area) between the FE model and FM. As shown in Figs. 14 and 15, the melting pool sizes computed via the FM are similar to that via the FE simulation. Therefore, the FM can be used to quickly estimate the melting pool sizes.

Fig. 13

The temperature evolutions predicted using FE model and FM at six selected points including substrate $\text {N}$ (a), clad $\text {P}_1$ (b), clad $\text {P}_2$ (c), clad $\text {P}_3$ (d), clad $\text {P}_4$ (e), and clad $\text {P}_5$ (f) for $Q_{{\text {laser}}} = 1.0Q_0$ with zoom on the cyclic zones

Fig. 14

The melting pool predicted by the FE model and FM at $t = 243.1\; \text {s}$ for $Q_{{\text {laser}}} = 1.0Q_0$ zoomed on the clad

Fig. 15

Melting pool width (a) and area (b) obtained with the FE model and FM for $Q_{{\text {laser}}} = 1.0Q_0$. The value of the melting pool sizes equal to zero means when the laser is switched off

Temporospatial temperature field prediction for $Q_{{\text {laser}}}$ randomly distributed on $[0.8, 1.2]Q_0$

We carry out the assessment of the predictive capability of the FM for $Q_{{\text {laser}}}$ randomly distributed on $[0.8, 1.2]Q_0$. Figure 16 shows the $R^2$ metrics of the FM prediction for different values of $Q_{{\text {laser}}}$. The FM predicts 16 new FE simulations associated with different values of $Q_{{\text {laser}}}$ with the $R^2$ metrics greater than 0.994. In addition, as observed in Fig. 16, farther from the training data, the obtained $R^2$ value is smaller and becomes the smallest near $Q_{{\text {laser}}} = 1Q_0$. For the scenario $Q_{{\text {laser}}} = 1Q_0$, we show in Sects. 4.1, 4.2, and “Temporospatial temperature field and melting pool sizes prediction for $Q_{\mathrm{laser}} = 1.0Q_{0}$” sections that the FM still accurately predicts the temporospatial temperature field of the DED process.

Distribution of the melting pool sizes inherited from laser power uncertainty

This section assesses the distribution of the melting pool sizes inherited from laser power uncertainty. First, the uncertainty in the $Q_{{\text {laser}}}$ is modeled as a uniform distribution bounded by $[0.8Q_0, 1.2Q_0]$. Then, we use the Monte-Carlo (MC) simulation (Arnst and Ponthot 2014) accelerated by the FM for propagating uncertainty to approximate the probability distribution of the melting pool sizes. In other words, we generate 1000 samples of $Q_{{\text {laser}}}$ in range $[0.8Q_0, 1.2Q_0]$, and use the FM to evaluate the temperature field and melting pool sizes for each sample.

Figure 17 shows the empirical distributions approximated using MC simulation with 1000 samples of the melting pool width (a) and area (b) located at the middle of each layer. The uncertainty of the melting pool sizes is negligible for the first layers (i.e., 1st to 6th). However, the uncertainty increases with the layer number and becomes significant for the last layers (i.e., 21st to 36th). The result affirms the extreme sensitivity of the melting pool sizes to the uncertainty of the laser power when printing products have several layers. As a consequence, optimization of the DED process parameters to maintain constant melting pool sizes, discussed in “Temporospatial temperature field and melting pool sizes prediction for $Q_{\mathrm{laser}} = 1.0Q_{0}$” section, is indeed challenging.

Computational efficiency assessment

This section compares the computational efficiency between the FM and the FE model for the temperature field prediction (“Assessment of predictive capability of the FFNN model” section) and the uncertainty quantification (“Distribution of the melting pool sizes inherited from laser power uncertainty” section). Table 3 reports the computational cost of the FM and FE model. A computer with the memory of 32GB RAM, the processor of Intel i7-6700 CPU, and the GPU of NVIDIA GeForce GTX 1660 Ti is used to perform the FE simulation and training of the FM. The total time required to build the training dataset $\varvec{D}_T$ by launching four FE simulations is approximately 2.4 hours. The training of the FM is about 0.5 hours. After training, the FM takes only 12 s for computing the temperature field corresponding to each sample of $Q_{{\text {laser}}}$.

For the MC simulation reported in “Distribution of the melting pool sizes inherited from laser power uncertainty” section, computing 1000 temperature fields requires 3.3 hours using the FFNN model. Whereas using the FE model, this process could require 600 hours (25 days). In total, using the FFNN model reduces the computational time by 105 compared with the FE model. In summary, because the FM requires FE simulations for training, there is no benefit in using the FM when only a few simulations are needed. In contrast, for uncertainty quantification or process optimization which require evaluation of many temperature fields, using the FM significantly improves the computational efficiency.

Fig. 16

The $R^2$ metrics of the FM prediction for different values of $Q_{{\text {laser}}}$

Conclusion

In this work, a DL-based approach for fast and accurate prediction of the temperature evolutions as well as the melting pool sizes in the DED process of a High-Speed Steel is developed. The FFNN model is trained using the data obtained from the FE simulations, which were validated by experiments. The main contributions of the work are:

• The temperature evolutions and the melting pool sizes of the DED process can be accurately predicted using a simple FFNN architecture. Owing to the fast execution of the FFNN model, the uncertainty quantification can be implemented efficiently (i.e., 3.3 hours compared with 25 days for computing 1000 temperature fields).

• A systematical procedure for feature enrichment and selection is developed. The FFNN model incorporates the physical knowledge about heat transfer problems into the input features of the FFNN model, which improves the accuracy of the model prediction, in particular the local behaviors such as temperature cycles and their peak values. Moreover, this work uses the SHAP method for measuring the contribution of the enriched features to the model accuracy and for interpreting the model.

• The trained FFNN model is validated for predicting the temperature evolutions of DED processes with effective laser input energies randomly distributed on the studied range.

Fig. 17

The empirical distributions approximated using MC simulation with 1000 samples of the melting pool width (a) and area (b) located at the middle of each layer

Table 3 The computational costs of the FM and FE model

In perspective, because the AM technology inherently includes multiple uncertainty sources and is highly sensitive to the manufacturing settings, a process parameter optimization under the presence of uncertainty will be developed based on this work. Our developed surrogate model in such numerical analyses improves computational efficiency, owing to its fast execution time. Also, the proposed framework will be extended to other AM technologies, new materials, and new physical phenomena (microstructure evolutions).

Appendices

Technical details of the FE simulation

In order to solve the non-linear equations of heat transfer energy in the entire volume of the material, the updated Lagrangian FE code “Lagamine”, which was developed by the ArGEnCo Department of the University of Liège (Jardin et al. 2019) was used.

To further improve the computation efficiency, the mesh was refined depending on the space position. The parts subjected to the laser source were refined to accurately model heat fluxes while the substrate bottom has meshed more coarsely. As shown in Fig. 2, a fine mesh was applied to the cladding. Here, an element width of 0.7 mm was selected to apply laser heat flux to two elements. The power density was considered constant for a radius of 0.7 mm related to the top hat profile of the laser. Transition mesh zones within the substrate ensure a correct link between the fine mesh of the clad and the coarse substrate mesh. In this FE model, the mesh comprises two kinds of elements, including quadrilateral elements to model thermal conduction for solid parts and linear interface elements to model radiation and convection phenomena. In this powder injection technology, the continuous addition of material on the substrate was modeled by the element birth and death technique.

It is noted that the effect of the latent heat of fusion and vaporization is integrated into the definition of $C_p$ - an apparent heat capacity within this FE solid approach. The fluid motion due to the thermo-capillary phenomenon (Marangoni flow) is not explicitly modeled. A modified conductivity above solidus temperature could be applied as in Kumar et al. (2012) and Zhang et al. (2016) to take into account this fluid motion. However, no multiplicative factor of k is used hereafter as the correct melt pool depth could be predicted without this factor.

All the material parameter sets such as conductivity, heat capacity, the density of the clad and substrate were measured and can be found in Jardin et al. (2020). Heat convection and radiation parameters for the bulk sample studied here were calibrated to recover both the experimental melt pool depth and the thermocouple temperature measurements. The FE model temperature histories of different material points were able to explain the heterogeneity of the microstructure (carbide nature and size) as shown in Jardin et al. (2019) for different locations within the clad. In addition, the process parameters of the DED manufacturing of the M4 bulk sample are reported in Table 4.

Table 4 The process parameters of the DED manufacturing of the M4 bulk sample

Note that ongoing research by the authors at the MSM unit aims to validate further the FE model using micro-structures measurements (Jardin et al. 2019), to verify the assumptions of the 2D model and to identify correctly model parameters, which are essential to demonstrate the applicability of the model in practice. However, these research directions are beyond the scope of this paper, which focuses on the development of DL-based surrogate model to replace the FE model for the prediction of temperature evolutions in the DED process.

Training procedure of the FFNN model

The architecture of the FFNN model, such as the number of nodes and neurons, is chosen based on a trial and error procedure (Stathakis 2009). In detail, this procedure has three steps: (i) start from an over-fitting architecture; (ii) reduce the number of hidden layers progressively; and (iii) monitor the improvement of the FFNN model. Referring to Fig. 4, an optimal architecture of the FFNN model, is found to have four hidden layers, whose numbers of neurons are 400, 200, 200, and 100, respectively.

Fig. 18

Training and non-biased cross-validation losses of the FFNN model

Figure 18 shows the training and non-biased cross-validation losses of the FFNN model. The so-called epoch, training loss, and non-biased cross-validation loss in Fig. 18 are the optimization step to identify $\varvec{W}$, the MSE evaluated with $\varvec{D}_T^\text {g}$, and that error computed with $\varvec{D}_T^\text {nb}$, respectively (see “Training procedure of DL-based surrogate model” section for the definitions of these datasets). The training ends at the $300^{th}$ epoch as no further significant decrease of the non-biased cross-validation loss is observed.